Multiparameter Neural Network Modeling of Facilitated Transport Mixed Matrix Membranes for Carbon Dioxide Removal
Abstract
:1. Introduction
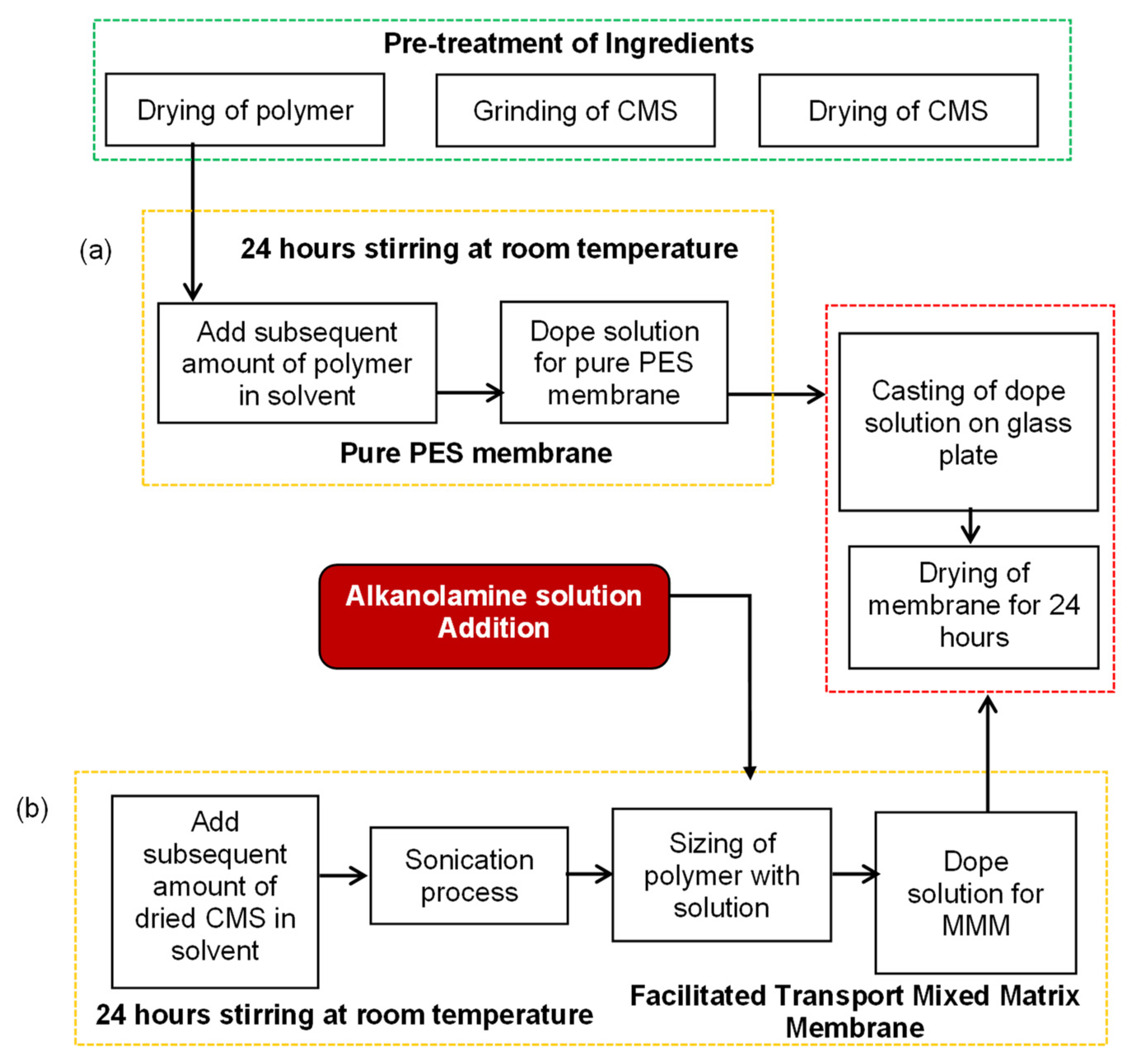
2. Membrane Synthesis, Characterization, and Gas Performance
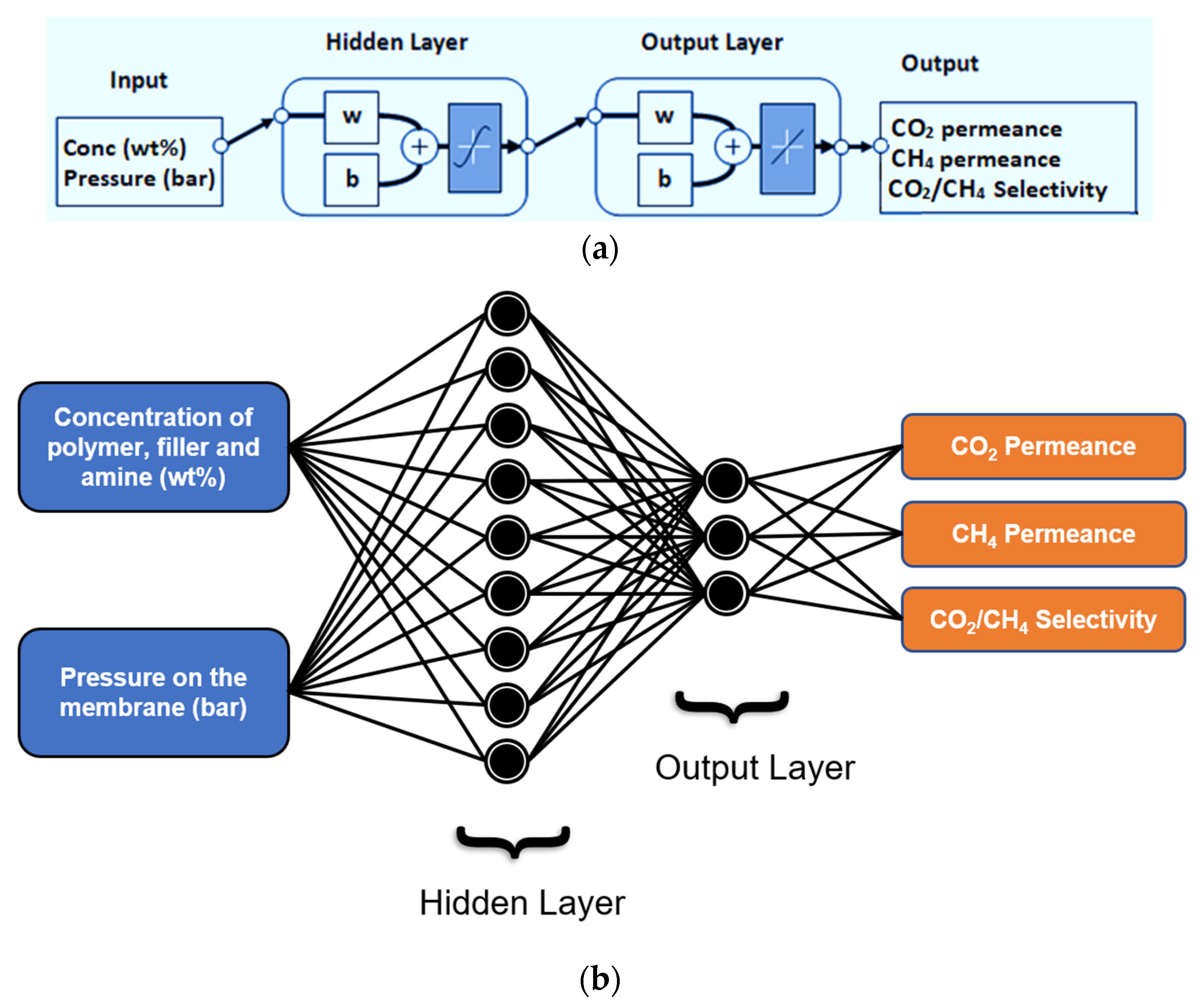
3. Methodology for ANN Development
4. Results and Discussion
4.1. Effect of Pressure on the Permeance
4.2. ANN Predictability
4.3. Relative Importance of Variables
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alalwan, H.A.; Alminshid, A.H. CO2 capturing methods: Chemical looping combustion (CLC) as a promising technique. Sci. Total Environ. 2021, 788, 147850. [Google Scholar] [CrossRef] [PubMed]
- Smith, K.H.; Anderson, C.J.; Tao, W.; Endo, K.; Mumford, K.A.; Kentish, S.E.; Qader, A.; Hooper, B.; Stevens, G.W. Pre-combustion capture of CO2—Results from solvent absorption pilot plant trials using 30 wt% potassium carbonate and boric acid promoted potassium carbonate solvent. Int. J. Greenh. Gas Control 2012, 10, 64–73. [Google Scholar] [CrossRef]
- Ahmad, N.N.R.; Leo, C.P.; Mohammad, A.W.; Shaari, N.; Ang, W.L. Recent progress in the development of ionic liquid-based mixed matrix membrane for CO2 separation: A review. Int. J. Energy Res. 2021, 45, 9800–9830. [Google Scholar] [CrossRef]
- Liu, M.; Nothling, M.D.; Zhang, S.; Fu, Q.; Qiao, G.G. Thin film composite membranes for postcombustion carbon capture: Polymers and beyond. Prog. Polym. Sci. 2022, 126, 101504. [Google Scholar] [CrossRef]
- Yousef, A.M.; El-Maghlany, W.M.; Eldrainy, Y.A.; Attia, A. New approach for biogas purification using cryogenic separation and distillation process for CO2 capture. Energy 2018, 156, 328–351. [Google Scholar] [CrossRef]
- Ghazali, Z.; Suhaili, N.; Tahari, M.N.A.; Yarmo, M.A.; Hassan, N.H.; Othaman, R. Impregnating deep eutectic solvent choline chloride:urea:polyethyleneimine onto mesoporous silica gel for carbon dioxide capture. J. Mater. Res. Technol. 2020, 9, 3249–3260. [Google Scholar] [CrossRef]
- Yong, J.K.; Stevens, G.W.; Caruso, F.; Kentish, S.E. The use of carbonic anhydrase to accelerate carbon dioxide capture processes. J. Chem. Technol. Biotechnol. 2015, 90, 3–10. [Google Scholar] [CrossRef]
- Davarpanah, E.; Hernández, S.; Latini, G.; Pirri, C.F.; Bocchini, S. Enhanced CO2 Absorption in Organic Solutions of Biobased Ionic Liquids. Adv. Sustain. Syst. 2020, 4, 1900067. [Google Scholar] [CrossRef] [Green Version]
- Yoro, K.O.; Sekoai, P.T.; Isafiade, A.J.; Daramola, M.O. A review on heat and mass integration techniques for energy and material minimization during CO2 capture. Int. J. Energy Environ. Eng. 2019, 10, 367–387. [Google Scholar] [CrossRef] [Green Version]
- Ismail, A.F.; Khulbe, K.C.; Matsuura, T. Gas separation membrane materials and structures. In Gas Separation Membranes; Springer: Berlin, Germany, 2015; pp. 37–192. [Google Scholar]
- Abdullah, N.; Rahman, M.A.; Dzarfan Othman, M.H.; Jaafar, J.; Ismail, A.F. Chapter 2—Membranes and Membrane Processes: Fundamentals. In Current Trends and Future Developments on (Bio-) Membranes; Basile, A., Mozia, S., Molinari, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 45–70. [Google Scholar]
- Nagy, E. Chapter 18—Membrane Gas Separation. In Basic Equations of Mass Transport through a Membrane Layer, 2nd ed.; Nagy, E., Ed.; Elsevier: New York, NY, USA, 2019; pp. 457–481. [Google Scholar]
- Ion-Ebrasu, D.; Pollet, B.G.; Caprarescu, S.; Chitu, A.; Trusca, R.; Niculescu, V.; Gabor, R.; Carcadea, E.; Varlam, M.; Vasile, B.S. Graphene inclusion effect on anion-exchange membranes properties for alkaline water electrolyzers. Int. J. Hydrogen Energy 2020, 45, 17057–17066. [Google Scholar] [CrossRef]
- Sandu, T.; Chiriac, A.L.; Tsyntsarski, B.; Stoycheva, I.; Căprărescu, S.; Damian, C.M.; Iordache, T.V.; Pătroi, D.; Marinescu, V.; Sârbu, A. Advanced hybrid membranes for efficient nickel retention from simulated wastewater. Polym. Int. 2021, 70, 866–876. [Google Scholar] [CrossRef]
- Ng, L.Y.; Mohammad, A.W.; Leo, C.P.; Hilal, N. Polymeric membranes incorporated with metal/metal oxide nanoparticles: A comprehensive review. Desalination 2013, 308, 15–33. [Google Scholar] [CrossRef]
- Ion-Ebrașu, D.; Andrei, R.D.; Enache, S.; Căprărescu, S.; Negrilă, C.C.; Jianu, C.; Enache, A.; Boerașu, I.; Carcadea, E.; Varlam, M. Nitrogen functionalization of cvd grown three-dimensional graphene foam for hydrogen evolution reactions in alkaline media. Materials 2021, 14, 4952. [Google Scholar] [CrossRef] [PubMed]
- Sasikumar, B.; Arthanareeswaran, G.; Ismail, A.F. Recent progress in ionic liquid membranes for gas separation. J. Mol. Liq. 2018, 266, 330–341. [Google Scholar] [CrossRef]
- Valappil, R.S.K.; Ghasem, N.; Al-Marzouqi, M.; Al-Marzouqi, M. Current and future trends in polymer membrane-based gas separation technology: A comprehensive review. J. Ind. Eng. Chem. 2021, 98, 103–129. [Google Scholar] [CrossRef]
- Chen, X.; Liu, G.; Jin, W. Natural gas purification by asymmetric membranes: An overview. Green Energy Environ. 2021, 6, 176–192. [Google Scholar] [CrossRef]
- Klemm, A.; Lee, Y.-Y.; Mao, H.; Gurkan, B. Facilitated transport membranes with ionic liquids for CO2 separations. Front. Chem. 2020, 8, 637. [Google Scholar] [CrossRef]
- Hu, L.; Clark, K.; Alebrahim, T.; Lin, H. Mixed matrix membranes for post-combustion carbon capture: From materials design to membrane engineering. J. Membr. Sci. 2022, 644, 120140. [Google Scholar] [CrossRef]
- Cakal, U.; Yilmaz, L.; Kalipcilar, H. Effect of feed gas composition on the separation of CO2/CH4 mixtures by PES-SAPO 34-HMA mixed matrix membranes. J. Membr. Sci. 2012, 417, 45–51. [Google Scholar] [CrossRef]
- Shabani, F.; Aroon, M.A.; Matsuura, T.; Farhadi, R. CO2/CH4 separation properties of PES mixed matrix membranes containing Fullerene-MWCNTs hybrids. Sep. Purif. Technol. 2021, 277, 119636. [Google Scholar] [CrossRef]
- Miri, S.; Omidkhah, M.; Ebadi Amooghin, A.; Matsuura, T. Membrane-based gas separation accelerated by quaternary mixed matrix membranes. J. Nat. Gas Sci. Eng. 2020, 84, 103655. [Google Scholar] [CrossRef]
- Mohshim, D.F.; Mukhtar, H.; Man, Z. The effect of incorporating ionic liquid into polyethersulfone-SAPO34 based mixed matrix membrane on CO2 gas separation performance. Sep. Purif. Technol. 2014, 135, 252–258. [Google Scholar] [CrossRef]
- Shin, J.E.; Lee, S.K.; Cho, Y.H.; Park, H.B. Effect of PEG-MEA and graphene oxide additives on the performance of Pebax®1657 mixed matrix membranes for CO2 separation. J. Membr. Sci. 2019, 572, 300–308. [Google Scholar] [CrossRef]
- Suleman, H.; Maulud, A.S.; Man, Z. Review and selection criteria of classical thermodynamic models for acid gas absorption in aqueous alkanolamines. Rev. Chem. Eng. 2015, 31, 599–639. [Google Scholar] [CrossRef]
- Ozcan, A.; Semino, R.; Maurin, G.; Yazaydin, A.O. Modeling of gas transport through polymer/MOF interfaces: A microsecond-scale concentration gradient-driven molecular dynamics study. Chem. Mater. 2020, 32, 1288–1296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarfraz, M.; Arshad, A.; Ba-Shammakh, M. Predicting Gas Permeability through Mixed-matrix Membranes Filled with Nanofillers of Different Shapes. Arab. J. Sci. Eng. 2021, 47, 1–13. [Google Scholar] [CrossRef]
- Zarabadipoor, M.; Maghami, S.; Mehrabani-Zeinabad, A.; Sadeghi, M. A comprehensive modeling approach for determining the role and nature of interfacial morphology in mixed matrix membranes. Comput. Mater. Sci. 2021, 197, 110590. [Google Scholar] [CrossRef]
- Sanaeepur, H.; Ebadi Amooghin, A.; Khademian, E.; Kargari, A.; Omidkhah, M. Gas permeation modeling of mixed matrix membranes: Adsorption isotherms and permeability models. Polym. Compos. 2018, 39, 4560–4568. [Google Scholar] [CrossRef]
- Vinh-Thang, H.; Kaliaguine, S. Predictive models for mixed-matrix membrane performance: A review. Chem. Rev. 2013, 113, 4980–5028. [Google Scholar] [CrossRef]
- Ghasemzadeh, K.; Aghaeinejad-Meybodi, A.; Basile, A. Hydrogen production as a green fuel in silica membrane reactor: Experimental analysis and artificial neural network modeling. Fuel 2018, 222, 114–124. [Google Scholar] [CrossRef]
- Asghari, M.; Dashti, A.; Rezakazemi, M.; Jokar, E.; Halakoei, H. Application of neural networks in membrane separation. Rev. Chem. Eng. 2020, 36, 265–310. [Google Scholar] [CrossRef]
- Apsemidis, A.; Psarakis, S.; Moguerza, J.M. A review of machine learning kernel methods in statistical process monitoring. Comput. Ind. Eng. 2020, 142, 106376. [Google Scholar] [CrossRef]
- Dufour, E.; Gassara, S.; Petit, E.; Pochat-Bohatier, C.; Deratani, A. Quantitative PVP mapping in PVDF hollow fiber membranes by using Raman spectroscopy coupled with spectral chemiometrics analysis. Eur. Phys. J. Spec. Top. 2015, 224, 1911–1919. [Google Scholar] [CrossRef]
- Chen, W.; Qian, C.; Zhou, K.-G.; Yu, H.-Q. Molecular Spectroscopic Characterization of Membrane Fouling: A Critical Review. Chem 2018, 4, 1492–1509. [Google Scholar] [CrossRef] [Green Version]
- Han, F.; Tian, Y.; Zou, Q.; Zhang, X. Research on the Fault Diagnosis of a Polymer Electrolyte Membrane Fuel Cell System. Energies 2020, 13, 2531. [Google Scholar] [CrossRef]
- Pirdashti, M.; Curteanu, S.; Kamangar, M.H.; Hassim, M.H.; Khatami, M.A. Artificial neural networks: Applications in chemical engineering. Rev. Chem. Eng. 2013, 29, 205–239. [Google Scholar] [CrossRef]
- Park, S.; Baek, S.-S.; Pyo, J.; Pachepsky, Y.; Park, J.; Cho, K.H. Deep neural networks for modeling fouling growth and flux decline during NF/RO membrane filtration. J. Membr. Sci. 2019, 587, 117164. [Google Scholar] [CrossRef]
- Jawad, J.; Hawari, A.H.; Zaidi, S.J. Artificial neural network modeling of wastewater treatment and desalination using membrane processes: A review. Chem. Eng. J. 2021, 419, 129540. [Google Scholar] [CrossRef]
- Rezakazemi, M.; Azarafza, A.; Dashti, A.; Shirazian, S. Development of hybrid models for prediction of gas permeation through FS/POSS/PDMS nanocomposite membranes. Int. J. Hydrogen Energy 2018, 43, 17283–17294. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, G.; Long, Y.; Teng, J.; You, X.; Liao, B.-Q.; Lin, H. Application of radial basis function artificial neural network to quantify interfacial energies related to membrane fouling in a membrane bioreactor. Bioresour. Technol. 2019, 293, 122103. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nasir, R.; Mukhtar, H.; Man, Z.; Dutta, B.K.; Shaharun, M.S.; Abu Bakar, M.Z. Mixed matrix membrane performance enhancement using alkanolamine solution. J. Membr. Sci. 2015, 483, 84–93. [Google Scholar] [CrossRef]
- Nasir, R.; Mukhtar, H.; Man, Z.; Shaharun, M.S.; Abu Bakar, M.Z. Effect of fixed carbon molecular sieve (CMS) loading and various di-ethanolamine (DEA) concentrations on the performance of a mixed matrix membrane for CO2/CH4 separation. RSC Adv. 2015, 5, 60814–60822. [Google Scholar] [CrossRef]
- Nasir, R.; Mukhtar, H.; Man, Z.; Shaharun, M.S.B.; Bakar, M.Z.A. Performance Enhancement of Mixed Matrix Membranes through the Incorporation of Alkanolamines for CO2/CH4 Separation. ASEAN J. Chem. Eng. 2014, 14, 28–37. [Google Scholar] [CrossRef]
- Suleman, H.; Maulud, A.S.; Man, Z. Reconciliation of outliers in CO2-alkanolamine-H2O datasets by robust neural network winsorization. Neural Comput. Appl. 2017, 28, 2621–2632. [Google Scholar] [CrossRef]
- Gurney, K. An Introduction to Neural Networks; CRC Press: New York, NY, USA, 2018. [Google Scholar]
- Balchandani, S.C.; Dey, A. Prediction of CO2 solubility in potential blends of ionic liquids with Alkanolamines using statistical non-rigorous and ANN based modeling: A comprehensive simulation study for post combustion CO2 capture. Int. Commun. Heat Mass Transf. 2022, 132, 105866. [Google Scholar] [CrossRef]
- Sharma, P.N.; Shmueli, G.; Sarstedt, M.; Danks, N.; Ray, S. Prediction-oriented model selection in partial least squares path modeling. Decis. Sci. 2021, 52, 567–607. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Hissel, D.; Lu, J.; Hou, M.; Shao, Z. Prognostics methods and degradation indexes of proton exchange membrane fuel cells: A review. Renew. Sustain. Energy Rev. 2020, 123, 109721. [Google Scholar] [CrossRef]
- Reprint of: Mahalanobis, P.C. (1936) On the Generalised Distance in Statistics. Sankhya A 2018, 80, 1–7.
- Sabetghadam, A.; Seoane, B.; Keskin, D.; Duim, N.; Rodenas, T.; Shahid, S.; Sorribas, S.; Guillouzer, C.L.; Clet, G.; Tellez, C. Metal organic framework crystals in mixed-matrix membranes: Impact of the filler morphology on the gas separation performance. Adv. Funct. Mater. 2016, 26, 3154–3163. [Google Scholar] [CrossRef]
- Cheng, Y.; Ying, Y.; Zhai, L.; Liu, G.; Dong, J.; Wang, Y.; Christopher, M.P.; Long, S.; Wang, Y.; Zhao, D. Mixed matrix membranes containing MOF@COF hybrid fillers for efficient CO2/CH4 separation. J. Membr. Sci. 2019, 573, 97–106. [Google Scholar] [CrossRef]
- Shahid, S.; Nijmeijer, K. High pressure gas separation performance of mixed-matrix polymer membranes containing mesoporous Fe(BTC). J. Membr. Sci. 2014, 459, 33–44. [Google Scholar] [CrossRef]
- Luo, J.; Guo, R.; Zhang, M.; Li, J. Gas permeation properties of polymer membranes containing pendant tertiary amine groups. High Perform. Polym. 2015, 28, 1005–1014. [Google Scholar] [CrossRef]
- Ghasemzadeh, K.; Ahmadnejad, F.; Aghaeinejad-Meybodi, A.; Basile, A. Hydrogen production by a PdAg membrane reactor during glycerol steam reforming: ANN modeling study. Int. J. Hydrogen Energy 2018, 43, 7722–7730. [Google Scholar] [CrossRef]
- Dashti, A.; Harami, H.R.; Rezakazemi, M. Accurate prediction of solubility of gases within H2-selective nanocomposite membranes using committee machine intelligent system. Int. J. Hydrogen Energy 2018, 43, 6614–6624. [Google Scholar] [CrossRef]
- Rostamizadeh, M.; Rezakazemi, M.; Shahidi, K.; Mohammadi, T. Gas permeation through H2-selective mixed matrix membranes: Experimental and neural network modeling. Int. J. Hydrogen Energy 2013, 38, 1128–1135. [Google Scholar] [CrossRef]
- Asteris, P.G.; Koopialipoor, M.; Armaghani, D.J.; Kotsonis, E.A.; Lourenço, P.B. Prediction of cement-based mortars compressive strength using machine learning techniques. Neural Comput. Appl. 2021, 33, 13089–13121. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasir, R.; Suleman, H.; Maqsood, K. Multiparameter Neural Network Modeling of Facilitated Transport Mixed Matrix Membranes for Carbon Dioxide Removal. Membranes 2022, 12, 421. https://doi.org/10.3390/membranes12040421
Nasir R, Suleman H, Maqsood K. Multiparameter Neural Network Modeling of Facilitated Transport Mixed Matrix Membranes for Carbon Dioxide Removal. Membranes. 2022; 12(4):421. https://doi.org/10.3390/membranes12040421
Chicago/Turabian StyleNasir, Rizwan, Humbul Suleman, and Khuram Maqsood. 2022. "Multiparameter Neural Network Modeling of Facilitated Transport Mixed Matrix Membranes for Carbon Dioxide Removal" Membranes 12, no. 4: 421. https://doi.org/10.3390/membranes12040421
APA StyleNasir, R., Suleman, H., & Maqsood, K. (2022). Multiparameter Neural Network Modeling of Facilitated Transport Mixed Matrix Membranes for Carbon Dioxide Removal. Membranes, 12(4), 421. https://doi.org/10.3390/membranes12040421







