Abstract
In this paper, the joint impact of the interior heating and chemical reaction on the double diffusive convective flow in porous membrane enclosures soaked by a non-Newtonian Maxwell fluid is investigated applying linear and nonlinear stability techniques. The porous enclosures are square, slender and rectangular. Using the linear stability analysis, the expression for the critical thermal Rayleigh–Darcy number, above which the convective movement occurs, is derived analytically in terms of associated physical parameters. A nonlinear stability examination reliant on the Fourier double series is executed to calculate the convective heat and mass transports of the arrangement. It is observed that the pattern of convective activity is oscillatory only in the occurrence of a relaxation parameter and the threshold value of the relaxation parameter for the occurrence of the oscillatory pattern depends on the other physical parameters. The onset of convective instability accelerates with the increasing chemical reacting parameter, the interior heating parameter, the solute Rayleigh–Darcy number, the Lewis number, the Vadasz number, and the relaxation parameter, while it delays with the heat capacity ratio. The convective heat and mass transfers increase with the solute Rayleigh–Darcy number, the Vadasz number, the relaxation parameter, and the aspect ratio (for rectangular enclosure), while it decreases with the heat capacity ratio and the aspect ratio (for slender enclosure). Additionally, the convective heat transfer enhances with the interior heating parameter, while the convective mass transfer enhances with the chemical reacting parameter and the Lewis number. The effects of Vadasz number, heat capacity ratio, and relaxation parameter are witnessed only on the oscillatory pattern of convection and unsteady convective heat and mass transfers. Further, some existing literature results are compared with the current findings.
1. Introduction
Double diffusive convective motion is encouraged by two components whose densities are different. These density gradients result in two different diffusion rates which are very crucial for this type of convection. Convection that occurs due to concentration and temperature gradients has gained popularity in previous years because of its realistic applications in science and engineering. Some of the vital sectors of relevances in engineering contain foodstuff and chemical processes [1,2,3,4], casting of metals [5,6,7], crystal growth [8], petroleum production [9,10,11], biomechanical and geosciences applications [12,13,14,15]. The problem of the double diffusive convective progress in a porous layer was explored by Poulikakos [16]. He derived the boundaries describing the areas of direct and overstable styles in terms of critical parameters. The anisotropic effect on the double diffusive convective movement in a porous surrounding substance was explored by Gaikwad et al. [17]. They considered the impacts of anisotropy parameters, solute Rayleigh number, the Soret, and the Dufour factors on the stationary and oscillatory convections as well as on the warmth and mass carrying. Kuznetsov and Nield [18] investigated the heterogeneity effect on the beginning of double diffusive convective movement analytically exploiting linear stability theory. The impact of throughflow on the onset of double-diffusive motion in a permeable layer was explored by Kiran [19] and Shivakumara and Khalili [20]. They found that the consequence of throughflow has either to become stable or to unsettle the arrangement. It depends on the direction of throughflow. Javaheri et al. [21] deliberated the double diffusive convective flow as a purpose for the geological congregation of carbon dioxide. The exponential discrepancy of boundary conditions on the unsteady double diffusive natural convective progress inside the porous enclosures was investigated by Al-Mudhaf [22]. Altawallbeh et al. [23] calculated the power of internal heating on binary instability in a permeable layer. They obtained the critical Rayleigh number and wave number for the stationary and oscillatory mode of convections exploiting the linear hypothesis. Malashetty and Biradar [24] examined the consequence of chemical feedback on the binary diffusive instability in a porous medium layer. They found that the chemical feedback may have a stabilizing or destabilizing influence on the stability criterion. An outstanding review of the studies associated with the double-diffusive instability has been provided by Nield and Bejan [13], Yadav [25], Mojtabi and Charrier-Mojtabi [26], and Vafai [27].
It is known that fluids that take place in the majority of the above-mentioned applications and in nature exhibit non-Newtonian fluid features [28,29,30,31,32,33,34,35,36,37,38]. The problem of double-diffusive instability in a porous medium layer drenched by non-Newtonian fluid taking an Oldroyd model was explored by Malashetty and Swamy [39]. They derived the arrival conditions for stationary, oscillatory, and finite amplitude convective motions analytically. They found a contrast amid the progression of thermal transmission, solute transmission, and viscoelasticity to establish the convective motion as an oscillatory pattern. Malashetty et al. [40] and Kumar and Bhadauria [41] extended this problem with the thermal non-equilibrium effect. The linear stability examination of a Maxwell liquid with double-diffusive motion was undertaken by Awad et al. [42]. They demonstrate that the critical Darcy–Rayleigh number reduces with the relaxation time. Wang and Tan [43] inspected the dual-diffusive instability for non-Newtonian liquid in an absorbent medium considering an amalgamation of Maxwell and Darcy models. They observed that the Soret outcome and relaxation time sped up the onset of convection. The consequence of interior heating on the beginning of double diffusive instability in a coupled stress non-Newtonian liquid flooded porous layer was scrutinized by Gaikwad and Kouser [44]. They found that the arrival of both stationary and oscillatory convective movement is increased by the interior Rayleigh number. Gaikwad and Dhanraj [45] scrutinized the combined weight of anisotropic and interior heating on the binary flow in a non-Newtonian Maxwell liquid flooded permeable layer. They observed that the inner Rayleigh number, mechanical anisotropy factor, and relaxation parameter sped up the start of convective activity, while the thermal anisotropy factor delayed it. Very recently, the impact of larger frequency pulsation in the gravity force on the double-diffusive convective activity with non-Newtonian viscoelastic liquid-filled porous matrix was inspected by Zhao et al. [46].
From the literature inspection, clearly no effort has been made to determine the mutual impact of chemical response and interior heating on the beginning of double diffusive convective motion in a permeable layer flooded by a non-Newtonian fluid. However, there are several practical applications in enhanced oil recovery systems (such as during polymer-flooding practices), a packed bed reactor, chemical privilege equipment, food manufacturing, metal casting procedures, and geophysical arrangements where the porous material may offer its source of warmth and the chemical reaction can take place among the chemical species in the porous substance and the non-Newtonian fluid. Therefore, the present effort intends to inspect the mutual effect of the interior heating and chemical reaction on the double diffusive convective motion in permeable enclosures flooded by a non-Newtonian fluid applying linear and nonlinear stability techniques. To model the non-Newtonian behavior of the fluid, the Maxwell model is used. This is a rate variety of non-Newtonian fluid models in which stress relaxation is known. The Maxwell fluid model acceptably describes the flow behavior of non-Newtonian fluids consisting of a substructure, for instance lubricants with polymer additions, electro-rheological fluids, liquid crystals, blood, and suspension fluids [47,48,49,50]. This work is presented as follows: In Section 1, an introduction of the problem under investigation is provided. In Section 2, the mathematical formulation of the problem is presented. The perturbation equations are obtained in Section 3. In Section 4, the conditions for the start of binary convective flow are derived. The convective heat and mass transports are derived in Section 5. Section 6 presents key results and discussion. At last, this work is completed with a conclusion in Section 7.
2. Mathematical Formulation
The system examined is a non-Newtonian Maxwell fluid-saturated porous cavity of length and width with a third dimension infinitely extended so that the fluid flow and heat and mass transport can be taken as two dimensional [29,51], as demonstrated in Figure 1.
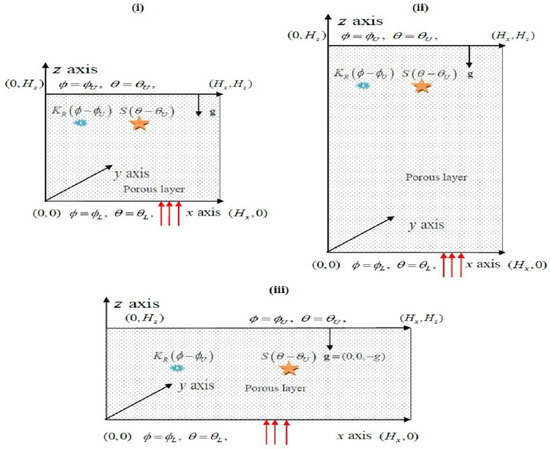
Figure 1.
Physical configuration of the problem: (i) square enclosure, (ii) slender vertical enclosure, and (iii) rectangular.
It is assumed that the porous cavity is subjected to an internal heat supply of strength and first-order chemical response of rate among a chemical genus in the permeable matrix and the Maxwell fluid. The temperatures and , and solute concentrations and , are consistently forced on the bottom and top boundary walls such that and , while other boundary walls are accepted to be insulated and impermeable to mass transmission. It is specified that the porous cavity is homogeneous and in local thermal balance with Maxwell fluid.
The continuity equation for the Maxwell fluid in a porous cavity is [52,53,54]:
Here, is Darcy’s velocity of the Maxwell fluid, and, and are unit vectors in and paths.
The momentum equation by taking the Darcy rule for the porous medium, the Maxwell model for non-Newtonian fluid, and the Boussinesq approximation for density disparity with temperature and solute concentration in the buoyancy force is [55,56,57]:
where, represents the time, symbolizes the temperature, represents the solute concentration, symbolizes the density at , represents the permeability of the porous medium, symbolizes the stress relaxation feature time constant, symbolizes the viscosity of Maxwell fluid, symbolizes the pressure, and symbolize the thermal and solute expansion coefficients, respectively.
The energy equation for a Maxwell fluid in a heat-generating permeable cavity is [31,58,59]:
Here, symbolizes the power of the interior heating, symbolizes the effectual thermal conductivity of the porous medium, and symbolize the heat capacities of the Maxwell fluid and effectual permeable medium, correspondingly.
The conservation equation for the solute with the chemical reaction of rate in the porous matrix is [60]
Here, is the solutal diffusivity and is the porosity of the permeable medium.
On eliminating the pressure term and using the stream function as and , the Equations (1)–(4) can be written as:
The boundary situations are:
For no-dimensional examination, the dimensionless variables are described as:
where . Then, the dimensionless forms of Equations (5)–(8) become:
Here, , , (relaxation parameter), (Vadasz number), (aspect ratio), (thermal Rayleigh–Darcy number), (heat capacity ratio), (solute Rayleigh–Darcy number), (interior heating parameter), (Lewis number), and (chemical reacting parameter).
Basic Condition
For a time-free calm solution of Equations (10)–(12), it is assumed that the temperature and solute distributions for the basic solution are:
On solving the Equations (11)–(13) for the basic solution, we have:
In the lack of interior heating and chemical reaction, Equations (15) and (16) give:
Equation (17) is the one found by Kuznetsov and Nield [61] for the case of pure fluid.
3. Perturbation Equation
Now, perturbation on the basic condition is imposed as:
where, , , and are the perturbed variables on their basic estimates. Replacing Equation (18) into Equations (10)–(13), we have:
4. Linear Stability Consideration
In this segment, the thresholds of the marginal and oscillatory type of convective flows are determined applying linear theory. Now, it is supposed that the amplitudes of the perturbation are extremely small and expressed as [13,29,60,62]:
where and represent the wavenumber and enlargement rate of disturbances, correspondingly.
On using Equation (23) in Equations (19)–(22) and avoiding the nonlinear terms with perturbed variables, we have:
Here, . To find an approximate solution to the system of Equations (24)–(27), the Galerkin routine is utilized [63,64,65,66,67,68]. The trial functions (fulfilling the boundary circumstances) are picked as:
where, , and are unidentified coefficients. On applying Equation (28) into Equations (24)–(26) and for the non-singular solution, we have:
where, , and .
Now, from Equation (25), we have:
where,
4.1. Marginal Pattern of Convection
The marginal pattern of convection can happen, if . Thus, Equation (30) gives the marginal thermal Rayleigh–Darcy number as:
The threshold of the signifying the beginning of marginal convection occurs at where satisfies the equation:
In the nonattendance of chemical response (), Equations (33) and (34) turn into:
For the case of a single component (), Equations (35) and (36) give:
The Equations (37) and (38) are the same as found by Yadav and Maqhusi [29] for the lack of viscosity variation.
In the nonattendance of interior heating (), Equations (35) and (36) provide:
Equations (39) and (40) are the standard results for a dual diffusive convective motion in a permeable medium for cases [13,50,69].
For the case of one component (), Equations (39) and (40) offer the critical marginal thermal Rayleigh–Darcy number as:
This coincides with the conclusion of Nield and Kuznetsov [70] for the convection in a rectangular box. Additionally, Equation (41) agrees with the experimental results obtained by Horton and Rogers [71] and Katto and Masuoka [72].
4.2. Oscillatory Pattern of Convection
The oscillatory pattern of convective motion occurs when and . Then, Equation (30) proposes the oscillatory thermal Rayleigh–Darcy number as:
Additionally, from Equation (30), the rate of oscillation satisfies the following dispersion relation:
Here,
From Equation (43), it is clear that the oscillatory manner of convective flow is conceivable only if . The analytical appearance for specified by Equation (42) is minimized respecting the wave number numerically when for diverse estimates of involved physical parameters to identify their impacts on the start of the oscillatory type of convective motion.
5. Weak Nonlinear Stability Investigation
The linear stability inquiry offers the threshold for the start of convective movement of the Maxwell fluid in terms of but does not calculate the convective heat and mass transport. To get these extra details, here the weak nonlinear stability analysis is used as [17,44,56,60,73]:
where, , and are undetermined amplitudes and to be determined. On replacing Equations (44)–(46) into Equations (19)–(21), we obtain the nonlinear stability equations as:
where , and .
The above nonlinear equations are not fit for analytical inspection for the time-reliant variables. Thus, we solved it numerically utilizing the Runge–Kutta–Fehlberg technique (RKF45). The results are also validated with ODE45 solver in MATLAB. For the initial state, we select , and .
5.1. Steady Motion
For steady motion, Equations (47)–(51) become:
On solving Equations (52)–(56) analytically, we have:
Here,
5.2. Convective Heat and Mass Transports
Convective heat and mass transfers play a very vital role in detecting the convective motion in more early stages. Heat and mass transfers can be calculated in spans of Nusselt number and Sherwood number , individually, and described as [17,44,56,60,73]:
On applying Equations (15), (16), (45) and (46) into Equations (62) and (63), we have:
6. Results and Discussion
The impact of interior heating and chemical reaction on the beginning of dual diffusive convective motion and the convective heat and mass transfers in non-Newtonian Maxwell fluid-saturated permeable square , slender , and rectangular enclosures were explored. Employing the linear stability philosophy, the criteria for the start of the marginal and oscillatory pattern of convective motions were derived analytically in terms of , which is the function of physical parameters , and . Applying the weakly nonlinear theory, the convective heat and mass transports were calculated in spans of the Nusselt number and Sherwood number , individually. The results are presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 and Table 1, Table 2, Table 3 and Table 4. To create the numerical results and figures, the MATLAB software (R2018b) was used. The range of the physical parameters that were considered for making the results are given in the figure captions and obtained from the available literature [31,50,55,60,73,74,75].

Figure 2.
Distributions of basic state temperature () and solute concentration ( ) with the depth of Maxwell fluid layer .
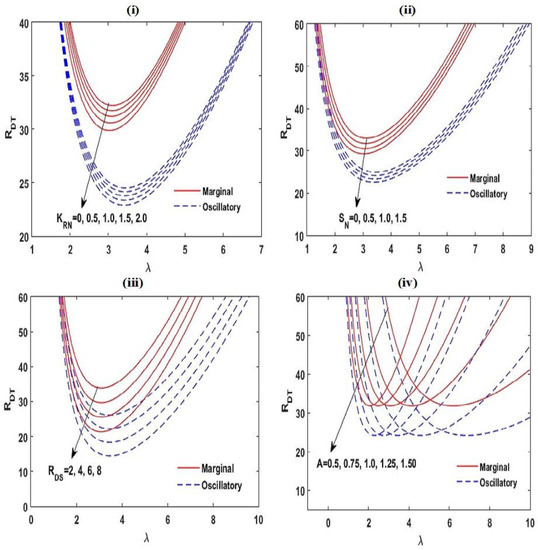
Figure 3.
The effect of , , , and on the neutral stability curves at , , , , , , , and with variation in one of these parameters.
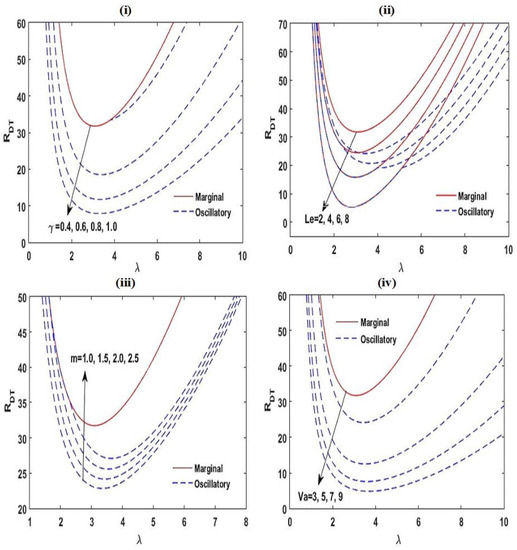
Figure 4.
The effect of , , , and on the neutral stability curves at , , , , , , , and with variation in one of these parameters.
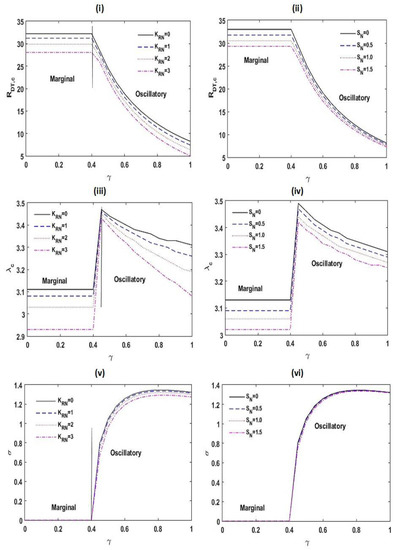
Figure 5.
Variation in , , and with for different values of and at , , , , , , and .
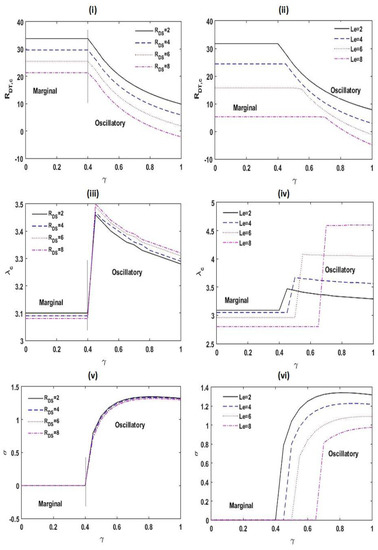
Figure 6.
Variation in , , and with for different values of and at , , , , , , and .

Figure 7.
Variation in , , and with for different values of and at , , , , , , and .
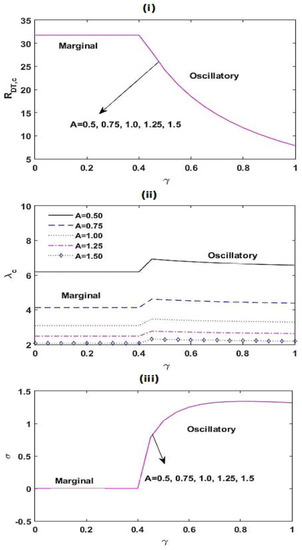
Figure 8.
Variation in , , and with for different values of at , , , , , , and .
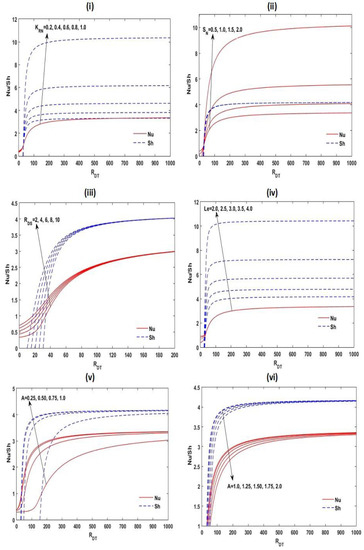
Figure 9.
Disparity of the steady and with at , , , , and for different values of one of these parameters.
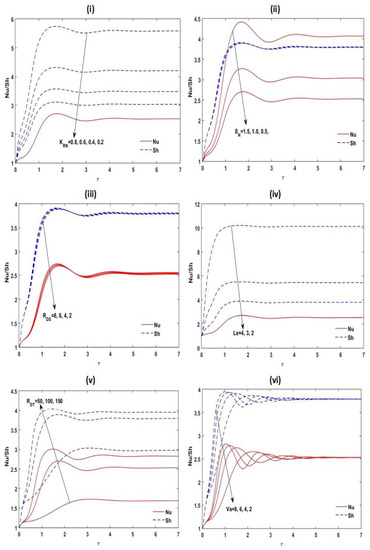
Figure 10.
Disparity of the unsteady and with for different values of , , , , , and at , , , , , ,, and .
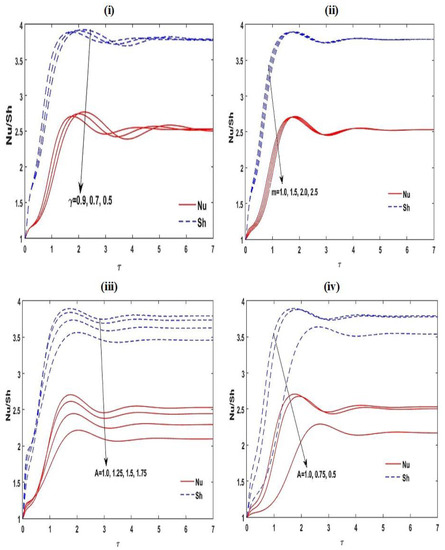
Figure 11.
Disparity of the unsteady and with for different values of , , and at , , , , , ,, and .

Table 1.
Comparison of , , and for different values of , , and at , , , , , , and .

Table 2.
Comparison of , , and for diverse values of , , and at , , , , , , and .

Table 3.
Comparison of , , and for diverse values of , , and at , , , , , , and .

Table 4.
Comparison of , , and for diverse values of , , and at , , , , , , and .
Figure 2 illustrates the impact of on the distribution of basic state temperature , and the impact of and on the allocation of basic state solute concentration . From Figure 2i, it is recognized that the power of the basic temperature allocation increases with accumulating interior heating parameters and the profile of basic temperature allocation alters from linear to nonlinear with . This happened because the increasing provides more warming to the Maxwell fluid layer, which enhances the strength of buoyancy force and as a result, more disturbances are seen in the system. From Figure 2ii, we observed a similar result on the allocation of basic state solute concentration with increasing and . This happened because an increase in the strength of and creates more disturbances in the system.
Figure 3 and Figure 4 exhibit the neutral curves for diverse values of the chemical reacting parameter (Figure 3i), the interior heating parameter (Figure 3ii), the solute Rayleigh–Darcy number (Figure 3iii), the aspect ratio (Figure 3iv), the relaxation parameter (Figure 4i), the Lewis number (Figure 4ii), the heat capacity ratio (Figure 4iii), and the Vadasz number (Figure 4iv). From these plots, it is found that the neutral curves are linked in a topological way. This establishes that the linear stability of the arrangement is specified in the span of , which at lower values the arrangement is stable and at somewhat greater than , convective activity starts. From these figures, it is also established that by increasing the values of , , , , and , the estimate of tends to lessen, i.e., the arrangement goes to destabilize, while has a stabilizing impact on the stability of the structure. The aspect ratio does not affect . The marginal pattern of the convective motion is found to be free with , , and .
Figure 5 illustrates the variations in , , and as a function of for varied estimates of the chemical reacting parameter and the interior heating parameter . From Figure 5i,ii, we found that with a boost in the values of , , and , the critical thermal Rayleigh–Darcy number diminishes. This shows that the chemical reacting parameter , the interior heating parameter , and the relaxation parameter speed up the beginning of convective activities. This is due to the fact that increasing the chemical reacting parameter and the interior heating parameter creates more disturbances by increasing the energy supply to the system. Further, the destabilizing effect of the relaxation parameter is found because thermal diffusivity of the system increases with (from the definition of ). From Figure 5iii,iv, it is noted that the critical wave number decreases with , , and . This illustrates that the magnitude of convection cells increases with , , and . From Figure 5v,vi, we detected that the frequency of oscillations decreases with accumulating and , while an opposite result is seen with .
Figure 6 exhibits the impact of and on the stability of the scheme. From Figure 6i,ii, it is noticed that an improvement in the estimation of and is to speed up the marginal and oscillatory patterns of convective motions.
This is on the ground that the disturbance to the arrangement increases with and . Furthermore, an increase in the estimate of increases the threshold estimate of at which the pattern of instability is amended. From Figure 6iii,iv, it is found that the critical wave number declines with and for a marginal pattern of convection, while a reverse result is seen for an oscillatory pattern of convection. From Figure 6v,vi, it is established that the frequency of oscillations shrinks with and .
The impacts of the heat capacity ratio and the Vadasz number on , , and are exposed in Figure 7. From Figure 7i,ii, it is found that surges with for oscillatory pattern of convection, while this result is opposite with . This appears that the outcome of delays the start of an oscillatory pattern of convection. This is due to fact that the energy restoring capacity of arrangement enhances with escalating the heat capacity ratio .
Further, the Vadasz number advances the start of the oscillatory type of movement. A similar result of the Vadasz number on the system was also observed by Kumar and Bhadauria [41] and Malashetty and Biradar [76]. From Figure 7iii,iv, it is proven that the critical wave number increases with and . The frequency of oscillations diminishes with m, while this result is opposite with as found from Figure 7v,vi. From Figure 7, it is also noticed that increasing decreases the threshold estimate of at which the pattern of instability alters, while this result is reversed with .
Figure 8 demonstrates the power of the aspect ratio on the stability of the system. From this graph, it is found that reduces with escalating . This illustrates that the dimension of convective cells enhances with increasing the aspect ratio . From Figure 8, it is also found that has no control on and .
To observe the effect of , and on steady-state heat and mass spreads, the Nusselt number and Sherwood number are plotted in Figure 9 as a function for diverse values of these parameters. From this figure, we recognize that if increases from one to five or six times of , the heat and mass transport increased significantly, and if increases more, it remains moderately constant.
The convective steady mass transfer increased with increasing , and for the slender enclosure , while it decreased with for rectangular enclosure . From Figure 9, it is also found that increases in the values of , , and for the slender enclosure amplify the convective heat transport in the scheme, while for a rectangular enclosure , convective heat transport decreases with .
The nonlinear unsteady ordinary differential Equations (47)–(51) are solved numerically by applying the RKF45 method with realistic initial circumstances. The achieved outcomes are presented in Figure 10 and Figure 11. It is noticed that the greatest increase in Nusselt number and Sherwood number appear near to the opening time; it reveals the spatial progress of increasing frequency. Lastly, the oscillations reach the steady situation for a sufficiently large amount of time. From Figure 10 and Figure 11, it is also found that increases in the estimates of for the slender enclosure and enhance the convective unsteady mass transmission in the arrangement, while it decreases with for rectangular enclosure and . The convective unsteady heat transportation in the structure increases with increasing for the slender enclosure and , whereas it reduces with for the rectangular enclosure and .
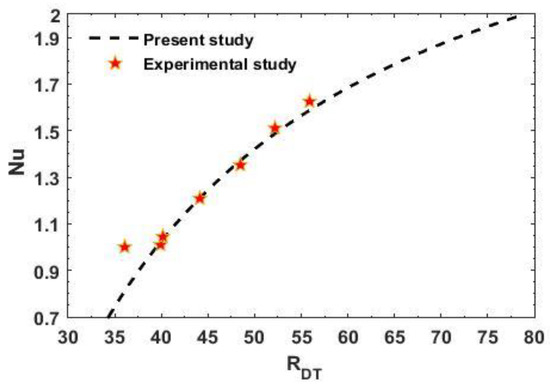
Figure 12.
Contrast of the Nusselt number in the particular case of the present analysis with experimental results found by Serkitjis [77].
In Figure 12, a comparison is made between the obtained results and the experimental results offered by Serkitjis [77] for normal fluid. From this figure, it is noticed that the heat spread observed by the experiment are very close to our outcomes if , whereas for , the experimental results are slightly lower, here .
7. Conclusions
The double diffusive convective progress in a Maxwell fluid occupying the interior heat-generating and chemical reacting porous enclosures was investigated analytically as well as numerically taking linear and weak nonlinear stability theories. The considered enclosures were rectangular , square , and slender . The impact of various parameters on the onset of the convective flow, and on the convective heat and mass transports of the system were achieved. The important conclusions are as follows:
- Increasing the chemical reacting parameter , the interior heating parameter , the solute Rayleigh–Darcy number , the relaxation parameter , the Lewis number , and the Vadasz number accelerates the onset of double diffusive convective motion, while it delays with increasing the heat capacity ratio m.
- The dimension of convective cells enhances by increasing the aspect ratio , the chemical reacting parameter , the interior heating parameter , and the relaxation parameter , while it decreases with the heat capacity ratio .
- Increasing and enhances the size of marginal convective cells, while this result is opposite for oscillatory convection.
- The convective mass transfer in the system is augmented with increasing (for the slender enclosure) and , while it reduces with (for rectangular enclosure) and .
- The convective heat transport in the system is enhanced with increasing (for the slender enclosure) and , whereas it reduces with (for rectangular enclosure) and .
- The marginal pattern of the convective motion and steady heat and mass transport are observed to be free with , , and .
Author Contributions
Conceptualization, writing—original draft preparation, methodology, writing—review and editing, D.Y. and M.A.-S. (Maimouna Al-Siyabi); software, A.A.-R.; validation, M.K.A. and R.R.; formal analysis, K.B. and M.K.A.; investigation, D.Y. and S.A.-N.; resources, M.A.-S. (Maimouna Al-Siyabi); data curation, M.A.-S. (Maryam Al-Subhi) and S.A.-N. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the TRC Undergraduate Research Grant (Grant No.: BFP/URG/CBS/21/024), the Sultanate of Oman, and the University of Nizwa Research Grant (Grant No.: A/2021-2022-UoN/3/CAS/IF), the Sultanate of Oman.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are thankful for continuous support and encouragement from the administration of University of Nizwa, Sultanate of Oman.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| aspect ratio | |
| specific heat | |
| solutal diffusivity | |
| gravity vector | |
| dimensional Maxwell fluid layer length | |
| dimensional Maxwell fluid layer width | |
| permeability of the porous matrix | |
| km | effectual thermal conductivity of the porous matrix |
| chemical reaction rate | |
| chemical reacting parameter | |
| Lewis number | |
| heat capacity ratio | |
| pressure | |
| thermal Rayleigh–Darcy number | |
| solute Rayleigh–Darcy number | |
| strength of the internal heat supply | |
| interior heating parameter | |
| Vadasz number | |
| Darcy’s velocity | |
| space coordinates | |
| Greek symbols | |
| effectual thermal diffusivity | |
| the thermal expansion coefficient | |
| the solute expansion coefficient | |
| relaxation parameter | |
| the stress relaxation | |
| dimensionless wave number | |
| viscosity | |
| density | |
| temperature | |
| concentration of solute | |
| stream function | |
| the porosity of the porous matrix | |
| enlargement rate of disturbance | |
| time | |
| Superscripts | |
| ′ | perturbed quantities |
| dimensionless variables | |
| Subscripts | |
| reference estimate | |
| effectual estimate | |
| estimate at the lower boundary | |
| estimate at the upper boundary | |
| basic flow | |
| critical | |
References
- Datta, A. Porous media approaches to studying simultaneous heat and mass transfer in food processes. II: Property data and representative results. J. Food Eng. 2007, 80, 96–110. [Google Scholar] [CrossRef]
- Purlis, E. Modelling convective drying of foods: A multiphase porous media model considering heat of sorption. J. Food Eng. 2019, 263, 132–146. [Google Scholar] [CrossRef]
- Steinberg, V.; Brand, H. Convective instabilities of binary mixtures with fast chemical reaction in a porous medium. J. Chem. Phys. 1983, 78, 2655–2660. [Google Scholar] [CrossRef]
- Beckermann, C.; Viskanta, R. Double-diffusive convection during dendritic solidification of a binary mixture. Phys. Hydrodyn. 1988, 10, 195–213. [Google Scholar]
- Coriell, S.; Cordes, M.; Boettinger, W.; Sekerka, R. Convective and interfacial instabilities during unidirectional solidification of a binary alloy. J. Cryst. Growth 1980, 49, 13–28. [Google Scholar] [CrossRef]
- Copley, S.; Giamei, A.F.; Johnson, S.; Hornbecker, M. The origin of freckles in unidirectionally solidified castings. Metall. Trans. 1970, 1, 2193–2204. [Google Scholar] [CrossRef]
- Prescott, P.; Incropera, F. Magnetically damped convection during solidification of a binary metal alloy. J. Heat Transfer. 1993, 115, 302–310. [Google Scholar] [CrossRef]
- Zhou, H.; Zebib, A. Oscillatory double diffusive convection in crystal growth. J. Cryst. Growth 1994, 135, 587–593. [Google Scholar] [CrossRef]
- Abbasi, M.; Khazali, N.; Sharifi, M. Analytical model for convection-conduction heat transfer during water injection in fractured geothermal reservoirs with variable rock matrix block size. Geothermics 2017, 69, 1–14. [Google Scholar] [CrossRef]
- Love, A.J.; Simmons, C.T.; Nield, D. Double-diffusive convection in groundwater wells. Water Resour. Res. 2007, 43, W08428. [Google Scholar] [CrossRef]
- Islam, A.W.; Sharif, M.A.; Carlson, E.S. Numerical investigation of double diffusive natural convection of CO2 in a brine saturated geothermal reservoir. Geothermics 2013, 48, 101–111. [Google Scholar] [CrossRef]
- Fournier, R.O. Double-diffusive convection in geothermal systems: The Salton Sea, California, geothermal system as a likely candidate. Geothermics 1990, 19, 481–496. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 2006; Volume 3. [Google Scholar]
- Yoshida, J.; Nagashima, H. Numerical experiments on double-diffusive intrusions in the ocean and their relation to laboratory experiments. Prog. Oceanogr. 2003, 56, 549–557. [Google Scholar] [CrossRef]
- Pop, I.; Ingham, D.B. Convective Heat Transfer: Mathematical and Computational Modelling of Viscous Fluids and Porous Media; Elsevier: Oxford, UK, 2001. [Google Scholar]
- Poulikakos, D. Double diffusive convection in a horizontal sparcely packed porous layer. Int. Commun. Heat Mass Transf. 1986, 13, 587–598. [Google Scholar] [CrossRef]
- Gaikwad, S.; Malashetty, M.; Prasad, K.R. Linear and non-linear double diffusive convection in a fluid-saturated anisotropic porous layer with cross-diffusion effects. Transp. Porous Media 2009, 80, 537–560. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Nield, D. The effects of combined horizontal and vertical heterogeneity on the onset of convection in a porous medium: Double diffusive case. Transp. Porous Media 2008, 72, 157–170. [Google Scholar] [CrossRef]
- Kiran, P. Throughflow and non-uniform heating effects on double diffusive oscillatory convection in a porous medium. Ain Shams Eng. J. 2016, 7, 453–462. [Google Scholar] [CrossRef]
- Shivakumara, I.; Khalili, A. On the stability of double diffusive convection in a porous layer with throughflow. Acta Mech. 2001, 152, 165–175. [Google Scholar] [CrossRef]
- Javaheri, M.; Abedi, J.; Hassanzadeh, H. Linear stability analysis of double-diffusive convection in porous media, with application to geological storage of CO2. Transp. Porous Media 2010, 84, 441–456. [Google Scholar] [CrossRef]
- Al-Mudhaf, A.F.; Rashad, A.; Ahmed, S.E.; Chamkha, A.J.; El-Kabeir, S. Soret and Dufour effects on unsteady double diffusive natural convection in porous trapezoidal enclosures. Int. J. Mech. Sci. 2018, 140, 172–178. [Google Scholar] [CrossRef]
- Altawallbeh, A.; Bhadauria, B.; Hashim, I. Linear and nonlinear double-diffusive convection in a saturated anisotropic porous layer with Soret effect and internal heat source. Int. J. Heat Mass Transf. 2013, 59, 103–111. [Google Scholar] [CrossRef]
- Malashetty, M.; Biradar, B.S. The onset of double diffusive reaction-convection in an anisotropic porous layer. Phys. Fluids 2011, 23, 064102. [Google Scholar] [CrossRef]
- Yadav, D. Hydrodynamic and Hydromagnetic Instability in Nanofluids; Lap Lambert Academic Publishing: Saarbrücken, Germany, 2014. [Google Scholar]
- Mojtabi, A.; Charrier-Mojtabi, M.-C. Double-diffusive convection in porous media. Handb. Porous Media 2005, 2, 269–320. [Google Scholar]
- Vafai, K. Handbook of Porous Media; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Yadav, D. The effect of viscosity and Darcy number on the start of convective motion in a rotating porous medium layer saturated by a couple-stress fluid. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 235, 999–1007. [Google Scholar] [CrossRef]
- Yadav, D.; Maqhusi, M. Influence of temperature dependent viscosity and internal heating on the onset of convection in porous enclosures saturated with viscoelastic fluid. Asia-Pac. J. Chem. Eng. 2020, 15, e2514. [Google Scholar] [CrossRef]
- Yadav, D. Influence of anisotropy on the Jeffrey fluid convection in a horizontal rotary porous layer. Heat Transf.—Asian Res. 2021, 50, 4595–4606. [Google Scholar] [CrossRef]
- Yadav, D.; Mahabaleshwar, U.S.; Wakif, A.; Chand, R. Significance of the inconstant viscosity and internal heat generation on the occurrence of Darcy-Brinkman convective motion in a couple-stress fluid saturated porous medium: An analytical solution. Int. Commun. Heat Mass Transf. 2021, 122, 105165. [Google Scholar] [CrossRef]
- Dawar, A.; Saeed, A.; Shah, Z.; Kumam, W.; Islam, S.; Kumam, P. Analytical Simulation for Magnetohydrodynamic Maxwell Fluid Flow Past an Exponentially Stretching Surface with First-Order Velocity Slip Condition. Coatings 2021, 11, 1009. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Nasir, S.; Islam, S.; Deebani, W.; Shutaywi, M. Application of Arrhenius chemical process on unsteady mixed bio-convective flows of third-grade fluids having temperature-dependent in thermo-rheological properties. Waves Random Complex Media 2022, 1–20. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Tassaddiq, A.; Islam, S.; Kumam, P. Joule heating in magnetohydrodynamic micropolar boundary layer flow past a stretching sheet with chemical reaction and microstructural slip. Case Stud. Therm. Eng. 2021, 25, 100870. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Islam, S.; Alshehri, A.; Alrabaiah, H. A comparative analysis of MHD Casson and Maxwell flows past a stretching sheet with mixed convection and chemical reaction. Waves Random Complex Media 2021, 1–16. [Google Scholar] [CrossRef]
- Awais, M.; Awan, S.E.; Rehman, S.U.; Raja, M.A.Z. Hydromagnetic Falkner-Skan fluid rheology with heat transfer properties. Therm. Sci. 2020, 24 Pt A, 339–346. [Google Scholar] [CrossRef]
- Awais, M.; Awan, S.E.; Muqaddass, N.; Rehman, S.U.; Raja, M.A.Z. Numerical and analytical approach for Sakiadis rheology of generalized polymeric material with magnetic field and heat source/sink. Therm. Sci. 2020, 24 Pt B, 1183–1194. [Google Scholar] [CrossRef]
- Awan, S.E.; Awais, M.; Qayyum, A.; Rehman, S.U.; Khan, A.; Ali, H.; Raja, M.A.Z. Numerical computing paradigms for the dynamics of squeezing rheology of third grade fluid. Therm. Sci. 2020, 24 Pt B, 4173–4182. [Google Scholar] [CrossRef]
- Malashetty, M.; Swamy, M. The onset of double diffusive convection in a viscoelastic fluid layer. J. Non-Newton. Fluid Mech. 2010, 165, 1129–1138. [Google Scholar] [CrossRef]
- Malashetty, M.; Hill, A.A.; Swamy, M. Double diffusive convection in a viscoelastic fluid-saturated porous layer using a thermal non-equilibrium model. Acta Mech. 2012, 223, 967–983. [Google Scholar] [CrossRef]
- Kumar, A.; Bhadauria, B. Double diffusive convection in a porous layer saturated with viscoelastic fluid using a thermal non-equilibrium model. Phys. Fluids 2011, 23, 054101. [Google Scholar] [CrossRef]
- Awad, F.; Sibanda, P.; Motsa, S.S. On the linear stability analysis of a Maxwell fluid with double-diffusive convection. Appl. Math. Model. 2010, 34, 3509–3517. [Google Scholar] [CrossRef]
- Wang, S.; Tan, W. Stability analysis of soret-driven double-diffusive convection of Maxwell fluid in a porous medium. Int. J. Heat Fluid Flow 2011, 32, 88–94. [Google Scholar] [CrossRef]
- Gaikwad, S.N.; Kouser, S. Double diffusive convection in a couple stress fluid saturated porous layer with internal heat source. Int. J. Heat Mass Transf. 2014, 78, 1254–1264. [Google Scholar] [CrossRef]
- Gaikwad, S.; Dhanraj, M. Onset of double diffusive convection in a Maxwell fluid saturated anisotropic porous layer with internal heat source. Spec. Top. Rev. Porous Media Int. J. 2013, 4, 359–374. [Google Scholar] [CrossRef]
- Zhao, M.; Zhao, H.; Wang, S.; Yin, C. The Onset of Double-Diffusive Convection in a Two-Layer System with a Viscoelastic Fluid-Saturated Porous Medium Under High-Frequency Vibration. J. Heat Transf. 2021, 143, 012601. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.; Thammanna, G.; Shehzad, S.; Abbasi, F.; Gorla, R. Nonlinear convection in nano Maxwell fluid with nonlinear thermal radiation: A three-dimensional study. Alex. Eng. J. 2018, 57, 1927–1935. [Google Scholar] [CrossRef]
- Rajagopal, K. A note on novel generalizations of the Maxwell fluid model. Int. J. Non-Linear Mech. 2012, 47, 72–76. [Google Scholar] [CrossRef]
- Khan, M.I.; Waqas, M.; Hayat, T.; Khan, M.I.; Alsaedi, A. Chemically reactive flow of upper-convected Maxwell fluid with Cattaneo–Christov heat flux model. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 4571–4578. [Google Scholar] [CrossRef]
- Chand, R.; Rana, G. Double diffusive convection in a layer of Maxwell viscoelastic fluid in porous medium in the presence of Soret and Dufour effects. J. Fluids 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Siddheshwar, P.; Kanchana, C. Unicellular unsteady Rayleigh–Bénard convection in Newtonian liquids and Newtonian nanoliquids occupying enclosures: New findings. Int. J. Mech. Sci. 2017, 131, 1061–1072. [Google Scholar] [CrossRef]
- Yadav, D. Thermal non-equilibrium effects on the instability mechanism in a non-Newtonian Jeffery fluid saturated porous layer. J. Porous Media 2022, 25, 1–12. [Google Scholar] [CrossRef]
- Yadav, D.; Awasthi, M.K.; Al-Siyabi, M.; Al-Nadhairi, S.; Al-Rahbi, A.; Al-Subhi, M.; Ragoju, R.; Bhattacharyya, K. Double diffusive convective motion in a reactive porous medium layer saturated by a non-Newtonian Kuvshiniski fluid. Phys. Fluids 2022, 34, 024104. [Google Scholar] [CrossRef]
- Park, H.M.; Lee, H.S. Nonlinear hydrodynamic stability of viscoelastic fluids heated from below. J. Non-Newton. Fluid Mech. 1995, 60, 1–26. [Google Scholar] [CrossRef]
- D’Hernoncourt, J.; De Wit, A.; Zebib, A. Double-diffusive instabilities of autocatalytic chemical fronts. J. Fluid Mech. 2007, 576, 445–456. [Google Scholar] [CrossRef][Green Version]
- Umavathi, J.; Yadav, D.; Mohite, M.B. Linear and nonlinear stability analyses of double-diffusive convection in a porous medium layer saturated in a Maxwell nanofluid with variable viscosity and conductivity. Elixir Mech Eng. 2015, 79, 30407–30426. [Google Scholar]
- Tan, W.; Masuoka, T. Stability analysis of a Maxwell fluid in a porous medium heated from below. Phys. Lett. A 2007, 360, 454–460. [Google Scholar] [CrossRef]
- Yadav, D. The Onset of Convective Activity in an Anisotropic Porous Medium Layer with Internal Heating and Inconsistent Gravity Effects. Rev. Cuba. Física 2020, 37, 24–33. [Google Scholar]
- Bhadauria, B.S. Double-diffusive convection in a saturated anisotropic porous layer with internal heat source. Transp. Porous Media 2012, 92, 299–320. [Google Scholar] [CrossRef]
- Yadav, D. Impact of chemical reaction on the convective heat transport in nanofluid occupying in porous enclosures: A realistic approach. Int. J. Mech. Sci. 2019, 157–158, 357–373. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Nield, D. The onset of double-diffusive nanofluid convection in a layer of a saturated porous medium. Transp. Porous Media 2010, 85, 941–951. [Google Scholar] [CrossRef]
- Nouri-Borujerdi, A.; Noghrehabadi, A.R.; Rees, D.A.S. Influence of Darcy number on the onset of convection in a porous layer with a uniform heat source. Int. J. Therm. Sci. 2008, 47, 1020–1025. [Google Scholar] [CrossRef]
- Chand, R.; Yadav, D.; Rana, G. Electrothermo convection in a horizontal layer of rotating nanofluid. Int. J. Nanoparticles 2015, 8, 241–261. [Google Scholar] [CrossRef]
- Rana, G.C.; Chand, R.; Yadav, D. The onset of electrohydrodynamic instability of an elastico-viscous Walters’ (model B’) dielectric fluid layer. FME Trans. 2015, 43, 154–160. [Google Scholar] [CrossRef]
- Chand, R.; Rana, G.; Yadav, D. Thermal instability in a layer of couple stress nanofluid saturated porous medium. J. Theor. Appl. Mech. 2017, 47, 69–84. [Google Scholar] [CrossRef]
- Yadav, D.; Wakif, A.; Boulahia, Z.; Sehaqui, R. Numerical examination of the thermo-electro-hydrodynamic convection in a horizontal dielectric nanofluid layer using the power series method. J. Nanofluids 2019, 8, 117–131. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The onset of convection in a horizontal nanofluid layer of finite depth. Eur. J. Mech.—B/Fluids 2010, 29, 217–223. [Google Scholar] [CrossRef]
- Nield, D.; Kuznetsov, A. The onset of convection in a horizontal nanofluid layer of finite depth: A revised model. Int. J. Heat Mass Transf. 2014, 77, 915–918. [Google Scholar] [CrossRef]
- Motsa, S. On the onset of convection in a porous layer in the presence of Dufour and Soret effects. SAMSA J. Pure Appl. Math. 2008, 3, 58–65. [Google Scholar]
- Nield, D.A.; Kuznetsov, A.V. The effect of vertical throughflow on the onset of convection in a porous medium in a rectangular box. Transp. Porous Media 2011, 90, 993–1000. [Google Scholar] [CrossRef]
- Horton, C.; Rogers, F., Jr. Convection currents in a porous medium. J. Appl. Phys. 1945, 16, 367–370. [Google Scholar] [CrossRef]
- Katto, Y.; Masuoka, T. Criterion for the onset of convective flow in a fluid in a porous medium. Int. J. Heat Mass Transf. 1967, 10, 297–309. [Google Scholar] [CrossRef]
- Umavathi, J.C.; Sheremet, M.A.; Ojjela, O.; Reddy, G.J. The onset of double-diffusive convection in a nanofluid saturated porous layer: Cross-diffusion effects. Eur. J. Mech.—B/Fluids 2017, 65, 70–87. [Google Scholar] [CrossRef]
- Yadav, D.; Wang, J. Convective heat transport in a heat generating porous layer saturated by a non-Newtonian nanofluid. Heat Transf. Eng. 2019, 40, 1363–1382. [Google Scholar] [CrossRef]
- Narayana, M.; Sibanda, P.; Motsa, S.; Lakshmi-Narayana, P. Linear and nonlinear stability analysis of binary Maxwell fluid convection in a porous medium. Heat Mass Transf. 2012, 48, 863–874. [Google Scholar] [CrossRef]
- Malashetty, M.; Biradar, B.S. The onset of double diffusive convection in a binary Maxwell fluid saturated porous layer with cross-diffusion effects. Phys. Fluids 2011, 23, 064109. [Google Scholar] [CrossRef]
- Serkitjis, M. Natural convection in a superposed air and porous layer when heated from below. Proc. Int. Build. Perform. Simul. Assoc. Build. Simul. 1997, 5, 129–136. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).