Characterization of Commercial Gas Diffusion Layers (GDL) by Liquid Extrusion Porometry (LEP) and Gas Liquid Displacement Porometry (GLDP)
Abstract
:1. Introduction
2. Materials and Methods
2.1. GDLs
2.2. Gas Liquid Displacement Porometry (GLDP) Method
2.3. Liquid Extrusion Porometry (LEP) Method
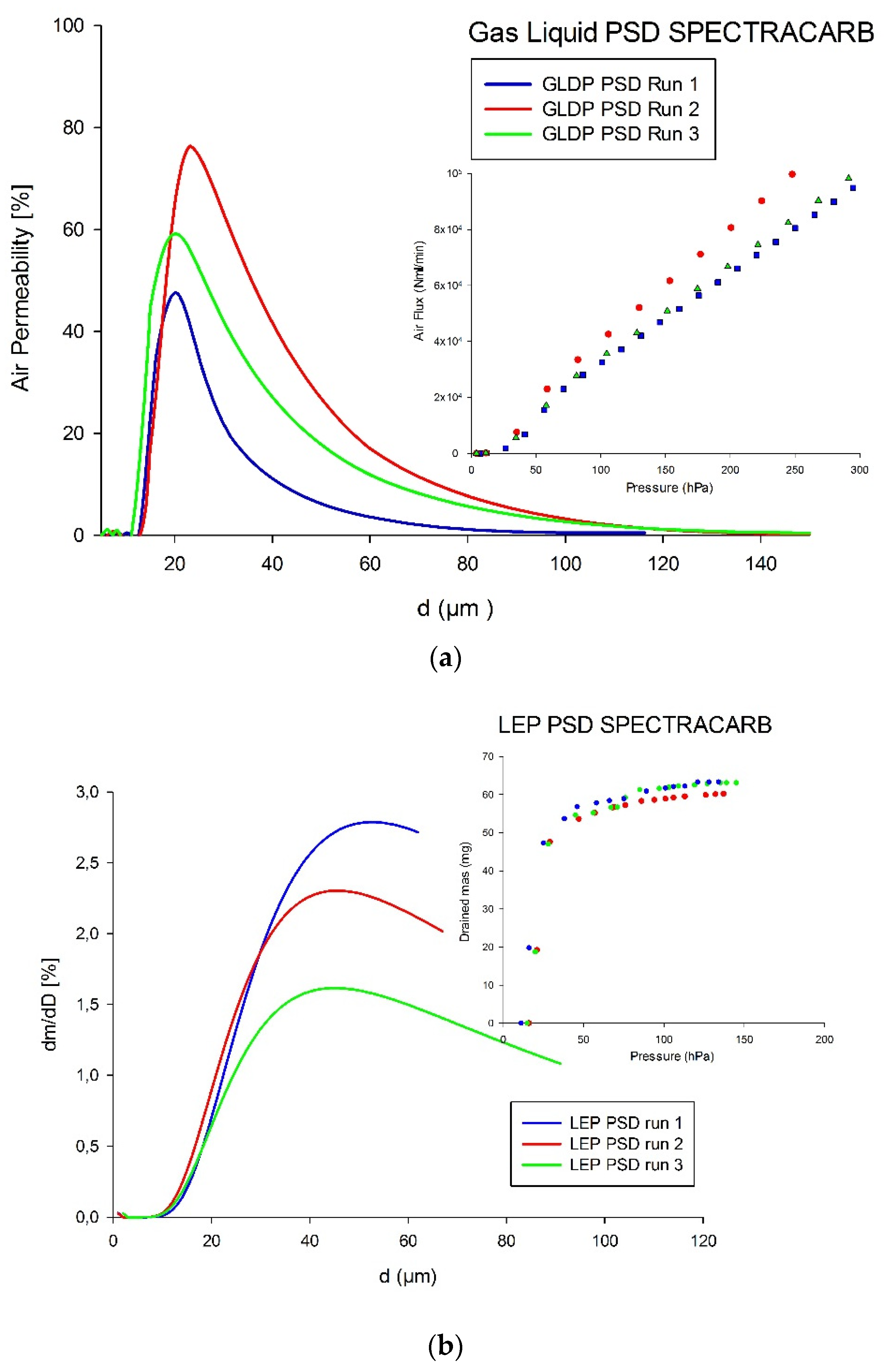
3. Results and Discussion
3.1. Flux vs. Pressure for GLDP Technique
3.2. Drained Mass vs. Capillary Pressure for LEP Technique
3.3. Comparison of Pore-Size Distributions (PSDs)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Δm | Differential mass (mg) |
| Δt | Differential time (s) |
| Δd | Differential pore diameter (m) |
| CN | Cellulose nitrate |
| CFP | Capillary flow porometry |
| d | Pore diameter (m) |
| davg | Mean pore diameter (m) |
| dmod | More frequent pore diameter (m) |
| DMFC | Direct methanol fuel cell |
| FC | Fuel Cell |
| GLDP | Gas-liquid displacement porometry |
| HgP | Mercury porometry |
| h | Distance between the liquid reservoir level and sample surface (LEP porometry) |
| IFTS | Institut de la Filtration et des Techniques Séparatives |
| LEP | Liquid extrusion porometry |
| m | Drained mass (mg) |
| MEA | Membrane electrode assembly |
| MPS | Macroporous substrate |
| MPL | Microporous layer |
| MF | Micro filtration |
| PF | Particle filtration |
| PEMFC | Polymer electrolyte membrane fuel cells |
| PG | Gas pressure (Pa) |
| PAtm | Atmospheric pressure (Pa) |
| Pc | Capillary pressure (Pa) |
| PNS | Pore network simulation |
| PSD | Pore size distribution |
| SEM | Scanning electron microscope |
| TSD | Throat pore size distribution |
| UF | Ultrafiltration |
| γ | Surface tension of the fluid pairs (mN/m) |
References
- IEA. World Energy Outlook 2014; International Energy Agency: Paris, France, 2014. [Google Scholar]
- Wilberforce, T.; Alaswad, A.; Palumbo, A.; Dassisti, M.; Olabi, A.G. Advances in stationary and portable fuel cell applications. Int. J. Hydrogen Energy 2016, 41, 16509–16522. [Google Scholar] [CrossRef] [Green Version]
- Dekel, D.R. Review of cell performance in anion exchange membrane fuel cells. J. Power Sources 2018, 375, 158–169. [Google Scholar] [CrossRef]
- Islam, M.R.; Shabani, B.; Rosengarten, G. Nanofluids to improve the performance of pem fuel cell cooling systems: A theoretical approach. Appl. Energy 2016, 178, 660–671. [Google Scholar] [CrossRef]
- Shabani, B.; Andrews, J.; Subic, A.; Paul, B. Novel concept of long-haul trucks powered by hydrogen fuel cells. In Proceedings of the FISITA 2012 World Automotive Congress; Springer: Berlin/Heidelberg, Germany, 2013; pp. 823–834. [Google Scholar]
- Panagopoulos, P.; Andrews, J.; Shabani, B. Towards a sustainable strategy for road transportation in Australia: The potential contribution of hydrogen. Renew. Sustain. Energy Rev. 2015, 52, 24–34. [Google Scholar]
- Frischauf, N. 5—hydrogen-fueled spacecraft and other space applications of hydrogen. In Compendium of Hydrogen Energy; Basile, A., Veziroglu, T.N., Eds.; Woodhead Publishing: Oxford, UK, 2016; pp. 87–107. [Google Scholar]
- Nguyen, H.Q.; Aris, A.M.; Shabani, B. Pem fuel cell heat recovery for preheating inlet air in standalone solar-hydrogen systems for telecommunication applications: An exergy analysis. Int. J. Hydrogen Energy 2016, 41, 2987–3003. [Google Scholar] [CrossRef]
- Aris, A.; Shabani, B. Sustainable power supply solutions for off-grid base stations. Energies 2015, 8, 10904–10941. [Google Scholar] [CrossRef] [Green Version]
- Shabani, B.; Andrews, J. Standalone solar-hydrogen systems powering fire contingency networks. Int. J. Hydrogen Energy 2015, 40, 5509–5517. [Google Scholar] [CrossRef]
- Paul, B.; Andrews, J. Optimal coupling of PV arrays to PEM electrolysers in solar hydrogen systems for remote area power supply. Int. J. Hydrogen Energy 2008, 33, 490–498. [Google Scholar] [CrossRef]
- Shabani, B. Solar-Hydrogen Combined Heat and Power Systems for Remote Area Power Supply. Ph.D. Thesis, School of Aerospace, Mechanical and Manufacturing Engineering, RMIT University, Melbourne, Australia, 2010. [Google Scholar]
- Assaf, J.; Shabani, B. Experimental study of a novel hybrid solar-thermal/pv-hydrogen system: Towards 100% renewable heat and power supply to standalone applications. Energy 2018, 157, 862–876. [Google Scholar] [CrossRef]
- Assaf, J.; Shabani, B. Multi-objective sizing optimisation of a solar-thermal system integrated with a solar-hydrogen combined heat and power system, using genetic algorithm. Energy Convers. Manag. 2018, 164, 518–532. [Google Scholar] [CrossRef]
- Omrani, R.; Shabani, B. Review of gas diffusion layer for proton exchange membrane-based technologies with a focus on unitised regenerative fuel cells. Int. J. Hydrogen Energy 2019, 44, 3834–3860. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Zamel, N.; Li, X. Transient analysis of carbon monoxide poisoning and oxygen bleeding in a PEM fuel cell anode catalyst layer. Int. J. Hydrogen Energy 2008, 33, 1335–1344. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, K.S.; Mishler, J.; Cho, S.C.; Adroher, X.C. A review of polymer electrolyte membrane fuel cells: Technology, applications, and needs on fundamental research. Appl. Energy 2011, 88, 981–1007. [Google Scholar] [CrossRef] [Green Version]
- Morgan, J.M.; Datta, R. Understanding the gas diffusion layer in proton exchange membrane fuel cells. I. How its structural characteristics affect diffusion and performance. J. Power Sources 2014, 251, 269–278. [Google Scholar] [CrossRef]
- Chan, C.; Zamel, N.; Li, X.; Shen, J. Experimental measurement of effective diffusion coefficient of gas diffusion layer/microporous layer in PEM fuel cells. Electrochim. Acta 2012, 65, 13–21. [Google Scholar] [CrossRef] [Green Version]
- Shahgaldi, S.; Zhao, J.; Alaefour, I.; Li, X. Investigation of catalytic vs reactant transport effect of catalyst layers on proton exchange membrane fuel cell performance. Fuel 2017, 208, 321–328. [Google Scholar] [CrossRef]
- Majlan, E.H.; Rohendi, D.; Daud, W.R.W.; Husaini, T.; Haque, M.A. Electrode for proton exchange membrane fuel cells: A review. Renew. Sustain. Energy Rev. 2018, 89, 117–134. [Google Scholar] [CrossRef]
- Ozden, A.; Shahgaldi, S.; Li, X.; Hamdullahpur, F. A review of gas diffusion layers for proton exchange membrane fuel cells—With a focus on characteristics, characterization techniques, materials and designs. Prog. Energy Combust. Sci. 2019, 74, 50–102. [Google Scholar] [CrossRef]
- Bresciani, F.; Rabissi, C.; Zago, M.; Marchesi, R.; Casalegno, A. On the effect of gas diffusion layers hydrophobicity on direct methanol fuel cell performance and degradation. J. Power Sources 2015, 273, 680–687. [Google Scholar] [CrossRef]
- Barbir, F. Chapter four—Main cell components, material properties, and processes. In Pem Fuel Cells, 2nd ed.; Barbir, F., Ed.; Academic Press: Boston, MA, USA, 2013; pp. 73–117. [Google Scholar]
- Jayakumar, A.; Sethu, S.; Ramos, M.; Robertson, J.; Al-Jumaily, A. A technical review on gas diffusion, mechanism and medium of pem fuel cell. Ionics 2014, 21, 1–18. [Google Scholar] [CrossRef]
- Cindrella, L.; Kannan, A.M.; Lin, J.F.; Saminathan, K.; Ho, Y.; Lin, C.W.; Wertz, J. Gas diffusion layer for proton exchange membrane fuel cellsda review. J. Power Sources 2009, 194, 146–160. [Google Scholar] [CrossRef]
- Gostick, J.T.; Ioannidis, M.A.; Fowler, M.W.; Pritzker, M.D. Wettability and capillary behavior of fibrous gas diffusion media for polymer electrolyte membrane fuel cells. J. Power Sources 2009, 194, 433–444. [Google Scholar] [CrossRef]
- Park, S.; Lee, J.-W.; Popov, B.N. A review of gas diffusion layer in PEM fuel cells: Materials and designs. Int. J. Hydrogen Energy 2012, 37, 5850–5865. [Google Scholar] [CrossRef]
- Arvay, A.; Yli-Rantala, E.; Liu, C.-H.; Peng, X.-H.; Koski, P.; Cindrella, L.; Kauranen, P.; Wilde, P.M.; Kannan, A.M. Characterization techniques for gas diffusion layers for proton exchange membrane fuel cells—A review. J. Power Sources 2012, 213, 317–337. [Google Scholar] [CrossRef]
- Li, Y.; Yuan, F.; Weng, R.; Xi, F.; Liu, W. Variational-principle-optimized porosity distribution in gas diffusion layer of high-temperature PEM fuel cells. Energy 2021, 235, 121350. [Google Scholar] [CrossRef]
- Xia, L.; Ni, M.; He, Q.; Xu, Q.; Cheng, C. Optimization of gas diffusion layer in high temperature PEMFC with the focuses on thickness and porosity. Appl. Energy 2021, 300, 117357. [Google Scholar] [CrossRef]
- Cheung, P.; Fairweather, J.F.; Schwartz, D.T. Probing liquid distribution in partially saturated porous materials with hydraulic admittance. Rev. Sci. Instrum. 2011, 82, 095102. [Google Scholar] [CrossRef]
- Agaesse, T.; Lamibrac, A.; Buechi, F.; Pauchet, J.; Prat, M. Validation of pore network simulations of ex-situ water distributions in a gas diffusion layer of proton exchange membrane fuel cells with X-ray tomographic images. J. Power Sources 2016, 331, 462–474. [Google Scholar] [CrossRef] [Green Version]
- Wilkinson, D.; Willemsen, J.F. Invasion percolation: A new form of percolation theory. J. Phys. A Math. Gen. 1983, 16, 3365–3376. [Google Scholar] [CrossRef]
- Joekar-Niasar, V.; Hassanizadeh, S.M.; Leijnse, A. Insights into the relationships among capillary pressure, saturation, interfacial area and relative permeability using pore-network modelling. Transp. Porous Media 2008, 74, 201–219. [Google Scholar] [CrossRef] [Green Version]
- Maalal, O.; Prat, M.; Peinador, R.; Lasseux, D. Determination of the throat size distribution of a porous medium as an inverse optimization problem combining pore network modeling and genetic and hill climbing algorithms. Phys. Rev. E 2021, 103, 023303. [Google Scholar] [CrossRef]
- Jena, A.; Gupta, K. Characterization of Pore Structure of Fuel Cell Components Containing Hydrophobic and Hydrophilic Pores. In Proceedings of the 41st Power Sources Conference, Philadelphia, PA, USA, 14–17 June 2004; Available online: http://www.pmiapp.com/publications/index.html (accessed on 8 March 2012).
- Peinador, R.I.; Calvo, J.I.; Aim, R.B. Comparison of Capillary Flow Porometry (CFP) and Liquid Extrusion Porometry (LEP) Techniques for the Characterization of Porous and Face Mask Membranes. Appl. Sci. 2020, 10, 5703. [Google Scholar] [CrossRef]
- Jena, A.; Gupta, K. Advances in pore structure evaluation by porometry. Chem. Eng. Technol. 2010, 33, 1241–1250. [Google Scholar] [CrossRef]
- Maalal, O. Porométrie Liquide-Liquide, Evaporométrie et Simulations sur Réseau de Pores. Ph.D. Thesis, Institut National Polytechnique de Toulouse (Toulouse INP), University of Toulouse, Toulouse, France, 2020. [Google Scholar]




| Manufacturer/Model |
|---|
| AVCARB MGL280, Lowell, MA, USA |
| SIGRACET 39AA, Seattle, WA, USA |
| SPECTRACARB 2050A-0850, Shelton, CT, USA |
| GDL | davg (µm) GLDP | davg (µm) LEP | dmod (µm) GLDP | dmod (µm) LEP |
|---|---|---|---|---|
| AVCARB | 19.4 ± 1.5% | 26.3 ± 3.0% | 14.2 ± 5.1% | 19.6 ± 9.2% |
| SPECTRACARB | 26.6 ± 6.9% | 47.3 ± 12.9% | 22.6 ± 4.3% | 41.0 ± 5.1% |
| SIGRACET | 30.4 ± 29% | 42.1 ± 0.9% | 22.2 ± 6.0% | 22.8 ± 12.8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peinador, R.I.; Abba, O.; Calvo, J.I. Characterization of Commercial Gas Diffusion Layers (GDL) by Liquid Extrusion Porometry (LEP) and Gas Liquid Displacement Porometry (GLDP). Membranes 2022, 12, 212. https://doi.org/10.3390/membranes12020212
Peinador RI, Abba O, Calvo JI. Characterization of Commercial Gas Diffusion Layers (GDL) by Liquid Extrusion Porometry (LEP) and Gas Liquid Displacement Porometry (GLDP). Membranes. 2022; 12(2):212. https://doi.org/10.3390/membranes12020212
Chicago/Turabian StylePeinador, René I., Oumaima Abba, and José I. Calvo. 2022. "Characterization of Commercial Gas Diffusion Layers (GDL) by Liquid Extrusion Porometry (LEP) and Gas Liquid Displacement Porometry (GLDP)" Membranes 12, no. 2: 212. https://doi.org/10.3390/membranes12020212
APA StylePeinador, R. I., Abba, O., & Calvo, J. I. (2022). Characterization of Commercial Gas Diffusion Layers (GDL) by Liquid Extrusion Porometry (LEP) and Gas Liquid Displacement Porometry (GLDP). Membranes, 12(2), 212. https://doi.org/10.3390/membranes12020212








