Solvent–Solute Interaction Effect on Permeation Flux through Forward Osmosis Membranes Investigated by Non-Equilibrium Molecular Dynamics
Abstract
:1. Introduction
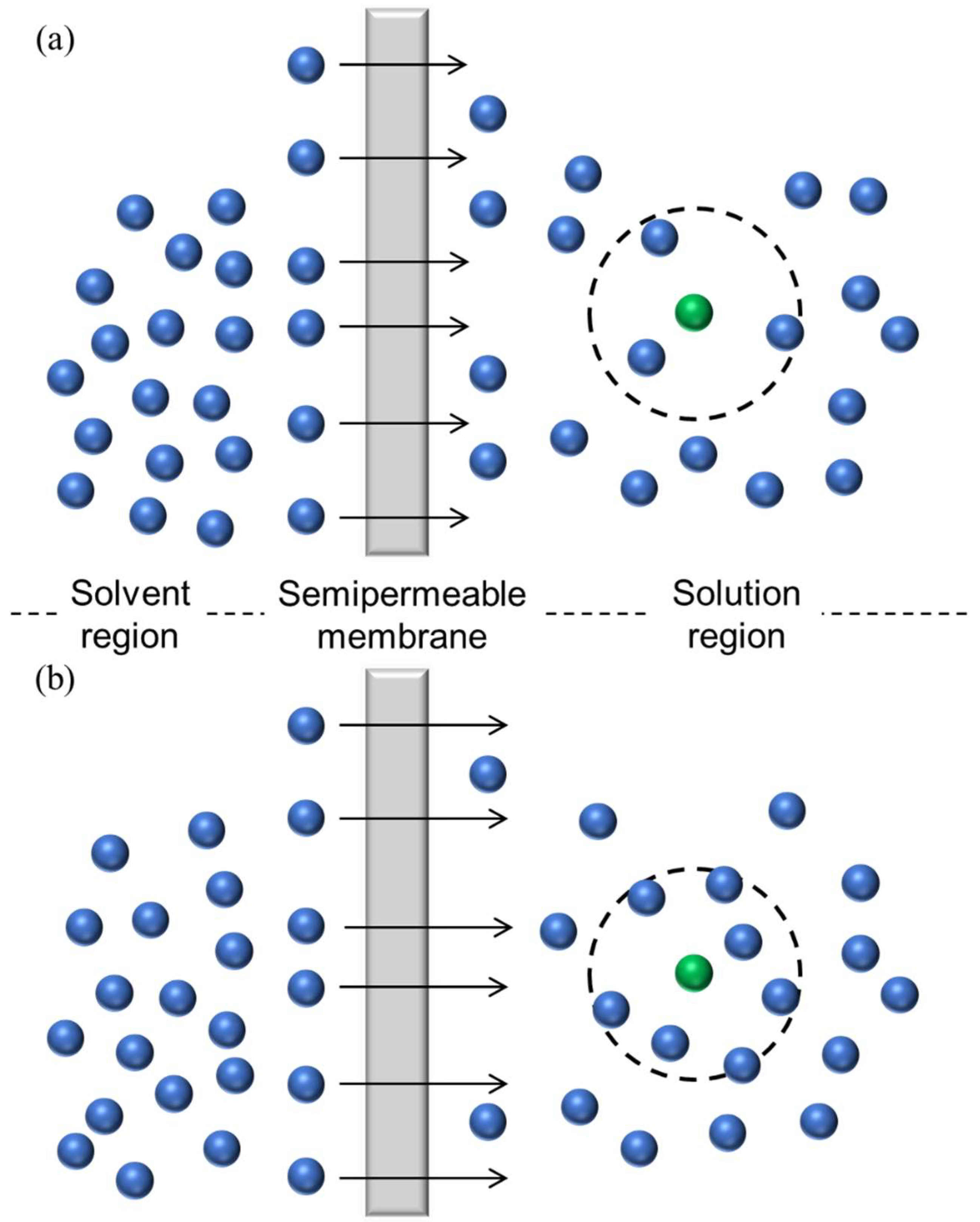
2. Calculation Method
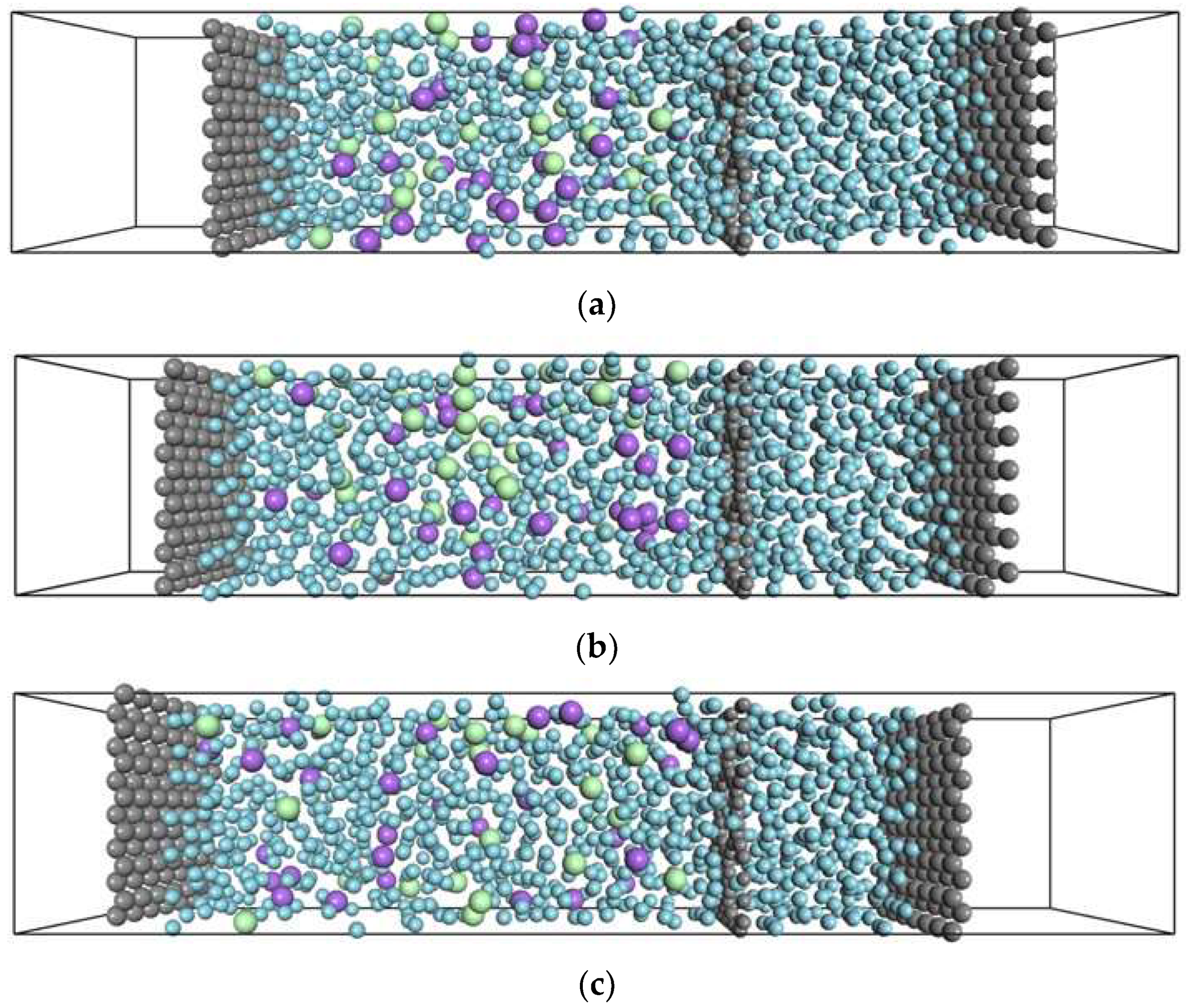
3. Results and Discussion
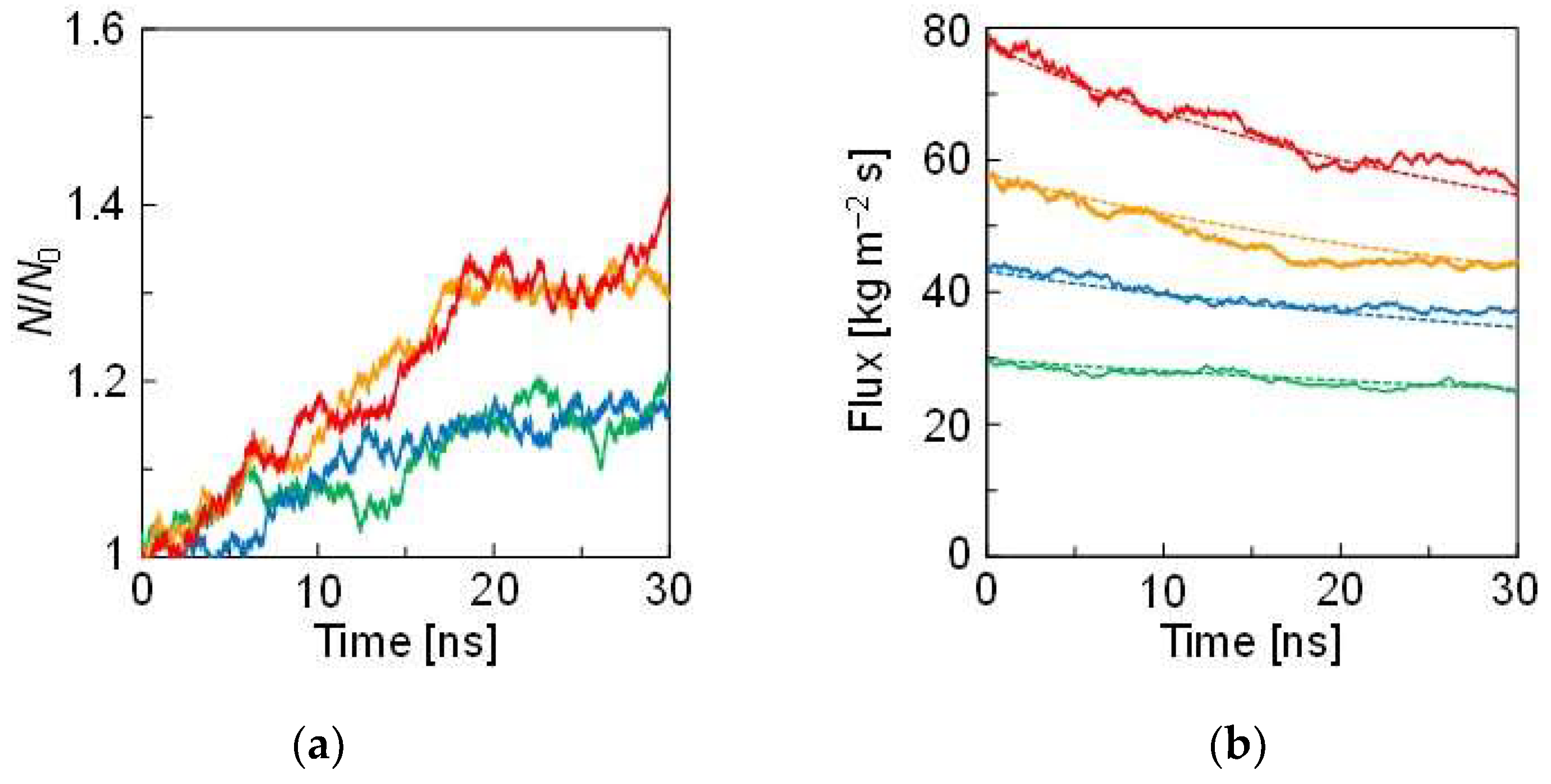
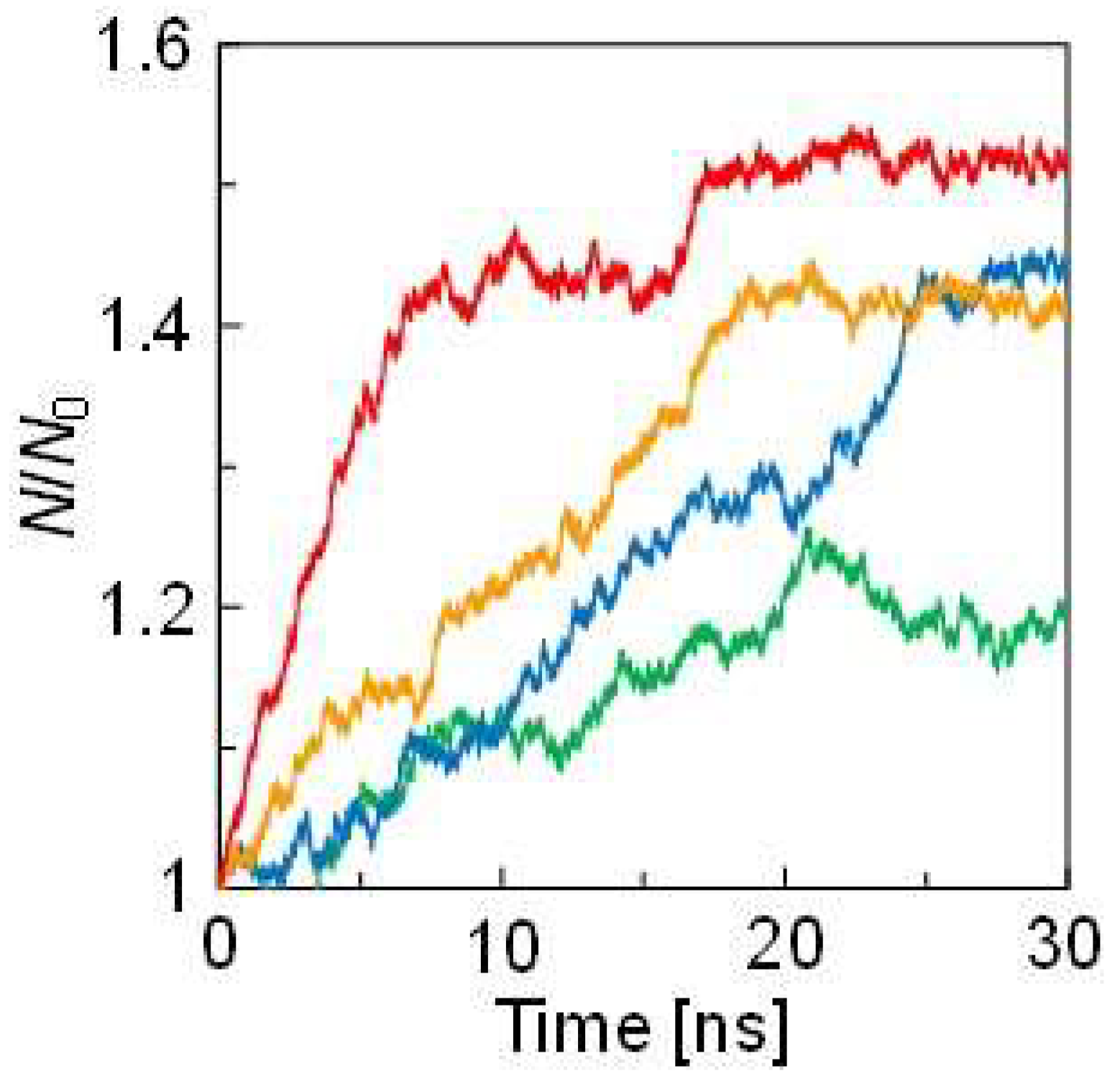
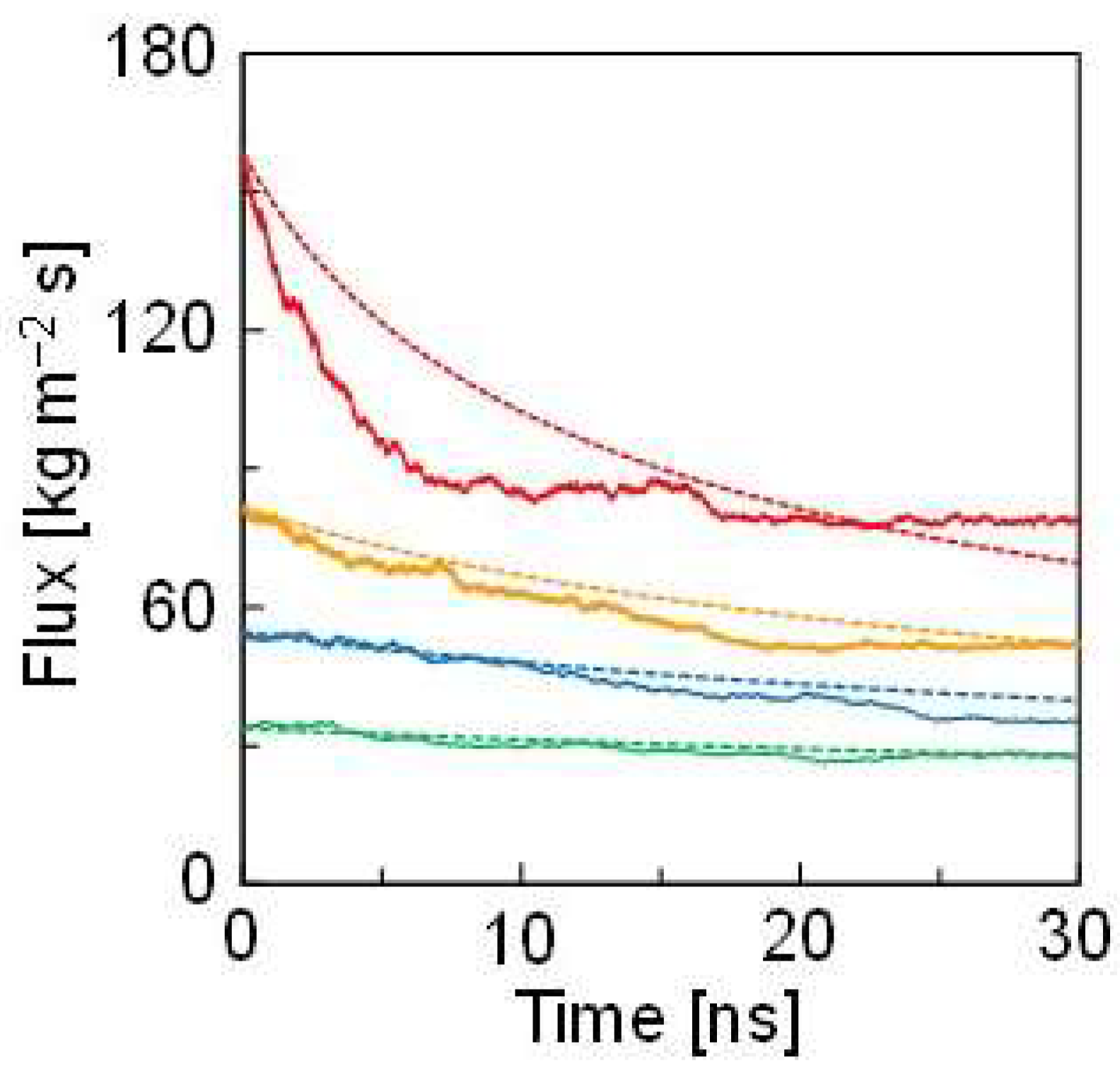
3.1. Model Validation
3.2. Effect of the Interaction between Solute and Solvent on Forward Osmosis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thakura, R.; Chakrabortty, S.; Pal, P. Treating complex industrial wastewater in a new membrane-integrated closed loop system for recovery and reuse. Clean Technol. Environ. Policy 2015, 17, 2299–2310. [Google Scholar] [CrossRef]
- Zhao, S.; Zou, L.; Tang, C.Y.; Mulcahy, D. Recent developments in forward osmosis: Opportunities and challenges. J. Membr. Sci. 2012, 396, 1–21. [Google Scholar] [CrossRef]
- Loeb, S. Production of energy from concentrated brines by pressure-retarded osmosis: I. Preliminary technical and economic correlations. J. Membr. Sci. 1976, 1, 49–63. [Google Scholar] [CrossRef]
- Lee, S.; Boo, C.; Elimelech, M.; Hong, S. Comparison of fouling behavior in forward osmosis (FO) and reverse osmosis (RO). J. Membr. Sci. 2010, 365, 34–39. [Google Scholar] [CrossRef]
- Gray, G.T.; McCutcheon, J.R.; Elimelech, M. Internal concentration polarization in forward osmosis: Role of membrane orientation. Desalination 2006, 197, 1–8. [Google Scholar] [CrossRef]
- McCutcheon, J.R.; Elimelech, M. Influence of concentrative and dilutive internal concentration polarization on flux behavior in forward osmosis. J. Membr. Sci. 2006, 284, 237–247. [Google Scholar] [CrossRef]
- Nagy, E. A general, resistance-in-series, salt- and water flux models for forward osmosis and pressure-retarded osmosis for energy generation. J. Membr. Sci. 2014, 460, 71–81. [Google Scholar] [CrossRef]
- Zhang, Y.; Nakagawa, K.; Shibuya, M.; Sasaki, K.; Takahashi, T.; Shintani, T.; Yoshioka, T.; Kamio, E.; Kondo, A.; Matsuyama, H. Molecular Dynamics Simulation Study of Polyamide Membrane Structures and RO/FO Water Permeation Properties. J. Membr. Sci. 2018, 566, 15–24. [Google Scholar] [CrossRef]
- Wang, L.; Dumont, R.S.; Dickson, J.M. Molecular dynamic simulations of pressure-driven water transport through polyamide nanofiltration membranes at different membrane densities. RSC Adv. 2016, 6, 63586–63596. [Google Scholar] [CrossRef]
- Takaba, H.; Onumata, Y.; Nakao, S. Molecular Simulation of Pressure-driven Fluid Flow in Nanoporous Membranes. J. Chem. Phys. 2007, 127, 054073. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Dumont, R.S.; Dickson, J.M. Nonequilibrium molecular dynamics simulation for studying the effect of pressure difference and periodic boundary conditions on water transport through a CNT membrane. Mol. Phys. 2017, 115, 981–990. [Google Scholar] [CrossRef]
- Strong, S.E.; Eaves, J.D. Atomistic hydrodynamics and the dynamical hydrophobic effect in porous graphene. J. Phys. Chem. Lett. 2016, 7, 1907–1912. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, M.; Lueptow, S.K.R.M. Dynamics of water and solute transport in polymeric reverse osmosis membranes via molecular dynamics simulations. J. Membr. Sci. 2016, 506, 95–108. [Google Scholar] [CrossRef] [Green Version]
- Murad, S.; Powles, J.G. A computer simulation of the classic experiment on osmosis and osmotic pressure. J. Chem. Phys. 1993, 99, 7271–7272. [Google Scholar] [CrossRef]
- Liu, B.; Law, A.-W.-K.; Zhou, K. Strained single-layer C2N membrane for efficient seawater desalination via forward osmosis: A molecular dynamics study. J. Membr. Sci. 2018, 550, 554–562. [Google Scholar] [CrossRef]
- Gogoi, A.; Anki, K.; Mondal, R.P. Multilayer Graphene Oxide Membrane in Forward Osmosis: Molecular Insights. ACS Appl. Nano Mater. 2018, 1, 4450–4460. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]


| Pair | Mw [×10−3 kg/mol] | ||
|---|---|---|---|
| SAr–SAr, MAr–MAr | 1.71 | 3.42 | SAr = 39.948 |
| Solute–solute | 1.71 | 5.13 | Na = 23.000 |
| Cl = 35.500 |
| Solution | Coordination Number | ||
|---|---|---|---|
| ε | Doubled ε | Increased Amount | |
| 3.0 wt% | 13.7 | 16.7 | 3.0 |
| 4.5 wt% | 12.8 | 16.6 | 3.8 |
| 5.9 wt% | 12.3 | 16.4 | 4.1 |
| 9.1 wt% | 11.0 | 15.4 | 4.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Higuchi, H.; Miyagawa, M.; Takaba, H. Solvent–Solute Interaction Effect on Permeation Flux through Forward Osmosis Membranes Investigated by Non-Equilibrium Molecular Dynamics. Membranes 2022, 12, 1249. https://doi.org/10.3390/membranes12121249
Higuchi H, Miyagawa M, Takaba H. Solvent–Solute Interaction Effect on Permeation Flux through Forward Osmosis Membranes Investigated by Non-Equilibrium Molecular Dynamics. Membranes. 2022; 12(12):1249. https://doi.org/10.3390/membranes12121249
Chicago/Turabian StyleHiguchi, Hayato, Masaya Miyagawa, and Hiromitsu Takaba. 2022. "Solvent–Solute Interaction Effect on Permeation Flux through Forward Osmosis Membranes Investigated by Non-Equilibrium Molecular Dynamics" Membranes 12, no. 12: 1249. https://doi.org/10.3390/membranes12121249
APA StyleHiguchi, H., Miyagawa, M., & Takaba, H. (2022). Solvent–Solute Interaction Effect on Permeation Flux through Forward Osmosis Membranes Investigated by Non-Equilibrium Molecular Dynamics. Membranes, 12(12), 1249. https://doi.org/10.3390/membranes12121249







