Application of Support Vector Machine to Obtain the Dynamic Model of Proton-Exchange Membrane Fuel Cell
Abstract
1. Introduction
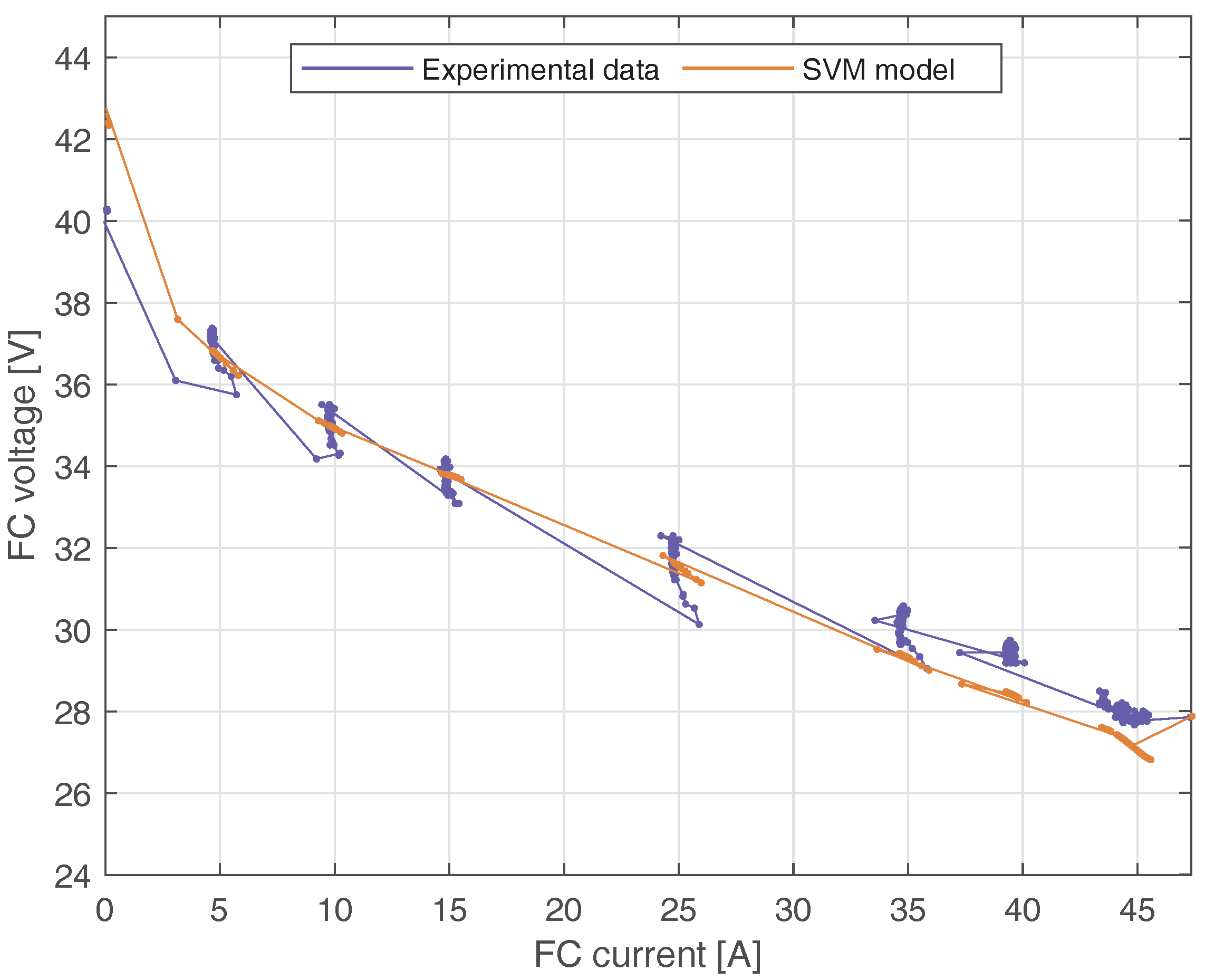
- The proposed model has been able to model the static and dynamic characteristics of the polarization curve in all operating regions. Two different FC current profiles have been used, with the aim to evaluate the generalization of the proposed model to predict the fuel cell voltage under different operating conditions.
- We provide a method to model the PEMFC based on SVM, considering a significant reduction in the number of samples used in the training phase, compared with the number of samples used in the training phase of the models proposed in [18,22]. In the same way, the number of samples used in the validation phase is much higher than the number of samples used in the validation phase of the model proposed in [21].
- Real measurements were used in the training and validation phase of the SVM model. The data correspond to a commercial Nexa fuel cell power module, with a rated power up to kW.
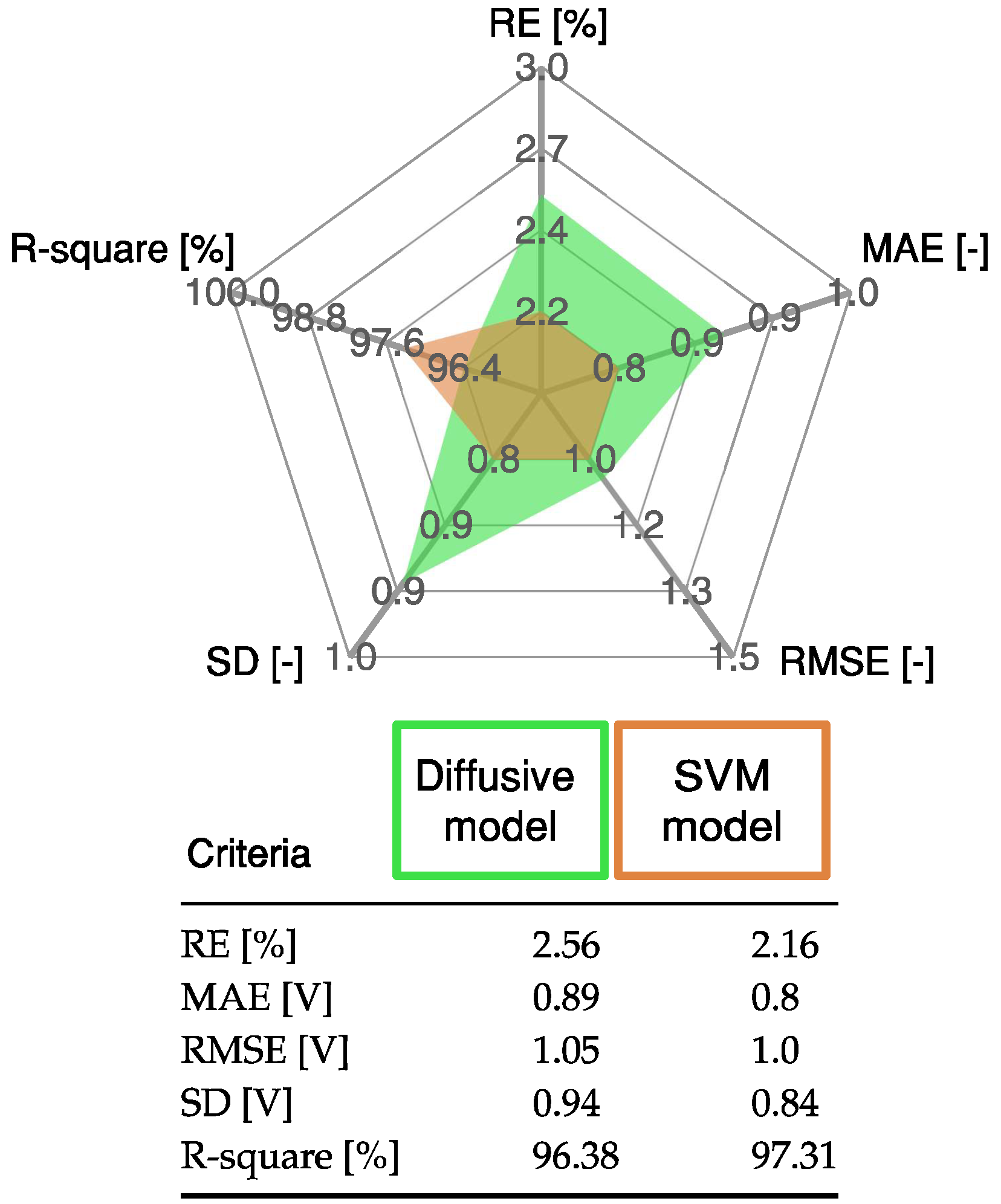
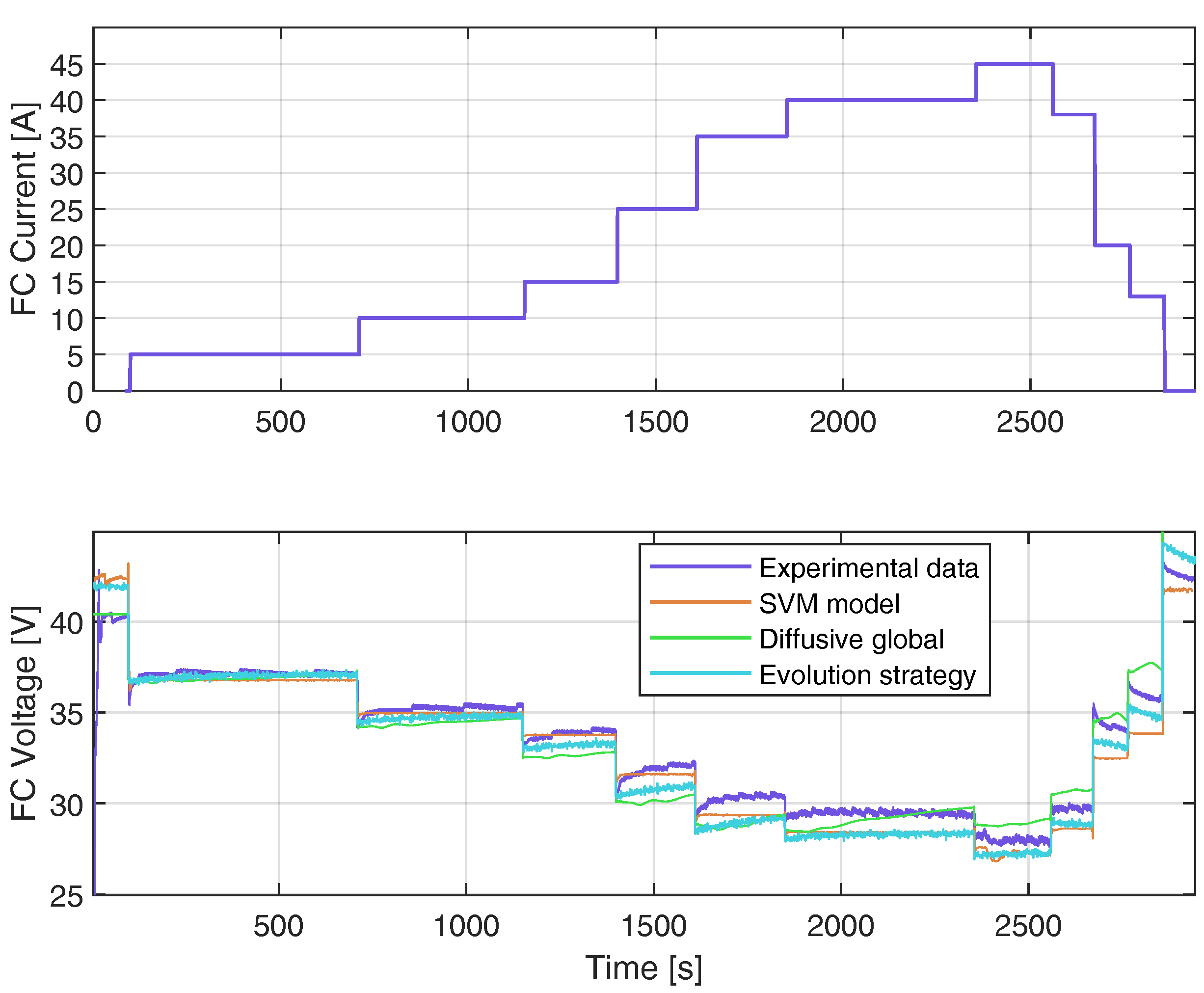
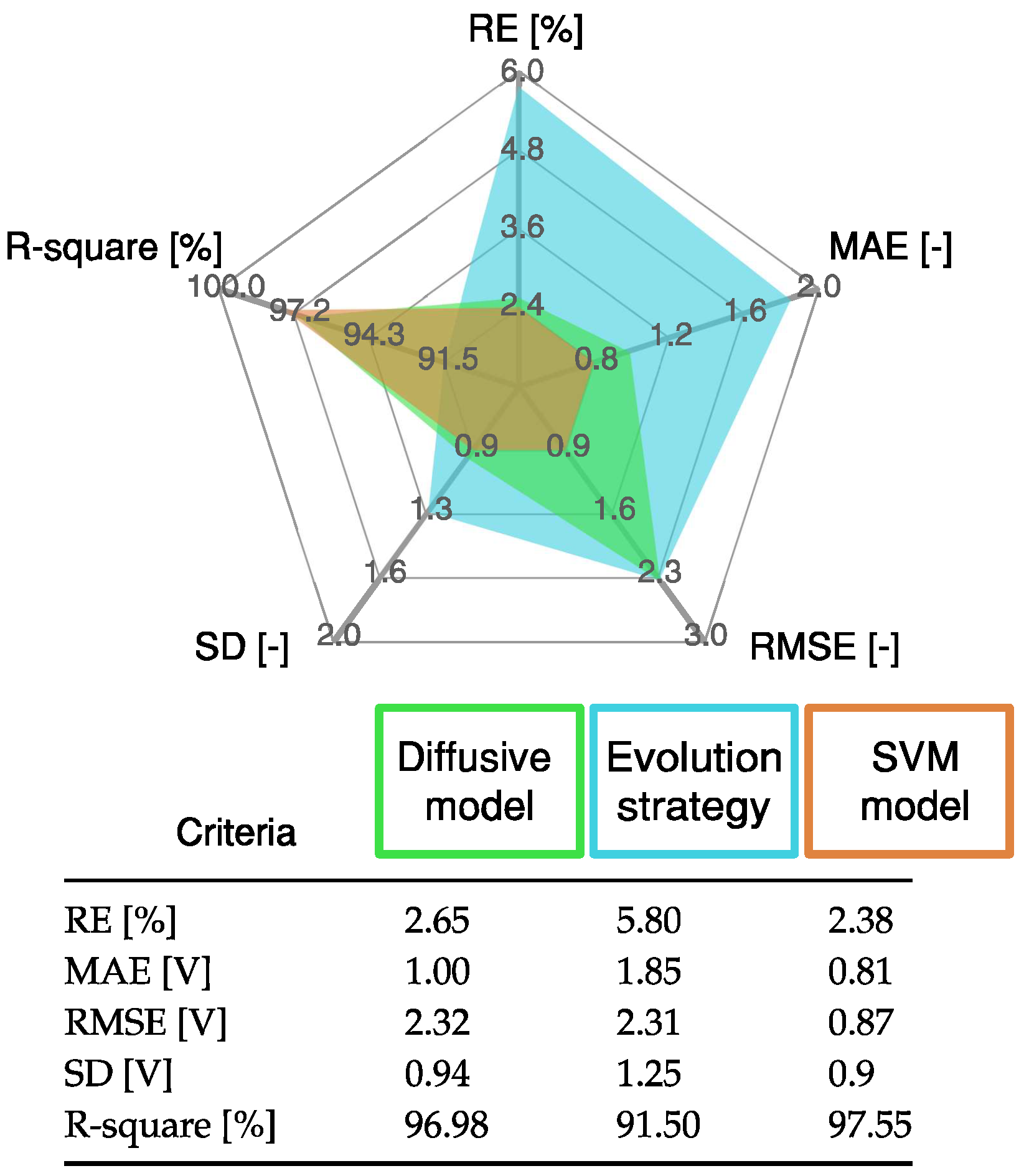
- The proposed model is accurate. The results showed a high similarity between the voltage predictions obtained by the SVM model and the actual data, obtaining root mean squared errors (RMSEs) of less than . Likewise, the root mean squared error obtained with the proposed model is lower than the evolution strategy [18] and the diffusive model [22]. Therefore, the obtained results prove the effectiveness of the proposed FC model compared with other models.
2. A Multi-Output Support Vector Machine
3. Proposed Model of the PEMFC Based on SVM
4. Experimental Results
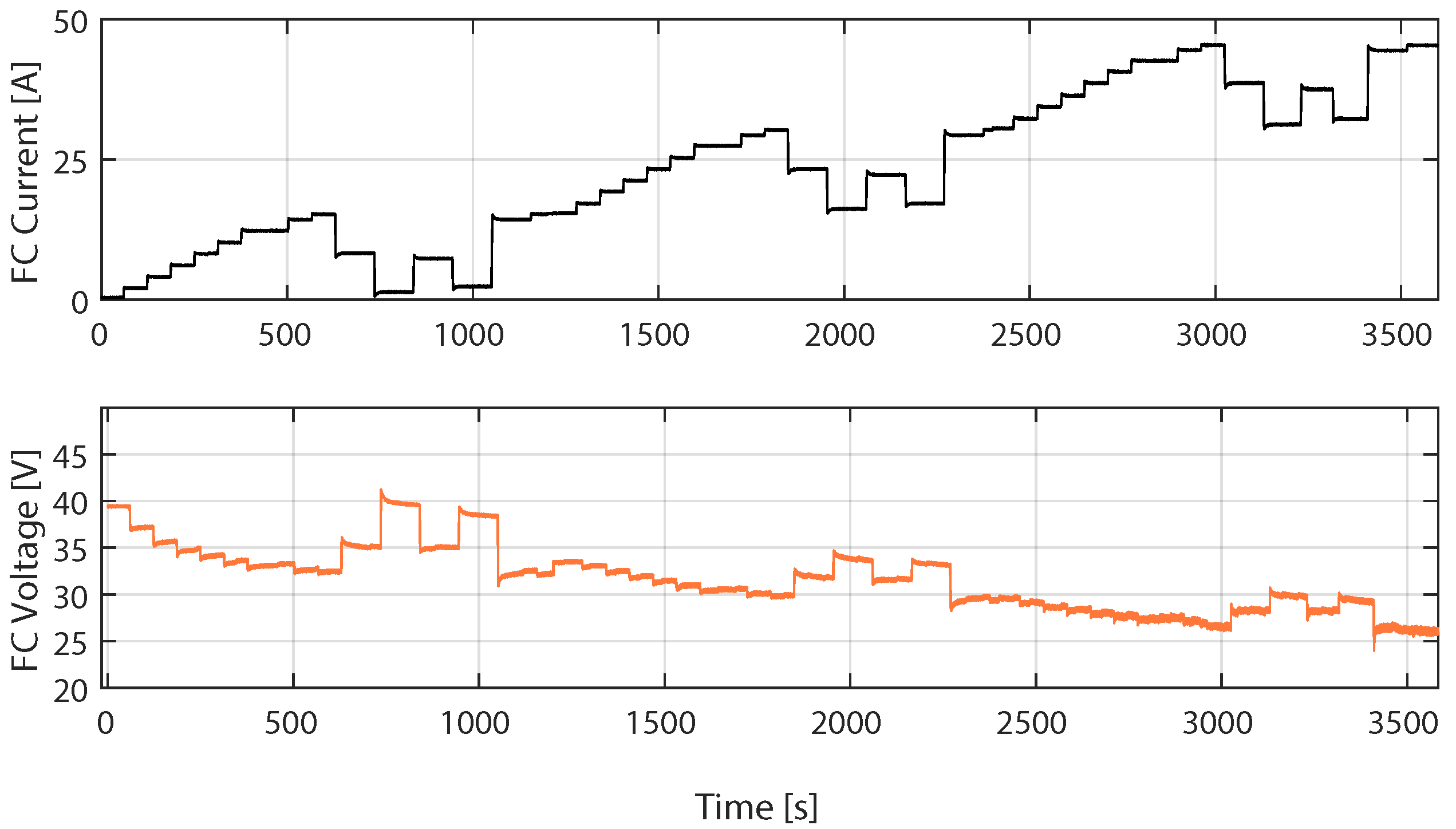
4.1. Dataset Measured from the PEMFC
4.2. Training Phase of the SVC Model with the First FC Load Current Profile
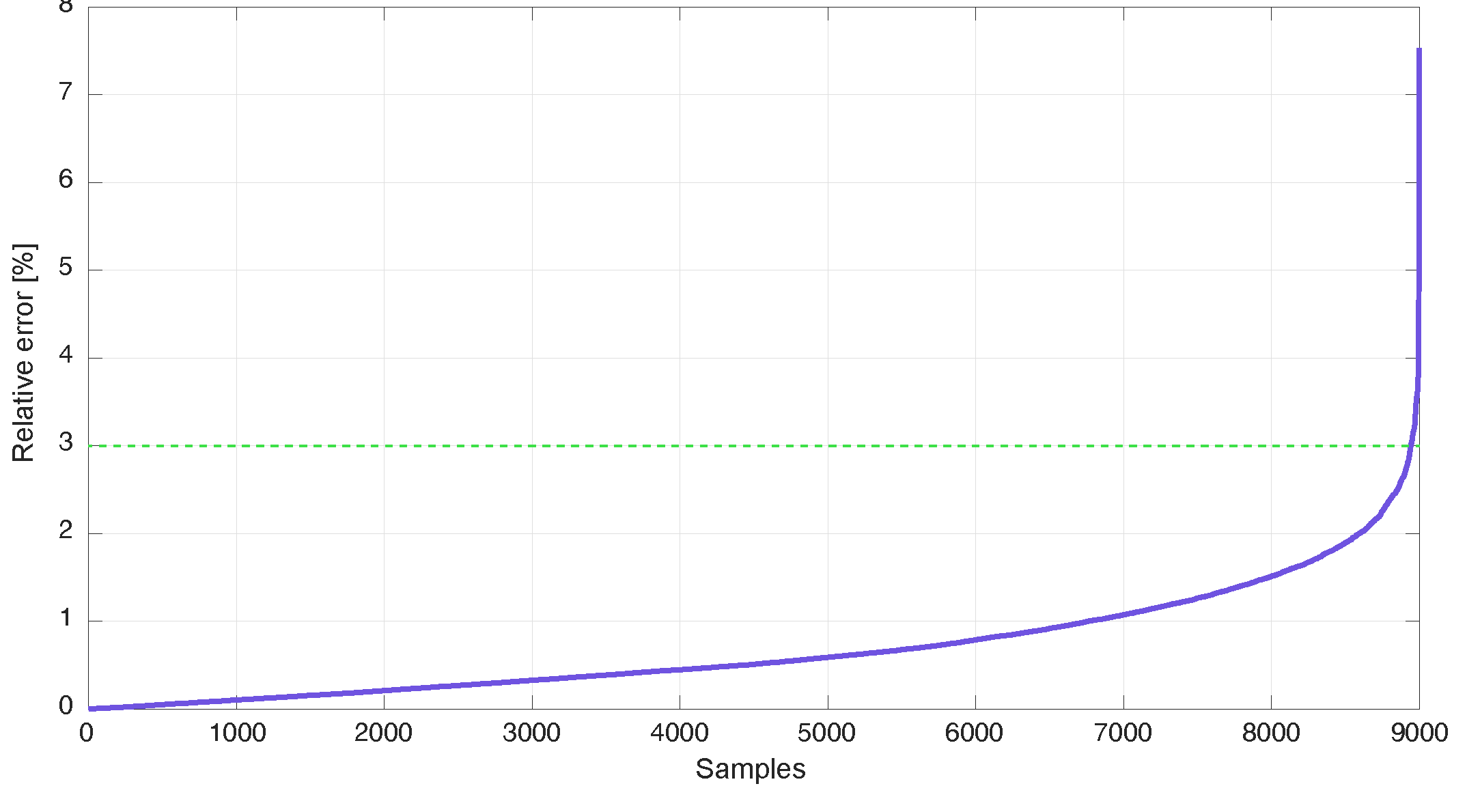
4.3. Validation of the SVM Model with the First FC Load Current Profile
4.4. Training of SVM Model with the Second FC Load Current Profile
4.5. Validation of SVM Model with the Second FC Load Current Profile
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASO | Atom search optimization |
| ARX | Autoregressive exogenous |
| ABC | Artificial bee colony |
| DG | Diffusive global |
| ES | Evolution strategy |
| FC | Fuel cell |
| MAE | Mean absolute error |
| PEMFC | Proton-exchange membrane fuel cell |
| RE | Relative error |
| RLS | Recursive least square |
| SD | Standard deviation |
| SVM | Support vector machine |
| SVR | Support vector regression |
| VSDE | Vortex search differential evolution |
Appendix A
References
- Zhang, W.; Wang, N.; Yang, S. Hybrid artificial bee colony algorithm for parameter estimation of proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2013, 38, 5796–5806. [Google Scholar] [CrossRef]
- Ding, R.; Zhang, S.; Chen, Y.; Rui, Z.; Hua, K.; Wu, Y.; Li, X.; Duan, X.; Wang, X.; Li, J.; et al. Application of Machine Learning in Optimizing Proton Exchange Membrane Fuel Cells: A Review. Energy AI 2022, 9, 100170. [Google Scholar] [CrossRef]
- Han, I.S.; Chung, C.B. A hybrid model combining a support vector machine with an empirical equation for predicting polarization curves of PEM fuel cells. Int. J. Hydrogen Energy 2017, 42, 7023–7028. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Z.; Jiang, J. Fuel cell technology for distributed generation: An overview. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; Volume 2, pp. 1613–1618. [Google Scholar]
- Menesy, A.S.; Sultan, H.M.; Selim, A.; Ashmawy, M.G.; Kamel, S. Developing and applying chaotic harris hawks optimization technique for extracting parameters of several proton exchange membrane fuel cell stacks. IEEE Access 2019, 8, 1146–1159. [Google Scholar] [CrossRef]
- Ali, M.; El-Hameed, M.; Farahat, M. Effective parameters’ identification for polymer electrolyte membrane fuel cell models using grey wolf optimizer. Renew. Energy 2017, 111, 455–462. [Google Scholar] [CrossRef]
- Mo, Z.J.; Zhu, X.J.; Wei, L.Y.; Cao, G.Y. Parameter optimization for a PEMFC model with a hybrid genetic algorithm. Int. J. Energy Res. 2006, 30, 585–597. [Google Scholar] [CrossRef]
- Menesy, A.S.; Sultan, H.M.; Korashy, A.; Banakhr, F.A.; Ashmawy, M.G.; Kamel, S. Effective parameter extraction of different polymer electrolyte membrane fuel cell stack models using a modified artificial ecosystem optimization algorithm. IEEE Access 2020, 8, 31892–31909. [Google Scholar] [CrossRef]
- Fathy, A.; Abd Elaziz, M.; Alharbi, A.G. A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew. Energy 2020, 146, 1833–1845. [Google Scholar] [CrossRef]
- Agwa, A.M.; El-Fergany, A.A.; Sarhan, G.M. Steady-state modeling of fuel cells based on atom search optimizer. Energies 2019, 12, 1884. [Google Scholar] [CrossRef]
- Louzazni, M.; Al-Dahidi, S.; Mussetta, M. Fuel Cell Characteristic Curve Approximation Using the Bézier Curve Technique. Sustainability 2020, 12, 8127. [Google Scholar] [CrossRef]
- Zhong, Z.D.; Zhu, X.J.; Cao, G.Y. Modeling a PEMFC by a support vector machine. J. Power Sources 2006, 160, 293–298. [Google Scholar] [CrossRef]
- Kheirandish, A.; Shafiabady, N.; Dahari, M.; Kazemi, M.S.; Isa, D. Modeling of commercial proton exchange membrane fuel cell using support vector machine. Int. J. Hydrogen Energy 2016, 41, 11351–11358. [Google Scholar] [CrossRef]
- Li, C.H.; Zhu, X.J.; Cao, G.Y.; Sui, S.; Hu, M.R. Identification of the Hammerstein model of a PEMFC stack based on least squares support vector machines. J. Power Sources 2008, 175, 303–316. [Google Scholar] [CrossRef]
- Pinagapani, A.K.; Mani, G.; Chandran, K.; Pandian, K.; Sawantmorye, E.; Vaghela, P. Dynamic Modeling and Validation of PEM Fuel Cell via System Identification Approach. J. Electr. Eng. Technol. 2021, 16, 2211–2220. [Google Scholar] [CrossRef]
- San Martín, I.; Ursúa, A.; Sanchis, P. Modelling of PEM fuel cell performance: Steady-state and dynamic experimental validation. Energies 2014, 7, 670–700. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H.; Shaw, S.R. Dynamic models and model validation for PEM fuel cells using electrical circuits. IEEE Trans. Energy Convers. 2005, 20, 442–451. [Google Scholar] [CrossRef]
- Restrepo, C.; Konjedic, T.; Garces, A.; Calvente, J.; Giral, R. Identification of a proton-exchange membrane fuel cell’s model parameters by means of an evolution strategy. IEEE Trans. Ind. Inform. 2014, 11, 548–559. [Google Scholar] [CrossRef]
- Marulanda-Durango, J.; Escobar-Mejía, A.; Alzate-Gómez, A.; Álvarez López, M. A Support Vector machine-Based method for parameter estimation of an electric arc furnace model. Electr. Power Syst. Res. 2021, 196, 107228. [Google Scholar] [CrossRef]
- González-Castaño, C.; Marulanda, J.; Restrepo, C.; Kouro, S.; Alzate, A.; Rodriguez, J. Hardware-in-the-Loop to Test an MPPT Technique of Solar Photovoltaic System: A Support Vector Machine Approach. Sustainability 2021, 13, 3000. [Google Scholar] [CrossRef]
- İskenderoğlu, F.C.; Baltacioğlu, M.K.; Demir, M.H.; Baldinelli, A.; Barelli, L.; Bidini, G. Comparison of support vector regression and random forest algorithms for estimating the SOFC output voltage by considering hydrogen flow rates. Int. J. Hydrogen Energy 2020, 45, 35023–35038. [Google Scholar] [CrossRef]
- Restrepo, C.; Garcia, G.; Calvente, J.; Giral, R.; Martínez-Salamero, L. Static and dynamic current–voltage modeling of a proton exchange membrane fuel cell using an input–output diffusive approach. IEEE Trans. Ind. Electron. 2015, 63, 1003–1015. [Google Scholar] [CrossRef]
- Sánchez-Fernández, M.; de Prado-Cumplido, M.; Arenas-García, J.; Pérez-Cruz, F. SVM multiregression for nonlinear channel estimation in multiple-input multiple-output systems. IEEE Trans. Signal Process. 2004, 52, 2298–2307. [Google Scholar] [CrossRef]
- Murphy, K. Machine Learning: A Probabilistic Perspective; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Bonhoff, K. The NEXATM 1200 Watt Compact Power Supply; The Fuel Cell World: Lucerne, Switzerland, 1–5 July 2002. [Google Scholar]





| FC Model Strategy | Ref. | Static Model | V-I Dynamic Model | Variables Used to Evaluate the Model | Training Complexity | Implementation Cost | Tested with a Real FC |
|---|---|---|---|---|---|---|---|
| SVM PEMFC | [12] |  |  | , | M | H |  |
| SVR | [13] |  |  | M | H |  | |
| ABC | [1] |  |  | M | M |  | |
| Hybrid SVM | [3] |  |  | , , , , | M | H |  |
| MIMO SVM-ARX | [14] |  |  | , , , , | H | H |  |
| VSDE | [9] |  |  | , , , , | M | H |  |
| ASO | [10] |  |  | , , , , | H | H |  |
| ARX-RLS | [15] |  |  | , , , , | L | H |  |
| Electrical model | [16] |  |  | , , , , |  | H |  |
| Electrical circuit | [17] |  |  | , , , , |  | H |  |
| ES | [18] |  |  | , , , , |  | H |  |
| Diffusive model | [22] |  |  | H | M |  | |
| This work | [-] |  |  | M | M |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durango, J.M.; González-Castaño, C.; Restrepo, C.; Muñoz, J. Application of Support Vector Machine to Obtain the Dynamic Model of Proton-Exchange Membrane Fuel Cell. Membranes 2022, 12, 1058. https://doi.org/10.3390/membranes12111058
Durango JM, González-Castaño C, Restrepo C, Muñoz J. Application of Support Vector Machine to Obtain the Dynamic Model of Proton-Exchange Membrane Fuel Cell. Membranes. 2022; 12(11):1058. https://doi.org/10.3390/membranes12111058
Chicago/Turabian StyleDurango, James Marulanda, Catalina González-Castaño, Carlos Restrepo, and Javier Muñoz. 2022. "Application of Support Vector Machine to Obtain the Dynamic Model of Proton-Exchange Membrane Fuel Cell" Membranes 12, no. 11: 1058. https://doi.org/10.3390/membranes12111058
APA StyleDurango, J. M., González-Castaño, C., Restrepo, C., & Muñoz, J. (2022). Application of Support Vector Machine to Obtain the Dynamic Model of Proton-Exchange Membrane Fuel Cell. Membranes, 12(11), 1058. https://doi.org/10.3390/membranes12111058












