Emerging Diamond Quantum Sensing in Bio-Membranes
Abstract
1. Introduction
2. Overview of Bio-Membranes
2.1. Structures and Compositions
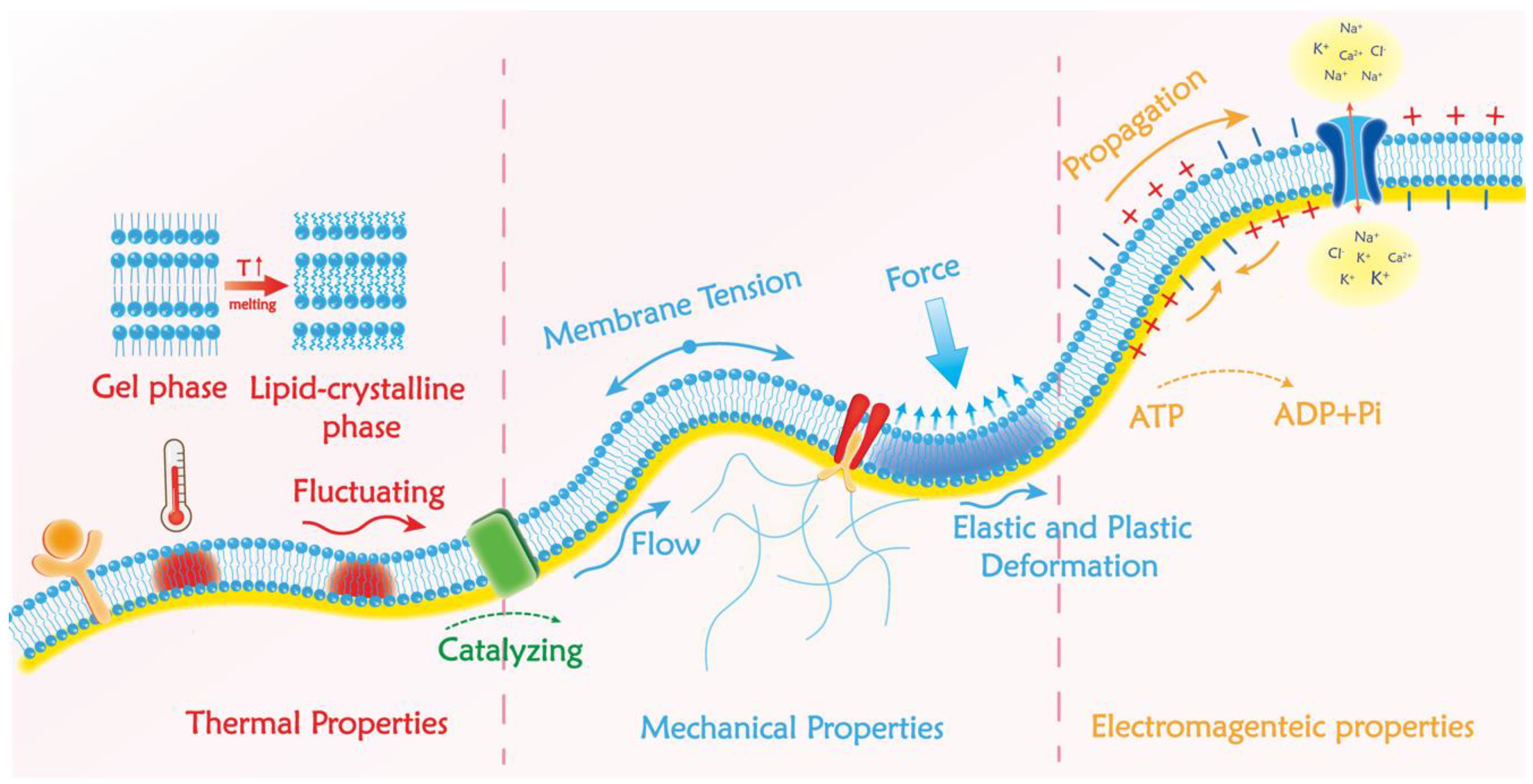
2.2. Biophysical Properties of Bio-Membranes
2.2.1. Mechanical Properties of Bio-Membranes and Available Detection Methods
2.2.2. Electronic Properties in the Bio-Membrane and Available Detection Methods
2.2.3. Thermal Properties of the Plasma Membrane and Available Detection Methods
3. The Rising Diamond Quantum Sensing
3.1. NV-Center Based Quantum Sensing
3.2. Enabled Bio-Oriented Sensing Quantities
3.2.1. Magnetic Field Sensing
3.2.2. Electric Field Sensing
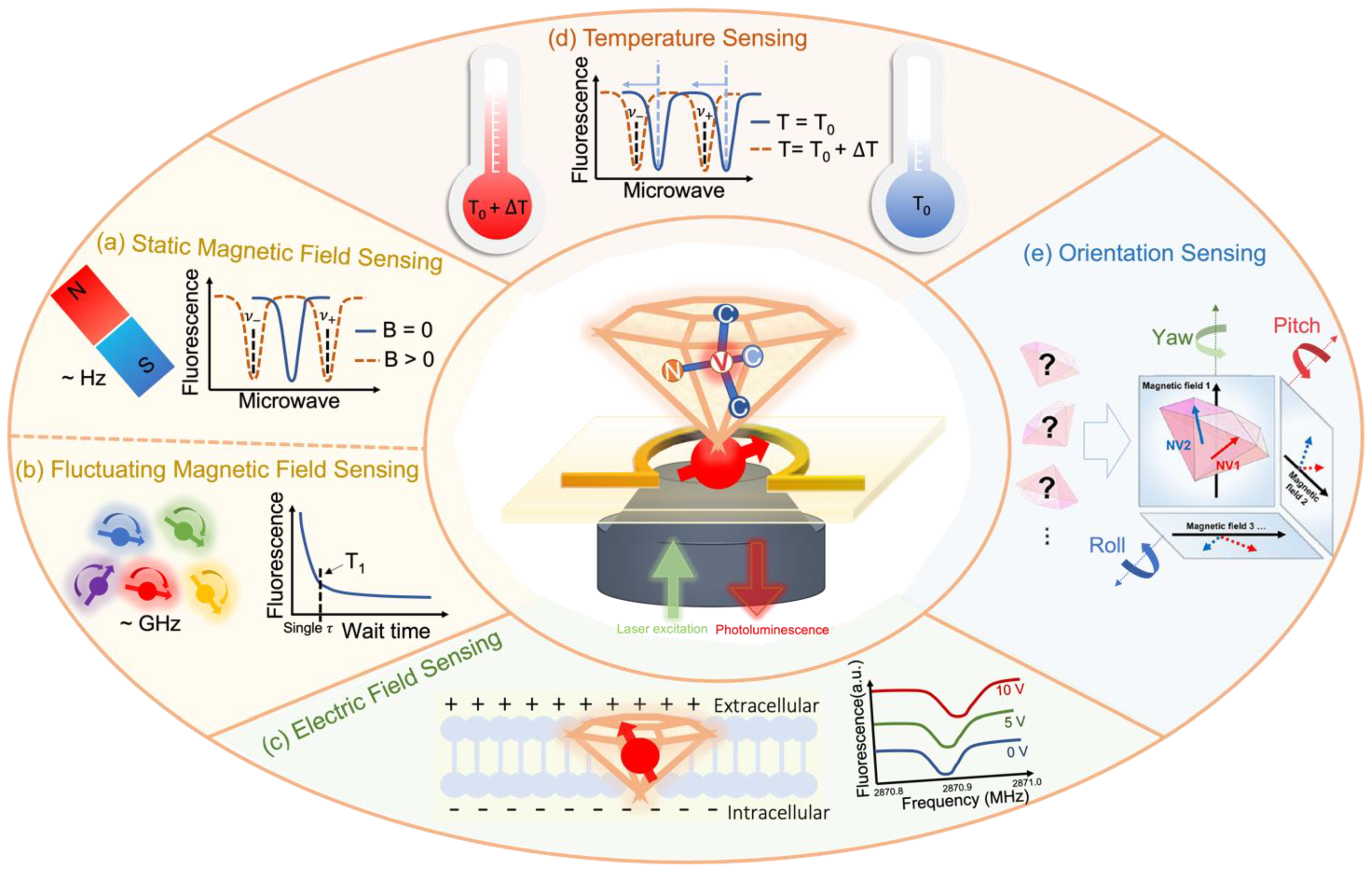
3.2.3. Temperature Sensing
3.2.4. Orientation Sensing
4. Emerging Applications of Diamond Quantum Sensing in Membrane Systems
4.1. Measurements of Physical Events in Membrane Systems
4.1.1. Membrane Structure-Related Measurements
- Lipid Bilayers
- Ion motions through ion-channels
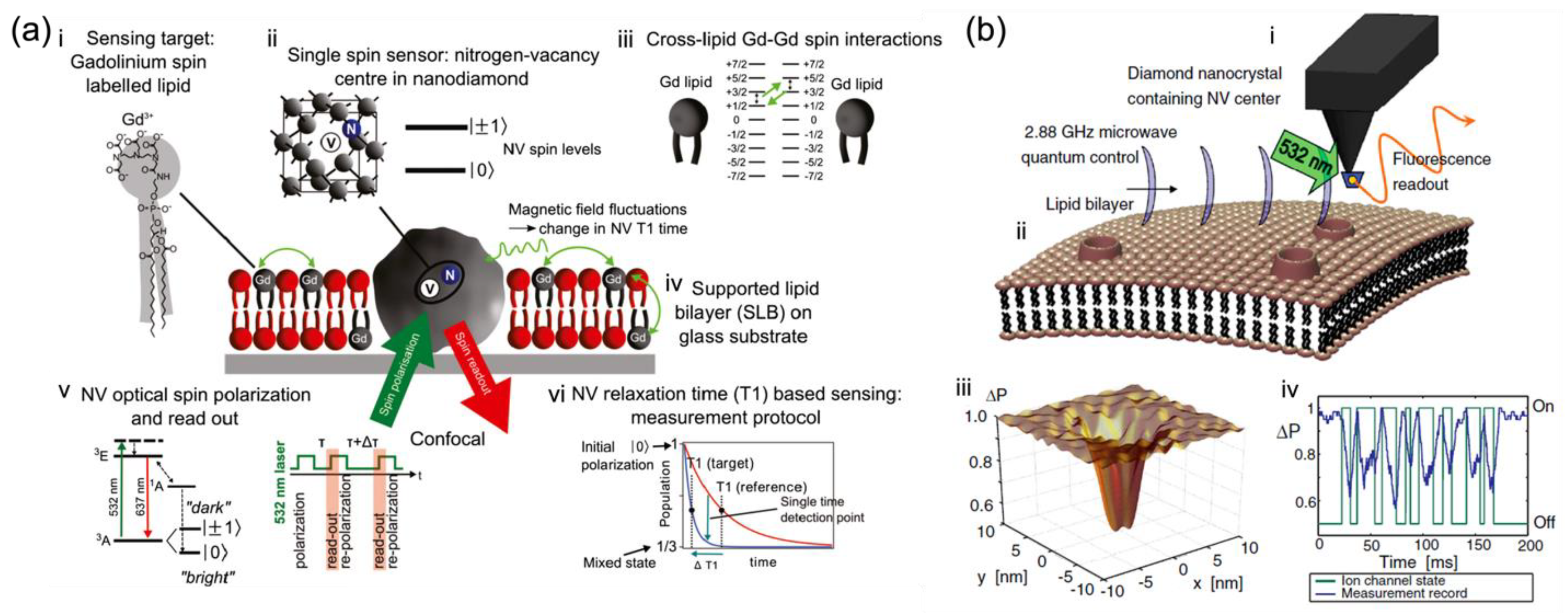
4.1.2. Membrane Motion Dynamics and Fluidity Measurement
- Membrane motion tracking
- Membrane elasticity measurement
- Lipid phase change with temperature
4.1.3. Membrane Potential and Polarity Measurement
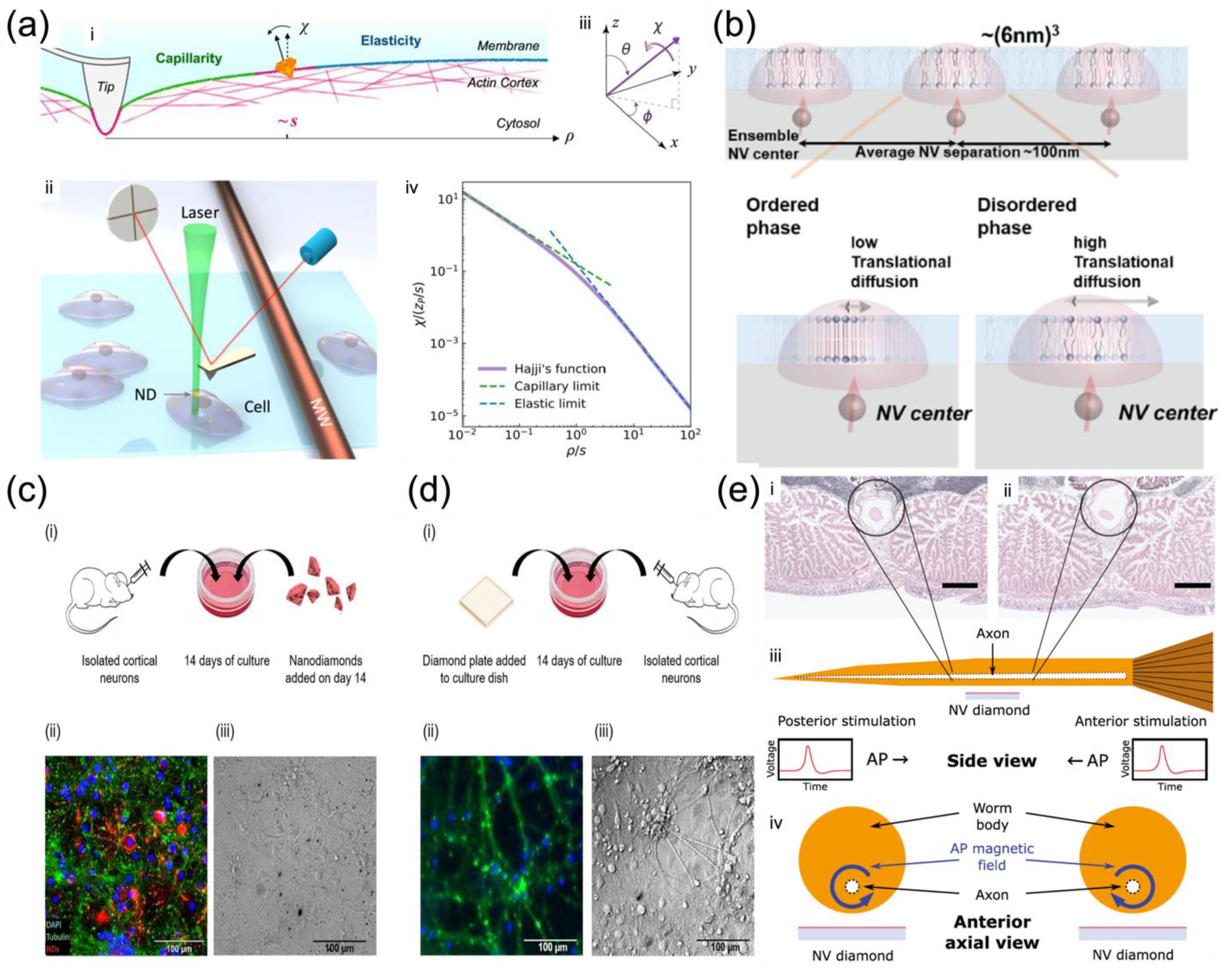
4.1.4. Nanoscale Thermometry in Membrane
4.2. Measurement of Chemical Events in Membrane Systems
5. Prospects: Limitations and Opportunities
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Gaber, B.P.; Easwaran, K.R.K. Biomembrane Structure and Functions—The State of the Art; Adenine Press: New York, NY, USA, 1992. [Google Scholar]
- Simons, K.; Vaz, W.L.C. Model systems, lipid rafts, and cell membranes. Annu. Rev. Biophys. Biomol. Struct. 2004, 33, 269–295. [Google Scholar] [CrossRef]
- Merla, C.; Liberti, M.; Apollonio, F.; Nervi, C.; d’Inzeo, G. A 3D microdosimetric study on blood cells: A permittivity model of cell membrane and stochastic electromagnetic analysis. IEEE Trans. Microw. Theory Tech. 2010, 58, 691–698. [Google Scholar] [CrossRef]
- Janshoff, A.; Steinem, C. Mechanics of lipid bilayers: What do we learn from pore-spanning membranes? Biochim. Biophys. Acta. Mol. Cell. Res. 2015, 1853, 2977–2983. [Google Scholar] [CrossRef] [PubMed]
- Itel, F.; Al-Samir, S.; Öberg, F.; Chami, M.; Kumar, M.; Supuran, C.T.; Endeward, V. CO2 permeability of cell membranes is regulated by membrane cholesterol and protein gas channels. FASEB J. 2012, 26, 5182–5191. [Google Scholar] [CrossRef] [PubMed]
- Ranjbar-Slamloo, Y.; Fazlali, Z. Dopamine and noradrenaline in the brain; overlapping or dissociate functions? Front. Mol. Neurosci. 2020, 12, 334. [Google Scholar] [CrossRef] [PubMed]
- Abdul Kadir, L.; Stacey, M.; Barrett-Jolley, R. Emerging roles of the membrane potential: Action beyond the action potential. Front. Physiol. 2018, 9, 1661. [Google Scholar] [CrossRef]
- Deng, Q.; Liu, L.; Sharma, P. Flexoelectricity in soft materials and biological membranes. J. Mech. Phys. Solids 2014, 62, 209–227. [Google Scholar] [CrossRef]
- Pelling, A.E.; Veraitch, F.S.; Chu, C.P.K.; Mason, C.; Horton, M.A. Mechanical dynamics of single cells during early apoptosis. Cell Motil. Cytoskelet. 2009, 66, 409–422. [Google Scholar] [CrossRef] [PubMed]
- Efros, A.L.; Delehanty, J.B.; Huston, A.L.; Medintz, I.L.; Barbic, M.; Harris, T.D. Evaluating the potential of using quantum dots for monitoring electrical signals in neurons. Nature Nanotech. 2018, 13, 278–288. [Google Scholar] [CrossRef]
- Escobar, J.F.; Vaca-González, J.J.; Guevara, J.M.; Garzón-Alvarado, D.A. Effect of magnetic and electric fields on plasma membrane of single cells: A computational approach. Eng. Rep. 2020, 2, e12125. [Google Scholar] [CrossRef]
- Escobar, J.F.; Vaca-González, J.J.; Guevara, J.M.; Garzón-Alvarado, D.A. How a high-gradient magnetic field could affect cell life. Sci. Rep. 2016, 6, 37407. [Google Scholar]
- Howard, R.; Scheiner, A.; Cunningham, J.; Gatenby, R. Cytoplasmic convection currents and intracellular temperature gradients. PLoS Comput. Biol. 2019, 15, e1007372. [Google Scholar] [CrossRef] [PubMed]
- Pompeu, P.; Lourenço, P.S.; Ether, D.S.; Soares, J.; Farias, J.; Maciel, G.; Pontes, B. Protocol to measure the membrane tension and bending modulus of cells using optical tweezers and scanning electron microscopy. STAR Protoc. 2021, 2, 100283. [Google Scholar] [CrossRef] [PubMed]
- Basoli, F.; Giannitelli, S.M.; Gori, M.; Mozetic, P.; Bonfanti, A.; Trombetta, M.; Rainer, A. Biomechanical characterization at the cell scale: Present and prospects. Front. Physiol. 2018, 9, 1449. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, A.; Waghmare, D.; Dasgupta, R.; Majumder, S.K. Red blood cell membrane damage by light-induced thermal gradient under optical trap. J. Biophotonics 2018, 11, e201700222. [Google Scholar] [CrossRef]
- Zhang, T.; Pramanik, G.; Zhang, K.; Gulka, M.; Wang, L.; Jing, J.; Chu, Z. Toward quantitative bio-sensing with nitrogen–vacancy center in diamond. ACS Sens. 2021, 6, 2077–2107. [Google Scholar] [CrossRef]
- Schirhagl, R.; Chang, K.; Loretz, M.; Degen, C.L. Nitrogen-vacancy centers in diamond: Nanoscale sensors for physics and biology. Annu. Rev. Phys. Chem. 2014, 65, 83–105. [Google Scholar] [CrossRef]
- Neumann, P.; Jakobi, I.; Dolde, F.; Burk, C.; Reuter, R.; Waldherr, G.; Wrachtrup, J. High-precision nanoscale temperature sensing using single defects in diamond. Nano Lett. 2013, 13, 2738–2742. [Google Scholar] [CrossRef]
- Fujiwara, M.; Shikano, Y. Diamond quantum thermometry: From foundations to applications. Nanotechnology 2021, 32, 482002. [Google Scholar] [CrossRef]
- Udvarhelyi, P.; Shkolnikov, V.O.; Gali, A.; Burkard, G.; Pályi, A. Spin-strain interaction in nitrogen-vacancy centers in diamond. Phys. Rev. B 2018, 98, 75201. [Google Scholar] [CrossRef]
- Reineck, P.; Capelli, M.; Lau, D.W.M.; Jeske, J.; Field, M.R.; Ohshima, T.; Gibson, B.C. Bright and photostable nitrogen-vacancy fluorescence from unprocessed detonation nanodiamond. Nanoscale 2017, 9, 497–502. [Google Scholar] [CrossRef] [PubMed]
- Yang, N.J.; Hinner, M.J. Getting across the cell membrane: An overview for small molecules, peptides, and proteins. In Site-Specific Protein Labeling, 1st ed.; Arnaud, G., Marlon, J.H., Eds.; Humana: New York, NY, USA, 2015; pp. 29–53. [Google Scholar]
- Hartman, N.C.; Groves, J.T. Signaling clusters in the cell membrane. Curr. Opin. Cell Biol. 2011, 23, 370–376. [Google Scholar] [CrossRef] [PubMed]
- Cho, W.; Stahelin, R.V. Membrane-protein interactions in cell signaling and membrane trafficking. Annu. Rev. Biophys. Biomol. Struct. 2005, 34, 119–151. [Google Scholar] [CrossRef]
- Shan, Y.; Wang, H. The structure and function of cell membranes examined by atomic force microscopy and single-molecule force spectroscopy. Chem. Soc. Rev. 2015, 44, 3617–3638. [Google Scholar] [CrossRef]
- Singer, S.J.; Nicolson, G.L. The fluid mosaic model of the structure of cell membranes: Cell membranes are viewed as two-dimensional solutions of oriented globular proteins and lipids. Science 1972, 175, 720–731. [Google Scholar] [CrossRef] [PubMed]
- Nicolson, G.L. Update of the 1972 Singer-Nicolson fluid-mosaic model of membrane structure. Discoveries 2013, 1, e3. [Google Scholar] [CrossRef][Green Version]
- Cheng, X.; Smith, J.C. Biological membrane organization and cellular signaling. Chem. Rev. 2019, 119, 5849–5880. [Google Scholar] [CrossRef]
- Peterka, D.S.; Takahashi, H.; Yuste, R. Imaging voltage in neurons. Neuron 2011, 69, 9–21. [Google Scholar] [CrossRef]
- Hübner, C.A.; Jentsch, T.J. Ion channel diseases. Hum. Mol. Genet. 2002, 11, 2435–2445. [Google Scholar] [CrossRef]
- Amin, A.S.; Tan, H.L.; Wilde, A.A. Cardiac ion channels in health and disease. Heart Rhythm 2010, 7, 117–126. [Google Scholar] [CrossRef]
- Bates, E. g36 Ion channels in development and cancer. Annu. Rev. Cell Dev. Biol. 2015, 31, 231–247. [Google Scholar] [CrossRef] [PubMed]
- Hollan, S. Membrane fluidity of blood cells. Haematologia 1996, 27, 109–127. [Google Scholar]
- Marguet, D.; Lenne, P.F.; Rigneault, H.; He, H.T. Dynamics in the plasma membrane: How to combine fluidity and order. EMBO J. 2006, 25, 3446–3457. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Nagatoishi, S.; Kuroda, D.; Suzuki, N.; Murata, T.; Tsumoto, K. Phospholipid membrane fluidity alters ligand binding activity of a G protein-coupled receptor by shifting the conformational equilibrium. Biochemistry 2019, 58, 504–508. [Google Scholar] [CrossRef] [PubMed]
- Butler, P.J.; Norwich, G.; Weinbaum, S.; Chien, S. Shear stress induces a time-and position-dependent increase in endothelial cell membrane fluidity. Am. J. Physiol. Cell Physiol. 2001, 280, C962–C969. [Google Scholar] [CrossRef]
- Los, D.A.; Murata, N. Membrane fluidity and its roles in the perception of environmental signals. Biochim. Biophys. Acta-Biomembr. 2004, 1666, 142–157. [Google Scholar] [CrossRef]
- Moeendarbary, E.; Harris, A.R. Cell mechanics: Principles, practices, and prospects. Wiley Interdiscip. Rev. Syst. Biol. Med. 2014, 6, 371–388. [Google Scholar] [CrossRef] [PubMed]
- Janmey, P.A.; McCulloch, C.A. Cell mechanics: Integrating cell responses to mechanical stimuli. Annu. Rev. Biomed. Eng. 2007, 9, 1–34. [Google Scholar] [CrossRef]
- Fletcher, D.A.; Mullins, R.D. Cell mechanics and the cytoskeleton. Nature 2010, 463, 485–492. [Google Scholar] [CrossRef]
- Rebelo, L.M.; de Sousa, J.S.; Mendes Filho, J.; Radmacher, M. Comparison of the viscoelastic properties of cells from different kidney cancer phenotypes measured with atomic force microscopy. Nanotechnology 2013, 24, 55102. [Google Scholar] [CrossRef]
- Martinac, B.; Nikolaev, Y.A.; Silvani, G.; Bavi, N.; Romanov, V.; Nakayama, Y.; Martinac, A.D.; Rohde, P.; Bavi, O.; Cox, C.D. Cell membrane mechanics and mechanosensory transduction. Curr. Top. Membr. 2020, 86, 83–141. [Google Scholar] [PubMed]
- Hochmuth, R.; Waugh, R. Erythrocyte membrane elasticity and viscosity. Annu. Rev. Physiol. 1987, 49, 209–219. [Google Scholar] [CrossRef] [PubMed]
- Pontes, B.; Monzo, P.; Gauthier, N.C. Membrane tension: A challenging but universal physical parameter in cell biology. Semin. Cell Dev. Biol. 2017, 71, 30–41. [Google Scholar] [CrossRef] [PubMed]
- Diz-Muñoz, A.; Fletcher, D.A.; Weiner, O.D. Use the force: Membrane tension as an organizer of cell shape and motility. Trends Cell Biol. 2013, 23, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Lieber, A.D.; Yehudai-Resheff, S.; Barnhart, E.L.; Theriot, J.A.; Keren, K. Membrane tension in rapidly moving cells is determined by cytoskeletal forces. Curr. Biol. 2013, 23, 1409–1417. [Google Scholar] [CrossRef]
- Yang, X.; Askarova, S.; Lee, J. Membrane biophysics and mechanics in Alzheimer’s disease. Mol. Neurobiol. 2010, 41, 138–148. [Google Scholar] [CrossRef]
- Ren, J.; Huang, H.; Liu, Y.; Zheng, X.; Zou, Q. An atomic force microscope study revealed two mechanisms in the effect of anticancer drugs on rate-dependent Young’s modulus of human prostate cancer cells. PLoS ONE 2015, 10, e0126107. [Google Scholar] [CrossRef]
- Legant, W.R.; Choi, C.K.; Miller, J.S.; Shao, L.; Gao, L.; Betzig, E.; Chen, C.S. Multidimensional traction force microscopy reveals out-of-plane rotational moments about focal adhesions. Proc. Natl. Acad. Sci. USA 2013, 110, 881–886. [Google Scholar] [CrossRef]
- Capozza, R.; Caprettini, V.; Gonano, C.A.; Bosca, A.; Moia, F.; Santoro, F.; De Angelis, F. Cell membrane disruption by vertical micro-/nanopillars: Role of membrane bending and traction forces. ACS Appl. Mater. Interface 2018, 10, 29107–29114. [Google Scholar] [CrossRef]
- Al-Rekabi, Z.; Contera, S. Multifrequency AFM reveals lipid membrane mechanical properties and the effect of cholesterol in modulating viscoelasticity. Proc. Natl. Acad. Sci. USA 2018, 115, 2658–2663. [Google Scholar] [CrossRef]
- Nussenzveig, H.M. Cell membrane biophysics with optical tweezers. Eur. Biophys. J. 2018, 47, 499–514. [Google Scholar] [CrossRef] [PubMed]
- Hosu, B.G.; Sun, M.; Marga, F.; Grandbois, M.; Forgacs, G. Eukaryotic membrane tethers revisited using magnetic tweezers. Phys. Biol. 2007, 4, 67. [Google Scholar] [CrossRef] [PubMed]
- Michels, L.; Gorelova, V.; Harnvanichvech, Y.; Borst, J.W.; Albada, B.; Weijers, D.; Sprakel, J. Complete microviscosity maps of living plant cells and tissues with a toolbox of targeting mechanoprobes. Proc. Natl. Acad. Sci. USA 2020, 117, 18110–18118. [Google Scholar] [CrossRef] [PubMed]
- Hur, S.S.; Jeong, J.H.; Ban, M.J.; Park, J.H.; Yoon, J.K.; Hwang, Y. Traction force microscopy for understanding cellular mechanotransduction. BMB Rep. 2020, 53, 74. [Google Scholar] [CrossRef] [PubMed]
- Neuman, K.C.; Nagy, A. Single-molecule force spectroscopy: Optical tweezers, magnetic tweezers and atomic force microscopy. Nat. Methods 2008, 5, 491–505. [Google Scholar] [CrossRef]
- Liu, Y.; Galior, K.; Ma, V.P.-Y.; Salaita, K. Molecular tension probes for imaging forces at the cell surface. Acc. Chem. Res. 2017, 50, 2915–2924. [Google Scholar] [CrossRef]
- Zhu, R.; Avsievich, T.; Popov, A.; Meglinski, I. Optical tweezers in studies of red blood cells. Cells 2020, 9, 545. [Google Scholar] [CrossRef]
- Colin-York, H.; Fritzsche, M. The future of traction force microscopy. Curr. Opin. Biomed. Eng. 2018, 5, 1–5. [Google Scholar] [CrossRef]
- De Vlaminck, I.; Dekker, C. Recent advances in magnetic tweezers. Annu. Rev. Biophys 2012, 41, 453–472. [Google Scholar] [CrossRef]
- Li, M.; Dang, D.; Liu, L.; Xi, N.; Wang, Y. Atomic force microscopy in characterizing cell mechanics for biomedical applications: A review. IEEE Trans. Nanobiosci. 2017, 16, 523–540. [Google Scholar] [CrossRef]
- McCormick, D.A. Membrane potential and action potential. In From Molecules to Networks, 3rd ed.; John, H.B., Ruth, H., Waxham, M.N., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 351–376. [Google Scholar]
- Wright, S.H. Generation of resting membrane potential. Adv. Physiol. Educ. 2004, 28, 139–142. [Google Scholar] [CrossRef] [PubMed]
- Sundelacruz, S.; Levin, M.; Kaplan, D.L. Role of membrane potential in the regulation of cell proliferation and differentiation. Stem Cell Rev. Rep. 2009, 5, 231–246. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, M.; Fee, D.; Barkhaus, P.E. Generation and propagation of the action potential. Handb. Clin. Neurol. 2019, 160, 3–22. [Google Scholar] [PubMed]
- Polder, H.R.; Weskamp, M.; Linz, K.; Meyer, R. Voltage-clamp and patch-clamp techniques. In Practical Methods in Cardiovascular Research, 1st ed.; Stefan, D., Friedrich, W.M., Mario, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 272–323. [Google Scholar]
- Bébarová, M. Advances in patch clamp technique: Towards higher quality and quantity. Gen. Physiol. Biophys. 2012, 31, 131–140. [Google Scholar] [CrossRef]
- Kornreich, B.G. The patch clamp technique: Principles and technical considerations. J. Vet. Cardiol. 2007, 9, 25–37. [Google Scholar] [CrossRef]
- Gao, J.; Liao, C.; Liu, S.; Xia, T.; Jiang, G. Nanotechnology: New opportunities for the development of patch-clamps. J. Nanobiotechnol. 2021, 19, 97. [Google Scholar] [CrossRef]
- Rad, M.S.; Choi, Y.; Cohen, L.B.; Baker, B.J.; Zhong, S.; Storace, D.A.; Braubach, O.R. Voltage and calcium imaging of brain activity. Biophys. J. 2017, 113, 2160–2167. [Google Scholar]
- Grienberger, C.; Konnerth, A. Imaging calcium in neurons. Neuron 2012, 73, 862–885. [Google Scholar] [CrossRef]
- Chemla, S.; Chavane, F. Voltage-sensitive dye imaging: Technique review and models. J. Physiol. Paris 2010, 104, 40–50. [Google Scholar] [CrossRef]
- Cossart, R.; Ikegaya, Y.; Yuste, R. Calcium imaging of cortical networks dynamics. Cell Calcium 2005, 37, 451–457. [Google Scholar] [CrossRef]
- Ali, F.; Kwan, A.C. Interpreting in vivo calcium signals from neuronal cell bodies, axons, and dendrites: A review. Neurophotonics 2019, 7, 11402. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Kim, C.K.; Ting, A.Y. Molecular tools for imaging and recording neuronal activity. Nat. Chem. Biol. 2019, 15, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Tajima, K.; Gershfeld, N. Phospholipid surface bilayers at the air-water interface. I. Thermodynamic properties. Biophys. J. 1985, 47, 203–209. [Google Scholar] [CrossRef]
- Gershfeld, N.L.; Murayama, M. Thermal instability of red blood cell membrane bilayers: Temperature dependence of hemolysis. J. Membr. Biol. 1988, 101, 67–72. [Google Scholar] [CrossRef] [PubMed]
- Koynova, R.; Tenchov, B. Transitions between lamellar and non-lamellar phases in membrane lipids and their physiological roles. OA Biochem. 2013, 1, 9. [Google Scholar] [CrossRef][Green Version]
- Evans, A.A.; Bhaduri, B.; Popescu, G.; Levine, A.J. Geometric localization of thermal fluctuations in red blood cells. Proc. Natl. Acad. Sci. USA 2017, 114, 2865–2870. [Google Scholar] [CrossRef]
- Waugh, R.; Evans, E.A. Thermoelasticity of red blood cell membrane. Biophys. J. 1979, 26, 115–131. [Google Scholar] [CrossRef]
- Thompson, S.M.; Masukawa, L.M.; Prince, D.A. Temperature dependence of intrinsic membrane properties and synaptic potentials in hippocampal CA1 neurons in vitro. J. Neurosci. 1985, 5, 817–824. [Google Scholar] [CrossRef] [PubMed]
- Bai, T.; Gu, N. Micro/nanoscale thermometry for cellular thermal sensing. Small 2016, 12, 4590–4610. [Google Scholar] [CrossRef] [PubMed]
- Jaque, D.; Vetrone, F. Luminescence nanothermometry. Nanoscale 2012, 4, 4301–4326. [Google Scholar] [CrossRef]
- del Rosal, B.; Ximendes, E.; Rocha, U.; Jaque, D. In vivo luminescence nanothermometry: From materials to applications. Adv. Opt. Mater. 2017, 5, 1600508. [Google Scholar] [CrossRef]
- Okabe, K.; Sakaguchi, R.; Shi, B.; Kiyonaka, S. Intracellular thermometry with fluorescent sensors for thermal biology. Pfluegers Arch. Eur. J. Phy. 2018, 470, 717–731. [Google Scholar] [CrossRef]
- Lucia, U. Bioengineering thermodynamics of biological cells. Theor. Biol. Med. Model. 2015, 12, 29. [Google Scholar] [CrossRef] [PubMed]
- Genet, S.; Costalat, R.; Burger, J. The influence of plasma membrane electrostatic properties on the stability of cell ionic composition. Biophys. J. 2001, 81, 2442–2457. [Google Scholar] [CrossRef]
- Wan, J.; Zhang, X.; Zhang, K.; Su, Z. Biological nanoscale fluorescent probes: From structure and performance to bioimaging. Rev. Anal. Chem. 2020, 39, 209–221. [Google Scholar] [CrossRef]
- Aharonovich, I.; Castelletto, S.; Simpson, D.A.; Su, C.H.; Greentree, A.D.; Prawer, S. Diamond-based single-photon emitters. Rep. Prog. Phys. 2011, 74, 76501. [Google Scholar] [CrossRef]
- Coe, S.E.; Sussmann, R.S. Optical, thermal and mechanical properties of CVD diamond. Diam. Relat. Mater. 2000, 9, 1726–1729. [Google Scholar] [CrossRef]
- Levine, E.V.; Turner, M.J.; Kehayias, P.; Hart, C.A.; Langellier, N.; Trubko, R.; Walsworth, R.L. Principles and techniques of the quantum diamond microscope. Nanophotonics 2019, 8, 1945–1973. [Google Scholar] [CrossRef]
- Aharonovich, I.; Greentree, A.D.; Prawer, S. Diamond photonics. Nat. Photonics 2011, 5, 397–405. [Google Scholar] [CrossRef]
- Casola, F.; Van Der Sar, T.; Yacoby, A. Probing condensed matter physics with magnetometry based on nitrogen-vacancy centres in diamond. Nat. Rev. Mater. 2018, 3, 17088. [Google Scholar] [CrossRef]
- Chu, Z.; Miu, K.; Lung, P.; Zhang, S.; Zhao, S.; Chang, H.C.; Li, Q. Rapid endosomal escape of prickly nanodiamonds: Implications for gene delivery. Sci. Rep. 2015, 5, 11661. [Google Scholar] [CrossRef] [PubMed]
- Wort, C.J.H.; Balmer, R.S. Diamond as an electronic material. Mater. Today 2008, 11, 22–28. [Google Scholar] [CrossRef]
- Momenzadeh, S.A.; Stohr, R.J.; De Oliveira, F.F.; Brunner, A.; Denisenko, A.; Yang, S.; Wrachtrup, J. Nanoengineered diamond waveguide as a robust bright platform for nanomagnetometry using shallow nitrogen vacancy centers. Nano Lett. 2015, 15, 165–169. [Google Scholar] [CrossRef]
- Maletinsky, P.; Hong, S.; Grinolds, M.S.; Hausmann, B.; Lukin, M.D.; Walsworth, R.L.; Yacoby, A. A robust scanning diamond sensor for nanoscale imaging with single nitrogen-vacancy centres. Nat. Nanotechnol. 2012, 7, 320–324. [Google Scholar] [CrossRef] [PubMed]
- Jelezko, F.; Wrachtrup, J. Single defect centres in diamond: A review. Phys. Status Solidi A 2006, 203, 3207–3225. [Google Scholar] [CrossRef]
- Toyli, D.M.; de Las Casas, C.F.; Christle, D.J.; Dobrovitski, V.V.; Awschalom, D.D. Fluorescence thermometry enhanced by the quantum coherence of single spins in diamond. Proc. Natl. Acad. Sci. USA 2013, 110, 8417–8421. [Google Scholar] [CrossRef]
- Gruber, A.; Drabenstedt, A.; Tietz, C.; Fleury, L.; Wrachtrup, J.; Borczyskowski, C.V. Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 1997, 276, 2012–2014. [Google Scholar] [CrossRef]
- Cui, Y.; Leong, W.H.; Liu, C.F.; Xia, K.; Feng, X.; Gergely, C.; Li, Q. Measurement of single-cell elasticity by nanodiamond-sensing of non-local deformation. arXiv 2021, arXiv:2109.13812. [Google Scholar]
- Glushkov, E.; Navikas, V.; Radenovic, A. Fluorescent nanodiamonds as versatile intracellular temperature sensors. CHIMIA Int. J. Chem. 2019, 73, 73–77. [Google Scholar] [CrossRef]
- Chipaux, M.; van der Laan, K.J.; Hemelaar, S.R.; Hasani, M.; Zheng, T.; Schirhagl, R. Nanodiamonds and their applications in cells. Small 2018, 14, 1704263. [Google Scholar] [CrossRef]
- Hemmer, E.; Benayas, A.; Légaré, F.; Vetrone, F. Exploiting the biological windows: Current perspectives on fluorescent bioprobes emitting above 1000 nm. Nanoscale Horiz. 2016, 1, 168–184. [Google Scholar] [CrossRef]
- Goovaerts, E. Optically detected magnetic resonance (ODMR). Emagres 2017, 6, 343–358. [Google Scholar]
- Le Sage, D.; Arai, K.; Glenn, D.; DeVience, S.; Pham, L.; Walsworth, R. Optical magnetic imaging of living cells. Nature 2013, 496, 486–489. [Google Scholar] [CrossRef]
- McCoey, J.M.; Matsuoka, M.; de Gille, R.W.; Hall, L.T.; Shaw, J.A.; Tetienne, J.P.; Simpson, D.A. Quantum magnetic imaging of iron biomineralization in teeth of the chiton Acanthopleura hirtosa. Small Methods 2020, 4, 1900754. [Google Scholar] [CrossRef]
- Fescenko, I.; Laraoui, A.; Smits, J.; Mosavian, N.; Kehayias, P.; Seto, J.; Acosta, V.M. Diamond magnetic microscopy of malarial hemozoin nanocrystals. Phys. Rev. Appl. 2019, 11, 34029. [Google Scholar] [CrossRef]
- Faivre, D.; Schuler, D. Magnetotactic bacteria and magnetosomes. Chem. Rev. 2008, 108, 4875–4898. [Google Scholar] [CrossRef] [PubMed]
- Kumar, C.S.S.R.; Mohammad, F. Magnetic nanomaterials for hyperthermia-based therapy and controlled drug delivery. Adv. Drug Deliv. Rev. 2011, 63, 789–808. [Google Scholar] [CrossRef]
- Veiseh, O.; Gunn, J.W.; Zhang, M. Design and fabrication of magnetic nanoparticles for targeted drug delivery and imaging. Adv. Drug Deliv. Rev. 2010, 62, 284–304. [Google Scholar] [CrossRef] [PubMed]
- Etoc, F.; Vicario, C.; Lisse, D.; Siaugue, J.M.; Piehler, J.; Coppey, M.; Dahan, M. Magnetogenetic control of protein gradients inside living cells with high spatial and temporal resolution. Nano Lett. 2015, 15, 3487–3494. [Google Scholar] [CrossRef] [PubMed]
- Aschner, M.; Guilarte, T.R.; Schneider, J.S.; Zheng, W. Manganese: Recent advances in understanding its transport and neurotoxicity. Toxicol. Appl. Pharmacol. 2007, 221, 131–147. [Google Scholar] [CrossRef]
- Yoneda, M.; Nozaki, Y.; Endo, H.; Mawatari, H.; Iida, H.; Fujita, K.; Nakajima, A. Serum ferritin is a clinical biomarker in Japanese patients with nonalcoholic steatohepatitis (NASH) independent of HFE gene mutation. Dig. Dis. Sci. 2010, 55, 808–814. [Google Scholar] [CrossRef] [PubMed]
- Droge, W. Free radicals in the physiological control of cell function. Physiol. Rev. 2002, 82, 47–95. [Google Scholar] [CrossRef] [PubMed]
- Sushkov, A.O.; Chisholm, N.; Lovchinsky, I.; Kubo, M.; Lo, P.K.; Bennett, S.D.; Lukin, M.D. All-optical sensing of a single-molecule electron spin. Nano Lett. 2014, 14, 6443–6448. [Google Scholar] [CrossRef] [PubMed]
- Schmid-Lorch, D.; Häberle, T.; Reinhard, F.; Zappe, A.; Slota, M.; Bogani, L.; Wrachtrup, J. Relaxometry and dephasing imaging of superparamagnetic magnetite nanoparticles using a single qubit. Nano Lett. 2015, 15, 4942–4947. [Google Scholar] [CrossRef] [PubMed]
- Barton, J.; Gulka, M.; Tarabek, J.; Mindarava, Y.; Wang, Z.; Schimer, J.; Cigler, P. Nanoscale dynamic readout of a chemical redox process using radicals coupled with nitrogen-vacancy centers in nanodiamonds. ACS Nano 2020, 14, 12938–12950. [Google Scholar] [CrossRef] [PubMed]
- Steinert, S.; Ziem, F.; Hall, L.T.; Zappe, A.; Schweikert, M.; Götz, N.; Wrachtrup, J. Magnetic spin imaging under ambient conditions with sub-cellular resolution. Nat. Commun. 2013, 4, 1607. [Google Scholar] [CrossRef]
- Ziem, F.C.; Götz, N.S.; Zappe, A.; Steinert, S.; Wrachtrup, J. Highly sensitive detection of physiological spins in a microfluidic device. Nano Lett. 2013, 13, 4093–4098. [Google Scholar] [CrossRef]
- Doherty, M.W.; Dolde, F.; Fedder, H.; Jelezko, F.; Wrachtrup, J.; Manson, N.B.; Hollenberg, L.C.L. Theory of the ground-state spin of the NV–center in diamond. Phys. Rev. B 2012, 85, 205203. [Google Scholar] [CrossRef]
- Dolde, F.; Fedder, H.; Doherty, M.W.; Nöbauer, T.; Rempp, F.; Balasubramanian, G.; Wrachtrup, J. Electric-field sensing using single diamond spins. Nat. Phys. 2011, 7, 459–463. [Google Scholar] [CrossRef]
- Kaufmann, S.; Simpson, D.A.; Hall, L.T.; Perunicic, V.; Senn, P.; Steinert, S.; Hollenberg, L. Detection of atomic spin labels in a lipid bilayer using a single-spin nanodiamond probe. Proc. Natl. Acad. Sci. USA 2013, 110, 10894–10898. [Google Scholar] [CrossRef]
- Igarashi, R.; Sugi, T.; Sotoma, S.; Genjo, T.; Kumiya, Y.; Walinda, E.; Shirakawa, M. Tracking the 3D rotational dynamics in nanoscopic biological systems. J. Am. Chem. Soc. 2020, 142, 7542–7554. [Google Scholar] [CrossRef]
- Acosta, V.M.; Bauch, E.; Ledbetter, M.P.; Waxman, A.; Bouchard, L.S.; Budker, D. Temperature dependence of the nitrogen-vacancy magnetic resonance in diamond. Phys Rev Lett. 2010, 104, 70801. [Google Scholar] [CrossRef] [PubMed]
- Fukami, M.; Yale, C.G.; Andrich, P.; Liu, X.; Heremans, F.J.; Nealey, P.F.; Awschalom, D.D. All-optical cryogenic thermometry based on nitrogen-vacancy centers in nanodiamonds. Phys. Rev. Appl. 2019, 12, 14042. [Google Scholar] [CrossRef]
- Liu, G.Q.; Feng, X.; Wang, N.; Li, Q.; Liu, R.B. Coherent quantum control of nitrogen-vacancy center spins near 1000 kelvin. Nat. Commun. 2019, 10, 1344. [Google Scholar] [PubMed]
- Takei, Y.; Arai, S.; Murata, A.; Takabayashi, M.; Oyama, K.; Ishiwata, S.I.; Suzuki, M. A nanoparticle-based ratiometric and self-calibrated fluorescent thermometer for single living cells. ACS Nano 2014, 8, 198–206. [Google Scholar] [CrossRef]
- Chen, D.P.; Eisenberg, R.S.; Jerome, J.W.; Shu, C.W. Hydrodynamic model of temperature change in open ionic channels. Biophysical J. 1995, 69, 2304–2322. [Google Scholar] [CrossRef]
- El Hady, A.; Machta, B.B. Mechanical surface waves accompany action potential propagation. Nat. Commun. 2015, 6, 6697. [Google Scholar] [CrossRef]
- Guatteo, E.; Chung, K.K.; Bowala, T.K.; Bernardi, G.; Mercuri, N.B.; Lipski, J. Temperature sensitivity of dopaminergic neurons of the substantia nigra pars compacta: Involvement of transient receptor potential channels. J. Clin. Neurophysiol. 2005, 94, 3069–3080. [Google Scholar] [CrossRef]
- Tsai, P.C.; Chen, O.Y.; Tzeng, Y.K.; Hui, Y.Y.; Guo, J.Y.; Wu, C.C.; Chang, H.C. Gold/diamond nanohybrids for quantum sensing applications. EPJ Quantum Technol. 2015, 2, 19. [Google Scholar] [CrossRef]
- Yoshinari, Y.; Kalay, Z.; Harada, Y. Observing the rotational diffusion of nanodiamonds with arbitrary nitrogen vacancy center configurations. Phys. Rev. B 2013, 88, 235206. [Google Scholar] [CrossRef]
- McGuinness, L.P.; Yan, Y.; Stacey, A.; Simpson, D.A.; Hall, L.T.; Maclaurin, D.; Hollenberg, L.C.L. Quantum measurement and orientation tracking of fluorescent nanodiamonds inside living cells. Nat. Nanotechnol. 2011, 6, 358–363. [Google Scholar] [CrossRef] [PubMed]
- Pace, R.J.; Chan, S.I. Molecular motions in lipid bilayers. III. Lateral and transverse diffusion in bilayers. J. Chem. Phys. 1982, 76, 4241–4247. [Google Scholar] [CrossRef]
- Frey, F.; Ziebert, F.; Schwarz, U.S. Dynamics of particle uptake at cell membranes. Phys. Rev. E 2019, 100, 52403. [Google Scholar] [CrossRef] [PubMed]
- Friedhoff, L.T. The effect of ion channels on cell membrane motion. J. Theor. Biol. 1983, 101, 205–210. [Google Scholar] [CrossRef]
- Atia, L.; Givli, S. A theoretical study of biological membrane response to temperature gradients at the single-cell level. J. R. Soc. Interface 2014, 11, 20131207. [Google Scholar] [CrossRef]
- Bayley, H.; Cremer, P.S. Stochastic sensors inspired by biology. Nature 2001, 413, 226–230. [Google Scholar] [CrossRef]
- Borbat, P.P.; Costa-Filho, A.J.; Earle, K.A.; Moscicki, J.K.; Freed, J.H. Electron spin resonance in studies of membranes and proteins. Science 2001, 291, 266–269. [Google Scholar] [CrossRef]
- Ide, T.; Takeuchi, Y.; Aoki, T.; Yanagida, T. Simultaneous optical and electrical recording of a single ion-channel. Jpn. J. Physiol. 2002, 52, 429–434. [Google Scholar] [CrossRef][Green Version]
- Baaken, G.; Sondermann, M.; Schlemmer, C.; Rühe, J.; Behrends, J.C. Planar microelectrode-cavity array for high-resolution and parallel electrical recording of membrane ionic currents. Lab Chip 2008, 8, 938–944. [Google Scholar] [CrossRef] [PubMed]
- Damjanovich, S. Biophysical Aspects of Transmembrane Signaling, 1st ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2005; pp. 298–302. [Google Scholar]
- Hall, L.T.; Hill, C.D.; Cole, J.H.; Städler, B.; Caruso, F.; Mulvaney, P.; Hollenberg, L.C. Monitoring ion-channel function in real time through quantum decoherence. Proc. Natl. Acad. Sci. USA 2010, 107, 18777–18782. [Google Scholar] [CrossRef]
- Hall, L.T.; Cole, J.H.; Hill, C.D.; Hollenberg, L.C. Sensing of fluctuating nanoscale magnetic fields using nitrogen-vacancy centers in diamond. Phys. Rev. Lett. 2009, 103, 220802. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Gupta, N. Fundamentals of Bacterial Physiology and Metabolism, 1st ed.; Springer: Singapore, 2021; p. 183. [Google Scholar]
- Feng, X.; Leong, W.H.; Xia, K.; Liu, C.F.; Liu, G.Q.; Rendler, T.; Li, Q. Association of nanodiamond rotation dynamics with cell activities by translation-rotation tracking. Nano Lett. 2021, 21, 3393–3400. [Google Scholar] [CrossRef] [PubMed]
- Safran, S.A.; Gov, N.; Nicolas, A.; Schwarz, U.S.; Tlusty, T. Physics of cell elasticity, shape and adhesion. Phys. A Stat. Mech. Appl. 2005, 352, 171–201. [Google Scholar] [CrossRef]
- Nawaz, S.; Sánchez, P.; Bodensiek, K.; Li, S.; Simons, M.; Schaap, I.A. Cell visco-elasticity measured with AFM and optical trapping at sub-micrometer deformations. Biophys. J. 2013, 104, 478a. [Google Scholar] [CrossRef]
- Sokolov, I.; Dokukin, M.E.; Guz, N.V. Method for quantitative measurements of the elastic modulus of biological cells in AFM indentation experiments. Methods 2013, 60, 202–213. [Google Scholar] [CrossRef] [PubMed]
- Van Meer, G.; de Kroon, A.I.P.M. Lipid map of the mammalian cell. J. Cell. Sci. 2011, 124, 5–8. [Google Scholar] [CrossRef]
- Lombard, J. Once upon a time the cell membranes: 175 years of cell boundary research. Biol. Direct. 2014, 9, 32. [Google Scholar] [CrossRef]
- Kučerka, N.; Nieh, M.P.; Katsaras, J. Fluid phase lipid areas and bilayer thicknesses of commonly used phosphatidylcholines as a function of temperature. Biochim. Biophys. Acta-Biomembr. 2011, 1808, 2761–2771. [Google Scholar] [CrossRef]
- Waheed, Q.; Tjörnhammar, R.; Edholm, O. Phase transitions in coarse-grained lipid bilayers containing cholesterol by molecular dynamics simulations. Biophys. J. 2012, 103, 2125–2133. [Google Scholar] [CrossRef]
- Van Meer, G.; Voelker, D.R.; Feigenson, G.W. Membrane lipids: Where they are and how they behave. Nat. Rev. Mol. Cell Biol. 2008, 9, 112–124. [Google Scholar] [CrossRef]
- Eggeling, C.; Ringemann, C.; Medda, R.; Schwarzmann, G.; Sandhoff, K.; Polyakova, S.; Hell, S.W. Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature 2009, 457, 1159–1162. [Google Scholar] [CrossRef] [PubMed]
- Skocaj, Á.; Bakrac, B.; Krizaj, I.; Macek, P.; Anderluh, G.; Sepcic, K. The sensing of membrane microdomains based on pore-forming toxins. Curr. Med. Chem. 2013, 20, 491–501. [Google Scholar] [PubMed]
- Ishiwata, H.; Watanabe, H.C.; Hanashima, S.; Iwasaki, T.; Hatano, M. Label-free phase change detection of lipid bilayers using nanoscale diamond magnetometry. Adv. Quantum Technol. 2021, 4, 2000106. [Google Scholar] [CrossRef]
- Pavel, M.A.; Petersen, E.N.; Wang, H.; Lerner, R.A.; Hansen, S.B. Studies on the mechanism of general anesthesia. Proc. Natl. Acad. Sci. USA 2020, 117, 13757–13766. [Google Scholar] [CrossRef]
- Barry, J.F.; Turner, M.J.; Schloss, J.M.; Glenn, D.R.; Song, Y.; Lukin, M.D.; Walsworth, R.L. Optical magnetic detection of single-neuron action potentials using quantum defects in diamond. Proc. Natl. Acad. Sci. USA 2016, 113, 14133–14138. [Google Scholar] [CrossRef]
- Price, J.C.; Mesquita-Ribeiro, R.; Dajas-Bailador, F.; Mather, M.L. Widefield, spatiotemporal mapping of spontaneous activity of mouse cultured neuronal networks using quantum diamond sensors. Front. Phys. 2020, 8, 255. [Google Scholar] [CrossRef]
- Epperla, C.P.; Chen, O.Y.; Chang, H.C. Gold/diamond nanohybrids may reveal how hyperlocalized hyperthermia kills cancer cells. Nanomedicine 2016, 11, 443–445. [Google Scholar] [CrossRef]
- Tsai, P.C.; Epperla, C.P.; Huang, J.S.; Chen, O.Y.; Wu, C.C.; Chang, H.C. Measuring nanoscale thermostability of cell membranes with single gold–diamond nanohybrids. Angew. Chem. Int. Ed. 2017, 56, 3025–3030. [Google Scholar] [CrossRef]
- Lanin, A.A.; Fedotov, I.V.; Ermakova, Y.G.; Sidorov-Biryukov, D.A.; Fedotov, A.B.; Hemmer, P.; Zheltikov, A.M. Fiber-optic electron-spin-resonance thermometry of single laser-activated neurons. Opt. Lett. 2016, 41, 5563–5566. [Google Scholar] [CrossRef]
- Meng, D.; Zhang, P.; Zhang, L.; Wang, H.; Ho, C.T.; Li, S.; Shahidi, F.; Zhao, H. Detection of Cellular Redox Reactions and Antioxidant Activity Assays. J. Funct. Foods. 2017, 37, 467–479. [Google Scholar] [CrossRef]
- Manganas, P.; MacPherson, L.; Tokatlidis, K. Oxidative Protein Biogenesis and Redox Regulation in the Mitochondrial Intermembrane Space. Cell Tissue Res. 2017, 367, 43–57. [Google Scholar] [CrossRef] [PubMed]
- Hosios, A.M.; Vander Heiden, M.G. The Redox Requirements of Proliferating Mammalian Cells. J. Biol. Chem. 2018, 293, 74907498. [Google Scholar] [CrossRef] [PubMed]
- Nie, L.; Nusantara, A.C.; Damle, V.G.; Sharmin, R.; Evans, E.P.P.; Hemelaar, S.R.; Schirhagl, R. Quantum monitoring of cellular metabolic activities in single mitochondria. Sci. Adv. 2021, 7, eabf0573. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Hou, Y.; Zhang, T.; Wei, X.; Zhou, Y.; Lei, D.; Wei, Q.; Lin, Y.; Chu, Z. All-Optical Modulation of Single Defects in Nanodiamonds: Revealing Rotational and Translational Motions in Cell Traction Force Fields. Nano Lett. 2022, 22, 7714–7723. [Google Scholar] [CrossRef]
- Duan, D.; Kavatamane, V.K.; Arumugam, S.R.; Tzeng, Y.K.; Chang, H.C.; Balasubramanian, G. Tapered ultra-high numerical aperture optical fiber tip for nitrogen vacancy ensembles based endoscope in a fluidic environment. Appl. Phys. Lett. 2020, 116, 113701. [Google Scholar] [CrossRef]
- Sturner, F.M.; Brenneis, A.; Buck, T.; Kassel, J.; Rölver, R.; Fuchs, T.; Savitsky, A.; Suter, D.; Grimmel, J.; Hengesbach, S.; et al. Integrated and portable magnetometer based on nitrogen-vacancy ensembles in diamond. Adv. Quantum Technol. 2021, 4, 2000111. [Google Scholar] [CrossRef]
- Fedotov, I.V.; Doronina-Amitonova, L.V.; Voronin, A.A.; Levchenko, A.O.; Zibrov, S.A.; Sidorov-Biryukov, D.A.; Fedotov, A.B.; Velichansky, V.L.; Zheltikov, A.M. Electron spin manipulation and readout through an optical fiber. Sci. Rep. 2015, 4, 5362. [Google Scholar] [CrossRef]
- Boss, J.M.; Cujia, K.S.; Zopes, J.; Degen, C.L. Quantum sensing with arbitrary frequency resolution. Science 2017, 356, 837–840. [Google Scholar] [CrossRef]
- Lovchinsky, I.; Sushkov, A.O.; Urbach, E.; de Leon, N.P.; Choi, S.; De Greve, K.; Lukin, M.D. Nuclear magnetic resonance detection and spectroscopy of single proteins using quantum logic. Science 2016, 351, 836–841. [Google Scholar] [CrossRef]
- Taylor, J.M.; Cappellaro, P.; Childress, L.; Jiang, L.; Budker, D.; Hemmer, P.R.; Lukin, M.D. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 2008, 4, 810–816. [Google Scholar] [CrossRef]
- Degen, C.L. Scanning magnetic field microscope with a diamond single-spin sensor. Appl. Phys. Lett. 2008, 92, 243111. [Google Scholar] [CrossRef]
- Wolf, T.; Neumann, P.; Nakamura, K.; Sumiya, H.; Ohshima, T.; Isoya, J.; Wrachtrup, J. Subpicotesla diamond magnetometry. Phys. Rev. X 2015, 5, 41001. [Google Scholar] [CrossRef]
- Petrini, G.; Moreva, E.; Bernardi, E.; Traina, P.; Tomagra, G.; Carabelli, V.; Genovese, M. Is a quantum biosensing revolution approaching? Perspectives in NV-assisted current and thermal biosensing in living cells. Adv. Quant. Technol. 2020, 3, 2000066. [Google Scholar] [CrossRef]
- Ofori-Okai, B.K.; Pezzagna, S.; Chang, K.; Loretz, M.; Schirhagl, R.; Tao, Y.; Degen, C.L. Spin properties of very shallow nitrogen vacancy defects in diamond. Phys. Rev. B 2012, 86, 81406. [Google Scholar] [CrossRef]
- Barnard, A.S. Optimal vacancy concentrations to maximize the N–V yield in nanodiamonds. Mater. Horiz. 2014, 1, 286–291. [Google Scholar] [CrossRef]
- Knowles, H.S.; Kara, D.M.; Atatüre, M. Observing bulk diamond spin coherence in high-purity nanodiamonds. Nat. Mater 2014, 13, 21–25. [Google Scholar] [CrossRef]
- Wu, Y.; Weil, T. Recent developments of nanodiamond quantum sensors for biological applications. Adv. Sci. 2022, 9, 2200059. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Y.; Hu, X.; Hou, Y.; Chu, Z. Emerging Diamond Quantum Sensing in Bio-Membranes. Membranes 2022, 12, 957. https://doi.org/10.3390/membranes12100957
Tan Y, Hu X, Hou Y, Chu Z. Emerging Diamond Quantum Sensing in Bio-Membranes. Membranes. 2022; 12(10):957. https://doi.org/10.3390/membranes12100957
Chicago/Turabian StyleTan, Yayin, Xinhao Hu, Yong Hou, and Zhiqin Chu. 2022. "Emerging Diamond Quantum Sensing in Bio-Membranes" Membranes 12, no. 10: 957. https://doi.org/10.3390/membranes12100957
APA StyleTan, Y., Hu, X., Hou, Y., & Chu, Z. (2022). Emerging Diamond Quantum Sensing in Bio-Membranes. Membranes, 12(10), 957. https://doi.org/10.3390/membranes12100957







