Model of Hydraulic Resistance When Forecasting Reverse Osmosis in Water Treatment
Abstract
1. Introduction
Forecasting the Efficiency of Membranes in Reverse Osmosis in the Process of Purification of Infiltration Water with Increased Concentration of Nitrogen Compounds, Based on the Model of the Hydraulic Filtration Resistance
2. Materials and Methods
2.1. Subject of Study
2.2. Technological Research
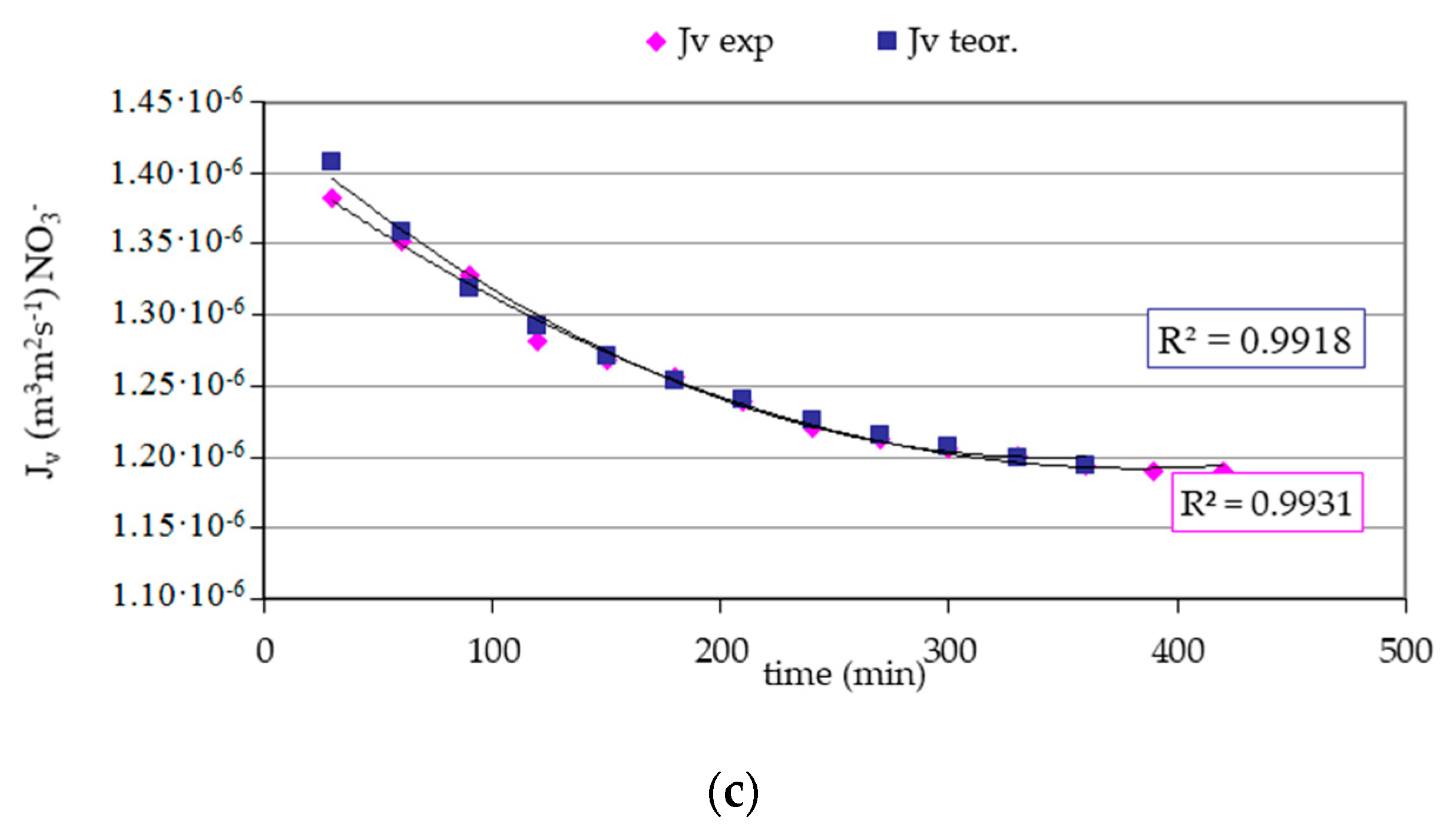
3. Results and Discussion
4. Conclusions
- The obtained high values of the correlation coefficients in the case of comparing the instantaneous values of the experimental permeate fluxes with the theoretical instantaneous fluxes allow for the conclusion that that the model of hydraulic filtration resistance used in the calculations allows the forecasting of the membrane efficiency in the discussed process.
- The resistance model for reversible contamination is correct. In order to determine this resistance, it is essential to obtain the membrane characteristics with deionized water, both for the new membrane and after the “working” process.
- The value of irreversible fouling resistance is higher than the reversible resistance, indicating additional unrecognized contaminants in the water.
- The analysis of the experimental data obtained in the process of purification of water with an increased concentration of nitrogen compounds with the use of the series resistances model enables the determination of the primary mass transport resistances, the resistance of the active layer of the membrane, as well as reversible and irreversible fouling, and also the identification and evaluation of the range of phenomena reducing the membrane’s efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Piekutin, J. Membrane processes associated with classical to surface water treatment. Pol. J. Environ. Stud. 2009, 2, 51–55. [Google Scholar]
- Dziubek, A.M.; Maćkiewicz, J. Direct filtration applied to infiltrated water treatment. Environ. Prot. Eng. 2002, 28, 39–45. [Google Scholar]
- Luo, M.; Wang, Z. Complex fouling and cleaning-in-place of a reverse osmosis desalination system. Desalination 2001, 141, 15–22. [Google Scholar] [CrossRef]
- Awadalla, F.T.; Striez, C.; Lamb, K. Removal of ammonium and nitrate ions from mine effluents by membrane technology. Sep. Sci. Technol. 1994, 29, 483–495. [Google Scholar] [CrossRef]
- Ghyoot, W.; Vandaele, S. Nitrogen removal from sludge reject water with a membrane-assisted bioreactor. Water Res. 1999, 33, 23–32. [Google Scholar] [CrossRef]
- Koyuncu, I.; Topacik, D. Application of the membrane technology to control ammonia in surface water. Water Sci. Technol. 2001, 1, 117–124. [Google Scholar] [CrossRef]
- Mielczarek, K.; Bohdziewicz, J. Performance prediction of ultrafiltration Treatment of post-process coke wastewater based on the assumptions of hydraulic filtration resistance model. Arch. Environ. Prot. 2011, 37, 107–118. [Google Scholar]
- Szaniawska, D.; Kuca, M. Fouling of ceramic membranes in the ultrafiltration process of protein and sodium chloride solutions. Inż. Ap. Chem. 2010, 49, 109–110. [Google Scholar]
- Bodzek, M.; Konieczny, K. Membrane Techniques in the Removal of Inorganic Anionic Micropollutants from Water Environment–State of the Art. Arch. Environ. Prot. 2011, 37, 15–29. [Google Scholar]
- Piekutin, J. Estimate of possibilities removal of selected nitrogen forms from infiltration water and optimization of reversed osmosis system. ECE 2008, 15, 9–16. [Google Scholar]
- ASTM. Standard Test Method for Silt Density Index (SDI) of Water, in Designation: D 4189—95 (Reapproved 2002); ASTM International: West Conshohocken, PA, USA, 2002. [Google Scholar]
- Lee, S.; Lueptow, R.M. Rotating reverse osmosis: A dynamic model for flux and rejection. J. Membr. Sci. 2001, 192, 129–143. [Google Scholar] [CrossRef]
- Costa, M.L.; Dickons, J.M. Modelling of modules and systems in reverse osmosis. Part I: Theoretical system design model development. Desalination 1991, 80, 251–274. [Google Scholar] [CrossRef]
- Konieczny, K.; Rafa, J. Modeling of the membrane filtration process of natural waters. Pol. J. Environ. Stud. 2000, 9, 57–64. [Google Scholar]
- Kargol, A. Mechanistic model of transport processes in porous membranes generated by osmotic and hydrostatic pressures. J. Membr. Sci. 2001, 19, 61–69. [Google Scholar] [CrossRef]
- Chen, K.L.; Song, L.; Ong, S.L.; Ng, W.J. The development of membrane fouling in full-scale RO processes. J. Membr. Sci. 2004, 232, 63–72. [Google Scholar] [CrossRef]
- Košutić, K.; Kunst, B. RO and NF membrane fouling and cleaning and pore size distribution variations. Desalination 2002, 150, 113–120. [Google Scholar] [CrossRef]
- Konieczny, K. Ultrafiltration and microfiltration in water treatment for municipal purposes. Sci. J. Sil. Univ. Technol. 2002, 42, 29–39. (In Polish) [Google Scholar]
- Amiri, M.C.; Samiei, M. Enhancing permeate flux in a RO plant by controlling membrane fouling. Desalination 2007, 207, 361–369. [Google Scholar] [CrossRef]
- Ruiz-García, A.; Melián-Martel, N.; Nuez, I. Short Review on Predicting Fouling in RO. Membranes 2017, 7, 62. [Google Scholar] [CrossRef]
- Jepsen, K.L.; Bram, M.V.; Pedersen, S.; Yang, Z. Membrane Fouling for Produced Water Treatment: A Review Study From a Process Control Perspective. Water 2018, 10, 847. [Google Scholar] [CrossRef]
- Carter, J.W.; Hoyland, G.; Hasting, A.P.M. Concentration polarisation in reverse osmosis flow systems under laminar conditions. Effect of surface roughness and fouling. Chem. Eng. Sci. 1974, 29, 1651–1658. [Google Scholar] [CrossRef]
- Hirose, M.; Ito, H.; Kamiyama, Y. Effect of skin layer surface structures on the flux behaviour of RO membranes. J. Membr. Sci. 1996, 121, 209–215. [Google Scholar] [CrossRef]
- Mohammadi, T.; Kazemimoghadam, M.; Saadabadi, M. Modeling of membrane fouling and flux decline in reverse osmosis during separation of oil in water emulsions. Desalination 2003, 157, 369–375. [Google Scholar] [CrossRef]
- Kostogloua, M.; Karabelasb, A.J. A mathematical study of the evolution of fouling and operating parameters throughout membrane sheets comprising spiral wound modules. Chem. Eng. J. 2012, 187, 222–231. [Google Scholar] [CrossRef]
- Li, H.; Xia, H.; Mei, Y.X. Modeling organic fouling of reverse osmosis membrane: From adsorption to fouling layer formation. Desalination 2016, 386, 25–31. [Google Scholar] [CrossRef]
- Pascual, X.; Gub, H.; Bartman, A.R.; Zhu, A.; Rahardianto, A.; Giralt, J.; Rallo, R.; Christofides, P.D.; Cohen, Y. Data-driven models of steady state and transient operations of spiral-wound RO plant. Desalination 2013, 316, 154–161. [Google Scholar] [CrossRef]
- Weinrich, L.; Haas, C.N.; LeChevallier, M.W. Recent advances in measuring and modeling reverse osmosis membrane fouling in seawater desalination: A review. J. Water Reuse Desalination 2013, 3, 85–101. [Google Scholar] [CrossRef][Green Version]
- Hadadian, Z.; Zahmatkesh, S.; Ansari, M.; Haghighi, A.; Moghimipour, E. Mathematical and experimental modeling of reverse osmosis (RO) process. Sep. Technol. Thermodyn. 2021, 38, 366–379. [Google Scholar]
- Xianhui, L.; Danyan, Y.; Genghong, A.; Dawei, J.; Jianxin, L. Fouling and Cleaning of Reverse Osmosis Membranes duing Municipal Tap Water Treatment on a Pilot-Scale Plant. J. Water Sustain. 2011, 1, 139–151. [Google Scholar]
- Zhang, Z.; Li, S.; Mi, B.; Wang, J.; Jianning, D. Surface slip on rotating graphene membrane enables the temporal selectivity that breaks the permeability-selectivity trade-off. Sci. Adv. 2020, 6, eaba9471. [Google Scholar] [CrossRef]
- Mi, B. Scaling up nanoporous graphene membranes. Science 2019, 364, 1033–1034. [Google Scholar] [CrossRef] [PubMed]
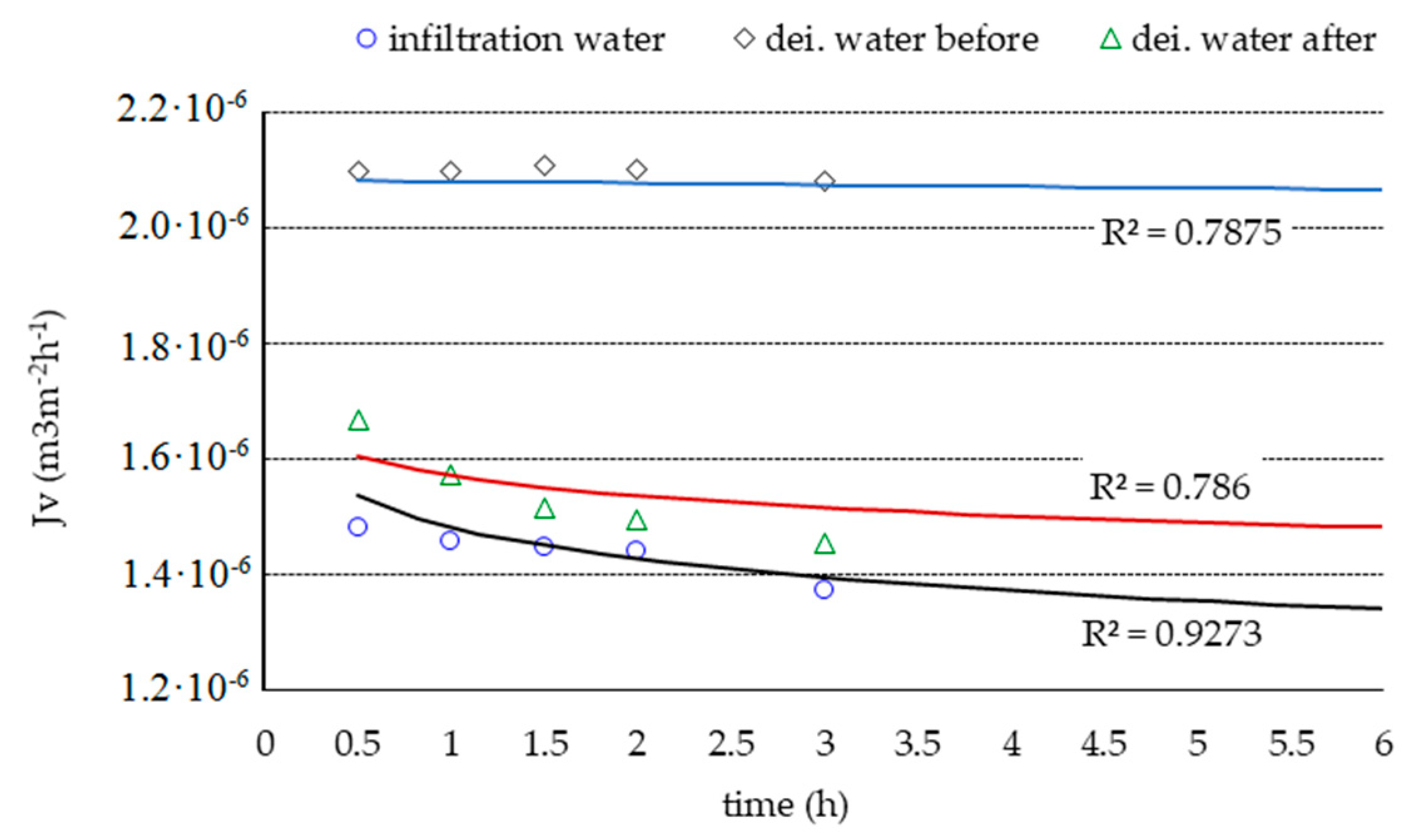
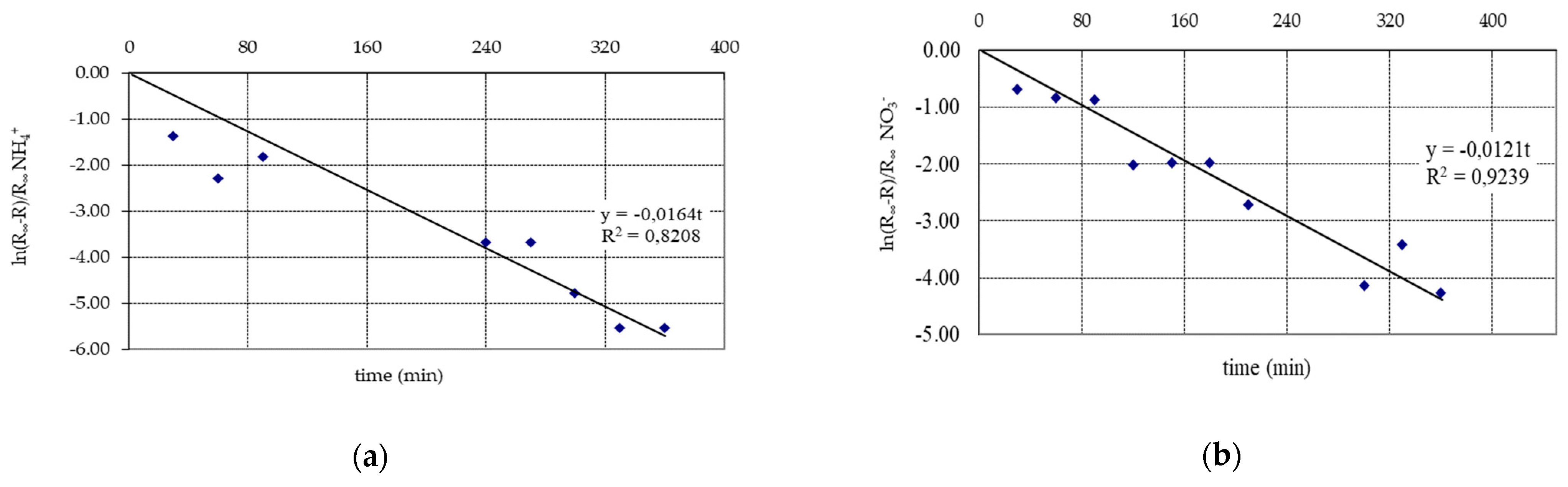
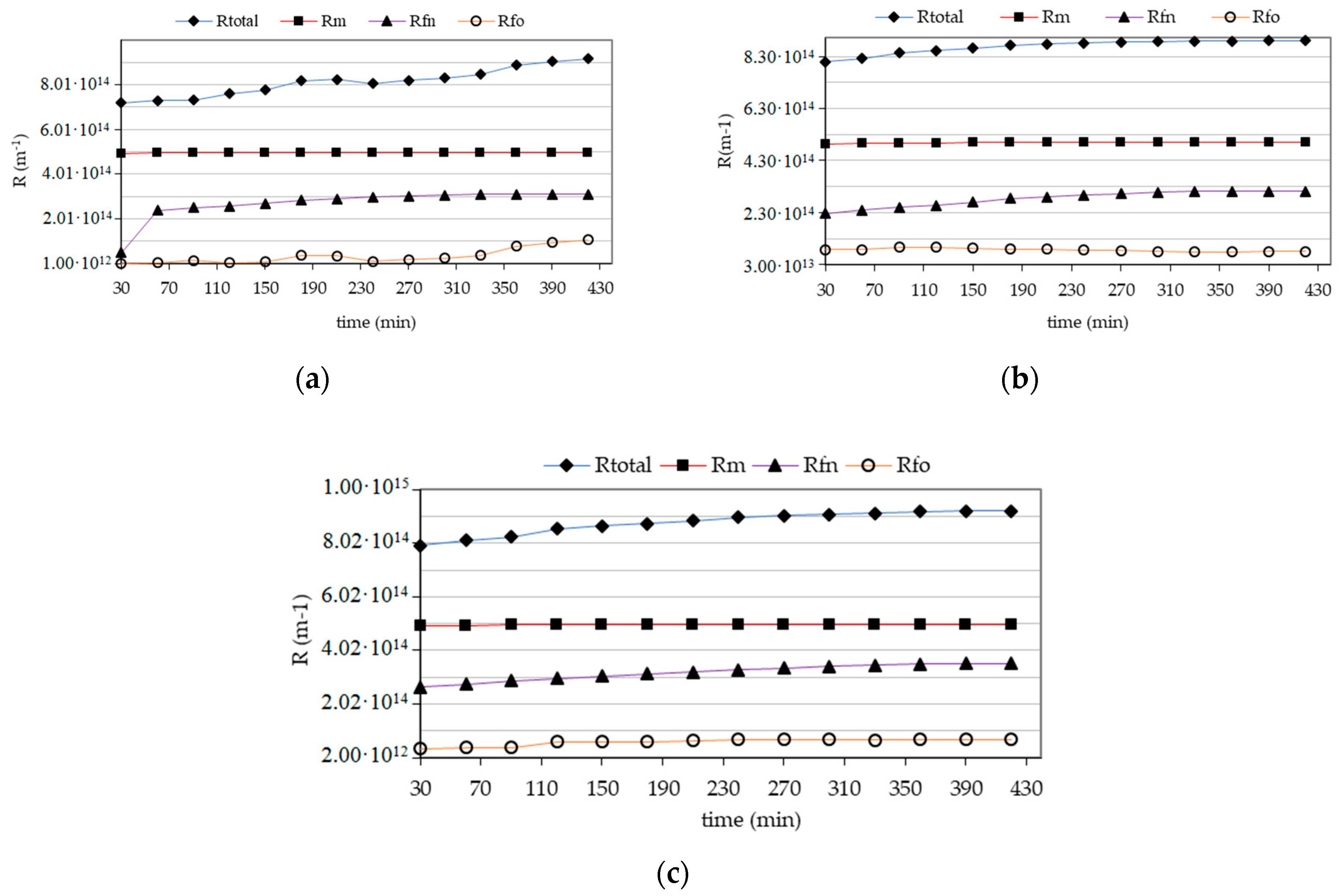
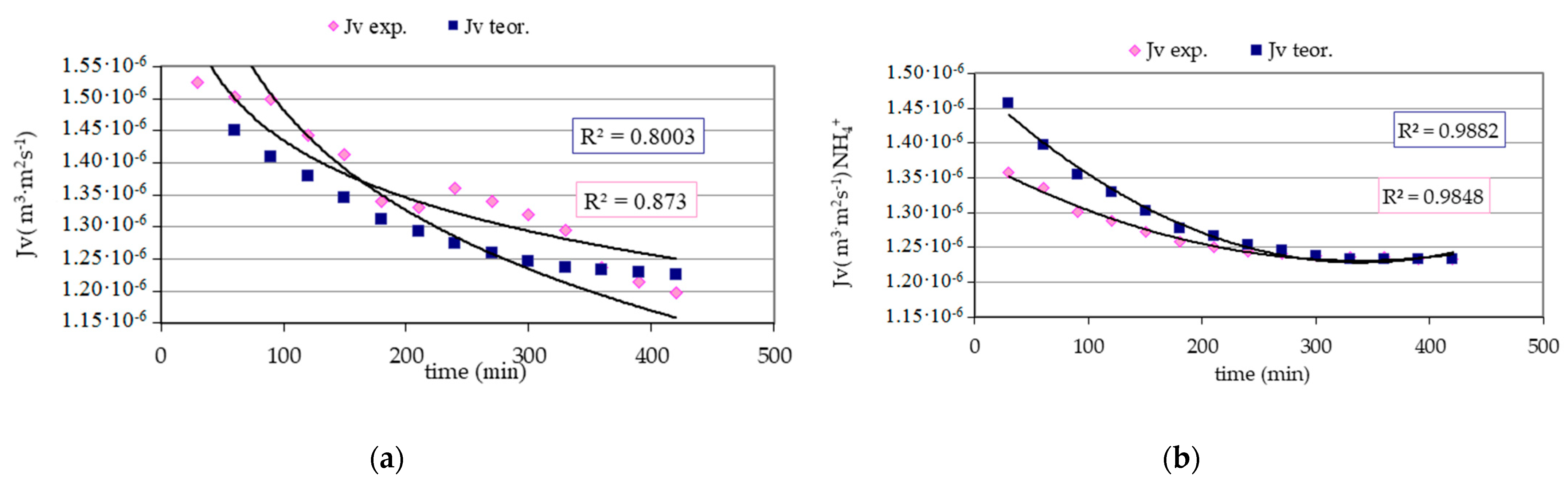
| Test Parameter | Unit | Raw Water | Infiltrate | Retention Factor R (%) | |||
|---|---|---|---|---|---|---|---|
| Values | Values | Values | |||||
| Mean | Median | Mean | Median | Mean | Median | ||
| Color | mg Pt/L | 42.46 | 44.00 | 1.23 | 1.00 | 97.31 | 97.42 |
| Turbidity | mg SiO2/L | 5.64 | 2.00 | 0.0 | 0.0 | 100.0 | 100.0 |
| Conductivity | µS/cm | 433.0 | 424.00 | 7.54 | 7.00 | 98.40 | 98.40 |
| Reaction | pH | 7.18 | 7.20 | 6.08 | 6.00 | - | - |
| Calcium | mg Ca2+/L | 84.93 | 82.30 | 0.89 | 0.00 | 99.21 | 100.0 |
| Manganese | mg Mn/L | 0.19 | 0.19 | 0.05 | 0.04 | 77.71 | 78.90 |
| Ferrumtot. | mg Fe/L | 0.71 | 0.61 | 0.03 | 0.03 | 95.70 | 95.71 |
| Chlorides | mg Cl−/L | 19.30 | 14.00 | 0.85 | 0.70 | 94.90 | 93.83 |
| Nitrate(V) | mg NO3−/L | 3.355 | 3.80 | 0.045 | 0.020 | 99.11 | 100.00 |
| Nitrate(III) | mg NO2−/L | 0.025 | 0.025 | 0.013 | 0.013 | 49.60 | 50.81 |
| Ammonia ion | mg NH4+/L | 0.587 | 0.45 | 0.022 | 0.020 | 95.10 | 96.00 |
| CODMn | mg O2/L | 10.02 | 9.20 | 0.43 | 0.33 | 89.39 | 90.15 |
| Test Parameter | Value | Retention Factor [%] |
|---|---|---|
| Color [mg Pt/L] | 39.0 | 74.3 |
| Turbidity [SiO2/L] | 39.0 | 100 |
| Conductance [µS/cm] | 543 | 88.45 |
| pH | 7.30 | - |
| Calcium [mg Ca2+/L] | 82.6 | 92.4 |
| Manganese [mg Mn/L] | 0.18 | 75.0 |
| Ferrum [mg Fe/L] | 0.67 | 84.8 |
| Chlorides [mg Cl−/L] | 16.2 | 76,0 |
| Nitrate(V) [mg NO3−/L] | 148 | 71.3 |
| Nitrate(III) [mg NO2−/L] | 0.02 | 88.0 |
| Ammonia ion [mg NH4+/L] | 12.6 | 83.6 |
| CODMn [mg O2/L] | 10.7 | 70.7 |
| Water Type | Resistance Rfo Determined from the Experiment (m−1) | Resistance Rfo Calculated from the Formula (m−1) | tRO Calculated from the Formula (min) |
|---|---|---|---|
| Infiltration water | 1.829 × 1013 | 6.974 × 1013 | 156.0 |
| Infiltration water amended with NH4+ | 8.722 × 1013 | 5.140 × 1013 | 65.0 |
| Infiltration water amended with NO3− | 4.085 × 1013 | 4.671 × 1013 | 83.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piekutin, J.; Kotowska, U. Model of Hydraulic Resistance When Forecasting Reverse Osmosis in Water Treatment. Membranes 2021, 11, 314. https://doi.org/10.3390/membranes11050314
Piekutin J, Kotowska U. Model of Hydraulic Resistance When Forecasting Reverse Osmosis in Water Treatment. Membranes. 2021; 11(5):314. https://doi.org/10.3390/membranes11050314
Chicago/Turabian StylePiekutin, Janina, and Urszula Kotowska. 2021. "Model of Hydraulic Resistance When Forecasting Reverse Osmosis in Water Treatment" Membranes 11, no. 5: 314. https://doi.org/10.3390/membranes11050314
APA StylePiekutin, J., & Kotowska, U. (2021). Model of Hydraulic Resistance When Forecasting Reverse Osmosis in Water Treatment. Membranes, 11(5), 314. https://doi.org/10.3390/membranes11050314







