A Study on the Evaluation of Flow Distribution Evenness in Parallel-Arrayed-Type Low-Pressure Membrane Module Piping
Abstract
1. Introduction
2. Research Methods
2.1. Membrane Filtration Process for Drinking Water Treatment
2.2. Flow Distribution Measurement Using an Ultrasonic Flow Meter
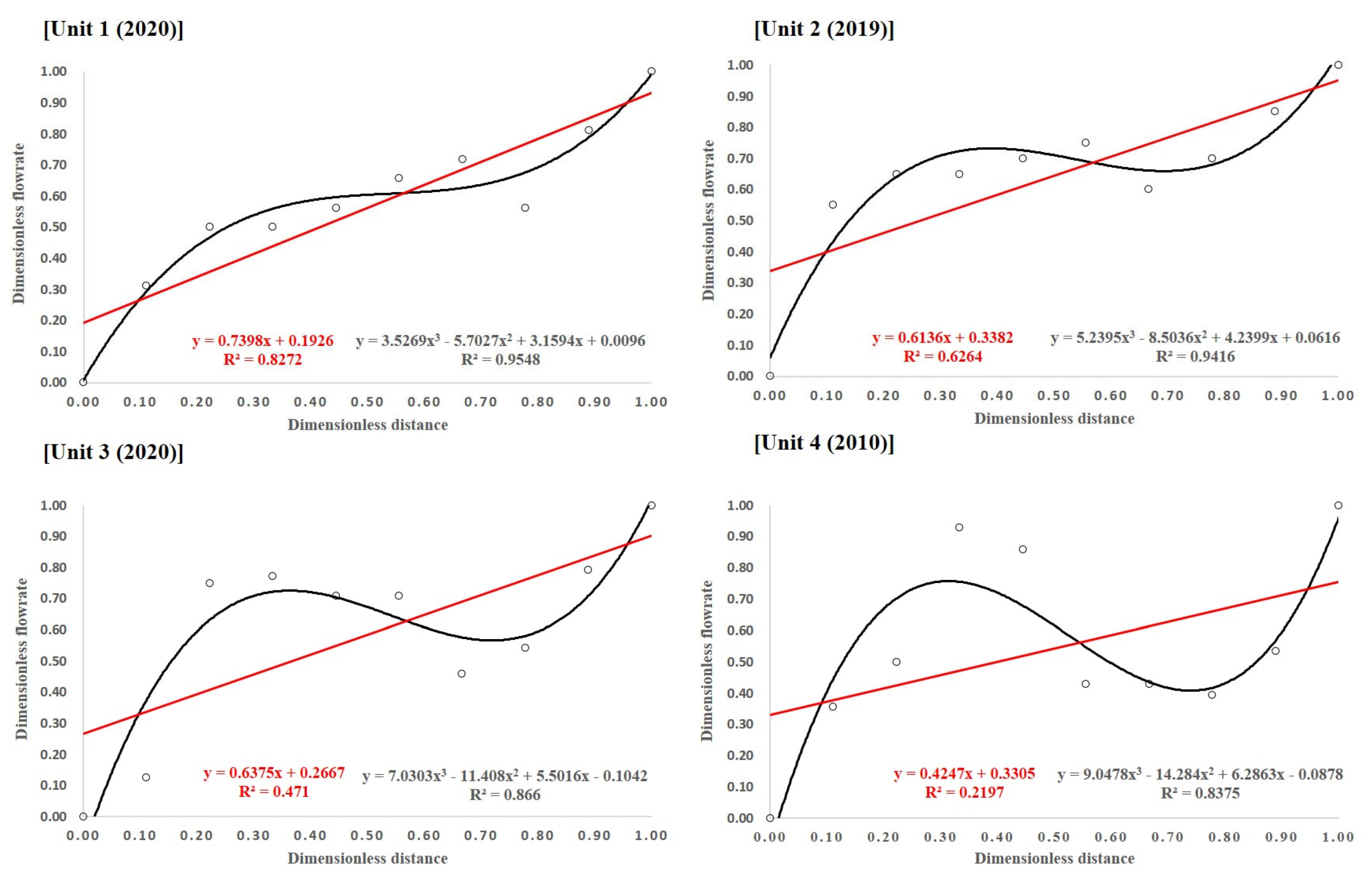
2.3. Statistical Processing of Experimental Data
2.4. Methodology of CFD Simulations
3. Results and Discussion
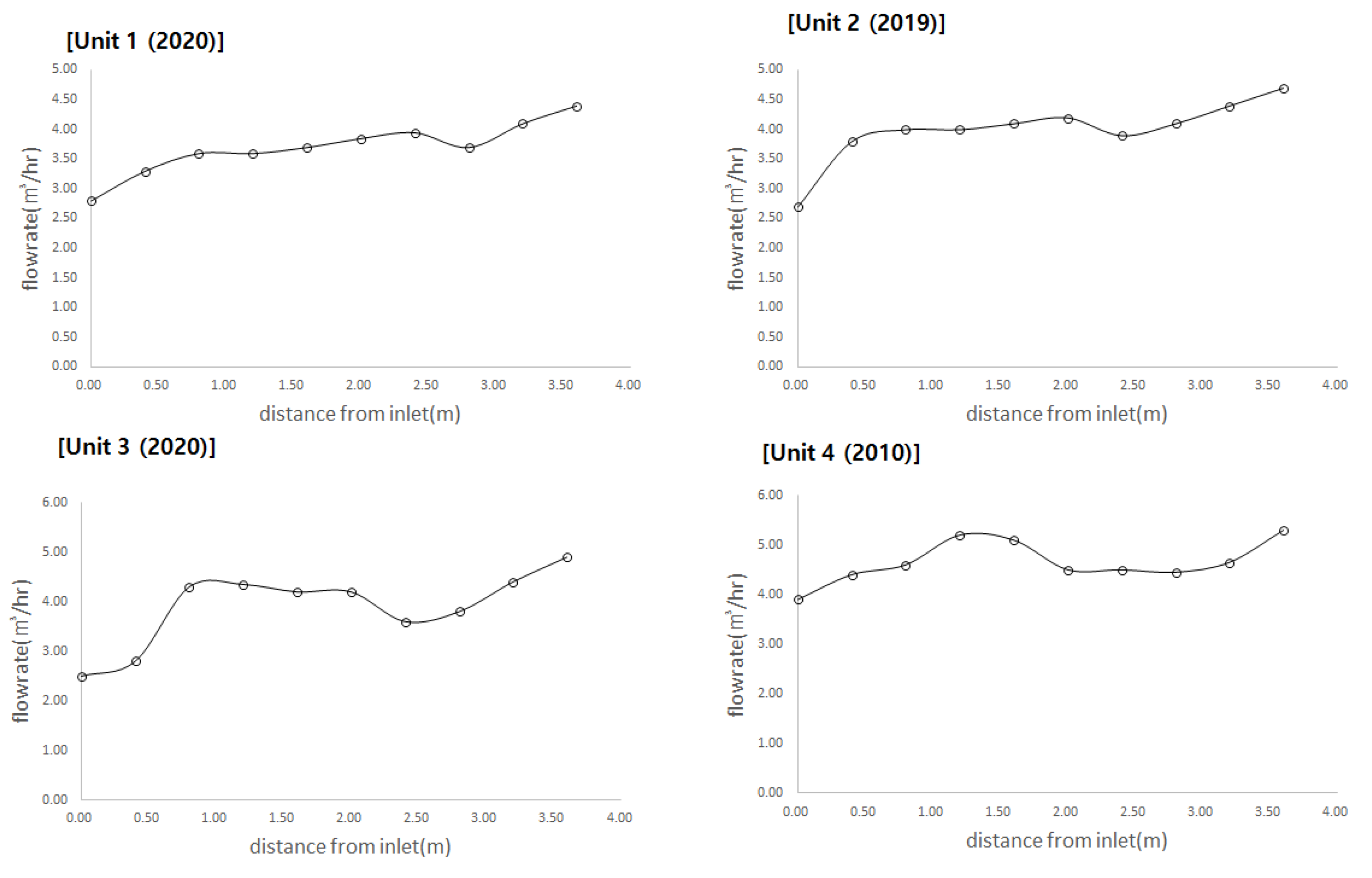
3.1. Flow Distribution Measurement Results
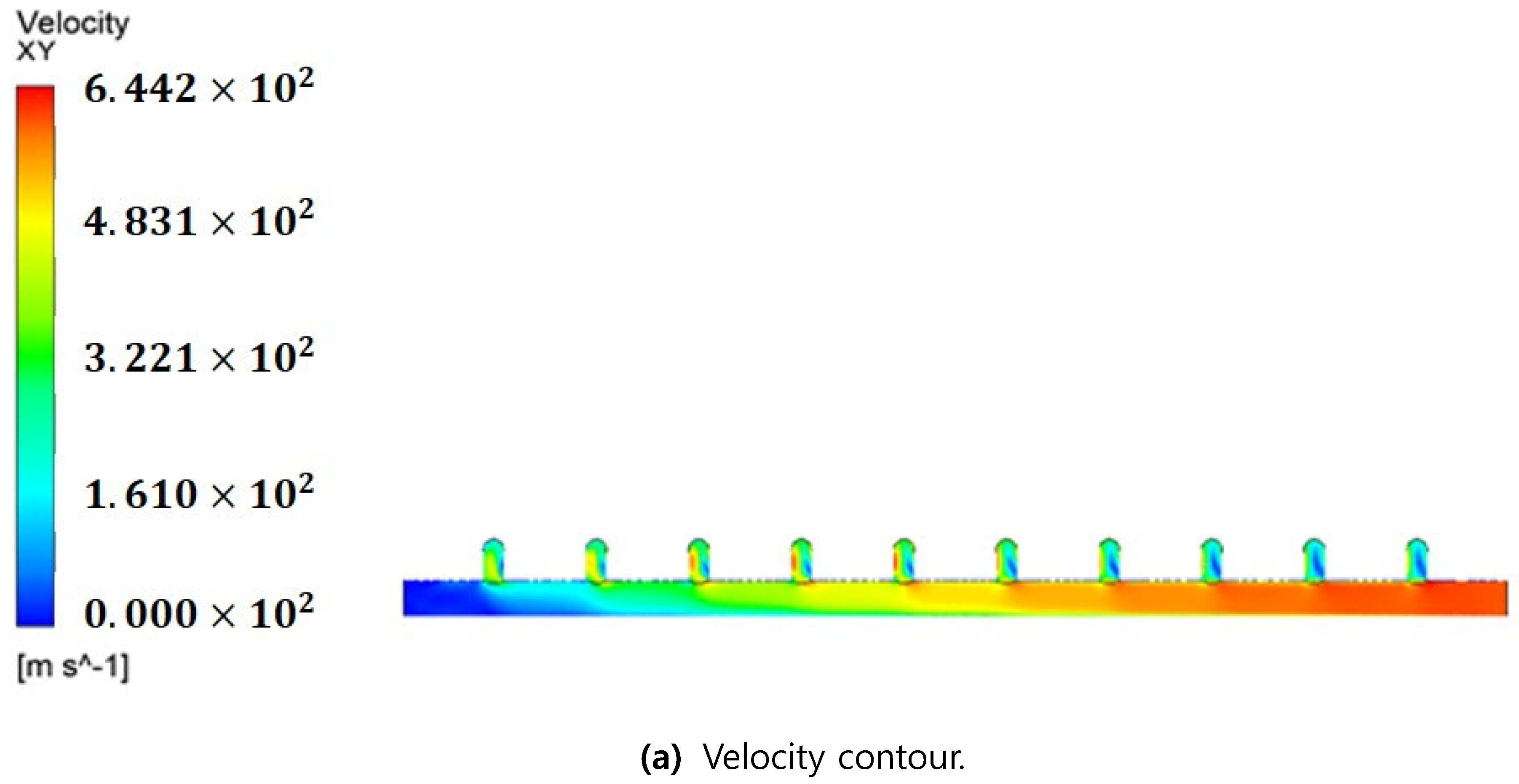
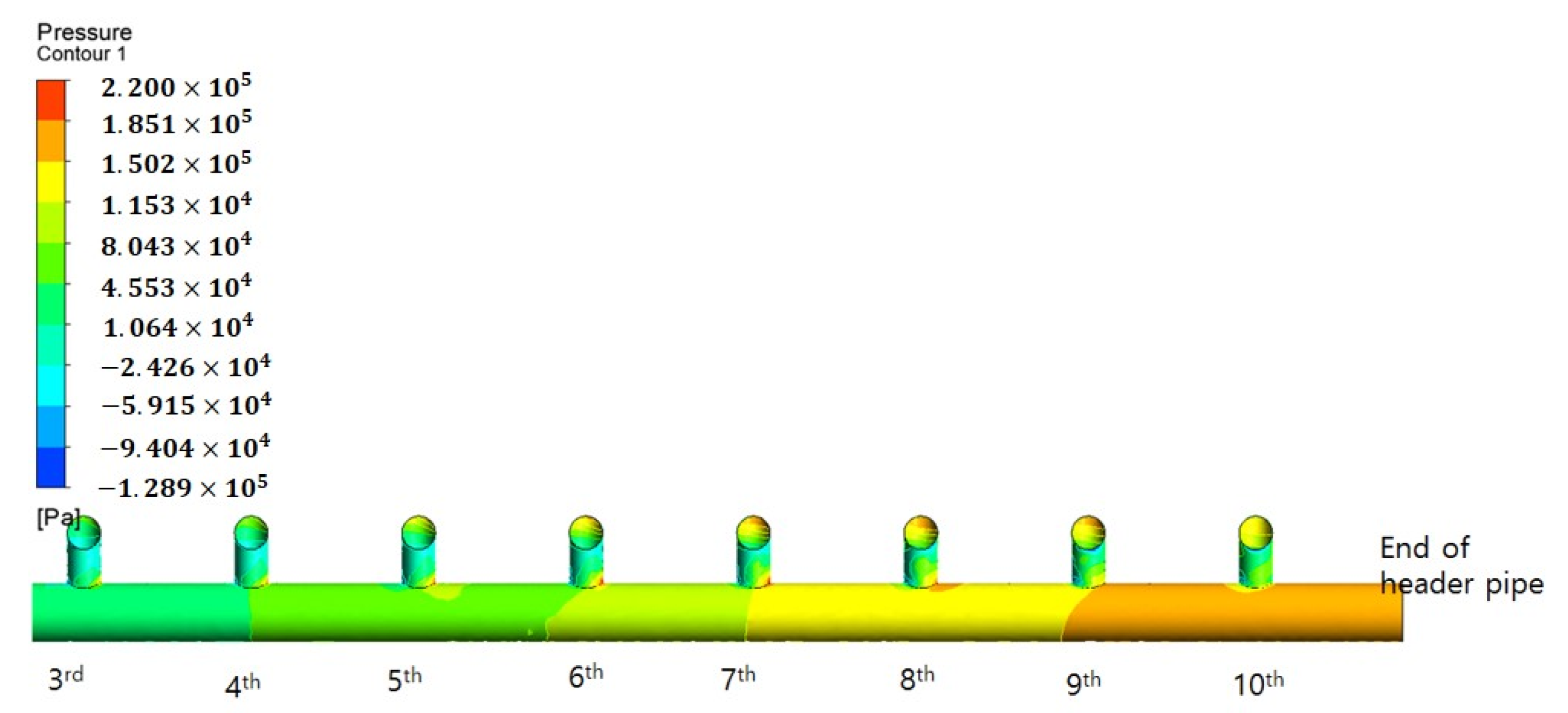
3.2. Results of CFD Simulations
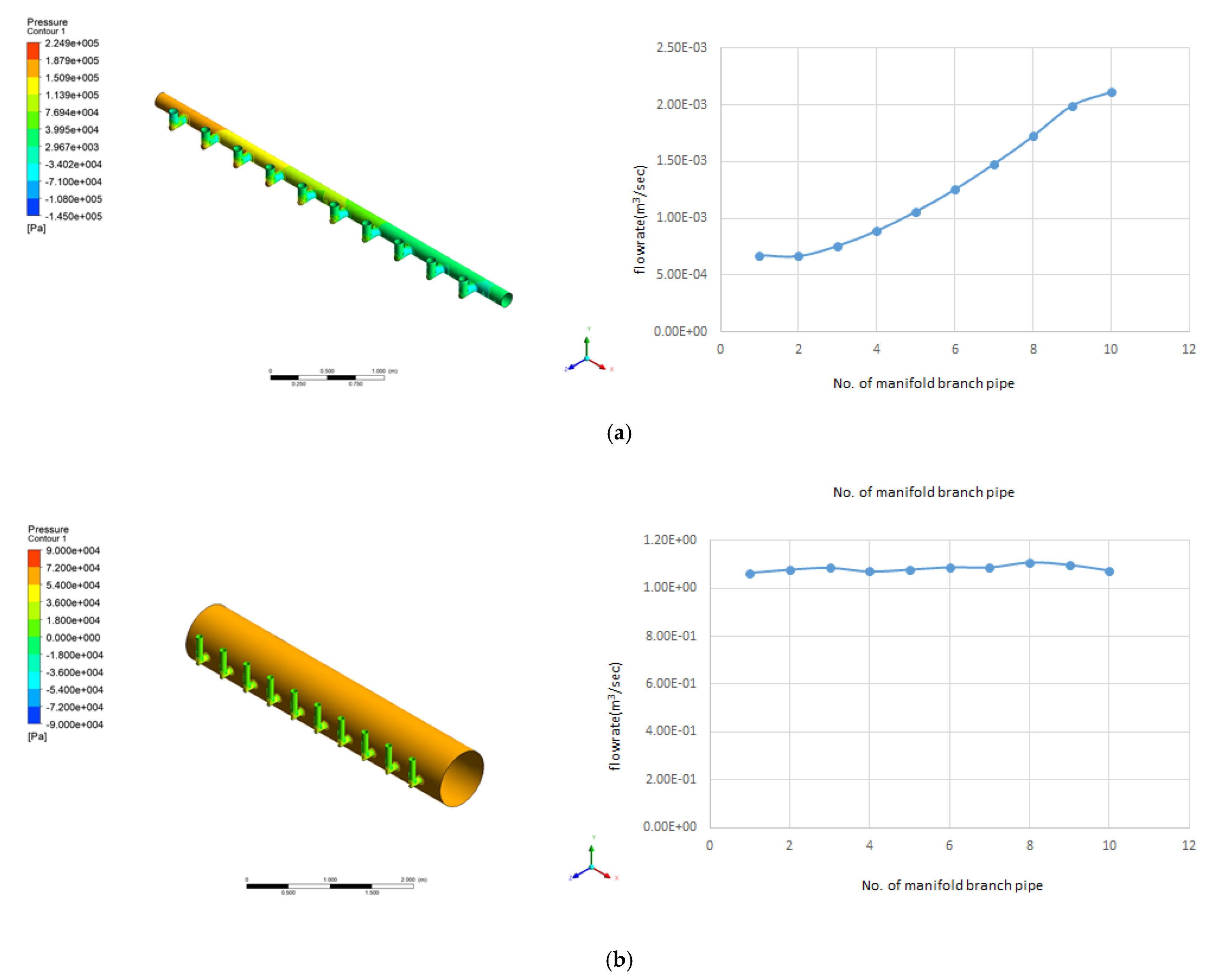
3.3. Header Pipe Cross-Sectional Area Expansion
4. Conclusions
- (1)
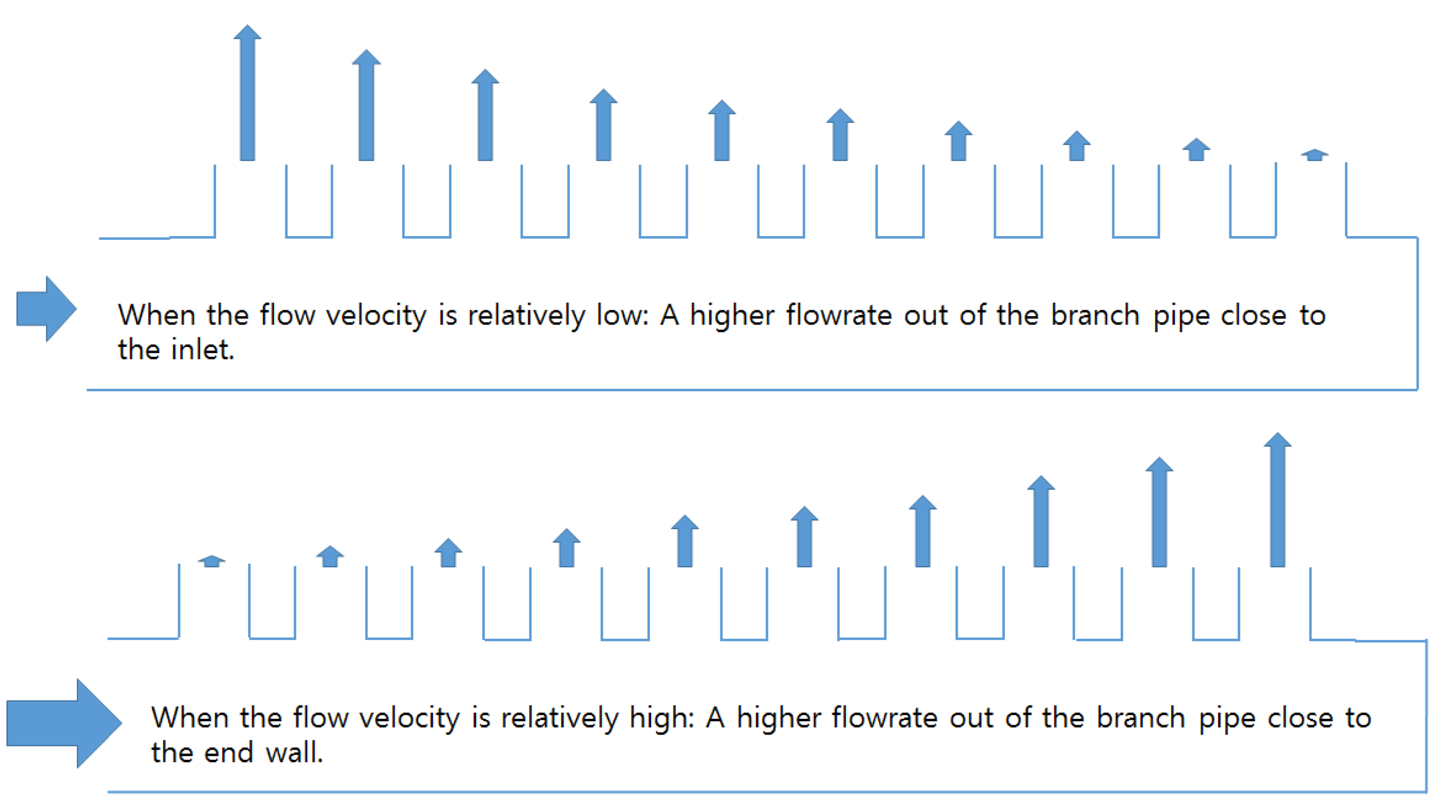
- From the actual measurement using an ultrasonic flow meter and the obtained CFD simulation results, it was verified that the flow rate increased toward the end of the header pipe, instead of the branch pipe close to the inlet in the header pipe of the membrane units. The flow rate from the first branch pipe in the inlet and the branch pipe located at the end of the header pipe differed approximately by a factor of 3.
- (2)
- The outflow into membrane modules increased toward the end of the header pipe because the pressure difference between each membrane module increased toward the end of the header pipe.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, C.; Yoon, S.; Kim, S.-S.; Park, N.-S. A Study on the Appropriateness Evaluation of Membrane Module Piping Design using CFD Simulation Technique. J. Korean Soc. Environ. Eng. 2018, 240, 103–110. [Google Scholar]
- Li, Y.L.; Tung, K.L. CFD simulation of fluid flow through spacer-filled membrane module: Selecting suitable cell types for periodic boundary conditions. Desalination 2008, 233, 351–358. [Google Scholar] [CrossRef]
- Ko, B.G.; Na, J.H.; Nam, D.H.; Kang, K.H.; Lee, C.Y. Fouling mitigation for pressurized membrane of side-stream MBR process at abnormal operation condition. J. Korean Soc. Environ. Eng. 2016, 38, 323–328. [Google Scholar] [CrossRef][Green Version]
- Hoinkis, J.; Deowan, S.A.; Panten, V.; Figoli, A.; Huang, R.R.; Drioli, E. Membrane bioreactor (MBR) technology- a promising approach for industrial water reuse. Procedia Eng. 2012, 33, 234–241. [Google Scholar] [CrossRef]
- Ahn, Y.; Kang, S.; Bae, B.U.; Lee, C.; Lee, W. Direct measurement of cake fouling potentials by powdered activated carbon during microfiltration of surface water. Desalin. Water Treat. 2016, 57, 7449–7455. [Google Scholar] [CrossRef]
- Kim, S.H.; Moon, S.Y.; Yoon, C.H.; Yim, S.K.; Cho, J.W. Role of coagulation in membrane filtration of wastewater for reuse. Desalination 2005, 173, 301–307. [Google Scholar] [CrossRef]
- Shen, P.I. The effect of friction on flow distribution in dividing and combining flow manifold. J. Fluids Eng. Trans. ASME 1992, 114, 121–123. [Google Scholar] [CrossRef]
- Choi, S.H.; Shin, S.; Cho, Y.I. The effect of area ratio on the flow distribution in liquid cooling module manifolds for electronic packaging. Int. Comm. Heat Mass Transf. 1993, 20, 221–234. [Google Scholar] [CrossRef]
- Datta, A.B.; Majumdar, A.K. Flow distribution in parallel and reverse flow manifolds. Int. J. Heat Fluid Flow 1990, 2, 253–262. [Google Scholar] [CrossRef]
- Eguchi, A.; Kuragasaki, M.; Sueoka, Y. Performance improvement on ACDEFLO headbox of paper machine. Mitsubishi Heavy Ind. Tech. Rev. 1988, 25, 191–196. [Google Scholar]
- Hong, J.C.; Riggs, J.B. Flow distribution in tapered, rectangular cross section manifolds. J. Chin. Inst. Chem. Eng. 1987, 18, 193–202. [Google Scholar]
- Muhana, A.; Novog, D.R. Validation of fluent for prediction of flow distribution and pressure gradients in a multi-branch header under low flow conditions. In Proceedings of the 16th International Conference on Nuclear Engineering, ICONE16, Orlando, FL, USA, 28 May 2008. [Google Scholar]
- Ding, W.; Shuyang, J.S. Application of CFD in Membrane Technique. Doctor Dissertation, Universität Duisburg-Essen, Duisburg and Essen, Germany, 2012. Available online: https://d-nb.info/1035066459/34 (accessed on 15 July 2021).
- Chang, P.A.; St-Pierre, J.; Stumper, J.; Wetton, B. Flow distribution in proton exchange membrane fuel cell stacks. J. Power Sour. 2006, 162, 340–355. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, H.D.; Lee, H.J.; Hwang, S.Y. A CFD Analysis of Gas Flow through an Ultrasonic meter. In Proceedings of the KSME Conference; The Korean Society of Mechanical Engineer: Seoul, Korea, 2003; pp. 998–1003. [Google Scholar]
- Oh, J.I.; Choi, J.W.; Lim, J.L.; Kim, D.; Park, N.S. A Study on Hydraulic Modifications of Low-Pressure Membrane Inlet Structure with CFD and PIV Techniques. J. Korean Soc. Environ. Eng. 2015, 37, 607–618. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS CFX-Solver Modeling Guide Release 15.0; ANSYS, Inc.: Canonsburg, PA, USA, 2013; Available online: https://manualzz.com/doc/42882899/cfx-solver-modeling-guide (accessed on 8 May 2021).
- Park, J.; Yoon, S.; Kim, S.; Park, N. Physical Modifications for improving inlet flow distribution evenness in multiple parallel-arrayed membrane modules. Desalin. Water Treat. 2018, 119, 1–8. [Google Scholar] [CrossRef]



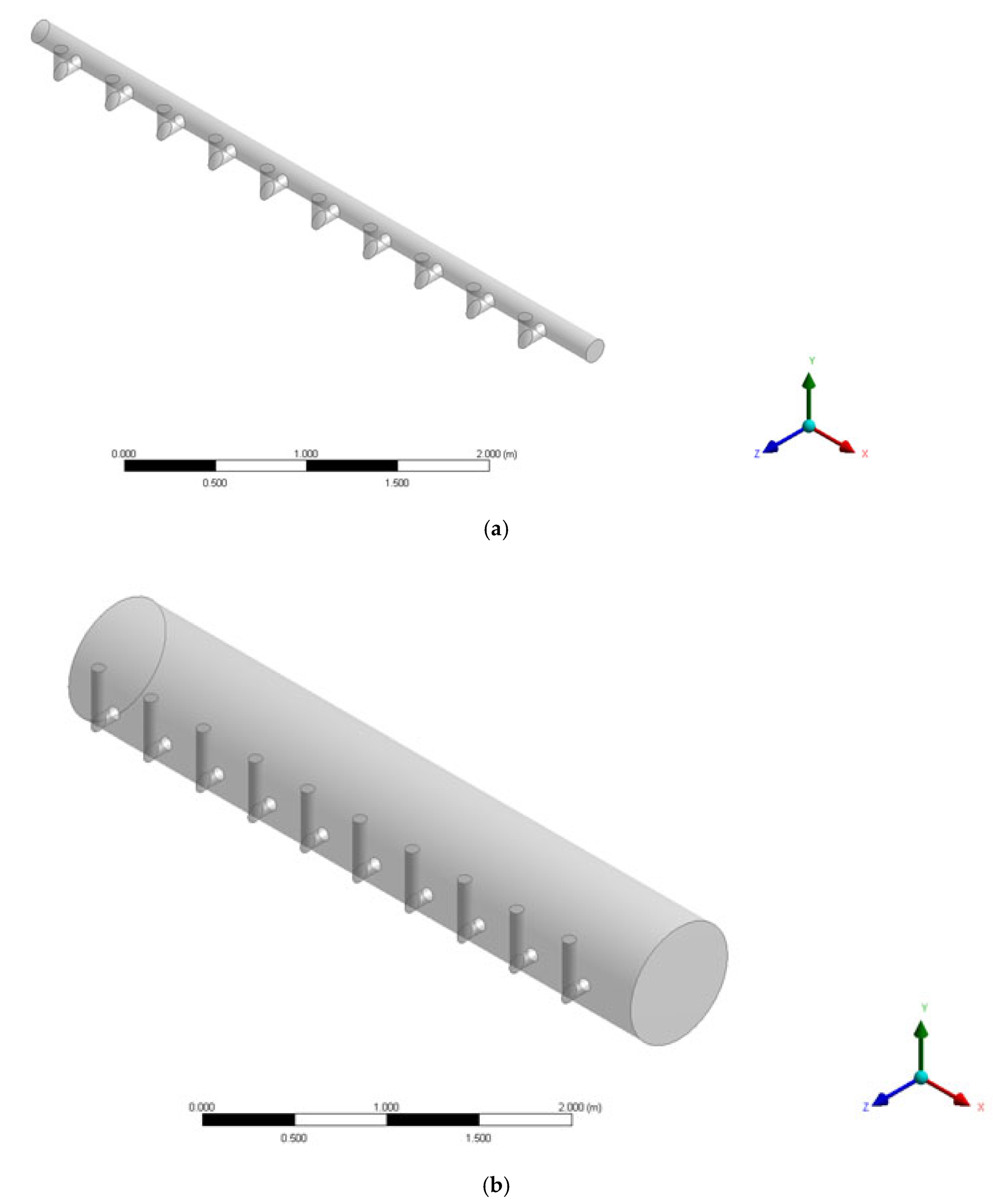


| Membrane manufacturer | Toray, HFS-2020 |
| Membrane type | Microfiltration (MF) |
| Membrane module shape | External-pressure-type hollow fiber membrane (casing) |
| Hollow fiber | Inner D 0.9 mm/external D 1.4 mm |
| Pore size | 0.05 µm |
| Membrane material | PVDF |
| Flux | (Ordinary) 1.0 m3/m2·day (Max.) 1.33 m3/m2·day |
| Module Size | D 216 mm × L 2160 mm |
| Membrane area | 72 m2/module |
| Allowable pressure | 300 kPa |
| Allowable pH | 1~10 at filtration, 1~12 at chemical cleaning |
| Flow Meter | PT878 | Transducer Type | Clamp-On |
|---|---|---|---|
| Flow type | All acoustically conductive fluids | Applications | Liquid |
| Pipe size | 12.7 mm~7.6 m | Compatible meters | PT878 |
| Pipe wall thickness | Up to 76.2 mm | Frequency | 1MHz |
| Pipe materials | All metals and most plastics | Process temp. | −20–210 °C |
| Repeatability | ±0.1% to 0.3% of reading | Ambient temp. | −20–40 °C |
| Range | −12.2 to 12.2 m/s | Materials of construction | Metals and plastics |
| Range ability | 400:1 | - | - |
| Measurement parameters | Volumetric flow, totalized flow, and flow velocity | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, N.-S.; Yoon, S.; Jeong, W.; Jeong, Y.-W. A Study on the Evaluation of Flow Distribution Evenness in Parallel-Arrayed-Type Low-Pressure Membrane Module Piping. Membranes 2021, 11, 751. https://doi.org/10.3390/membranes11100751
Park N-S, Yoon S, Jeong W, Jeong Y-W. A Study on the Evaluation of Flow Distribution Evenness in Parallel-Arrayed-Type Low-Pressure Membrane Module Piping. Membranes. 2021; 11(10):751. https://doi.org/10.3390/membranes11100751
Chicago/Turabian StylePark, No-Suk, Sukmin Yoon, Woochang Jeong, and Yong-Wook Jeong. 2021. "A Study on the Evaluation of Flow Distribution Evenness in Parallel-Arrayed-Type Low-Pressure Membrane Module Piping" Membranes 11, no. 10: 751. https://doi.org/10.3390/membranes11100751
APA StylePark, N.-S., Yoon, S., Jeong, W., & Jeong, Y.-W. (2021). A Study on the Evaluation of Flow Distribution Evenness in Parallel-Arrayed-Type Low-Pressure Membrane Module Piping. Membranes, 11(10), 751. https://doi.org/10.3390/membranes11100751






