Electrical Properties of Membrane Phospholipids in Langmuir Monolayers
Abstract
1. Introduction
2. Materials and Methods
2.1. Surface Potential Measurements
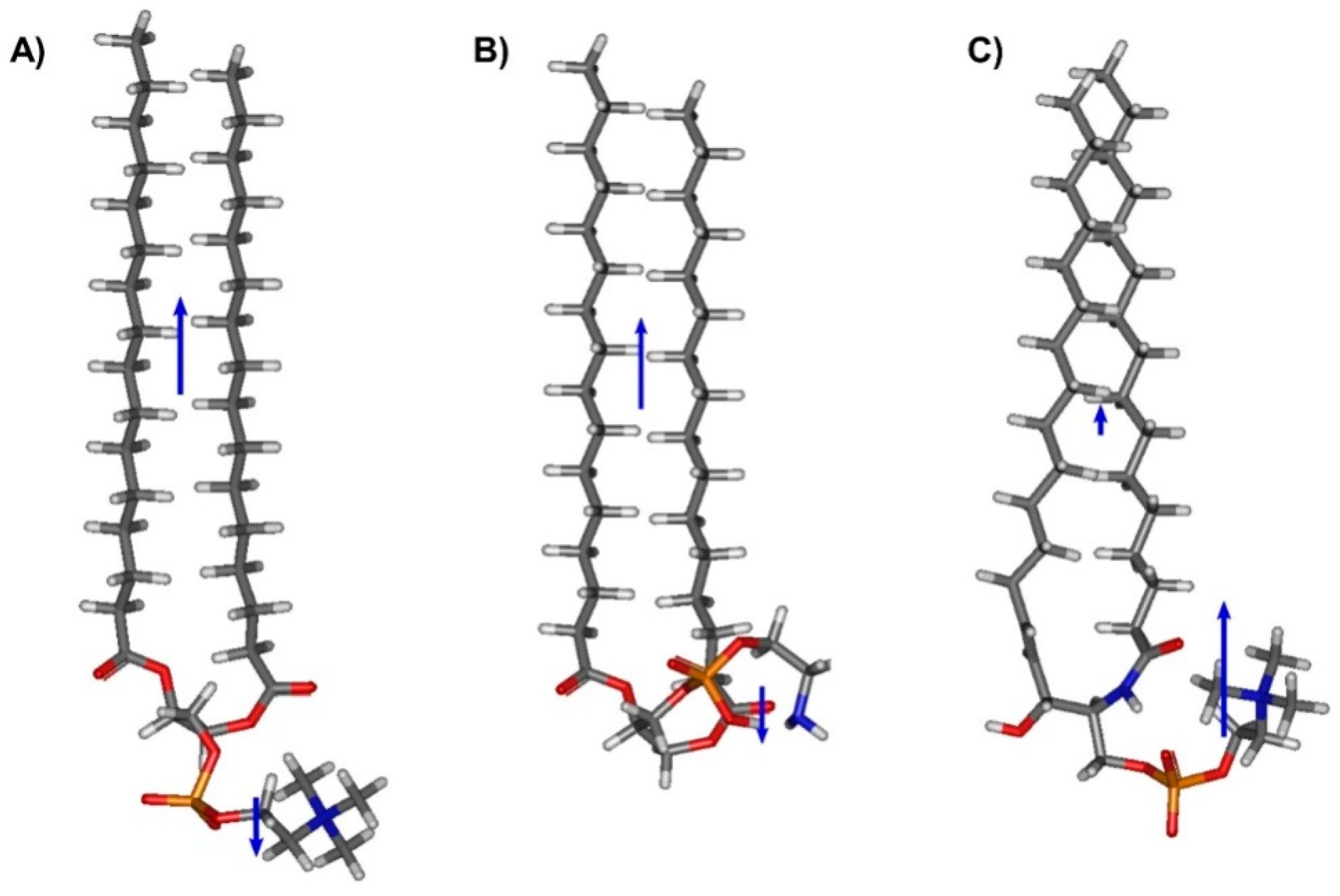
2.2. Theoretical Calculations
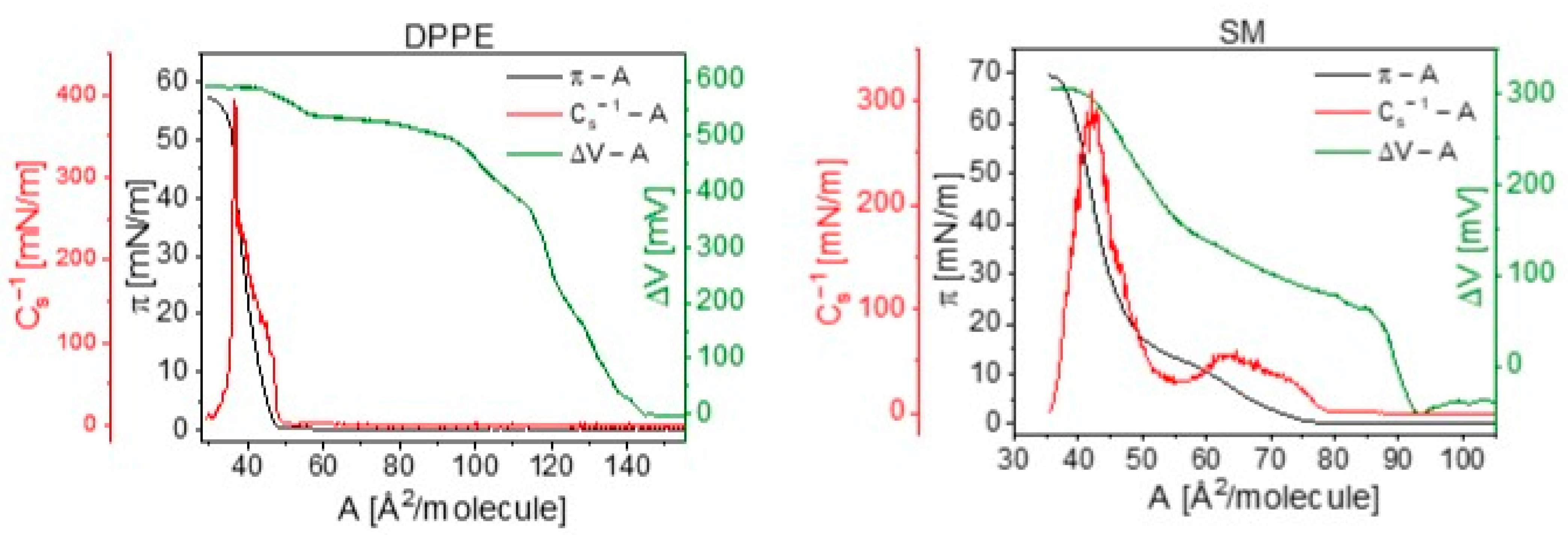
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Barnes, G.; Gentle, I. Interfacial Science: An Introduction, 2nd ed.; Oxford University Press: Oxford, UK, 2011; ISBN 9780199571185. [Google Scholar]
- Daear, W.; Mahadeo, M.; Prenner, E.J. Applications of Brewster angle microscopy from biological materials to biological systems. Biochim. Biophys. Acta Biomembr. 2017, 1859, 1749–1766. [Google Scholar] [CrossRef] [PubMed]
- Stottrup, B.L.; Nguyen, A.H.; Tüzel, E. Taking another look with fluorescence microscopy: Image processing techniques in Langmuir monolayers for the twenty-first century. Biochim. Biophys. Acta Biomembr. 2010, 1798, 1289–1300. [Google Scholar] [CrossRef] [PubMed]
- Nobre, T.M.; Pavinatto, F.J.; Caseli, L.; Barros-Timmons, A.; Dynarowicz-Łatka, P.; Oliveira, O.N. Interactions of bioactive molecules & nanomaterials with Langmuir monolayers as cell membrane models. Thin Solid Films 2015, 593, 158–188. [Google Scholar]
- Jaroque, G.N.; Sartorelli, P.; Caseli, L. The effect of the monocyclic monoterpene tertiary alcohol γ-terpineol on biointerfaces containing cholesterol. Chem. Phys. Lipids 2020, 230, 104915. [Google Scholar] [CrossRef]
- Ceridório, L.F.; Caseli, L.; Oliveira, O.N. Chondroitin sulfate interacts mainly with headgroups in phospholipid monolayers. Colloids Surf. B. Biointerfaces 2016, 141, 595–601. [Google Scholar] [CrossRef]
- Nakahara, H.; Hagimori, M.; Mukai, T.; Shibata, O. Monolayers of a tetrazine-containing gemini amphiphile: Interplays with biomembrane lipids. Colloids Surf. B. Biointerfaces 2018, 164, 1–10. [Google Scholar] [CrossRef]
- Nakahara, H.; Hagimori, M.; Mukai, T.; Shibata, O. Interactions of a Tetrazine Derivative with Biomembrane Constituents: A Langmuir Monolayer Study. Langmuir 2016, 32, 6591–6599. [Google Scholar] [CrossRef]
- Dynarowicz, P. Recent developments in the modeling of the monolayers structure at the water/air interface. Adv. Colloid Interface Sci. 1993, 45, 215–241. [Google Scholar] [CrossRef]
- Oliveira, O.N.; Bonardi, C. The Surface Potential of Langmuir Monolayers Revisited. Langmuir 1997, 13, 5920–5924. [Google Scholar] [CrossRef]
- Adam, N.K.; Danielli, J.F.; Harding J., B. The structure of surface films XXI—Surface potentials of dibasic esters, alcohols, aldoximes, and ketones. Proc. Math. Phys. Eng. Sci. 1934, 147, 491–499. [Google Scholar]
- Schuhmann, D. Electrical properties of adsorbed or spread films: The effective value of permittivities in the Helmholtz equation (plane distribution of point dipoles). J. Colloid Interface Sci. 1990, 134, 152–160. [Google Scholar] [CrossRef]
- Broniatowski, M.; Macho, I.S.; Miñones, J.; Dynarowicz-Łatka, P. Langmuir monolayers characteristic of (Perfluorodecyl)-alkanes. J. Phys. Chem. B. 2004, 108, 13403–13411. [Google Scholar] [CrossRef]
- Shibata, O.; Krafft, M.P. Mixed Langmuir monolayers made from single-chain perfluoroalkylated amphiphiles. Langmuir 2000, 16, 10281–10286. [Google Scholar] [CrossRef]
- Oliveira, O.N.; Taylor, D.M.; Morgan, H. Modelling the surface potential-area dependence of a stearic acid monolayer. Thin Solid Films 1992, 210–211, 76–78. [Google Scholar] [CrossRef]
- Demchak, R.J.; Fort, T. Surface dipole moments of close-packed un-ionized monolayers at the air-water interface. J. Colloid Interface Sci. 1974, 46, 191–202. [Google Scholar] [CrossRef]
- Dynarowicz, P.; Paluch, M. Electrical properties of some adsorbed films at the water-air interface. J. Colloid Interface Sci. 1985, 107, 75–80. [Google Scholar] [CrossRef]
- Oliveira, O.N.; Taylor, D.M.; Lewis, T.J.; Salvagno, S.; Stirling, C.J.M. Estimation of group dipole moments from surface potential measurements on Langmuir monolayers. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1989, 85, 1009–1018. [Google Scholar] [CrossRef]
- Petrov, J.G.; Polymeropoulos, E.E.; Möhwald, H. Three-capacitor model for surface potential of insoluble monolayers. J. Phys. Chem. 1996, 100, 9860–9869. [Google Scholar] [CrossRef]
- Mozaffary, H. On the sign and origin of the surface potential of phospholipid monolayers. Chem. Phys. Lipids 1991, 59, 39–47. [Google Scholar] [CrossRef]
- Beitinger, H.; Vogel, V.; Möbius, D.; Rahmann, H. Surface potentials and electric dipole moments of ganglioside and phospholipid monolayers: Contribution of the polar headgroup at the water/lipid interface. Biochim. Biophys. Acta Biomembr. 1989, 984, 293–300. [Google Scholar] [CrossRef]
- Smaby, J.M.; Brockman, H.L. Surface dipole moments of lipids at the argon-water interface. Similarities among glycerol-ester-based lipids. Biophys. J. 1990, 58, 195–204. [Google Scholar] [CrossRef]
- Nakahara, H.; Nakamura, S.; Nakamura, K.; Inagaki, M.; Aso, M.; Higuchi, R.; Shibata, O. Cerebroside Langmuir monolayers originated from the echinoderms: I. Binary systems of cerebrosides and phospholipids. Colloids Surf. B. Biointerfaces 2005, 42, 157–174. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, S.; Nakahara, H.; Shibata, O. Miscibility behavior of sphingomyelin with phytosterol derivatives by a Langmuir monolayer approach. J. Oleo Sci. 2013, 62, 809–824. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Stefaniu, C.; Brezesinski, G.; Möhwald, H. Polymer-capped magnetite nanoparticles change the 2D structure of DPPC model membranes. Soft Matter 2012, 8, 7952–7959. [Google Scholar] [CrossRef]
- Kilic, S.; Bolukcu, E.S. Phase behavior of DSPC/PEG40St mixtures at higher emulsifier contents. Colloids Surf. B. Biointerfaces 2018, 171, 368–376. [Google Scholar] [CrossRef]
- Borden, M.A.; Pu, G.; Runner, G.J.; Longo, M.L. Surface phase behavior and microstructure of lipid/PEG-emulsifier monolayer-coated microbubbles. Colloids Surf. B Biointerfaces 2004, 35, 209–223. [Google Scholar] [CrossRef] [PubMed]
- Raju, R.; Torrent-Burgués, J.; Bryant, G. Interactions of cryoprotective agents with phospholipid membranes—A Langmuir monolayer study. Chem. Phys. Lipids 2020, 231, 104949. [Google Scholar] [CrossRef] [PubMed]
- Korchowiec, B.; Paluch, M.; Corvis, Y.; Rogalska, E. A Langmuir film approach to elucidating interactions in lipid membranes: 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine/cholesterol/metal cation systems. Chem. Phys. Lipids 2006, 144, 127–136. [Google Scholar] [CrossRef] [PubMed]
- Wnętrzak, A.; Makyła-Juzak, K.; Filiczkowska, A.; Kulig, W.; Dynarowicz-Latka, P. Oxysterols Versus Cholesterol in Model Neuronal Membrane. I. The Case of 7-Ketocholesterol. The Langmuir Monolayer Study. J. Membr. Biol. 2017, 250, 553–564. [Google Scholar] [CrossRef] [PubMed]
- Davies, J.T.; Rideal, E.K. Interfacial phenomena; Academic Press: Cambridge, MA, USA, 1963; ISBN 9780123956095. [Google Scholar]
- Gragson, D.E.; Beaman, D.; Porter, R. Using compression isotherms of phospholipid monolayers to explore critical phenomena. A biophysical chemistry experiment. J. Chem. Educ. 2008, 85, 272–275. [Google Scholar] [CrossRef]
- Taylor, D.M.; De Oliveira, O.N.; Morgan, H. Models for interpreting surface potential measurements and their application to phospholipid monolayers. J. Colloid Interface Sci. 1990, 139, 508–518. [Google Scholar] [CrossRef]
- Sanchez, J.; Badia, A. Spatial variation in the molecular tilt orientational order within the solid domains of phase-separated, mixed dialkylphosphatidylcholine monolayers. Chem. Phys. Lipids 2008, 152, 24–37. [Google Scholar] [CrossRef]
- Peterson, U.; Mannock, D.A.; Lewis, R.N.A.H.; Pohl, P.; McElhaney, R.N.; Pohl, E.E. Origin of membrane dipole potential: Contribution of the phospholipid fatty acid chains. Chem. Phys. Lipids 2002, 117, 19–27. [Google Scholar] [CrossRef]
- Pasenkiewicz-Gierula, M.; Baczynski, K.; Markiewicz, M.; Murzyn, K. Computer modelling studies of the bilayer/water interface. Biochim. Biophys. Acta Biomembr. 2016, 1858, 2305–2321. [Google Scholar] [CrossRef] [PubMed]
- Disalvo, E.A.; Lairion, F.; Martini, F.; Almaleck, H.; Diaz, S.; Gordillo, G. Water in biological membranes at interfaces: Does it play a functional role? An. des la Asoc. Quim. Argentina 2004, 92, 1–22. [Google Scholar]
- Kodama, M.; Abe, M.; Kawasaki, Y.; Hayashi, K.; Ohira, S.; Nozaki, H.; Katagiri, C.; Inoue, K.; Takahashi, H. Estimation of interlamellar water molecules in sphingomyelin bilayer systems studied by DSC and X-ray diffraction. Thermochim. Acta 2004, 416, 105–111. [Google Scholar]



| Phospholipid | ||||||
|---|---|---|---|---|---|---|
| DPPC 1 | 96.2 | 139.0 | 47.8 | 509 | 0.64 | 0.05 |
| DSPC 2 | 57.2 | 96.2 | 45.8 | 684 | 0.83 | 0.05 |
| DAPC 3 | 58.5 | 82.6 | 43.7 | 614 | 0.71 | 0.05 |
| DOPC 4 | 116.8 | 162.3 | 64.0 | 358 | 0.61 | 0.04 |
| DPPE 5 | 62.2 | 144.2 | 47.7 | 573 | 0.73 | 0.05 |
| SM 6 | 78.3 | 92.9 | 42.0 | 295 | 0.33 | 0.03 |
| Phospholipid | Molecular Dipole Moment in Vacuum (D) | Group Dipole Moment (D) | |||
|---|---|---|---|---|---|
| DPPC | 13.07 | 13.05 | 0.66 | −1.89 | 2.55 |
| DSPC | 13.01 | 13.00 | 0.55 | −2.16 | 2.71 |
| DAPC | 13.07 | 13.02 | 1.06 | −1.43 | 2.49 |
| DOPC | 13.04 | 11.88 | 5.39 | 3.40 | 1.99 |
| DPPE | 8.63 | 8.57 | 0.94 | −1.00 | 1.94 |
| SM | 14.33 | 9.94 | 10.33 | 10.30 | 0.03 |
| Phospholipid | Apparent Dipole Moment (D) | |||
|---|---|---|---|---|
| DPPC | 0.32 | 0.60 | 0.44 | 0.68 |
| DSPC | 0.27 | 0.57 | 0.40 | 0.83 |
| DAPC | 0.27 | 0.55 | 0.40 | 0.67 |
| DOPC | 0.86 | 1.18 | 0.96 | 0.61 |
| DPPE | 0.27 | 0.47 | 0.37 | 0.13 |
| SM | 1.40 | 1.55 | 1.40 | −0.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chachaj-Brekiesz, A.; Kobierski, J.; Wnętrzak, A.; Dynarowicz-Latka, P. Electrical Properties of Membrane Phospholipids in Langmuir Monolayers. Membranes 2021, 11, 53. https://doi.org/10.3390/membranes11010053
Chachaj-Brekiesz A, Kobierski J, Wnętrzak A, Dynarowicz-Latka P. Electrical Properties of Membrane Phospholipids in Langmuir Monolayers. Membranes. 2021; 11(1):53. https://doi.org/10.3390/membranes11010053
Chicago/Turabian StyleChachaj-Brekiesz, Anna, Jan Kobierski, Anita Wnętrzak, and Patrycja Dynarowicz-Latka. 2021. "Electrical Properties of Membrane Phospholipids in Langmuir Monolayers" Membranes 11, no. 1: 53. https://doi.org/10.3390/membranes11010053
APA StyleChachaj-Brekiesz, A., Kobierski, J., Wnętrzak, A., & Dynarowicz-Latka, P. (2021). Electrical Properties of Membrane Phospholipids in Langmuir Monolayers. Membranes, 11(1), 53. https://doi.org/10.3390/membranes11010053






