Filtration of Elastic Polymers and Spherical Gels through a Silica-Deposited Layer on a Porous Membrane
Abstract
1. Introduction
2. Theory
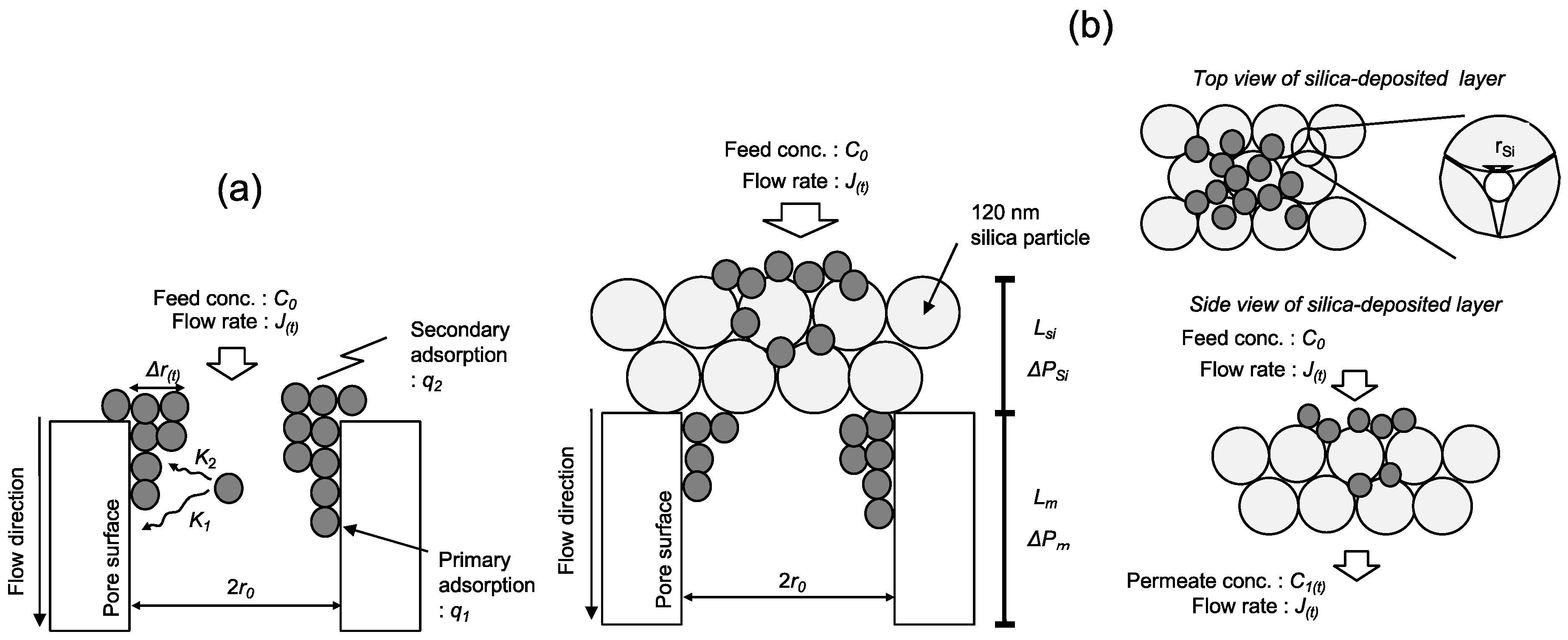
2.1. Calculation of Silica Layer Thickness
2.2. Mathematical Model of Filtration by the PE Membrane
2.3. Mathematical Model of Filtration by the Silica-Deposited Membrane
3. Experiments
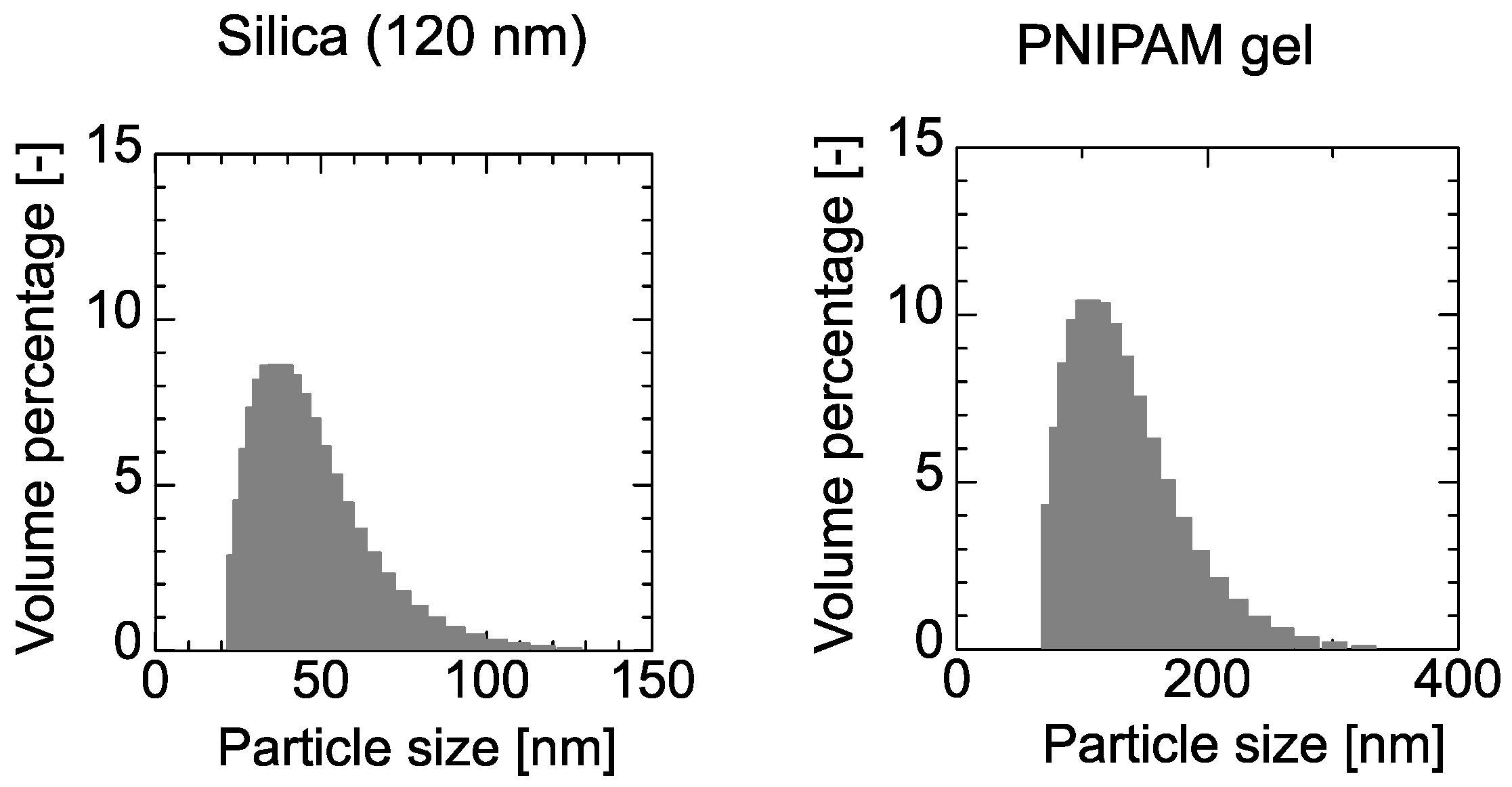
3.1. Materials
3.2. Preparation of PNIPAM Gel
3.3. Batch-Mode Adsorption of PNIPAM Gel and Dextran to the PE Membrane and 120-nm Silica
3.4. Deposition of Silica on the PE Membrane
3.5. Permeation of Colloidal Suspension through the Membrane
4. Results
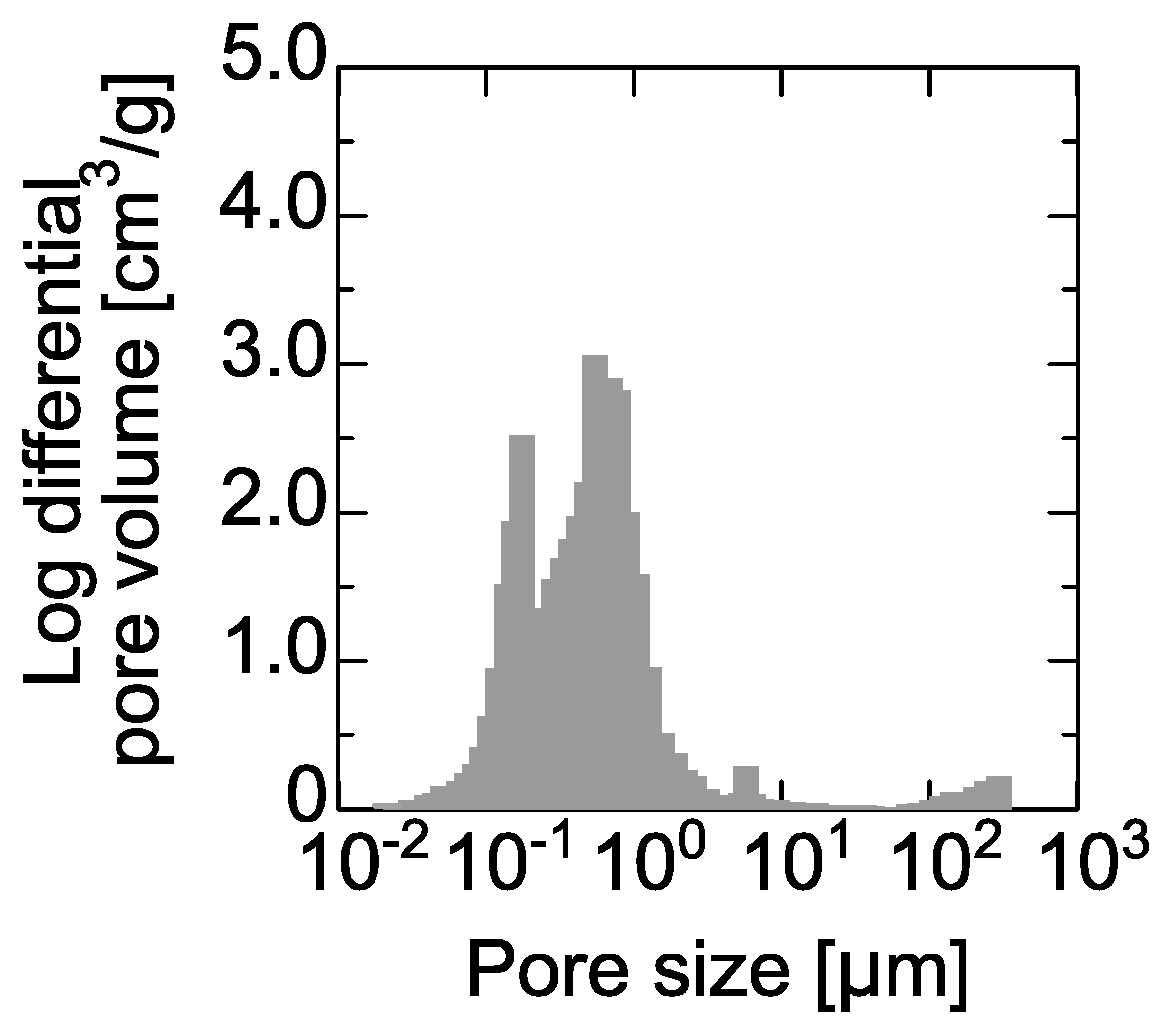
4.1. Silica Deposition on PE Membrane Surface
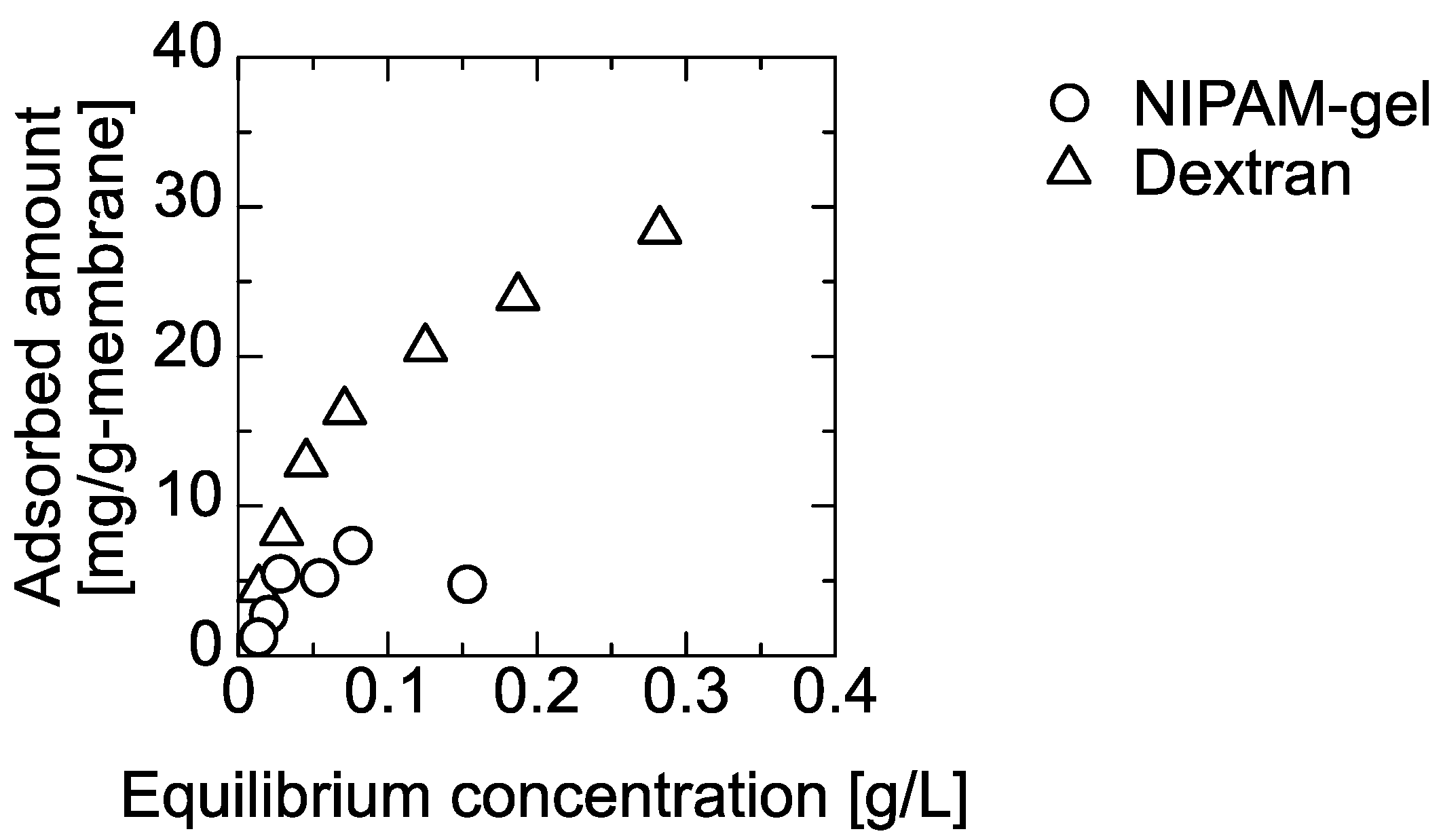
4.2. Adsorption of PNIPAM Gel and Dextran on the PE Membrane and 120-nm Silica
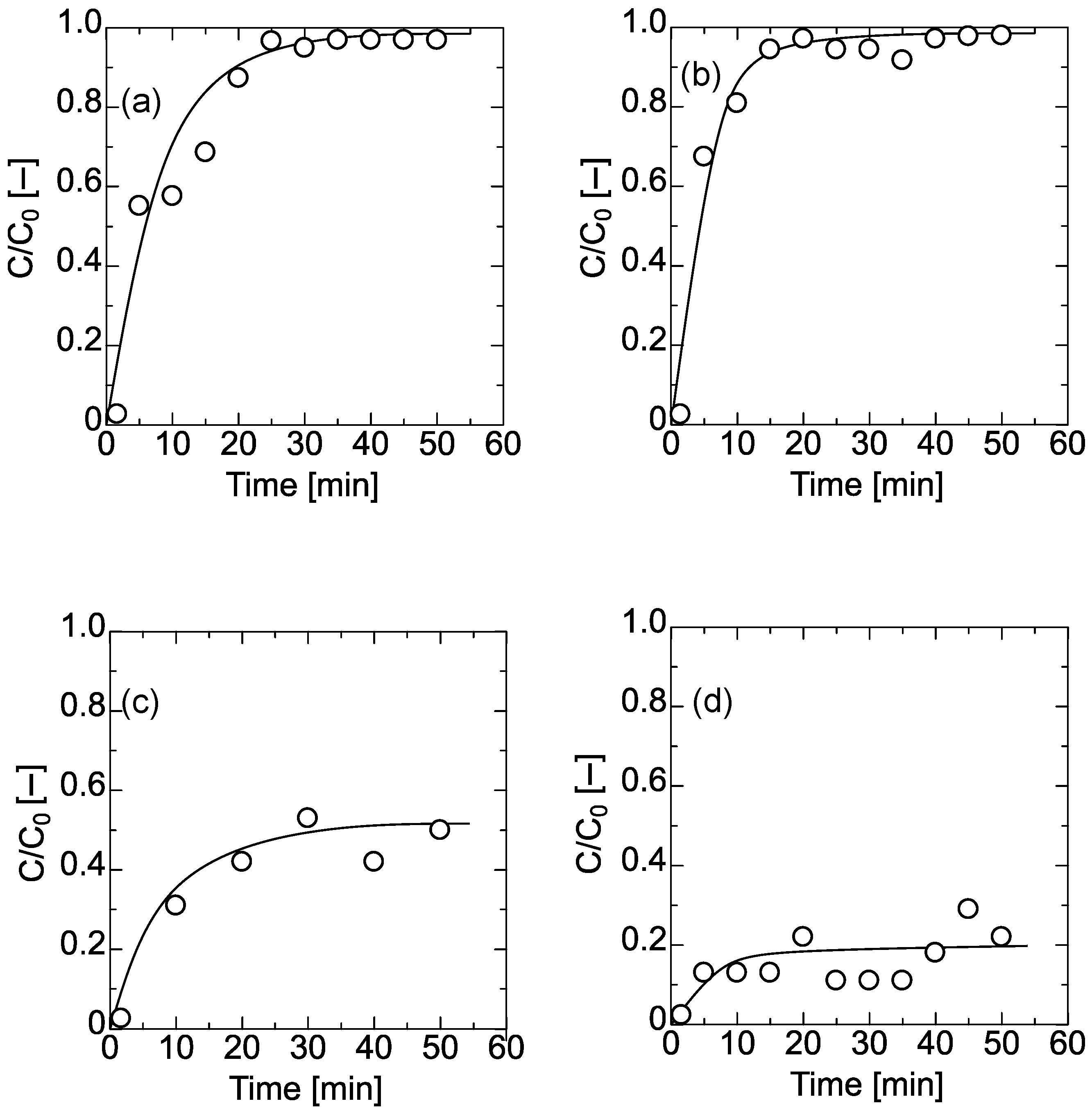
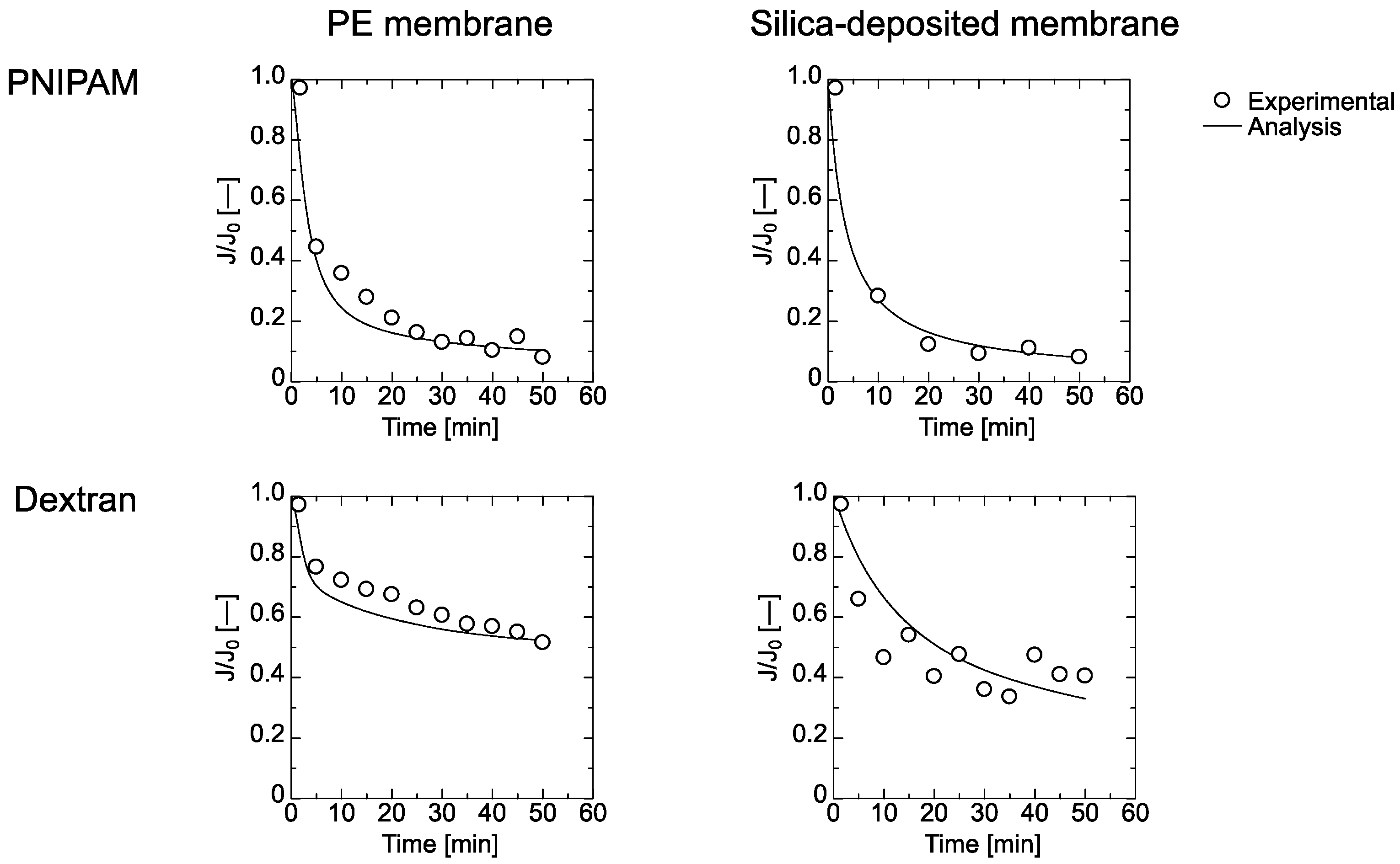
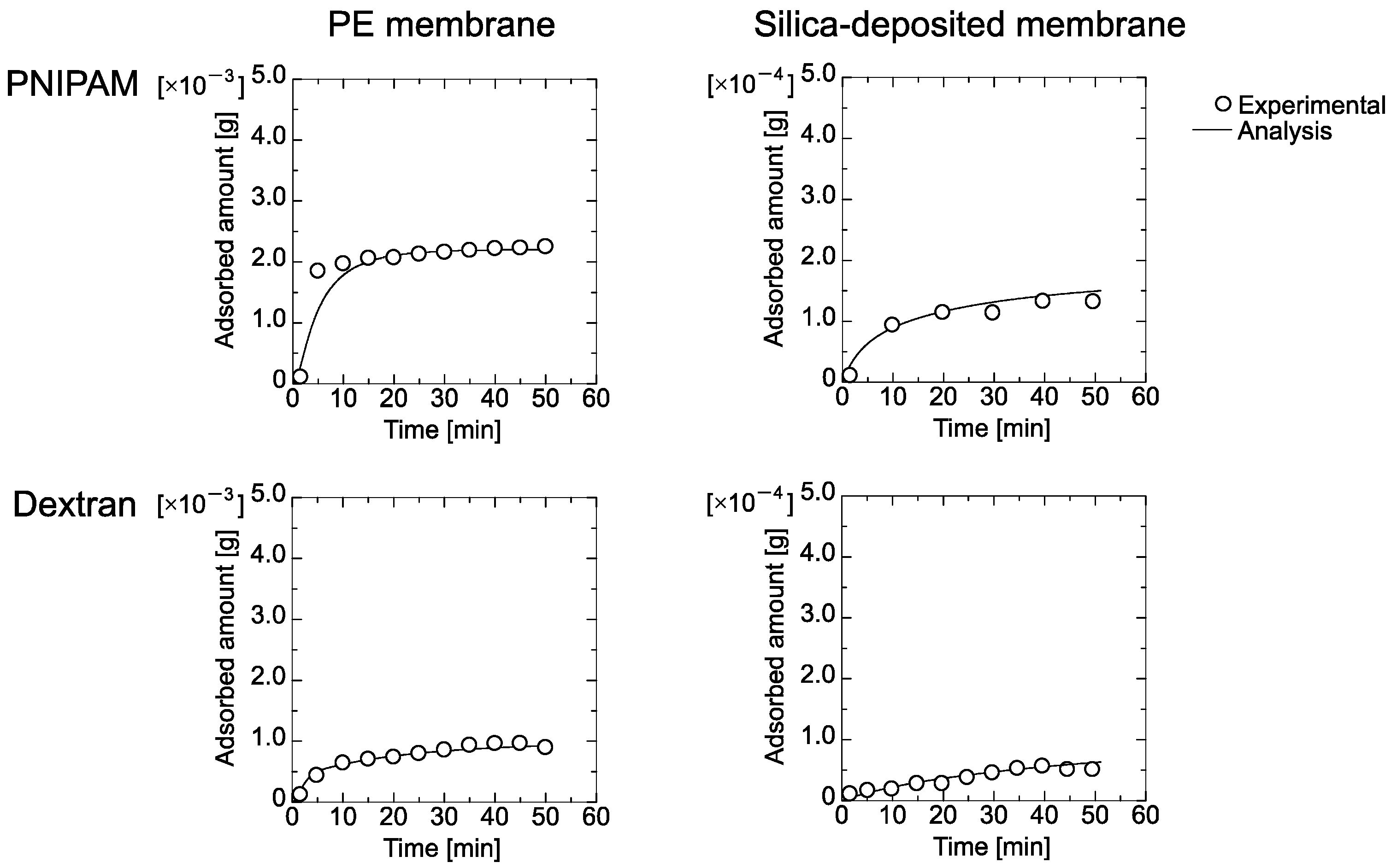
4.3. Filtration of PNIPAM Gel and Dextran through the Membrane
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | effective membrane area, m2 |
| B1 | thickness of first layer per unit amount of adsorbed colloid mass, pore-narrowing factor, m/g |
| B2 | thickness of second layer per unit amount of adsorbed colloid mass, pore-narrowing factor, m/g |
| BSi | thickness of adsorbed colloid per amount of adsorbed colloid in silica-deposited layer, m/g |
| C0 | initial concentration of colloidal suspension, g/m3 |
| Ci | concentration of each fraction from the membrane, g/m3 |
| J0 | water-permeation flux of silica-deposited membrane, m/s |
| Jm0 | water flux through PE membrane, m/s |
| JSi | imaginary flux through silica-deposited layer, m/s |
| J(t) | filtration flux, m/s |
| K1 | adsorption coefficient on the membrane pore, 1/m |
| K2 | adsorption coefficient on the adsorbed colloids, 1/m |
| KSi | adsorption coefficient of colloid on the silica-deposited layer, 1/m |
| Lm | thickness of PE membrane, m |
| LSi | thickness of silica-deposited layer, m |
| Nm | pore density of PE membrane, 1/m2 |
| NSi | pore number density of silica-deposited layer, 1/m2 |
| ΔP | pressure drop, Pa |
| ΔPm | pressure drop in PE membrane, Pa |
| ΔPSi | pressure drop in silica-deposited layer, Pa |
| q1(t) | amounts adsorbed to the membrane pore surface, g |
| q2(t) | amounts adsorbed to the previously adsorbed surface of the colloids, g |
| Qmax1 | maximum amount of colloid adsorbed, g |
| Qmax2 | maximum amount to the previously adsorbed colloid, g |
| QmaxSi | maximum amount adsorbed to the silica-deposited layer, g |
| rPE | radius of pore of PE membrane, m |
| rSi | pore-gap radius in silica-deposited layer, m |
| Rm | PE membrane resistance, 1/m |
| RSi | resistance of silica-deposited layer, 1/m |
| Rtotal | total membrane resistance, 1/m |
| Vi | volume of effluent from the membrane, m3 |
| µ | viscosity, Pa·s |
Appendix A
References
- Anantharaman, A.; Chun, Y.; Hua, T.; Chew, J.W.; Wang, R. Pre-deposited dynamic membrane filtration-A review. Water Res. 2020, 173, 115558. [Google Scholar] [CrossRef] [PubMed]
- Yue, X.; Li, W.; Li, Z.; Qiu, F.; Pan, J.; Zhang, T. Laminated super wetting aerogel/membrane composite with large pore sizes for efficient separation of surfactant-stabilized water-in-oil emulsions. Chem. Eng. Sci. 2020, 215, 115450. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, T.; Sun, H.; Wang, W. Preparation and application of titanium dioxide membranes in microfiltration of oil-in-water emulsions. Sep. Purif. Technol. 2012, 89, 78–83. [Google Scholar] [CrossRef]
- Fujii, T.; Yano, T.; Nakamura, K.; Miyawaki, O. The sol-gel preparation and characterization of nanoporous silica membrane with controlled pore size. J. Membr. Sci. 2001, 187, 171–180. [Google Scholar] [CrossRef]
- Van Oers, C.W.; Vorstman, M.A.G.; Kerkhof, P.J.A.M. Solute rejection in the presence of a deposited layer during ultrafiltration. J. Membr. Sci. 1995, 107, 173–192. [Google Scholar] [CrossRef][Green Version]
- Zamani, A.; Maini, B. Flow of dispersed particles through porous media – Deep bed filtration. J. Petrol. Sci. Eng. 2009, 69, 71–88. [Google Scholar] [CrossRef]
- Ho, C.C.; Zydney, A.L. Effect of membrane morphology on the initial rate of protein fouling during microfiltration. J. Membr. Sci. 1999, 155, 261–275. [Google Scholar] [CrossRef]
- Yoshida, M.; Taniguchi, M.; Tanaka, T. Depth filtration of cell suspensions of agglomerated steptobacteria by biodegradable membranes. J. Chem. Eng. Jpn. 2012, 45, 778–784. [Google Scholar] [CrossRef]
- Latulippe, D.A.; Zydney, A.L. Elongational flow model for transmission of supercoiled plasmid DNA during membrane ultrafiltration. J. Membr. Sci. 2009, 329, 201–208. [Google Scholar] [CrossRef]
- Mochizuki, S.; Zydney, A.L. Dextran transport through asymmetric ultrafiltration membranes: Comparison with hydrodynamic models. J. Membr. Sci. 1992, 68, 21–41. [Google Scholar] [CrossRef]
- Tai, J.; Lim, C.P.; Lam, Y.C. Visualization of polymer relaxation in viscoelastic turbulent microchannel flow. Sci. Rep. 2015, 5, 16633. [Google Scholar] [CrossRef] [PubMed]
- Nirs, O.; Trieu, T.; Bannwarth, S.; Wessling, M. Microfiltration of deformable microgels. Soft Matter 2016. [Google Scholar] [CrossRef]
- Linkhorst, J.; Beckmann, T.; Go, D.; Kuehne, A.J.C.; Wessling, M. Microfluidic colloidal filtration. Sci. Rep. 2016, 6, 22376. [Google Scholar] [CrossRef] [PubMed]
- Hendrickson, G.R.; Lyon, L.A. Microgel translocation through pores under confinement. Angew. Chem. Int. Ed. 2010, 49, 2193–2197. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, K.; Matsumoto, K. Properties of protein adsorption onto pore surface during microfiltration: Effects of solution environment and membrane hydrophobicity. J. Membr. Sci. 2006, 280, 363–374. [Google Scholar] [CrossRef]
- Nakamura, K.; Matsumoto, K. Protein adsorption properties on a microfiltration membrane: A comparison between static and dynamic adsorption methods. J. Membr. Sci. 2006, 285, 126–136. [Google Scholar] [CrossRef]
- Bacchin, P.; Si-Hassen, D.; Starov, V.; Clifton, M.J.; Aimar, P. A unifying model for concentration polarization, gel-layer formation and particle deposition in cross-flow membrane filtration of colloidal suspensions. Chem. Eng. Sci. 2002, 57, 77–91. [Google Scholar] [CrossRef]
- Hwang, K.-J.; Huang, P.-S. Cross-flow microfiltration of dilute macromolecular suspension. Sep. Purif. Technol. 2009, 68, 328–334. [Google Scholar] [CrossRef]
- Harouna, B.M.; Bekortbi, O.; Hanini, S.; Amrane, A. Modeling of transition pore blockage to cake filtration and modified fouling index – Dynamical surface phenomena in membrane filtration. Chem. Eng. Sci. 2019, 193, 298–311. [Google Scholar] [CrossRef]
- Iritani, E.; Katagiri, N.; Takenaka, T.; Yamashita, Y. Membrane pore blocking during cake formation in constant pressure and constant flux dead-end microfiltration of very dilute colloids. Chem. Eng. Sci. 2015, 122, 465–473. [Google Scholar] [CrossRef]
- Tien, C.; Ramarao, B.V.; Yasarla, R. A blocking model of membrane filtration. Chem. Eng. Sci. 2014, 111, 421–431. [Google Scholar] [CrossRef]
- Lebrun, L.; Junter, G.-A. Diffusion of dextran through microporous membrane. J. Membr. Sci. 1994, 88, 253–261. [Google Scholar] [CrossRef]
- Zhou, M.-Y.; Chu, L.-Y.; Chen, W.-M.; Ju, X.-J. Flow and aggregation characteristics of thermo-responsive poly(N-isopropylacrylamide) spheres during the phase transition. Chem. Eng. Sci. 2006, 61, 6337–6347. [Google Scholar] [CrossRef]
- Wickramansinghe, S.R.; Bower, S.E.; Chen, Z.; Mukherjee, A.; Husson, S.M. Relating the pore size distribution of ultrafiltration membranes to dextran rejection. J. Membr. Sci. 2009, 340, 1–8. [Google Scholar] [CrossRef]
- Marszaleck, P.E.; Oberhauser, A.F.; Pang, Y.-P.; Fernandez, J.M. Polysaccharide elasticity governed by chair-boat transitions of the glucopyranose ring. Nature 1998, 396, 661–664. [Google Scholar] [CrossRef]
- Neelov, I.M.; Adolf, D.B.; Mcleish, T.C.B.; Oaci, E. Molecular dynamics simulation of dextran extension by constant force in single molecule AFM. Biophys. J. 2006, 91, 3579–3588. [Google Scholar] [CrossRef]


| pore number density of silica deposited layer, NSi [m−2] | 4.1 × 1016 |
| effective membrane area, A [m2] | 3.1 × 10−4 |
| pore-gap radius in silica deposited layer, rSi [m] | 1.7 × 10−8 |
| K1 (m−1) | K2 (m−1) | Qmax1 (g) | Qmax2 (g) | B1 (m/g) | B2 (m/g) | |
|---|---|---|---|---|---|---|
| PNIPAM | 1.0 × 10−3 | 1.5 × 100 | 8.0 × 10−5 | 2.2 × 10−3 | 1.0 × 10−3 | 2.0 × 10−5 |
| Dextran | 1.0 × 10−2 | 5.0 × 10−1 | 6.0 × 10−4 | 3.7 × 10−4 | 3.0 × 10−5 | 3.0 × 10−5 |
| K1 (m−1) | K2 (m−1) | Qmax1 (g) | |
|---|---|---|---|
| PNIPAM | 1.7 × 10−1 | 2.0 × 10−4 | 5.5 × 10−4 |
| Dextran | 2.3 × 10−2 | 3.0 × 10−5 | 1.3 × 10−3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hidane, T.; Kitani, H.; Morisada, S.; Ohto, K.; Kawakita, H.; Furuta, S. Filtration of Elastic Polymers and Spherical Gels through a Silica-Deposited Layer on a Porous Membrane. Membranes 2021, 11, 22. https://doi.org/10.3390/membranes11010022
Hidane T, Kitani H, Morisada S, Ohto K, Kawakita H, Furuta S. Filtration of Elastic Polymers and Spherical Gels through a Silica-Deposited Layer on a Porous Membrane. Membranes. 2021; 11(1):22. https://doi.org/10.3390/membranes11010022
Chicago/Turabian StyleHidane, Takanori, Hidemi Kitani, Shintaro Morisada, Keisuke Ohto, Hidetaka Kawakita, and Sachiko Furuta. 2021. "Filtration of Elastic Polymers and Spherical Gels through a Silica-Deposited Layer on a Porous Membrane" Membranes 11, no. 1: 22. https://doi.org/10.3390/membranes11010022
APA StyleHidane, T., Kitani, H., Morisada, S., Ohto, K., Kawakita, H., & Furuta, S. (2021). Filtration of Elastic Polymers and Spherical Gels through a Silica-Deposited Layer on a Porous Membrane. Membranes, 11(1), 22. https://doi.org/10.3390/membranes11010022







