Experimental Investigation of the Oxidative Coupling of Methane in a Porous Membrane Reactor: Relevance of Back-Permeation
Abstract
1. Introduction
2. Materials and Methods
2.1. Catalyst Preparation
2.2. Membrane Preparation
2.3. Experimental Procedure
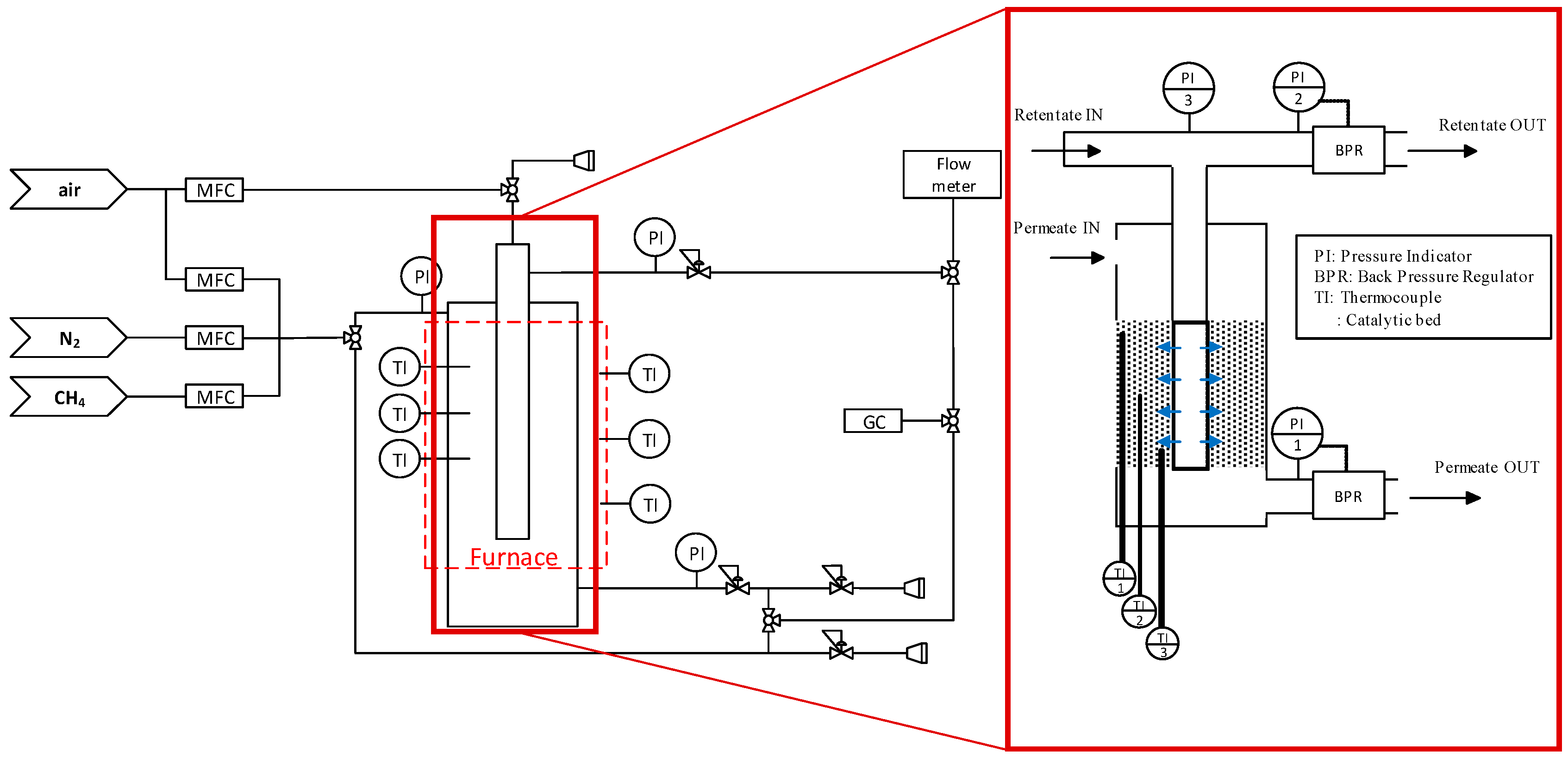
2.3.1. Reactor Section
2.3.2. Analysis Section
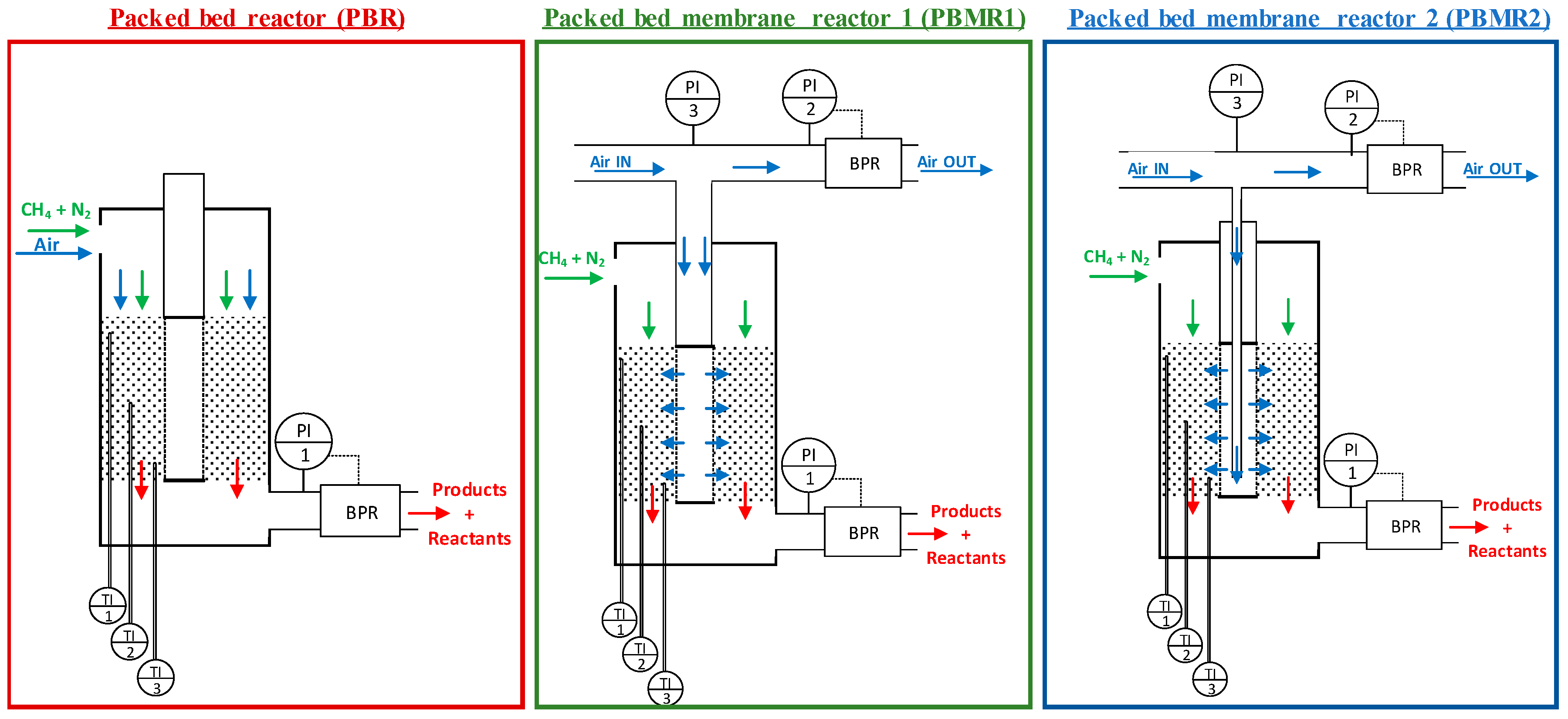
2.4. Reactor Configuartions
3. Results
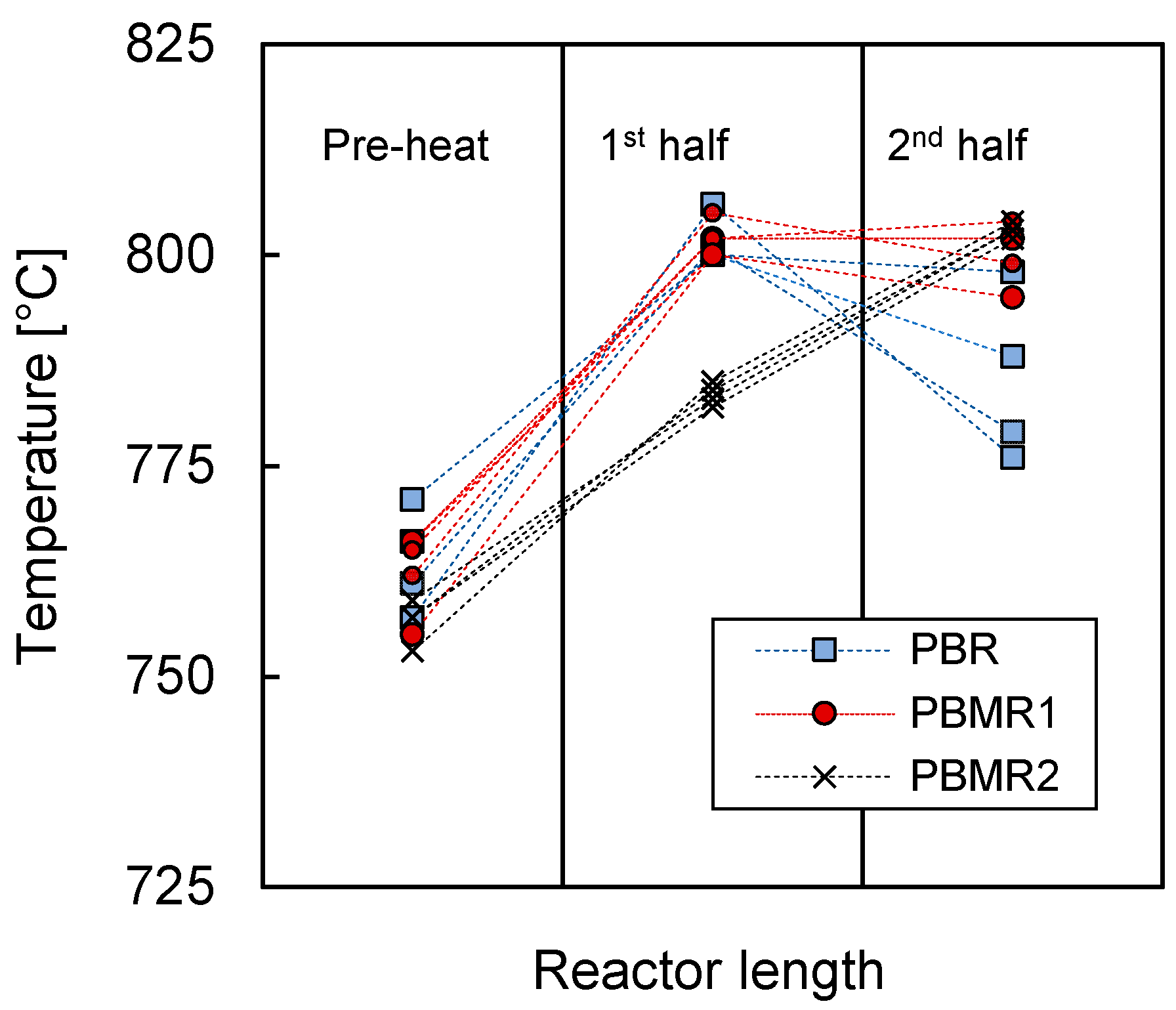
3.1. Mass and Heat Transfer Limitations
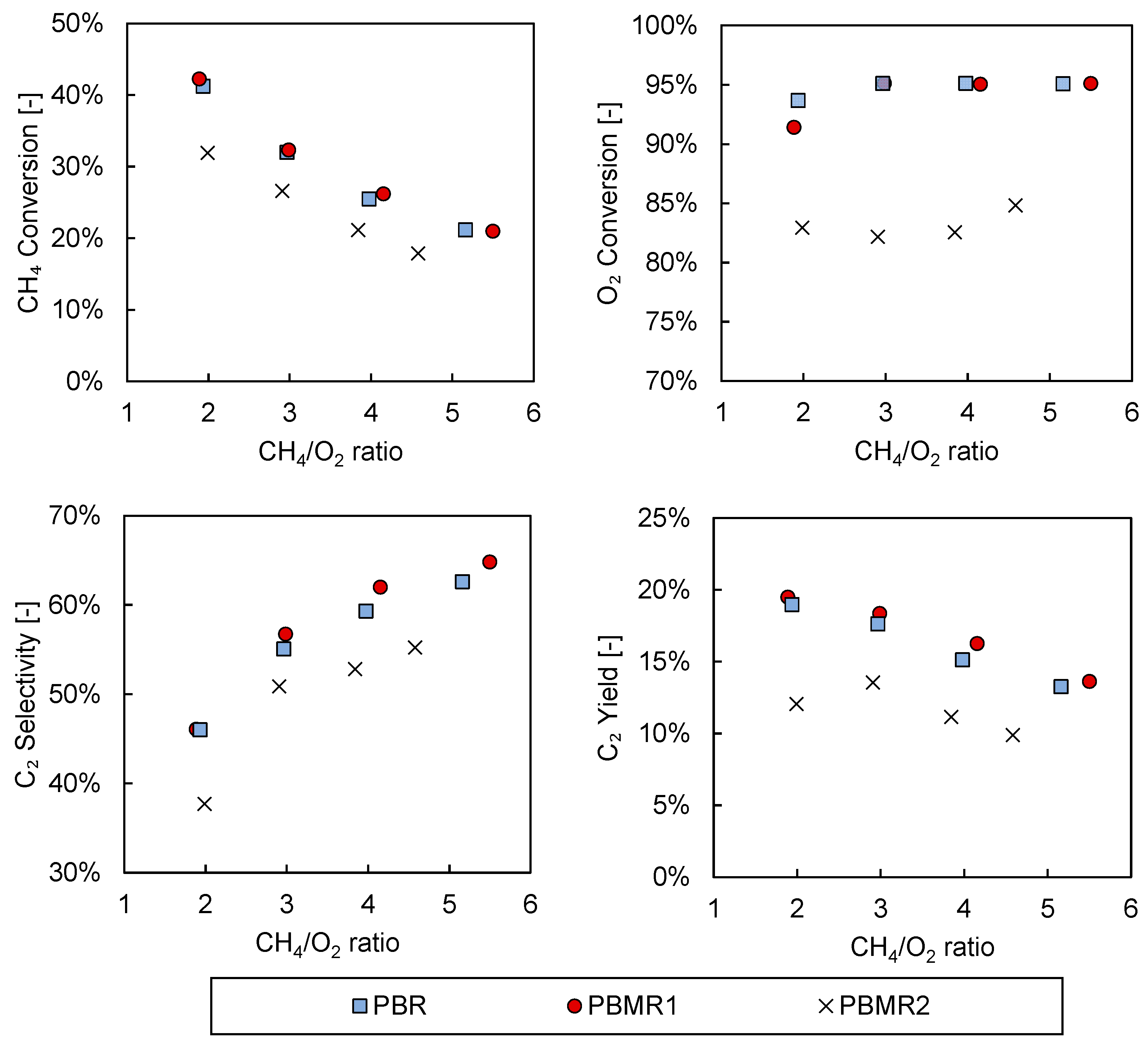
3.2. Packed Bed versus Packed Bed Porous Membrane Reactor
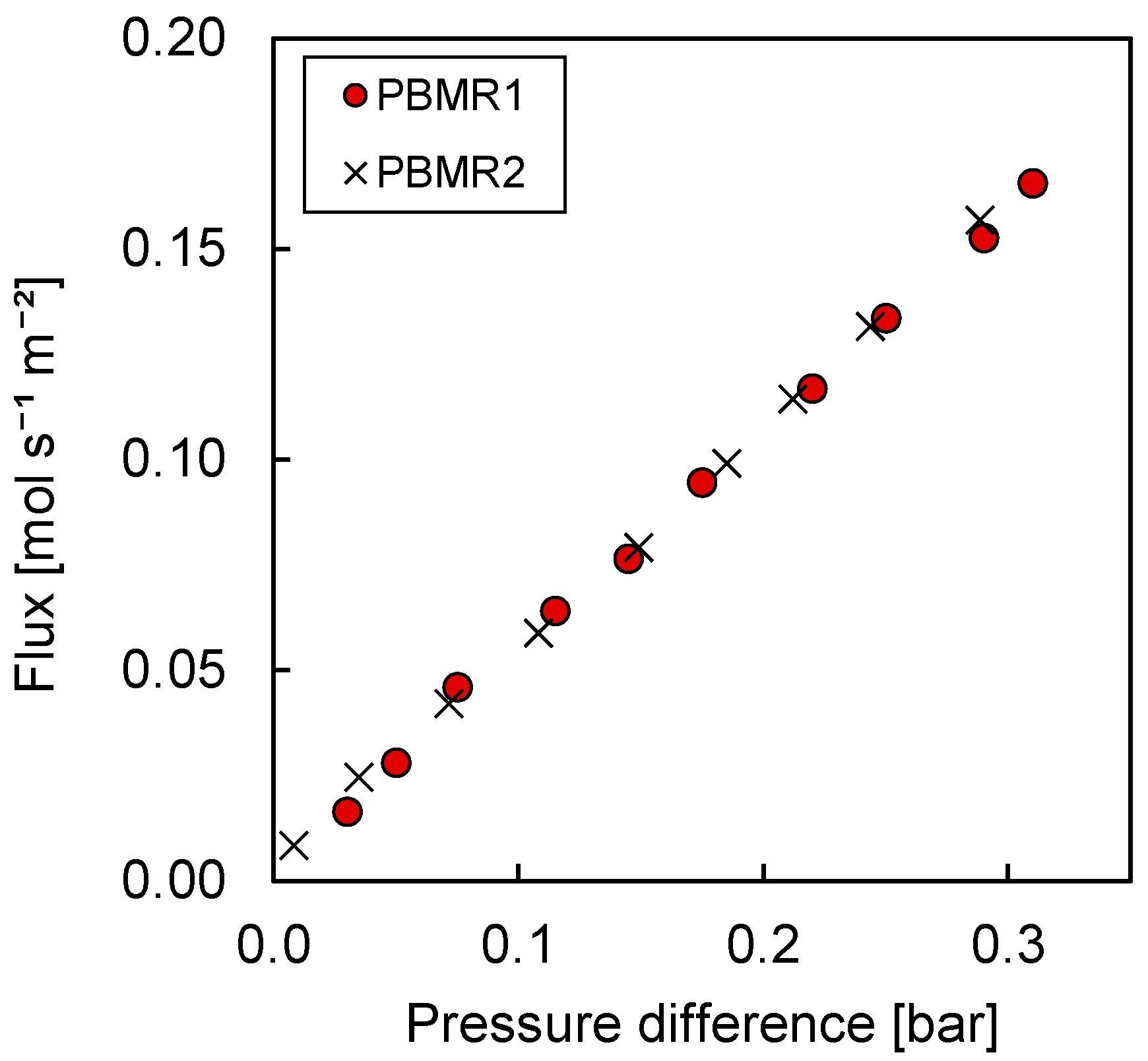
Membrane Characterization
3.3. Membrane Reactor Experiments
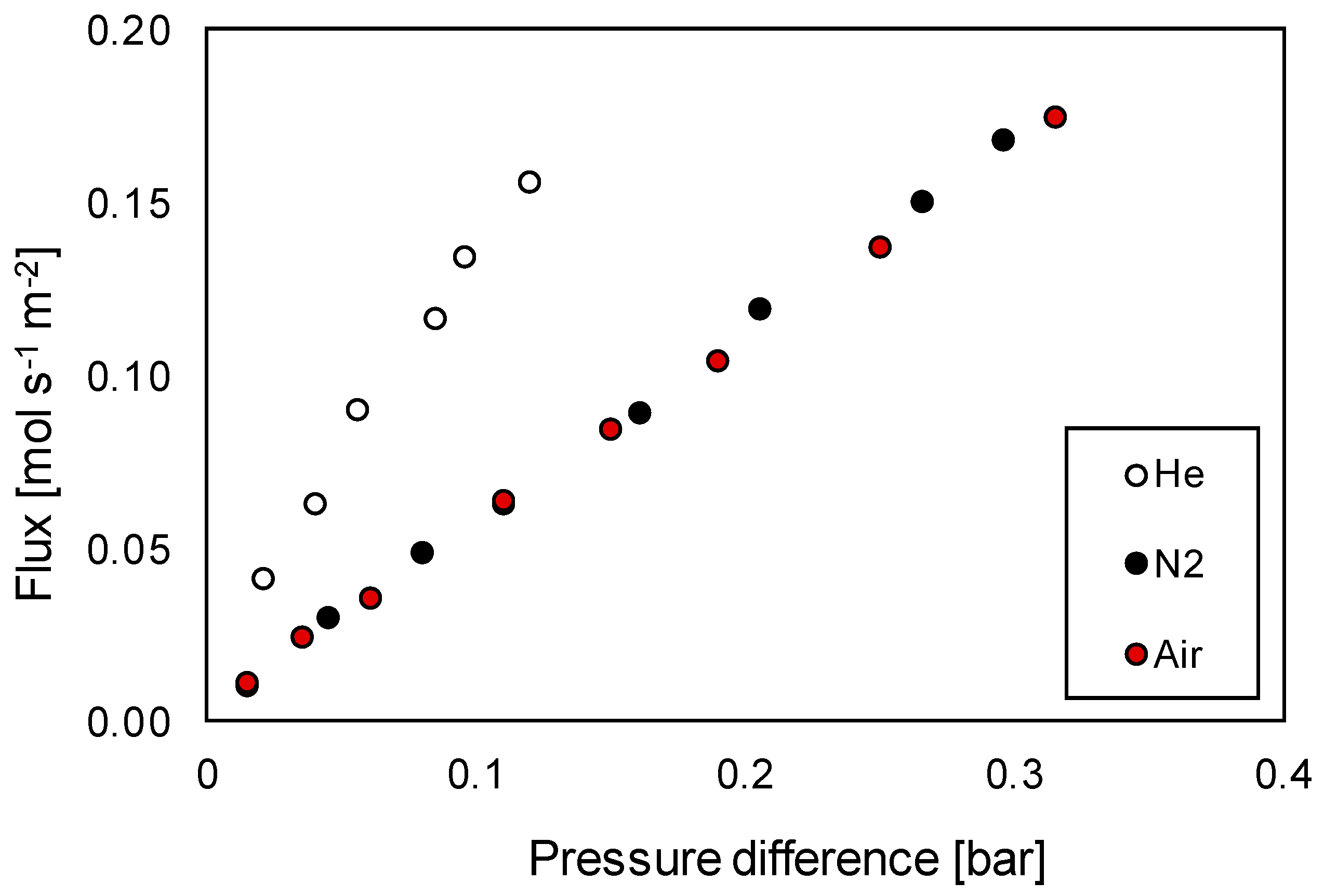
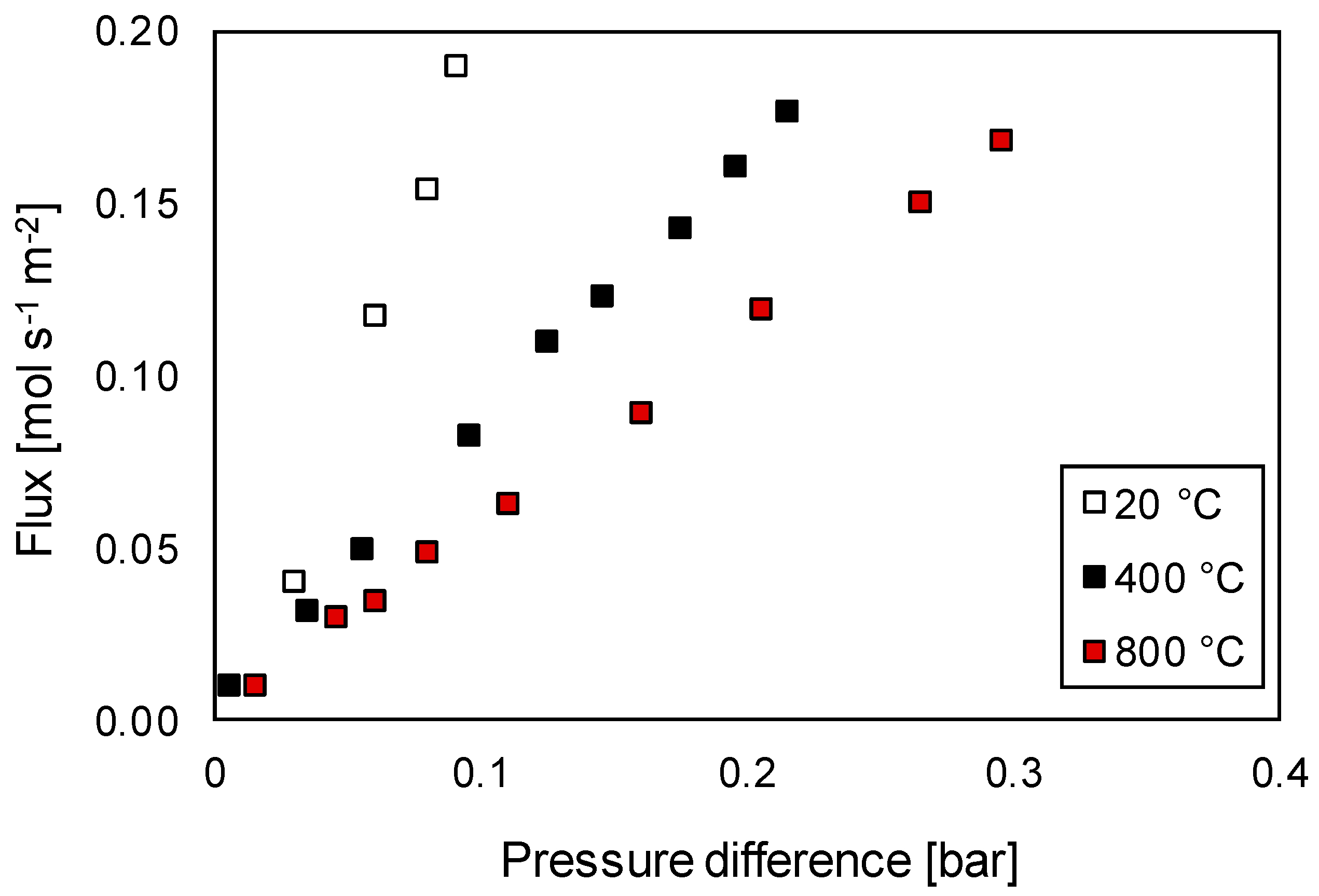
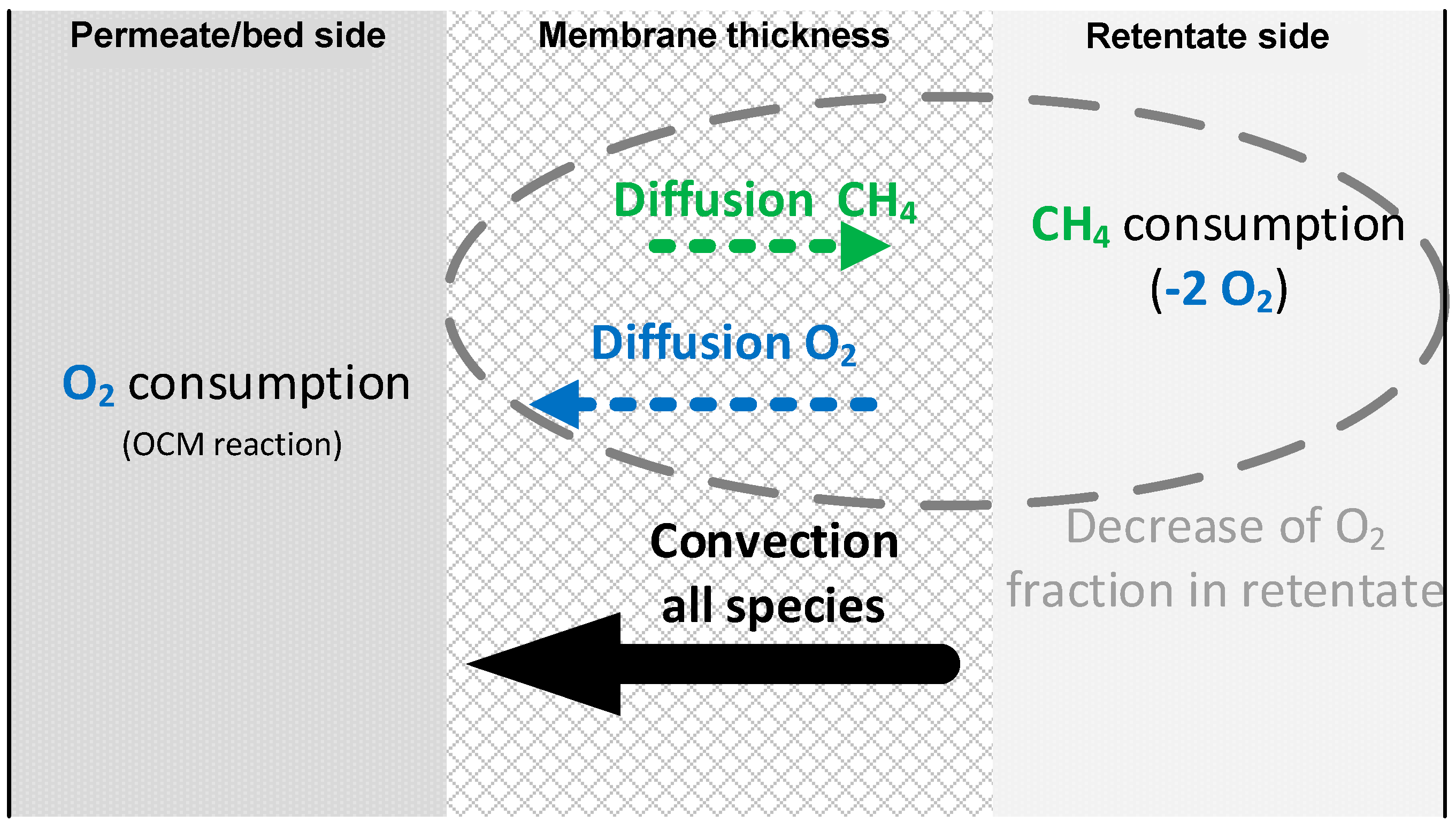
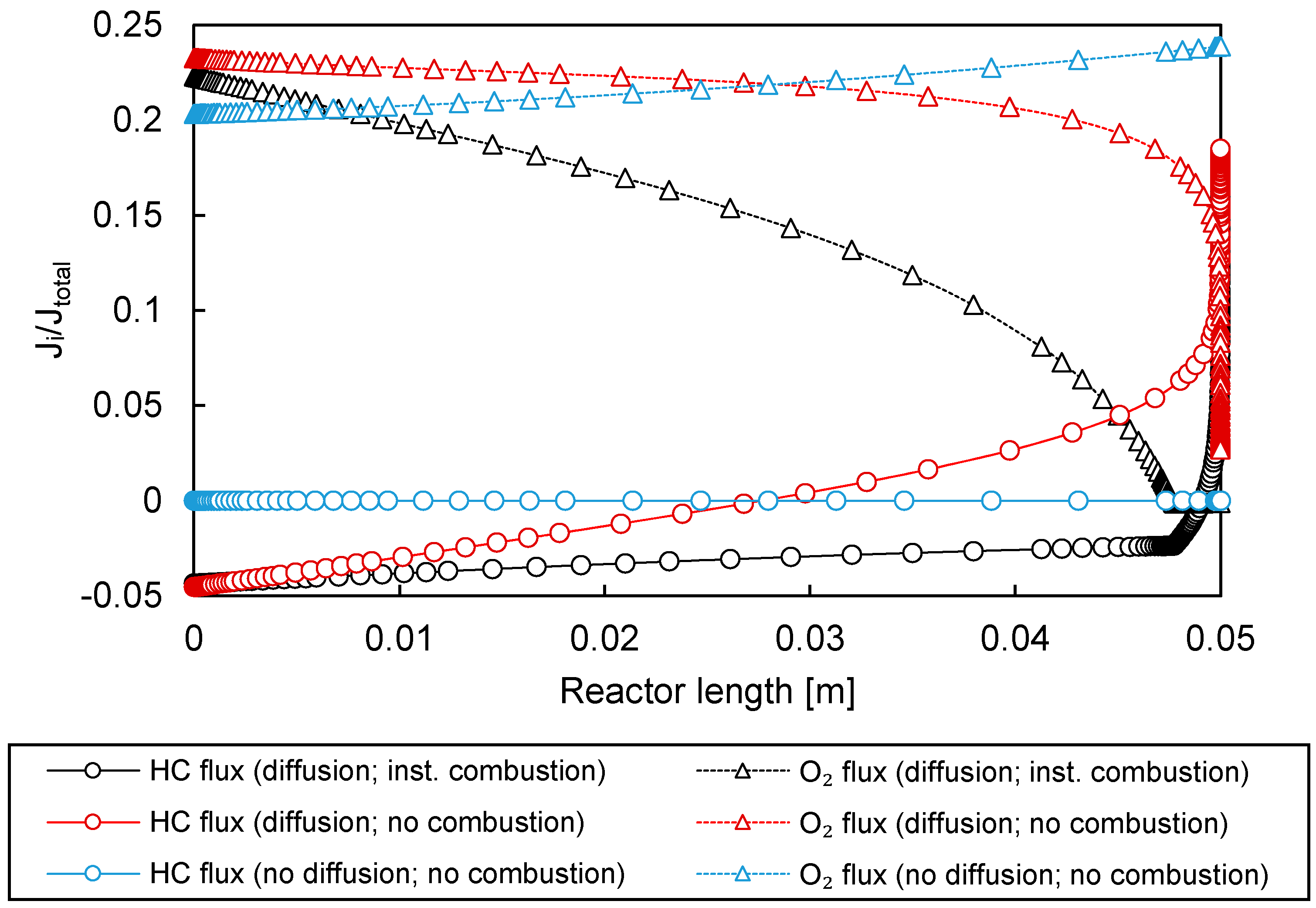
3.3.1. Permeation Mechanisms through the Porous Membrane
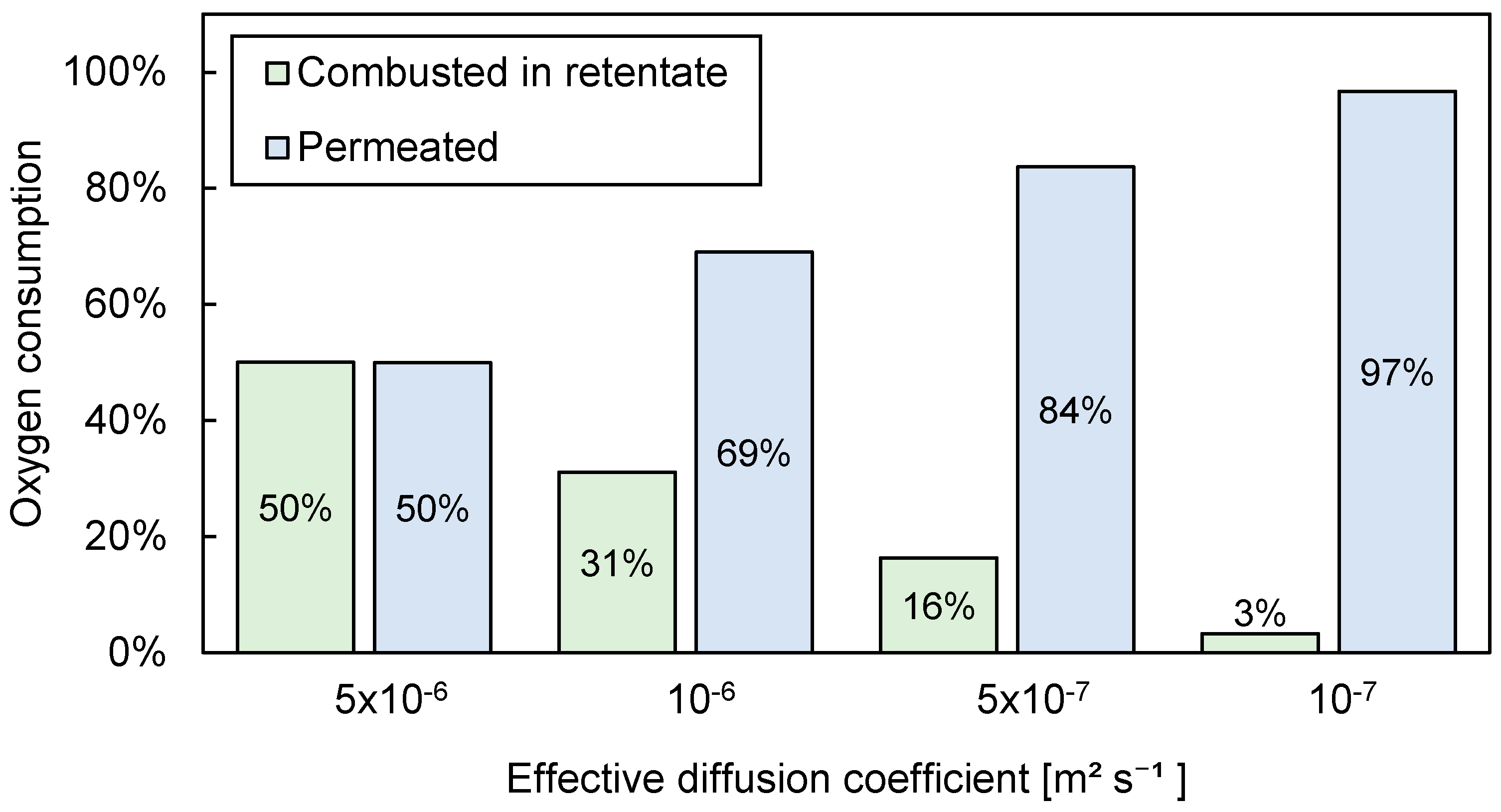
3.3.2. Influence of Effective Diffusion Coefficient
4. Conclusions
Author Contributions
Funding

Conflicts of Interest
Appendix A.
Appendix A.1. Mass and Heat Transfer Limitations
Appendix A.1.1. External Mass Transfer Limitations
Appendix A.1.2. Internal Mass Transfer Limitations
Appendix A.1.3. Heat Transfer Limitations
Appendix B.
References
- Spallina, V.; Velarde, I.C.; Jimenez, J.A.M.; Godini, H.R.; Gallucci, F.; Van Sint Annaland, M. Techno-economic assessment of different routes for olefins production through the oxidative coupling of methane (OCM): Advances in benchmark technologies. Energy Convers. Manag. 2017, 154, 244–261. [Google Scholar] [CrossRef]
- World Energy Outlook, International Energy Agency. 2017. Available online: www.Iea.Org/Weo/ (accessed on 3 April 2020).
- Stansch, Z.; Mleczko, L.; Baerns, M. Comprehensive kinetics of oxidative coupling of methane over the La2O3/CaO catalyst. Ind. Eng. Chem. Res. 1997, 36, 2568–2579. [Google Scholar] [CrossRef]
- Keller, G.E.; Bhasin, M.M. Synthesis of Ethylene via Oxidative Coupling of Methane. I. Determination of active catalysts. J. Catal. 1982, 73, 9–19. [Google Scholar] [CrossRef]
- Cruellas, A.; Bakker, J.J.; van Sint Annaland, M.; Medrano, J.A.; Gallucci, F. Techno-economic analysis of oxidative coupling of methane: Current state of the art and future perspectives. Energy Convers. Manag. 2019, 198, 111789. [Google Scholar] [CrossRef]
- Lomonosov, V.I.; Sinev, M.Y. Oxidative coupling of methane: Mechanism and kinetics. Kinet. Catal. 2016, 57, 647–676. [Google Scholar] [CrossRef]
- Kiani, D.; Sourav, S.; Baltrusaitis, J.; Wachs, I.E. Oxidative Coupling of Methane (OCM) by SiO2-Supported Tungsten Oxide Catalysts Promoted with Mn and Na. ACS Catal. 2019, 9, 5912–5928. [Google Scholar] [CrossRef]
- Vamvakeros, A.; Jacques, S.D.M.; Middelkoop, V.; di Michiel, M.; Egan, C.K.; Ismagilov, I.Z.; Vaughan, G.B.M.; Gallucci, F.; van Sint Annaland, M.; Shearing, P.R.; et al. Real time chemical imaging of a working catalytic membrane reactor during oxidative coupling of methane. Chem. Commun. 2015, 51, 12752–12755. [Google Scholar] [CrossRef]
- Matras, D.; Jacques, S.D.M.; Godini, H.R.; Khadivi, M.; Drnec, J.; Poulain, A.; Cernik, R.J.; Beale, A.M. Real-Time Operando Diffraction Imaging of La–Sr/CaO During the Oxidative Coupling of Methane. J. Phys. Chem. C 2018, 122, 2221–2230. [Google Scholar] [CrossRef]
- Matras, D.; Jacques, S.D.M.; Poulston, S.; Grosjean, N.; Bosch, C.E.; Rollins, B.; Wright, J.; di Michiel, M.; Vamvakeros, A.; Cernik, R.J.; et al. Operando and Postreaction Diffraction Imaging of the La–Sr/CaO Catalyst in the Oxidative Coupling of Methane Reaction. J. Phys. Chem. C 2019, 123, 1751–1760. [Google Scholar] [CrossRef]
- Ito, T.; Wang, J.; Lin, C.H.; Lunsford, J.H. Oxidative dimerization of methane over a lithium-promoted magnesium oxide catalyst. J. Am. Chem. Soc. 1985, 107, 5062–5068. [Google Scholar] [CrossRef]
- Vatani, A.; Jabbari, E.; Askarieh, M.; Torangi, M.A. Kinetic modeling of oxidative coupling of methane over Li/MgO catalyst by genetic algorithm. J. Nat. Gas Sci. Eng. 2014, 20, 347–356. [Google Scholar] [CrossRef]
- Arndt, S.; Laugel, G.; Levchenko, S.; Horn, R.; Baerns, M.; Scheffler, M.; Schlögl, R.; Schomäcker, R. A Critical Assessment of Li/MgO-Based Catalysts for the Oxidative Coupling of Methane. Catal. Rev. 2011, 53, 424–514. [Google Scholar] [CrossRef]
- Alexiadis, V.I.; Chaar, M.; van Veen, A.; Muhler, M.; Thybaut, J.W.; Marin, G.B. Quantitative screening of an extended oxidative coupling of methane catalyst library. Appl. Catal. B Environ. 2016, 199, 252–259. [Google Scholar] [CrossRef]
- Choudhary, V.R.; Mulla, S.A.R.; Rane, V.H. Surface basicity and acidity of alkaline earth-promoted La2O3 catalysts and their performance in oxidative coupling of methane. J. Chem. Technol. Biotechnol. 1998, 72, 125–130. [Google Scholar] [CrossRef]
- Koirala, R.; Büchel, R.; Pratsinis, S.E.; Baiker, A. Oxidative coupling of methane on flame-made Mn-Na2WO4/SiO2: Influence of catalyst composition and reaction conditions. Appl. Catal. A Gen. 2014, 484, 97–107. [Google Scholar] [CrossRef]
- Pak, S.; Lunsford, J.H. Thermal effects during the oxidative coupling of methane over Mn/Na2WO4/SiO2 and Mn/Na2WO4/MgO catalysts. Appl. Catal. A Gen. 1998, 168, 131–137. [Google Scholar] [CrossRef]
- Elkins, T.W.; Hagelin-Weaver, H.E. Characterization of Mn/Na2WO4/SiO2 and Mn/Na2WO4/MgO catalysts for the oxidative coupling of methane. Appl. Catal. A Gen. 2015, 497, 96–106. [Google Scholar] [CrossRef]
- Karakaya, C.; Kee, R.J. Progress in the direct catalytic conversion of methane to fuels and chemicals. Prog. Energy Combust. Sci. 2016, 55, 60–97. [Google Scholar] [CrossRef]
- Arndt, S.; Otremba, T.; Simon, U.; Yildiz, M.; Schubert, H.; Schomäcker, R. Mn-Na2WO4/SiO2 as catalyst for the oxidative coupling of methane. What is really known? Appl. Catal. A Gen. 2012, 425–426, 53–61. [Google Scholar] [CrossRef]
- Cruellas, A.; Melchiori, T.; Gallucci, F.; van Sint Annaland, M. Advanced reactor concepts for oxidative coupling of methane. Catal. Rev. 2018, 59, 234–294. [Google Scholar] [CrossRef]
- Zarrinpashne, S.; Ahmadi, R.; Zekordi, S.M. Catalyst direct conversion of methane to ethane and ethylene. U.S. Patent 7,902,113, 8 March 2011. [Google Scholar]
- Wang, J.; Chou, L.; Zhang, B.; Song, H.; Zhao, J.; Yang, J.; Li, S. Comparative study on oxidation of methane to ethane and ethylene over Na2WO4-Mn/SiO2 catalysts prepared by different methods. J. Mol. Catal. A Chem. 2006, 245, 272–277. [Google Scholar] [CrossRef]
- Gambo, Y.; Jalil, A.A.; Triwahyono, S.; Abdulrasheed, A.A. Recent advances and future prospect in catalysts for oxidative coupling of methane to ethylene: A review. J. Ind. Eng. Chem. 2018, 59, 218–229. [Google Scholar] [CrossRef]
- Cruellas, A.; Melchiori, T.; Gallucci, F.; van Sint Annaland, M. Oxidative Coupling of Methane: A Comparison of Different Reactor Configurations. Energy Technol. 2019, 1900148. [Google Scholar] [CrossRef]
- Cheng, Z.; Baser, D.S.; Nadgouda, S.G.; Qin, L.; Fan, J.A.; Fan, L.-S. C2 Selectivity Enhancement in Chemical Looping Oxidative Coupling of Methane over a Mg–Mn Composite Oxygen Carrier by Li-Doping-Induced Oxygen Vacancies. ACS Energy Lett. 2018, 3, 1730–1736. [Google Scholar] [CrossRef]
- Chung, E.Y.; Wang, W.K.; Nadgouda, S.G.; Baser, D.S.; Sofranko, J.A.; Fan, L.-S. Catalytic Oxygen Carriers and Process Systems for Oxidative Coupling of Methane Using the Chemical Looping Technology. Ind. Eng. Chem. Res. 2016, 55, 12750–12764. [Google Scholar] [CrossRef]
- Fleischer, V.; Littlewood, P.; Parishan, S.; Schomäcker, R. Chemical looping as reactor concept for the oxidative coupling of methane over a Na2WO4/Mn/SiO2 catalyst. Chem. Eng. J. 2016, 306, 646–654. [Google Scholar] [CrossRef]
- Parishan, S.; Littlewood, P.; Arinchtein, A.; Fleischer, V.; Schomäcker, R. Chemical looping as a reactor concept for the oxidative coupling of methane over the MnxOy-Na2WO4/SiO2 catalyst, benefits and limitation. Catal. Today 2018, 311, 40–47. [Google Scholar] [CrossRef]
- Fleischer, V.; Simon, U.; Parishan, S.; Colmenares, M.G.; Görke, O.; Gurlo, A.; Riedel, W.; Thum, L.; Schmidt, J.; Risse, T.; et al. Investigation of the role of the Na2WO4/Mn/SiO2 catalyst composition in the oxidative coupling of methane by chemical looping experiments. J. Catal. 2018, 360, 102–117. [Google Scholar] [CrossRef]
- Santamaría, J.; Menéndez, M.; Peña, J.A.; Barahona, J.I. Methane oxidative coupling in fixed bed catalytic reactors with a distributed oxygen feed. A simulation study. Catal. Today 1992, 13, 353–360. [Google Scholar] [CrossRef]
- Baerns, M.; Hinsen, W. Process for the Production of Ethane and/or Ethylene from Methane. U.S. Patent 4,608,449, 2 June 1983. [Google Scholar]
- Plazaola, A.A.; Labella, A.C.; Liu, Y.; Porras, N.B.; Tanaka, A.D.P.; Annaland, V.M.S.; Gallucci, F. Mixed Ionic-Electronic Conducting Membranes (MIEC) for Their Application in Membrane Reactors: A Review. Processes 2019, 7, 128. [Google Scholar] [CrossRef]
- Lafarga, D.; Santamaria, J.; Menéndez, M. Methane oxidative coupling using porous ceramic membrane reactors—I. reactor development. Chem. Eng. Sci. 1994, 49, 2005–2013. [Google Scholar] [CrossRef]
- Tan, X.; Pang, Z.; Gu, Z.; Liu, S. Catalytic perovskite hollow fibre membrane reactors for methane oxidative coupling. J. Membr. Sci. 2007, 302, 109–114. [Google Scholar] [CrossRef]
- Lu, Y.; Dixon, A.G.; Moser, W.R.; Hua, Y.; Balachandran, U. Oxygen-permeable dense membrane reactor for the oxidative coupling of methane. J. Membr. Sci. 2000, 170, 27–34. [Google Scholar] [CrossRef]
- Czuprat, O.; Schiestel, T.; Voss, H. Oxidative Coupling of Methane in a BCFZ Perovskite Hollow Fiber Membrane Reactor. Ind. Eng. Chem. Res. 2010, 49, 10230–10236. [Google Scholar] [CrossRef]
- Wang, H.; Cong, Y.; Yang, W. Oxidative coupling of methane in Ba0.5Sr0.5Co0.8Fe0.2O3−δ tubular membrane reactors. Catal. Today 2005, 104, 160–167. [Google Scholar] [CrossRef]
- Olivier, L.; Haag, S.; Mirodatos, C.; van Veen, A.C. Oxidative coupling of methane using catalyst modified dense perovskite membrane reactors. Catal. Today 2009, 142, 34–41. [Google Scholar] [CrossRef]
- Akin, F.T.; Lin, Y.S. Controlled Oxidative Coupling of Methane by Ionic Conducting Ceramic Membrane. Catal. Lett. 2002, 78, 239–242. [Google Scholar] [CrossRef]
- Bhatia, S.; Thien, C.Y.; Mohamed, A.R. Oxidative coupling of methane (OCM) in a catalytic membrane reactor and comparison of its performance with other catalytic reactors. Chem. Eng. J. 2009, 148, 525–532. [Google Scholar] [CrossRef]
- Othman, N.H.; Wu, Z.; Li, K. An oxygen permeable membrane microreactor with an in-situ deposited Bi1.5Y0.3Sm0.2O3−δ catalyst for oxidative coupling of methane. J. Membr. Sci. 2015, 488, 182–193. [Google Scholar] [CrossRef]
- Arratibel, A.; Astobieta, U.; Tanaka, D.A.P.; van Sint Annaland, M.; Gallucci, F. N2, He and CO2 diffusion mechanism through nanoporous YSZ/γ-Al2O3 layers and their use in a pore-filled membrane for hydrogen membrane reactors. Int. J. Hydrog. Energy 2016, 41, 8732–8744. [Google Scholar] [CrossRef]
- Cruellas, A.; Heezius, J.; Spallina, V.; van Sint Annaland, M.; Medrano, J.A.; Gallucci, F. Oxidative Coupling of Methane in Membrane Reactors; A Techno-Economic Assessment. Processes 2020, 8, 274. [Google Scholar] [CrossRef]
- Chen, H.; Li, L.; Kemps, R.; Michielsen, B.; Jacobs, M.; Snijkers, F.; Middelkoop, V. Reactive air brazing for sealing mixed ionic electronic conducting hollow fibre membranes. Acta Mater. 2015, 88, 74–82. [Google Scholar] [CrossRef]
- Wakao, N.; Funazkri, T. Effect of fluid dispersion coefficients on particle-to-fluid mass transfer coefficients in packed beds. Chem. Eng. Sci. 1978, 33, 1375–1384. [Google Scholar] [CrossRef]
- Appamana, W.; Charojrochkul, S.; Assabumrungrat, S.; Wiyaratn, W. Synthesis of Na2WO4-Mn Supported YSZ as a Potential Anode Catalyst for Oxidative Coupling of Methane in SOFC Reactor. Eng. J. 2015, 19, 13–20. [Google Scholar] [CrossRef]
- TTiemersma, P.; Tuinier, M.J.; Gallucci, F.; Kuipers, J.A.M.; Annaland, M.V.S. A kinetics study for the oxidative coupling of methane on a Mn/Na2WO4/SiO2 catalyst. Appl. Catal. A Gen. 2012, 433–434, 96–108. [Google Scholar] [CrossRef]
- Jašo, S.; Godini, H.R.; Arellano-Garcia, H.; Omidkhah, M.; Wozny, G. Analysis of attainable reactor performance for the oxidative methane coupling process. Chem. Eng. Sci. 2010, 65, 6341–6352. [Google Scholar] [CrossRef]
- Aseem, A.; Harold, M.P. C2 yield enhancement during oxidative coupling of methane in a nonpermselective porous membrane reactor. Chem. Eng. Sci. 2018, 175, 199–207. [Google Scholar] [CrossRef]
- Papavassiliou, V.; Lee, C.; Nestlerode, J.; Harold, M.P. Pneumatically Controlled Transport and Reaction in Inorganic Membranes. Ind. Eng. Chem. Res. 1997, 36, 4954–4964. [Google Scholar] [CrossRef]
- Daneshpayeh, M.; Khodadadi, A.; Mostoufi, N.; Mortazavi, Y.; Sotudeh-Gharebagh, R.; Talebizadeh, A. Kinetic modeling of oxidative coupling of methane over Mn/Na2WO4/SiO2 catalyst. Fuel Process. Technol. 2009, 90, 403–410. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Godini, H.R.; Xiao, S.; Kim, M.; Holst, N.; Jašo, S.; Görke, O.; Steinbach, J.; Wozny, G. Experimental and model-based analysis of membrane reactor performance for methane oxidative coupling: Effect of radial heat and mass transfer. J. Ind. Eng. Chem. 2014, 20, 1993–2002. [Google Scholar] [CrossRef]
- Mears, D.E. Tests for Transport Limitations in Experimental Catalytic Reactors. Ind. Eng. Chem. Process Des. Dev. 1971, 10, 541–547. [Google Scholar] [CrossRef]
- Pushnov, A.S. Calculation of average bed porosity. Chem. Pet. Eng. 2006, 42, 14–17. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 4th ed.; Pearson: Amsterdam, The Nederlands, 2014. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Weisz, P.B.; Prater, C.D. Interpretation of Measurements in Experimental Catalysis. Adv. Catal. 1954, 6, 143–196. [Google Scholar] [CrossRef]
- Zhang, L.-Z. Conjugate Heat and Mass Transfer in Adsorbent Ducts; Elsiever: Amsterdam, The Nederlands, 2013. [Google Scholar] [CrossRef]
- Vandewalle, L.A.; Van de Vijver, R.; Van Geem, K.M.; Marin, G.B. The role of mass and heat transfer in the design of novel reactors for oxidative coupling of methane. Chem. Eng. Sci. 2018. [Google Scholar] [CrossRef]
- Wakao, N.; Kaguei, S.; Funazkri, T. Effect of fluid dispersion coefficients on particle-to-fluid heat transfer coefficients in packed beds. Correlation of nusselt numbers. Chem. Eng. Sci. 1979, 34, 325–336. [Google Scholar] [CrossRef]



| Condition | Value |
|---|---|
| Temperature [°C] | 800 |
| Gas dilution [%] | 70 (N2) |
| Catalyst dilution [%] | 50 (quartz) |
| Type of catalyst | Mn-Na2WO4/SiO2 |
| Amount of solid in the bed [g.] | 3–6 |
| Permeate pressure [bar] | 2 |
| Retentate pressure [bar] | 2.1–2.3 |
| Total flow [NmL/min] | 250–750 |
| CH4/O2 ratio | 2–10 |
| Membrane type | Porous MgO |
| Membrane length [mm] | 50 |
| Membrane outer diameter [mm] | 10 |
| Membrane inner diameter [mm] | 7 |
| Reactor diameter [mm] | 16 |
| Condition | Value |
|---|---|
| Inlet flow rate [mL/min] | 360 |
| CH4/O2 ratio | 5 |
| Gas dilution | 70% (N2) |
| Temperature [°C] | 800 |
| Pressure [bar] | 2 |
| Observed CH4 conversion [%] | 14.5 |
| Observed O2 conversion [%] | 45.8 |
| Criterion | Value | Restriction | |
|---|---|---|---|
| Mears criterion (external mass transfer) | 0.056 a | 0.11 b | <0.15 a,b |
| Weisz–Prater criterion (internal mass transfer) | 0.41 c | 0.086 d | <1 c,d |
| Effectiveness factor (intraparticle) | 0.974 c | 0.994 d | − |
| Mears criterion (external heat transfer) | 6.38 × 10−4 e | 7.23 × 10−4 f | <0.0063 e <0.0136 f |
| Mears criterion (internal heat transfer) | 1.53 × 10−5 e | 1.74 × 10−5 f | <0.0315 e <0.0679 f |
| Operating Condition | Value |
|---|---|
| Retentate inlet flow rate [NmL/min] | 545 |
| Permeate inlet flow rate [NmL/min] | 545 |
| Retentate gas composition [%] | 79% N2, 21% O2 (air) |
| Permeate gas composition [%] | 79% N2, 21% O2 (air) |
| Retentate pressure [bar] | From 2.01 to 2.3 |
| Permeate pressure [bar] | 2 |
| Temperature [°C] | 700 |
| Membrane type | MgO |
| Membrane outer diameter [mm] | 10 |
| Membrane inner diameter [mm] | 7 |
| Membrane length [mm] | 50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruellas, A.; Ververs, W.; Annaland, M.v.S.; Gallucci, F. Experimental Investigation of the Oxidative Coupling of Methane in a Porous Membrane Reactor: Relevance of Back-Permeation. Membranes 2020, 10, 152. https://doi.org/10.3390/membranes10070152
Cruellas A, Ververs W, Annaland MvS, Gallucci F. Experimental Investigation of the Oxidative Coupling of Methane in a Porous Membrane Reactor: Relevance of Back-Permeation. Membranes. 2020; 10(7):152. https://doi.org/10.3390/membranes10070152
Chicago/Turabian StyleCruellas, Aitor, Wout Ververs, Martin van Sint Annaland, and Fausto Gallucci. 2020. "Experimental Investigation of the Oxidative Coupling of Methane in a Porous Membrane Reactor: Relevance of Back-Permeation" Membranes 10, no. 7: 152. https://doi.org/10.3390/membranes10070152
APA StyleCruellas, A., Ververs, W., Annaland, M. v. S., & Gallucci, F. (2020). Experimental Investigation of the Oxidative Coupling of Methane in a Porous Membrane Reactor: Relevance of Back-Permeation. Membranes, 10(7), 152. https://doi.org/10.3390/membranes10070152






