Thin Graphene–Nanotube Films for Electronic and Photovoltaic Devices: DFTB Modeling
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
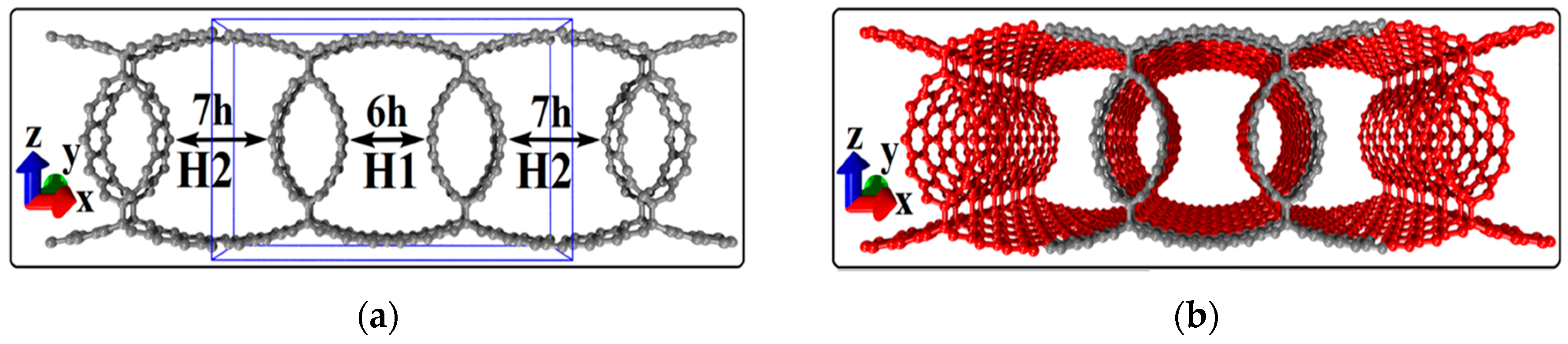
3.1. Topological Models of Supercells of Graphene/SWCNTComposite Films
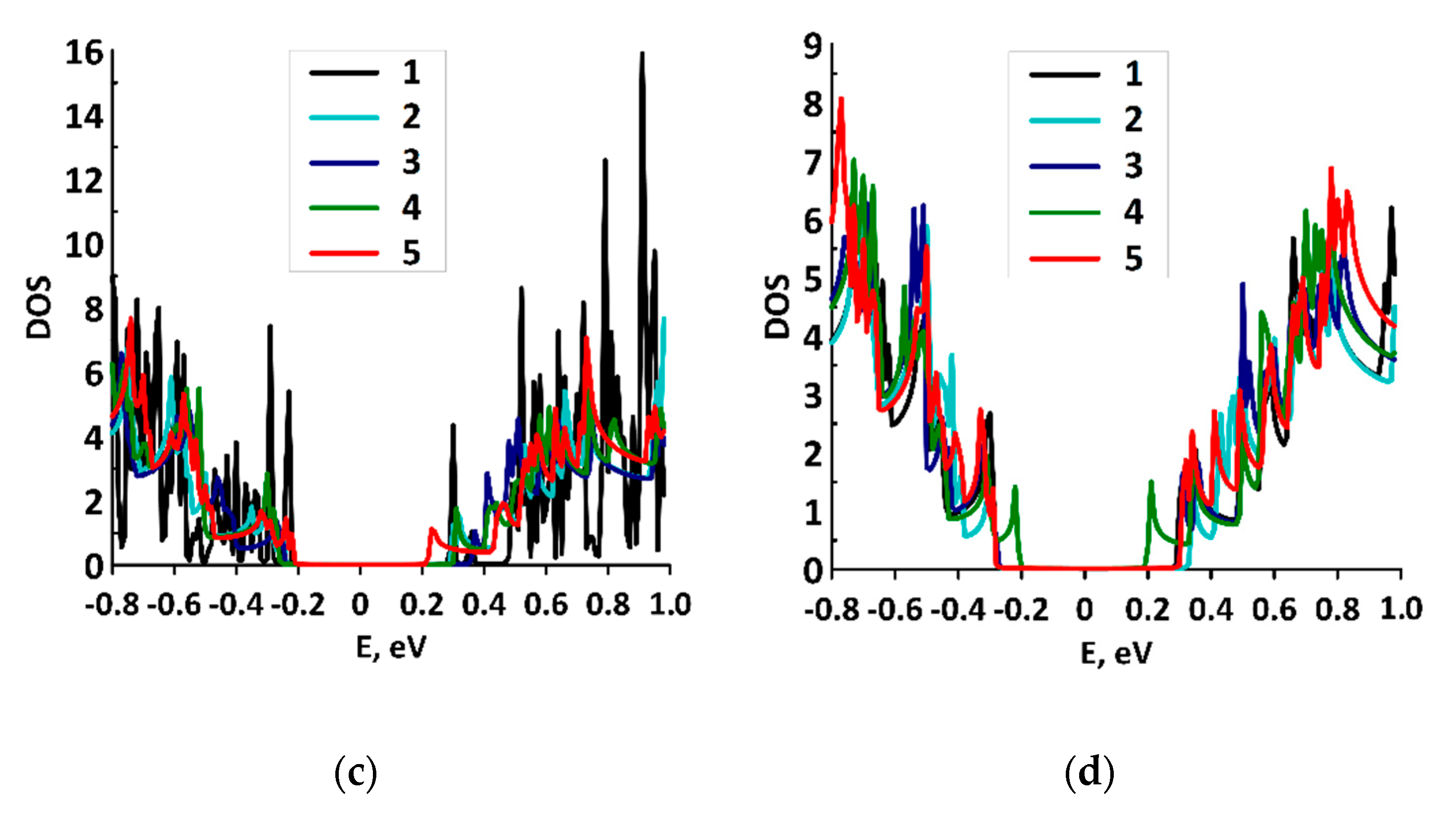
3.2. Electrical Properties of Graphene/SWCNT Composite Films
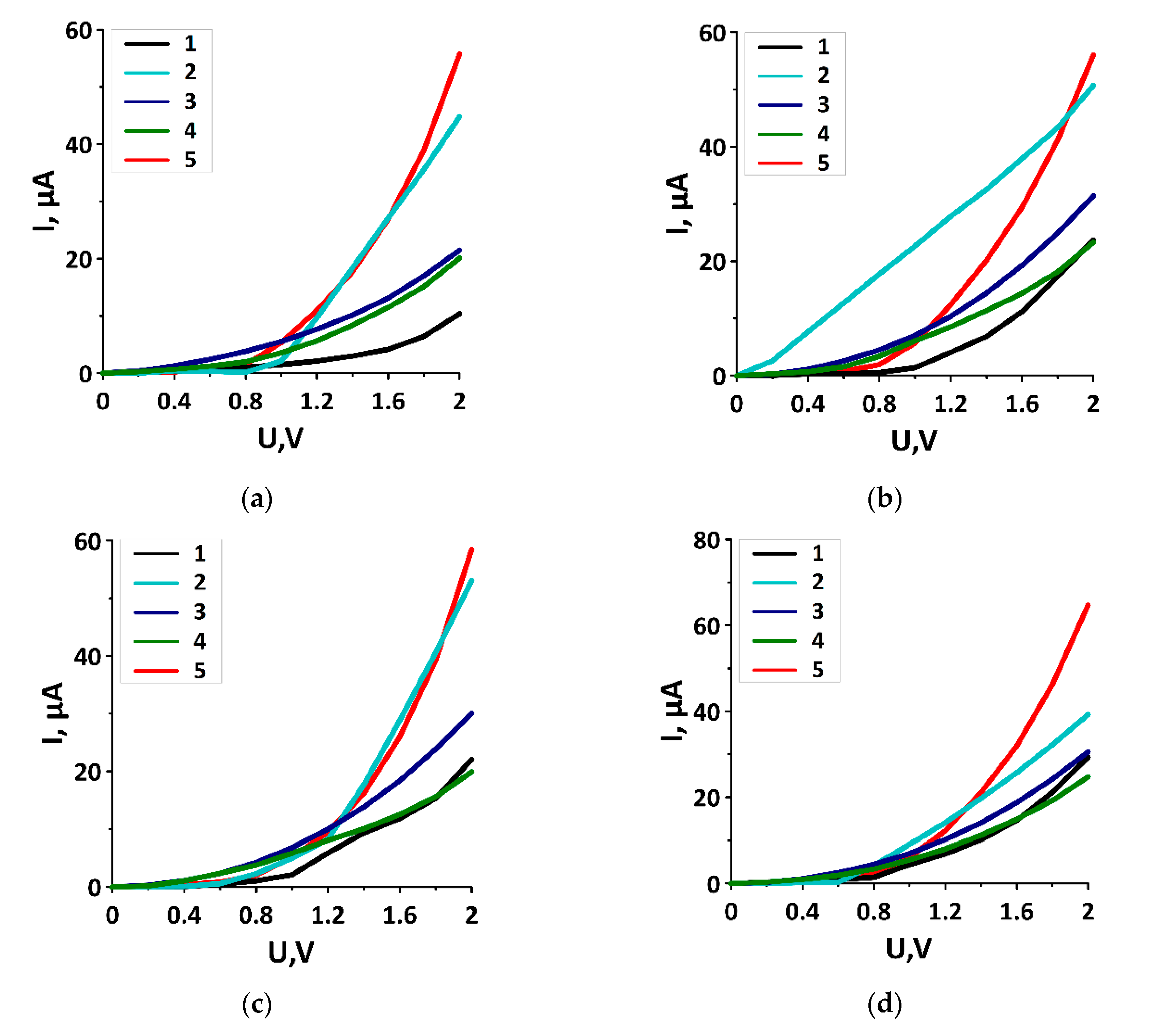
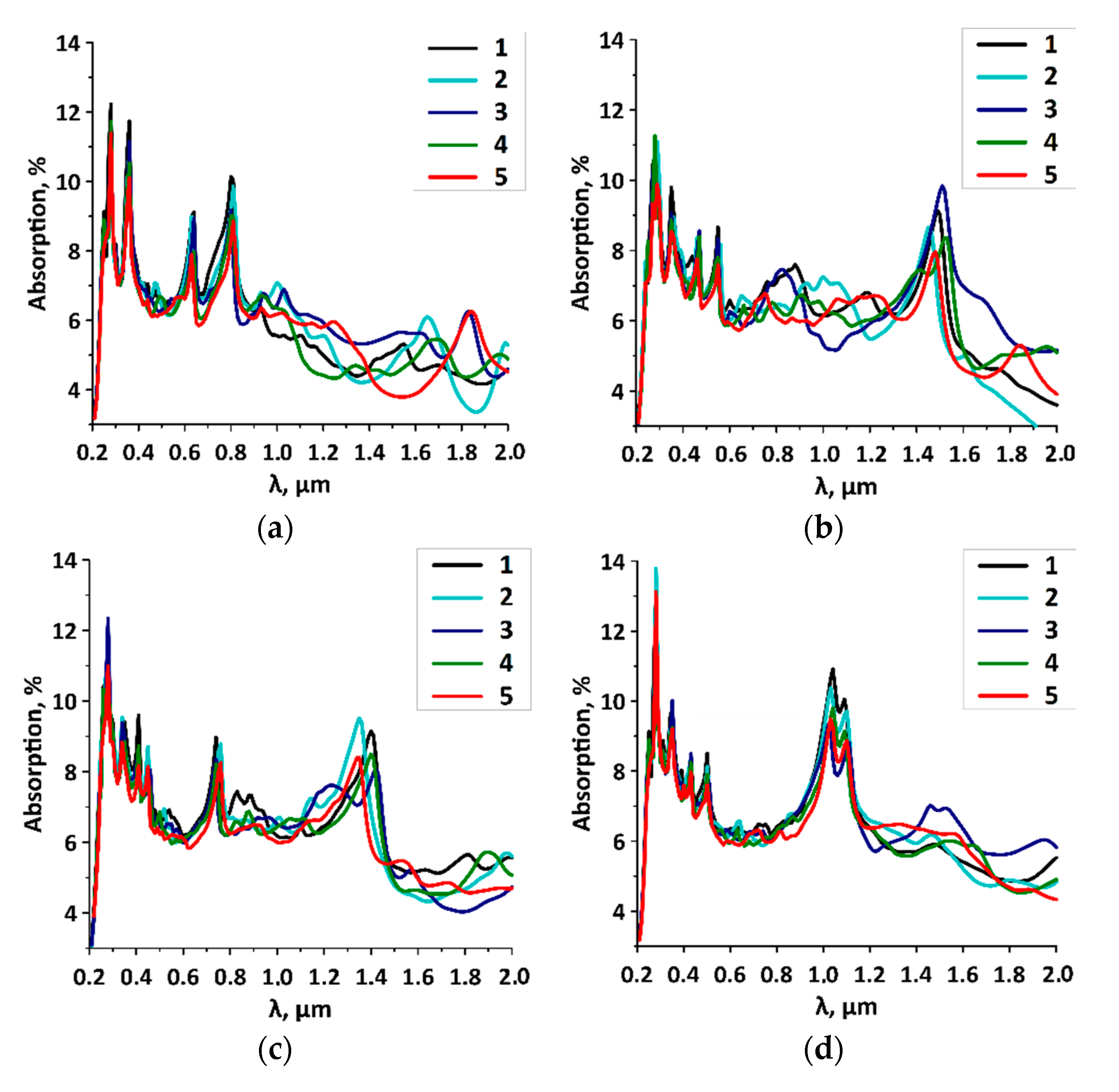
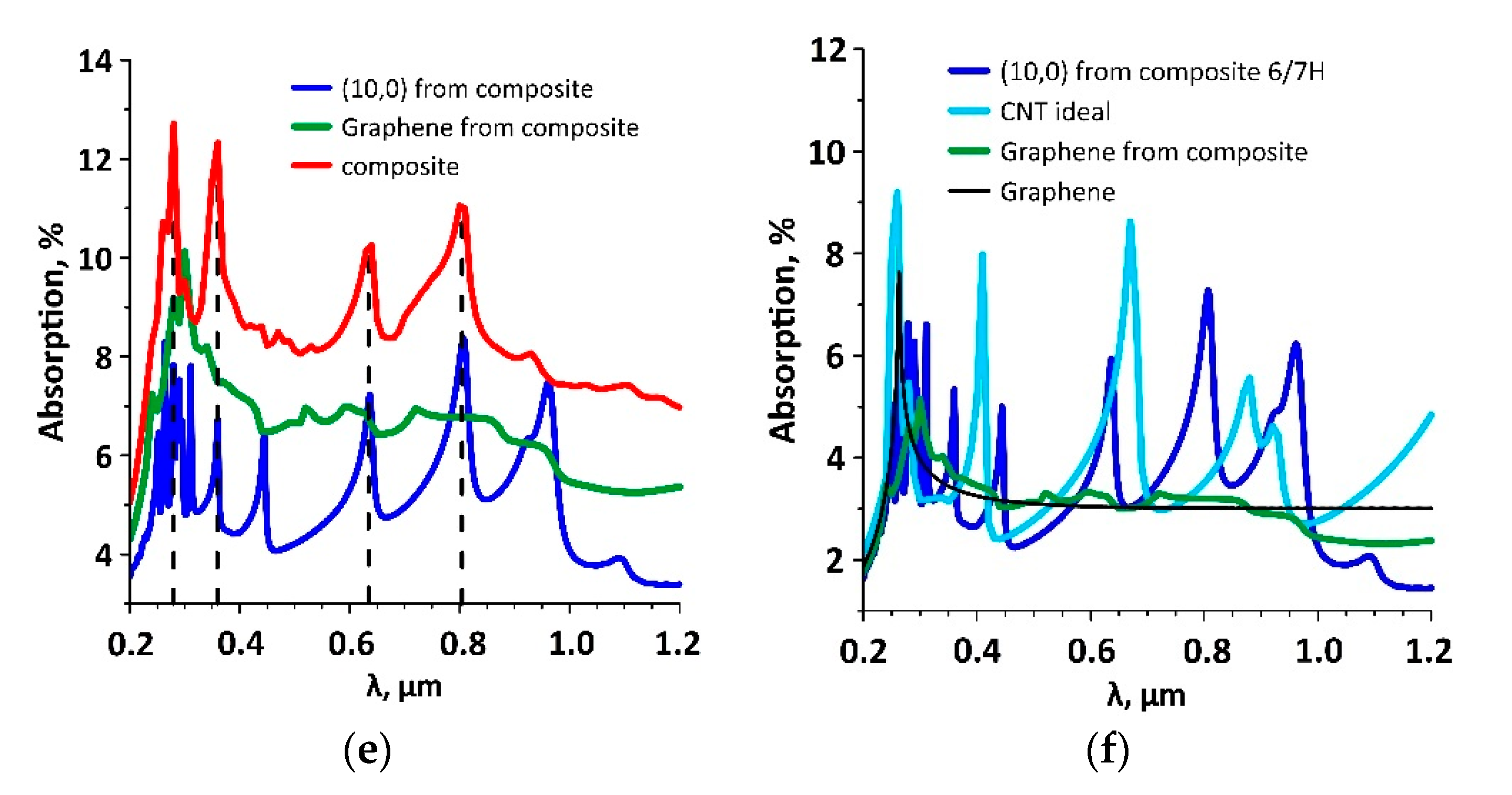
3.3. Dynamic Conductivity and Photocurrent of Graphene/SWCNT Composite Films
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shi, E.; Li, H.; Yang, L.; Hou, J.; Li, Y.; Li, L.; Cao, A.; Fang, Y. Carbon nanotube network embroidered graphene films for monolithic all-carbon electronics. Adv. Mater. 2015, 27, 682–688. [Google Scholar] [CrossRef]
- Wang, R.; Hong, T.; Xu, Y.Q. Ultrathin single-walled carbon nanotube network framed graphene hybrids. ACS Appl. Mater. Interfaces 2015, 7, 5233–5238. [Google Scholar] [CrossRef] [PubMed]
- Yun, H.; Kwak, J.; Kim, S.; Seo, H.; Bang, I.; Kim, S.Y.; Kang, S.; Kwon, S. High performance all-carbon composite transparent electrodes containing uniform carbon nanotube networks. J. Alloys Compd. 2016, 675, 37–45. [Google Scholar] [CrossRef]
- Seo, H.; Yun, H.D.; Kwon, S.Y.; Bang, I.C. Hybrid Graphene and Single-Walled Carbon Nanotube Films for Enhanced Phase-Change Heat Transfer. Nano Lett. 2016, 16, 932–938. [Google Scholar] [CrossRef]
- Chi, X.; Zhang, J.; Nshimiyimana, J.P.; Hu, X.; Wu, P.; Liu, S.; Liu, J.; Chu, W.; Sun, L. Wettability of monolayer graphene/single-walled carbon nanotube hybrid films. RSC Adv. 2017, 7, 48184–48188. [Google Scholar] [CrossRef]
- Liao, Y.; Mustonen, K.; Tulić, S.; Skákalová, V.; Khan, S.A.; Laiho, P.; Zhang, Q.; Li, C.; Monazam, M.; Kotakoski, J.; et al. Enhanced Tunneling in a Hybrid of Single-Walled Carbon Nanotubes and Graphene. ACS Nano 2019, 13, 11522–11529. [Google Scholar] [CrossRef]
- Tavakkoli, M.; Flahaut, E.; Peljo, P.; Sainio, J.; Davodi, F.; Lobiak, E.V.; Mustonen, K.; Kauppinen, E. Mesoporous Single-Atom-Doped Graphene–Carbon Nanotube Hybrid: Synthesis and Tunable Electrocatalytic Activity for Oxygen Evolution and Reduction Reactions. ACS Catal. 2020, 10, 4647–4658. [Google Scholar] [CrossRef]
- Adhikari, P.D.; Ko, Y.; Jung, D.; Park, C. Single-wall carbon nanotube hybridized graphene films: Self assembly and electrical properties. New Carbon Mater. 2015, 30, 342–348. [Google Scholar] [CrossRef]
- Lv, R.T.; Cruz, E.-S.; Terrones, M. Building complex hybrid carbon architectures by covalent interconnections: Graphene-nanotube hybrids and more. ACS Nano 2014, 8, 4061–4069. [Google Scholar] [CrossRef]
- Yan, Z.; Peng, Z.W.; Casillas, G.; Lin, J.; Xiang, C.S.; Zhou, H.Q.; Yang, Y.; Ruan, G.D.; Raji, A.-R.O.; Samuel, E.L.G.; et al. Rebar graphene. ACS Nano 2014, 8, 5061–5068. [Google Scholar] [CrossRef]
- Li, X.L.; Sha, J.W.; Lee, S.K.; Li, Y.L.; Ji, Y.S.; Zhao, Y.J.; Tour, J.M. Rivet graphene. ACS Nano 2016, 10, 7307–7313. [Google Scholar] [CrossRef] [PubMed]
- Gan, X.; Lv, R.; Bai, J.; Zhang, Z.; Wei, J.; Huang, Z.H.; Zhu, H.; Kang, F.; Terrones, M. Efficient photovoltaic conversion of graphene—Carbon nanotube hybrid films grown from solid precursors. 2D Mater. 2015, 2, 034003. [Google Scholar] [CrossRef]
- Dang, V.T.; Nguyen, D.D.; Cao, T.T.; Le, P.H.; Tran, D.L.; Phan, N.M.; Nguyen, V.C. Recent trends in preparation and application of carbon nanotube–graphene hybrid thin films. Adv. Nat. Sci. Nanosci. Nanotechnol. 2016, 7, 033002. [Google Scholar] [CrossRef]
- Lin, X.Y.; Liu, P.; Wei, Y.; Li, Q.Q.; Wang, J.P.; Wu, Y.; Feng, C.; Zhang, L.N.; Fan, S.S.; Jiang, K.L. Development of an ultra-thin film comprised of a graphene membrane and carbon nanotube vein support. Nat. Commun. 2013, 4, 2920. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.D.; Li, X.M.; Cheng, H.Y.; Liu, Z.J.; Zhao, L.Y.; Yang, T.T.; Dai, Z.H.; Cheng, Z.G.; Shi, E.Z.; Yang, L.; et al. Graphene reinforced carbon nanotube networks for wearable strain sensors. Adv. Funct. Mater. 2016, 26, 2078–2084. [Google Scholar] [CrossRef]
- Liu, Y.D.; Wang, F.Q.; Wang, X.M.; Wang, X.Z.; Flahaut, E.; Liu, X.L.; Li, Y.; Wang, X.R.; Xu, Y.B.; Shi, Y.; et al. Planar carbon nanotube-graphene hybrid films for high-performance broadband photodetectors. Nat. Commun. 2015, 6, 8589. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.H.; Song, W.; Jung, M.W.; Kang, M.A.; Kim, K.; Chang, S.J.; Lee, S.S.; Lim, J.; Hwang, J.; Myung, S.; et al. Carbon nanotube and graphene hybrid thin film for transparent electrodes and field effect transistors. Adv. Mater. 2014, 26, 4247–4252. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Tiwari, R.N.; Matsuoka, Y.; Hashimoto, G.; Rokuta, E.; Chen, Y.-Z.; Chueh, Y.-L.; Yoshimura, M. Low vacuum annealing of cellulose acetate on nickel towards transparent conductive CNT-graphene hybrid films. ACS Appl. Mater. Interfaces 2014, 6, 9071–9077. [Google Scholar] [CrossRef]
- Kholmanov, I.N.; Magnuson, C.W.; Piner, R.; Kim, J.Y.; Aliev, A.E.; Tan, C.; Kim, T.Y.; Zakhidov, A.A.; Sberveglieri, G.; Baughman, R.H.; et al. Optical, electrical, and electromechanical properties of hybrid graphene/carbon nanotube films. Adv. Mater. 2015, 27, 3053–3059. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.; Jeong, H.S.; Kim, H.; Lee, H.; Ha, J.M.; Choi, S.M.; Kim, T.H.; Nah, Y.C.; Shin, T.J.; et al. Spontaneous hybrids of graphene and carbon nanotube arrays at the liquid-gas interface for Li-ion battery anodes. Chem. Commun. 2018, 54, 5229–5232. [Google Scholar] [CrossRef]
- Paulus, G.L.; Wang, Q.H.; Ulissi, Z.W.; McNicholas, T.P.; Vijayaraghavan, A.; Shih, C.J.; Jin, Z.; Strano, M.S. Charge transfer at junctions of a single layer of graphene and a metallic single walled carbon nanotube. Small 2013, 9, 1954–1963. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Liu, Y.; Qin, S.; Xu, Y.; Zhang, R.; Wang, F. Graphene-carbon nanotube hybrid films for high-performance flexible photodetectors. Nano Res. 2016, 10, 1880–1887. [Google Scholar] [CrossRef]
- Maarouf, A.; Kasry, A.; Chandra, B.; Martyna, G. A graphene–carbon nanotube hybrid material for photovoltaic applications. Carbon 2015, 102, 74–80. [Google Scholar] [CrossRef]
- Cao, J.; Zou, Y.; Gong, X.; Qian, R.; An, Z. Scalable Production of Graphene/Semiconducting Single-Wall Carbon Nanotube Film Schottky Broadband Photodiode Array with Enhanced Photoresponse. Appl. Sci. 2018, 8, 2369. [Google Scholar] [CrossRef]
- Cao, J.; Zou, Y.; Gong, X.; Gou, P.; Qian, J.; Qian, R.; An, Z. Double-layer heterostructure of graphene/carbon nanotube films for highly efficient broadband photodetector. Appl. Phys. Lett. 2018, 113, 061112. [Google Scholar] [CrossRef]
- Mitrofanov, V.V.; Slepchenkov, M.M.; Zhang, G.; Glukhova, O.E. Hybrid carbon nanotube-graphene monolayer films: Regularities of structure, electronic and optical properties. Carbon 2017, 115, 803–810. [Google Scholar] [CrossRef]
- Liu, A.; Stuart, S.J. Empirical Bond-Order Potential for Hydrocarbons: Adaptive Treatment of van der Waals Interactions. J. Comput. Chem. 2008, 29, 601–611. [Google Scholar] [CrossRef]
- Elstner, M.; Seifert, G. Density functional tight binding. Philos. Trans. R. Soc. A 2014, 372, 20120483. [Google Scholar] [CrossRef]
- Li, M.; Liu, X.; Zhao, X.; Yang, F.; Wang, X.; Li, Y. Metallic Catalysts for Structure-Controlled Growth of Single-Walled Carbon Nanotubes. Top. Curr. Chem. 2017, 375, 29. [Google Scholar] [CrossRef]
- Yang, F.; Wang, X.; Li, M.; Liu, X.; Zhao, X.; Zhang, D.; Zhang, Y.; Yang, J.; Li, Y. Templated Synthesis of Single-Walled Carbon Nanotubes with Specific Structure. Acc. Chem. Res. 2016, 49, 606–615. [Google Scholar] [CrossRef]
- Datta, S. Coherent Transport. In Quantum Transport: Atom to Transistor; Cambridge University Press: New York, NY, USA, 2005; pp. 232–240. [Google Scholar]
- Glukhova, O.E.; Nefedov, I.S.; Shalin, A.S.; Slepchenkov, M.M. New 2D graphene hybrid composites as an effective base element of optical nanodevices. Beilstein J. Nanotechnol. 2018, 9, 1321–1327. [Google Scholar] [CrossRef] [PubMed]
- Calderín, L.; Karasiev, V.V.; Trickey, S.B. Kubo-Greenwood electrical conductivity formulation and implementation for projector augmented wave datasets. Comput. Phys. Commun. 2017, 221, 118–142. [Google Scholar] [CrossRef]
- Stauber, T.; Peres, N.M.R.; Geim, A.K. Optical conductivity of graphene in the visible region of the spectrum. Phys. Rev. B 2008, 78, 085432. [Google Scholar] [CrossRef]
- Zhou, H.; Qu, Y.; Zeid, T.; Duan, X. Towards highly efficient photocatalysts using semiconductor nanoarchitectures. Energy Environ. Sci. 2012, 5, 6732–6743. [Google Scholar] [CrossRef]
- NREL Website. Solar Resource Data and Tools. Available online: http://rredc.nrel.gov (accessed on 16 September 2020).
- Bernardi, M.; Palummo, M.; Grossman, J. Extraordinary Sunlight Absorption and One Nanometer Thick Photovoltaics Using Two-Dimensional Monolayer Materials. Nano Lett. 2013, 13, 3664–3670. [Google Scholar] [CrossRef]


| Parameters | H1/H2 | Lx, Å | Ly, Å | h, nm | ΔHf, kcal/mol∙atom | Ef, eV | Egap, eV |
|---|---|---|---|---|---|---|---|
| (10,0) | 6/7 6/8 6/9 6/10 6/11 | 32.07 34.46 36.79 39.38 41.72 | 4.28 4.28 4.29 4.28 4.28 | 1.645 1.633 1.641 1.634 1.627 | −0.23 −0.35 −0.27 −0.22 −0.32 | −4.63 −4.63 −4.66 −4.67 −4.63 | 0.73 0.69 0.6 0.56 0.69 |
| (12,0) | 7/8 7/9 7/10 7/11 7/12 | 36.97 39.33 41.84 44.23 46.67 | 4.28 4.29 4.28 4.28 4.29 | 1.897 1.897 1.881 1.884 1.881 | −0.19 −0.16 −0.24 −0.19 −0.13 | −4.69 −4.69 −4.69 −4.69 −4.69 | 0.53 0.53 0.52 0.51 0.51 |
| (14,0) | 8/9 8/10 8/11 8/12 8/13 | 41.75 44.28 46.68 49.12 51.59 | 4.28 4.27 4.28 4.28 4.27 | 2.167 2.146 2.144 2.120 2.132 | −0.22 −0.16 −0.18 −0.21 −0.15 | −4.64 −4.66 −4.63 −4.67 −4.69 | 0.6 0.53 0.61 0.56 0.43 |
| (16,0) | 9/10 9/11 9/12 9/13 9/14 | 46.75 49.16 51.6 54 56.53 | 4.28 4.28 4.29 4.28 4.28 | 2.427 2.380 2.367 2.376 2.357 | −0.04 −0.12 −0.07 −0.03 −0.10 | −4.69 −4.67 −4.68 −4.70 −4.68 | 0.57 0.62 0.58 0.43 0.59 |
| Structure Type | (10,0) | (12,0) | (14,0) | (16,0) |
|---|---|---|---|---|
| Graphene/SWCNT Composite Film | 55.73 µA | 56.02 µA | 58.45 µA | 64.72 µA |
| Ideal Graphene | 21.49 µA | 34.42 µA | 30.06 µA | 30.55 µA |
| Ideal SWCNT | 44.81 µA | 50.7 µA | 53.03 µA | 39.24 µA |
| Graphene in a Composite Film | 20.1 µA | 23.3 µA | 19.89 µA | 24.73 µA |
| SWCNT as Part of a Composite Film | 10.38 µA | 23.69 µA | 22.05 µA | 29.3 µA |
| AM0 | |||||||
| Isum for the Emission Spectrum 200–2000 nm, | |||||||
| (10,0) | (12,0) | (14,0) | (16,0) | ||||
| 6/7 | 5.19 | 7/8 | 5.48 | 8/9 | 5.60 | 9/10 | 5.61 |
| 6/8 | 5.22 | 7/9 | 5.28 | 8/10 | 5.48 | 9/11 | 5.57 |
| 6/9 | 5.31 | 7/10 | 5.46 | 8/11 | 5.39 | 9/12 | 5.59 |
| 6/10 | 4.98 | 7/11 | 5.31 | 8/12 | 5.34 | 9/13 | 5.40 |
| 6/11 | 5.01 | 7/12 | 5.17 | 8/13 | 5.26 | 9/14 | 5.39 |
| Isum for the Visible Part of the Solar Spectrum 380–780 nm, | |||||||
| (10,0) | (12,0) | (14,0) | (16,0) | ||||
| 6/7 | 2.19 | 7/8 | 2.08 | 8/9 | 2.11 | 9/10 | 2.02 |
| 6/8 | 2.10 | 7/9 | 2.03 | 8/10 | 2.07 | 9/11 | 1.98 |
| 6/9 | 2.08 | 7/10 | 1.99 | 8/11 | 2.04 | 9/12 | 1.96 |
| 6/10 | 2.01 | 7/11 | 1.96 | 8/12 | 2.00 | 9/13 | 1.93 |
| 6/11 | 1.96 | 7/12 | 1.95 | 8/13 | 1.97 | 9/14 | 1.92 |
| AM1.5 | |||||||
| Isum for the Emission Spectrum 200–2000 nm, | |||||||
| (10,0) | (12,0) | (14,0) | (16,0) | ||||
| 6/7 | 3.90 | 7/8 | 4.03 | 8/9 | 4.06 | 9/10 | 4.17 |
| 6/8 | 3.96 | 7/9 | 3.87 | 8/10 | 3.98 | 9/11 | 4.13 |
| 6/9 | 3.94 | 7/10 | 3.99 | 8/11 | 3.94 | 9/12 | 4.09 |
| 6/10 | 3.73 | 7/11 | 3.87 | 8/12 | 3.86 | 9/13 | 4.02 |
| 6/11 | 3.72 | 7/12 | 3.76 | 8/13 | 3.85 | 9/14 | 3.99 |
| Isum for the Visible Part of the Solar Spectrum 380–780 nm, | |||||||
| (10,0) | (12,0) | (14,0) | (16,0) | ||||
| 6/7 | 1.78 | 7/8 | 1.68 | 8/9 | 1.72 | 9/10 | 1.64 |
| 6/8 | 1.71 | 7/9 | 1.65 | 8/10 | 1.67 | 9/11 | 1.60 |
| 6/9 | 1.69 | 7/10 | 1.64 | 8/11 | 1.65 | 9/12 | 1.59 |
| 6/10 | 1.63 | 7/11 | 1.59 | 8/12 | 1.63 | 9/13 | 1.56 |
| 6/11 | 1.60 | 7/12 | 1.58 | 8/13 | 1.60 | 9/14 | 1.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolosov, D.A.; Mitrofanov, V.V.; Slepchenkov, M.M.; Glukhova, O.E. Thin Graphene–Nanotube Films for Electronic and Photovoltaic Devices: DFTB Modeling. Membranes 2020, 10, 341. https://doi.org/10.3390/membranes10110341
Kolosov DA, Mitrofanov VV, Slepchenkov MM, Glukhova OE. Thin Graphene–Nanotube Films for Electronic and Photovoltaic Devices: DFTB Modeling. Membranes. 2020; 10(11):341. https://doi.org/10.3390/membranes10110341
Chicago/Turabian StyleKolosov, Dmitry A., Vadim V. Mitrofanov, Michael M. Slepchenkov, and Olga E. Glukhova. 2020. "Thin Graphene–Nanotube Films for Electronic and Photovoltaic Devices: DFTB Modeling" Membranes 10, no. 11: 341. https://doi.org/10.3390/membranes10110341
APA StyleKolosov, D. A., Mitrofanov, V. V., Slepchenkov, M. M., & Glukhova, O. E. (2020). Thin Graphene–Nanotube Films for Electronic and Photovoltaic Devices: DFTB Modeling. Membranes, 10(11), 341. https://doi.org/10.3390/membranes10110341







