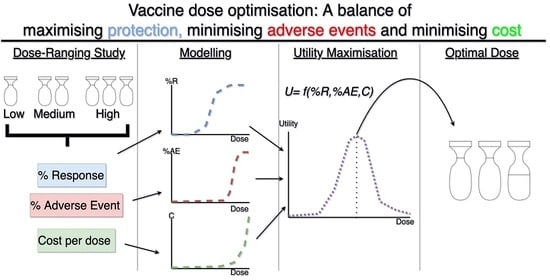
Optimising Vaccine Dose in Inoculation against SARS-CoV-2, a Multi-Factor Optimisation Modelling Study to Maximise Vaccine Safety and Efficacy
Abstract
1. Introduction
- (1)
- Using published data, calibrate mathematical models to the relationship between dose and seroconversion, safety and cost of a single inoculation.
- (2)
- Identify the minimum dose that is predicted to theoretically induce herd immunity.
- (3)
- Identify the dose that maximises immunogenicity and safety.
- (4)
- Identify the dose that maximises immunogenicity and safety whilst minimising cost.
2. Materials and Methods
2.1. Data
2.2. Objective 1. Using Published Data, Calibrate Mathematical Models to the Relationship between Dose and Seroconversion, Safety and Cost of a Single Inoculation
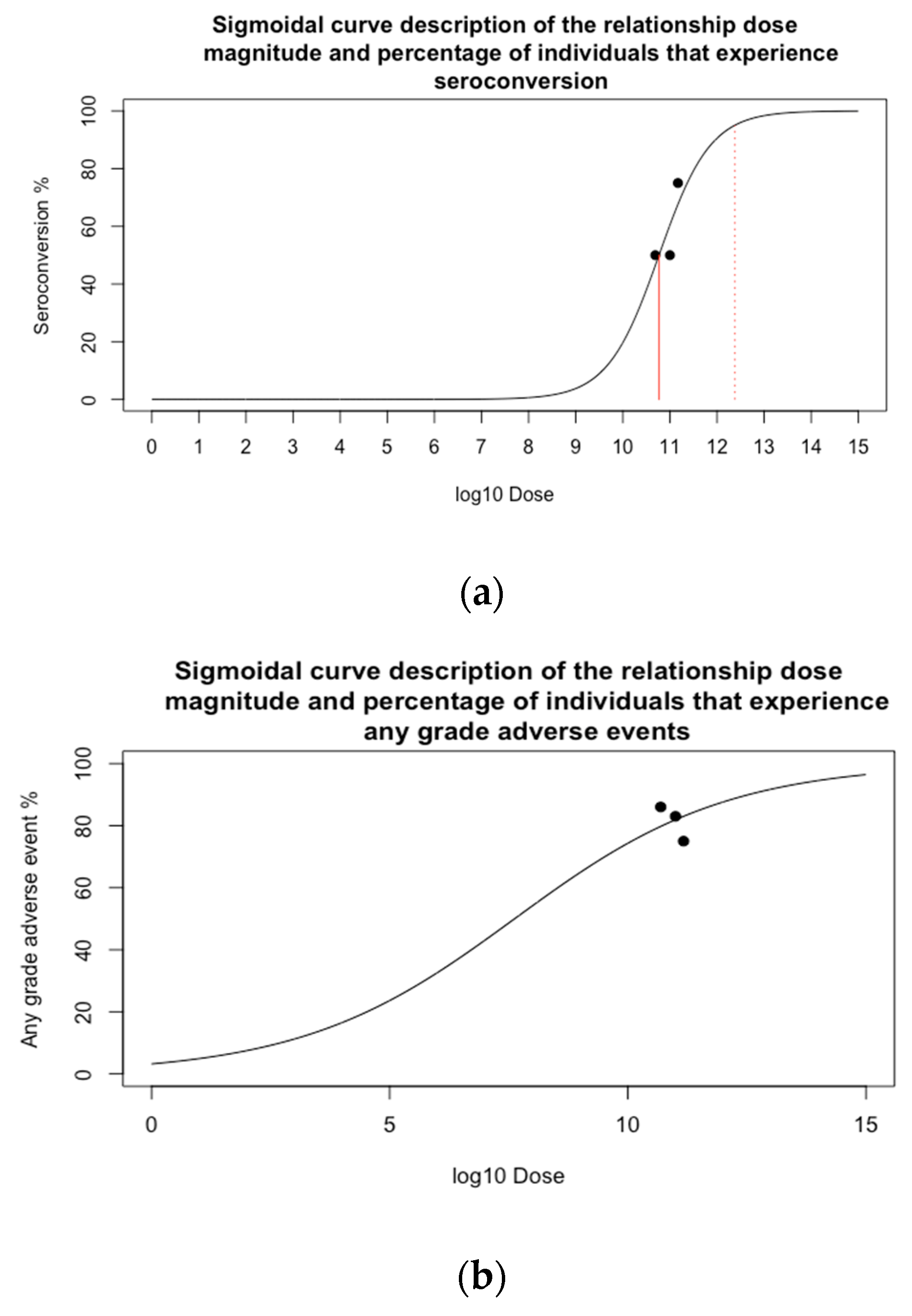
2.2.1. Dose-Seroconversion Relationship
2.2.2. Dose-Safety Relationship
2.2.3. Dose-Cost Relationship
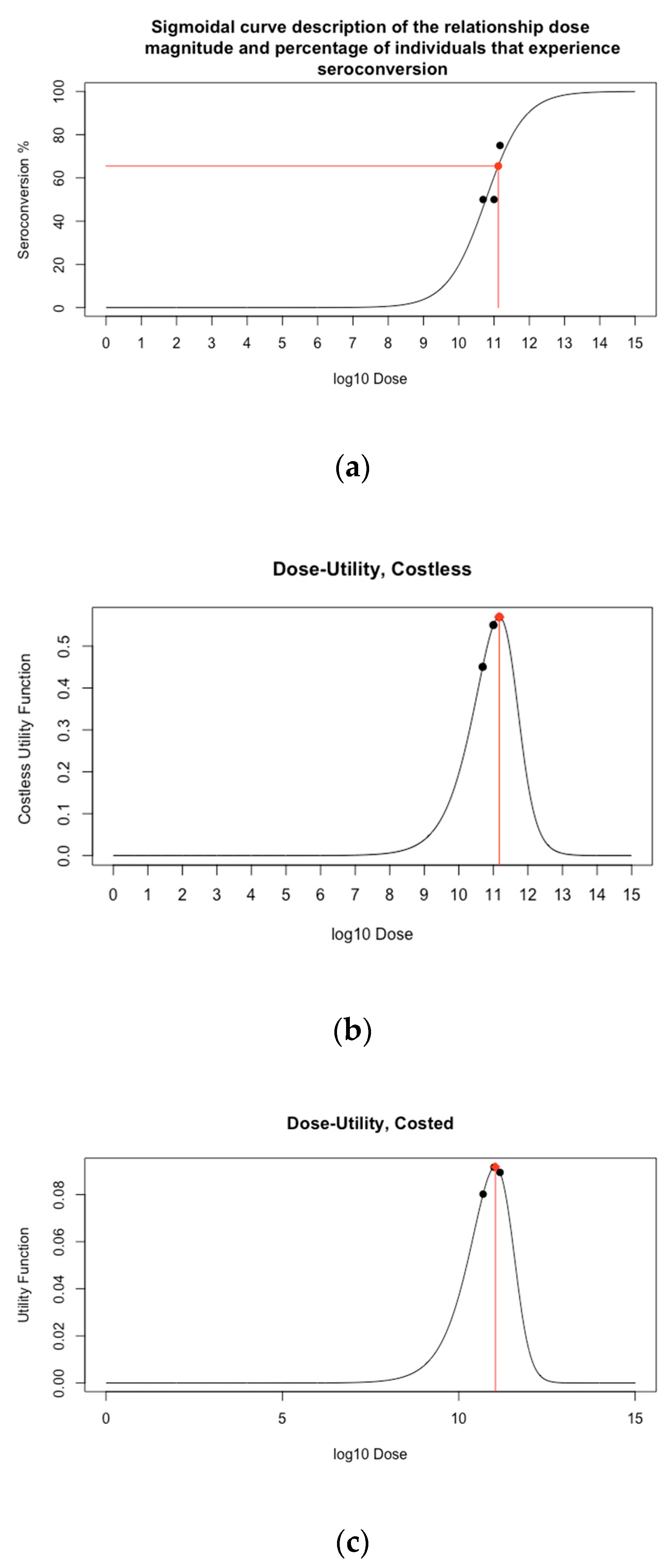
2.3. Objective 2. Identify the Minimum Dose that Is Predicted to Theoretically Induce Herd Immunity
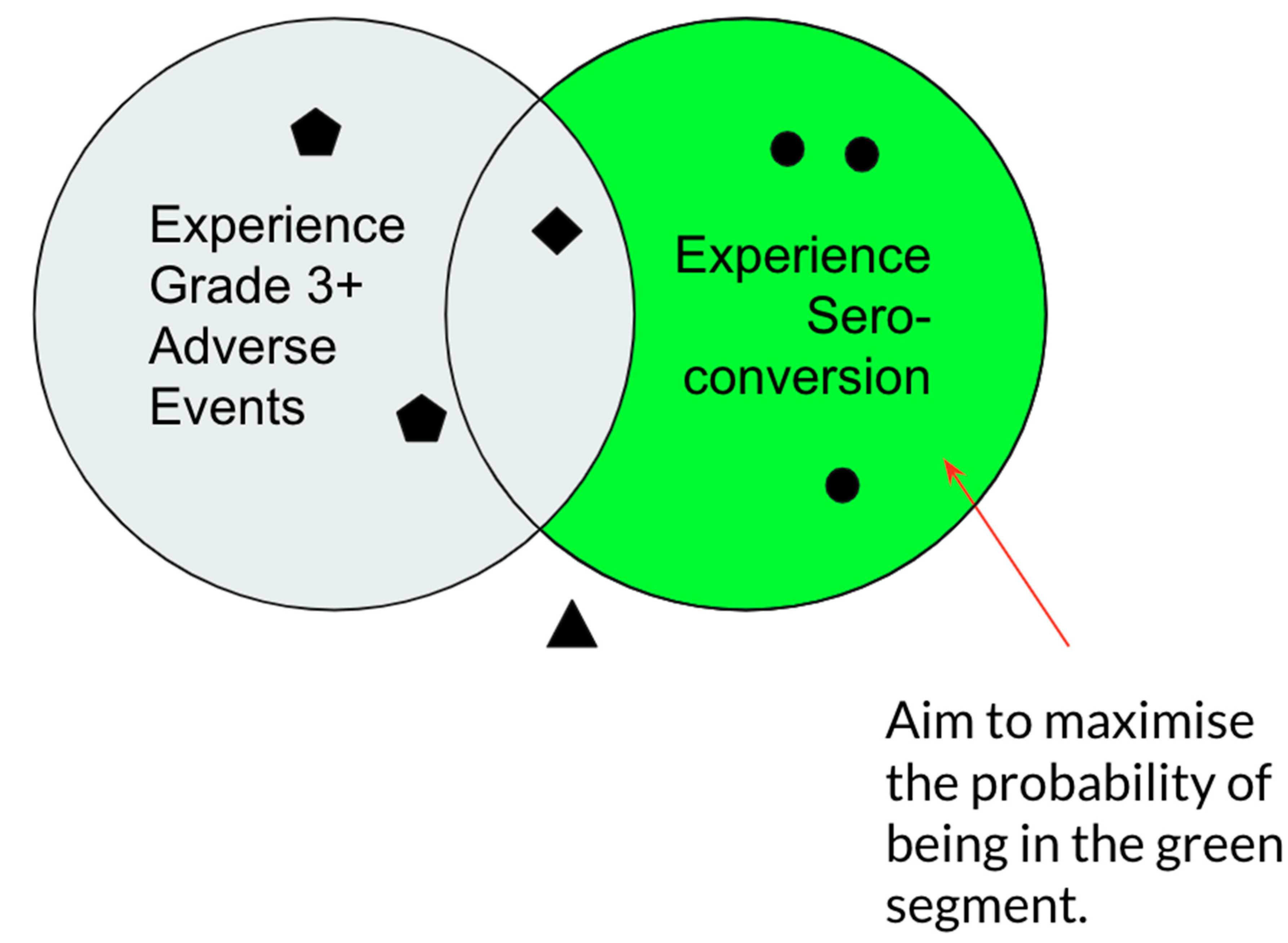
2.4. Objective 3. Identify the Dose that Maximises Immunogenicity and Safety
2.5. Objective 4. Identify the Dose that Maximises Immunogenicity and Safety Whilst Minimising Cost
Threshold Analysis
3. Results
3.1. Objective 1. Using Published Data, Calibrate Mathematical Models to the Relationship between Dose and Seroconversion, Safety, and Cost of a Single Inoculation
3.1.1. Does-Seroconversion Relationship
3.1.2. Dose-Safety Relationship
3.2. Objective 2. Identify the Minimum Dose that Is Predicted to Theoretically Induce Herd Immunity
3.3. Objective 3. Identify the Dose that Maximises Immunogenicity and Safety
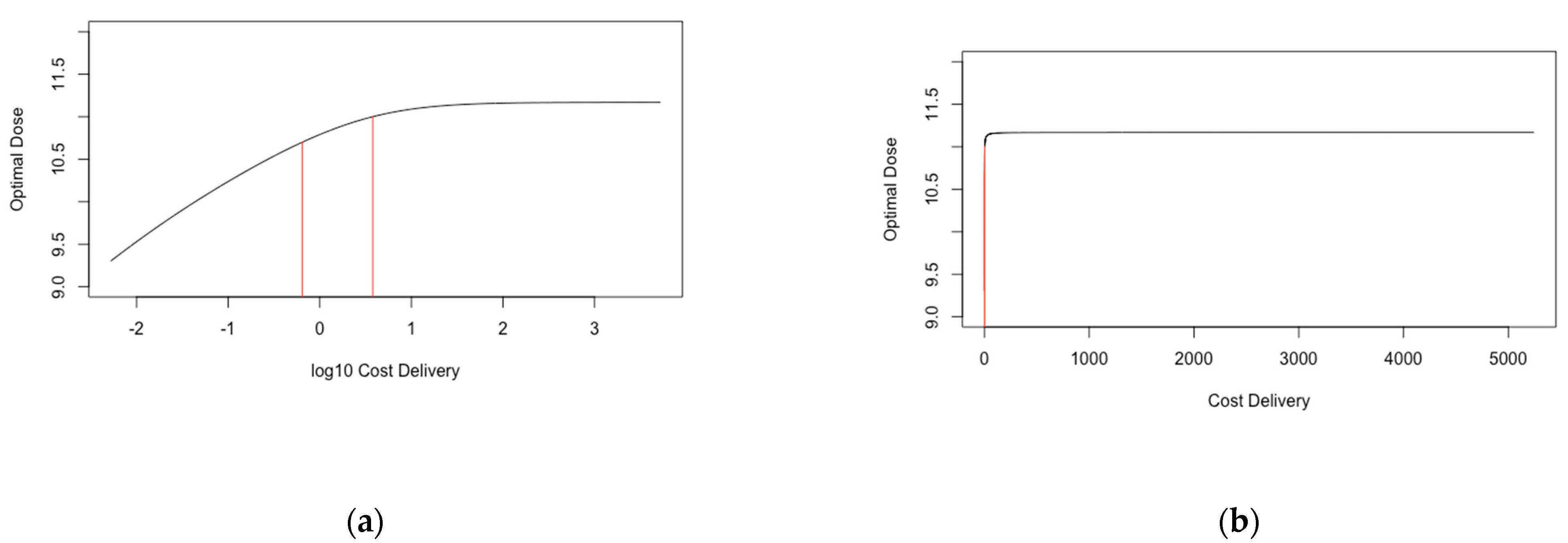
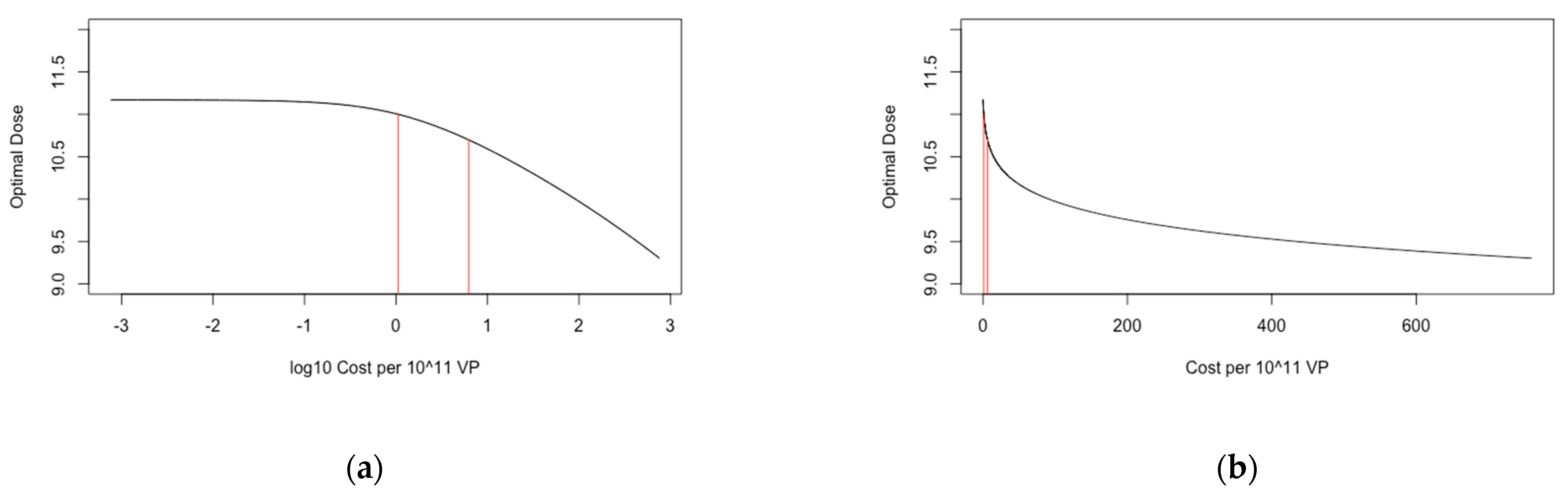
3.4. Objective 4. Identify the Dose that Maximises Immunogenicity and Safety Whilst Minimising Cost
Threshold Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sharma, A.; Tiwari, S.; Deb, M.K.; Marty, J.L. Severe Acute Respiratory Syndrome Coronavirus-2 (SARS-CoV-2): A Global Pandemic and Treatment Strategies. Int. J. Antimicrob. Agents 2020, 56, 106054. [Google Scholar] [CrossRef] [PubMed]
- Nicola, M.; Alsafi, Z.; Sohrabi, C.; Kerwan, A.; Al-Jabir, A.; Iosifidis, C.; Agha, M.; Agha, R. The Socio-Economic Implications of the Coronavirus Pandemic (COVID-19): A Review. Int. J. Surg. 2020, 78, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Greenwood, B. The Contribution of Vaccination to Global Health: Past, Present and Future. Philos. Trans. R. Soc. B Biol. Sci. 2014, 369, 20130433. [Google Scholar] [CrossRef] [PubMed]
- Kaur, S.P.; Gupta, V. COVID-19 Vaccine: A Comprehensive Status Report. Virus Res. 2020, 288, 198114. [Google Scholar] [CrossRef]
- Rhodes, S.J.; Knight, G.M.; Kirschner, D.E.; White, R.G.; Evans, T.G. Dose Finding for New Vaccines: The Role for Immunostimulation/Immunodynamic Modelling. J. Theor. Biol. 2019, 465, 51–55. [Google Scholar] [CrossRef]
- Handel, A.; Li, Y.; McKay, B.; Pawelek, K.A.; Zarnitsyna, V.; Antia, R. Exploring the Impact of Inoculum Dose on Host Immunity and Morbidity to Inform Model-Based Vaccine Design. PLoS Comput. Biol. 2018, 14, e1006505. [Google Scholar] [CrossRef]
- Rhodes, S.J.; Zelmer, A.; Knight, G.M.; Prabowo, S.A.; Stockdale, L.; Evans, T.G.; Lindenstrøm, T.; White, R.G.; Fletcher, H. The TB Vaccine H56+IC31 Dose-Response Curve Is Peaked Not Saturating: Data Generation for New Mathematical Modelling Methods to Inform Vaccine Dose Decisions. Vaccine 2016, 34, 6285–6291. [Google Scholar] [CrossRef]
- Benest, J.; Rhodes, S.; Afrough, S.; Evans, T.; White, R. Response Type and Host Species May Be Sufficient to Predict Dose-Response Curve Shape for Adenoviral Vector Vaccines. Vaccines 2020, 8, 155. [Google Scholar] [CrossRef]
- Frazão, T.D.C.; Camilo, D.G.G.; Cabral, E.L.S.; Souza, R.P. Multicriteria Decision Analysis (MCDA) in Health Care: A Systematic Review of the Main Characteristics and Methodological Steps. BMC Med. Inform. Decis. Mak. 2018, 18, 90. [Google Scholar] [CrossRef]
- World Health Organisation. DRAFT Landscape of COVID-19 Candidate Vaccines. Available online: https://www.who.int/publications/m/item/draft-landscape-of-covid-19-candidate-vaccines (accessed on 9 September 2020).
- Izda, V.; Jeffries, M.A.; Sawalha, A.H. COVID-19: A Review of Therapeutic Strategies and Vaccine Candidates. Clin. Immunol. 2020, 222, 108634. [Google Scholar] [CrossRef]
- Oxford University Breakthrough on Global COVID-19 Vaccine | University of Oxford. Available online: https://www.ox.ac.uk/news/2020-11-23-oxford-university-breakthrough-global-covid-19-vaccine (accessed on 30 November 2020).
- Mahase, E. COVID-19: Vaccine Candidate May Be More than 90% Effective, Interim Results Indicate. BMJ 2020, 371, m4347. [Google Scholar] [CrossRef] [PubMed]
- Mullard, A. COVID-19 Vaccine Development Pipeline Gears Up. Lancet 2020, 395, 1751–1752. [Google Scholar] [CrossRef]
- Zhu, F.-C.; Li, Y.-H.; Guan, X.-H.; Hou, L.-H.; Wang, W.-J.; Li, J.-X.; Wu, S.-P.; Wang, B.-S.; Wang, Z.; Wang, L.; et al. Safety, Tolerability, and Immunogenicity of a Recombinant Adenovirus Type-5 Vectored COVID-19 Vaccine: A Dose-Escalation, Open-Label, Non-Randomised, First-in-Human Trial. Lancet 2020, 395, 1845–1854. [Google Scholar] [CrossRef]
- Manners, C.; Larios Bautista, E.; Sidoti, H.; Lopez, O.J. Protective Adaptive Immunity Against Severe Acute Respiratory Syndrome Coronaviruses 2 (SARS-CoV-2) and Implications for Vaccines. Cureus 2020, 12, e8399. [Google Scholar] [CrossRef]
- US Food and Drug Administration. Guidance for Industry: Toxicity Grading Scale for Healthy Adult and Adolescent Volunteers Enrolled in Preventive Vaccine Clinical Trials; US Department of Health and Human Services, Food and Drug Administration: Silver Spring, MD, USA, 2007.
- Sibille, M.; Patat, A.; Caplain, H.; Donazzolo, Y. A Safety Grading Scale to Support Dose Escalation and Define Stopping Rules for Healthy Subject First-Entry-into-Man Studies. Br. J. Clin. Pharmacol. 2010, 70, 736–748. [Google Scholar] [CrossRef]
- Grothendieck, G. Nls2: Non-Linear Regression with Brute Force, R package version 0.2; 2013. Available online: https://CRAN.R-project.org/package=nls2 (accessed on 5 January 2019).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Afrough, S.; Rhodes, S.; Evans, T.; White, R.; Benest, J. Immunologic Dose-Response to Adenovirus-Vectored Vaccines in Animals and Humans: A Systematic Review of Dose-Response Studies of Replication Incompetent Adenoviral Vaccine Vectors When Given via an Intramuscular or Subcutaneous Route. Vaccines 2020, 8, 131. [Google Scholar] [CrossRef]
- Wang, C.; Rosner, G.L.; Roden, R.B.S. A Bayesian Design for Phase I Cancer Therapeutic Vaccine Trials. Stat. Med. 2019, 38, 1170–1189. [Google Scholar] [CrossRef]
- Wages, N.A.; Slingluff, C.L. Flexible Phase I–II Design for Partially Ordered Regimens with Application to Therapeutic Cancer Vaccines. Stat. Biosci. 2020, 12, 104–123. [Google Scholar] [CrossRef]
- Le Tourneau, C.; Lee, J.J.; Siu, L.L. Dose Escalation Methods in Phase I Cancer Clinical Trials. JNCI J. Natl. Cancer Inst. 2009, 101, 708–720. [Google Scholar] [CrossRef]
- Safety Information by Vaccine | CDC. Available online: https://www.cdc.gov/vaccinesafety/vaccines/index.html (accessed on 15 October 2020).
- Average for the Year to 31 March 2020—GOV.UK. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/885947/Spot.csv/preview (accessed on 16 October 2020).
- Inflation Calculator. Available online: http://www.bankofengland.co.uk/monetary-policy/inflation/inflation-calculator (accessed on 16 October 2020).
- Agenda for Change—Pay Rates. Available online: https://www.healthcareers.nhs.uk/working-health/working-nhs/nhs-pay-and-benefits/agenda-change-pay-rates (accessed on 16 October 2020).
- Annual Leave and Holiday | Advice Guides | Royal College of Nursing. Available online: /get-help/rcn-advice/annual-leave-and-holiday-pay (accessed on 16 October 2020).
- Vaccinating Adults: A Step-by-Step Guide; Centers for Disease Control and Prevention: St. Paul, MI, USA, 2017.
- Pereira, C.C.; Bishai, D. Vaccine Presentation in the USA: Economics of Prefilled Syringes versus Multidose Vials for Influenza Vaccination. Expert Rev. Vaccines 2010, 9, 1343–1349. [Google Scholar] [CrossRef]
- GE Healthcare. Scalable Process for Adenovirus Production 2018. Available online: https://cdn.cytivalifesciences.com/dmm3bwsv3/AssetStream.aspx?mediaformatid=10061&destinationid=10016&assetid=27018 (accessed on 15 October 2020).
- Kwok, K.O.; Lai, F.; Wei, W.I.; Wong, S.Y.S.; Tang, J.W.T. Herd Immunity—Estimating the Level Required to Halt the COVID-19 Epidemics in Affected Countries. J. Infect. 2020, 80, e32–e33. [Google Scholar] [CrossRef] [PubMed]
- Raja, A.T.; Alshamsan, A.; Al-jedai, A. Current COVID-19 Vaccine Candidates: Implications in the Saudi Population. Saudi Pharm. J. SPJ 2020, 28, 1743–1748. [Google Scholar] [CrossRef] [PubMed]
- Rhodes, S.J.; Guedj, J.; Fletcher, H.A.; Lindenstrøm, T.; Scriba, T.J.; Evans, T.G.; Knight, G.M.; White, R.G. Using Vaccine Immunostimulation/Immunodynamic Modelling Methods to Inform Vaccine Dose Decision-Making. NPJ Vaccines 2018, 3, 36. [Google Scholar] [CrossRef] [PubMed]
- Newall, A.T.; Chaiyakunapruk, N.; Lambach, P.; Hutubessy, R.C.W. WHO Guide on the Economic Evaluation of Influenza Vaccination. Influenza Other Respir. Viruses 2018, 12, 211–219. [Google Scholar] [CrossRef]
- World Health Organistaion. Guidelines for Estimating Costs of Introducing New Vaccines into the National Immunization System; World Health Organisation: Geneva, Switzerland, 2002. [Google Scholar]
- Murray, C.J. Quantifying the Burden of Disease: The Technical Basis for Disability-Adjusted Life Years. Bull. World Health Organ. 1994, 72, 429–445. [Google Scholar]
- Mercado, N.B.; Zahn, R.; Wegmann, F.; Loos, C.; Chandrashekar, A.; Yu, J.; Liu, J.; Peter, L.; McMahan, K.; Tostanoski, L.H.; et al. Single-Shot Ad26 Vaccine Protects against SARS-CoV-2 in Rhesus Macaques. Nature 2020, 586, 583–588. [Google Scholar] [CrossRef]
- Oland, G.A.; Ovsyannikova, I.G.; Kennedy, R.B. SARS-CoV-2 Immunity: Review and Applications to Phase 3 Vaccine Candidates. Lancet 2020, 396, 1595–1606. [Google Scholar] [CrossRef]
- Deng, W.; Bao, L.; Liu, J.; Xiao, C.; Liu, J.; Xue, J.; Lv, Q.; Qi, F.; Gao, H.; Yu, P.; et al. Primary Exposure to SARS-CoV-2 Protects against Reinfection in Rhesus Macaques. Science 2020, 369, 818–823. [Google Scholar] [CrossRef]

| Adverse Reaction Grade | General Descriptions |
|---|---|
| 1 | Mild. Does not interfere with normal activity |
| 2 | Moderate. Interference with normal activity. Little or no treatment required. |
| 3 | Severe. Prevents normal activity. Requires treatment. |
| 4 | Serious or Potentially Life-Threatening. Generally requires hospitalisation and stopping of any clinical trial where this grade is observed. |
| Name of Parameter | Value | Unit | Description | References |
|---|---|---|---|---|
| 30,615 | GBP per NHS Band 5 Income per annum (2020/21) | [28] | ||
| 1740 | Work hours per year for average UK nurse | [29] | ||
| 0.25 | Recommended hours per vaccination appointment | [30] | ||
| 0.014 | GBP per vaccination per month’s storage. Converted and adjusted for inflation from $0.014 2010 USD. | [31] | ||
| 0.08 | GBP of gloves for one vaccination. Converted and adjusted for inflation from $0.08 USD. | [31] | ||
| 0.03 | GBP of sterilising alcohol for one vaccination. Converted and adjusted for inflation from $0.03 2010 USD. | [31] | ||
| 0.40 | GBP of the pre-filled syringe for one vaccination. Converted and adjusted for inflation from $0.39 2010 USD. | [31] | ||
| 0.32 | GBP of needle for one vaccination. Converted and adjusted for inflation from $0.31 2010 USD. | [31] | ||
| 342,000 | GBP per single-use reference process batch (converted from 450,000 US Dollars) | [32] | ||
| 9 × 1013 | Viral Particles per litre in single-use reference process batch | [32] | ||
| 500 | Volume of Adenovirus produced in single-use reference process batch | [32] | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benest, J.; Rhodes, S.; Quaife, M.; Evans, T.G.; White, R.G. Optimising Vaccine Dose in Inoculation against SARS-CoV-2, a Multi-Factor Optimisation Modelling Study to Maximise Vaccine Safety and Efficacy. Vaccines 2021, 9, 78. https://doi.org/10.3390/vaccines9020078
Benest J, Rhodes S, Quaife M, Evans TG, White RG. Optimising Vaccine Dose in Inoculation against SARS-CoV-2, a Multi-Factor Optimisation Modelling Study to Maximise Vaccine Safety and Efficacy. Vaccines. 2021; 9(2):78. https://doi.org/10.3390/vaccines9020078
Chicago/Turabian StyleBenest, John, Sophie Rhodes, Matthew Quaife, Thomas G. Evans, and Richard G. White. 2021. "Optimising Vaccine Dose in Inoculation against SARS-CoV-2, a Multi-Factor Optimisation Modelling Study to Maximise Vaccine Safety and Efficacy" Vaccines 9, no. 2: 78. https://doi.org/10.3390/vaccines9020078
APA StyleBenest, J., Rhodes, S., Quaife, M., Evans, T. G., & White, R. G. (2021). Optimising Vaccine Dose in Inoculation against SARS-CoV-2, a Multi-Factor Optimisation Modelling Study to Maximise Vaccine Safety and Efficacy. Vaccines, 9(2), 78. https://doi.org/10.3390/vaccines9020078