Expected Evolution of COVID-19 Epidemic in France for Several Combinations of Vaccination Strategies and Barrier Measures
Abstract
:1. Introduction
2. Results
2.1. Dynamics of the Epidemic with the Historical Strain without Vaccination
2.2. Dynamics of the Epidemic with the Introduction of the Alpha Variant without Vaccination
2.3. Effects of a 6-Month Vaccination Campaign with Intensive-NPIs
2.4. Effects of a 9-Month Vaccination Campaign with Intensive-NPIs
2.5. Effects of a 12-Month Vaccination Campaign with Intensive-NPIs
2.6. Effects of a 18-Month Vaccination Campaign with Intensive-NPIs
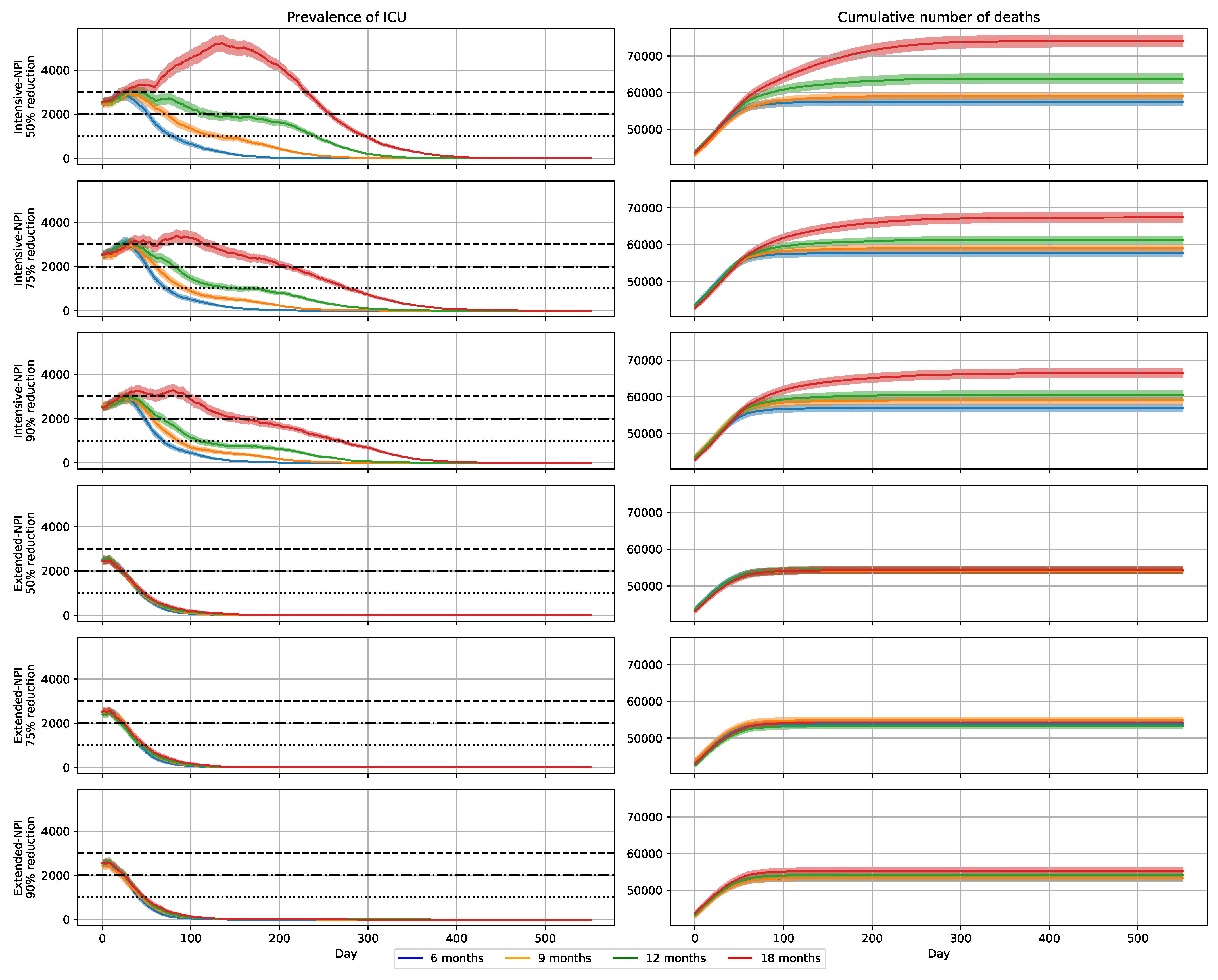
2.7. Impact of Transmission Reduction on Vaccination Campaign Efficacy
2.8. Impact of Extended-NPIs on Vaccination Campaign Efficacy
2.9. Reduction in Disease Transmission by NPIs and Relative Contagiousness of the Alpha Variant
3. Discussion
4. Methods
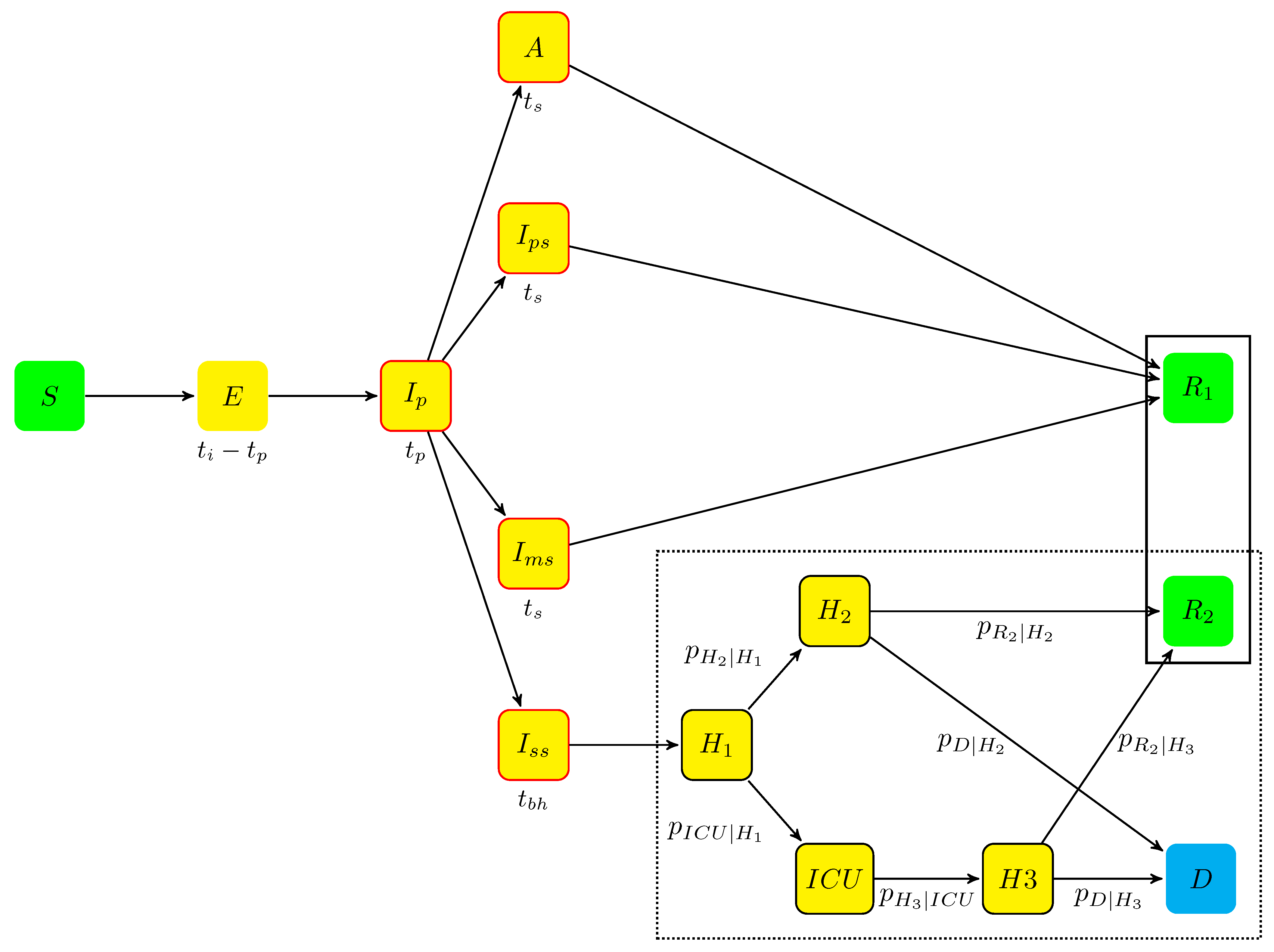
4.1. The Agent-Based Model
4.1.1. The Model States
- Individuals who were not infected by the virus begin in state S (susceptible);
- The incubation period includes two states:
- -
- when infected (see next section), an individual moves from state S to state E (exposed), which contains infected individuals who did not develop symptoms yet and are not contagious. The mean sojourn time in E was , being the incubation period and the duration of the prodromal state (see next item);
- -
- when contagious, an individual is transferred from state E to state (prodromal phase, which is the short phase that follows contamination without symptoms but with possible non-specific prodromes). After an average stay , the individuals moved to one of the four states A, , , and , defined hereafter.
- A (asymptomatic state, with probability ): individuals who completed the incubation period, became infectious, but without disease symptoms. The mean sojourn time in A was ;
- The symptomatic infectious period includes three states for individuals developing symptoms, (with probability ):
- -
- (paucisymptomatic disease): individuals with weak disease symptoms;
- -
- (medium symptoms): individuals with disease symptoms (e.g., fever or cough) who did not require hospitalization. The average sojourn time in states and are the same as in state A;
- -
- (severe symptoms): individuals severely infected requiring hospitalization. They stayed in before being hospitalized. The mean sojourn time in was .
Given the onset of symptoms, the probabilities of states , , and are, respectively, , , and (probabilities summing to one).An individual leaving states A, or ends in state (removed individuals). - When leaving , individuals enter the hospitalization period, which corresponds to four states:
- -
- : individuals hospitalized before it was determined whether they needed intensive care or not;
- -
- : individuals hospitalized without the need for ICU;
- -
- : individuals hospitalized in ICU;
- -
- : individuals hospitalized after leaving ICU.
From hospital, all individuals end in one of the two absorbing states:- -
- D (deceased at hospital);
- -
- (removed): individuals who recovered.
During the hospitalization period, each individual follows a Markov chain dynamics (the dotted frame in Figure 4), with daily transition probabilities noted , , , , , , and .
4.1.2. Transition Probabilities
- was the estimated baseline probability of infection, as a function of age (based on the age of the susceptible individual).
- , , estimated the effects of three NPI levels: moderate, intensive, and extended. The underlying hypotheses were that the NPI effects are independent from the state of the infectious individual, age group, or virus strain. Fixing , parameters , and estimated the relative reductions in disease transmission under intensive- and extensive-NPIs, in comparison to moderate-NPIs. Parameter was interpreted as a coefficient, reducing the mean number of daily contacts, mean duration of contacts, and/or their infectiousness ().
- , , estimated the relative contagiousness of each virus strains, , estimating the relative contagiousness of the Alpha variant, compared to that of the historical strain ().
- is the state of the infectious individual, being the relative infectiousness of individuals in state Z. It was fixed to 1 for and states (reference states), and to 0.55 for , , and states, according to the literature (Table 7).
4.2. Scenarios
4.2.1. Vaccination Effects
4.2.2. Statistical Analyses
4.2.3. Outcome Criteria
4.3. Model Calibration
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Members of the CovDyn (Covid Dynamics) Group, by Main Affiliation
- LBBE–HCL
- LSAF
- LAMA
- CIRI-HCL
- LMFA
- LTDS
- INL
- LIRIS
- ICJ
- INRIA
- CHU de Rouen Unité INSERM 1018, CESP
- CHU de Rouen LIMICS INSERM U1142, Université de Rouen/Sorbonne Université
- CHU de NICE, Université de Nice
References
- Zhu, N.; Zhang, D.; Wang, W.; Li, X.; Yang, B.; Song, J.; Zhao, X.; Huang, B.; Shi, W.; Lu, R.; et al. A Novel Coronavirus from Patients with Pneumonia in China, 2019. N. Engl. J. Med. 2020, 382, 727–733. [Google Scholar] [CrossRef] [PubMed]
- Volz, E.; Mishra, S.; Chand, M.; Barrett, J.C.; Johnson, R.; Geidelberg, L.; Hinsley, W.R.; Laydon, D.J.; Dabrera, G.; O’Toole, Á.; et al. Transmission of SARS-CoV-2 Lineage B.1.1.7 in England: Insights from linking epidemiological and genetic data. medRxiv 2021. [Google Scholar] [CrossRef]
- European Centre for Disease Prevention and Control. Emergence of SARS-CoV-2 B.1.617 Variants in India and Situation in the EU/EEA; European Centre for Disease Prevention and Control: Solna, Sweden, 2021.
- Voysey, M.; Clemens, S.A.C.; Madhi, S.A.; Weckx, L.Y.; Folegatti, P.M.; Aley, P.K.; Angus, B.; Baillie, V.L.; Barnabas, S.L.; Bhorat, Q.E.; et al. Safety and efficacy of the ChAdOx1 nCoV-19 vaccine (AZD1222) against SARS-CoV-2: An interim analysis of four randomised controlled trials in Brazil, South Africa, and the UK. Lancet 2021, 397, 99–111. [Google Scholar] [CrossRef]
- Baden, L.R.; El Sahly, H.M.; Essink, B.; Kotloff, K.; Frey, S.; Novak, R.; Diemert, D.; Spector, S.A.; Rouphael, N.; Creech, C.B.; et al. Efficacy and safety of the mRNA-1273 SARS-CoV-2 vaccine. N. Engl. J. Med. 2021, 384, 403–416. [Google Scholar] [CrossRef] [PubMed]
- Polack, F.P.; Thomas, S.J.; Kitchin, N.; Absalon, J.; Gurtman, A.; Lockhart, S.; Perez, J.L.; Pérez Marc, G.; Moreira, E.D.; Zerbini, C.; et al. Safety and efficacy of the BNT162b2 mRNA Covid-19 vaccine. N. Engl. J. Med. 2020, 383, 2603–2615. [Google Scholar] [CrossRef] [PubMed]
- Pageaud, S.; Ponthus, N.; Gauchon, R.; Pothier, C.; Rigotti, C.; Eyraud-Loisel, A.; Bertoglio, J.P.; Bienvenüe, A.; Gueyffier, F.; Vanhems, P.; et al. Adapting French COVID-19 vaccination campaign duration to variant dissemination. medRxiv 2021. [Google Scholar] [CrossRef]
- Davies, N.G.; Abbott, S.; Barnard, R.C.; Jarvis, C.I.; Kucharski, A.J.; Munday, J.D.; Pearson, C.A.B.; Russell, T.W.; Tully, D.C.; Washburne, A.D.; et al. Estimated transmissibility and impact of SARS-CoV-2 lineage B.1.1.7 in England. Science 2021, 372, 141–150. [Google Scholar] [CrossRef] [PubMed]
- Bosetti, P.; Kiem, C.T.; Andronico, A.; Paireau, J.; Bruhl, D.L.; Lina, B.; Yazdanpanah, Y.; Fontanet, A.; Colizza, V.; Boëlle, P.Y.; et al. A Race between SARS-CoV-2 Variants and Vaccination: The Case of the B.1.1.7 Variant in France. HAL-Pasteur-03149525. 2021. Available online: https://hal-pasteur.archives-ouvertes.fr/pasteur-03149525 (accessed on 2 March 2021).
- Challen, R.; Brooks-Pollock, E.; Read, J.M.; Dyson, L.; Tsaneva-Atanasova, K.; Danon, L. Increased hazard of mortality in cases compatible with SARS-CoV-2 variant of concern 202012/1-a matched cohort study. medRxiv 2021. [Google Scholar] [CrossRef]
- Barda, N.; Dagan, N.; Ben-Shlomo, Y.; Kepten, E.; Waxman, J.; Ohana, R.; Hernán, M.A.; Lipsitch, M.; Kohane, I.; Netzer, D.; et al. Safety of the BNT162b2 mRNA Covid-19 vaccine in a nationwide setting. N. Engl. J. Med. 2021, 385, 1078–1090. [Google Scholar] [CrossRef] [PubMed]
- Pottegård, A.; Lund, L.C.; Karlstad, Ø.; Dahl, J.; Andersen, M.; Hallas, J.; Lidegaard, Ø.; Tapia, G.; Gulseth, H.L.; Ruiz, P.L.D.; et al. Arterial events, venous thromboembolism, thrombocytopenia, and bleeding after vaccination with Oxford-AstraZeneca ChAdOx1-S in Denmark and Norway: Population based cohort study. BMJ 2021, 373, n1114. [Google Scholar] [CrossRef] [PubMed]
- Kiem, C.T.; Massonnaud, C.R.; Levy-Bruhl, D.; Poletto, C.; Colizza, V.; Bosetti, P.; Fontanet, A.; Gabet, A.; Olié, V.; Zanetti, L.; et al. A modelling study investigating short and medium-term challenges for COVID-19 vaccination: From prioritisation to the relaxation of measures. EClinicalMedicine 2021, 38, 101001. [Google Scholar] [CrossRef] [PubMed]
- Di Domenico, L.; Pullano, G.; Sabbatini, C.E.; Boëlle, P.Y.; Colizza, V. Impact of lockdown on COVID-19 epidemic in Île-de-France and possible exit strategies. BMC Med. 2020, 18, 240. [Google Scholar] [CrossRef] [PubMed]
- Gauchon, R.; Ponthus, N.; Pothier, C.; Rigotti, C.; Volpert, V.; Derrode, S.; Bertoglio, J.P.; Bienvenue, A.; Goffard, P.O.; Eyraud-Loisel, A.; et al. Lessons learnt from the use of compartmental models over the COVID-19 induced lockdown in France. medRxiv 2021. [Google Scholar] [CrossRef]
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science 2020, 368, 489–493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beale, S.; Hayward, A.; Shallcross, L.; Aldridge, R.W.; Fragaszy, E. A Rapid Review of the Asymptomatic Proportion of PCR-Confirmed SARS-CoV-2 Infections in Community Settings. 2020. Available online: https://www.gov.uk/government/publications/nervtag-rapid-review-of-the-asymptomatic-proportion-of-pcr-confirmed-sars-cov-2-infections-in-community-settings-9-september-2020 (accessed on 23 October 2020).
- Prem, K.; Cook, A.R.; Jit, M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput. Biol. 2017, 13, e1005697. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Nair, M.S.; Liu, L.; Iketani, S.; Luo, Y.; Guo, Y.; Wang, M.; Yu, J.; Zhang, B.; Kwong, P.D.; et al. Antibody Resistance of SARS-CoV-2 Variants B.1.351 and B.1.1.7. Nature 2021, 593, 130–135. [Google Scholar] [CrossRef] [PubMed]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
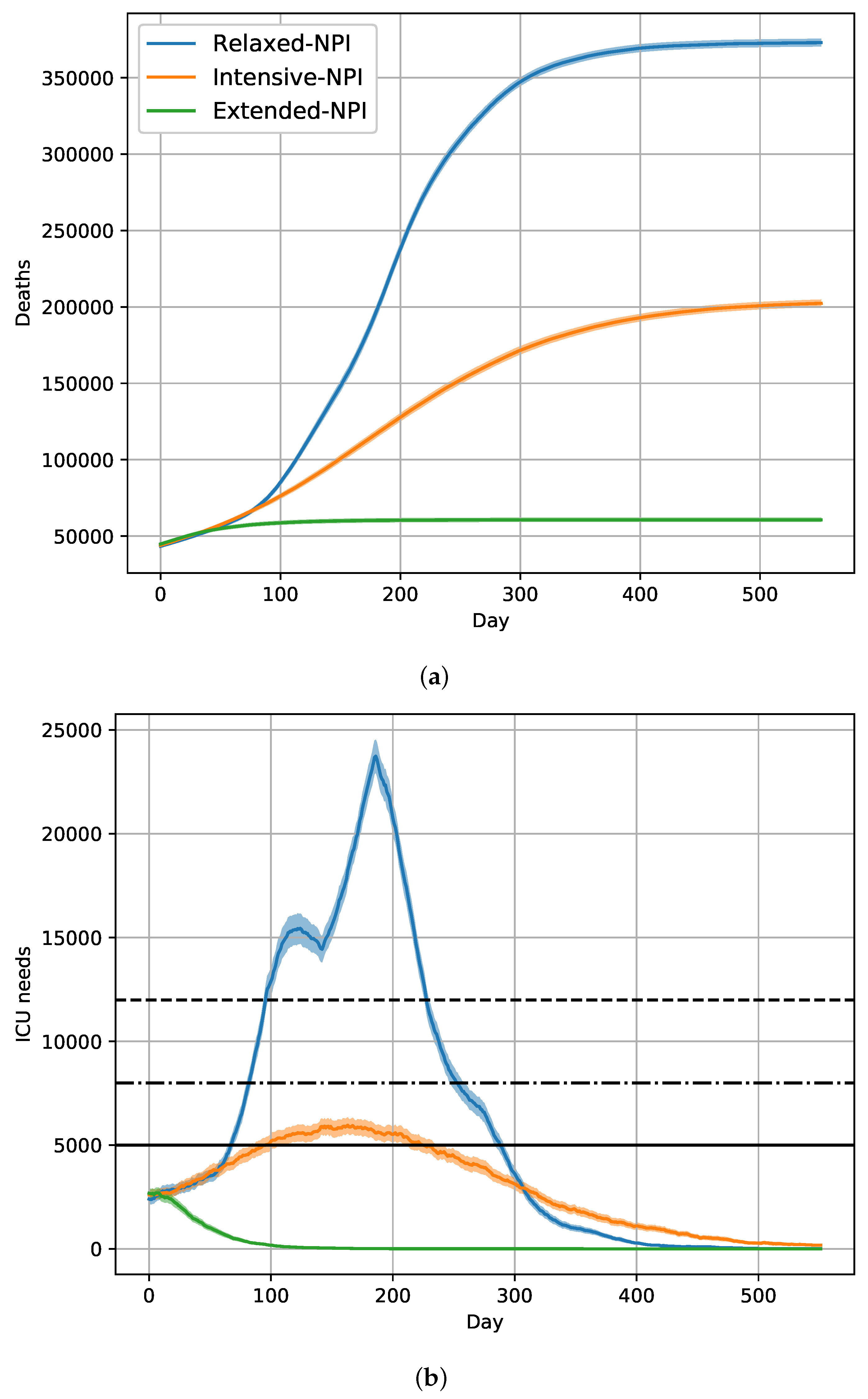
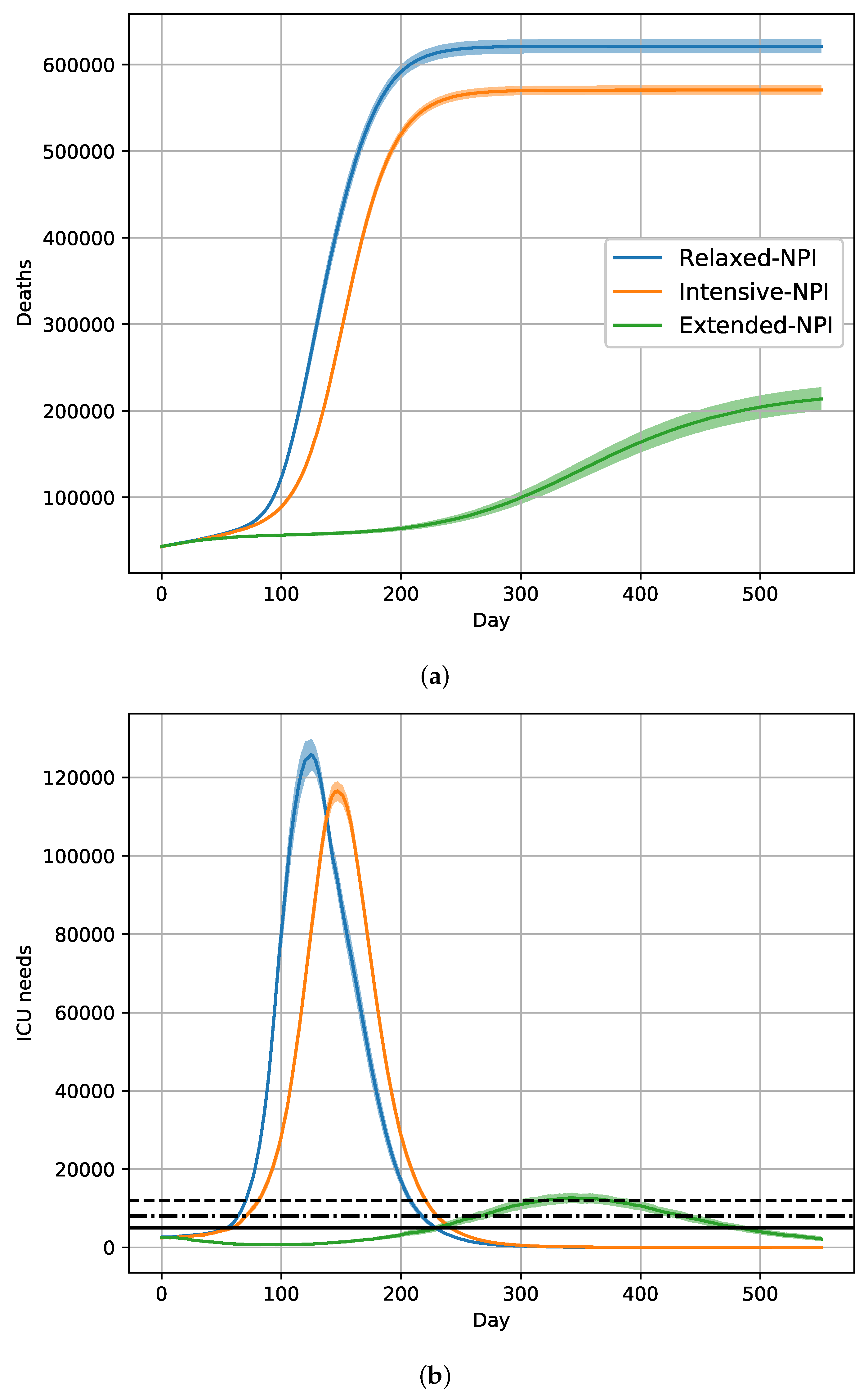
| NPIs | Removed | Deceased |
|---|---|---|
| Relaxed-NPIs | 26,397,570 | 372,973 |
| Intensive-NPIs | 16,688,896 | 202,411 |
| Extended-NPIs | 7,906,676 | 60,771 |
| NPIs | Removed | Deceased |
|---|---|---|
| Relaxed-NPIs | 48,293,980 | 621,289 |
| Intensive-NPIs | 45,537,214 | 570,555 |
| Extended-NPIs | 20,551,828 | 213,715 |
| NPIs | Vaccination Ages | Campaign Duration (Days) | Removed | Deceased | Cumulative ICU Bed-Days | Max Bed-Days /On Day | Days of ICU Overload If Max Available Beds Is | ||
|---|---|---|---|---|---|---|---|---|---|
| 1000 | 2000 | 3000 | |||||||
| Intensive-NPIs | 10+ | 180 | 8,625,521 | 56,916 | 192,728 | 2926/30 | 69 | 48 | 0 |
| Intensive-NPIs | 10+ | 270 | 9,446,952 | 59,006 | 253,715 | 2928/30 | 86 | 57 | 0 |
| Intensive-NPIs | 10+ | 360 | 10,715,225 | 60,552 | 341,083 | 3001/27 | 109 | 69 | 1 |
| Intensive-NPIs | 10+ | 540 | 14,160,343 | 66,375 | 662,125 | 3281/80 | 270 | 155 | 72 |
| Intensive-NPIs | All | 180 | 8,537,674 | 56,466 | 180,477 | 2853/26 | 65 | 46 | 0 |
| Intensive-NPIs | All | 270 | 9,190,934 | 57,836 | 230,283 | 2855/30 | 79 | 52 | 0 |
| Intensive-NPIs | All | 360 | 10,074,304 | 58,819 | 304,086 | 2883/29 | 100 | 61 | 0 |
| Intensive-NPIs | All | 540 | 13,321,101 | 65,539 | 556,832 | 3250/36 | 256 | 107 | 27 |
| Extended-NPIs | 10+ | 180 | 7,681,105 | 53,277 | 101,474 | 2553/3 | 42 | 23 | 0 |
| Extended-NPIs | 10+ | 270 | 7,702,427 | 53,331 | 107,054 | 2461/7 | 44 | 22 | 0 |
| Extended-NPIs | 10+ | 360 | 7,725,029 | 54,139 | 118,005 | 2634/7 | 47 | 26 | 0 |
| Extended-NPIs | 10+ | 540 | 7,816,371 | 55,280 | 122,126 | 2578/4 | 47 | 25 | 0 |
| Extended-NPIs | All | 180 | 7,695,726 | 53,418 | 106,390 | 2592/3 | 44 | 24 | 0 |
| Extended-NPIs | All | 270 | 7,785,962 | 54,464 | 116,136 | 2633/7 | 47 | 26 | 0 |
| Extended-NPIs | All | 360 | 7,734,358 | 53,728 | 113,134 | 2615/7 | 45 | 23 | 0 |
| Extended-NPIs | All | 540 | 7,749,345 | 54,387 | 113,459 | 2517/7 | 46 | 22 | 0 |
| NPIs | Vaccination Ages | Campaign Duration (Days) | Removed | Deceased | Cumulative ICU Bed-Days | Max Bed-Days /On Day | Days of ICU Overload If Max Available Beds Is | ||
|---|---|---|---|---|---|---|---|---|---|
| 1000 | 2000 | 3000 | |||||||
| Intensive-NPIs | 10+ | 180 | 8,848,757 | 57,720 | 207,524 | 3087/25 | 73 | 51 | 10 |
| Intensive-NPIs | 10+ | 270 | 9,726,806 | 58,995 | 270,539 | 2958/30 | 94 | 61 | 0 |
| Intensive-NPIs | 10+ | 360 | 11,501,532 | 61,280 | 397,393 | 3088/32 | 154 | 81 | 13 |
| Intensive-NPIs | 10+ | 540 | 15,243,733 | 67,387 | 741,392 | 3378/84 | 278 | 210 | 76 |
| Intensive-NPIs | All | 180 | 8,574,155 | 55,863 | 182,187 | 2787/20 | 67 | 47 | 0 |
| Intensive-NPIs | All | 270 | 9,427,345 | 58,267 | 248,697 | 2950/28 | 86 | 57 | 0 |
| Intensive-NPIs | All | 360 | 10,826,562 | 60,202 | 360,763 | 3061/31 | 123 | 73 | 12 |
| Intensive-NPIs | All | 540 | 14,114,090 | 65,830 | 629,200 | 3090/37 | 265 | 137 | 24 |
| Extended-NPIs | 10+ | 180 | 7,726,318 | 53,926 | 106,497 | 2544/8 | 43 | 24 | 0 |
| Extended-NPIs | 10+ | 270 | 7,799,063 | 54,892 | 114,168 | 2553/7 | 45 | 25 | 0 |
| Extended-NPIs | 10+ | 360 | 7,689,234 | 53,274 | 109,427 | 2497/8 | 44 | 21 | 0 |
| Extended-NPIs | 10+ | 540 | 7,782,863 | 54,260 | 122,188 | 2565/7 | 48 | 24 | 0 |
| Extended-NPIs | All | 180 | 7,691,260 | 52,927 | 103,575 | 2496/8 | 43 | 23 | 0 |
| Extended-NPIs | All | 270 | 7,801,188 | 54,828 | 113,826 | 2726/7 | 45 | 25 | 0 |
| Extended-NPIs | All | 360 | 7,760,065 | 54,589 | 115,912 | 2535/7 | 47 | 25 | 0 |
| Extended-NPIs | All | 540 | 7,857,610 | 56,095 | 127,551 | 2746/8 | 49 | 27 | 0 |
| NPIs | Vaccination Ages | Campaign Duration (Days) | Removed | Deceased | Cumulative ICU Bed-Days | Max Bed-Days /On Day | Days of ICU Overload If Max Available Beds Is | ||
|---|---|---|---|---|---|---|---|---|---|
| 1000 | 2000 | 3000 | |||||||
| Intensive-NPIs | 10+ | 180 | 9,202,882 | 57,504 | 216,751 | 2870/17 | 80 | 52 | 0 |
| Intensive-NPIs | 10+ | 270 | 11,043,587 | 59,056 | 336,887 | 2926/31 | 131 | 72 | 0 |
| Intensive-NPIs | 10+ | 360 | 14,036,762 | 63,840 | 556,218 | 3031/38 | 241 | 119 | 11 |
| Intensive-NPIs | 10+ | 540 | 19,133,475 | 74,014 | 1,106,397 | 5219/134 | 298 | 258 | 207 |
| Intensive-NPIs | All | 180 | 9,023,689 | 56,264 | 202,522 | 2830/25 | 75 | 49 | 0 |
| Intensive-NPIs | All | 270 | 10,527,221 | 59,584 | 310,561 | 3071/28 | 113 | 62 | 10 |
| Intensive-NPIs | All | 360 | 13,036,072 | 62,685 | 481,481 | 3117/27 | 218 | 96 | 22 |
| Intensive-NPIs | All | 540 | 17,927,080 | 70,458 | 926,777 | 3877/145 | 291 | 249 | 181 |
| Extended-NPIs | 10+ | 180 | 7,771,015 | 54,196 | 107,426 | 2530/2 | 44 | 24 | 0 |
| Extended-NPIs | 10+ | 270 | 7,772,026 | 54,103 | 111,120 | 2502/8 | 45 | 23 | 0 |
| Extended-NPIs | 10+ | 360 | 7,782,238 | 54,307 | 117,712 | 2541/9 | 46 | 22 | 0 |
| Extended-NPIs | 10+ | 540 | 7,775,685 | 54,302 | 122,420 | 2486/8 | 48 | 23 | 0 |
| Extended-NPIs | All | 180 | 7,705,102 | 53,347 | 106,052 | 2571/7 | 43 | 23 | 0 |
| Extended-NPIs | All | 270 | 7,778,149 | 54,255 | 110,905 | 2553/7 | 46 | 22 | 0 |
| Extended-NPIs | All | 360 | 7,784,818 | 54,110 | 120,321 | 2593/6 | 48 | 24 | 0 |
| Extended-NPIs | All | 540 | 7,836,271 | 55,120 | 128,861 | 2655/5 | 48 | 26 | 0 |
| Age | 0–9 | 10–19 | 20–29 | 30–39 | 40–49 | 50–59 | 60–69 | 70–79 | 80+ |
|---|---|---|---|---|---|---|---|---|---|
| Left-hand part of the model | |||||||||
| 0.01 | 0.01 | 0.017 | 0.008 | 0.007 | 0.012 | 0.016 | 0.16 | 0.164 | |
| 0.249 | 0.249 | 0.247 | 0.243 | 0.242 | 0.225 | 0.209 | 0.189 | 0.031 | |
| 0.746 | 0.748 | 0.741 | 0.730 | 0.727 | 0.674 | 0.626 | 0.568 | 0.092 | |
| 0.006 | 0.003 | 0.012 | 0.026 | 0.031 | 0.102 | 0.166 | 0.243 | 0.877 | |
| 0.783 for all ages | |||||||||
| 0.534 for all ages | |||||||||
| 1.572 for all ages | |||||||||
| Right-hand part of the model for historical strain (calibration period September 2020–December 2020) | |||||||||
| 0.151 | 0.5 | 0.077 | 0.078 | 0.117 | 0.146 | 0.228 | 0.227 | 0.128 | |
| 0.849 | 0.95 | 0.923 | 0.922 | 0.874 | 0.854 | 0.771 | 0.773 | 0.872 | |
| 0.149 | 0.055 | 0.143 | 0.065 | 0.058 | 0.049 | 0.051 | 0.062 | 0.22 | |
| 0 | 0 | 0 | 0.001 | 0.001 | 0.002 | 0.006 | 0.012 | 0.019 | |
| 0.526 | 0.462 | 0.442 | 0.265 | 0.188 | 0.142 | 0.098 | 0.07 | 0.036 | |
| 0.001 | 0.002 | 0.005 | 0.007 | 0.009 | 0.009 | 0.008 | |||
| 0.039 | 0.001 | 0.018 | 0.016 | 0.016 | 0.01 | 0.01 | 0.009 | 0.067 | |
| Right-hand part of the model for Alpha variant (calibration period March 2021–April 2021) | |||||||||
| 0.052 | 0.031 | 0.077 | 0.071 | 0.116 | 0.157 | 0.280 | 0.268 | 0.098 | |
| 0.948 | 0.967 | 0.902 | 0.918 | 0.873 | 0.841 | 0.396 | 0.732 | 0.895 | |
| 0.079 | 0.033 | 0.070 | 0.033 | 0.033 | 0.033 | 0.075 | 0.057 | 0.139 | |
| 0 | 0 | 0.001 | 0.001 | 0.002 | 0.003 | 0.009 | 0.012 | 0.016 | |
| 0.288 | 0.193 | 0.165 | 0.151 | 0.115 | 0.082 | 0.040 | 0.035 | 0.030 | |
| 0 | 0 | 0.001 | 0.005 | 0.004 | 0.007 | 0.001 | 0.004 | 0.014 | |
| 0.084 | 0.052 | 0.211 | 0.057 | 0.055 | 0.053 | 0.102 | 0.059 | 0.073 | |
| Parameter | Sources | Value |
|---|---|---|
| Sojourn time | ||
| see [15] | 5.1 | |
| see [15] | 1.5 | |
| see [15] | 7 | |
| see [15] | 3 | |
| Relative infectiousness | ||
| [16] | 1 | |
| [16] | 1 | |
| [16] | 0.55 | |
| [16] | 0.55 | |
| [16] | 0.55 | |
| Rate of asymptomatic subjects | ||
| [14,17] | 0.20 | |
| Proportion new variant (8 January 2021) | ||
| Alpha variant | Santé Publique France | 3.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pageaud, S.; Pothier, C.; Rigotti, C.; Eyraud-Loisel, A.; Bertoglio, J.-P.; Bienvenüe, A.; Leboisne, N.; Ponthus, N.; Gauchon, R.; Gueyffier, F.; et al. Expected Evolution of COVID-19 Epidemic in France for Several Combinations of Vaccination Strategies and Barrier Measures. Vaccines 2021, 9, 1462. https://doi.org/10.3390/vaccines9121462
Pageaud S, Pothier C, Rigotti C, Eyraud-Loisel A, Bertoglio J-P, Bienvenüe A, Leboisne N, Ponthus N, Gauchon R, Gueyffier F, et al. Expected Evolution of COVID-19 Epidemic in France for Several Combinations of Vaccination Strategies and Barrier Measures. Vaccines. 2021; 9(12):1462. https://doi.org/10.3390/vaccines9121462
Chicago/Turabian StylePageaud, Simon, Catherine Pothier, Christophe Rigotti, Anne Eyraud-Loisel, Jean-Pierre Bertoglio, Alexis Bienvenüe, Nicolas Leboisne, Nicolas Ponthus, Romain Gauchon, François Gueyffier, and et al. 2021. "Expected Evolution of COVID-19 Epidemic in France for Several Combinations of Vaccination Strategies and Barrier Measures" Vaccines 9, no. 12: 1462. https://doi.org/10.3390/vaccines9121462
APA StylePageaud, S., Pothier, C., Rigotti, C., Eyraud-Loisel, A., Bertoglio, J.-P., Bienvenüe, A., Leboisne, N., Ponthus, N., Gauchon, R., Gueyffier, F., Vanhems, P., Iwaz, J., Loisel, S., Roy, P., & on behalf of the Group CovDyn (Covid Dynamics). (2021). Expected Evolution of COVID-19 Epidemic in France for Several Combinations of Vaccination Strategies and Barrier Measures. Vaccines, 9(12), 1462. https://doi.org/10.3390/vaccines9121462







