To Vaccinate or Not: Impact of Bovine Viral Diarrhoea in French Cow-Calf Herds
Abstract
1. Introduction
2. Material and Methods
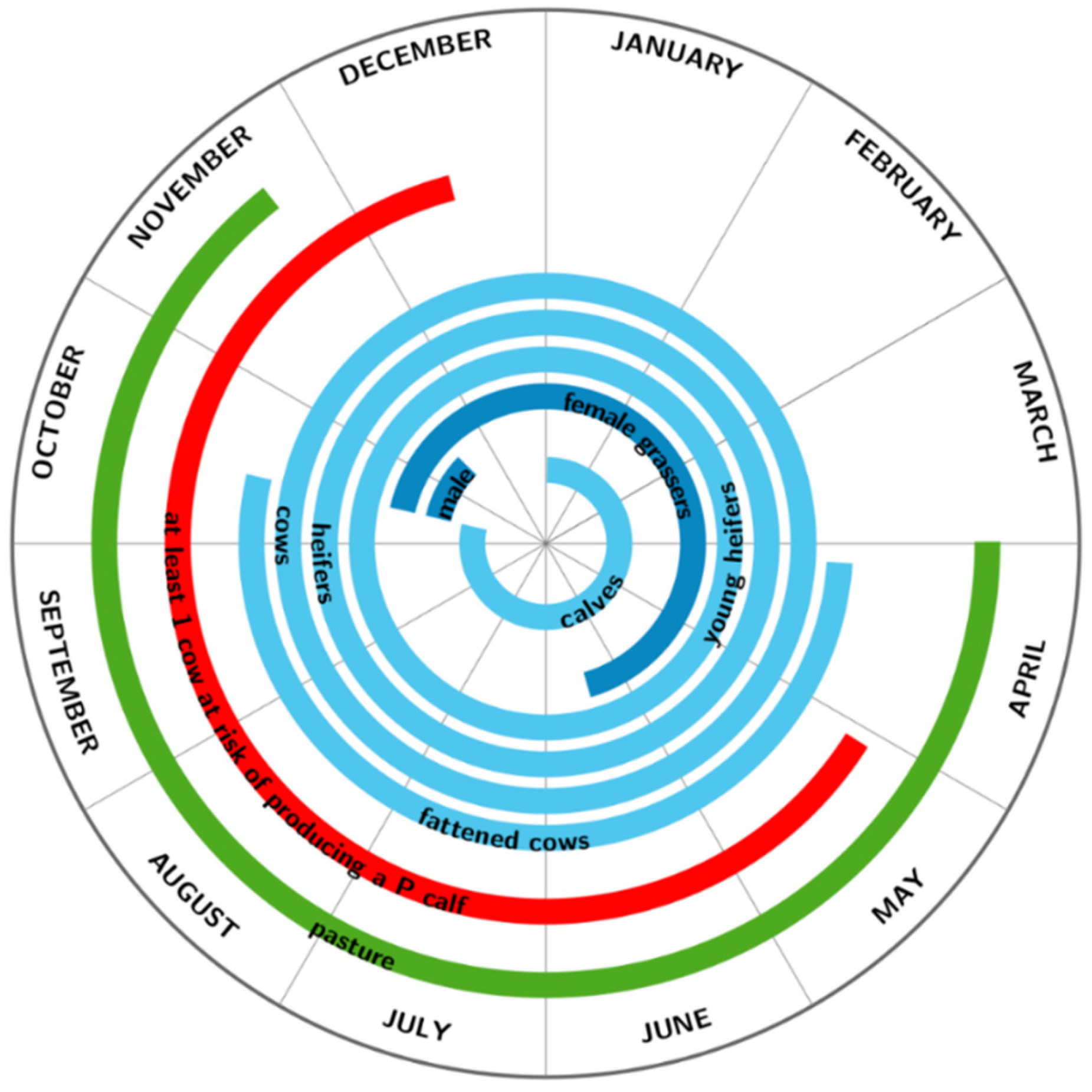
2.1. Herd Dynamics
2.2. Within-Herd Infection Dynamics and Vaccination
2.3. Model Outputs
2.4. Simulation Settings
2.5. Sensitivity Analysis
3. Results
3.1. BVD Impact and Vaccination Reward in Exposed Beef Cow-Calf Herds of Charolaise System
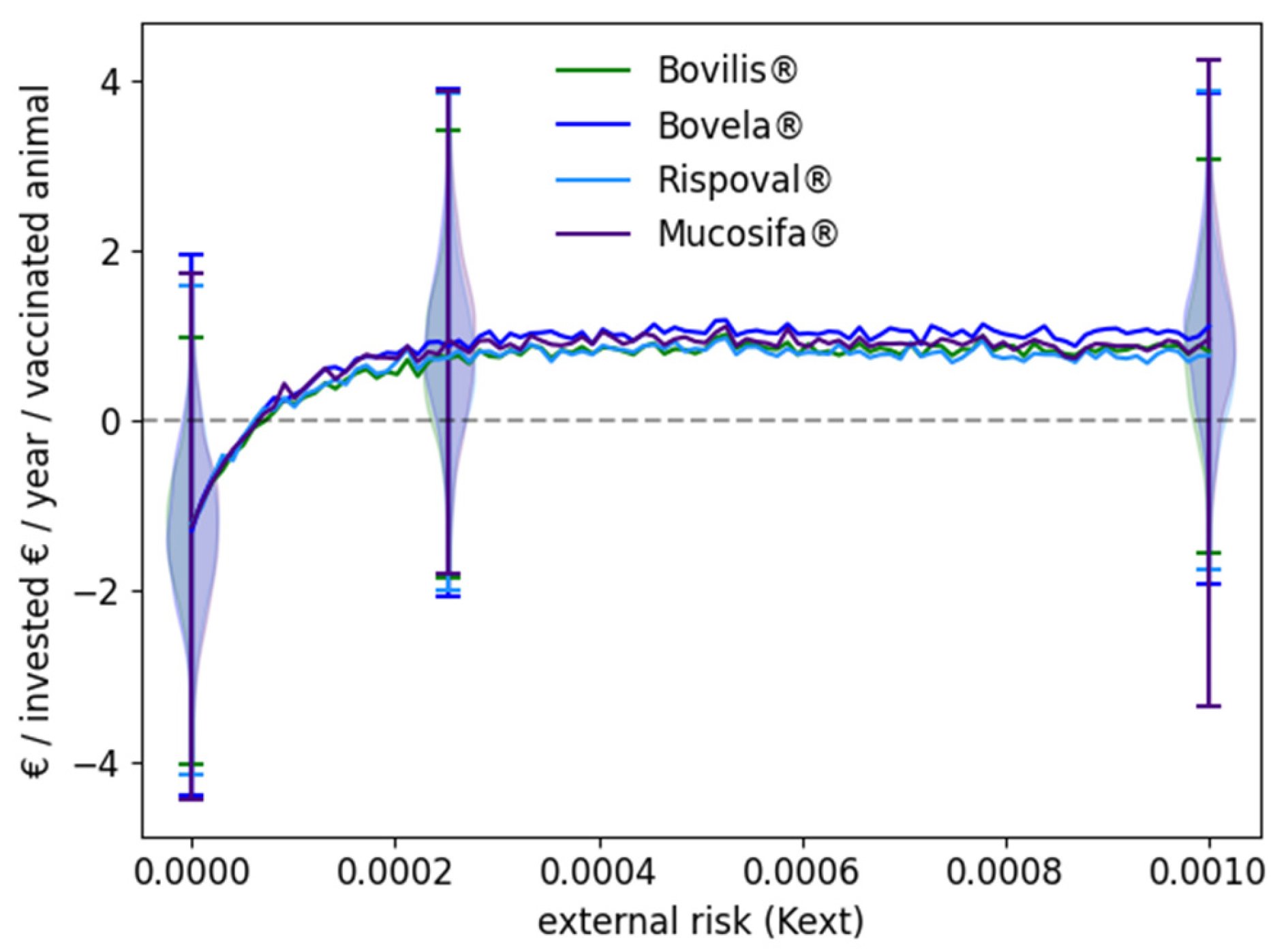
3.2. Influence of the Vaccine Used and of the External Risk of Virus Introduction
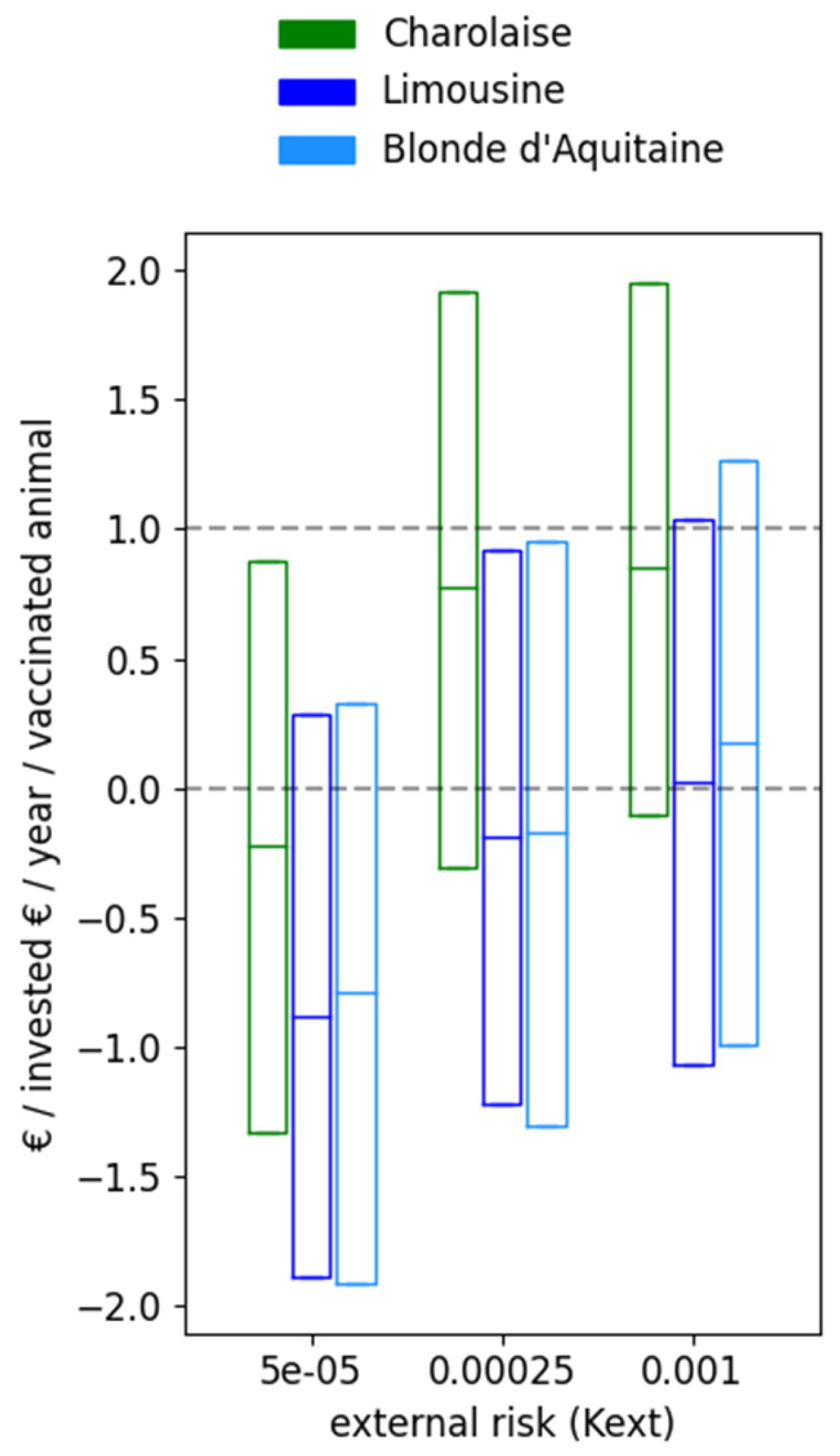
3.3. Comparison of Three French Farming Systems
3.4. When to Stop Vaccinating?
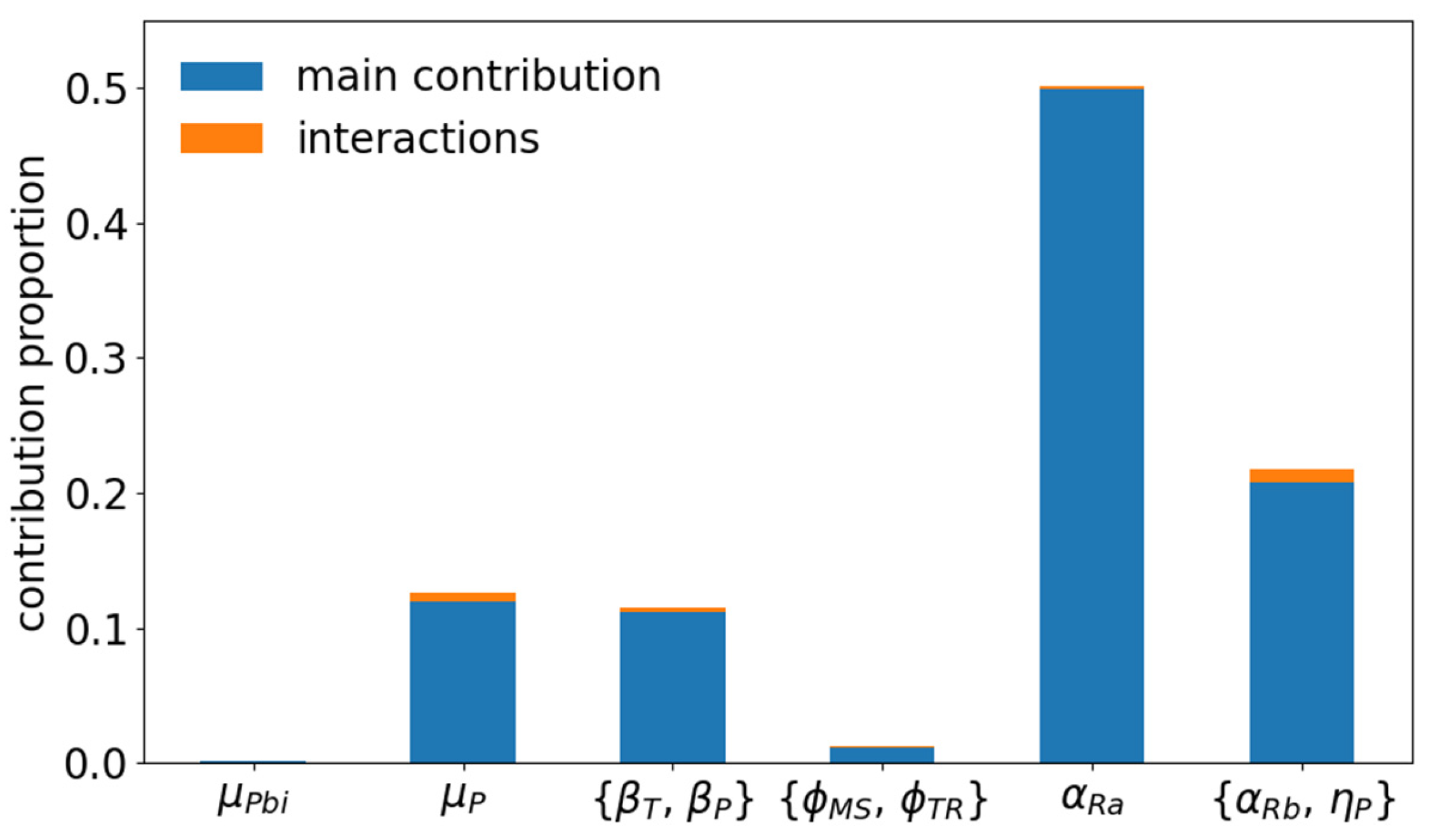
3.5. Sensitivity of BVD Impact and Vaccination Reward to Epidemiological Parameters
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pinior, B.; Firth, C.L.; Richter, V.; Lebl, K.; Trauffler, M.; Dzieciol, M.; Hutter, S.E.; Burgstaller, J.; Obritzhauser, W.; Winter, P.; et al. A Systematic Review of Financial and Economic Assessments of Bovine Viral Diarrhea Virus (BVDV) Prevention and Mitigation Activities Worldwide. Prev. Vet. Med. 2017, 137, 77–92. [Google Scholar] [CrossRef] [PubMed]
- Gates, M.C.; Humphry, R.W.; Gunn, G.J. Associations between Bovine Viral Diarrhoea Virus (BVDV) Seropositivity and Performance Indicators in Beef Suckler and Dairy Herds. Vet. J. 2013, 198, 631–637. [Google Scholar] [CrossRef] [PubMed]
- Richter, V.; Kattwinkel, E.; Firth, C.L.; Marschik, T.; Dangelmaier, M.; Trauffler, M.; Obritzhauser, W.; Baumgartner, W.; Käsbohrer, A.; Pinior, B. Mapping the Global Prevalence of Bovine Viral Diarrhoea Virus Infection and Its Associated Mitigation Programme. Vet. Rec. 2019, 184, 711. [Google Scholar] [CrossRef] [PubMed]
- Evans, C.A.; Pinior, B.; Larska, M.; Graham, D.; Schweizer, M.; Guidarini, C.; Decaro, N.; Ridpath, J.; Gates, M.C. Global Knowledge Gaps in the Prevention and Control of Bovine Viral Diarrhoea (BVD) Virus. Transbound. Emerg. Dis. 2019, 66, 640–652. [Google Scholar] [CrossRef]
- Brownlie, J.; Clarke, M.C.; Howard, C.J.; Pocock, D.H. Pathogenesis and Epidemiology of Bovine Virus Diarrhoea Virus Infection of Cattle. Ann. Vet. Res. 1987, 18, 157–166. [Google Scholar]
- Fray, M.D.; Paton, D.J.; Alenius, S. The Effects of Bovine Viral Diarrhoea Virus on Cattle Reproduction in Relation to Disease Control. Anim. Reprod. Sci. 2000, 60, 615–627. [Google Scholar] [CrossRef]
- Houe, H. Survivorship of Animals Persistently Infected with Bovine Virus Diarrhoea Virus (BVDV). Prev. Vet. Med. 1993, 15, 275–283. [Google Scholar] [CrossRef]
- Gates, M.C.; Woolhouse, M.E.J.; Gunn, G.J.; Humphry, R.W. Relative Associations of Cattle Movements, Local Spread, and Biosecurity with Bovine Viral Diarrhoea Virus (BVDV) Seropositivity in Beef and Dairy Herds. Prev. Vet. Med. 2013, 112, 285–295. [Google Scholar] [CrossRef]
- Graham, D.A.; Clegg, T.A.; Thulke, H.H.; O’Sullivan, P.; McGrath, G.; More, S.J. Quantifying the Risk of Spread of Bovine Viral Diarrhoea Virus (BVDV) between Contiguous Herds in Ireland. Prev. Vet. Med. 2016, 126, 30–38. [Google Scholar] [CrossRef]
- Damman, A.; Viet, A.-F.; Arnoux, S.; Guerrier-Chatellet, M.C.; Petit, E.; Ezanno, P. Modeling the Spread of Bovine Viral Diarrhea Virus (BVDV) in a Beef Cattle Herd and Its Impact on Herd Productivity. Vet. Res. 2015, 46. [Google Scholar] [CrossRef]
- Moennig, V.; Becher, P. Control of Bovine Viral Diarrhea. Pathogens 2018, 7, 29. [Google Scholar] [CrossRef]
- Gethmann, J.; Probst, C.; Bassett, J.; Blunk, P.; Hövel, P.; Conraths, F.J. An Epidemiological and Economic Simulation Model to Evaluate Strategies for the Control of Bovine Virus Diarrhea in Germany. Front. Vet. Sci. 2019, 6, 406. [Google Scholar] [CrossRef]
- Iotti, B.; Valdano, E.; Savini, L.; Candeloro, L.; Giovannini, A.; Rosati, S.; Colizza, V.; Giacobini, M. Farm Productive Contexts and the Dynamics of Bovine Viral Diarrhea (BVD) Transmission. Prev. Vet. Med. 2019, 165, 23–33. [Google Scholar] [CrossRef] [PubMed]
- Gunn, G.J.; Stott, A.W.; Humphry, R.W. Modelling and Costing BVD Outbreaks in Beef Herds. Vet. J. 2004, 167, 143–149. [Google Scholar] [CrossRef]
- Stott, A.W.; Lloyd, J.; Humphry, R.W.; Gunn, G.J. A Linear Programming Approach to Estimate the Economic Impact of Bovine Viral Diarrhoea (BVD) at the Whole-Farm Level in Scotland. Prev. Vet. Med. 2003, 59, 51–66. [Google Scholar] [CrossRef]
- Smith, R.L.; Sanderson, M.W.; Renter, D.G.; Larson, R.; White, B. A Stochastic Risk-Analysis Model for the Spread of Bovine Viral Diarrhea Virus after Introduction to Naive Cow-Calf Herds. Prev. Vet. Med. 2010, 95, 86–98. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.L.; Sanderson, M.W.; Jones, R.; N’Guessan, Y.; Renter, D.; Larson, R.; White, B.J. Economic Risk Analysis Model for Bovine Viral Diarrhea Virus Biosecurity in Cow-Calf Herds. Prev. Vet. Med. 2014, 113, 492–503. [Google Scholar] [CrossRef] [PubMed]
- Han, J.-H.; Weston, J.F.; Heuer, C.; Gates, M.C. Modelling the Economics of Bovine Viral Diarrhoea Virus Control in Pastoral Dairy and Beef Cattle Herds. Prev. Vet. Med. 2020, 182. [Google Scholar] [CrossRef]
- Cherry, B.R.; Reeves, M.J.; Smith, G. Evaluation of Bovine Viral Diarrhoea Virus Control Using a Mathematical Model of Infection Dynamics. Prev. Vet. Med. 1998, 33, 91–108. [Google Scholar] [CrossRef]
- Lindberg, A. Bovine Viral Diarrhoea Virus Infections and Its Control: A Review. Vet. Q. 2003, 25, 1–16. [Google Scholar] [CrossRef]
- Yesilbag, K.; Alpay, G.; Becher, P. Variability and Global Distribution of Subgenotypes of Bovine Viral Diarrhea Virus. Viruses 2017, 9, 128. [Google Scholar] [CrossRef]
- Sozzi, E.; Righi, C.; Boldini, M.; Bazzucchi, M.; Pezzoni, G.; Gradassi, M.; Petrini, S.; Lelli, D.; Ventura, G.; Pierini, I.; et al. Cross-Reactivity Antibody Response after Vaccination with Modified Live and Killed Bovine Viral Diarrhea Virus (BVD) Vaccines. Vaccines 2020, 8, 374. [Google Scholar] [CrossRef]
- Duffell, S.; Harkness, J. Bovine Virus Diarrhoea-Mucosal Disease Infection in Cattle. Vet. Rec. 1985, 117, 240–245. [Google Scholar] [CrossRef]
- Kendrick, J.; Franti, C. Bovine Viral Diarrhea: Decay of Colostrum-Conferred Antibody in the Calf. Am. J. Vet. Res. 1974, 35, 589–592. [Google Scholar]
- McGowan, M.; Kirkland, P.; Richards, S.; Littlejohns, I. Increased Reproductive Losses in Cattle Infected with Bovine Pestivirus Around the Time of Insemination. Vet. Rec. 1993, 133, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Viet, A.; Fourichon, C.; Seegers, H. Review and Critical Discussion of Assumptions and Modelling Options to Study the Spread of the Bovine Viral Diarrhoea Virus (BVDV) Within a Cattle Herd. Epidemiol. Inf. 2007, 135, 706–721. [Google Scholar] [CrossRef] [PubMed]
- Baker, J. Bovine Viral Diarrhoea Virus: A Review. J. Am. Vet. Med. Assoc. 1987, 190, 1449–1458. [Google Scholar]
- Moerman, A.; Straver, P.; de Jong, M.; Quak, J.; Baanvinger, T.; van Oirschot, J. A Long Term Epidemiological Study of Bovine Viral Diarrhoea Infections in a Large Herd of Dairy Cattle. Vet. Rec. 1993, 132, 622–626. [Google Scholar] [CrossRef]
- Carlsson, U.; Fredriksson, G.; Alenius, S.; Kindahl, H. Bovine Virus Diarrhoea Virus, a Cause of Early Pregnancy Failure in the Cow. J. Vet. Med. Ser. A 1989, 36, 15–23. [Google Scholar] [CrossRef]
- Done, J.; Terlecki, S.; Richardson, C.; Harkness, J.; Sands, J.; Patterson, D.; Sweasey, D.; Shaw, I.; Winkler, C.; Duffell, S. Bovine Virus Diarrhoea-Mucosal Disease Virus: Pathogenicity for the Fetal Calf Following Maternal Infection. Vet. Rec. 1980, 106, 473–479. [Google Scholar] [CrossRef]
- McClurkin, A.; Littledike, E.; Cutlip, R.; Frank, G.; Coria, M.; Bolin, S. Production of Cattle Immunotolerant to Bovine Viral Diarrhea Virus. Can. J. Comp. Med. 1984, 48, 156–161. [Google Scholar]
- Kendrick, J.W. Bovine Viral Diarrhea-Mucosal Disease Virus Infection in Pregnant Cows. Am. J. Vet. Res. 1971, 32, 533–544. [Google Scholar] [PubMed]
- Saltelli, A.; Chan, K.; Scott, E.M. Sensitivity Analysis; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Thulke, H.H.; Lange, M.; Tratalos, J.A.; Clegg, T.A.; McGrath, G.; O’Grady, L.; O’Sullivan, P.; Doherty, M.L.; Graham, D.A.; More, S.J. Eradicating BVD, Reviewing Irish Programme Data and Model Predictions to Support Prospective Decision Making. Prev. Vet. Med. 2018, 150, 151–161. [Google Scholar] [CrossRef]
- Metcalfe, L. An Update on the Status of BVD Control and Eradication in Europe. J. Vet. Sci. Med. 2019, 7. [Google Scholar] [CrossRef][Green Version]
- Sayers, R.G.; Sayers, G.P.; Graham, D.A.; Arkins, S. Impact of Three Inactivated Bovine Viral Diarrhoea Virus Vaccines on Bulk Milk p80 (NS3) ELISA Test Results in Dairy Herds. Vet. J. 2015, 205, 56–61. [Google Scholar] [CrossRef]
- Häsler, B.; Howe, K.S.; Presi, P.; Stärk, K.D. An economic model to evaluate the mitigation programme for bovine viral diarrhoea in Switzerland. Prev. Vet. Med. 2012, 106, 162–173. [Google Scholar] [CrossRef]
- Jackova, A.; Novackova, M.; Pelletier, C.; Audeval, C.; Gueneau, E.; Haffar, A.; Petit, E.; Rehby, L.; Vilcek, S. The Extended Genetic Diversity of BVDV-1, Typing of BVDV Isolates from France. Vet. Res. Commun. 2008, 32, 7–11. [Google Scholar] [CrossRef] [PubMed]
- Ridpath, J.F. Immunology of BVDV Vaccines: Biologicals, Aspects of Immunology of Bovine Viral Diarrhea. Virus 2013, 41, 14–19. [Google Scholar]
- Lanyon, S.R.; Hill, F.I.; Reichel, M.P.; Brownlie, J. Bovine Viral Diarrhoea: Pathogenesis and Diagnosis. Vet. J. 2014, 199, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Cristancho-Fajardo, L.; Ezanno, P.; Vergu, E. Integrative Modelling of Pathogen Spread through Animal Trade by Accounting for Farmers’ Control Decisions. Sci. Rep. 2021, 11. [Google Scholar] [CrossRef]



| Parameters | Charolaise | Limousine | Blonde d’Aquitaine |
|---|---|---|---|
| Number of cows kept for breeding | 68 | 56 | 53 |
| Number of heifers kept for breeding | 22 | 12 | 13 |
| Probability of infertility of cows | 0.061 | 0.048 | 0.080 |
| Probability of infertility of heifers | 0.039 | 0.026 | 0.058 |
| Probability of having twins | 0.023 | 0.004 | 0.022 |
| Probability of calf mortality before weaning | 0.08 | 0.05 | 0.07 |
| Weaning date | 14 October | 1 October | 29 August |
| Breeding period | 22 March–19 July | 4 February–4 June | 19 February–19 July |
| Pasture period | 1 April–22 November | 1 April–14 November | 10 April–9 November |
| Pasture length | 237 days | 229 days | 215 days |
| Sale period of male grassers | 15 November (+/−3 weeks) | 15 November (+/−3 weeks) | |
| Sale period of female grassers | 15 June (+/−3 weeks) | ||
| Number of heifers sold at breeding | 2 | 0 | 0 |
| Scheme | Definition | Value | Reference |
|---|---|---|---|
| μP,bi | Probability of mortality at birth of P calves | 0.0667 | [7,23] |
| μCa,bi | Probability of mortality at birth of non-P calves | 0.02 | |
| μP | Mortality of P animals per day | 0.0019 | [7,23] |
| μCa | Mortality of non-P calves per day | 0.000326 | |
| ФMS | Transition rate from state M to state S per day | 0.00667 | [24] |
| ФTR | Transition rate from state T to state R per day | 0.2 | [25] |
| ФVS | Transition rate from state V2 to state S per day | 1/ ΔV2 | |
| βT | Transmission rate for T animals | 0.03 | [26,27] |
| βP | Transmission rate for P animals | 0.5 | [26,28] |
| αRa | Abortion rate due to infection early pregnancy | 0.8 | [6,25,29] |
| αRb | Abortion rate due to infection mid-pregnancy | 0.2 | [6,30,31] |
| ηP ηM = ηR | Probability of giving birth to a calf in state P, M, or R if infection in mid-pregnancy and no abortion | 0.9375 0.03125 | [6,28,30,31,32] |
| Kext | External risk of virus introduction during pasture | 0–0.001 |
| Scheme | Definition | Bovilis® | Bovela® | Rispoval® | Mucosiffa® |
|---|---|---|---|---|---|
| ρH/C | Boolean | 1 if vaccination, 0 otherwise | |||
| λ | Probability of protection against infection £ | 0/1 * | 0 | 0 | 0 |
| ω | Probability of protection against vertical transmission § | 1/0 * | 0.985 | 0.9 | 0.9 |
| ΔV1 | Duration in V1 state (weeks) § | 52 | 52 | 52 | 52 |
| ΔV2 | Duration in V2 state (weeks) £ | 8 | 8 | 8 | 8 |
| cD | Dose cost (euro) § | 4.59 | 5.80 | 4.33 | 5.72 |
| n1 | Number of vaccine doses for the first shot § | 2 | 1 | 2 | 1 |
| n2 | Number of vaccine doses for the second shot § | 1 | 1 | 1 | 1 |
| Parameters | Charolaise | Limousine | Blonde d’Aquitaine | ||||
|---|---|---|---|---|---|---|---|
| € | Kg | € | Kg | € | Kg | ||
| Price and weight per animal type | Replacement calf | 352 | 47 | 352 | 42 | 352 | 46 |
| Gestating cow | 1689 | 747 | 1621 | 682 | 1828 | 814 | |
| Male grasser | 1051 | 420 | 966 | 315 | 915 | 260 | |
| Female grasser (sold in fall) | - | - | 793 | 300 | 724 | 240 | |
| Female grasser (sold in spring) | 985 | 400 | - | - | - | - | |
| Fattened heifer | 1330 | 630 | - | - | - | - | |
| Culled cow | 1337 | 700 | 1570 | 691 | 1710 | 798 | |
| Cprod | Production cost per kg | 0.754 | - | 0.652 | - | 0.775 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arnoux, S.; Bidan, F.; Damman, A.; Petit, E.; Assié, S.; Ezanno, P. To Vaccinate or Not: Impact of Bovine Viral Diarrhoea in French Cow-Calf Herds. Vaccines 2021, 9, 1137. https://doi.org/10.3390/vaccines9101137
Arnoux S, Bidan F, Damman A, Petit E, Assié S, Ezanno P. To Vaccinate or Not: Impact of Bovine Viral Diarrhoea in French Cow-Calf Herds. Vaccines. 2021; 9(10):1137. https://doi.org/10.3390/vaccines9101137
Chicago/Turabian StyleArnoux, Sandie, Fabrice Bidan, Alix Damman, Etienne Petit, Sébastien Assié, and Pauline Ezanno. 2021. "To Vaccinate or Not: Impact of Bovine Viral Diarrhoea in French Cow-Calf Herds" Vaccines 9, no. 10: 1137. https://doi.org/10.3390/vaccines9101137
APA StyleArnoux, S., Bidan, F., Damman, A., Petit, E., Assié, S., & Ezanno, P. (2021). To Vaccinate or Not: Impact of Bovine Viral Diarrhoea in French Cow-Calf Herds. Vaccines, 9(10), 1137. https://doi.org/10.3390/vaccines9101137






