New Insights into the Estimation of Reproduction Numbers during an Epidemic
Abstract
1. Introduction
2. Mathematical Models and Methods
2.1. A Standard Method to Estimate
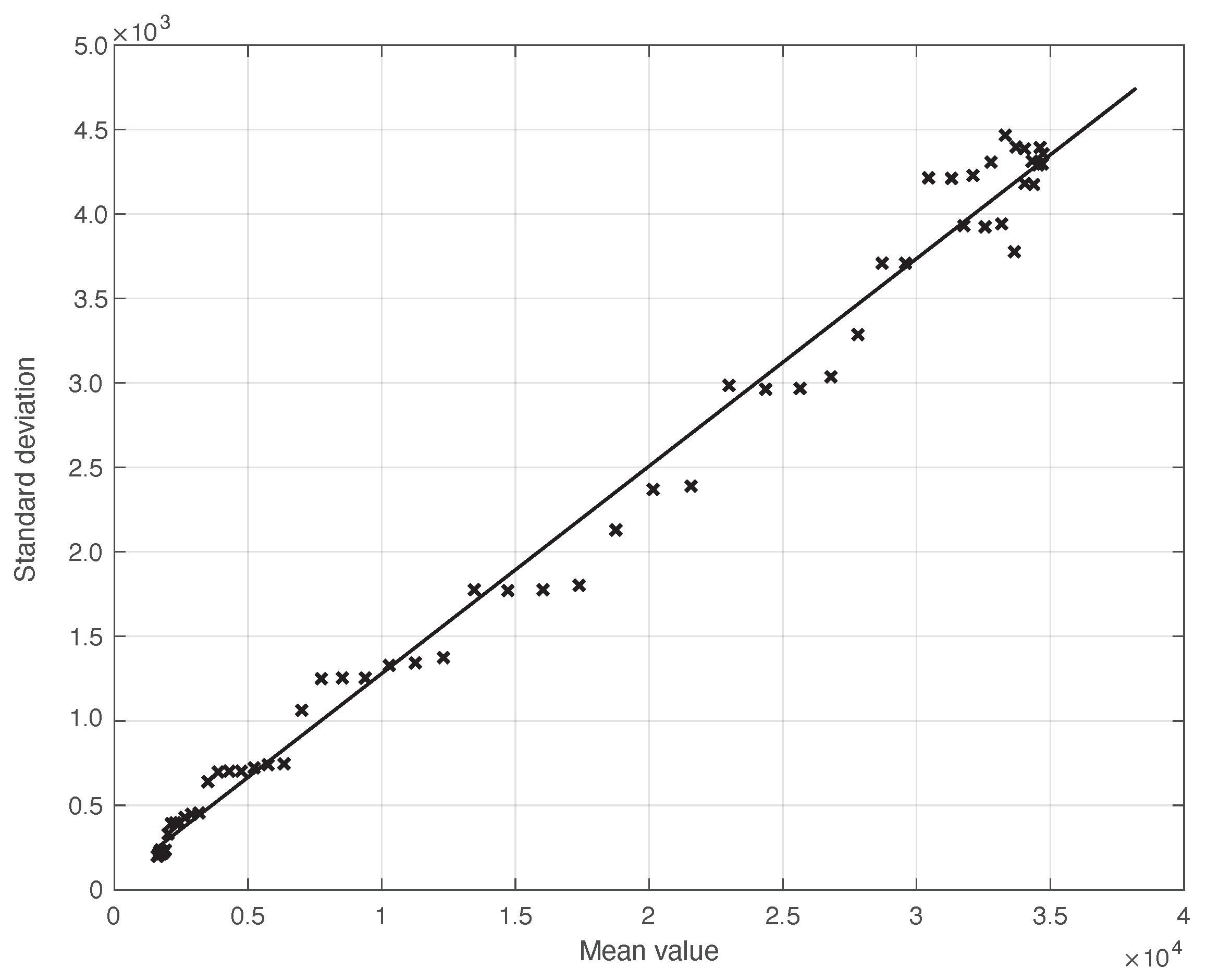
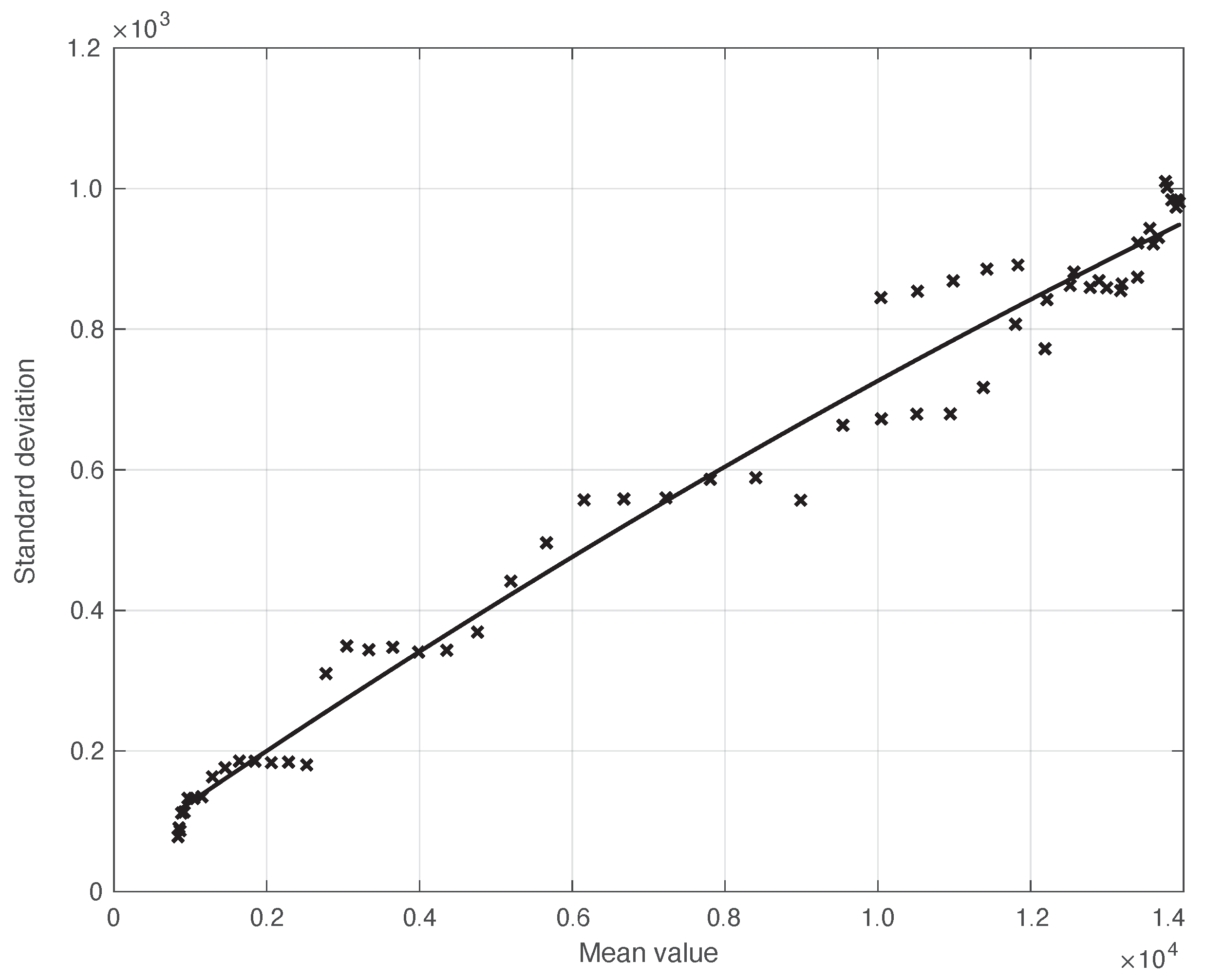
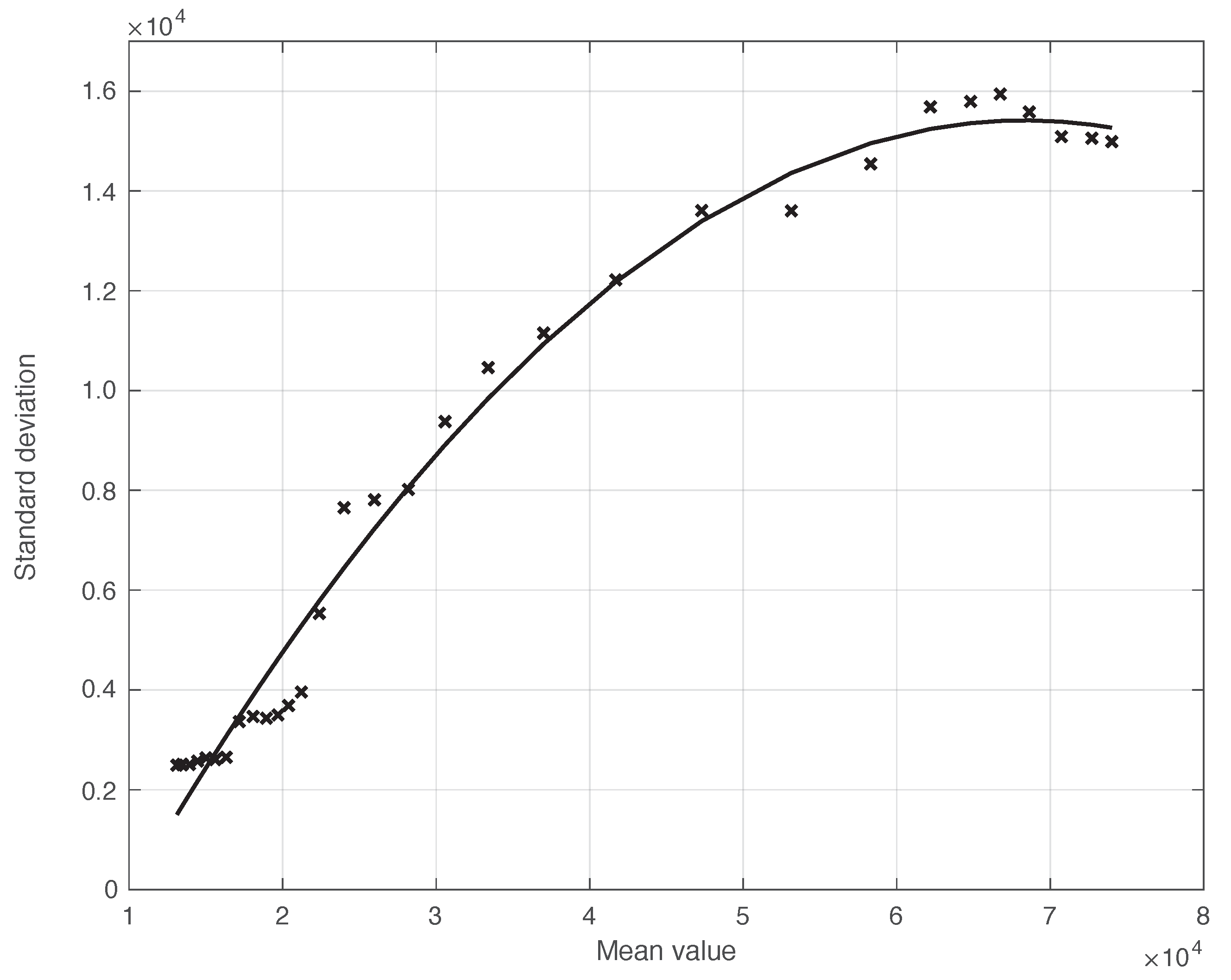
2.2. Data Error Reduction
2.3. Estimation of from Positive Test Data
2.4. A New Estimator for the Reproduction Number Sequence
3. Results
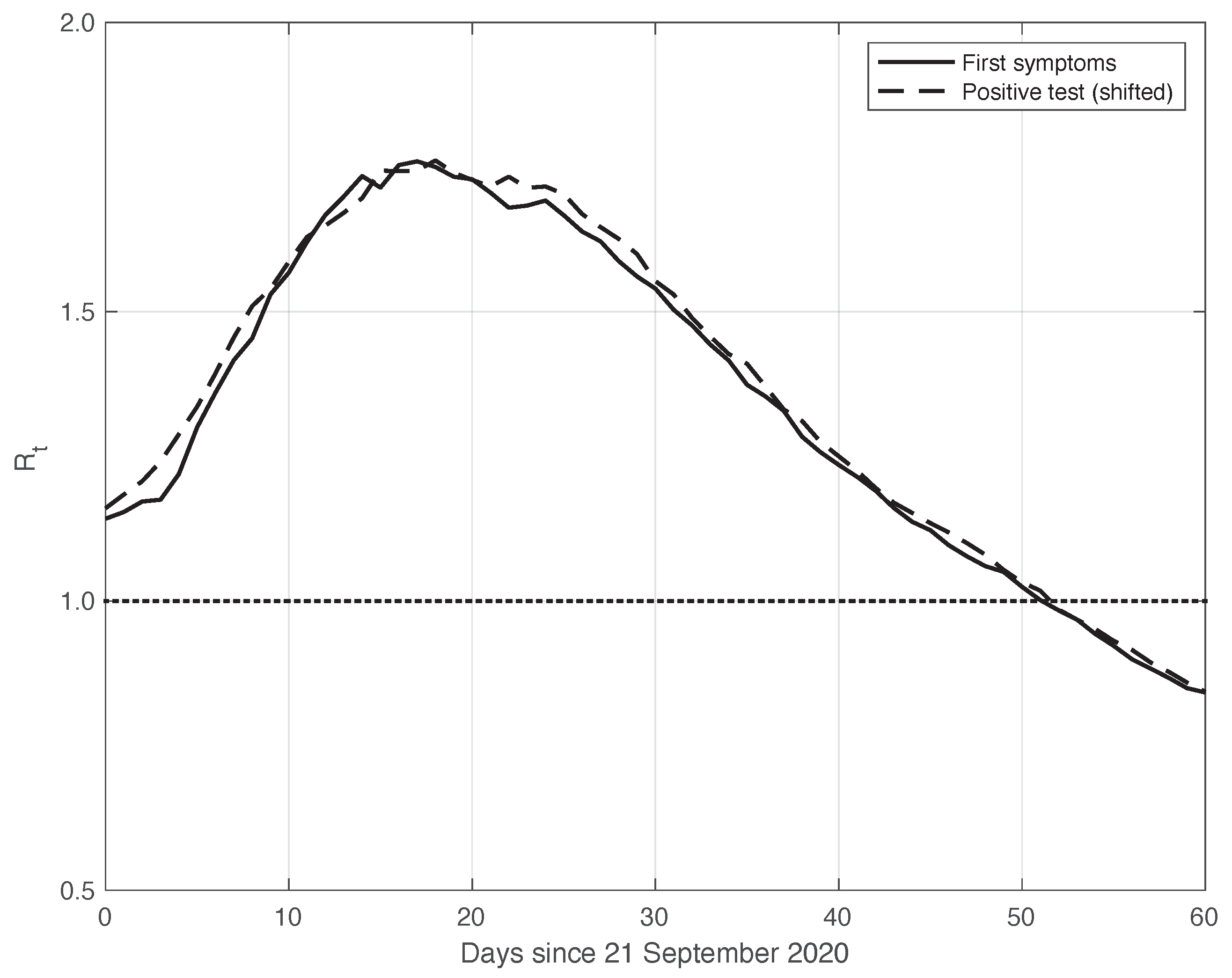
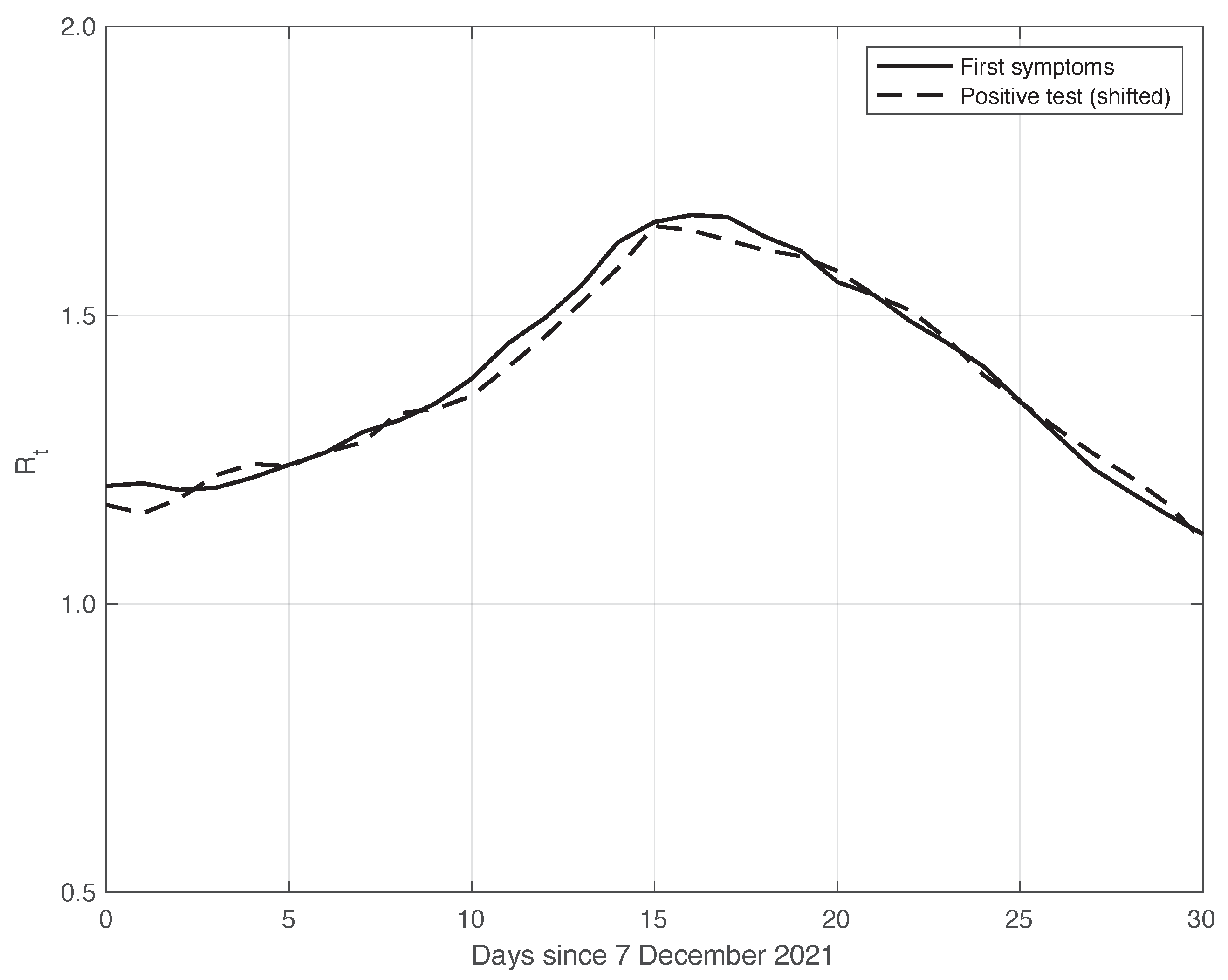
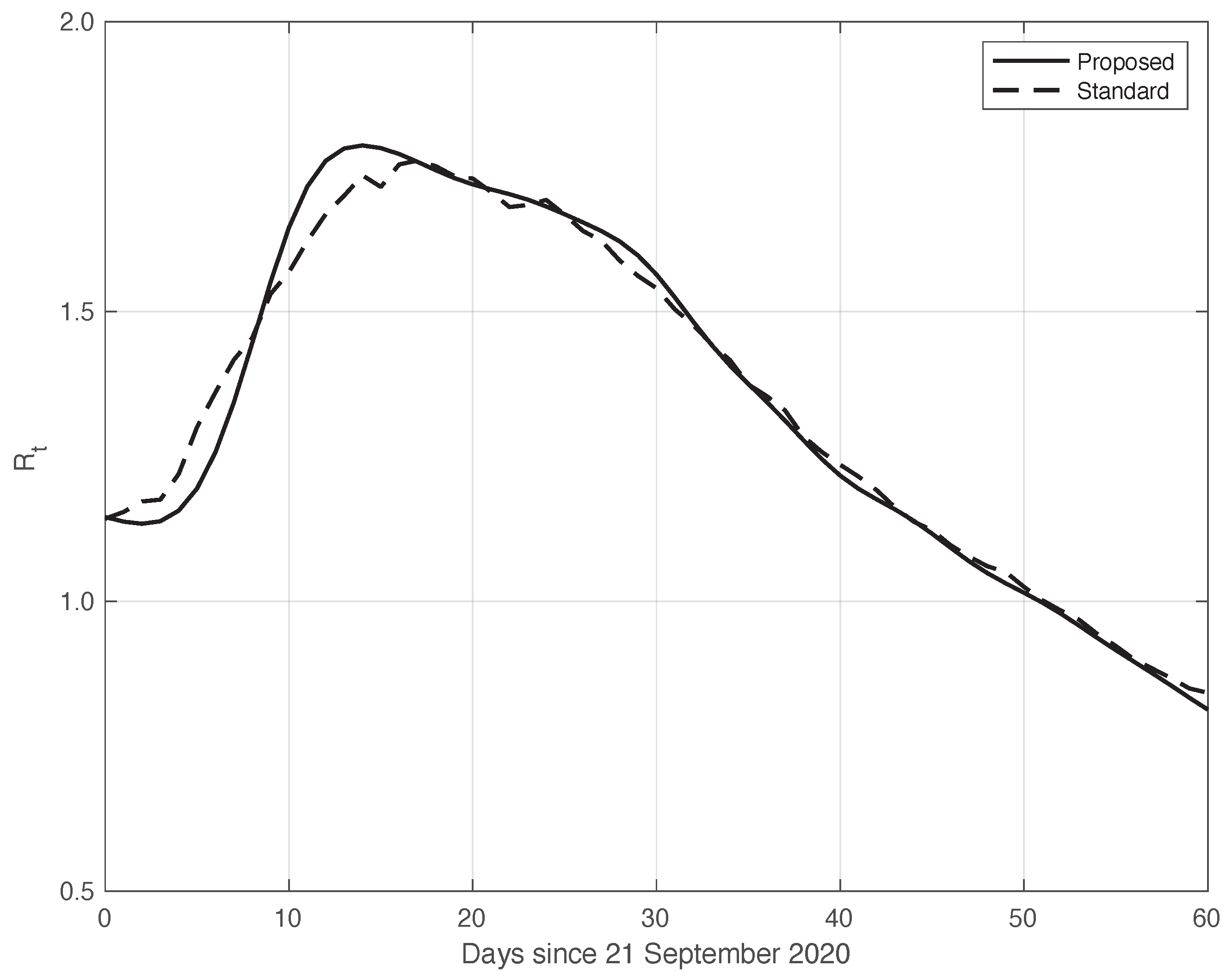
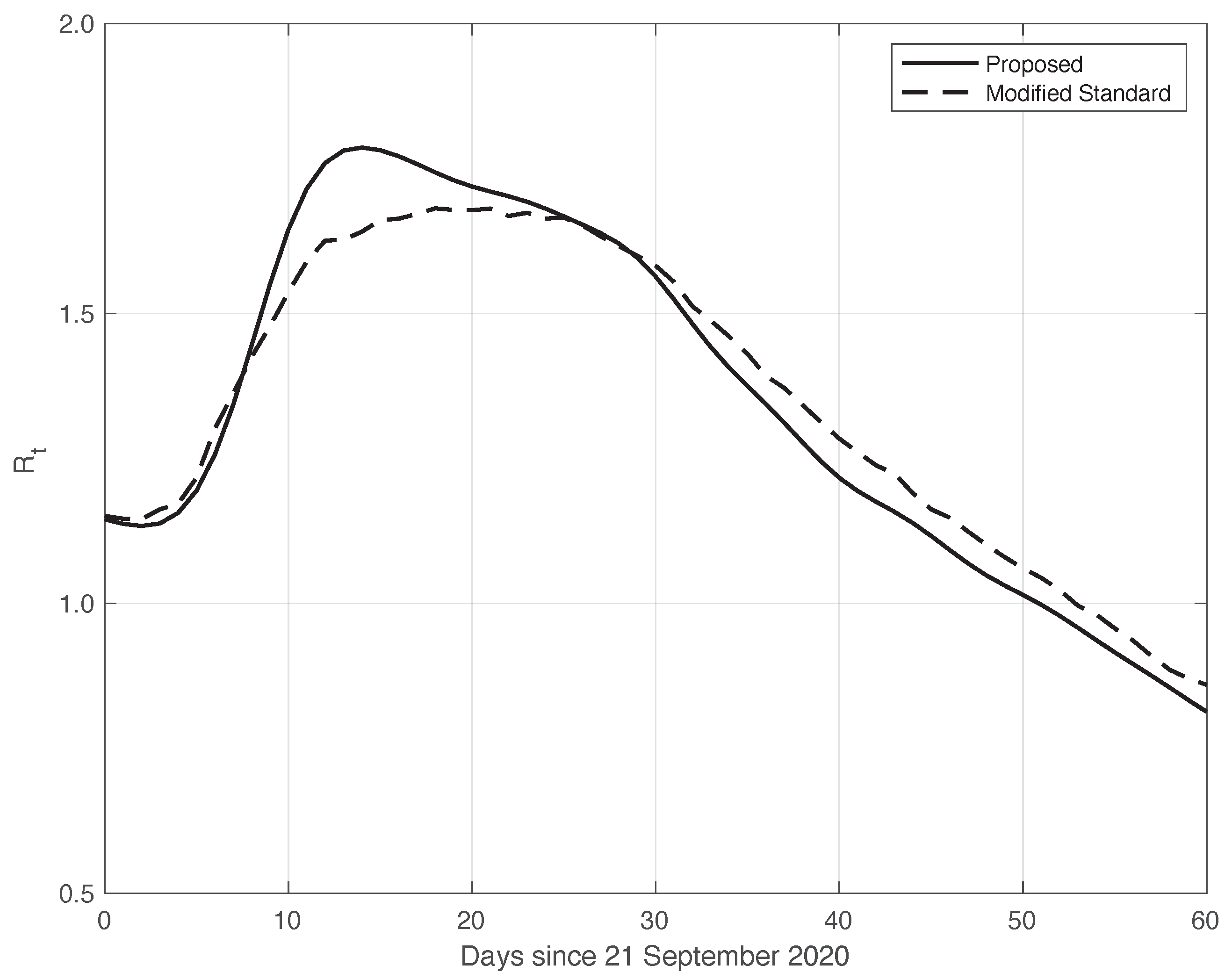
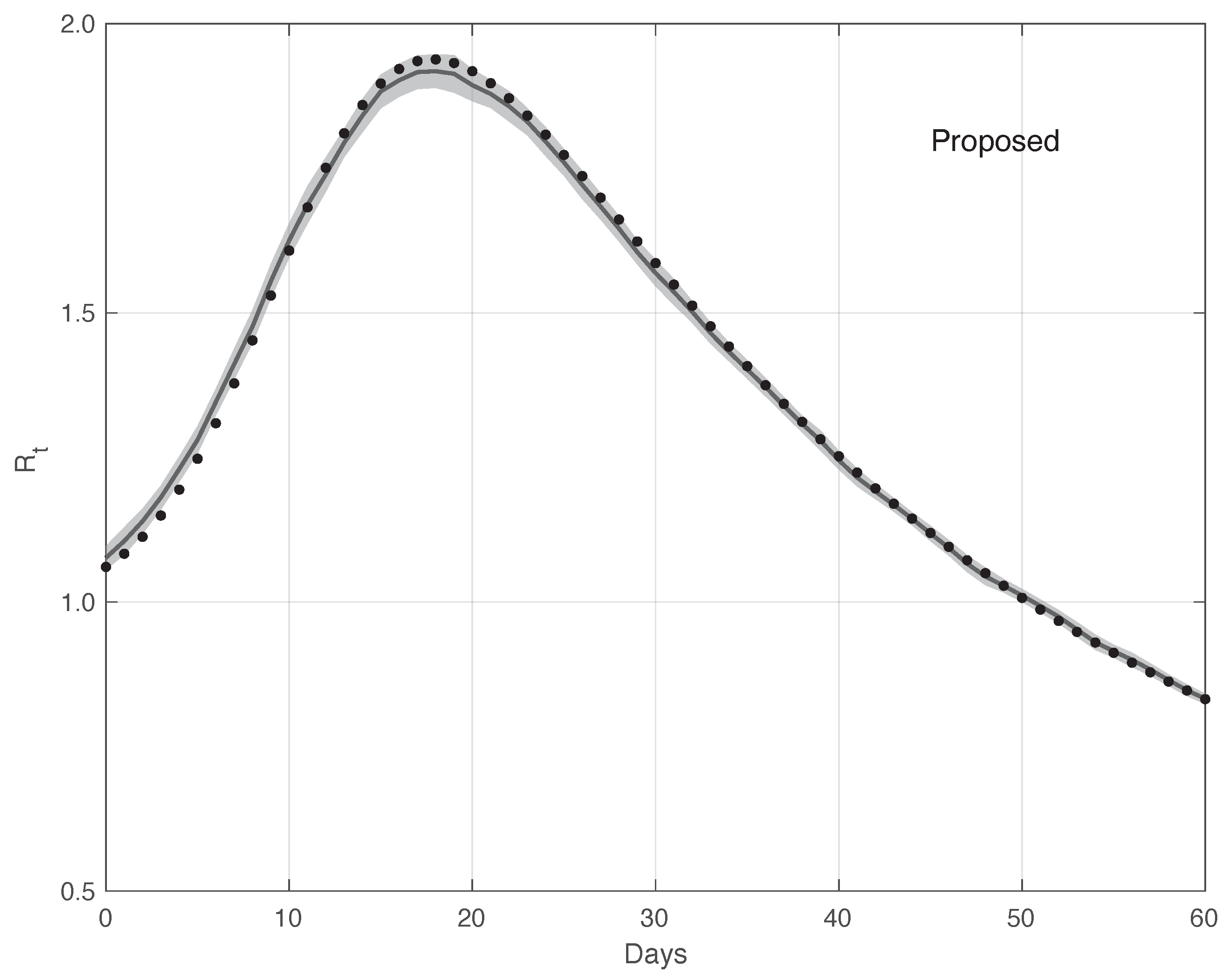
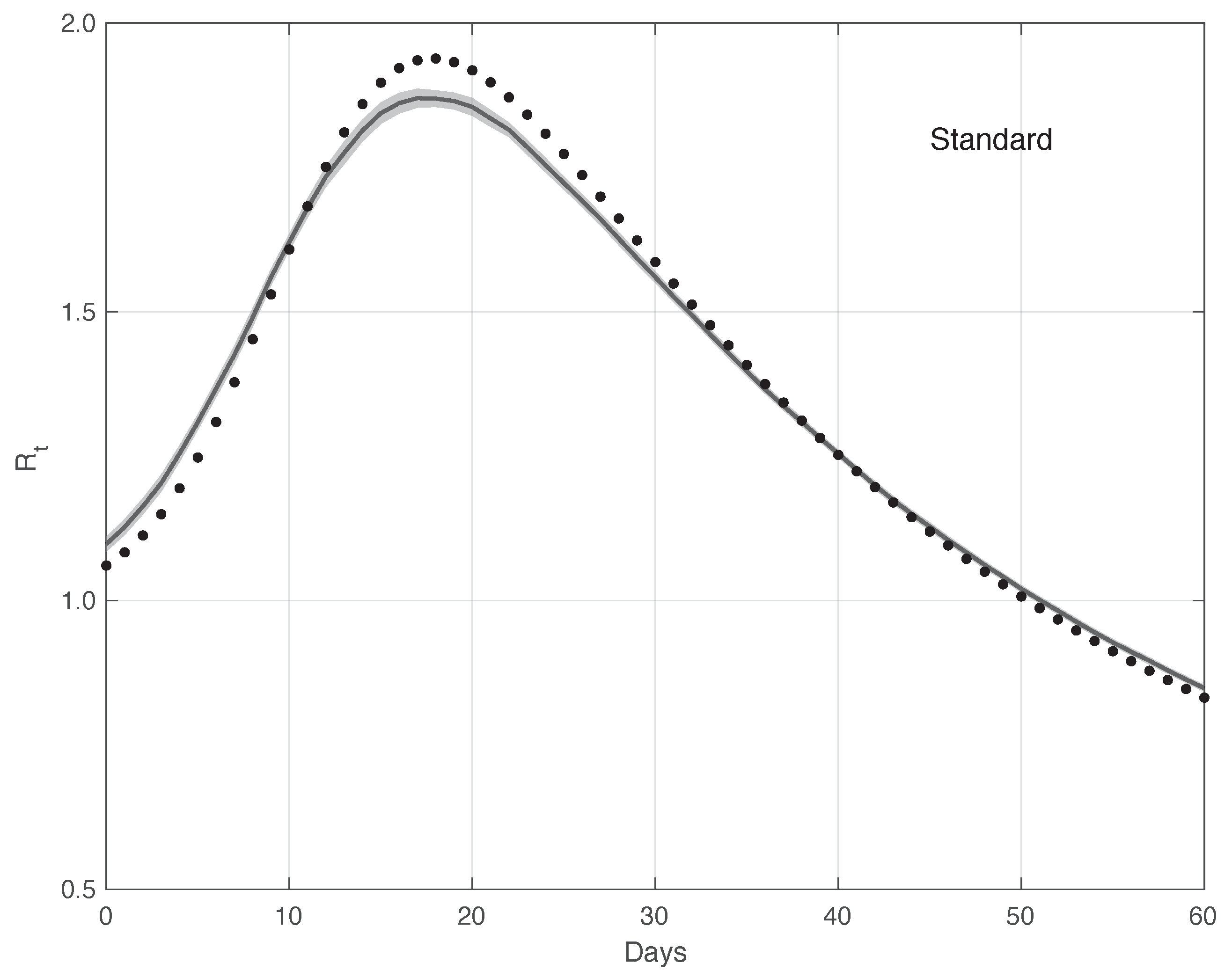
3.1. Real SARS-CoV-2 Italian Data
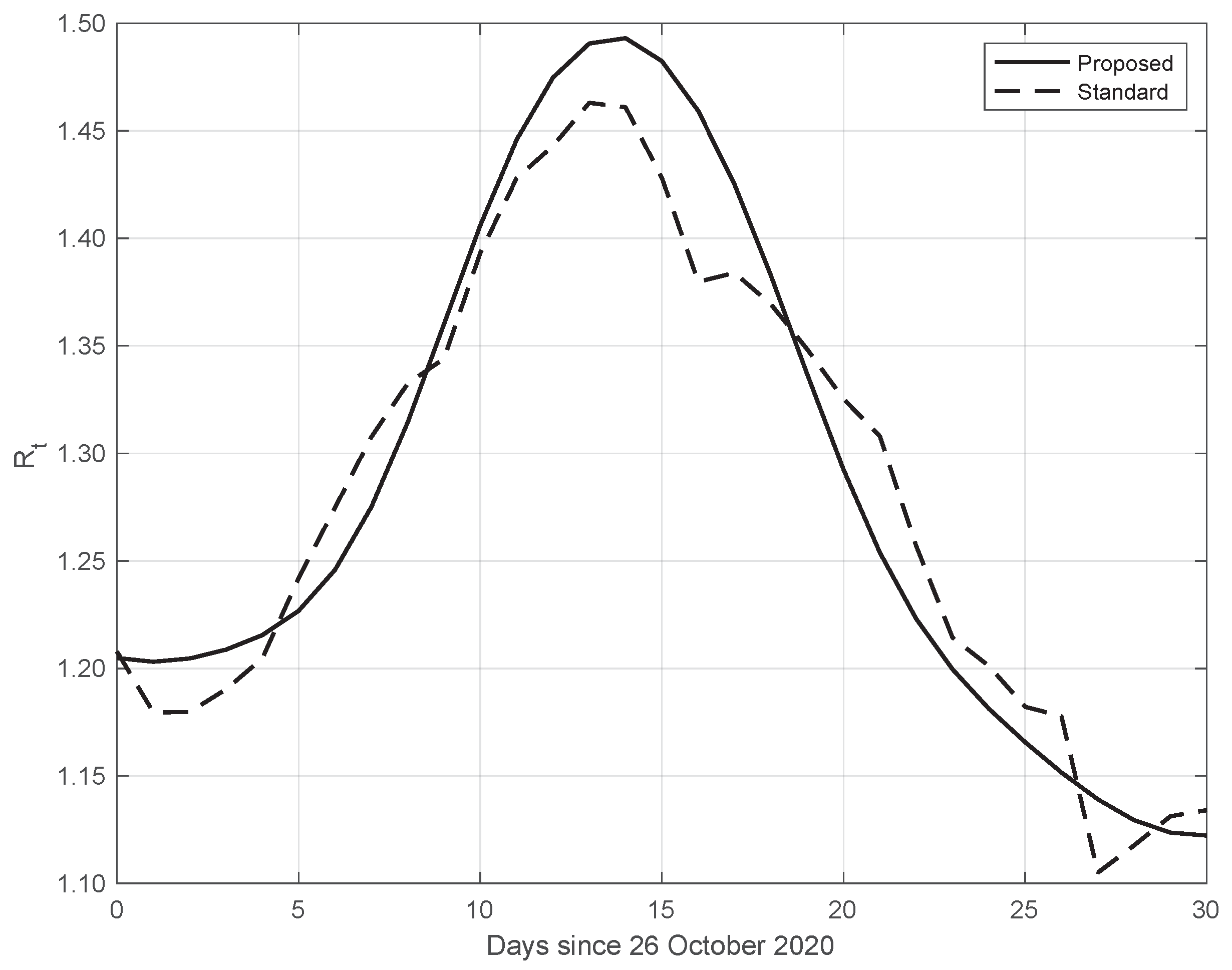
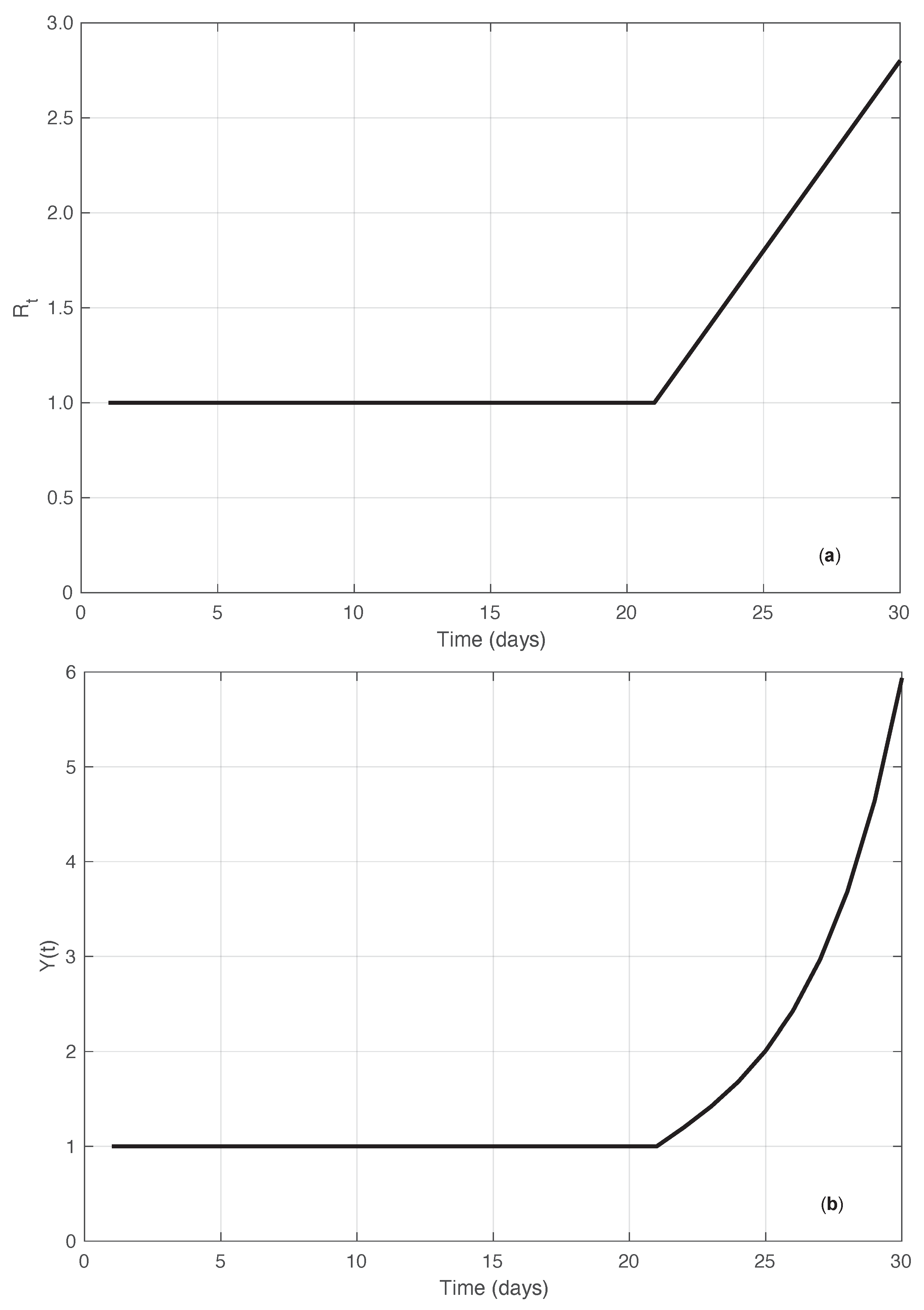
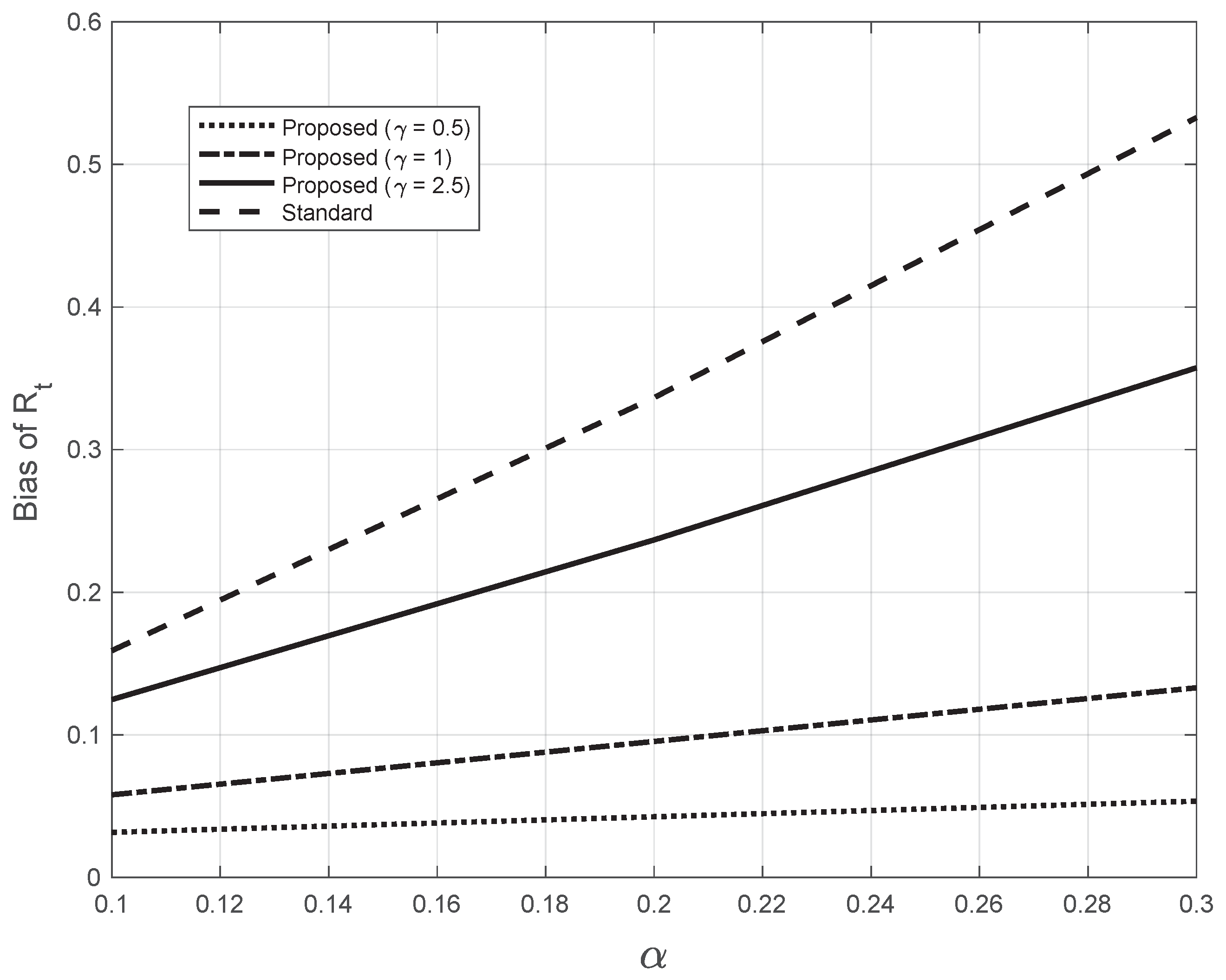
3.2. Synthetic Epidemic Data
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SARS-CoV-2 | Severe Acute Respiratory Syndrome CoronaVirus 2 |
| Probability Density Function | |
| i.i.d. | Independent and identically distributed |
| ISS | Istituto Superiore di Sanitá |
| NYC | New York City |
References
- Cauchemez, S.; Fraser, C.; Van Kerkhove, M.D.; Donnelly, C.A.; Riley, S.; Rambaut, A.; Enouf, V.; van der Werf, S.; Ferguson, N.M. Middle East respiratory syndrome coronavirus: Quantification of the extent of the epidemic, surveillance biases, and transmissibility. Lancet Infect. Dis. 2014, 14, 50–56. [Google Scholar] [CrossRef]
- Nouvellet, P.; Cori, A.; Garske, T.; Blake, I.M.; Dorigatti, I.; Hinsley, W.; Jombart, T.; Mills, H.L.; Nedjati-Gilani, G.; Van Kerkhove, M.D.; et al. A simple approach to measure transmissibility and forecast incidence. Epidemics 2018, 22, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Fraser, C. Estimating individual and household reproduction numbers in an emerging epidemic. PLoS ONE 2007, 2, e758. [Google Scholar] [CrossRef] [PubMed]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. London. Ser. A 1927, 115, 700–721. [Google Scholar]
- Murphy, G.F. COVID-19 and graft-versus-host disease: A tale of two diseases (and why age matters). Lab. Investig. 2021, 101, 274–279. [Google Scholar] [CrossRef]
- Saraceni, F.; Scortechini, I.; Mancini, G.; Mariani, M.; Federici, I.; Gaetani, M.; Barbatelli, P.; Minnucci, M.L.; Bagnarelli, P.; Olivieri, A. Severe COVID-19 in a patient with chronic graft-versus-host disease after hematopoietic stem cell transplant successfully treated with ruxolitinib. Transpl. Infect. Dis. 2021, 23, e13401. [Google Scholar] [CrossRef]
- Zhao, S.; Tang, B.; Musa, S.S.; Ma, S.; Zhang, J.; Zeng, M.; Yun, Q.; Guo, W.; Zheng, Y.; Yang, Z.; et al. Estimating the generation interval and inferring the latent period of COVID-19 from the contact tracing data. Epidemics 2021, 36, 100482. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Sebastiani, G.; Massa, M.; Riboli, E. Covid-19 epidemic in Italy: Evolution, projections and impact of government measures. Eur. J. Epidemiol. 2020, 35, 341–345. [Google Scholar] [CrossRef]
- Lin, Y.T.; Neumann, J.; Miller, E.F.; Posner, R.G.; Mallela, A.; Safta, C.; Ray, J.; Thakur, G.; Chinthavali, S.; Hlavacek, W.S. Daily forecasting of regional epidemics of Coronavirus Disease with Bayesian uncertainty quantification, United States. Emerg. Infect. Dis. 2021, 27, 767. [Google Scholar] [CrossRef]
- Trejo, I.; Lin, Y.T.; Patrick, A.L.; Hengartner, N. Nonparametric inference for the reproductive rate in generalized compartmental models. Preprint 2022. [Google Scholar] [CrossRef]
- Cori, A.; Ferguson, N.; Fraser, C.; Cauchemez, S. A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics. Am. J. Epidemiol. 2013, 178, 1505–1512. [Google Scholar] [CrossRef] [PubMed]
- EpiEstim R Package v2.2–3: A Tool to Estimate Time Varying Instantaneous Reproduction Number during Epidemics. 2021. Available online: https://cran.r-project.org/web/packages/EpiEstim/index.html (accessed on 31 March 2021).
- EpiEstim Microsoft Excel Spreadsheet. 2012. Available online: https://cran.r-project.org/web/packages/EpiEstim/index.html (accessed on 31 March 2021).
- Nash, R.K.; Nouvellet, P.; Cori, A. Real-time estimation of the epidemic reproduction number: Scoping review of the applications and challenges. PLoS Digit. Health 2022, 1, e0000052. [Google Scholar] [CrossRef]
- Ali, S.T.; Wang, L.; Lau, E.H.Y.; Xu, X.; Du, Z.; Wu, Y.; Leung, G.M.; Cowling, B.J. Serial interval of SARS-CoV-2 was shortened over time by nonpharmaceutical interventions. Science 2020, 369, 1106–1109. [Google Scholar] [CrossRef]
- Britton, T.; Scalia Tomba, G. Estimation in emerging epidemics: Biases and remedies. J. R. Soc. Interface 2019, 16, 20180670. [Google Scholar] [CrossRef]
- Cereda, D.; Manica, M.; Tirani, M.; Rovida, F.; Demicheli, V.; Ajelli, M.; Poletti, P.; Trentini, F.; Guzzetta, G.; Marziano, V.; et al. The early phase of the COVID-19 epidemic in Lombardy, Italy. Epidemics 2021, 37, 100528. [Google Scholar] [CrossRef]
- He, X.; Lau, E.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.C.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020, 26, 672–675. [Google Scholar] [CrossRef]
- Tindale, L.C.; Stockdale, J.E.; Coombe, M.; Garlock, E.S.; Lau, W.Y.V.; Saraswat, M.; Zhang, L.; Chen, D.; Wallinga, J.; Colijn, C. Evidence for transmission of COVID-19 prior to symptom onset. eLife 2020, 9, e57149. [Google Scholar] [CrossRef]
- Lehmann, E.L.; Casella, G. Theory of Point Estimation; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Spassiani, I.; Gubian, L.; Palù, G.; Sebastiani, G. Vaccination Criteria Based on Factors Influencing COVID-19 Diffusion and Mortality. Vaccines 2020, 8, 766. [Google Scholar] [CrossRef]
- O’Dea, E.B.; Drake, J.M. A semi-parametric, state-space compartmental model with time-dependent parameters for forecasting COVID-19 cases, hospitalizations and deaths. J. R. Soc. Interface 2022, 19, 20210702. [Google Scholar] [CrossRef]
- Eubank, R. Nonparametric Regression and Spline Smoothing; Statistics: A Series of Textbooks and Monographs; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Parzen, E. On Estimation of a Probability Density Function and Mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Sebastiani, G.; Palù, G. COVID-19 and school activities in Italy. Viruses 2020, 12, 1339. [Google Scholar] [CrossRef] [PubMed]
- Stefanelli, P.; Trentini, F.; Petrone, D.; Mammone, A.; Ambrosio, L.; Manica, M.; Guzzetta, G.; Andrea, V.D.; Marziano, V.; Zardini, A.; et al. Tracking the progressive spread of the SARS-CoV-2 Omicron variant in Italy, December 2021–January 2022. medRxiv 2022. [Google Scholar] [CrossRef]
- Spassiani, I.; Sebastiani, G.; Palù, G. Spatiotemporal analysis of COVID-19 incidence data. Viruses 2021, 13, 463. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sebastiani, G.; Spassiani, I. New Insights into the Estimation of Reproduction Numbers during an Epidemic. Vaccines 2022, 10, 1788. https://doi.org/10.3390/vaccines10111788
Sebastiani G, Spassiani I. New Insights into the Estimation of Reproduction Numbers during an Epidemic. Vaccines. 2022; 10(11):1788. https://doi.org/10.3390/vaccines10111788
Chicago/Turabian StyleSebastiani, Giovanni, and Ilaria Spassiani. 2022. "New Insights into the Estimation of Reproduction Numbers during an Epidemic" Vaccines 10, no. 11: 1788. https://doi.org/10.3390/vaccines10111788
APA StyleSebastiani, G., & Spassiani, I. (2022). New Insights into the Estimation of Reproduction Numbers during an Epidemic. Vaccines, 10(11), 1788. https://doi.org/10.3390/vaccines10111788






