A Theoretical Analysis of the Effects That the Glycocalyx and the Internal Elastic Lamina Have on Nitric Oxide Concentration Gradients in the Arterial Wall
Abstract
1. Introduction
2. Materials and Methods
2.1. The Creation of an Arteria 3D Digital Phantom
2.2. Calculations of the Convectional Field in the Phantom
2.3. Evaluation of the NO Gradients Using a Boundary Problem for the Convectional Reaction–Diffusion Equation
2.4. The Numerical Method of the Boundary Problem Evaluation Used in the Present Study
3. Results
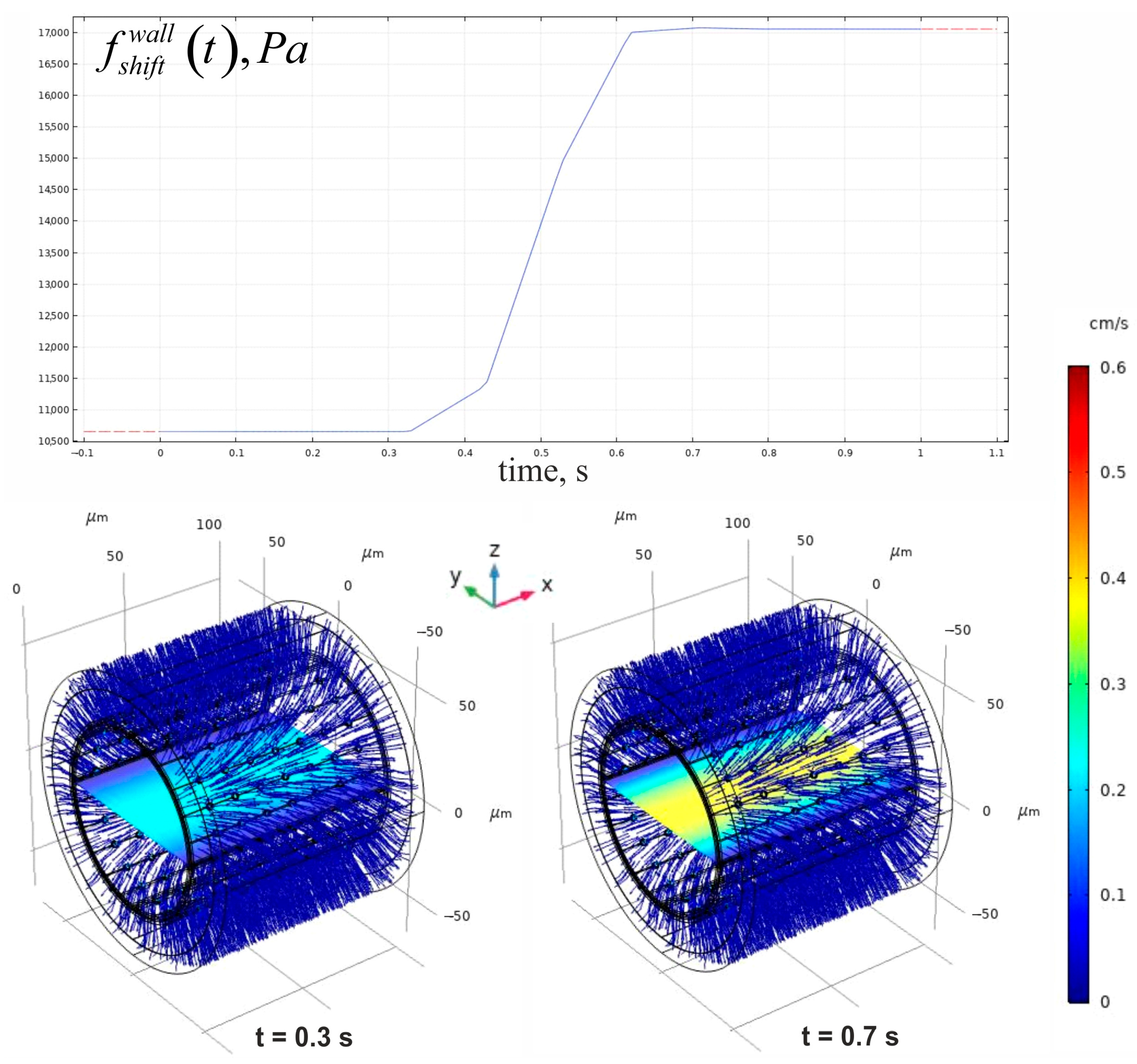
3.1. Evaluation of the Convectional Velocity Field in the Phantom
3.2. Evaluation of a Spatial-Temporal Distribution of NO Concentrations Considering the Effects of Blood Flow Velocities, ESG Permeability and IEL Fenestration
3.2.1. Forming a Gradient of NO Concentrations Under Different Blood Flow Rates
3.2.2. The Effect of IEL Pore Density and Diffusion Permeability of ESG on the NO Concentration Gradients
3.2.3. The Relationship Between eNOS Activity Levels and the Concentration Distribution of NO
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NO | Nitric oxide |
| NOS | Nitric oxide synthase |
| nNOS | The neuronal isoenzyme of nitric oxide synthase |
| iNOS | The inducible isoenzyme of nitric oxide synathase |
| eNOS | The endothelial isoenzyme of nitric oxide synthase |
| ROS | Reactive oxygen species |
| sGC | Soluble guanylyl cyclase |
| ONOO– | Peroxynitrite |
| IEL | The internal elastic lamina |
| ESG | A thin layer of endothelial surface glycocalyx |
| GACs | Glycosaminoglycans |
| FEM | The finite element method |
| HS | Heparan sulphate |
| HA | Hyaluronic acid (hyaluronan) |
| ATP | Adenosine triphosphate |
References
- Pacher, P.; Beckman, J.S.; Liaudet, L. Nitric Oxide and Peroxynitrite in Health and Disease. Physiol. Rev. 2007, 87, 315–424. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Vanhoutte, P.M.; Leung, S.W.S. Vascular nitric oxide: Beyond eNOS. J. Pharmacol. Sci. 2015, 129, 83–94. [Google Scholar] [CrossRef] [PubMed]
- Andrabi, S.M.; Sharma, N.S.; Karan, A.; Shahriar, S.M.S.; Cordon, B.; Ma, B.; Xie, J. Nitric Oxide: Physiological Functions, Delivery, and Biomedical Applications. Adv. Sci. 2023, 10, e2303259. [Google Scholar] [CrossRef] [PubMed]
- Alderton, W.K.; Cooper, C.E.; Knowles, R.G. Nitric oxide synthases: Structure, function and inhibition. Biochem. J. 2001, 357, 593–615. [Google Scholar] [CrossRef]
- Förstermann, U.; Sessa, W.C. Nitric oxide synthases: Regulation and function. Eur. Heart J. 2012, 33, 829–837. [Google Scholar] [CrossRef]
- Chachlaki, K.; Garthwaite, J.; Prevot, V. The gentle art of saying NO: How nitric oxide gets things done in the hypothalamus. Nat. Rev. Endocrinol. 2017, 13, 521–535. [Google Scholar] [CrossRef]
- Walford, G.; Loscalzo, J. Nitric oxide in vascular biology. J. Thromb. Haemost. 2003, 1, 2112–2118. [Google Scholar] [CrossRef]
- Toda, N.; Ayajiki, K.; Okamura, T. Cerebral blood flow regulation by nitric oxide: Recent advances. Pharmacol. Rev. 2009, 61, 62–97. [Google Scholar] [CrossRef]
- Belenichev, I.; Popazova, O.; Bukhtiyarova, N.; Savchenko, D.; Oksenych, V.; Kamyshnyi, O. Modulating Nitric Oxide: Implications for Cytotoxicity and Cytoprotection. Antioxidants 2024, 13, 504. [Google Scholar] [CrossRef]
- Brunori, M.; Forte, E.; Arese, M.; Mastronicola, D.; Giuffrè, A.; Sarti, P. Nitric oxide and the respiratory enzyme. Biochim. Et Biophys. Acta Bioenerg. 2006, 1757, 1144–1154. [Google Scholar] [CrossRef]
- Farah, C.; Michel, L.Y.M.; Balligand, J.L. Nitric oxide signalling in cardiovascular health and disease. Nat. Rev. Cardiol. 2018, 15, 292–316. [Google Scholar] [CrossRef] [PubMed]
- Qin, G.; Wang, L.; Hua, Y.; Hou, H.; Zou, Q.; Wang, D.; Hu, Z.; Lu, D. Comparative morphology of the internal elastic lamina of cerebral and peripheral arteries. Int. J. Clin. Exp. Pathol. 2020, 13, 764–770. [Google Scholar] [PubMed]
- Weinbaum, S.; Tarbell, J.; Damiano, E. The Structure and Function of the Endothelial Glycocalyx Layer. Annu. Rev. Biomed. Eng. 2007, 9, 121–167. [Google Scholar] [CrossRef] [PubMed]
- Tada, S.; Tarbell, J.M. Internal elastic lamina affects the distribution of macromolecules in the arterial wall: A computational study. Am. J. Physiol. Heart Circ. Physiol. 2004, 287, H905–H913. [Google Scholar] [CrossRef]
- Yen, W.; Cai, B.; Yang, J.; Zhang, L.; Zeng, M.; Tarbell, J.M.; Fu, B.M. Endothelial Surface Glycocalyx Can Regulate Flow—Induced Nitric Oxide Production in Microvessels In Vivo. PLoS ONE 2015, 10, e0117133. [Google Scholar] [CrossRef]
- Bartosch, A.M.W.; Mathews, R.; Tarbell, J.M. Endothelial Glycocalyx—Mediated Nitric Oxide Production in Response to Selective AFM Pulling. Biophys. J. 2017, 113, 101–108. [Google Scholar] [CrossRef]
- Oikonomou, E.; Tsalamandris, S.; Mourouzis, K.; Tousoulis, D. Chapter 1.1—Biology of the Vessel Wall. In Coronary Artery Disease; Tousoulis, D., Ed.; Academic Press: Cambridge, MA, USA, 2018; pp. 3–12. [Google Scholar]
- Itoh, Y.; Suzuki, N. Control of brain capillary blood flow. J. Cereb. Blood Flow Metab. 2012, 32, 1167–1176. [Google Scholar] [CrossRef]
- Ho, W.M.; Reis, C.; Akyol, O.; Zhang, J. Chapter 6-Cerebral Vasa Vasorum. In Primer on Cerebrovascular Diseases, 2nd ed.; Caplan, L.R., Biller, J., Leary, M.C., Lo, E.H., Thomas, A.J., Yenari, M., Zhang, J.H., Eds.; Academic Press: San Diego, CA, USA, 2017; pp. 37–42. [Google Scholar]
- Kopylova, V.S.; Boronovskiy, S.E.; Nartsissov, Y.R. Fundamental principles of vascular network topology. Biochem. Soc. Trans. 2017, 45, 839–844. [Google Scholar] [CrossRef]
- Blanco, P.J.; Watanabe, S.M.; Dari, E.A.; Passos, M.A.R.F.; Feijóo, R.A. Blood flow distribution in an anatomically detailed arterial network model: Criteria and algorithms. Biomech. Model. Mechanobiol. 2014, 13, 1303–1330. [Google Scholar] [CrossRef]
- Reitsma, S.; Slaaf, D.W.; Vink, H.; van Zandvoort, M.A.M.J.; oude Egbrink, M.G.A. The endothelial glycocalyx: Composition, functions, and visualization. Pflügers Arch. Eur. J. Physiol. 2007, 454, 345–359. [Google Scholar] [CrossRef]
- Krüger-Genge, A.; Blocki, A.; Franke, R.P.; Jung, F. Vascular endothelial cell biology: An update. Int. J. Mol. Sci. 2019, 20, 4411. [Google Scholar] [CrossRef] [PubMed]
- Schulze-Bauer, C.A.J.; Mörth, C.; Holzapfel, G.A. Passive biaxial mechanical response of aged human iliac arteries. J. Biomech. Eng. 2003, 125, 395–406. [Google Scholar] [CrossRef] [PubMed]
- Bukač, M.; Alber, M. Multi-component model of intramural hematoma. J. Biomech. 2017, 50, 42–49. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Aiello, V.D.; Gutierrez, P.S.; Chaves, M.J.F.; Lopes, A.A.B.; Higuchi, M.L.; Ramires, J.A.F. Morphology of the internal elastic lamina in arteries from pulmonary hypertensive patients: A confocal laser microscopy study. Mod. Pathol. 2003, 16, 411–416. [Google Scholar] [CrossRef]
- Nartsissov, Y.R. Application of a multicomponent model of convectional reaction-diffusion to description of glucose gradients in a neurovascular unit. Front. Physiol. 2022, 13, 843473. [Google Scholar] [CrossRef]
- Nartsissov, Y.R. The Effect of Flux Dysconnectivity Functions on Concentration Gradients Changes in a Multicomponent Model of Convectional Reaction—Diffusion by the Example of a Neurovascular Unit. Defect Diffus. Forum 2021, 413, 19–28. [Google Scholar] [CrossRef]
- Molla, M.M.; Paul, M.C. LES of non-Newtonian physiological blood flow in a model of arterial stenosis. Med. Eng. Phys. 2012, 34, 1079–1087. [Google Scholar] [CrossRef]
- Tamura, T. 5.05-Blood Flow Measurement. In Comprehensive Biomedical Physics; Brahme, A., Ed.; Elsevier: Oxford, UK, 2014; pp. 91–105. [Google Scholar]
- Ai, L.; Vafai, K. A coupling model for macromolecule transport in a stenosed arterial wall. Int. J. Heat Mass Transf. 2006, 49, 1568–1591. [Google Scholar] [CrossRef]
- Yang, N.; Vafai, K. Modeling of low-density lipoprotein (LDL) transport in the artery—Effects of hypertension. Int. J. Heat Mass Transf. 2006, 49, 850–867. [Google Scholar] [CrossRef]
- Chen, K.; Popel, A.S. Vascular and perivascular nitric oxide release and transport: Biochemical pathways of neuronal nitric oxide synthase (NOS1) and endothelial nitric oxide synthase (NOS3). Free. Radic. Biol. Med. 2007, 42, 811–822. [Google Scholar] [CrossRef][Green Version]
- Lamkin-Kennard, K.A.; Buerk, D.G.; Jaron, D. Interactions between NO and O2 in the microcirculation: A mathematical analysis. Microvasc. Res. 2004, 68, 38–50. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, Z.; Zhao, P.; Fan, Z.; Sun, A.; Zhan, F.; Fan, Y.; Deng, X. Nitric oxide transport in normal human thoracic aorta:Effects of hemodynamics and nitric oxide scavengers. PLoS ONE 2014, 9, e112395. [Google Scholar] [CrossRef]
- El-Farra, N.H.; Christofides, P.D.; Liao, J.C. Analysis of nitric oxide consumption by erythrocytes in blood vessels using a distributed multicellular model. Ann. Biomed. Eng. 2003, 31, 294–309. [Google Scholar] [CrossRef] [PubMed]
- Tsoukias, M.N.; Popel, A.S. A model of nitric oxide capillary exchange. Microcirculation 2003, 10, 479–495. [Google Scholar] [CrossRef]
- Haselden, W.D.; Kedarasetti, R.T.; Drew, P.J. Spatial and temporal patterns of nitric oxide diffusion and degradation drive emergent cerebrovascular dynamics. PLoS Comput. Biol. 2020, 16, e1008069. [Google Scholar] [CrossRef]
- Sriram, K.; Vázquez, B.Y.S.; Yalcin, O.; Johnson, P.C.; Intaglietta, M.; Tartakovsky, D.M. The effect of small changes in hematocrit on nitric oxide transport in arterioles. Antioxid. Redox Signal. 2011, 14, 175–185. [Google Scholar] [CrossRef]
- Chen, X.; Jaron, D.; Barbee, K.A.; Buerk, D.G. The influence of radial RBC distribution, blood velocity profiles, and glycocalyx on coupled NO/O2 transport. J. Appl. Physiol. 2006, 100, 482–492. [Google Scholar] [CrossRef]
- Vaughn, M.W.; Kuo, L.; Liao, J.C. Estimation of nitric oxide production and reaction rates in tissue by use of a mathematical model. Am. J. Physiol. 1998, 274, H2163–H2176. [Google Scholar]
- Hall, J.E.; Guyton, A.C. Guyton and Hall Textbook of Medical Physiology, 11th ed.; Elsevier: Amsterdam, The Netherlands, 2012; p. 1112. [Google Scholar]
- Tarbell, J.M.; Cancel, L.M. The glycocalyx and its significance in human medicine. J. Intern. Med. 2016, 280, 97–113. [Google Scholar] [CrossRef]
- Juffer, P.; Bakker, A.D.; Klein-Nulend, J.; Jaspers, R.T. Mechanical Loading by Fluid Shear Stress of Myotube Glycocalyx Stimulates Growth Factor Expression and Nitric Oxide Production. Cell Biochem. Biophys. 2014, 69, 411–419. [Google Scholar] [CrossRef]
- Jacob, M.; Rehm, M.; Loetsch, M.; Paul, J.O.; Bruegger, D.; Welsch, U.; Conzen, P.; Becker, B.F. The endothelial glycocalyx prefers albumin for evoking shear stress-induced, nitric oxide-mediated coronary dilatation. J. Vasc. Res. 2007, 44, 435–443. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Liu, H.; Yue, Y.; Wu, Q.; Jiang, W.; Qiu, Y.; Zeng, Y. Anisodamine Hydrobromide Protects Glycocalyx and Against the Lipopolysaccharide-Induced Increases in Microvascular Endothelial Layer Permeability and Nitric Oxide Production. Cardiovasc. Eng. Technol. 2021, 12, 91–100. [Google Scholar] [CrossRef]
- Kang, H.; Wu, C.; Qu, Y.; Gao, M.; Zhang, W.; Sun, A.; Deng, X. Adaptation of glycocalyx, nitric oxide synthase expression and vascular cell apoptosis in conduit arteries of tail-suspended rats. Clin. Exp. Pharmacol. Physiol. 2019, 46, 1013–1021. [Google Scholar] [CrossRef] [PubMed]
- Kurzelewski, M.; Czarnowska, E.; Berȩsewicz, A. Superoxide-and nitric oxide-derived species mediate endothelial dysfunction, endothelial glycocalyx disruption, and enhanced neutrophil adhesion in the post-ischemic guinea-pig heart. J. Physiol. Pharmacol. 2005, 56, 163–178. [Google Scholar] [PubMed]
- Bruegger, D.; Rehm, M.; Jacob, M.; Chappell, D.; Stoeckelhuber, M.; Welsch, U.; Conzen, P.; Becker, B.F. Exogenous nitric oxide requires an endothelial glycocalyx to prevent postischemic coronary vascular leak in guinea pig hearts. Crit. Care 2008, 12, R73. [Google Scholar] [CrossRef] [PubMed]
- Simon-Walker, R.; Romero, R.; Staver, J.M.; Zang, Y.; Reynolds, M.M.; Popat, K.C.; Kipper, M.J. Glycocalyx-inspired nitric oxide-releasing surfaces reduce platelet adhesion and activation on titanium. ACS Biomater. Sci. Eng. 2017, 3, 68–77. [Google Scholar] [CrossRef]
- Lyu, N.; Du, Z.; Qiu, H.; Gao, P.; Yao, Q.; Xiong, K.; Tu, Q.; Li, X.; Chen, B.; Wang, M.; et al. Mimicking the Nitric Oxide-Releasing and Glycocalyx Functions of Endothelium on Vascular Stent Surfaces. Adv. Sci. 2020, 7, 2002330. [Google Scholar] [CrossRef]
- Dragovich, M.A.; Chester, D.; Fu, B.M.; Wu, C.; Xu, Y.; Goligorsky, M.S.; Zhang, X.F. Mechanotransduction of the endothelial glycocalyx mediates nitric oxide production through activation of TRP channels. Am. J. Physiol. Cell Physiol. 2016, 311, C846–C853. [Google Scholar] [CrossRef]
- Kong, X.; Chen, L.; Ye, P.; Wang, Z.; Zhang, J.; Ye, F.; Chen, S. The role of HYAL2 in LSS-induced glycocalyx impairment and the PKA-mediated decrease in eNOS—Ser-633 phosphorylation and nitric oxide production. Mol. Biol. Cell 2016, 27, 3972–3979. [Google Scholar] [CrossRef]
- Kumagai, R.; Lu, X.; Kassab, G.S. Role of glycocalyx in flow-induced production of nitric oxide and reactive oxygen species. Free Radic. Biol. Med. 2009, 47, 600–607. [Google Scholar] [CrossRef]
- Prosi, M.; Zunino, P.; Perktold, K.; Quarteroni, A. Mathematical and numerical models for transfer of low-density lipoproteins through the arterial walls: A new methodology for the model set up with applications to the study of disturbed lumenal flow. J. Biomech. 2005, 38, 903–917. [Google Scholar] [CrossRef] [PubMed]
- Briones, A.; Gonzalez-Granado, J.; Somoza, B.; Giraldo, J.; Daly, C.; Vila, E.; González, M.C.; McGrath, J.C.; Arribas, S. Role of Elastin in Spontaneously Hypertensive Rat Small Mesenteric Artery Remodelling. J. Physiol. 2003, 552, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Masuda, H.; Zhuang, Y.-J.; Singh, T.M.; Kawamura, K.; Murakami, M.; Zarins, C.K.; Glagov, S. Adaptive Remodeling of Internal Elastic Lamina and Endothelial Lining During Flow-Induced Arterial Enlargement. Arterioscler. Thromb. Vasc. Biol. 1999, 19, 2298–2307. [Google Scholar] [CrossRef] [PubMed]
- Figueroa, X.F.; Lillo, M.A.; Gaete, P.S.; Riquelme, M.A.; Sáez, J.C. Diffusion of nitric oxide across cell membranes of the vascular wall requires specific connexin-based channels. Neuropharmacology 2013, 75, 471–478. [Google Scholar] [CrossRef]
- Seraya, I.P.; Nartsissov, Y.R. Theoretical approach to description of time-dependent nitric oxide effects in the vasculature. Mol. Biol. Rep. 2002, 29, 151–155. [Google Scholar] [CrossRef]
- Seraya, I.P.; Nartsissov, Y.R.; Brown, G.C. Mathematical modeling of nonstationary spatial nitric oxide gradients in vascular smooth muscle. Biophysics 2003, 48, 82–86. [Google Scholar]
- Horst, B.G.; Marletta, M.A. Physiological activation and deactivation of soluble guanylate cyclase. Nitric Oxide Biol. Chem. 2018, 77, 65–74. [Google Scholar] [CrossRef]
- Wood, K.C.; Batchelor, A.M.; Bartus, K.; Harris, K.L.; Garthwaite, G.; Vernon, J.; Garthwaite, J. Picomolar nitric oxide signals from central neurons recorded using ultrasensitive detector cells. J. Biol. Chem. 2011, 286, 43172–43181. [Google Scholar] [CrossRef]
- Manoury, B.; Montiel, V.; Balligand, J.-L. Nitric oxide synthase in post-ischaemic remodelling: New pathways and mechanisms. Cardiovasc. Res. 2012, 94, 304–315. [Google Scholar] [CrossRef][Green Version]
- Chen, K.; Pittman, R.N.; Popel, A.S. Nitric oxide in the vasculature: Where does it come from and where does it go? A quantitative perspective. Antioxid. Redox Signal. 2008, 10, 1185–1198. [Google Scholar] [CrossRef]

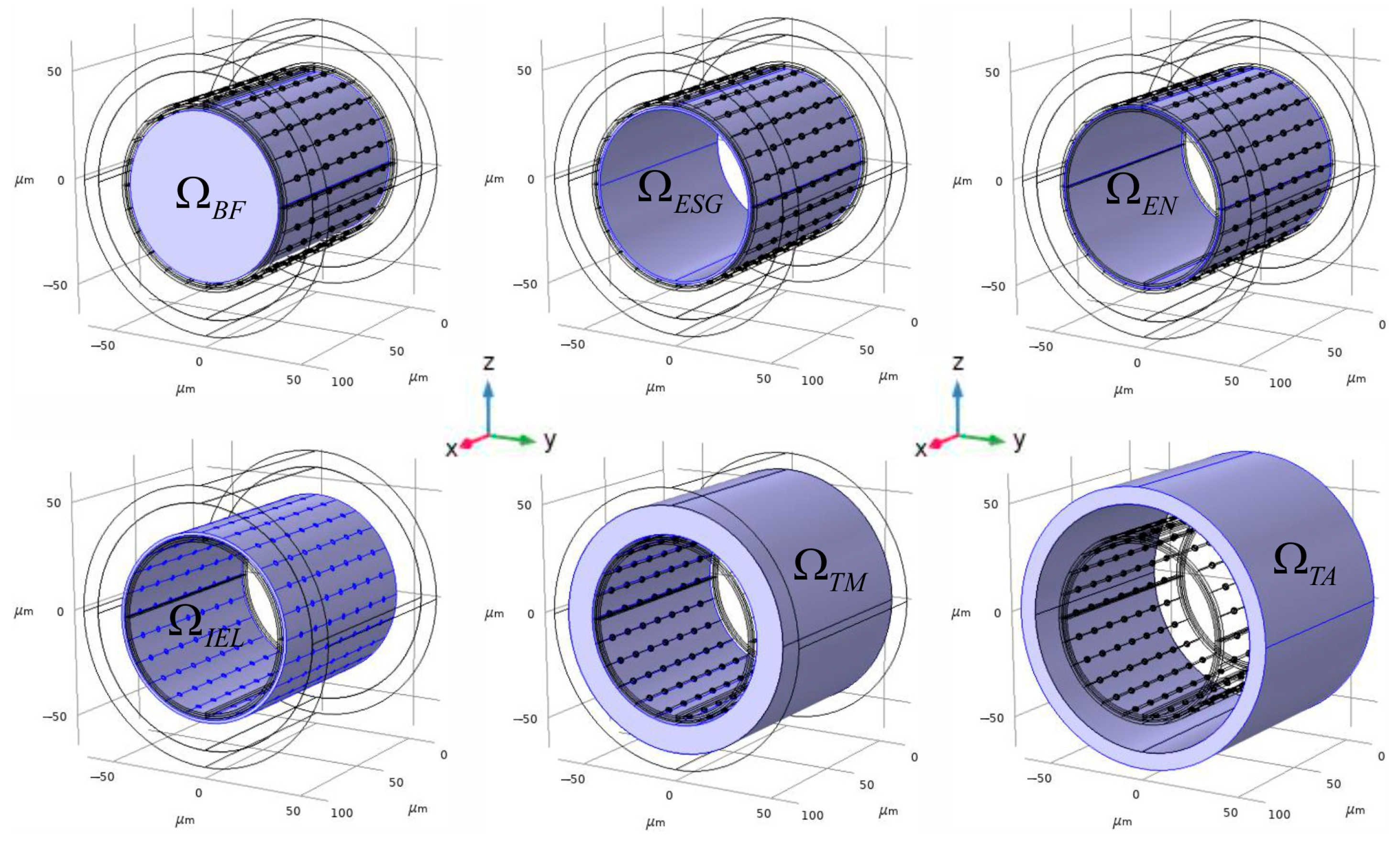
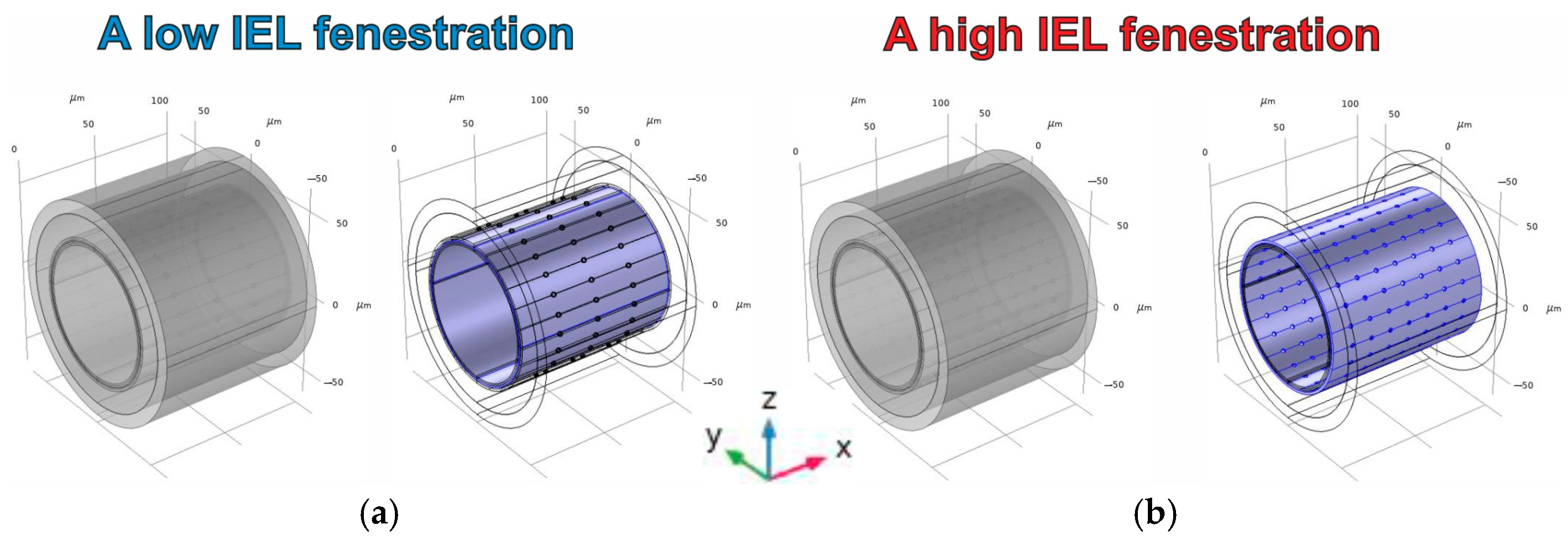
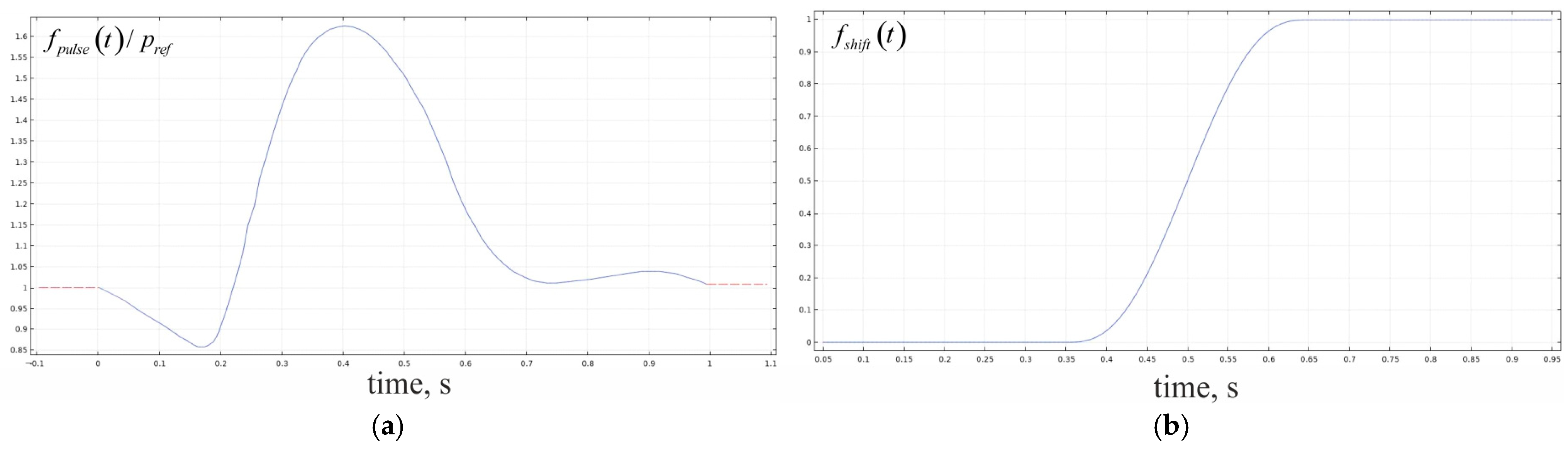
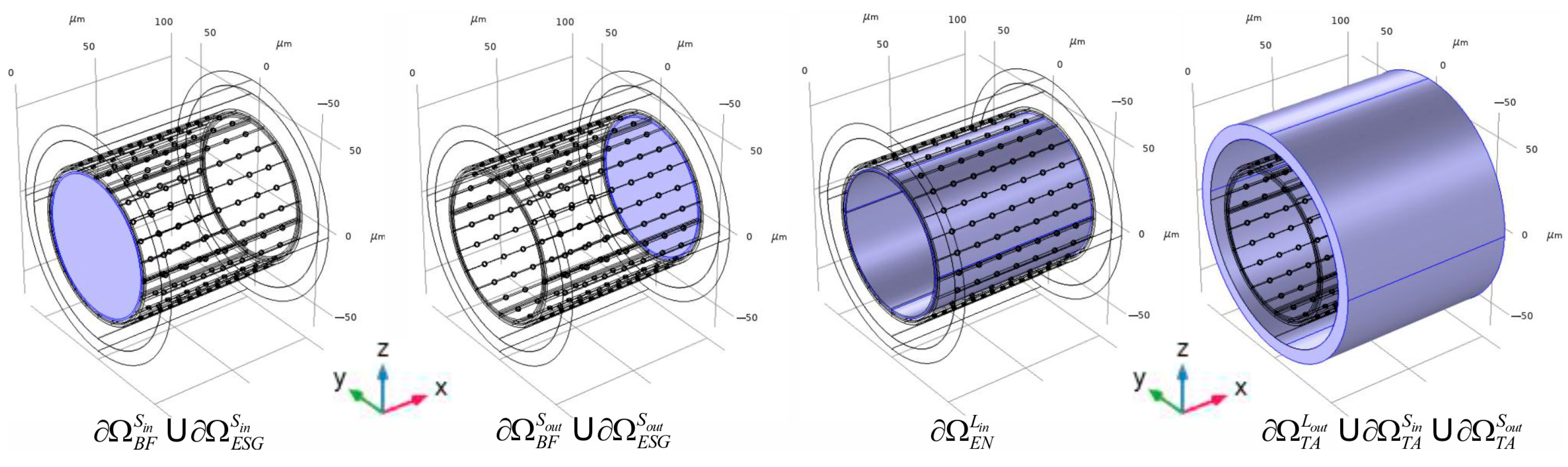



| Geometrical Parameter | Value (μm) | Literature and Comments |
|---|---|---|
| 100 | [20] 1 | |
| 40 | [20] 2 | |
| 51.3 | [21] 3 | |
| 1 | [13,22] | |
| 1 | [23] | |
| 10.39 | [24,25] 4 | |
| 1.38 | [26] | |
| 40.78 | [24,25] | |
| 24.79 | [24,25] | |
| 2.8 | [14] | |
| 5.6 | [14] |
| Structure | Value | Domains and Surfaces |
|---|---|---|
| A blood stream | ||
| Volume | 477,630.0 μm3 | |
| Surface area | 34,054.0 μm2 | |
| ESG | ||
| Volume | 24,821.0 μm3 | |
| Surface area | 50,128.0 μm2 | |
| The endothelium | ||
| Volume | 25,437.0 μm3 | |
| Surface area | 51,397.0 μm2 | |
| IEL | ||
| Volume | 36,920.0 μm3 | |
| Surface area | 52,717.0 μm2 | |
| Pores (a low IEL fenestration) | ||
| Volume | 557.19 μm3 | 1 |
| Surface area | 1539 μm2 | |
| Pores (a high IEL fenestration) | ||
| Volume | 1300.1 μm3 | The designations are the same as for a low IEL fenestration |
| Surface area | 3591.1 μm2 | - |
| The tunica media | ||
| Volume | 405,440.0 μm3 | |
| Surface area | 70,644.0 μm2 | |
| The tunica adventitia | ||
| Volume | 296,200.0 μm3 | |
| Surface area | 81,648.0 μm2 |
| Parameter | Value | Literature and Comments |
|---|---|---|
| 10,666 Pa | [30] | |
| 10,661 Pa | minus shift in pressure according to Poiseuille’s law | |
| 3.875 Pa | This value is calculated according to Poiseuille’s law for the minimal blood flow velocity | |
| 5.99 Pa | The same calculation as in a previous row, but it has been performed for the maximal blood flow velocity | |
| 1.6 | An empiric coefficient | |
| 2.6 | An empiric coefficient | |
| 2.7 | An empiric coefficient | |
| 3999.7 Pa | [31] | |
| 0.72 × 10−3 g/(mm∙s) | [32] | |
| 4.32 × 10−15 mm2 | [32] | |
| 2.00 × 10−10 mm2 | [32] | |
| 4.392 × 10−13 mm2 | [32] | |
| 2.00 × 10−12 mm2 | [32] | |
| 5.061 × 10−11 mm2 | The average value |
| Parameter | Value | Literature and Comments |
|---|---|---|
| 3.3 × 10−5 cm2/s | [37,38] | |
| 3.3 × 10−5 cm2/s | The assumed value 1 | |
| 1.65 × 10−5 cm2/s | [39] | |
| 3.3 × 10−6 cm2/s | [40] | |
| 3.18 × 10−11 cm2/s | [31] | |
| 0.01 1/s | [34,41] | |
| 0.05 1/(μM∙s) | [36,41] | |
| 1230 1/s | [33] | |
| 150 μM/s | [35] | |
| 2.4 Pa | [35] | |
| 1 or 5.46 | An empiric coefficient 2 |
| Meshes | Domain Elements | Boundary Elements | Edge Elements |
|---|---|---|---|
| Mesh #1 * | 9,948,439 | 1,361,050 | 19,861 |
| Mesh #2 | 602,764 | 130,592 | 8118 |
| Mesh #3 | 10,361,539 | 1,407,458 | 26,664 |
| Mesh #4 | 743,741 | 161,988 | 12,210 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nartsissov, Y.R.; Seraya, I.P. A Theoretical Analysis of the Effects That the Glycocalyx and the Internal Elastic Lamina Have on Nitric Oxide Concentration Gradients in the Arterial Wall. Antioxidants 2025, 14, 747. https://doi.org/10.3390/antiox14060747
Nartsissov YR, Seraya IP. A Theoretical Analysis of the Effects That the Glycocalyx and the Internal Elastic Lamina Have on Nitric Oxide Concentration Gradients in the Arterial Wall. Antioxidants. 2025; 14(6):747. https://doi.org/10.3390/antiox14060747
Chicago/Turabian StyleNartsissov, Yaroslav R., and Irena P. Seraya. 2025. "A Theoretical Analysis of the Effects That the Glycocalyx and the Internal Elastic Lamina Have on Nitric Oxide Concentration Gradients in the Arterial Wall" Antioxidants 14, no. 6: 747. https://doi.org/10.3390/antiox14060747
APA StyleNartsissov, Y. R., & Seraya, I. P. (2025). A Theoretical Analysis of the Effects That the Glycocalyx and the Internal Elastic Lamina Have on Nitric Oxide Concentration Gradients in the Arterial Wall. Antioxidants, 14(6), 747. https://doi.org/10.3390/antiox14060747









