1. Introduction
There is no question that speech perception is a multimodal process (see [
1,
2] for reviews). In face-to-face conversations, the listener receives both visual information from the speaker’s face (e.g., their lips, teeth, tongue, and non-mouth facial features) and acoustic signals from the speaker’s voice. In order to use these two sources of information, listeners must combine auditory and visual cues into an integrated percept during spoken language comprehension. A number of studies show that the reliable co-occurrence of synchronous and highly redundant visual and auditory cues supports this ability, leading to accurate speech comprehension by adults [
3,
4], especially in cases where the auditory signal is degraded due to background noise [
5,
6,
7,
8,
9]. Mismatching auditory and visual information also influences speech perception, as shown in the McGurk effect [
10,
11]: listening to the spoken syllable
/ba/ while simultaneously watching the visual movements for
/ga/ often results in the illusory perception of
/da/. The McGurk effect provides clear evidence that visual information is involved in speech perception even when the auditory signal is perfectly intelligible [
12].
How does the ability to perceive a unified audiovisual percept emerge over the course of development? Are the same developmental processes involved in infants’ acquisition of phonological categories via acoustic cues used for acquisition of categories based on visual cues? In this paper, we aim to address these questions by presenting a model of phonetic category acquisition that is trained on data derived from phonetic analyses of visual and auditory speech cues for stop consonants. The model uses the same statistical learning processes available to human infants; thus, in principle, it allows us to determine whether such processes are sufficient for the acquisition of integrated audiovisual percepts.
1.1. Audiovisual Speech Development in Infants
Despite the fact that multimodal inputs benefit speech perception in adults, it is not clear that integrated audiovisual inputs equally benefit infants’ speech perception [
13] or whether infants even form integrated audiovisual perceptual representations. This does not mean that infants do not use visual speech cues; indeed, research shows that infants can detect characteristics of both visual and auditory speech even before they can speak [
14]. Infants can also detect audiovisual temporal asynchrony in isolated syllables and continuous speech streams [
15,
16] and prefer to listen to fluent, synchronized speech [
17]. Thus, infants’ are able to track the co-occurrence of temporally-aligned cues, an ability that may provide a mechanism for later development of integrated perceptual representations.
There is some evidence that infants can detect cases where phonemic information is congruent between faces and voices. In several studies, infants were habituated with two side-by-side faces silently mouthing different phonemes that are reliably distinguished by visual cues, such as
/b/ and
/d/. The infants were then presented with a simultaneous auditory stimulus that matched one of the faces and their looking time to the two faces was measured. Four- to five-month-old [
18,
19,
20], two-month old [
21], and even newborn [
22] infants consistently look longer at the matching face than the mismatched face, providing evidence that infants can rapidly learn to track these phonological co-occurrences.
Research is more mixed as to when infants can detect cases where fluent (i.e., continuous) speech information matches between faces and voices. Using a similar paradigm to that described above, one study found that four- to eight-month-old infants did not show a preference for a face that was temporally synchronized and matched with the articulation of an auditory stimulus, whereas 12- to 14-month-olds did show such a preference [
23]. However, a different study found that eight-month-old infants did show a preference for congruent speech patterns across modalities, even with a visual signal that consisted only of animated markers on a talking face and with a low-pass filtered auditory signal [
24]. A similar study was done with newborns, who also showed a preference for the matching face and voice [
25]. Interestingly, infants can also match a multi-syllable auditory signal with the correct articulating face when the sound is sine wave speech (SWS, see [
26]), suggesting that infants may be relying on cues that are not necessarily phonetic to match auditory and visual speech [
27].
Studies examining the McGurk effect in infants provide even more ambiguous results. Several studies with infants as young as four months found that their pattern of illusory phoneme detection was similar to that of adults [
13,
28]. However, other studies have found different results in male and female infants depending on the experimental design [
29,
30], showing that the effect is not as strong or consistent as in adults. Therefore, the literature suggests that infants are sensitive to cases of temporal and phonological audiovisual synchrony, suggesting a possible innate audiovisual integration skill. However, it is not clear that this sensitivity assists them with the development and mastery of speech perception [
31], as it does for adults.
1.2. Audiovisual Speech Development in Older Children
Research with preschoolers and school-age children provides further evidence that children do not yet fully integrate multi-modal speech cues, and provides insights into the developmental time-course of this process. Children weight visual cues less, relative to adults, in speech categorization tasks involving cues from both modalities [
32]. In addition, a majority of research using McGurk-like paradigms (i.e., comparisons between congruent and incongruent audiovisual stimuli) show that children rely less on visual cues than adults. A number of studies find that the influence of the illusory phoneme varies as a direct function of age, with children aged four-to nine-years-old largely choosing a response consistent with the auditory stimulus and children ages 10–18 more often choosing the illusory phoneme (i.e., the response consistent with the visual stimulus; [
33,
34,
35,
36,
37]). This developmental time-course has also been observed in a recent event-related potential (ERP) study [
38]. In adult subjects, the amplitude of the N1 and P2 ERP components is reduced in the presence of incongruent audiovisual stimuli, relative to auditory-only stimuli, suggesting that visual speech information affects auditory perceptual representations. Knowland et al. [
38] found that this amplitude reduction for audiovisual stimuli emerges over development, occurring around the same age as corresponding behavioral effects for audiovisual speech. Research also shows that younger children do not benefit as much as adults from the addition of visual cues in noisy environments. Studies using noise-vocoded sentences [
39] and low auditory signal-to-noise (SNR) ratios [
31,
40,
41] have found that children do not fully utilize visual speech cues to enhance speech perception when the auditory signal is degraded.
Several possible explanations for the lack of integration have been offered. One explanation is that young children (i.e., four- to six-year-olds) have poor lip-reading ability. Indeed, one study found a positive correlation between lip-reading ability and the size of the visual contribution to audiovisual speech perception [
32]. Another explanation may be that young children (i.e., three- to five-year-olds) lack the necessary experience correctly producing the phoneme sounds in order to integrate this information during comprehension. In support of this explanation, one study found that preschool children who make phoneme articulation errors for consonant confusions are less influenced by visual cues than those children who correctly produce the consonants [
42]. A third possibility is that audiovisual speech allows for predictive coding (because the visual information normally arrives first), which can speed up processing in adult subjects [
43]; however, it is unclear how the ability to use this information might change over development.
However, not all results suggest the same developmental pattern. One study found a significant influence of visual speech in four year-olds and 10- to 14-year-olds, but not five- to nine-year-olds, proposing a temporary loss in sensitivity due to a reorganization of phonological knowledge during early school years [
44]. In contrast, other studies have shown an influence of visual speech in children as young as six-year-olds on detection, discrimination, and recognition audiovisual speech tasks [
45].
In general, the evidence reported here seems to suggest that although infants show early sensitivity to both auditory and visual speech information, the accuracy of using and combining information from multiple modalities to acquire phonological categories improves throughout childhood [
12,
38]. In addition, data on the developmental time-course of this process suggest that, in general, children rely more heavily on auditory speech cues than visual ones, relative to adults [
32]. Our goal here is to provide a mechanism that can explain how unified percepts are formed over development, and why these developmental patterns emerge.
1.3. Acquisition of Auditory Phonological Categories
There is an extensive literature on children’s acquisition of phonological distinctions in the auditory domain that may help shed light on the processes involved in the acquisition of multimodal phonological categories. Classic studies on infant speech sound discrimination [
46,
47] suggest differences between infant and adult speech sound discrimination. In some cases this manifests as increased sensitivity to non-native speech sound contrasts (e.g., for stop consonants; [
47]), while in other cases infants show decreased sensitivity to acoustic differences (e.g., for fricative distinctions; [
48]). Thus, there is evidence for a perceptual reorganization process over development; over the first year or two, infants learn phonological representations that are specific to their native language.
How do infants do this? Consider that any learning mechanism that seeks to explain the process of phonological acquisition faces a significant challenge: infants appear to learn their native-language speech sound categories without explicit feedback about how acoustic cues map onto different phonemes. They must sort out which acoustic cues are used in their native language and how many phoneme categories their language has along any given phonological feature dimension (e.g., English has two voicing categories, while Thai has three, [
49]). Infants also process input stochastically, updating their representations on a trial-by-trial basis.
These factors point towards a need for an
unsupervised learning process that allows for the gradual acquisition of speech sound categories over time. Statistical learning provides one possible mechanism for this. For example, previous work has demonstrated that infants can track the distributional statistics of phoneme transitions (i.e., the probability that a phoneme occurs within or at the end of a word) and can use this information to segment words [
50] in a discrimination task.
The same process can be applied to the acquisition of phonological categories based on the distributional statistics of acoustic-phonetic cues. For example, English has a two-way voicing distinction between unaspirated (typically referred to as “voiced”) and aspirated (typically referred to as “voiceless”) stop consonants. Word-initially, this distinction is primarily signaled by differences in voice onset time (VOT), a reliable cue that is used to mark voicing distinctions in many languages. The distribution of VOT values in English tends to form two clusters, one corresponding to voiced and one to voiceless consonants. Thus, the distributional statistics for VOT contain information needed to map specific cue-values onto phonemes.
Infants appear to be sensitive to this statistical information [
51]. Infants exposed to speech sounds that form a bimodal distribution (reflecting a two-category phonological distinction) will discriminate pairs of sounds that correspond to the two categories, whereas infants exposed to a unimodal distribution (reflecting an acoustic cue that is not used to provide a meaningful contrast in the language) show poorer discrimination. This is true even though the overall likelihood of hearing the specific tokens is the same in both conditions. Thus, infants are able to track the distributional statistics of specific acoustic cues, which can then be used to acquire phonological categories.
McMurray et al. [
52] implemented this unsupervised statistical learning mechanism in a Gaussian mixture model (GMM) of speech development. This approach provides a learning mechanism that requires few assumptions about the knowledge available to infants, as it does not require the modeler to specify the number of phonological categories or their statistical properties
a priori, and it involves learning categories using the same iterative statistical learning procedure available to infants. In their simulations, McMurray et al. demonstrated that phoneme categories based on VOT distinctions can be learned via statistical learning and winner-take-all competition. On each training trial, the phoneme category with the highest likelihood for the current input is updated, thus eliminating unnecessary Gaussians and eventually converging on the appropriate two-category voicing distributions. The model successfully accounts for different developmental trajectories, showing both overgeneration-and-pruning effects and phonological enhancement effects observed in human infants [
47,
48].
1.4. Cue Weighting in Speech
This statistical learning approach has also been extended to the acquisition of multiple acoustic cues. The speech signal contains redundant cues that provide information about specific phonological contrasts [
53,
54,
55]. For example, Lisker [
55] lists 16 cues to word-medial voicing in English. Thus, we must also consider how multiple acoustic cues are combined over the course of development. This can be extended to the questions about combining auditory and visual speech cues as well.
A few studies have examined how children combine multiple acoustic cues and how their cue weights change over time. Data on fricative classification (
/f/ vs.
/θ/ and
/s/ vs.
/ʃ/ distinctions) suggests that infants initially weight dynamic acoustic cues (formant transitions) more than static spectral differences (mean frication frequency) [
56]. However, the relative weights of these cues may be specific to those phonemes, as different patterns emerge for the relative weight of temporal and spectral cues to stop consonant voicing (
/d/ vs.
/t/; [
57,
58]). In both cases, however, it is clear that children’s cue weights are not the same as adults’ weights, suggesting some process that involves a change in cue weights over the course of development. This observation is similar to the work described above showing that children tend to weight visual speech cues less than adults overall.
The computational modeling approach described above has also been applied to the problem of the acquisition of multiple acoustic cues. Toscano and McMurray [
59] extended the GMM introduced by McMurray et al. [
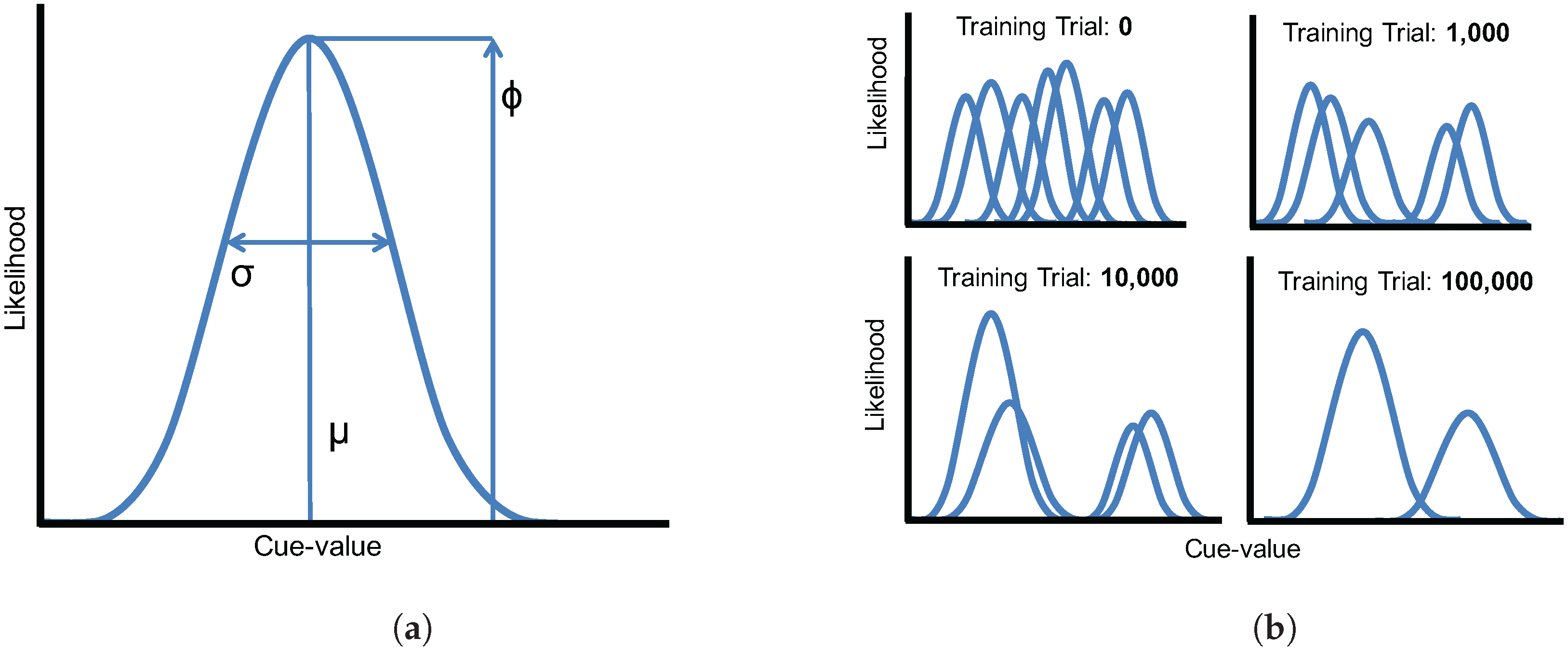
52] to allow the model to learn an arbitrary number of cues for any given phonological feature, combining them into a unified perceptual representation. In their simulations, they demonstrate that VOT and vowel length (VL, a secondary cue to voicing) are weighted approximately by their reliability. Weighting-by-reliability (an approach used in our model as well) derives from well-established effects in visual perception describing how observers combine cues to depth: cues are weighted inversely to the variance in the estimates they provide (i.e., cues that provide more consistent depth estimates are weighted higher). Thus, the weight of a cue can be described as the inverse of its variance,
where
σ is the standard deviation of the estimates provided by that cue. This metric can be applied to both multiple visual cues [
60] and cross-modal integration (i.e., combining visual and haptic cues; [
61]), and it describes an optimal method of weighting cues given their statistical reliability.
Although this approach works well for unimodal dimensions, it would not accurately describe cue reliability for a multimodal dimension where variability arises from naturally-occurring differences between category exemplars (as opposed to variability due to noise in the cue estimates, as in the models described above). The is the case for speech sounds, which are structured by phonological categories (e.g., voiced and voiceless VOT categories). If we ignore this category structure and apply Equation (
1), we will obtain a
lower cue weight for categories that are further spread apart, all other things being equal. This is precisely the opposite of how the metric should weight this cue. Toscano and McMurray [
59] present a different metric, implemented in a weighted Gaussian mixture model (WGMM), that applies the weighting-by-reliability principle to perceptual dimensions that contain a category structure, as acoustic and visual cues in speech do. For a two-way distinction (e.g.,
/b/ vs.
/d/), the cue weighting metric is
where
μ is the mean of each category,
σ is its standard deviation, and
ϕ is the category’s frequency of occurrence in the language (allowing the model to account for phoneme categories that are not equally likely).
m and
n correspond to values for the two phoneme categories. Thus, if the means of two categories are far apart, the cue dimension will be weighted higher; if the variances within each category are high, the cue will be weighted lower. Toscano and McMurray [
59] demonstrate that this cue weighing metric captures the way that listeners combine multiple acoustic cues in speech.
Critically, they also demonstrate that the developmental process matters. When cue weights are set strictly by their statistical reliability, the model underestimates the weight of the secondary cue (VL). However, when the model is allowed to learn the cue weights via an unsupervised statistical learning process, it arrives at category representations that more closely reflect those of adult listeners.
Other models describing acoustic cue-integration rely on similar principles [
62,
63,
64], and several models have been proposed to explain either perceptual integration more generally [
65] or audiovisual cue-integration in speech specifically [
66,
67,
68,
69]. Although previous audiovisual cue-integration models have not focused on describing the underlying developmental mechanisms, they still offer a number of insights.
Perhaps the most influential model in the audiovisual speech domain has been Massaro and colleagues’ fuzzy logical model of perception (FLMP) [
69], which extended the original implementation that was designed to handle multiple acoustic cues in speech [
62]. FLMP maps continuously-valued cues probabilistically onto phonological categories via a three-step process: (1) feature evaluation, the process of encoding features as initial perceptual representations; (2) prototype matching, which involves mapping feature-values onto stored category prototypes; and (3) pattern classification, which involves determining which prototype (category) best matches the input.
FLMP can also be fit to perceptual data from individual subjects performing audiovisual speech categorization tasks. While it provides a good fit to these data when cues are treated as independent [
69], as they are in the WGMM used here, there is debate about whether similar results can be achieved with fewer model parameters (e.g., in the early maximum likelihood estimation model; [
66]) or when cues are combined at a pre-categorization stage (as in the pre-labeling integration model; [
68]). Recent work has also aimed to incorporate the weighting-by-reliability perspective to explain audiovisual speech perception, taking the category structure of the acoustic and visual cue dimensions into account [
67], using a cue weighting metric similar to the one used in the WGMM (using the variance across the cue dimension, rather than the within-category variances, in the denominator). Overall, modeling work in audiovisual speech perception has generally supported the view that listeners combine cues probabilistically based on the amount of information provided by each cue. However, this work has not focused on describing the developmental mechanisms that give rise to these integrated percepts, which we plan to do here.
1.5. Approach
The main goal of the present study was to address two limitations of previous models: (a) previous audiovisual integration models have not sought to describe the developmental mechanisms that give rise to the changes in cue-weighting observed between children and adults (though they have sought to fit models to data from both children and adults; [
32]); and (b) previous cue integration models that do describe development (e.g., WGMM) [
59] have focused only on acoustic cues; they have not demonstrated that unsupervised statistical learning is sufficient to acquire these types of audiovisual representations.
Is it the case that listeners also use statistical learning for the complex problem of acquiring audiovisual speech categories, which require the learner to integrate information from multiple modalities? Can children learn to appropriately weight cues from different senses according to their reliability? Here, we ask whether WGMMs can be used to simulate the acquisition of phonological distinctions for voiced stop consonants (/b/, /d/, and /ɡ/) and capture the changes in cue weights for multiple auditory and visual cues observed over development.
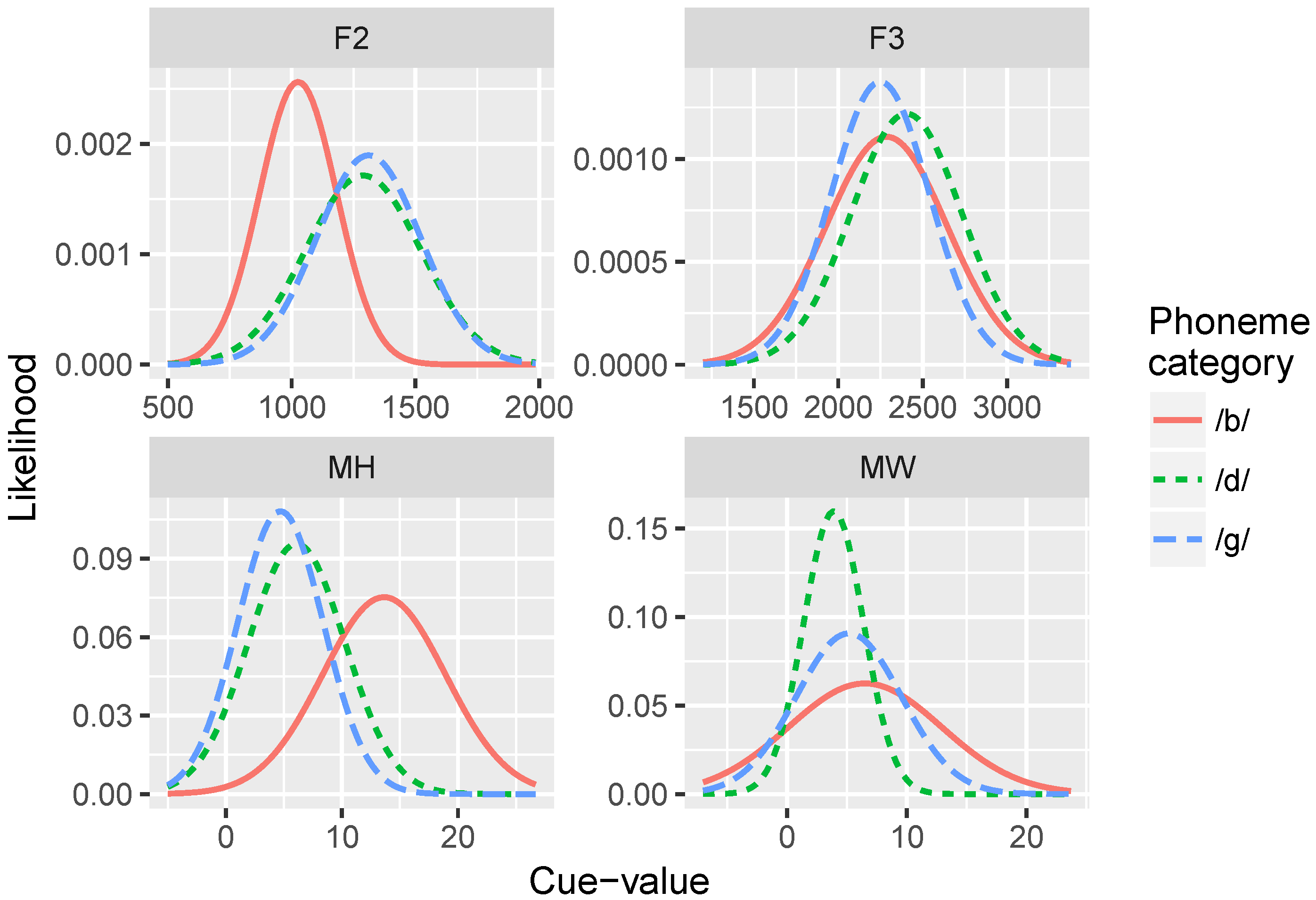
The data used in our simulations consists of distributions of acoustic and visual cue measurements from the Audio-Video Australian English Speech (AVOZES) data corpus [
70,
71] as reported in Goecke [
72]. The AVOZES corpus comprises 20 native speakers of Australian English (10 female and 10 male speakers) recorded producing phonemes using a non-intrusive 3D lip tracking algorithm. From the recordings, they extracted a number of auditory speech parameters (fundamental frequency F0, formant frequencies F1, F2, F3, and RMS energy) and visual speech parameters (mouth width, mouth height, protrusion of the upper lip, protrusion of the lower lip, and relative teeth count).
Our simulations examined four of these cues (two visual, and two acoustic) that we predicted would be the most reliable and uncorrelated with each other: (1) mouth width (
MW; defined as the 3D distance from lip corner to lip corner); (2) mouth height (
MH; 3D distance from the midpoint of upper lip to the midpoint of lower lip); (3) F2 onset (
F2), and F3 onset (
F3). F2 and F3 are canonical acoustic cues to place of articulation [
73], and MH and MW were predicted to be the most orthogonal to each other, given the visual cues in the AVOZES corpus (since they are measures of orthogonal dimensions in space). Although there are many more phonetic cues in speech for any given phonological dimension [
55], the subset of cues we use here are informative and approximate the categorization functions produced by human subjects, as evidenced by the identification curves produced by the model. In theory, we could add any number of cues to the simulations; the model should learn which cues are uninformative because their cue-weights should be near zero.
The purpose of our current approach was to simulate the developmental process of acquiring phonological categories from auditory and visual cues, asking whether simple statistical learning approaches are sufficient for learning multi-modal representations. Further, we use this information to explain audiovisual speech perception in adult perceivers, including cases where auditory and visual inputs are redundant and cases where the inputs are mismatched. Note that, unlike many of the previous studies aimed at modeling audiovisual cue-integration described above, our approach here is not to fit model parameters to specific subjects’ data, but rather to determine whether a model trained on speech input corresponding to what a human infant might hear will show the same developmental time-course and cue-weighting strategies as humans. This modeling approach is in the same spirit as connectionist simulations, where the goal is to uncover the underlying mechanisms that give rise to behavioral phenomena.
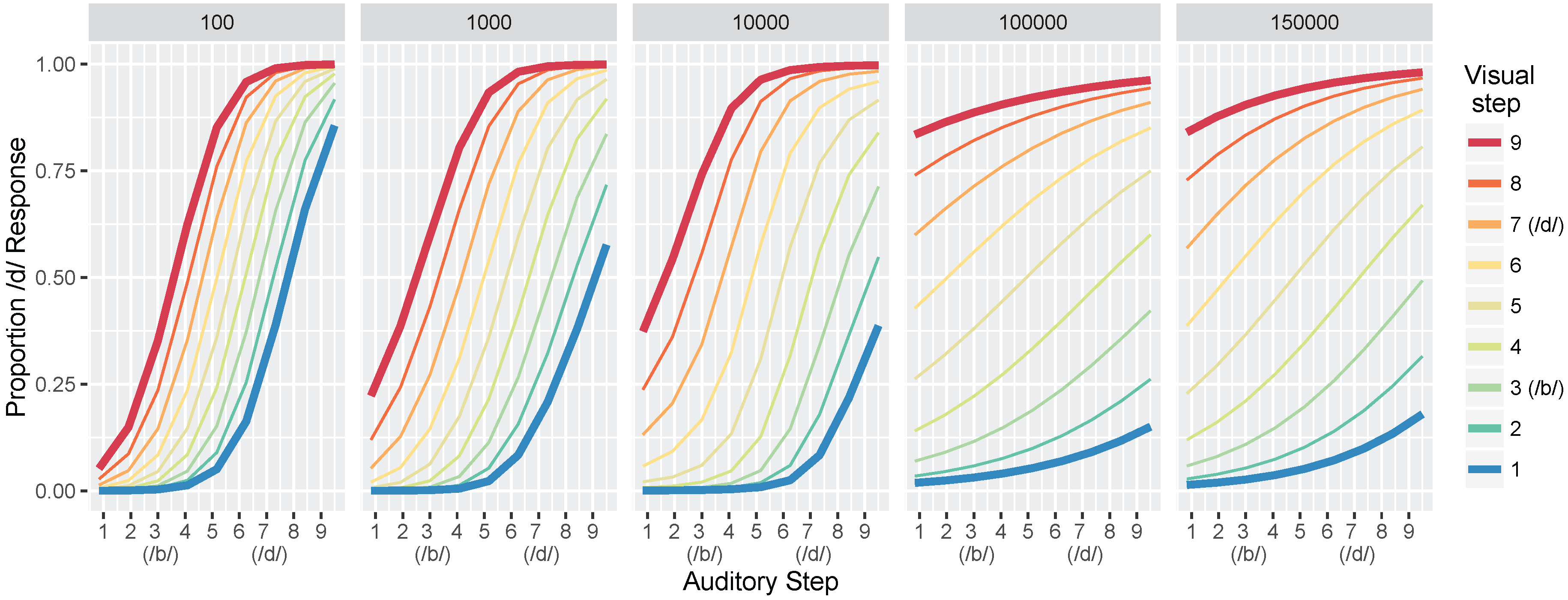
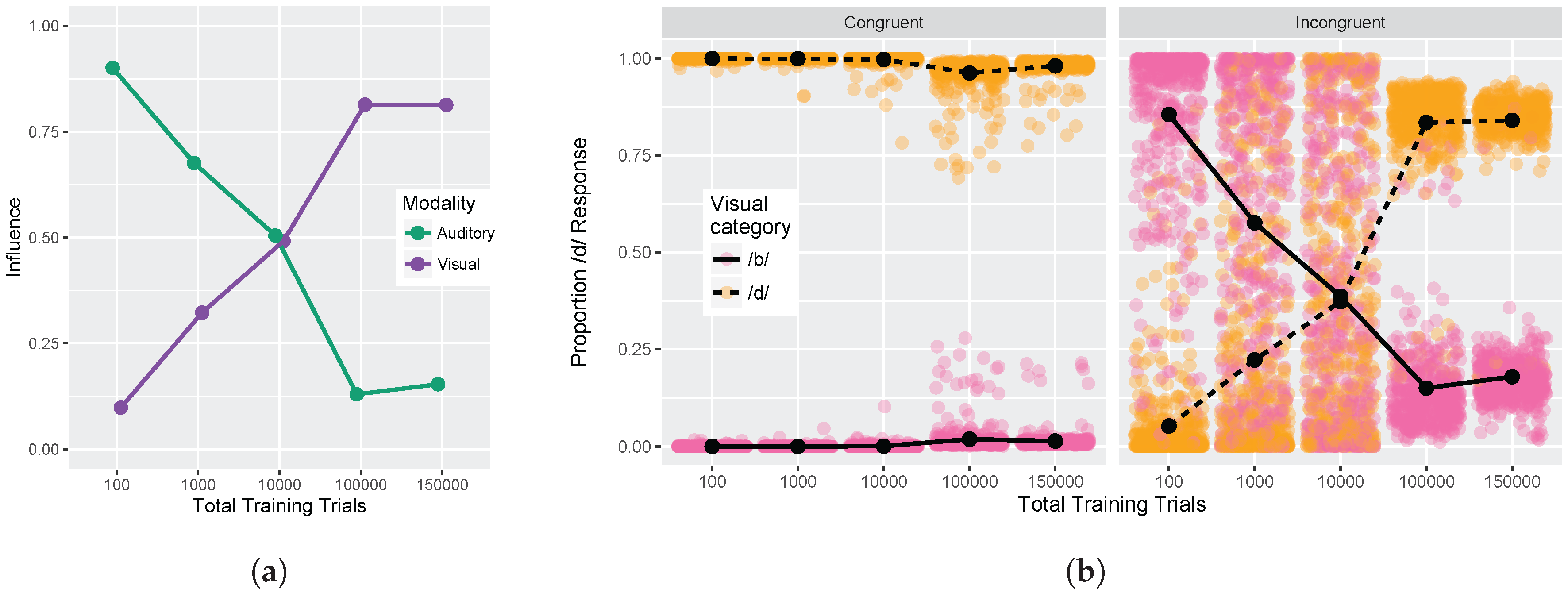
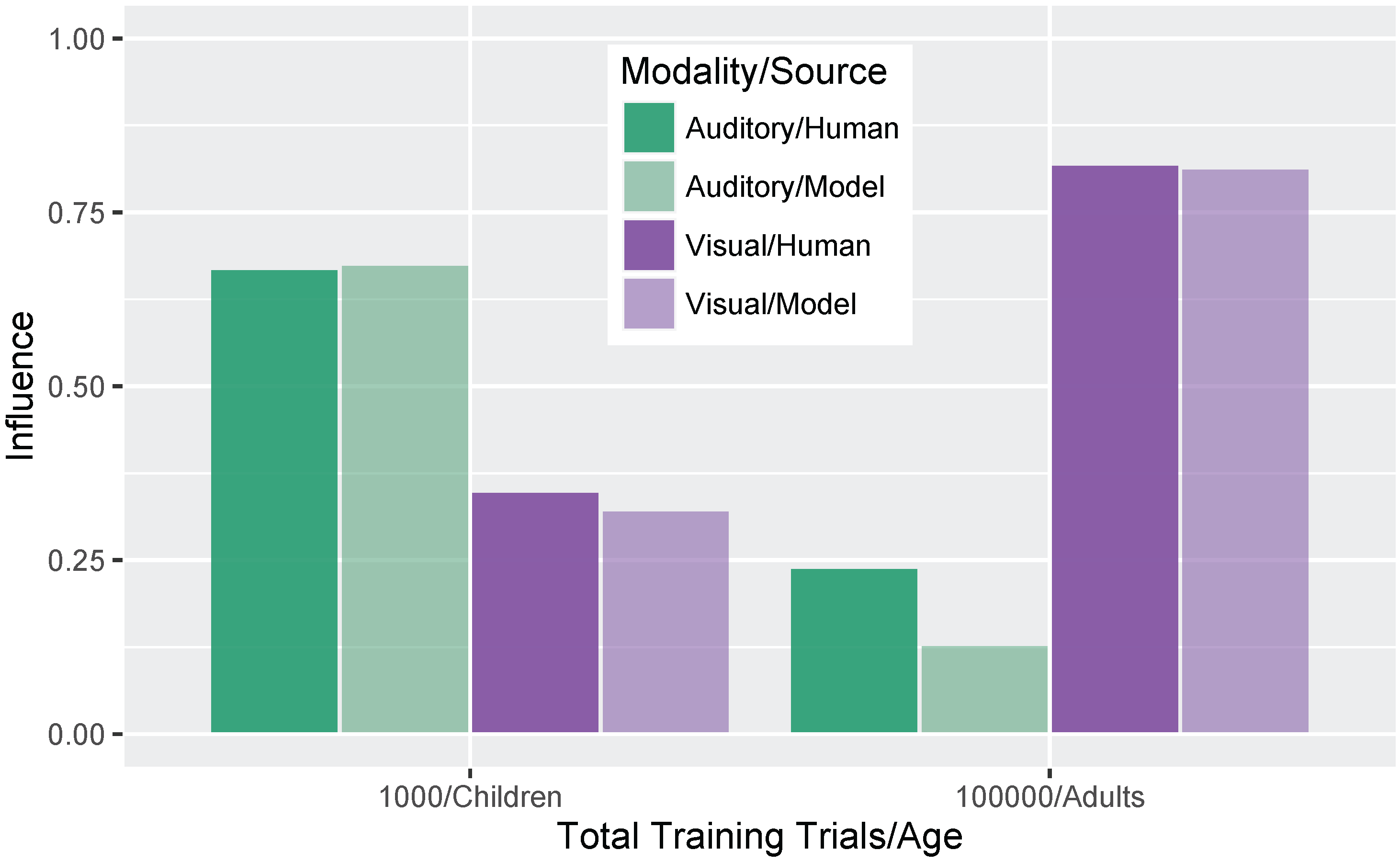
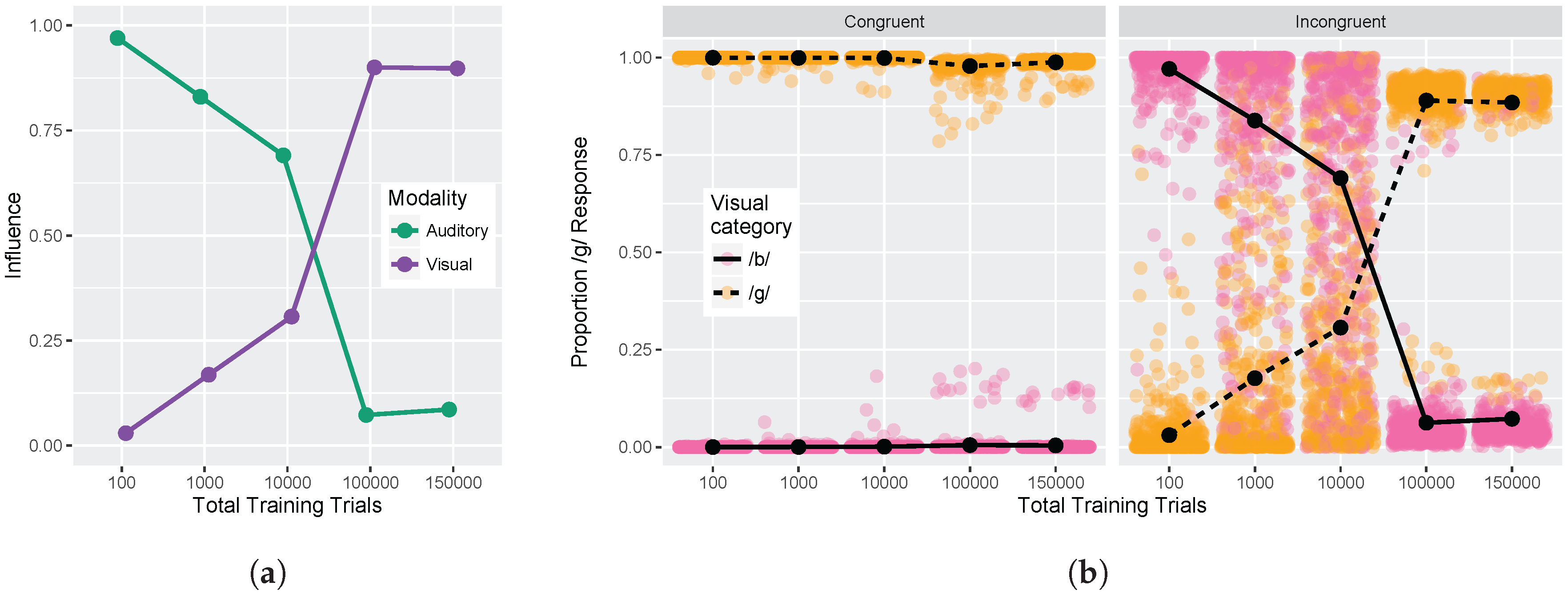
We conducted two sets of simulations with the WGMM trained on the four cues, testing the model at five different points during training. At each testing point during development, we measured the relative use of auditory and visual cues to see whether the model shows an increase in reliance on visual cues over the course of development (see
Figure 1a). This is similar to the approach used previously by Massaro and colleagues [
32,
35,
62] to examine changes in the proportion of
/b/ and
/d/ responses to audiovisual stimuli in a forced-choice experiment over the course of development. For children, the proportion of
/d/ responses is largely based on
auditory information. This is shown in schematic
Figure 1a (“Children” panel) by the closeness of red and blue lines. Additionally, each of the identification functions span from largely
/b/ to largely
/d/ responses across the auditory continuum. Later in development, the pattern changes, and the proportion of
/d/ responses is largely based on the
visual information. This is shown in
Figure 1a (“Adults” panel) by the spread of the red and blue lines. Additionally, individual identification functions no longer span the entire range of responses across the auditory continuum. We predict a similar pattern of developmental change for the model’s responses.
We also focused more closely on the differences between responses to congruent and incongruent audiovisual stimuli by examining the two endpoint steps from the auditory and visual continua. These proportions were derived from the full identification functions (
Figure 1a). The amount of
auditory influence when the modalities provide incongruent information is shown by the difference in response proportion between the endpoints of the auditory continuum for each visual phoneme, values of which are then averaged together:
where
is the auditory
/d/ paired with the visual
/b/; the same notation is used for the other stimulus combinations. The amount of
visual influence when the two modalities provide incongruent information is shown by the difference in response proportion between the visual phonemes at the two auditory continuum endpoints, values of which are then averaged together:
Given previous results [
32,
33,
34,
35,
36,
37], we predicted that the model should show that visual influence is small early in development and larger later in development, whereas auditory influence is large early in development and smaller later in development (see
Figure 1b).
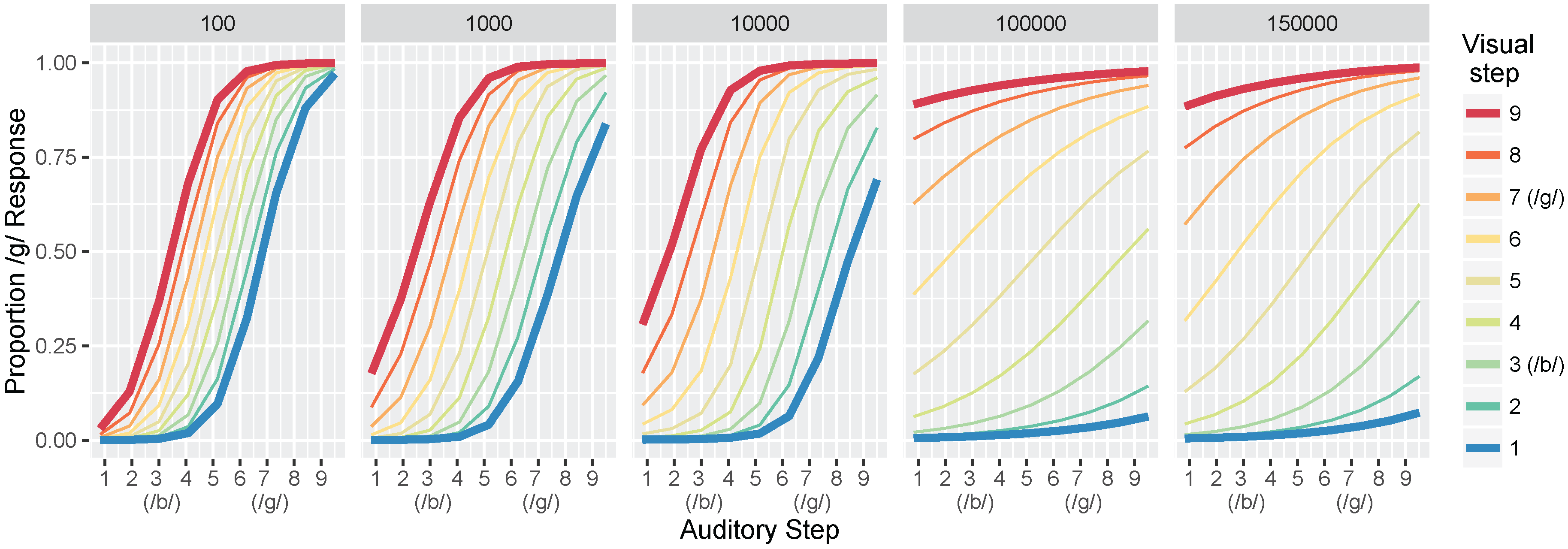
In Simulation 1, we examine the acquisition of /b/ vs. /d/ distinctions, and in Simulation 2, we examine /b/ vs. /ɡ/ distinctions. In both cases, the difference between the bilabial consonant and the other phoneme should be conveyed reliably by visual information in addition to being cued by auditory differences. Note that we did not train the model on all three phonemes simultaneously because the acoustic and visual cues used here do not reliably distinguish /d/ and /ɡ/ (see Discussion for further consideration of this point).
4. Discussion
We sought to investigate whether unsupervised, competitive, statistical learning mechanisms are sufficient for acquiring unified audiovisual perceptual representations. We also asked whether the model would show the same developmental trajectory as human listeners in terms of changes in its use of visual cue information (i.e., increased reliance of visual cues over the course of development), including changes in model responses to congruent and incongruent audiovisual stimuli.
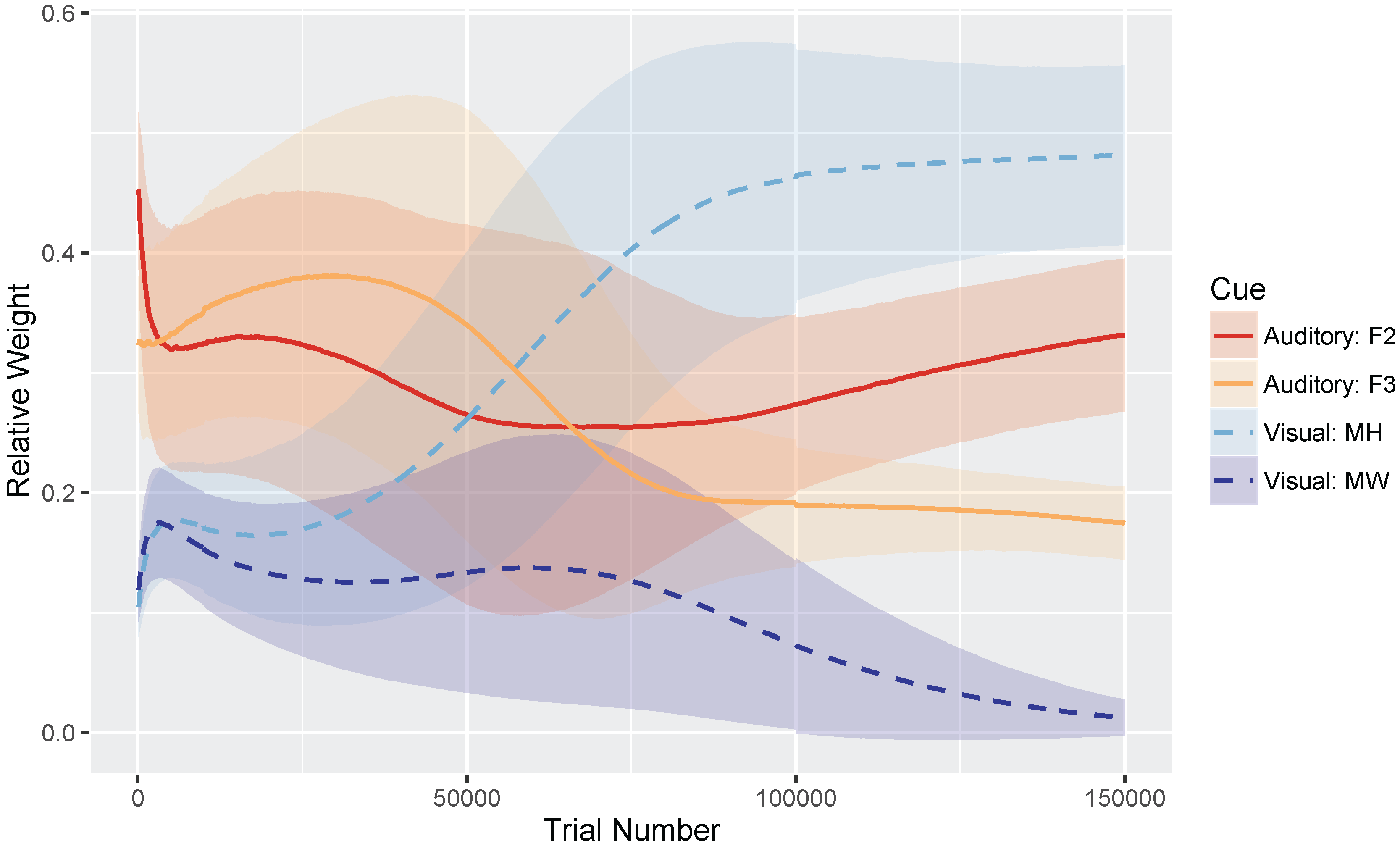
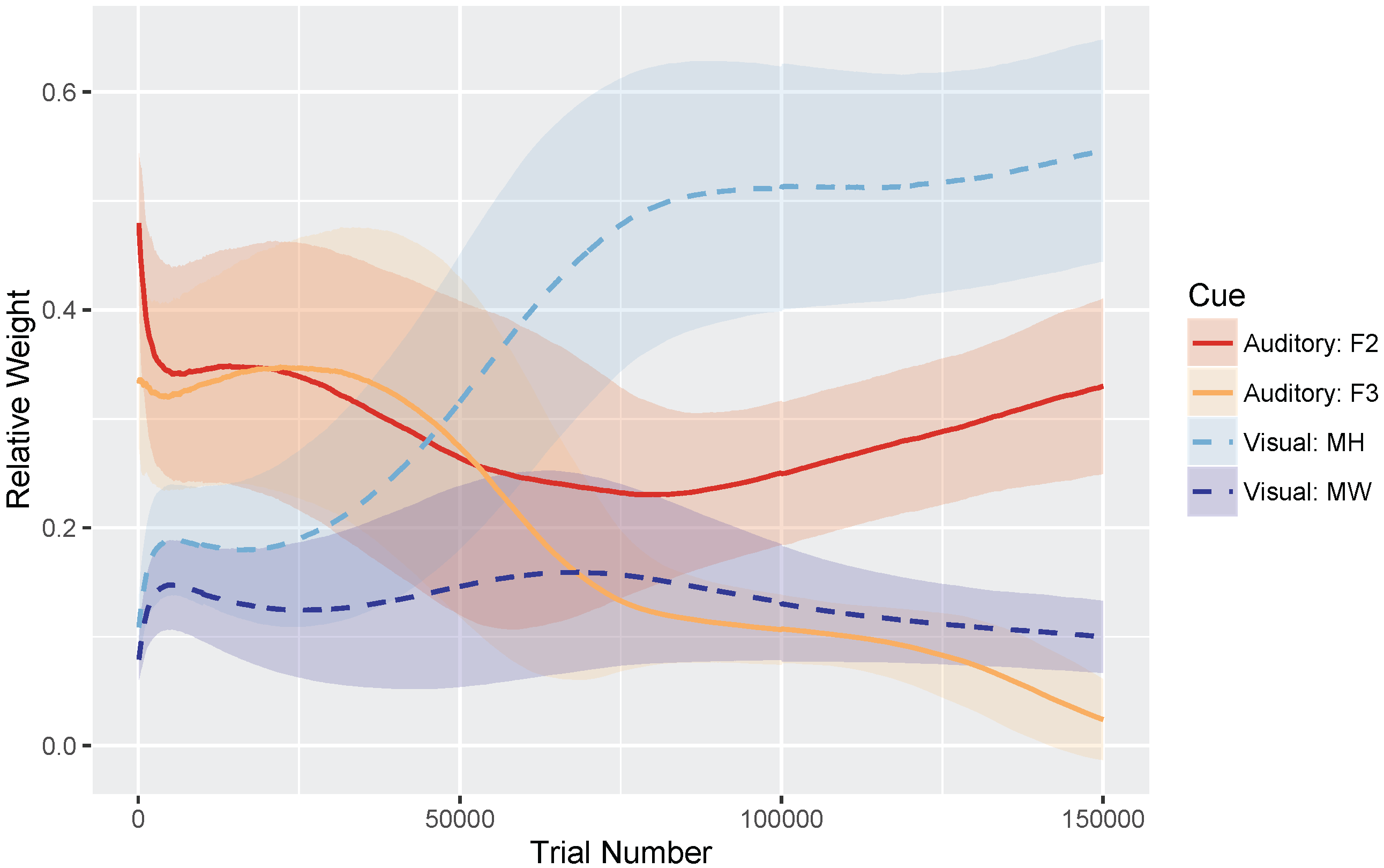
These hypotheses were supported by the model simulations. The simulations demonstrate that weighting-by-reliability can be used to successfully describe the developmental trajectory of audiovisual speech learning. Early in training, the model weights the two auditory cues higher than the two visual cues. Later in development, when the model has achieved a stable (i.e., adult-like) representation, it successfully weights the cues by their reliability in distinguishing the trained phonemes. When testing the model at various stages of development, we found that it showed increased effects of visual cues as a function of age, which is consistent with observations from human listeners: children show a much smaller effect of visual speech cues on categorization than adults do [
12,
32]. Further, we found that audiovisual congruency effects emerged over the course of learning, such that the model initially makes responses consistent with the auditory stimulus and then switches to visual-based responses with additional training. This is again consistent with what we observe with human infants and children [
33,
34,
35,
36,
37], with the size of the auditory and visual influence in the model closely matching the effect sizes seen in data from children and adults [
32].
Thus, we provide an existence proof that statistical learning, as implemented in the GMM [
52,
59], can be used to acquire unified audiovisual representations that follow the same developmental trajectory as human learners and produce categorization functions that mirror those obtained in behavioral experiments. This is significant because it provides a learning mechanism that makes few assumptions about the information available to infants and children. The learning algorithm and cue-weighting metric used in the model make no
a priori assumptions about the number of phonological categories, their distributional statistics, or the reliability of the cues. As the model learns, it weights and integrates inputs from each cue according to their reliability in order to learn the integrated audiovisual distinction between stop consonants. This learning process takes place iteratively, and at no point during training do we need to present labeled inputs to the model about which category is “correct”—these distinctions can all be learned using the same types of statistical learning mechanisms available to human infants.
This is also the first time GMM models have been used for visual inputs in addition to acoustic cues. The results suggest that the emergence of unified perceptual representations and phenomena like the McGurk effect do not require specialized learning mechanisms, though we cannot rule out the possibility that infants use additional mechanisms as well (the current results simply suggest that additional mechanisms are not necessary). Both auditory and visual speech cues can be represented as statistical distributions, putting them into a common representational frame that can then be used to acquire audiovisual speech categories.
It is worth noting that our model shows similar results regardless of audiovisual pairing (i.e., auditory
/ɡ/ + visual
/b/ is similar to auditory
/b/ + visual
/ɡ/), whereas studies of the original McGurk effect found an asymmetry depending on the pairing (i.e., auditory
/ɡ/ + visual
/b/ shows more auditory-bias than auditory
/b/ + visual
/ɡ/, which results in the fusion response
/d/). However, the original effect [
10,
11] was generated by asking participants to repeat what they heard in a task with an open-ended response. Therefore, our model is more similar to the two-alternative forced-choice task used by Massaro and colleagues [
32,
35,
62], and our results match nicely with the behavioral data they present.
Several of our model implementation choices deserve further discussion. Most importantly, we did not run a simulation including a three-way distinction between
/b/,
/d/, and
/ɡ/. Although this would allow a closer comparison to the original McGurk effect [
10], it was unrealistic given the dataset we had available in these simulations [
72]. Consider again the cue distributions shown in
Figure 3: notice that for the majority of the cues we chose, a three-way distinction is not obvious from the distributions. Even for the more reliable cues (F2 and MH), there seems to be a
/b/ vs. non-
/b/ category distinction, but not a
/d/ vs.
/ɡ/ distinction. However, the model could, in principle, be trained on a three-way distinction if a set of non-overlapping cue distributions existed with the same relative category order for each cue. The cue weighting metric is also generalizable to three-way distinctions. Thus, this is not a limitation of the model,
per se, but rather a limitation of the input data that necessitates our separate simulations for the
/b-d/ and
/b-g/ distinctions. In addition, several of the comparisons we make with data from human subjects rely on two-way distinctions, rather than a three-way
/b/-/d/-/g/ contrast.
Second, previous simulations using the GMM [
52,
59] did not include the scaling parameters for the normalized inputs (Equation (
9)) to account for extreme training values along the cue dimensions. We ran a set of 100 simulation runs without the parameters (i.e., with
t and
s ) for the
/b/-
/d/ distinction. The combined audiovisual mixture was not more likely to overgeneralize without these parameters (99% arrived at at least a two-category solution); however the inclusion of these parameters has merit developmentally. A human listener who hears or sees extreme input values (e.g., over-exaggerated mouth movements) would either ignore that instance or scale it into a more plausible value given the rest of its input (i.e., assign it to the closest matching phoneme category).
Third, we set the
ϕ learning rates (
) for the visual cues to be slower in comparison to the learning rates for the auditory cues (
Table 1). To confirm that this choice alone did not drive the pattern of results observed, we ran a set of 100 simulation runs with the auditory learning rates slowed down to be equal to the visual learning rates (
for all four cues) for the
/b/-
/d/ distinction. The combined audiovisual mixture overgeneralized slightly more often by 150,000 trials (93% converged on at least a two-category solution). This led to a more equal proportion of
/b/ and
/d/ responses for incongruent test stimuli than the simulations with faster auditory learning rates. This difference suggests that it is not the absolute learning rates impacting the model’s performance, but the
relative rate difference; the combined mixture overgeneralizes if all four cue rates are the same, but largely achieves a two-category solution if the visual cue learning rates are slower than the auditory rates. Indeed, it makes sense developmentally that visual cues would take longer to acquire than auditory cues, as infants are likely to have more learning opportunities on the basis of auditory input alone (i.e., they only get visual cues if they are looking at the talker).
Finally, although the initial cue weights (before training) were approximately equal across the four cues, as determined by the spread of the Gaussians in each mixture at the start of the simulation, there was a bias towards higher average weights for the auditory cues than the visual cues for the starting parameters we used. Although the selection of starting values is somewhat arbitrary, it was important to verify that our simulation outcome was not just a product of poor initial values. To test this, we updated the spread of the initial μ values for each cue to ensure that the initial weights were exactly the same (i.e., within 0.9% of each other), and ran a set of 100 simulation runs on the /b/-/d/ distinction. Despite closer relative cue weights between the four cues at trial 100, the testing results still showed an increase in the use of visual cues over the course of development, though the model was more likely to overgeneralize (89% converged on at least a two-category solution). This suggests that an early auditory bias is not needed to to show these effects, removing one additional assumption about what is needed for the effects to emerge.