Investigating Methodological Differences in the Assessment of Dendritic Morphology of Basolateral Amygdala Principal Neurons—A Comparison of Golgi–Cox and Neurobiotin Electroporation Techniques
Abstract
1. Introduction
2. Methods
2.1. Ethics Statement
2.2. Golgi–Cox Staining
2.3. Neurobiotin Electroporation
2.4. Neuronal Dendritic Morphology
2.5. Statistical Methods
3. Results
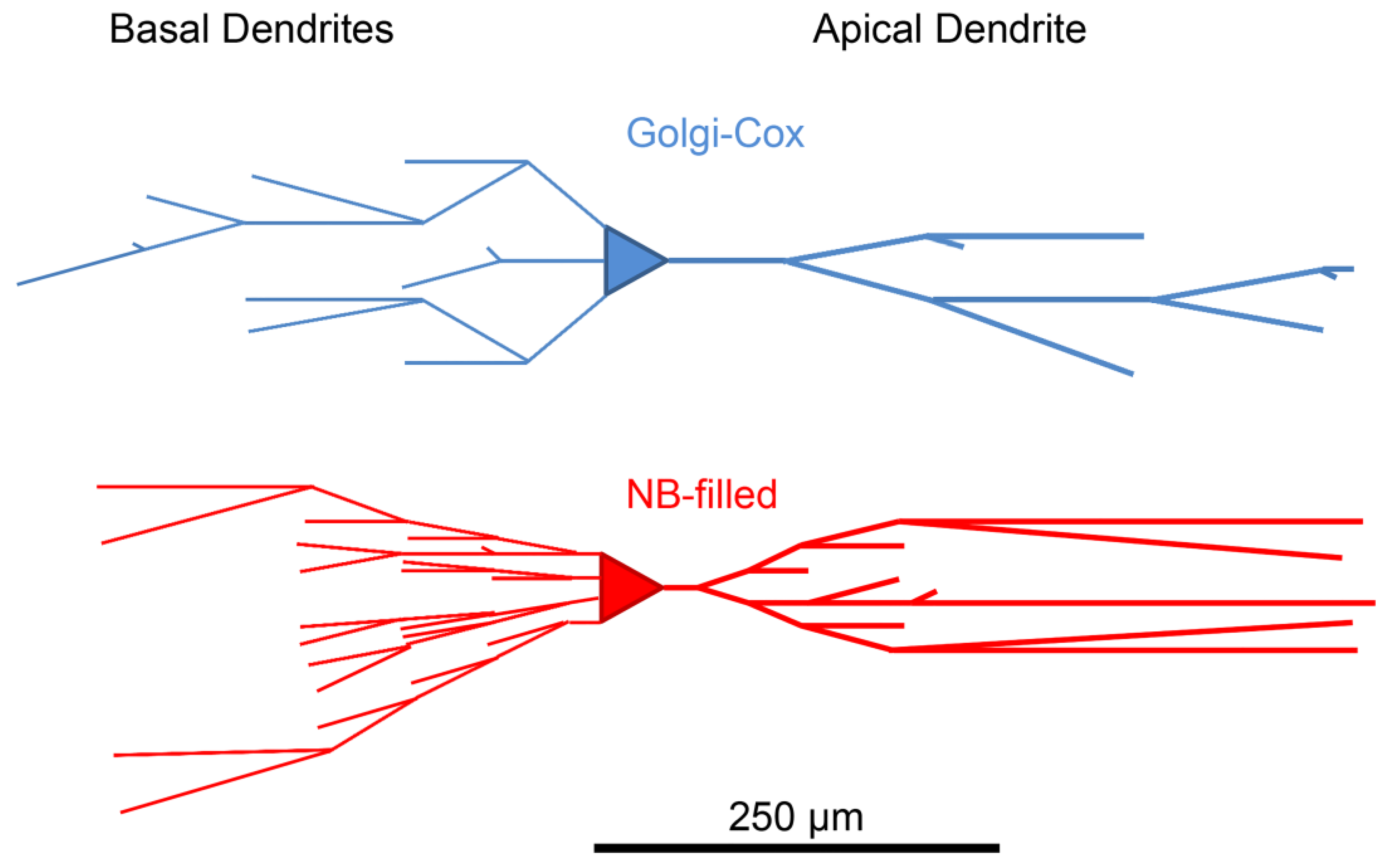
3.1. Neurobiotin-Filled Principal Neurons Have Longer Dendritic Arbor Length Compared to Golgi–Cox-Stained Principal Neurons within the BLA
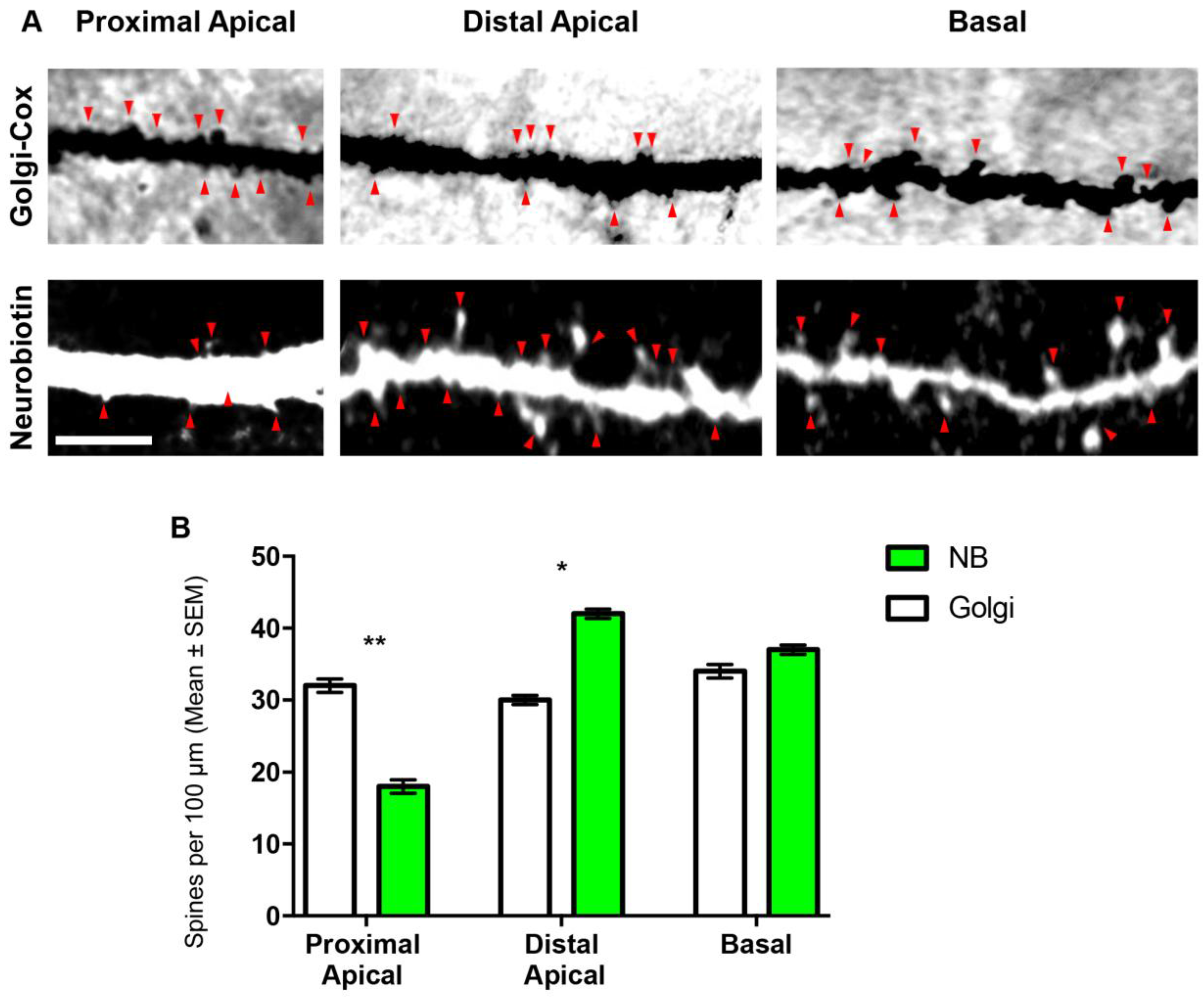
3.2. Comparison of Spines Densities from NB-Filled and Golgi–Cox-Stained BLA Principal Neurons
3.3. Branch Order Analysis of Dendritic Branch Segments, Dendritic Segment Length and Dendritic Spines from NB-Filled and Golgi–Cox-Stained BLA Principal Neurons
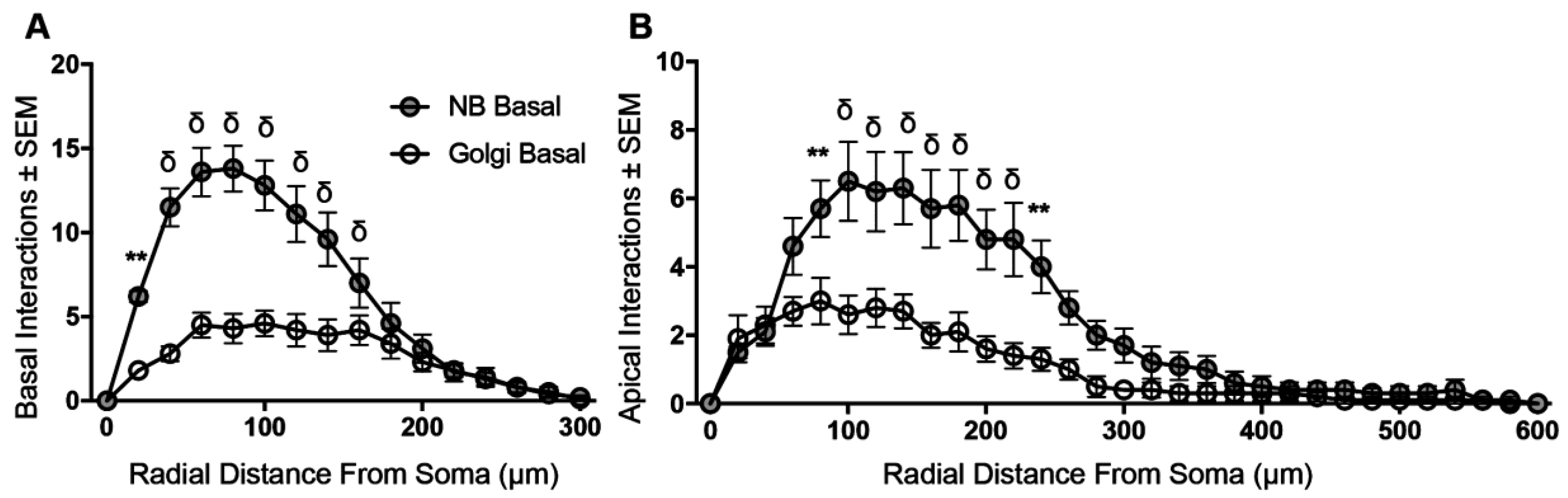
3.4. Sholl Analysis of Basal and Apical Dendrites from NB-Filled and Golgi–Cox-Stained BLA Principal Neurons
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Spruston, N. Pyramidal neurons: Dendritic structure and synaptic integration. Nat. Rev. Neurosci. 2008, 9, 206–221. [Google Scholar] [CrossRef] [PubMed]
- Cox, W.H. Imprägnation des centralen Nervensystems mit Quecksilber-salzen. Arch. Mikrosk. Anat. 1891, 37, 16–21. [Google Scholar] [CrossRef]
- Golgi, C. Sulla fina anatomia del cervelletto umano. Archivio Italiano per le Malattie Nervose 1874, 2, 90–107. [Google Scholar]
- Mazzararello, P. Golgi, a Biography of the Founder of Modern Neuroscience; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Senft, S.L. A brief history of neuronal reconstruction. Neuroinformatics 2011, 9, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Belmer, A.; Klenowski, P.M.; Patkar, O.L.; Bartlett, S.E. Mapping the connectivity of serotonin transporter immunoreactive axons to excitatory and inhibitory neurochemical synapses in the mouse limbic brain. Brain Struct. Funct. 2016. [Google Scholar] [CrossRef] [PubMed]
- Fogarty, M.J.; Hammond, L.A.; Kanjhan, R.; Bellingham, M.C.; Noakes, P.G. A method for the three-dimensional reconstruction of Neurobiotin-filled neurons and the location of their synaptic inputs. Front. Neural Circuits 2013, 7, 153. [Google Scholar] [CrossRef] [PubMed]
- Klenowski, P.M.; Fogarty, M.J.; Belmer, A.; Noakes, P.G.; Bellingham, M.C.; Bartlett, S.E. Structural and functional characterization of dendritic arbors and GABAergic synaptic inputs on interneurons and principal cells in the rat basolateral amygdala. J. Neurophysiol. 2015, 114, 942–957. [Google Scholar] [CrossRef] [PubMed]
- Parekh, R.; Ascoli, G.A. Neuronal morphology goes digital: A research hub for cellular and system neuroscience. Neuron 2013, 77, 1017–1038. [Google Scholar] [CrossRef] [PubMed]
- Vyas, A.; Mitra, R.; Shankaranarayana Rao, B.S.; Chattarji, S. Chronic stress induces contrasting patterns of dendritic remodeling in hippocampal and amygdaloid neurons. J. Neurosci. 2002, 22, 6810–6818. [Google Scholar] [PubMed]
- Padival, M.A.; Blume, S.R.; Rosenkranz, J.A. Repeated restraint stress exerts different impact on structure of neurons in the lateral and basal nuclei of the amygdala. Neuroscience 2013, 246, 230–242. [Google Scholar] [CrossRef] [PubMed]
- Koss, W.A.; Belden, C.E.; Hristov, A.D.; Juraska, J.M. Dendritic remodeling in the adolescent medial prefrontal cortex and the basolateral amygdala of male and female rats. Synapse 2014, 68, 61–72. [Google Scholar] [CrossRef] [PubMed]
- Faber, E.S.; Callister, R.J.; Sah, P. Morphological and electrophysiological properties of principal neurons in the rat lateral amygdala in vitro. J. Neurophysiol. 2001, 85, 714–723. [Google Scholar] [PubMed]
- Ryan, S.J.; Ehrlich, D.E.; Rainnie, D.G. Morphology and dendritic maturation of developing principal neurons in the rat basolateral amygdala. Brain Struct. Funct. 2016, 221, 839–854. [Google Scholar] [CrossRef] [PubMed]
- Sholl, D.A. Dendritic organization in the neurons of the visual and motor cortices of the cat. J. Anat. 1953, 87, 387–406. [Google Scholar] [PubMed]
- Fogarty, M.J.; Mu, E.W.; Noakes, P.G.; Lavidis, N.A.; Bellingham, M.C. Marked changes in dendritic structure and spine density precede significant neuronal death in vulnerable cortical pyramidal neuron populations in the SOD1(G93A) mouse model of amyotrophic lateral sclerosis. Acta Neuropathol. Commun. 2016, 4, 77. [Google Scholar] [CrossRef] [PubMed]
- Klenowski, P.M.; Shariff, M.R.; Belmer, A.; Fogarty, M.J.; Mu, E.W.; Bellingham, M.C.; Bartlett, S.E. Prolonged Consumption of Sucrose in a Binge-Like Manner, Alters the Morphology of Medium Spiny Neurons in the Nucleus Accumbens Shell. Front. Behav. Neurosci. 2016, 10, 54. [Google Scholar] [CrossRef] [PubMed]
- Rutledge, L.T.; Duncan, J.; Beatty, N. A study of pyramidal cell axon collaterals in intact and partially isolated adult cerebral cortex. Brain Res. 1969, 16, 15–22. [Google Scholar] [CrossRef]
- Ranjan, A.; Mallick, B.N. A modified method for consistent and reliable Golgi-cox staining in significantly reduced time. Front. Neurol. 2010, 1, 157. [Google Scholar] [CrossRef] [PubMed]
- Bellingham, M.C.; Berger, A.J. Presynaptic depression of excitatory synaptic inputs to rat hypoglossal motoneurons by muscarinic M2 receptors. J. Neurophysiol. 1996, 76, 3758–3770. [Google Scholar] [PubMed]
- Kanjhan, R.; Bellingham, M.C. Neurobiotin electroporation for combined structural and functional analysis of neurons in developing mouse brain slices. In Excitation and Inhibition of Neural Responses; Pilowsky, P.M., Farnham, M.M., Fong, A.Y., Eds.; Humana: New York, NY, USA, 2013; pp. 151–165. [Google Scholar]
- Fogarty, M.J.; Noakes, P.G.; Bellingham, M.C. Motor cortex layer V pyramidal neurons exhibit dendritic regression, spine loss, and increased synaptic excitation in the presymptomatic hSOD1(G93A) mouse model of amyotrophic lateral sclerosis. J. Neurosci. 2015, 35, 643–647. [Google Scholar] [CrossRef] [PubMed]
- Klenowski, P.M.; Fogarty, M.J.; Shariff, M.; Belmer, A.; Bellingham, M.C.; Bartlett, S.E. Increased Synaptic Excitation and Abnormal Dendritic Structure of Prefrontal Cortex Layer V Pyramidal Neurons following Prolonged Binge-Like Consumption of Ethanol. eNeuro 2016, 3. [Google Scholar] [CrossRef] [PubMed]
- Shariff, M.; Klenowski, P.; Morgan, M.; Patkar, O.; Mu, E.; Bellingham, M.; Belmer, A.; Bartlett, S.E. Binge-like sucrose consumption reduces the dendritic length and complexity of principal neurons in the adolescent rat basolateral amygdala. PLoS ONE 2017, 12, e0183063. [Google Scholar] [CrossRef] [PubMed]
- McDonald, A.J. Neurons of the lateral and basolateral amygdaloid nuclei: A Golgi study in the rat. J. Comp. Neurol. 1982, 212, 293–312. [Google Scholar] [CrossRef] [PubMed]
- McDonald, A.J. Neuronal organization of the lateral and basolateral amygdaloid nuclei in the rat. J. Comp. Neurol. 1984, 222, 589–606. [Google Scholar] [CrossRef] [PubMed]
- Washburn, M.S.; Moises, H.C. Electrophysiological and morphological properties of rat basolateral amygdaloid neurons in vitro. J. Neurosci. 1992, 12, 4066–4079. [Google Scholar] [PubMed]
- Louth, E.L.; Sutton, C.D.; Mendell, A.L.; MacLusky, N.J.; Bailey, C.D.C. Imaging Neurons within Thick Brain Sections Using the Golgi-Cox Method. J. Vis. Exp. 2017. [Google Scholar] [CrossRef] [PubMed]
- Uylings, H.B.; van Eden, C.G.; Hofman, M.A. Morphometry of size/volume variables and comparison of their bivariate relations in the nervous system under different conditions. J. Neurosci. Methods 1986, 18, 19–37. [Google Scholar] [CrossRef]
- Uylings, H.B.; van Pelt, J.; Verwer, R.W.; McConnel, P. Statistical analysis of neuronal populations. In Computer Techniques in Neuroanatomy; Capowski, J.J., Ed.; Plenum Press: New York, NY, USA, 1989; pp. 241–264. [Google Scholar]
- Van Pelt, J.; van Ooyen, A.; Uylings, H.B. Axonal and dendritic density field estimation from incomplete single-slice neuronal reconstructions. Front. Neuroanat. 2014, 8, 54. [Google Scholar] [CrossRef] [PubMed]
- Cullen, C.L.; Burne, T.H.; Lavidis, N.A.; Moritz, K.M. Low dose prenatal ethanol exposure induces anxiety-like behaviour and alters dendritic morphology in the basolateral amygdala of rat offspring. PLoS ONE 2013, 8, e54924. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Golgi–Cox (n = 10) | Neurobiotin (n = 10) | p-Value |
|---|---|---|---|
| Total dendritic length (µm) | 2251 ± 113 | 4349 ± 488 | 0.003 ** a |
| Apical dendritic length (µm) | 944 ± 116 | 1955 ± 285 | 0.007 ** a |
| Basal dendritic length (µm) | 1307 ± 102 | 2394 ± 278 | 0.01 * a |
| Mean basal tree length (µm) | 512 ± 58 | 589 ± 55 | 0.35 |
| Nodes and endings | 22 ± 2 | 70 ± 6 | <0.0001 **** a |
| Maximum apical terminal length (µm) | 484 ± 51 | 431 ± 51 | 0.47 |
| Parameter | Golgi–Cox (n = 10) | Neurobiotin (n = 10) | p-Value |
|---|---|---|---|
| Total spine density | 33 ± 2 | 38 ± 2 | 0.18 |
| Apical spine density | 31 ± 2 | 38 ± 2 | 0.16 |
| Basal spine density | 34 ± 3 | 37 ± 2 | 0.79 |
| Proximal basal spine density | 37 ± 4 | 30 ± 3 | 0.09 |
| Distal basal spine density | 32 ± 3 | 38 ± 3 | 0.12 |
| Proximal apical spine density | 40 ± 5 | 18 ± 3 | 0.0011 ** |
| Distal apical spine density | 30 ± 2 | 42 ± 2 | 0.002 * |
| Branch Order Properties | Golgi–Cox Basal | Neurobiotin Basal | Golgi–Cox Apical | Neurobiotin Apical | Adjusted p-Values |
|---|---|---|---|---|---|
| 1st order branch segments | 2.7 ± 0.1 | 4.0 ± 0.1 | 1.0 ± 0.0 | 1.0 ± 0.0 | B: p = 0.001 *** A: p > 0.99 |
| 1st order mean branch segment length (μm) | 64 ± 20 | 19 ± 4 | 72 ± 21 | 21 ± 7 | B: NS A: NS |
| 1st order branch mean spine density | 44.5 ± 5.7 | 17.4 ± 3.0 | 47.1 ± 1.8 | 11.4 ± 1.1 | B: NS A: p < 0.0001 **** |
| 2nd order branch segments | 4.6 ± 0.2 | 7.8 ± 0.1 | 2.0 ± 0.0 | 2.0 ± 0.0 | B: p < 0.0001 **** A: p > 0.99 |
| 2nd order mean branch segment length (μm) | 76 ± 12 | 49 ± 6 | 91 ± 15 | 31 ± 7 | B: NS A: NS |
| 2nd order branch mean spine density | 34.1 ± 2.9 | 32.0 ± 2.7 | 38.5 ± 1.6 | 21.8 ± 1.2 | B: NS A: p < 0.0001 **** |
| 3rd order branch segments | 4.2 ± 0.2 | 11.1 ± 0.4 | 2.9 ± 0.1 | 3.5 ± 0.1 | B: p < 0.0001 **** A: p < 0.004 ** |
| 3rd order mean branch segment length (μm) | 109 ± 14 | 56 ± 3 | 134 ± 37 | 37 ± 5 | B: NS A: NS |
| 3rd order branch mean spine density | 32.1 ± 3.0 | 36.2 ± 2.9 | 31.1 ± 0.7 | 30.9 ± 1.5 | B: NS A: p > 0.99 |
| 4th order branch segments | 1.8 ± 0.2 | 9.8 ± 0.5 | 2.6 ± 0.1 | 6.1 ± 0.2 | B: p < 0.0001 **** A: p < 0.0001 **** |
| 4th order mean branch segment length (μm) | 64 ± 29 | 65 ± 5 | 108 ± 44 | 64 ± 8 | B: NS A: NS |
| 4th order branch mean spine density | 32.9 ± 6.1 | 40.7 ± 2.6 | 29.1 ± 1.2 | 38.4 ± 1.5 | B: NS A: p < 0.0001 **** |
| ≥5th order branch segments | 1.0 ± 0.1 | 4.0 ± 0.2 | 2 ± 0.1 | 4.5 ± 0.2 | B: p < 0.0001 **** A: p > 0.99 |
| ≥5th order mean branch segment length (μm) | 79 ± 38 | 134 ± 27 | 19 ± 12 | 286 ± 46 | B: NS A: p < 0.0001 **** |
| ≥5th order mean spine density | 33.6 ± 3.2 | 45.3 ± 4.4 | 34.1 ± 1.9 | 40.2 ± 1.1 | B: NS A: p = 0.01 * |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klenowski, P.M.; Wright, S.E.; Mu, E.W.H.; Noakes, P.G.; Lavidis, N.A.; Bartlett, S.E.; Bellingham, M.C.; Fogarty, M.J. Investigating Methodological Differences in the Assessment of Dendritic Morphology of Basolateral Amygdala Principal Neurons—A Comparison of Golgi–Cox and Neurobiotin Electroporation Techniques. Brain Sci. 2017, 7, 165. https://doi.org/10.3390/brainsci7120165
Klenowski PM, Wright SE, Mu EWH, Noakes PG, Lavidis NA, Bartlett SE, Bellingham MC, Fogarty MJ. Investigating Methodological Differences in the Assessment of Dendritic Morphology of Basolateral Amygdala Principal Neurons—A Comparison of Golgi–Cox and Neurobiotin Electroporation Techniques. Brain Sciences. 2017; 7(12):165. https://doi.org/10.3390/brainsci7120165
Chicago/Turabian StyleKlenowski, Paul M., Sophie E. Wright, Erica W. H. Mu, Peter G. Noakes, Nickolas A. Lavidis, Selena E. Bartlett, Mark C. Bellingham, and Matthew J. Fogarty. 2017. "Investigating Methodological Differences in the Assessment of Dendritic Morphology of Basolateral Amygdala Principal Neurons—A Comparison of Golgi–Cox and Neurobiotin Electroporation Techniques" Brain Sciences 7, no. 12: 165. https://doi.org/10.3390/brainsci7120165
APA StyleKlenowski, P. M., Wright, S. E., Mu, E. W. H., Noakes, P. G., Lavidis, N. A., Bartlett, S. E., Bellingham, M. C., & Fogarty, M. J. (2017). Investigating Methodological Differences in the Assessment of Dendritic Morphology of Basolateral Amygdala Principal Neurons—A Comparison of Golgi–Cox and Neurobiotin Electroporation Techniques. Brain Sciences, 7(12), 165. https://doi.org/10.3390/brainsci7120165





