Evaluation of Teaching Signals for Motor Control in the Cerebellum during Real-World Robot Application
Abstract
:1. Introduction
2. Materials and Methods
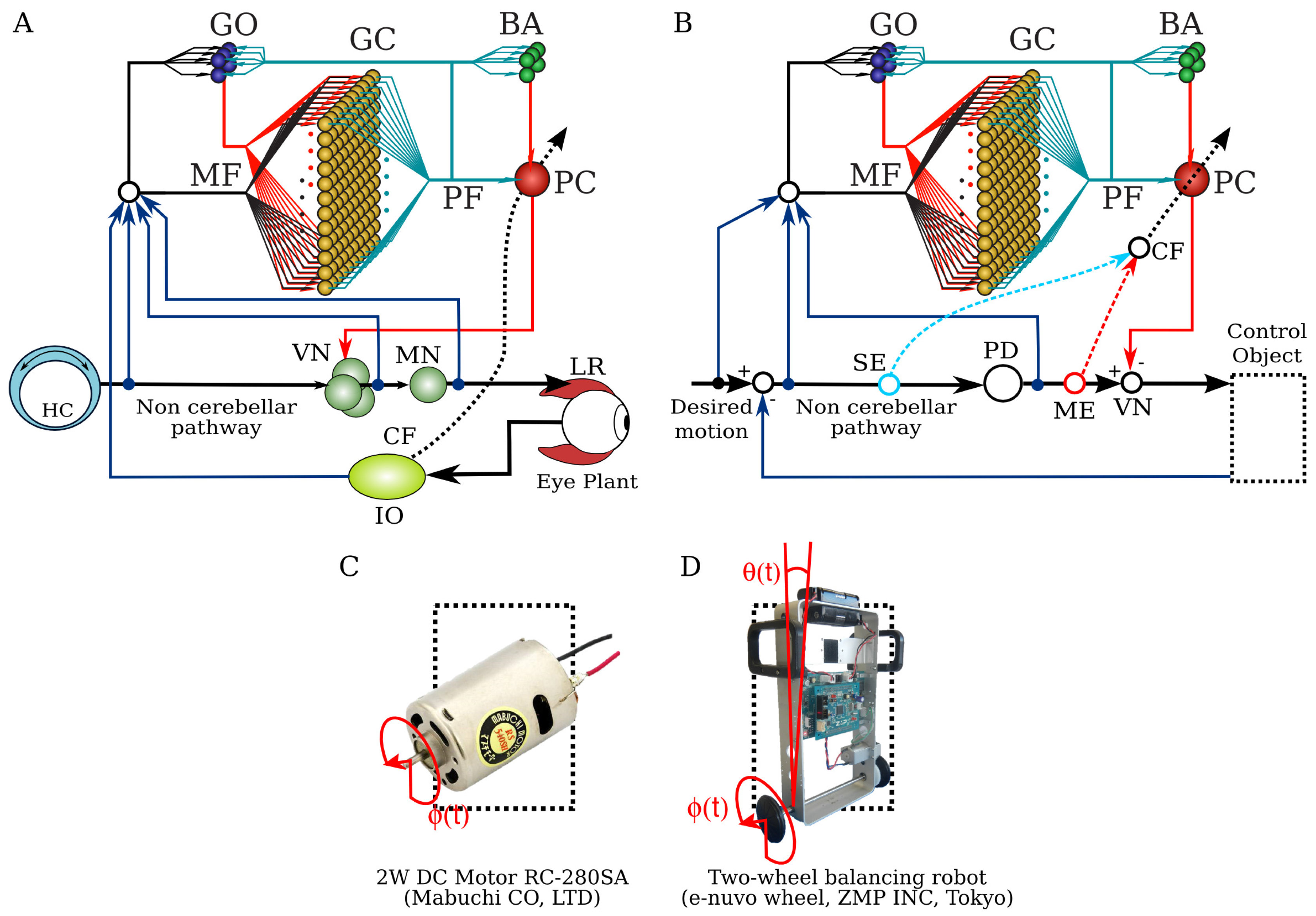
2.1. Neuronal Network Model of the Cerebellum
2.2. Equations of the Model
2.3. Control Plants
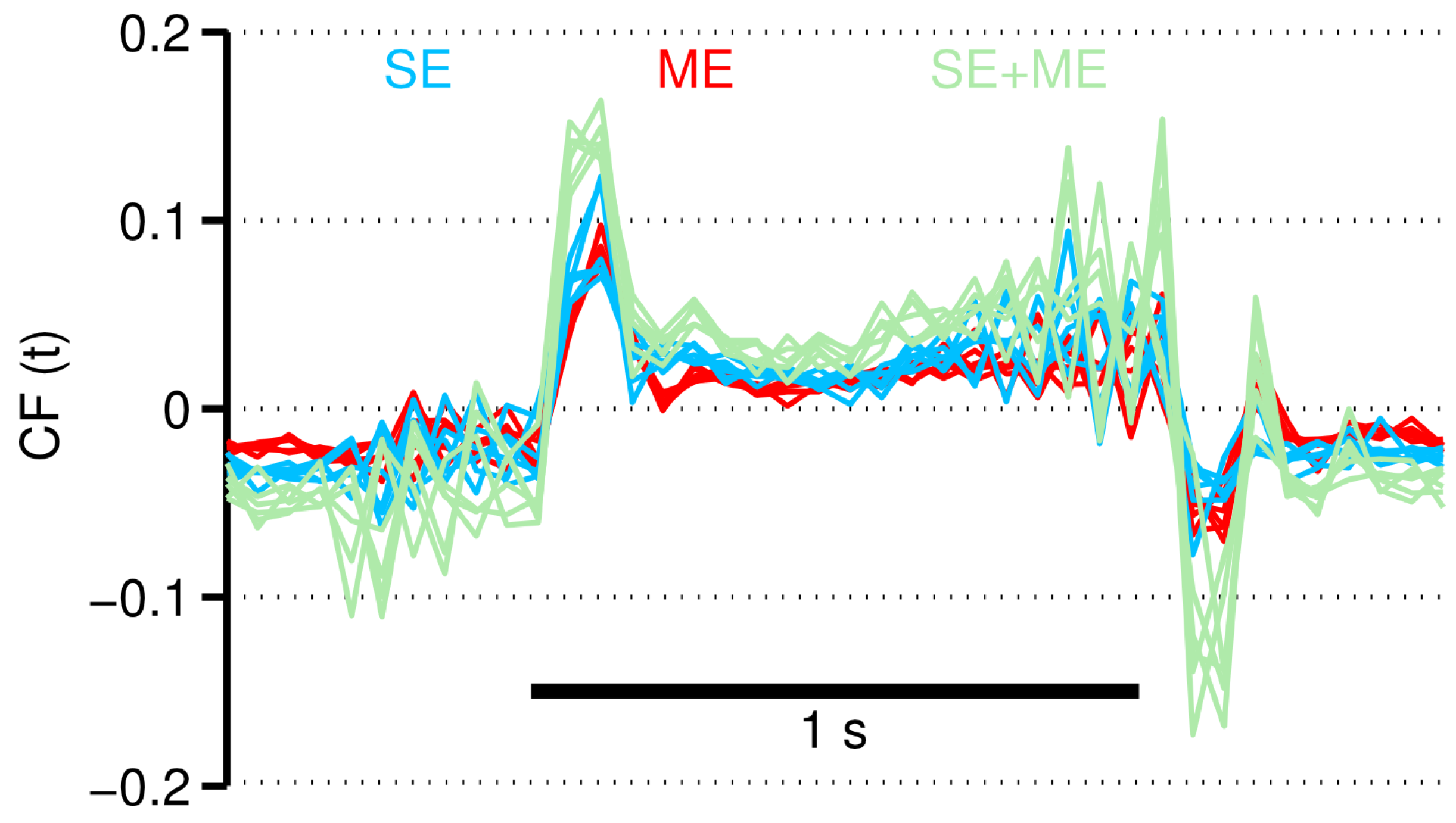
2.4. Two Types of Error Information in CF
2.5. Performance Assessment Methodology
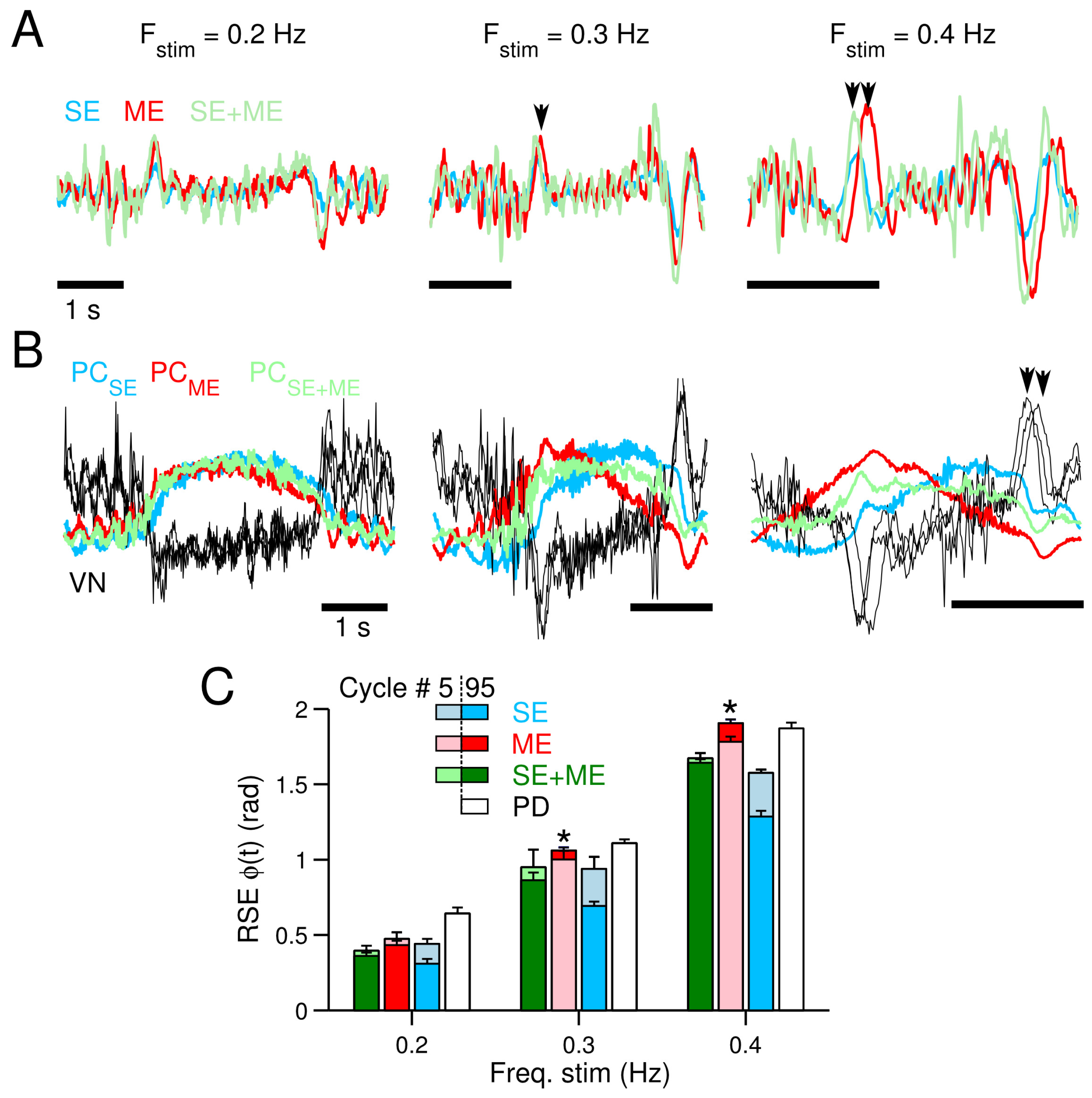
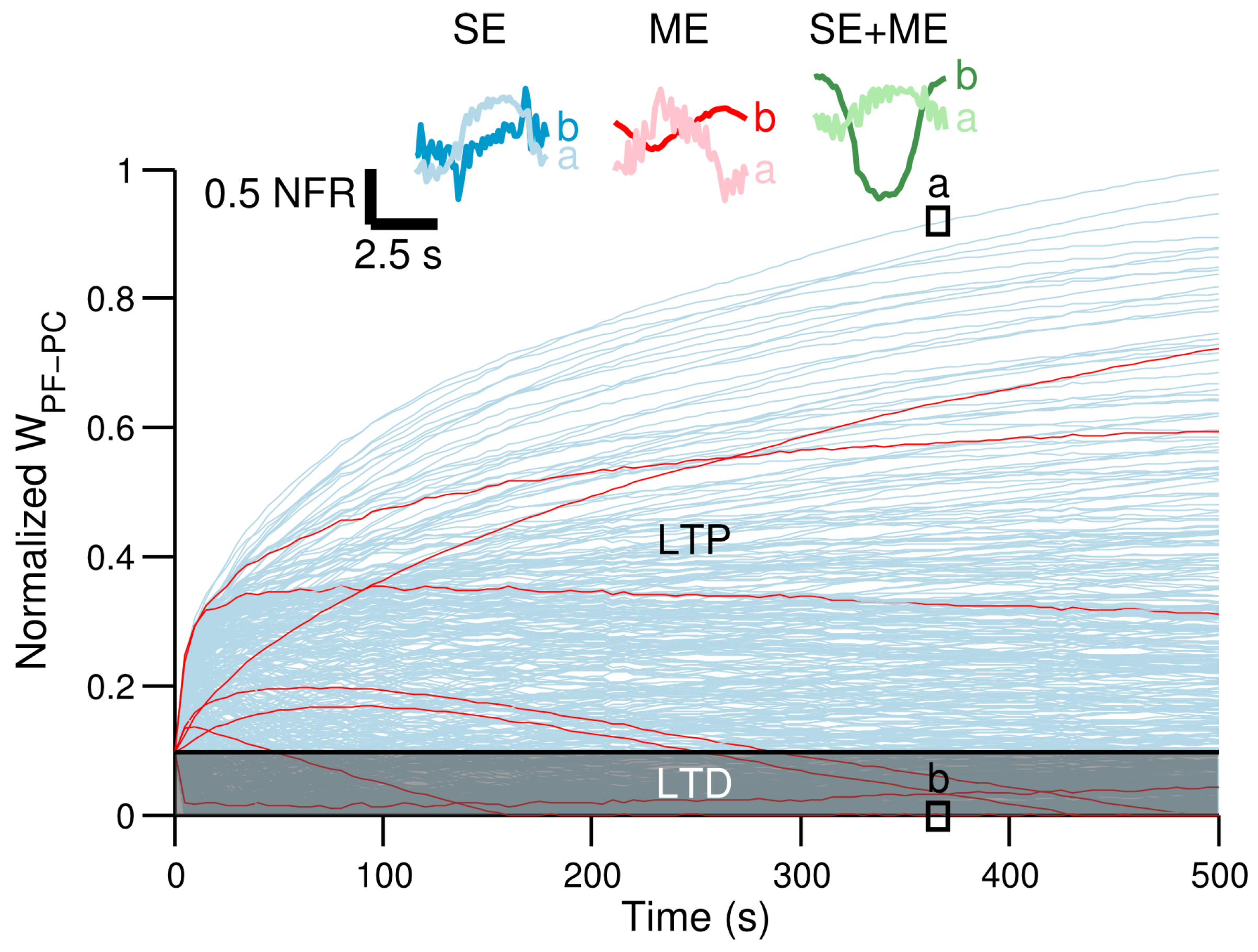
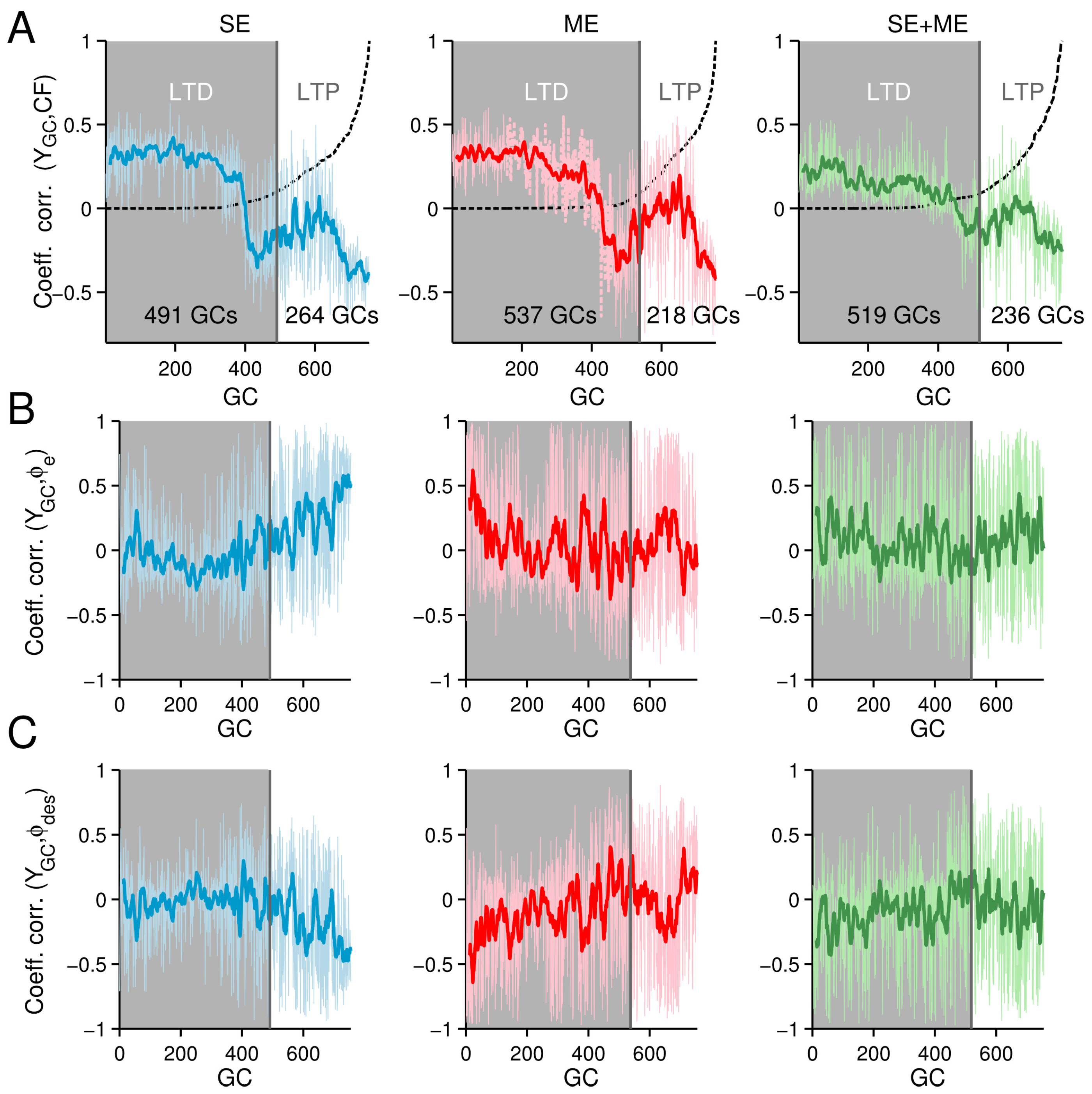
3. Results
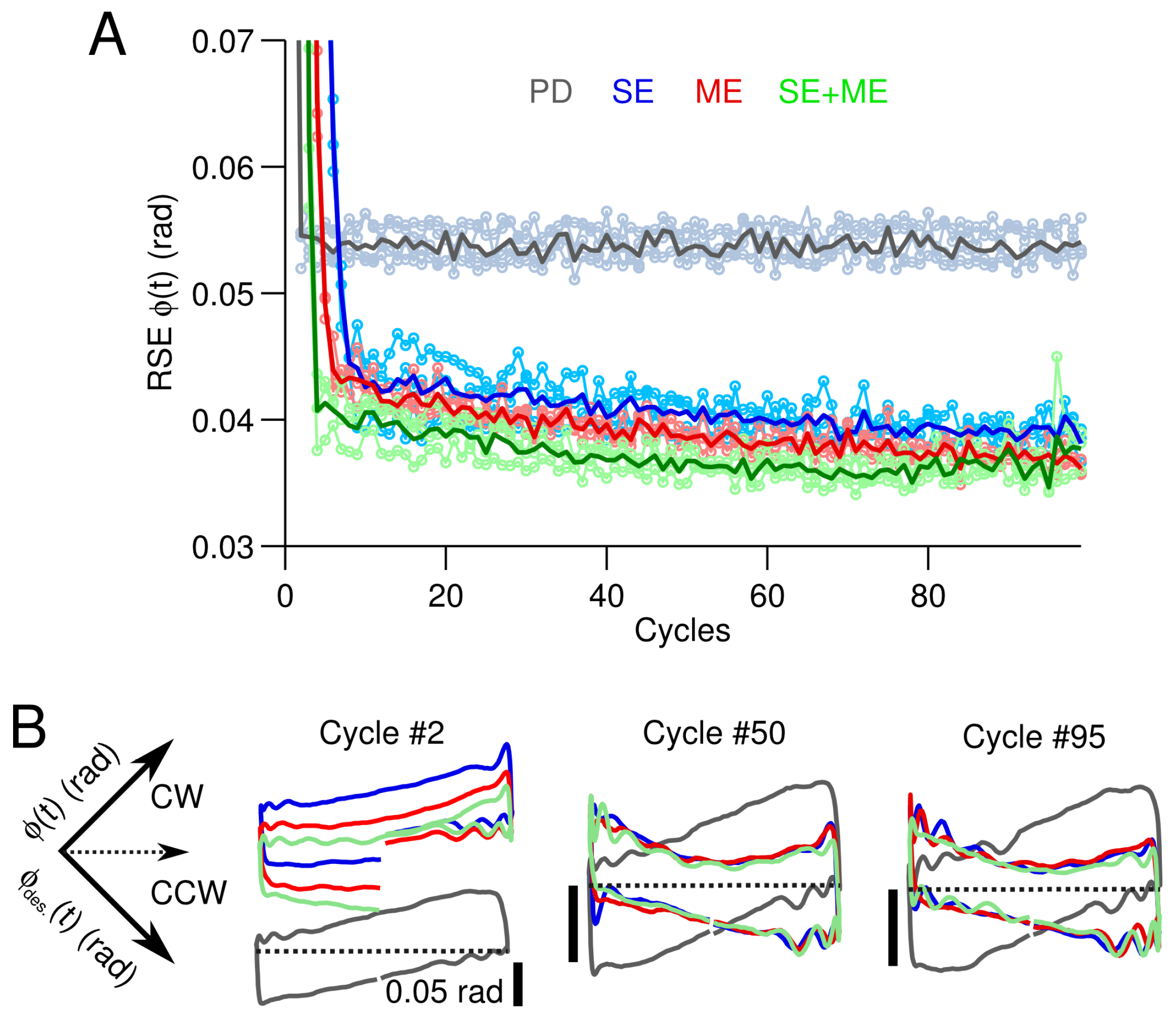
3.1. Simple Control Scenario
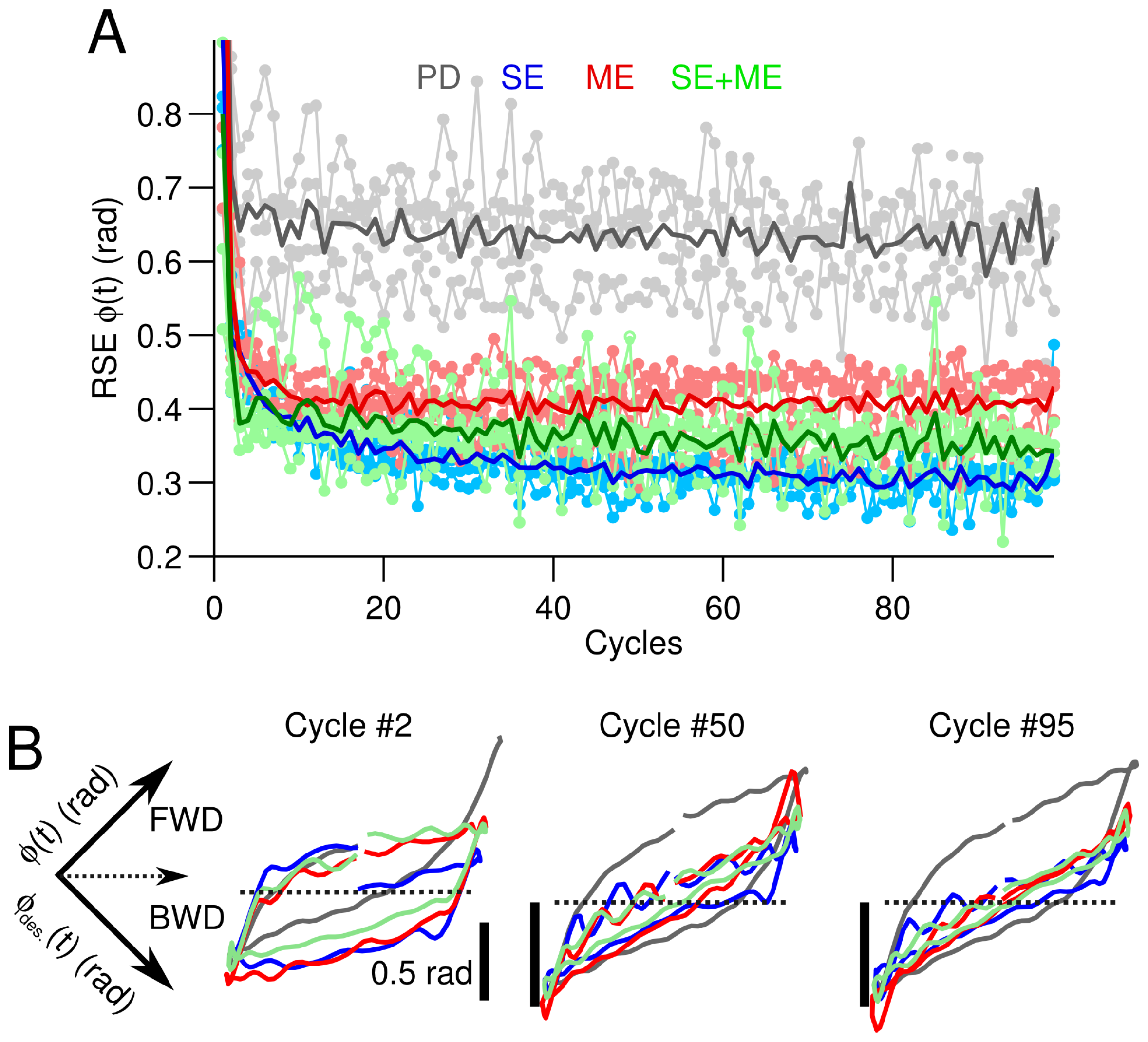
3.2. Difficult Control Scenario
3.3. Neural Consequences of the Different CF Types
4. Discussion
4.1. Type of Error Signal and the Yielded Robot Control Performance
4.2. Generalization and Limitation of the Current Results
4.3. Comparison with Other Cerebellar Models
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Manto, M.; Taib, N.O.B. The contributions of the cerebellum in sensorimotor control: What are the prevailing opinions which will guide forthcoming studies? Cerebellum 2013, 12, 313–315. [Google Scholar] [CrossRef] [PubMed]
- Ito, M. Error detection and representation in the olivo-cerebellar system. Front. Neural Circuits 2013, 7, 1. [Google Scholar] [CrossRef] [PubMed]
- Marr, D. A theory of cerebellar cortex. J. Physiol. 1969, 202, 437–470. [Google Scholar] [CrossRef] [PubMed]
- Albus, J.S. A theory of cerebellar function. Math. Biosci. 1971, 10, 25–61. [Google Scholar] [CrossRef]
- Dean, P.; Porrill, J.; Ekerot, C.F.; Jorntell, H. The cerebellar microcircuit as an adaptive filter: Experimental and computational evidence. Nat. Rev. Neurosci. 2010, 11, 30–43. [Google Scholar] [CrossRef] [PubMed]
- Kawato, M. Internal models for motor control and trajectory planning. Curr. Opin. Neurobiol. 1999, 9, 718–727. [Google Scholar] [CrossRef]
- Hofstotter, C.; Mintz, M.; Verschure, P.F.M.J. The cerebellum in action: A simulation and robotics study. Eur. J. Neurosci. 2002, 16, 1361–1376. [Google Scholar] [CrossRef] [PubMed]
- Carrillo, R.R.; Ros, E.; Boucheny, C.; Coenen, O.J.M. A real-time spiking cerebellum model for learning robot control. Biosystems 2008, 94, 18–27. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y.; Ohata, Y.; Kawamoto, T.; Hirata, Y. Adaptive control of 2-wheeled balancing robot by cerebellar neuronal network model. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Buenos Aires, Argentina, 31 August–4 September 2010; pp. 1589–1592.
- Garrido Alcazar, J.A.; Luque, N.R.; DAngelo, E.; Ros, E. Distributed cerebellar plasticity implements adaptable gain control in a manipulation task: A closed-loop robotic simulation. Front. Neural Circuits 2013, 7, 159. [Google Scholar]
- Pinzon-Morales, R.D.; Hirata, Y. Cerebellar-inspired bi-hemispheric neural network for adaptive control of an unstable robot. In Proceedings of the Biosignals and Biorobotics Conference (2013 BRC), Rio de Janeiro, Brazil, 18–20 February 2013; pp. 1–4.
- Yamazaki, T.; Igarashi, J. Realtime cerebellum: A large-scale spiking network model of the cerebellum that runs in realtime using a graphics processing unit. Neural Netw. 2013, 47, 103–111. [Google Scholar] [CrossRef] [PubMed]
- Graf, W.; Simpson, J.I.; Leonard, C.S. Spatial organization of visual messages of the rabbit’s cerebellar flocculus. II. Complex and simple spike responses of Purkinje cells. J. Neurophysiol. 1988, 60, 2091–2121. [Google Scholar] [PubMed]
- Stone, L.S.; Lisberger, S.G. Visual responses of Purkinje cells in the cerebellar flocculus during smooth-pursuit eye movements in monkeys. II. Complex spikes. J. Neurophysiol. 1990, 63, 1262–1275. [Google Scholar] [PubMed]
- Frens, M.A.; Mathoera, A.L.; van der Steen, J. Floccular complex spike response to transparent retinal slip. Neuron 2001, 30, 795–801. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Kawano, K.; Takemura, A.; Inoue, Y.; Kitama, T.; Gomi, H.; Kawato, M. Temporal firing patterns of purkinje cells in the cerebellar ventral paraflocculus during ocular following responses in monkeys II. Complex spikes. J. Neurophysiol. 1998, 80, 832–848. [Google Scholar] [PubMed]
- Kawato, M.; Gomi, H. The cerebellum and VOR/OKR learning models. Trends Neurosci. 1992, 15, 445–453. [Google Scholar] [CrossRef]
- Kawato, M.; Gomi, H. A computational model of four regions of the cerebellum based on feedback-error learning. Biol. Cybern. 1992, 68, 95–103. [Google Scholar] [CrossRef] [PubMed]
- Porrill, J.; Dean, P.; Anderson, S.R. Adaptive filters and internal models: Multilevel description of cerebellar function. Neural Netw. 2013, 47, 134–149. [Google Scholar] [CrossRef] [PubMed]
- Ito, M. The Cerebellum: Brain for an Implicit Self; FT Press Science: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Blazquez, P.M.; Hirata, Y.; Heiney, S.A.; Green, A.M.; Highstein, S.M. Cerebellar signatures of vestibulo-ocular reflex motor learning. J. Neurosci. 2003, 23, 9742–9751. [Google Scholar] [PubMed]
- Hirata, Y.; Highstein, S.M. Acute adaptation of the vestibuloocular reflex: Signal processing by floccular and ventral parafloccular purkinje cells. J. Neurophysiol. 2001, 85, 2267–2288. [Google Scholar] [PubMed]
- Huang, C.C.; Sugino, K.; Shima, Y.; Guo, C.; Bai, S.; Mensh, B.D.; Nelson, S.B.; Hantman, A.W. Convergence of pontine and proprioceptive streams onto multimodal cerebellar granule cells. eLife 2013, 2, e00400. [Google Scholar] [CrossRef] [PubMed]
- Atlassian Bitbucket. Available online: https://bitbucket.org/rdpinzonm/the-bicnn-model/downloads (accessed on 18 December 2016).
- Cerebellar Platform. Available online: https://cerebellum.neuroinf.jp/ (accessed on 18 December 2016).
- Li, Z.; Yang, C.; Fan, L. Advanced Control of Wheeled Inverted Pendulum Systems; Springer: London, UK, 2013. [Google Scholar]
- Ito, M. Cerebellar learning in the vestibulo-ocular reflex. Trends Cogn. Sci. 1998, 2, 313–321. [Google Scholar] [CrossRef]
- Solinas, S.; Nieus, T.; DAngelo, E. A realistic large-scale model of the cerebellum granular layer predicts circuit spatio-temporal filtering properties. Front. Cell. Neurosci. 2010, 4, 12. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. ASME 1942, 64, 759–768. [Google Scholar] [CrossRef]
- Pinzon-Morales, R.; Hirata, Y. A bi-hemispheric neuronal network model of the cerebellum with spontaneous climbing fiber firing produces asymmetrical motor learning during robot control. Front. Neural Circuits 2014, 8, 131. [Google Scholar] [CrossRef] [PubMed]
- Pinzon-Morales, R.; Hirata, Y. An stand-alone and portable bi-hemispherical neuronal network model of the cerebellum for engineering applications. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO), Bali, Indonesia, 5–10 December 2014; pp. 1–4.
- Hirata, Y.; Lockard, J.M.; Highstein, S.M. Capacity of vertical VOR adaptation in squirrel monkey. J. Neurophysiol. 2002, 88, 3194–3207. [Google Scholar] [CrossRef] [PubMed]
- Kitazawa, S.; Kimura, T.; Yin, P.B. Cerebellar complex spikes encode both destinations and errors in arm movements. Nature 1998, 392, 494–497. [Google Scholar] [CrossRef] [PubMed]
- Raymond, J.L.; Lisberger, S.G. Neural learning rules for the vestibulo-ocular reflex. J. Neurosci. 1998, 18, 9112–9129. [Google Scholar] [PubMed]
- Pinzon-Morales, R.D.; Hirata, Y. A realistic bi-hemispheric model of the cerebellum uncovers the purpose of the abundant granule cells during motor control. Front. Neural Circuits 2015, 9, 18. [Google Scholar] [CrossRef] [PubMed]
- Thach, W.T. On the specific role of the cerebellum in motor learning and cognition: Clues from PET activation and lesion studies in man. Behav. Brain Sci. 1996, 19, 411–433. [Google Scholar] [CrossRef]
- Wolpert, D.M.; Miall, R.; Kawato, M. Internal models in the cerebellum. Trends Cogn. Sci. 1998, 2, 338–347. [Google Scholar] [CrossRef]
- Ruan, X.; Chen, J. On-line NNAC for a balancing two-wheeled robot using feedback-error-learning on the neurophysiological mechanism. J. Comput. 2011, 6, 489–496. [Google Scholar] [CrossRef]
- Blazquez, P.M.; Hirata, Y.; Highstein, S.M. Chronic changes in inputs to dorsal Y neurons accompany VOR motor learning. J. Neurophysiol. 2006, 95, 1812–1825. [Google Scholar] [CrossRef] [PubMed]
- Takemura, A.; Inoue, Y.; Gomi, H.; Kawato, M.; Kawano, K. Change in neuronal firing patterns in the process of motor command generation for the ocular following response. J. Neurophysiol. 2001, 86, 1750–1763. [Google Scholar] [PubMed]
- Lisberger, S.G.; Pavelko, T.A.; Broussard, D.M. Neural basis for motor learning in the vestibuloocular reflex of primates. I. Changes in the responses of brain stem neurons. J. Neurophysiol. 1994, 72, 928–953. [Google Scholar] [PubMed]
- Kassardjian, C.D.; Tan, Y.F.; Chung, J.Y.J.; Heskin, R.; Peterson, M.J.; Broussard, D.M. The site of a motor memory shifts with consolidation. J. Neurosci. 2005, 25, 7979–7985. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Beugen, B.J.V.; De Zeeuw, C.I. Distributed synergistic plasticity and cerebellar learning. Nat. Rev. Neurosci. 2012, 13, 619–635. [Google Scholar] [CrossRef] [PubMed]
- McElvain, L.E.; Bagnall, M.W.; Sakatos, A.; du Lac, S. Bidirectional Plasticity gated by hyperpolarization controls the gain of postsynaptic firing responses at central vestibular nerve synapses. Neuron 2010, 68, 763–775. [Google Scholar] [CrossRef] [PubMed]
- Kettner, R.E.; Mahamud, S.; Leung, H.C.; Sitkoff, N.; Houk, J.C.; Peterson, B.W.; Barto, A.G. Prediction of complex two-dimensional trajectories by a cerebellar model of smooth pursuit eye movement. J. Neurophysiol. 1997, 77, 2115–2130. [Google Scholar] [PubMed]
- Lenz, A.; Anderson, S.; Pipe, A.; Melhuish, C.; Dean, P.; Porrill, J. Cerebellar-inspired adaptive control of a robot eye actuated by pneumatic artificial muscles. IEEE Trans. Syst. Man Cybern. B Cybern. 2009, 39, 1420–1433. [Google Scholar] [CrossRef] [PubMed]
- Eskiizmirliler, S.; Forestier, N.; Tondu, B.; Darlot, C. A model of the cerebellar pathways applied to the control of a single-joint robot arm actuated by McKibben artificial muscles. Biol. Cybern. 2002, 86, 379–394. [Google Scholar] [CrossRef] [PubMed]
- Inagaki, K.; Hirata, Y.; Blazquez, P.; Highstein, S. Computer simulation of vestibuloocular reflex motor learning using a realistic cerebellar cortical neuronal network model. In Neural Information Processing; Ishikawa, M., Doya, K., Miyamoto, H., Yamakawa, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 4984, pp. 902–912. [Google Scholar]
- Luque, N.R.; Garrido, J.A.; Carrillo, R.R.; Tolu, S.; Ros, E. Adaptive cerebellar spiking model embedded in the control loop: Context switching and robustness against noise. Int. J. Neural Syst. 2011, 21, 385–401. [Google Scholar] [CrossRef] [PubMed]
| No. of Cells | Divergence | Convergence | |
|---|---|---|---|
| Mossy fibers (MF) | 7/5 * | ||
| Golgi (GO) | 5 | ||
| Granule (GC) | 755 | ||
| Basket/stellate (BA) | 15 | ||
| Purkinje (PC) | 1 | ||
| Parallel fibers (PF) | 755 | ||
| MF → GC | 1:150 | 4:1 | |
| MF → GO | 1:5 | 50:1 | |
| GC (parallel fibers)→ GO | 1:4 | 150:1 | |
| GO → GC | 1:600 | 3:1 | |
| GC (PF)→ BA | 1:30 | 50:1 | |
| GC (PF)→ PC | 1:1 | 755:1 | |
| BA → PC | 1:1 | 15:1 |
| Object | Outputs (Sensors) | Mossy Fibers | Scaling Gain |
|---|---|---|---|
| Motor | shaft ang. pos. (rad) | 1-des. shaft ang. pos. | 0.1 |
| shaft ang. vel. (rad/s) | 2- des. shaft ang. vel. | s/rad | |
| 3- shaft ang. pos. error | |||
| 4- shaft ang. vel. error | s/rad | ||
| 5- efference copy | 1 | ||
| Robot | wheel angle (rad) | 1- des. wheel ang. pos. | 0.03 |
| wheel ang. vel. (rad/s) | 2- des. wheel ang. vel. | 0.04 s/rad | |
| body tilt ang. pos. (rad) | 3- body tilt ang. pos. error | 1 | |
| body tilt ang. vel. (rad/s) | 4- body tilt ang. vel. error | 0.5 s/rad | |
| 5- wheel ang. pos. error | 0.1 | ||
| 6- wheel ang. vel. error | 0.2 s/rad | ||
| 7- efference copy | 0.5 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinzon Morales, R.D.; Hirata, Y. Evaluation of Teaching Signals for Motor Control in the Cerebellum during Real-World Robot Application. Brain Sci. 2016, 6, 62. https://doi.org/10.3390/brainsci6040062
Pinzon Morales RD, Hirata Y. Evaluation of Teaching Signals for Motor Control in the Cerebellum during Real-World Robot Application. Brain Sciences. 2016; 6(4):62. https://doi.org/10.3390/brainsci6040062
Chicago/Turabian StylePinzon Morales, Ruben Dario, and Yutaka Hirata. 2016. "Evaluation of Teaching Signals for Motor Control in the Cerebellum during Real-World Robot Application" Brain Sciences 6, no. 4: 62. https://doi.org/10.3390/brainsci6040062
APA StylePinzon Morales, R. D., & Hirata, Y. (2016). Evaluation of Teaching Signals for Motor Control in the Cerebellum during Real-World Robot Application. Brain Sciences, 6(4), 62. https://doi.org/10.3390/brainsci6040062





