A Multi-Branch Network for Integrating Spatial, Spectral, and Temporal Features in Motor Imagery EEG Classification
Abstract
1. Introduction
- (1)
- To extract spatial and spectral features from EEG signals, a 3D PSD tensor is constructed as the primary network input. To compensate for the absence of temporal dynamics in the 3D PSD representation, 2D time-domain EEG signals are introduced as a complementary input.
- (2)
- To capture spatial, spectral, spatial-spectral joint, and temporal features of MI-EEG signals, while maintaining low computational complexity, four parallel feature extraction branches based on DSC modules are designed.
- (3)
- To evaluate the classification performance of the proposed model, comparative experiments are conducted on two publicly available MI-EEG datasets, benchmarking against state-of-the-art methods.
- (4)
- To enhance the model’s neurophysiological interpretability, gradient-weighted class activation mapping (Grad-CAM) is applied to visualize the brain regions and frequency bands most relevant to the classification tasks.
2. Materials and Methods
2.1. Dataset and Preprocessing
2.1.1. EEG Motor Movement/Imagery Database (EEGMMIDB)
2.1.2. BCI Competition IV Dataset 2a (BCIIV2A)
2.1.3. Data Preprocessing
- (1)
- Baseline Correction
- (2)
- Sampling Rate Alignment
- (3)
- Amplitude Conversion and Standardization
- (4)
- Sliding Window Segmentation
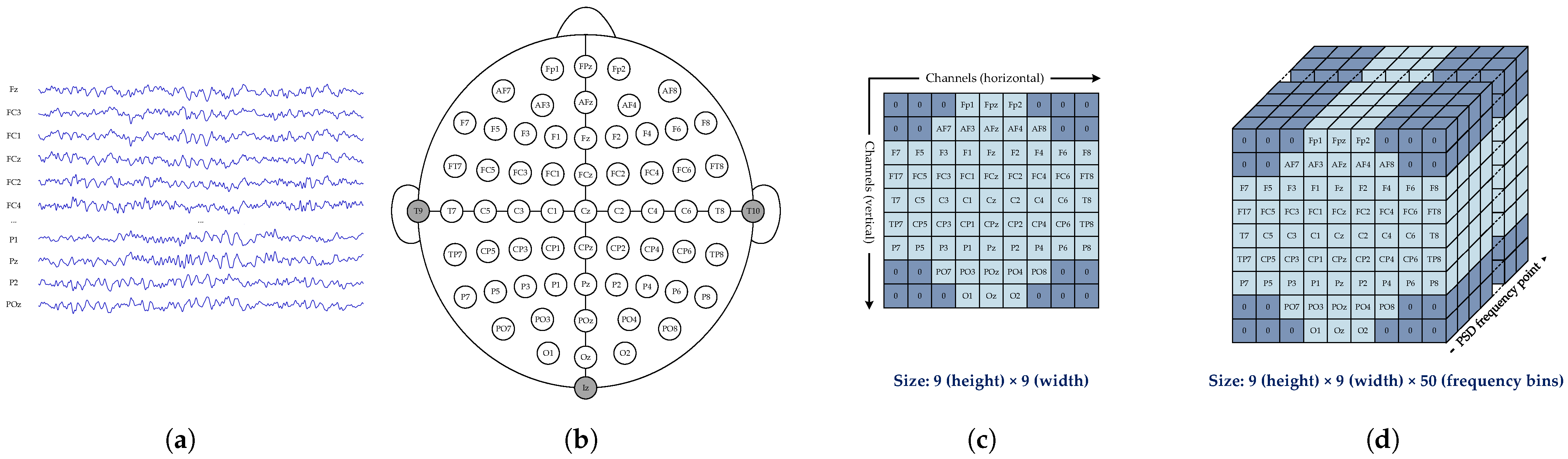
2.2. Three-Dimensional Power Spectral Density Matrix
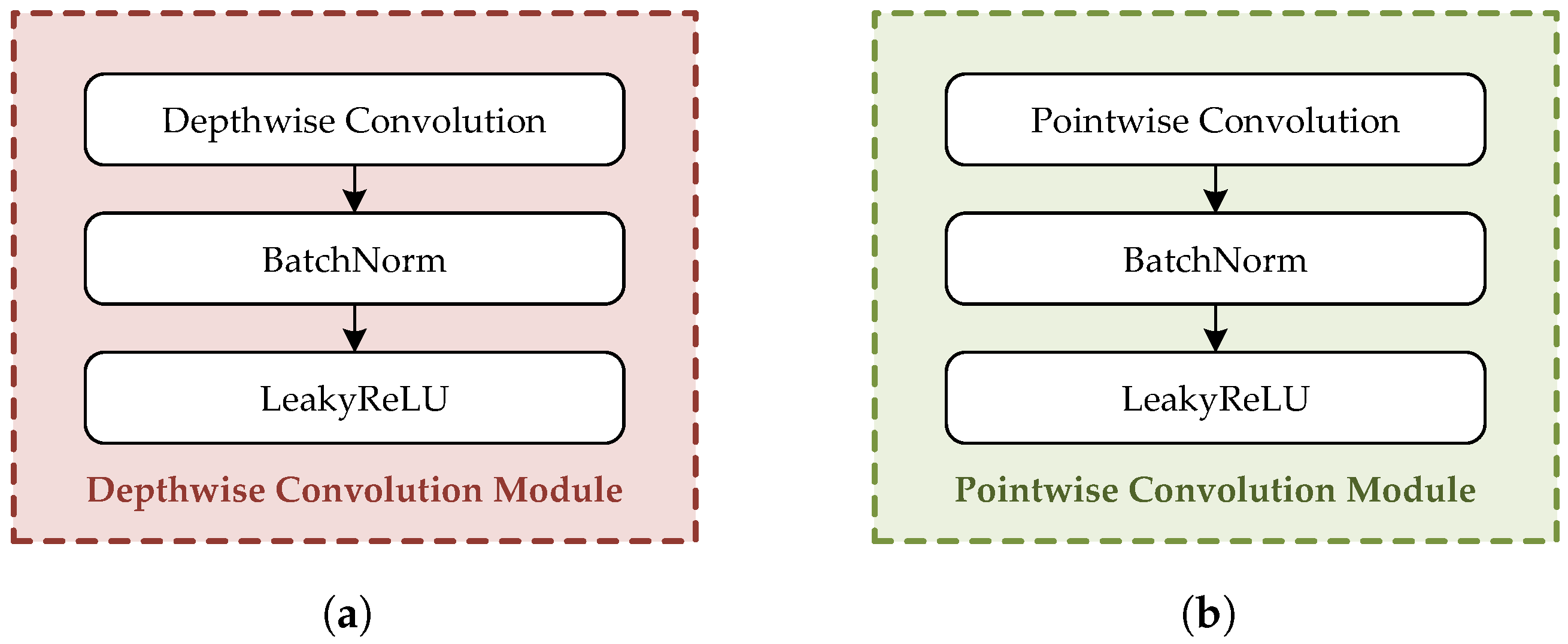
2.3. Depthwise Separable Convolution
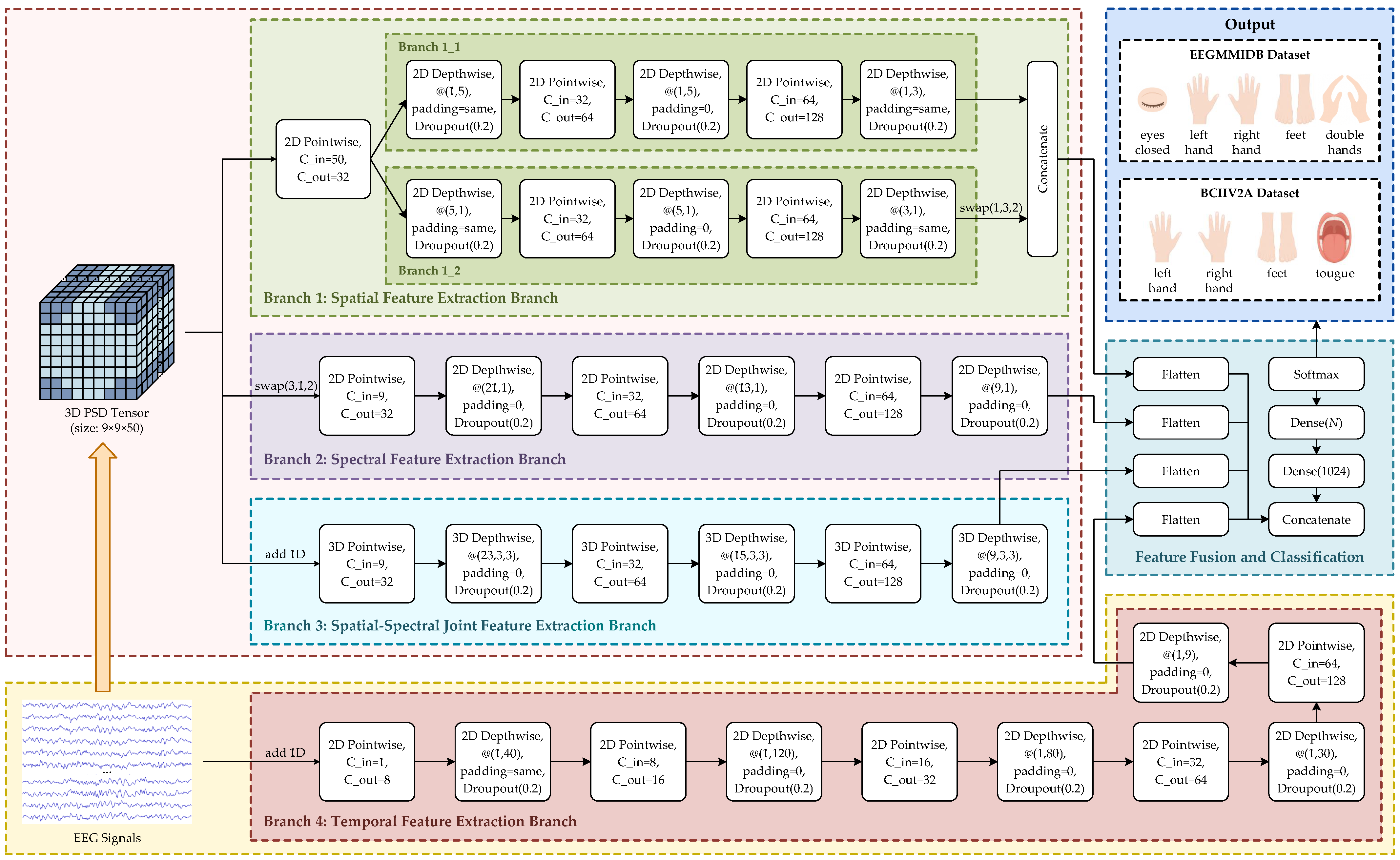
2.4. Network Architecture
2.4.1. Branch 1: Spatial Feature Extraction Branch
2.4.2. Branch 2: Spectral Feature Extraction Branch
2.4.3. Branch 3: Spatial-Spectral Joint Feature Extraction Branch
2.4.4. Branch 4: Temporal Feature Extraction Branch
3. Experiments and Results
3.1. Training Procedure
3.2. Evaluation Methods
- (1)
- Confusion Matrix
- (2)
- Accuracy
- (3)
- Kappa Coefficient
- (4)
- Grad-CAM Visualization
3.3. Experimental Results
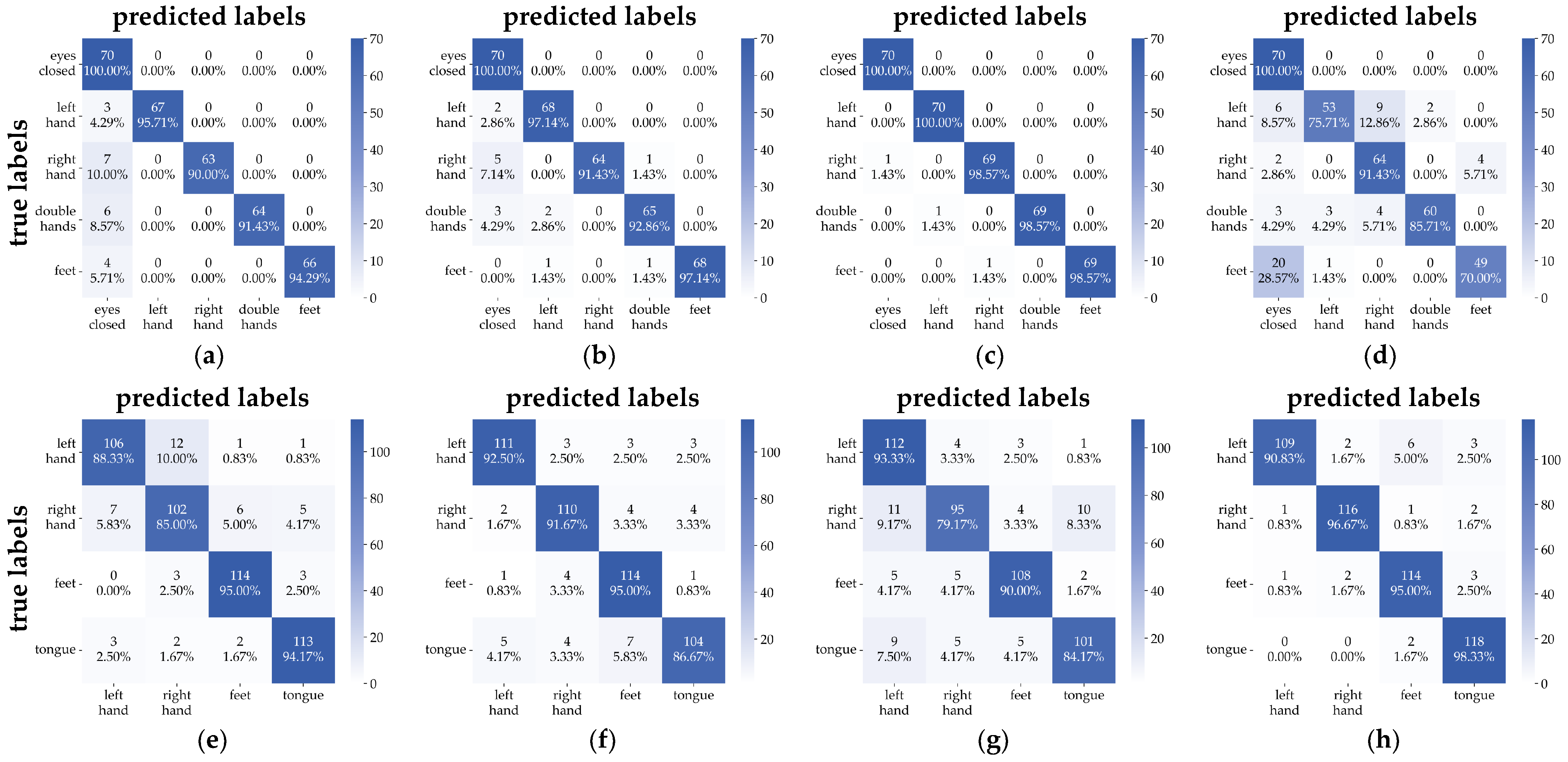
3.3.1. Confusion Matrix
3.3.2. Ablation Study
- (1)
- Single-branch models: Variants using only one of Branches 1, 2, 3, or 4 were evaluated to assess the independent modeling capabilities of each feature dimension.
- (2)
- Two-branch combination models: Four dual-branch variants (Branch 1+2, Branch 1+4, Branch 2+4, and Branch 3+4) were developed to explore the collaborative modeling effects of different feature dimensions and to analyze the complementarity among spatial, spectral, and temporal information.
- (3)
- Multi-branch combination models: In addition to the full MSSTNet architecture, variants combining Branch 1+2+3 and Branch 1+2+4 were also evaluated to assess the comprehensive performance under multi-dimensional feature fusion.
3.3.3. Performance Comparison
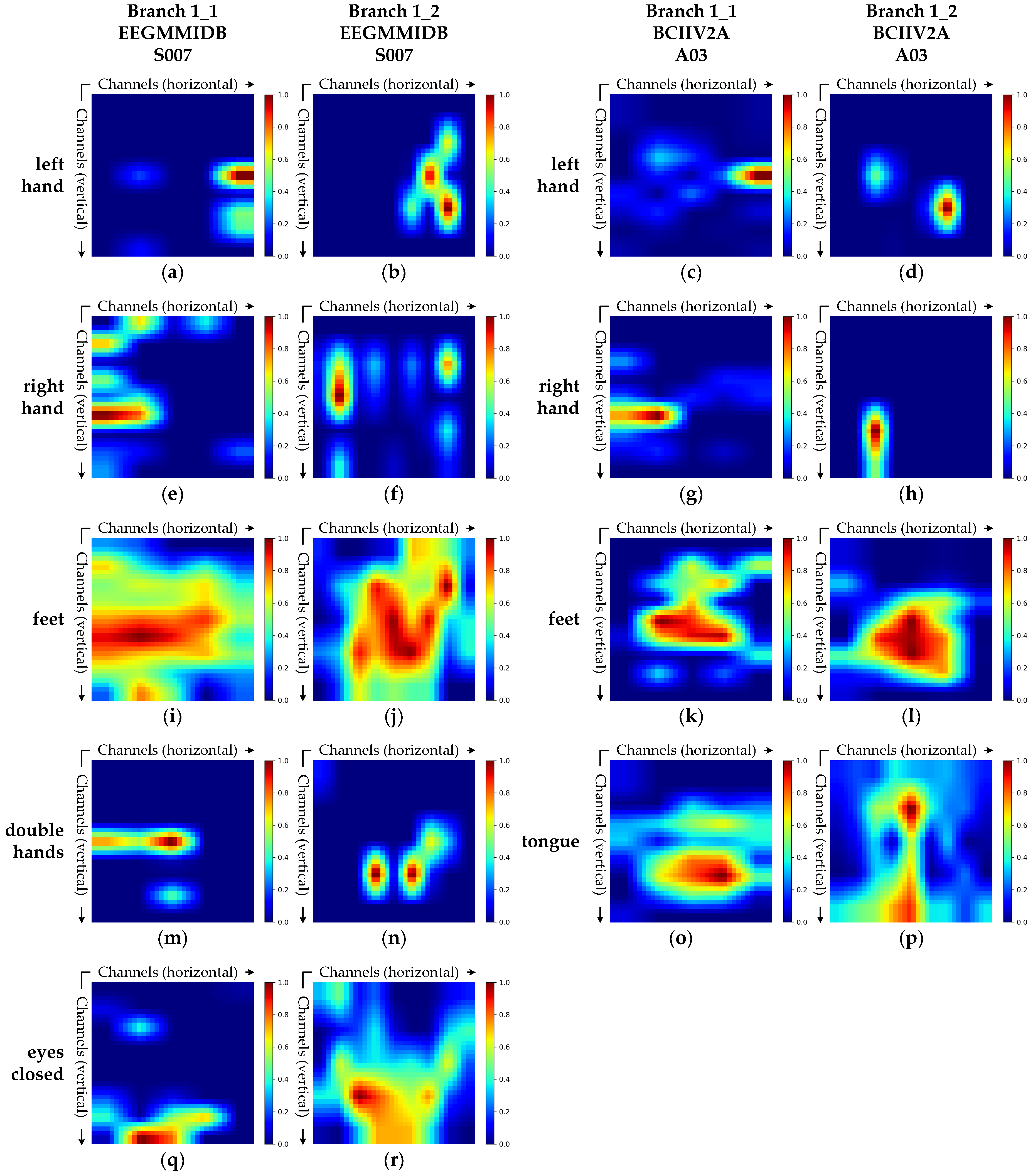
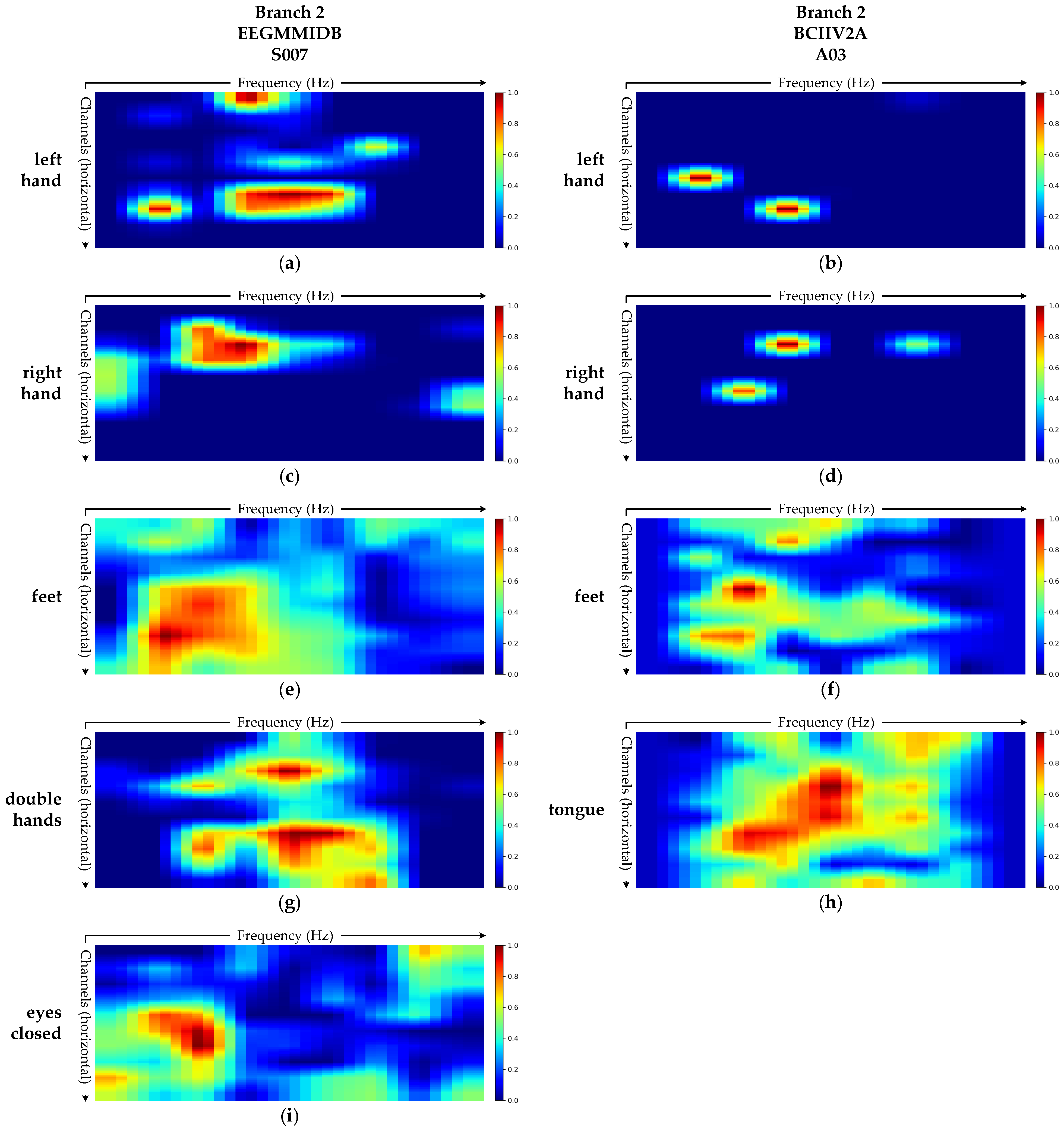
3.3.4. Grad-CAM Visualization Analysis
- (1)
- Branch 1: Spatial Feature Extraction Branch
- (2)
- Branch 2: Spectral Feature Extraction Branch
- (3)
- Branch 3: Spatial-Spectral Joint Feature Extraction Branch
4. Discussion
- (1)
- This study proposes MSSTNet, a multi-branch deep neural network that takes both 3D PSD representations and 2D time-domain EEG signals as dual inputs. These inputs enable the model to capture spatial, spectral, and temporal features effectively.
- (2)
- MSSTNet incorporates four specialized feature extraction branches and employs DSC modules as core components. This design achieves a balance between representational capacity and computational efficiency, ensuring robust decoding performance while reducing the computational overhead.
- (3)
- On the EEGMMIDB and BCIIV2A datasets, MSSTNet achieves accuracies of 86.34% and 83.43%, and kappa coefficients of 0.829 and 0.779, respectively, outperforming representative methods including EEGNet, ShallowFBCSPNet, EEGInception, CRGNet, and BrainGridNet.
- (4)
- Ablation experiments systematically quantify the independent contributions and complementarity of each branch. They reveal that hierarchical convolution-based cross-dimensional modeling more effectively captures spatial-spectral interactions during feature extraction. Meanwhile, the temporal branch provides essential complementary information, further enhancing overall discriminative performance.
- (5)
- Grad-CAM visualizations show that the model’s attention patterns align closely with established neurophysiological principles, thereby corroborating the physiological plausibility of its decision-making process from an interpretability perspective.
- (1)
- Although the multi-branch architecture effectively integrates spatial, spectral, and temporal features, the current fusion strategy relies on simple concatenation. This approach lacks explicit cross-dimensional interaction modeling, which may constrain further improvements in fusion effectiveness.
- (2)
- The training and evaluation in this study were conducted exclusively in a subject-dependent setting. The model’s generalization ability under cross-subject transfer or few-shot scenarios, which is critical for practical BCI system applications, has yet to be validated.
- (3)
- While the DSC modules outperform 2D standard convolutions in reducing parameter count and computational overhead, the overall network depth of MSSTNet remains relatively large. So its deployment efficiency on low-power or embedded devices could still be optimized compared with certain lightweight architectures, such as BrainGridNet.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Robinson, N.; Mane, R.; Chouhan, T.; Guan, C. Emerging trends in BCI-robotics for motor control and rehabilitation. Curr. Opin. Biomed. Eng. 2021, 20, 100354. [Google Scholar] [CrossRef]
- Lazcano-Herrera, A.G.; Fuentes-Aguilar, R.Q.; Chairez, I.; Alonso-Valerdi, L.M.; Gonzalez-Mendoza, M.; Alfaro-Ponce, M. Review on BCI virtual rehabilitation and remote technology based on EEG for assistive devices. Appl. Sci. 2022, 12, 12253. [Google Scholar] [CrossRef]
- Yoxon, E.; Welsh, T.N. Motor system activation during motor imagery is positively related to the magnitude of cortical plastic changes following motor imagery training. Behav. Brain Res. 2020, 390, 112685. [Google Scholar] [CrossRef] [PubMed]
- Palumbo, A.; Gramigna, V.; Calabrese, B.; Ielpo, N. Motor-imagery EEG-based BCIs in wheelchair movement and control: A systematic literature review. Sensors 2021, 21, 6285. [Google Scholar] [CrossRef] [PubMed]
- Altaheri, H.; Muhammad, G.; Alsulaiman, M.; Amin, S.U.; Altuwaijri, G.A.; Abdul, W.; Bencherif, M.A.; Faisal, M. Deep learning techniques for classification of electroencephalogram (EEG) motor imagery (MI) signals: A review. Neural Comput. Appl. 2023, 35, 14681–14722. [Google Scholar] [CrossRef]
- Koles, Z.J.; Lazar, M.S.; Zhou, S.Z. Spatial patterns underlying population differences in the background EEG. Brain Topogr. 1990, 2, 275–284. [Google Scholar] [CrossRef] [PubMed]
- Jiang, A.; Shang, J.; Liu, X.; Tang, Y.; Kwan, H.K.; Zhu, Y. Efficient CSP algorithm with spatio-temporal filtering for motor imagery classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1006–1016. [Google Scholar] [CrossRef] [PubMed]
- Blanco-Diaz, C.F.; Antelis, J.M.; Ruiz-Olaya, A.F. Comparative analysis of spectral and temporal combinations in CSP-based methods for decoding hand motor imagery tasks. J. Neurosci. Methods 2022, 371, 109495. [Google Scholar] [CrossRef] [PubMed]
- Mammone, N.; Ieracitano, C.; Adeli, H.; Morabito, F.C. AutoEncoder Filter Bank Common Spatial Patterns to Decode Motor Imagery from EEG. IEEE J. Biomed. Health Inform. 2023, 27, 2365–2376. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Wei, Q. Tensor decomposition-based channel selection for motor imagery-based brain-computer interfaces. Cogn. Neurodyn. 2024, 18, 877–892. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Gao, X.; Zhu, X.; Wang, B.; Lu, N.; Wang, J. Motor imagery EEG classification based on ensemble support vector learning. Comput. Methods Programs Biomed. 2020, 193, 105464. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, W.; Lin, C.; Pei, Z.; Chen, J.; Chen, Z. Boosting-LDA algriothm with multi-domain feature fusion for motor imagery EEG decoding. Biomed. Signal Process. Control 2021, 70, 102983. [Google Scholar] [CrossRef]
- Zhao, W.; Zhao, W.; Wang, W.; Jiang, X.; Zhang, X.; Peng, Y.; Zhang, B.; Zhang, G. A Novel Deep Neural Network for Robust Detection of Seizures Using EEG Signals. Comput. Math. Methods Med. 2020, 2020, 9689821. [Google Scholar] [CrossRef] [PubMed]
- Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef] [PubMed]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A compact convolutional neural network for EEG-based brain-computer interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef] [PubMed]
- Riyad, M.; Khalil, M.; Adib, A. A novel multi-scale convolutional neural network for motor imagery classification. Biomed. Signal Process Control 2021, 68, 102747. [Google Scholar] [CrossRef]
- Yu, S.; Wang, Z.; Wang, F.; Chen, K.; Yao, D.; Xu, P.; Zhang, T. Multiclass classification of motor imagery tasks based on multi-branch convolutional neural network and temporal convolutional network model. Cereb. Cortex. 2024, 34, bhad511. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Yang, B.; Ke, S.; Liu, P.; Rong, F.; Xia, X. M-FANet: Multi-feature attention convolutional neural network for motor imagery decoding. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 401–411. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, Y.; Qi, W.; Kong, D.; Wang, W. BrainGridNet: A two-branch depthwise CNN for decoding EEG-based multi-class motor imagery. Neural Netw. 2024, 170, 312–324. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Tangermann, M.; Müller, K.R.; Aertsen, A.; Birbaumer, N.; Braun, C.; Brunner, C.; Blankertz, B. Review of the BCI competition IV. Front. Neurosci. 2012, 6, 55. [Google Scholar] [CrossRef] [PubMed]
- Brundavani, P.; Vardhan, D.V. A novel approach for minimising anti-aliasing effects in EEG data acquisition. Open Life Sci. 2023, 18, 20220664. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Zhang, H.; Zhu, G.; You, F.; Kuang, S.; Sun, L. A multi-branch 3D convolutional neural network for EEG-based motor imagery classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 2164–2177. [Google Scholar] [CrossRef] [PubMed]
- Kaľavský, A.; Niesłony, A.; Huňady, R. Influence of PSD estimation parameters on fatigue life prediction in spectral method. Materials 2023, 16, 1007. [Google Scholar] [CrossRef] [PubMed]
- Dişli, F.; Gedikpınar, M.; Fırat, H.; Şengür, A.; Güldemir, H.; Koundal, D. Epilepsy diagnosis from EEG signals using continuous wavelet Transform-Based depthwise convolutional neural network model. Diagnostics 2025, 15, 84. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Zhang, T.; Feng, G. Channel compression: Rethinking information redundancy among channels in CNN architecture. IEEE Access. 2020, 8, 147265–147274. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- Hu, Y.; Tian, S.; Ge, J. Hybrid convolutional network combining multiscale 3D depthwise separable convolution and CBAM residual dilated convolution for hyperspectral image classification. Remote Sens. 2023, 15, 4796. [Google Scholar] [CrossRef]
- Salehin, I.; Kang, D.K. A review on dropout regularization approaches for deep neural networks within the scholarly domain. Electronics 2023, 12, 3106. [Google Scholar] [CrossRef]
- Thakur, A.; Gupta, M.; Sinha, D.K.; Mishra, K.K.; Venkatesan, V.K.; Guluwadi, S. Transformative breast Cancer diagnosis using CNNs with optimized ReduceLROnPlateau and Early stopping Enhancements. Int. J. Comput. Intell. Syst. 2024, 17, 14. [Google Scholar] [CrossRef]
- Krstinić, D.; Braović, M.; Šerić, L.; Božić-Štulić, D. Multi-label classifier performance evaluation with confusion matrix. Comput. Sci. Inf. Technol. 2020, 1, 1–14. [Google Scholar] [CrossRef]
- Fleiss, J.L.; Cohen, J. The equivalence of weighted kappa and the intraclass correlation coefficient as measures of reliability. Educ. Psychol. Meas. 1973, 33, 613–619. [Google Scholar] [CrossRef]
- Viera, A.J.; Garrett, J.M. Understanding interobserver agreement: The kappa statistic. Fam. Med. 2005, 37, 360–363. [Google Scholar] [PubMed]
- Zhang, Y.; Zhu, Y.; Liu, J.; Yu, W.; Jiang, C. An Interpretability optimization method for deep learning networks based on grad-CAM. IEEE Internet Things J. 2024, 12, 3961–3970. [Google Scholar] [CrossRef]
- Pfurtscheller, G.; Neuper, C. Motor imagery and direct brain-computer communication. Proc. IEEE 2001, 89, 1123–1134. [Google Scholar] [CrossRef]
- Santamaria-Vazquez, E.; Martinez-Cagigal, V.; Vaquerizo-Villar, F.; Hornero, R. EEG-inception: A novel deep convolutional neural network for assistive ERP-based brain-computer interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 2773–2782. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.; Liu, W.; Yang, X. Convolutional neural network and riemannian geometry hybrid approach for motor imagery classification. Neurocomputing 2022, 507, 180–190. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Song, Z. Classification of motor imagery electroencephalography signals based on image processing method. Sensors 2021, 21, 4646. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.; Liu, T.; Szarkowski, R.; Rios, C.; Ashe, J.; He, B. Negative covariation between task-related responses in alpha/beta-band activity and BOLD in human sensorimotor cortex: An EEG and fMRI study of motor imagery and movements. Neuroimage 2010, 49, 2596–2606. [Google Scholar] [CrossRef] [PubMed]
- Yi, W.; Qiu, S.; Qi, H.; Zhang, L.; Wan, B.; Ming, D. EEG feature comparison and classification of simple and compound limb motor imagery. J. Neuroeng. Rehabil. 2013, 10, 106. [Google Scholar] [CrossRef] [PubMed]
- Giannopulu, I.; Mizutani, H. Neural kinesthetic contribution to motor imagery of body parts: Tongue, hands, and feet. Front. Hum. Neurosci. 2021, 15, 602723. [Google Scholar] [CrossRef] [PubMed]
- Hohaia, W.; Saurels, B.W.; Johnston, A.; Yarrow, K.; Arnold, D.H. Occipital alpha-band brain waves when the eyes are closed are shaped by ongoing visual processes. Sci. Rep. 2022, 12, 1194. [Google Scholar] [CrossRef] [PubMed]
- Pfurtscheller, G.; Brunner, C.; Schlögl, A.; Da Silva, F.L. Mu rhythm (de) synchronization and EEG single-trial classification of different motor imagery tasks. Neuroimage 2006, 31, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Rimbert, S.; Al-Chwa, R.; Zaepffel, M.; Bougrain, L. Electroencephalographic modulations during an open-or closed-eyes motor task. PeerJ 2018, 6, e4492. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Li, M.; Li, J.; Guo, M.; Xu, G. A robust multi-branch multi-attention-mechanism EEGNet for motor imagery BCI decoding. J. Neurosci. Methods 2024, 405, 110108. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Wu, D. Transfer learning for brain-computer interfaces: A Euclidean space data alignment approach. IEEE Trans. Biomed. Eng. 2019, 67, 399–410. [Google Scholar] [CrossRef] [PubMed]


| Model | Subjects | Avg. Acc | Avg. Kappa | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S001 | S002 | S003 | S004 | S005 | S006 | S007 | S008 | S009 | S010 | |||
| Branch 1 | 85.14 | 80.86 | 78.29 | 87.71 | 73.14 | 69.43 | 88.57 | 74.57 | 70.00 | 76.57 | 78.43 | 0.729 |
| Branch 2 | 83.14 | 80.00 | 77.71 | 87.43 | 73.14 | 69.14 | 88.00 | 73.14 | 68.86 | 74.86 | 77.54 | 0.718 |
| Branch 3 | 88.29 | 83.43 | 80.86 | 91.14 | 75.14 | 72.29 | 92.00 | 75.43 | 72.29 | 78.57 | 80.94 | 0.761 |
| Branch 4 | 86.29 | 81.43 | 79.71 | 89.14 | 74.29 | 70.57 | 90.57 | 75.43 | 70.29 | 76.86 | 79.46 | 0.742 |
| Branch 1+2 | 87.14 | 82.86 | 81.14 | 90.57 | 74.86 | 71.71 | 91.43 | 75.71 | 71.14 | 77.43 | 80.40 | 0.754 |
| Branch 1+4 | 87.71 | 83.71 | 82.57 | 90.29 | 76.00 | 71.14 | 93.14 | 77.14 | 71.71 | 77.71 | 81.11 | 0.763 |
| Branch 2+4 | 88.29 | 82.86 | 81.71 | 90.86 | 75.43 | 71.43 | 92.29 | 75.71 | 72.57 | 78.57 | 80.97 | 0.762 |
| Branch 3+4 | 90.00 | 84.00 | 82.86 | 92.57 | 77.14 | 72.57 | 94.29 | 77.43 | 73.71 | 79.71 | 82.43 | 0.780 |
| Branch 1+2+3 | 91.43 | 84.57 | 83.43 | 92.86 | 78.00 | 74.00 | 96.29 | 78.00 | 75.14 | 81.43 | 83.52 | 0.799 |
| Branch 1+2+4 | 93.14 | 86.00 | 85.43 | 94.57 | 79.71 | 75.71 | 98.00 | 80.00 | 77.14 | 83.71 | 85.43 | 0.818 |
| MSSTNet | 94.29 | 87.43 | 87.14 | 95.71 | 80.29 | 76.00 | 99.14 | 81.43 | 77.43 | 84.57 | 86.34 | 0.829 |
| Model | Subject | Avg. Acc | Avg. Kappa | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A01 | A02 | A03 | A04 | A05 | A06 | A07 | A08 | A09 | |||
| Branch 1 | 83.54 | 60.21 | 89.17 | 68.33 | 51.46 | 67.08 | 85.83 | 83.96 | 81.67 | 74.58 | 0.661 |
| Branch 2 | 83.75 | 61.04 | 81.25 | 70.00 | 52.08 | 65.00 | 82.29 | 77.50 | 78.12 | 72.34 | 0.631 |
| Branch 3 | 89.17 | 67.50 | 86.04 | 73.96 | 58.33 | 64.58 | 82.71 | 87.82 | 82.29 | 76.93 | 0.693 |
| Branch 4 | 91.04 | 60.42 | 85.21 | 76.67 | 56.25 | 59.79 | 81.46 | 87.50 | 82.08 | 75.60 | 0.675 |
| Branch 1+2 | 90.00 | 62.08 | 87.29 | 63.96 | 62.71 | 70.83 | 88.54 | 84.58 | 76.25 | 76.25 | 0.683 |
| Branch 1+4 | 89.58 | 66.25 | 92.71 | 70.42 | 63.54 | 71.67 | 87.29 | 80.83 | 78.96 | 77.92 | 0.706 |
| Branch 2+4 | 83.54 | 67.92 | 86.88 | 78.33 | 61.25 | 58.33 | 87.08 | 87.71 | 83.96 | 77.22 | 0.696 |
| Branch 3+4 | 89.79 | 67.71 | 88.33 | 67.50 | 62.29 | 72.71 | 88.75 | 87.29 | 84.58 | 78.77 | 0.717 |
| Branch 1+2+3 | 88.54 | 65.00 | 92.50 | 73.75 | 63.54 | 72.92 | 91.04 | 87.29 | 86.46 | 80.12 | 0.736 |
| Branch 1+2+4 | 91.67 | 68.95 | 94.17 | 76.67 | 65.62 | 73.54 | 91.87 | 87.92 | 82.34 | 82.01 | 0.765 |
| MSSTNet | 92.29 | 70.83 | 95.83 | 77.29 | 67.92 | 75.21 | 92.92 | 88.75 | 89.79 | 83.43 | 0.779 |
| Model | Subjects | Avg. Acc | Avg. Kappa | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S001 | S002 | S003 | S004 | S005 | S006 | S007 | S008 | S009 | S010 | |||
| EEGNet | 68.57 | 65.14 | 69.71 | 59.43 | 56.86 | 54.86 | 78.86 | 63.43 | 53.71 | 61.71 | 63.40 | 0.537 |
| ShallowFBCSPNet | 79.71 | 87.43 | 77.14 | 67.43 | 58.29 | 61.43 | 89.43 | 74.29 | 60.29 | 71.14 | 72.83 | 0.682 |
| EEGInception | 77.71 | 76.00 | 78.86 | 72.86 | 69.43 | 73.14 | 80.29 | 73.71 | 65.14 | 64.29 | 74.13 | 0.700 |
| CRGNet | 82.28 | 89.43 | 74.57 | 73.43 | 68.29 | 63.71 | 94.57 | 80.86 | 58.29 | 68.57 | 76.16 | 0.712 |
| BrainGridNet | 89.71 | 83.14 | 75.71 | 87.71 | 75.43 | 78.86 | 93.43 | 77.43 | 75.71 | 74.29 | 81.90 | 0.756 |
| MSSTNet | 94.29 | 87.43 | 87.14 | 95.71 | 80.29 | 76.00 | 99.14 | 81.43 | 77.43 | 84.57 | 86.34 | 0.829 |
| Model | Subjects | Avg. Acc | Avg. Kappa | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A01 | A02 | A03 | A04 | A05 | A06 | A07 | A08 | A09 | |||
| EEGNet | 83.43 | 59.43 | 85.43 | 66.28 | 57.14 | 53.71 | 86.86 | 81.14 | 84.57 | 73.11 | 0.662 |
| ShallowFBCSPNet | 86.67 | 62.29 | 89.79 | 72.09 | 56.46 | 57.92 | 90.83 | 80.42 | 78.96 | 75.05 | 0.689 |
| EEGInception | 85.43 | 65.58 | 94.28 | 71.14 | 55.71 | 68.57 | 88.00 | 85.43 | 87.71 | 77.98 | 0.752 |
| CRGNet | 81.67 | 68.54 | 88.33 | 72.92 | 62.29 | 70.42 | 93.13 | 86.86 | 76.46 | 77.85 | 0.748 |
| BrainGridNet | 90.83 | 63.54 | 90.42 | 80.63 | 77.50 | 71.25 | 86.25 | 77.71 | 83.33 | 80.16 | 0.760 |
| MSSTNet | 92.29 | 70.83 | 95.83 | 77.29 | 67.92 | 75.21 | 92.92 | 88.75 | 89.79 | 83.43 | 0.779 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, X.; Liu, C.; Gao, C.; Deng, Z.; Guan, W.; Gong, Y. A Multi-Branch Network for Integrating Spatial, Spectral, and Temporal Features in Motor Imagery EEG Classification. Brain Sci. 2025, 15, 877. https://doi.org/10.3390/brainsci15080877
Lian X, Liu C, Gao C, Deng Z, Guan W, Gong Y. A Multi-Branch Network for Integrating Spatial, Spectral, and Temporal Features in Motor Imagery EEG Classification. Brain Sciences. 2025; 15(8):877. https://doi.org/10.3390/brainsci15080877
Chicago/Turabian StyleLian, Xiaoqin, Chunquan Liu, Chao Gao, Ziqian Deng, Wenyang Guan, and Yonggang Gong. 2025. "A Multi-Branch Network for Integrating Spatial, Spectral, and Temporal Features in Motor Imagery EEG Classification" Brain Sciences 15, no. 8: 877. https://doi.org/10.3390/brainsci15080877
APA StyleLian, X., Liu, C., Gao, C., Deng, Z., Guan, W., & Gong, Y. (2025). A Multi-Branch Network for Integrating Spatial, Spectral, and Temporal Features in Motor Imagery EEG Classification. Brain Sciences, 15(8), 877. https://doi.org/10.3390/brainsci15080877






