Predicting Brain Age and Gender from Brain Volume Data Using Variational Quantum Circuits
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Dataset
2.2. Image Processing and Feature Extraction
2.3. Machine Learning Algorithms
2.4. Model Training and Evaluation
3. Results
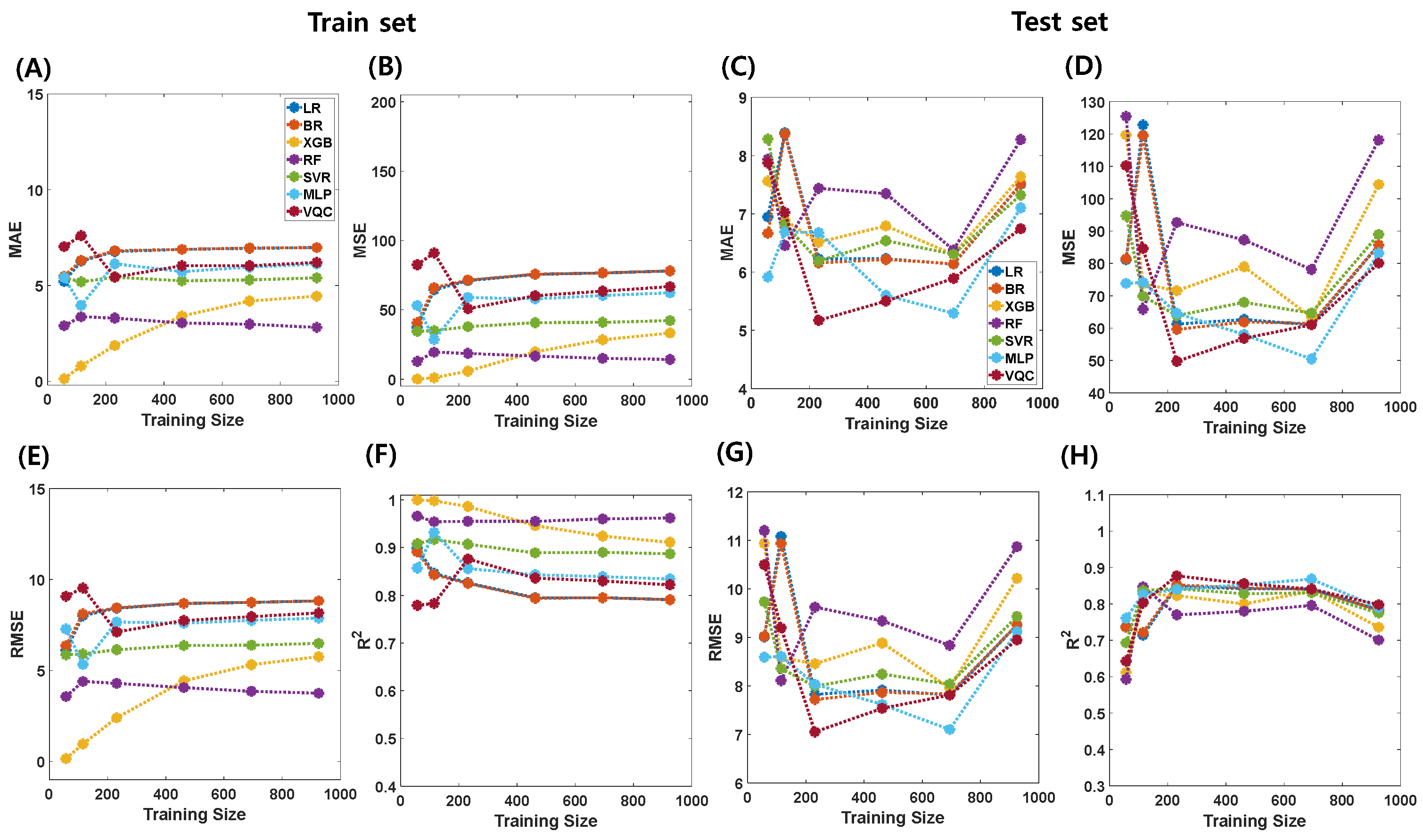
3.1. Algorithm Performance for Brain Age Prediction
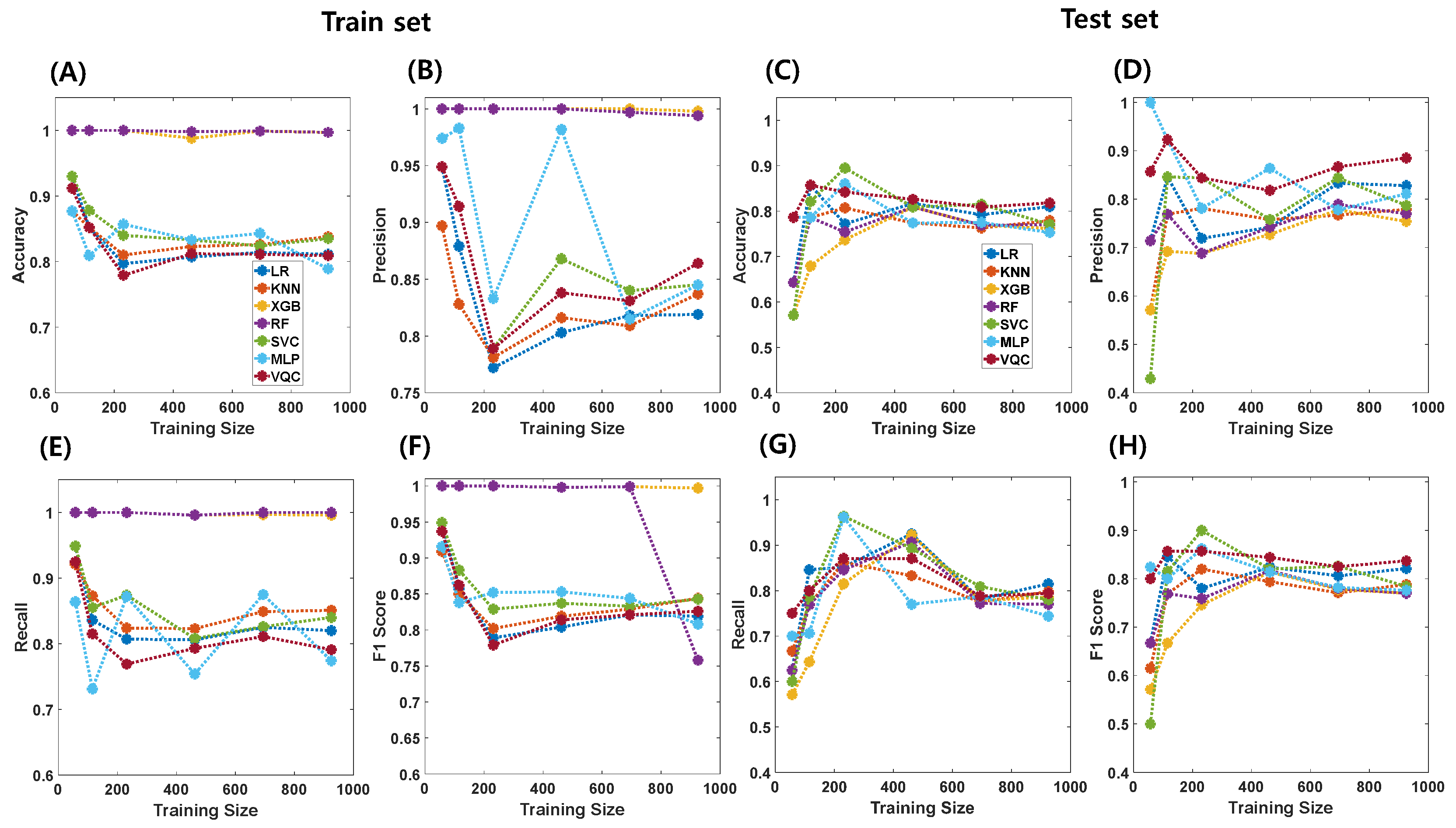
3.2. Algorithm Performance for Gender Prediction
3.3. Comparative Study for Brain Age Prediction
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baecker, L.; Garcia-Dias, R.; Vieira, S.; Scarpazza, C.; Mechelli, A. Machine learning for brain age prediction: Introduction to methods and clinical applications. eBioMedicine 2021, 72, 103600. [Google Scholar] [CrossRef] [PubMed]
- Mohajer, B.; Abbasi, N.; Mohammadi, E.; Khazaie, H.; Osorio, R.S.; Rosenzweig, I.; Eickhoff, C.R.; Zarei, M.; Tahmasian, M.; Eickhoff, S.B. Gray matter volume and estimated brain age gap are not linked with sleep-disordered breathing. Hum. Brain Mapp. 2020, 41, 3034–3044. [Google Scholar] [CrossRef] [PubMed]
- Pardoe, H.R.; Cole, J.H.; Blackmon, K.; Thesen, T.; Kuzniecky, R. Structural brain changes in medically refactory focal epilepsy resemble premature brain aging. Epilepsy Res. 2017, 133, 28–32. [Google Scholar] [CrossRef] [PubMed]
- Cole, J.H.; Raffel, J.; Friede, T.; Eshaghi, A.; Brownlee, W.J.; Chard, D.; Stefano, N.D.; Enzinger, C.; Pirpamer, L.; Filippi, M.; et al. Longitudinal Assessment of Multiple Sclerosis with the Brain-Age Paradigm. Ann. Neurol. 2020, 88, 93–105. [Google Scholar] [CrossRef] [PubMed]
- Savjani, R.R.; Taylor, B.A.; Acion, L.; Wilde, E.A.; Jorge, R.E. Accelerated Changes in Cortical Thickness Measurements with Age. J. Neurotrauma 2017, 34, 3107–3116. [Google Scholar] [CrossRef]
- Lee, W.H.; Antoniades, M.; Schnack, H.G.; Kahn, R.S.; Frangou, S. Brain age prediction in schizophrenia: Does the choice of machine learning algorithm matter? Psychiatry Res. Neuroimaging 2021, 310, 111270. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.D.; Tsai, S.J.; Lin, C.P.; Lee, Y.J.; Yang, A.C. Predicting aging trajectories of decline in brain volume, cortical thickness and fractional anisotropy in schizophrenia. Schizophrenia 2023, 9, 1. [Google Scholar] [CrossRef] [PubMed]
- Van Gestel, H.; Franke, K.; Petite, J.; Slaney, C.; Garnham, J.; Helmick, C.; Johnson, K.; Uher, R.; Alda, M.; Hajek, T. Brain age in bipolar disorders: Effects of lithium treatment. Aust. N. Z. J. Psychiatry 2019, 53, 1179–1188. [Google Scholar] [CrossRef]
- Han, L.K.L.; Dinga, R.; Hahn, T.; Ching, C.R.; Eyler, L.T.; Aftanas, L.; Aghajani, M.; Aleman, A.; Baune, B.T.; Berger, K.; et al. Brain aging in major depressive disorder: Results from the ENIGMA major depressive disorder working group. Mol. Psychiatry 2021, 26, 5124–5139. [Google Scholar] [CrossRef]
- Flint, C.; Forster, K.; Koser, S.A.; Konras, C.; Zwitserlood, P.; Berger, K.; Hermesdorf, M.; Kircher, T.; Nenadic, I.; Krug, A.; et al. Biological sex classification with structural MRI data shows increased misclassification in transgender women. Neuropsychopharmacology 2020, 45, 1758–1765. [Google Scholar] [CrossRef]
- Mendes, S.L.; Pinaya, W.H.L.; Pan, P.; Sata, J.R. Estimating Gender and Age from Brain Structural MRI of Children and Adolescents: A 3D Convolutional Neural Network Multitask Learning Model. Comput. Intell. Neurosci. 2021, 12, 5550914. [Google Scholar] [CrossRef] [PubMed]
- Ebel, M.; Domin, M.; Neumann, N.; Schmidt, C.O.; Lotze, M.; Stanke, M. Classifying sex with volume-matched brain MRI. Neuroimage Rep. 2023, 3, 110181. [Google Scholar] [CrossRef]
- Baecker, L.; Dafflon, J.; da Costa, P.F.; Garcia-Dias, R.; Vieira, S.; Scarpazza, C.; Calhoun, V.D.; Sato, J.R.; Mechelli, A.; Pinaya, W.H.L. Brain age prediction: A comparison between machine learning models using region- and voxel-based morphometric data. Hum. Brain Mapp. 2021, 42, 2332–2346. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Kim, S.Y.; Lee, J.; Lee, W.H. Brain Age Prediction: A Comparison between Machine Learning Models Using Brain Morphometric Data. Sensors 2022, 22, 8077. [Google Scholar] [CrossRef] [PubMed]
- Simfukwe, C.; Youn, Y.C. Prediction of East Asian Brain Age using Machine Learning Algorithms Trained With Community-based Healthy Brain MRI. Dement. Neurocogn. Disord. 2022, 21, 138–146. [Google Scholar] [CrossRef] [PubMed]
- More, S.; Antonopoulos, G.; Hoffstaedter, F.; Caspers, J.; Eickhoff, S.B.; Patil, K.R. Brain-age prediction: A systematic comparison of machine learning workflows. NeuroImage 2023, 270, 119947. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Gong, W.; Beckmann, C.F.; Vedaldi, A.; Smith, S.M. Accurate brain age prediction with lightweight deep neural networks. Med. Image Anal. 2021, 68, 101871. [Google Scholar] [CrossRef]
- Hwang, I.; Yeon, E.K.; Lee, J.Y.; Yoo, R.E.; Kang, K.M.; Yun, T.J.; Choi, S.H.; Sohn, C.H.; Kim, H.; Kim, J. Prediction of brain age from routine T2-weighted spin-echo brain magnetic resonance images with a deep convolutional neural network. Neurobiol. Aging 2021, 105, 78–85. [Google Scholar] [CrossRef]
- Johnsson, B.A.; Bjornsdottir, G.; Thorgeirsson, T.E.; Ellingsen, L.M.; Walters, G.B.; Gudbjartsson, D.F.; Stefansson, H.; Stefansson, K.; Ulfarsson, M.O. Brain age prediction using deep learning uncovers associated sequence variants. Nat. Commun. 2019, 10, 5409. [Google Scholar] [CrossRef]
- Tanveer, M.; Ganaie, M.A.; Beheshti, I.; Goel, T.; Ahmad, N.; Lai, K.T.; Kaizhu, H.; Zhang, Y.D.; Ser, J.D.; Lin, C.T. Deep learning for brain age estimation: A systematic review. Inf. Fusion 2023, 96, 130–143. [Google Scholar] [CrossRef]
- Aycheh, H.M.; Seong, J.K.; Shin, J.H.; Na, D.L.; Kang, B.; Seo, S.W.; Sohn, K.A. Biological Brain Age Prediction Using Cortical Thickness Data: A Large Scale Cohort Study. Front. Aging Neurosci. 2018, 10, 252. [Google Scholar] [CrossRef]
- Mouches, P.; Wilms, M.; Aulakh, A.; Langner, S.; Forkert, N.D. Multimodal brain age prediction fusing morphometric and imaging data and association with cardiovascular risk factors. Front. Neurol. 2022, 13, 979774. [Google Scholar] [CrossRef]
- Mouches, P.; Wilms, M.; Rajashekar, D.; Langner, S.; Forkert, N.D. Multimodal biological brain age prediction using magnetic resonance imaging and angiography with the identification of predictive regions. Hum. Brain Mapp. 2022, 43, 2554–2566. [Google Scholar] [CrossRef]
- Kharsa, R.; Bouridane, A.; Amira, A. Advances in Quantum Machine Learning and Deep Learning for Image Classification: A Survey. Neurocomputing 2023, 560, 126843. [Google Scholar] [CrossRef]
- Sagingalieva, A.; Kordzanganeh, M.; Kenbayev, N.; Kosichkina, D.; Tomashuk, T.; Melnikov, A. Hybrid Quantum Neural Network For Drug Response Prediction. Cancers 2023, 15, 2705. [Google Scholar] [CrossRef]
- Xiao, T.; Zhai, X.; Wu, X.; Fan, J.; Zeng, G. Practical advantage of quantum machine learning in ghost imaging. Commun. Phys. 2023, 6, 171. [Google Scholar] [CrossRef]
- Cho, H.; Seo, S.W.; Kim, J.H.; Kim, C.; Ye, B.S.; Kim, G.H.; Noh, Y.; Kim, H.J.; Yoon, C.W.; Seong, J.K.; et al. Changes in structures in early- versus late-onset Alzheimer’s disease. Neurobiol. Aging 2013, 34, 7. [Google Scholar] [CrossRef]
- Park, S.E.; Jeon, Y.J.; Baek, H.M. Functional and Structural Brain Abnormalities and Clinical Characteristics of Male Patients with Alcohol Dependence. Brain Sci. 2023, 13, 942. [Google Scholar] [CrossRef]
- Kim, A.Y.; Shim, J.H.; Choi, H.J.; Baek, H.M. Comparison of volumetric and shape changes of subcortical structures based on 3-dimensional image between obesity and normal-weighted subjects using 3.0 T MRI. J. Clin. Neurosci. 2020, 73, 280–287. [Google Scholar] [CrossRef]
- Henschel, L.; Kügler, D.; Reuter, M. FastSurferVINN: Building resolution-independence into deep learning segmentation methods—A solution for HighRes brain MRI. NeuroImage 2022, 251, 118933. [Google Scholar] [CrossRef]
- Fischl, B.; Salat, D.H.; Busa, E.; Albert, M.; Dieterich, M.; Haselgrove, C.; van der Kouwe, A.; Killiany, R.; Kennedy, D.; Klaveness, S.; et al. Whole Brain Segmentation: Automated Labeling of Neuroanatomical Structures in the Human Brain. Neuron 2002, 33, 341–355. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
- Zhang, S.X.; Allcock, J.; Wan, Z.Q.; Liu, S.; Sun, J.; Yu, H.; Yang, X.H.; Qiu, J.; Ye, Z.; Chen, Y.Q.; et al. TensorCircuit: A Quantum Software Framework for the NISQ Era. Quantum 2023, 7, 912. [Google Scholar] [CrossRef]
- Bergholm, V.; Izaac, J.; Schuld, M.; Gogolin, C.; Ahmed, S.; Ajith, V.; Alam, M.S.; Alonso-Linaje, G.; AkashNarayanan, B.; Asadi, A.; et al. PennyLane: Automatic differentiation of hybrid quantum-classical computations. arXiv 2018, arXiv:1811.04968. [Google Scholar]
- Cordier, B.A.; Sawaya, N.P.D.; Guerreschi, G.G.; McWeeney, S.K. Biology and medicine in the landscape of quantum advantages. J. R. Soc. Interface 2022, 19, 20220541. [Google Scholar] [CrossRef]
- Wang, J.; Knol, M.J.; Tuilpin, A.; Dubost, F.; de Bruijne, M.; Vernooij, M.W.; Adams, H.H.H.; Ikram, M.A.; Niessen, W.J.; Roshchupkin, G.V. Gray Matter Age Prediction as a Biomarker for Risk of Dementia. Proc. Natl. Acad. Sci. USA 2019, 116, 21213–21218. [Google Scholar] [CrossRef]
- Cong, I.; Choi, S.; Lukin, M.D. Quantum Convolutional Neural Networks. arXiv 2019, arXiv:1810.03787v2. [Google Scholar] [CrossRef]
- Henderson, M.; Shakya, S.; Pradhan, S.; Cook, T. Quanvolutional Neural Networks: Powering Image Recognition with Quantum Circuits. arXiv 2019, arXiv:1904.04767v1. [Google Scholar] [CrossRef]
- Perez-Salinas, A.; Cervera-Lierta, A.; Gil-Fuster, E.; Latorre, J.I. Data re-uploading for a universal quantum classifier. Quantum 2020, 4, 226. [Google Scholar] [CrossRef]
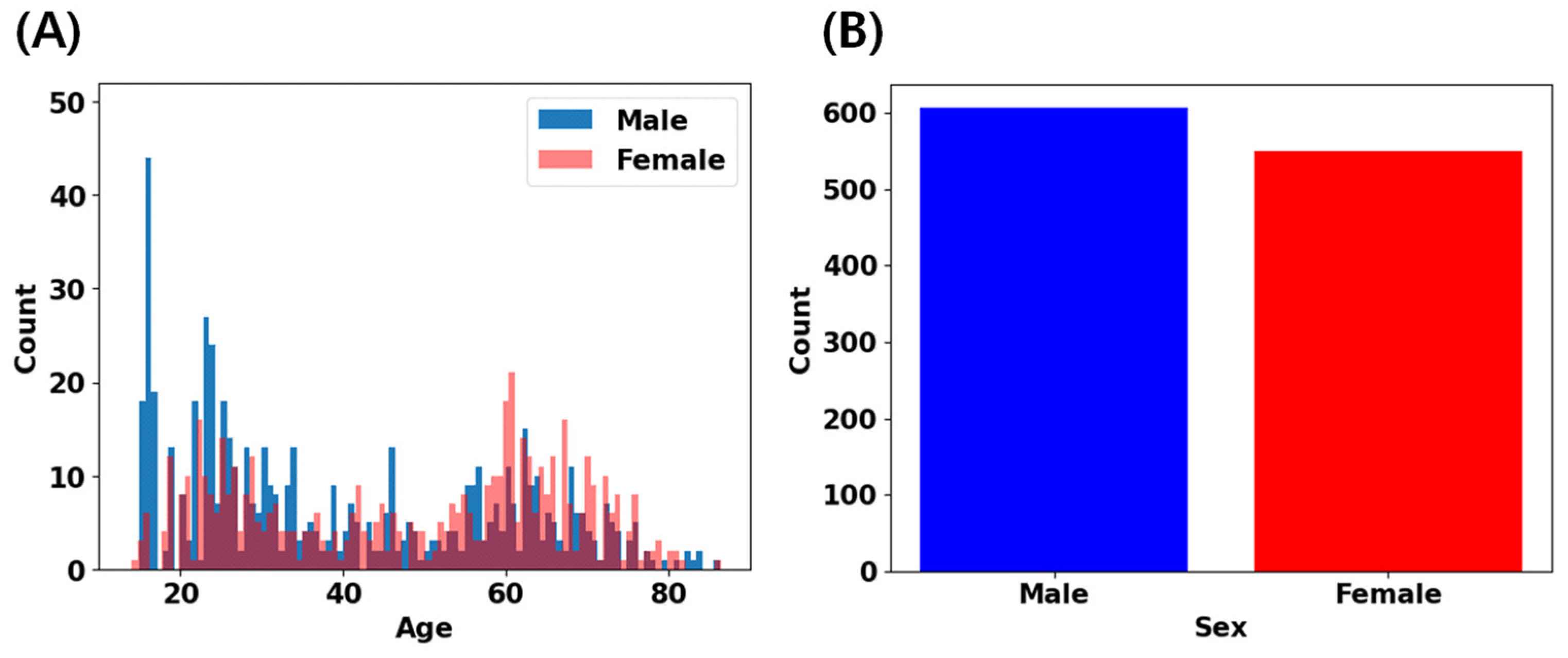

| Age Range | No. of Subjects | ||
|---|---|---|---|
| Male | Female | Total | |
| 14–19 | 96 | 27 | 123 |
| 20–29 | 159 | 120 | 279 |
| 30–39 | 86 | 54 | 140 |
| 40–49 | 59 | 60 | 119 |
| 50–59 | 69 | 83 | 152 |
| 60–69 | 95 | 134 | 229 |
| 70–79 | 36 | 66 | 102 |
| 80–89 | 7 | 6 | 13 |
| Total | 607 | 550 | 1157 |
| No. | Feature | No. | Feature |
|---|---|---|---|
| 1 | Left white matter | 18 | Right white matter |
| 2 | Left lateral ventricle | 19 | Right lateral ventricle |
| 3 | Left inferior lateral ventricle | 20 | Right inferior lateral ventricle |
| 4 | Left cerebellum white matter | 21 | Right cerebellum white matter |
| 5 | Left cerebellum cortex | 22 | Right cerebellum cortex |
| 6 | Left thalamus proper | 23 | Right thalamus proper |
| 7 | Left caudate | 24 | Right caudate |
| 8 | Left putamen | 25 | Right putamen |
| 9 | Left pallidum | 26 | Right pallidum |
| 10 | Left hippocampus | 27 | Right hippocampus |
| 11 | Left amygdala | 28 | Right amygdala |
| 12 | Left accumbens area | 29 | Right accumbens area |
| 13 | Left ventralDC | 30 | Right ventralDC |
| 14 | Left choroid plexus | 31 | Right choroid plexus |
| 15 | Left cerebral cortex | 32 | Right cerebral cortex |
| 16 | Cerebrospinal fluid | 33 | Brain stem |
| 17 | Third ventricle | 34 | Fourth ventricle |
| Name | Purpose | Matrix | Symbol |
|---|---|---|---|
| Parameterized X Rotation | around the x-axis | 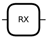 | |
| Parameterized Y Rotation | around the y-axis | 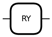 | |
| Parameterized Z Rotation | around the z-axis | 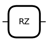 | |
| Controlled NOT (CNOT) | Entangle two qubits in a quantum circuit |  |
| Regressors | Train (N = 925) | Test (N = 231) | ||||||
|---|---|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | R2 | MAE | MSE | RMSE | R2 | |
| LR | 6.978 | 77.987 | 8.831 | 0.791 | 7.506 | 85.695 | 9.257 | 0.784 |
| BR | 6.982 | 78.013 | 8.833 | 0.791 | 7.512 | 85.733 | 9.259 | 0.783 |
| XGBoost | 4.437 | 33.259 | 5.767 | 0.911 | 7.639 | 104.394 | 10.217 | 0.736 |
| RF | 2.809 | 14.118 | 3.757 | 0.962 | 8.275 | 118.161 | 10.870 | 0.701 |
| SVR | 5.395 | 42.177 | 6.494 | 0.887 | 7.324 | 88.986 | 9.433 | 0.775 |
| MLP | 6.118 | 62.193 | 7.886 | 0.834 | 7.103 | 83.184 | 9.121 | 0.790 |
| VQC | 6.200 | 66.674 | 8.165 | 0.822 | 6.744 | 80.092 | 8.949 | 0.798 |
| Classifiers | Train (N = 925) | Test (N = 231) | ||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | Accuracy | Precision | Recall | F1-Score | |
| LR | 0.811 | 0.819 | 0.820 | 0.819 | 0.810 | 0.828 | 0.815 | 0.821 |
| KNN | 0.838 | 0.837 | 0.851 | 0.844 | 0.779 | 0.779 | 0.798 | 0.788 |
| XGBoost | 0.997 | 0.998 | 0.996 | 0.997 | 0.762 | 0.754 | 0.786 | 0.770 |
| RF | 0.997 | 0.994 | 1.000 | 0.758 | 0.770 | 0.770 | 0.770 | 0.770 |
| SVC | 0.835 | 0.845 | 0.840 | 0.843 | 0.771 | 0.787 | 0.780 | 0.784 |
| MLP | 0.789 | 0.845 | 0.774 | 0.808 | 0.753 | 0.811 | 0.744 | 0.776 |
| VQC | 0.809 | 0.864 | 0.791 | 0.826 | 0.818 | 0.885 | 0.794 | 0.837 |
| Author | Method | Model Performance (MAE) | Prediction Performance (MAE) |
|---|---|---|---|
| Han, J. et al. [14] | ARD | 7.4790 | 8.0453 |
| Proposed | VQC | 6.265 | 7.201 |
| Author | Method | MAE | MSE | RMSE | R2 |
|---|---|---|---|---|---|
| Simfukwe, C. et al. [15] | BR | 3.310 | 18.280 | 4.280 | 0.300 |
| Proposed | VQC | 3.302 | 16.675 | 4.083 | 0.425 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, Y.-J.; Park, S.-E.; Baek, H.-M. Predicting Brain Age and Gender from Brain Volume Data Using Variational Quantum Circuits. Brain Sci. 2024, 14, 401. https://doi.org/10.3390/brainsci14040401
Jeon Y-J, Park S-E, Baek H-M. Predicting Brain Age and Gender from Brain Volume Data Using Variational Quantum Circuits. Brain Sciences. 2024; 14(4):401. https://doi.org/10.3390/brainsci14040401
Chicago/Turabian StyleJeon, Yeong-Jae, Shin-Eui Park, and Hyeon-Man Baek. 2024. "Predicting Brain Age and Gender from Brain Volume Data Using Variational Quantum Circuits" Brain Sciences 14, no. 4: 401. https://doi.org/10.3390/brainsci14040401
APA StyleJeon, Y.-J., Park, S.-E., & Baek, H.-M. (2024). Predicting Brain Age and Gender from Brain Volume Data Using Variational Quantum Circuits. Brain Sciences, 14(4), 401. https://doi.org/10.3390/brainsci14040401





