Emotional Brain Network Community Division Study Based on an Improved Immunogenetic Algorithm
Abstract
:1. Introduction
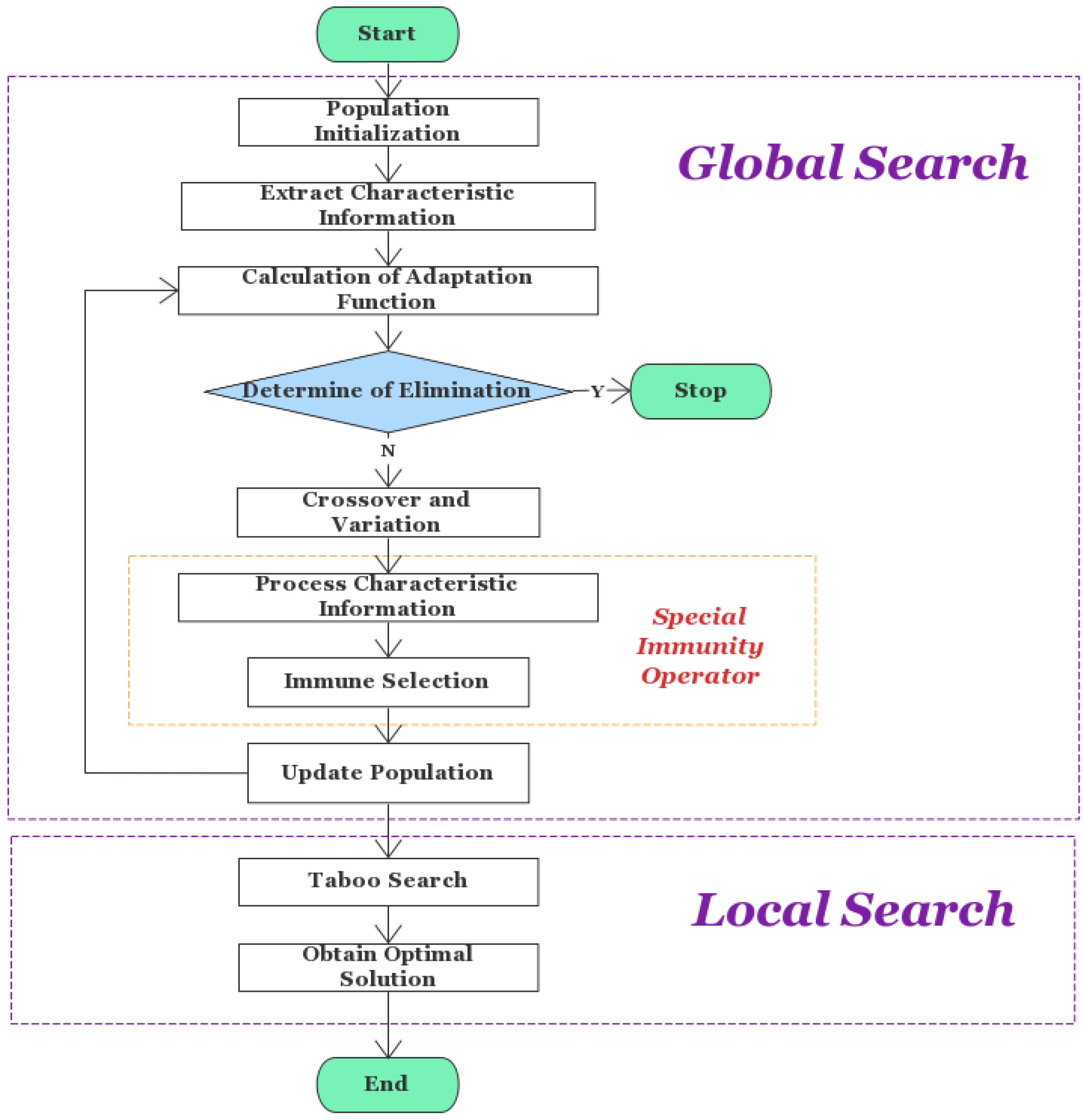
- Based on the traditional genetic algorithm, the specific immunity operator is introduced to improve the accuracy and accelerate the convergence of the algorithm, and the results are further optimized with a forbidden search algorithm;
- The adaptive threshold setting method is proposed to allow the threshold set by the binarization network to be dynamically altered in accordance with the different brain network features to increase the accuracy of the outcomes of brain division;
- Q and NMI metrics derived by the techniques are reliable and superior to the currently used brain network division algorithms under the same experimental settings;
- The algorithm is used to divide the brain network into communities in various emotional states and investigate changes in how the brain communicates across regions and interaction patterns when processing emotional activity, yielding results that are largely consistent with previous physiological findings.
2. Method
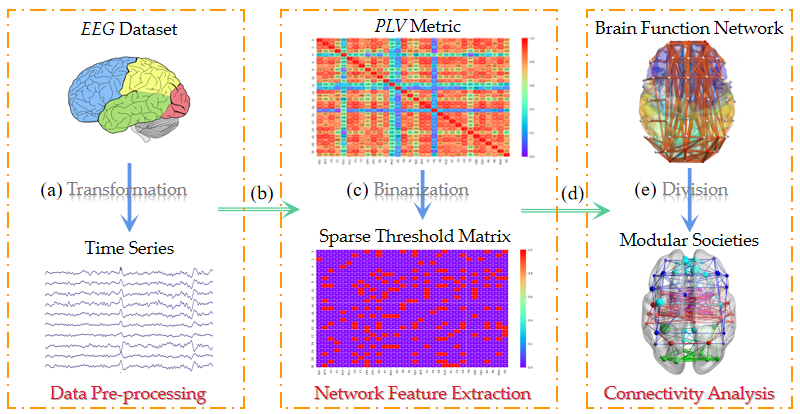
2.1. Algorithm Framework
2.2. Data Pre-Processing
2.2.1. EEG Emotional Database (DEAP)
2.2.2. Pre-Processing Methods
2.3. Network Feature Extraction
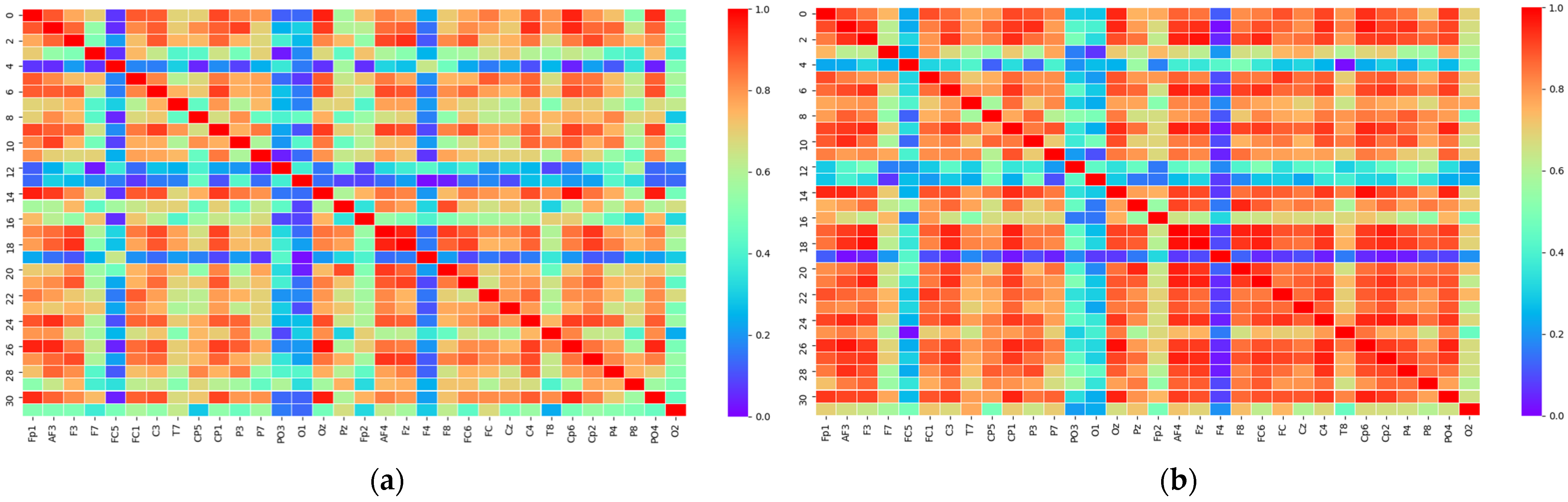
2.3.1. PLV Statistical Analysis
2.3.2. Matrix Binarization
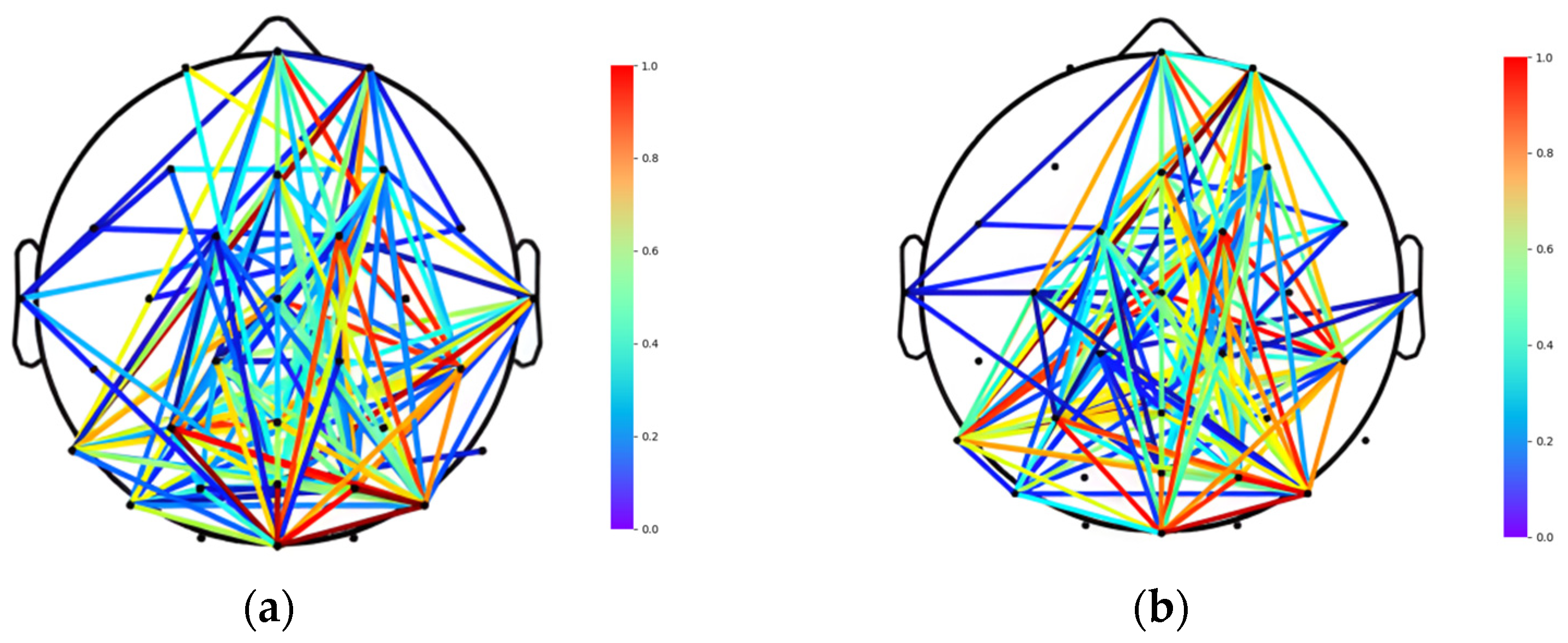
2.4. Connectivity Analysis
2.4.1. Brain Function Network Establishment
2.4.2. Brain Network Structure Division
2.5. Evaluation Function
2.5.1. Normalized Mutual Information
2.5.2. Modularity
3. Results and Discussion
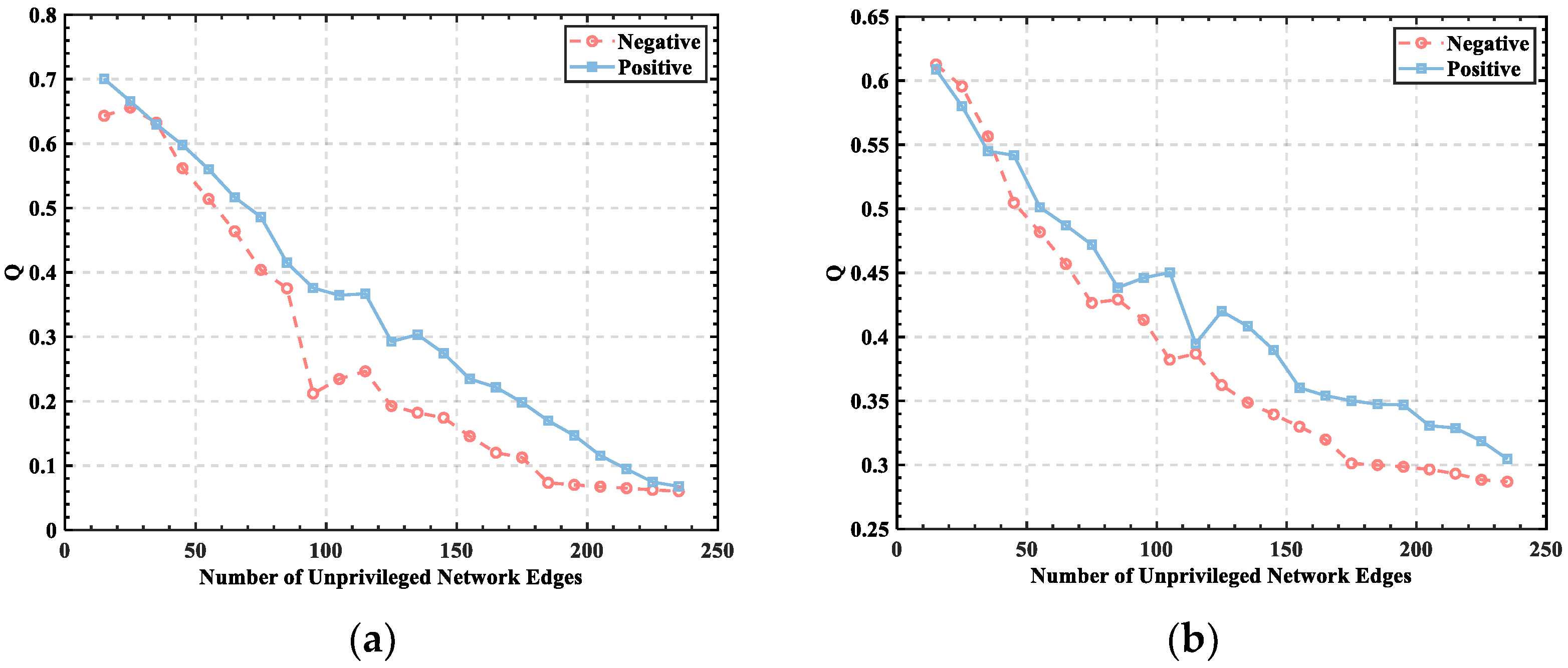
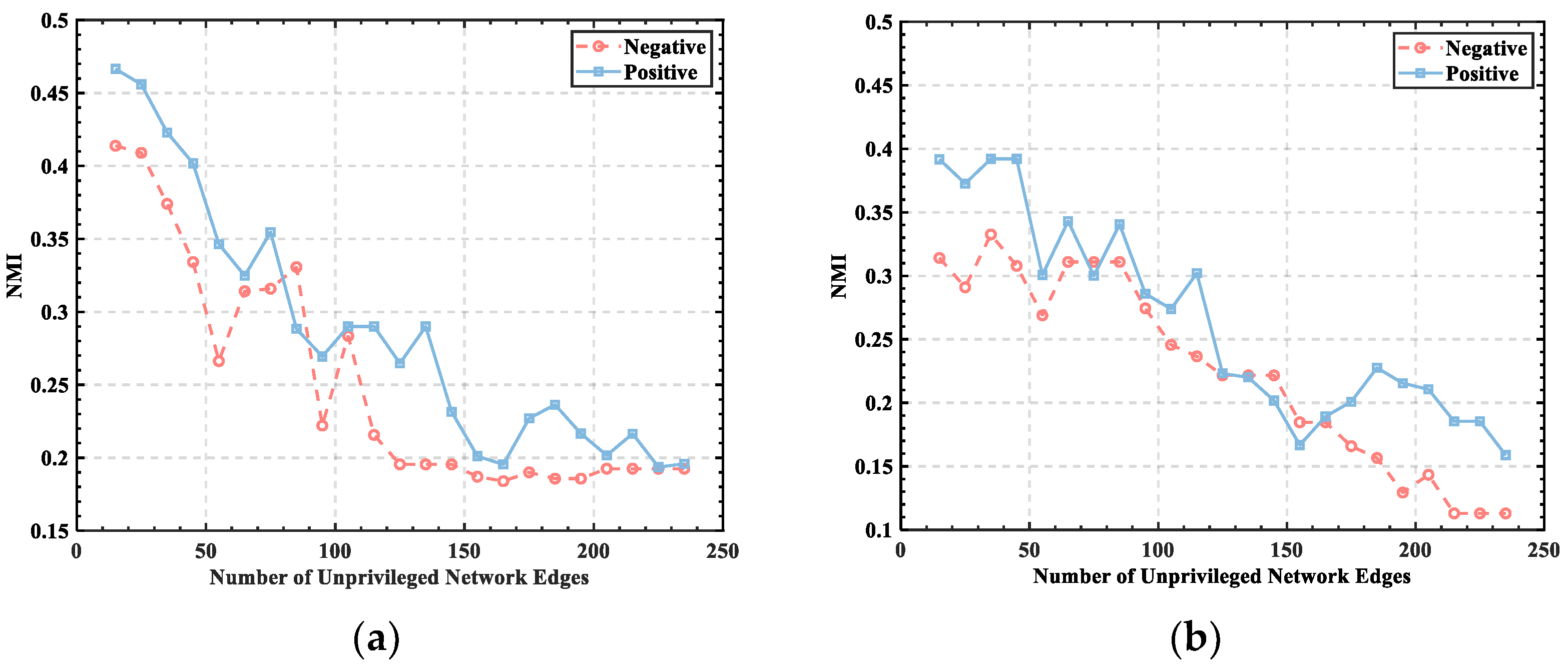
3.1. Threshold Determination
3.2. Division of Brain Functional Networks in Different Emotional States
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cowie, R.; Douglas-Cowie, E.; Tsapatsoulis, N.; Votsis, G.; Kolias, S.; Fellenz, W.; Taylor, J.G. Emotion Recognition in Human-Computer Interaction. IEEE Signal Processing Mag. 2001, 18, 32–80. [Google Scholar] [CrossRef]
- Scherer, K.R. What Are Emotions? And How Can They Be Measured? Soc. Sci. Inf. 2005, 44, 695–729. [Google Scholar] [CrossRef]
- Sander, D.; Grandjean, D.; Scherer, K.R. A Systems Approach to Appraisal Mechanisms in Emotion. Neural Netw. 2005, 18, 317–352. [Google Scholar] [CrossRef] [PubMed]
- Jenke, R.; Peer, A.; Buss, M. Feature Extraction and Selection for Emotion Recognition from EEG. IEEE Trans. Affect. Comput. 2014, 5, 327–339. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, G.; Hong, X.; Zheng, W.; Pietikäinen, M. Spontaneous Facial Micro-Expression Analysis Using Spatiotemporal Completed Local Quantized Patterns. Neurocomputing 2016, 175, 564–578. [Google Scholar] [CrossRef]
- Huang, X.; Wang, S.-J.; Liu, X.; Zhao, G.; Feng, X.; Pietikäinen, M. Discriminative Spatiotemporal Local Binary Pattern with Revisited Integral Projection for Spontaneous Facial Micro-Expression Recognition. IEEE Trans. Affect. Comput. 2017, 10, 32–47. [Google Scholar] [CrossRef]
- Yan, J.; Zheng, W.; Xin, M.; Yan, J. Integrating Facial Expression and Body Gesture in Videos for Emotion Recognition. IEICE Trans. Inf. Syst. 2014, 97, 610–613. [Google Scholar] [CrossRef]
- Khosrowabadi, R.; Quek, C.; Ang, K.K.; Wahab, A. ERNN: A Biologically Inspired Feedforward Neural Network to Discriminate Emotion from EEG Signal. IEEE Trans. Neural Netw. Learn. Syst. 2013, 25, 609–620. [Google Scholar] [CrossRef]
- Wang, X.-W.; Nie, D.; Lu, B.-L. Emotional State Classification from EEG Data Using Machine Learning Approach. Neurocomputing 2014, 129, 94–106. [Google Scholar] [CrossRef]
- Pfurtscheller, G.; Brunner, C.; Schlögl, A.; Da Silva, F.L. Mu Rhythm (de) Synchronization and EEG Single-Trial Classification of Different Motor Imagery Tasks. NeuroImage 2006, 31, 153–159. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, X.; Hong, B.; Gao, S. Practical Designs of Brain–Computer Interfaces Based on the Modulation of EEG Rhythms. In Brain-Computer Interfaces; Springer: Berlin/Heidelberg, Germany, 2009; pp. 137–154. [Google Scholar]
- Michel, C.M.; Murray, M.M. Towards the Utilization of EEG as a Brain Imaging Tool. NeuroImage 2012, 61, 371–385. [Google Scholar] [CrossRef] [PubMed]
- Ahmadlou, M.; Adeli, H. Functional Community Analysis of Brain: A New Approach for EEG Based Investigation of the Brain Pathology. NeuroImage 2011, 58, 401–408. [Google Scholar] [CrossRef] [PubMed]
- Hamann, S. Mapping Discrete and Dimensional Emotions onto the Brain: Controversies and Consensus. Trends Cogn. Sci. 2012, 16, 458–466. [Google Scholar] [CrossRef] [PubMed]
- Bullmore, E.; Sporns, O. Complex Brain Networks: Graph Theoretical Analysis of Structural and Functional Systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Bola, M.; Sabel, B.A. Dynamic Reorganization of Brain Functional Networks during Cognition. NeuroImage 2015, 114, 398–413. [Google Scholar] [CrossRef]
- Tabanfar, Z.; Yousefipoor, F.; Firoozabadi, M.; Khodakarami, Z.; Shankayi, Z. Recognition of Two Emotional States of Joy and Sadness Using Phase Lag Index and SVM Classifier. In Proceedings of the 2016 23rd Iranian Conference on Biomedical Engineering and 2016 1st International Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 24–25 November 2016; pp. 327–330. [Google Scholar]
- Magelinski, T.; Bartulovic, M.; Carley, K.M. Measuring Node Contribution to Community Structure with Modularity Vitality. IEEE Trans. Netw. Sci. Eng. 2021, 8, 707–723. [Google Scholar] [CrossRef]
- Micheloyannis, S.; Vourkas, M.; Tsirka, V.; Karakonstantaki, E.; Kanatsouli, K.; Stam, C.J. The Influence of Ageing on Complex Brain Networks: A Graph Theoretical Analysis. Hum. Brain Mapp. 2009, 30, 200–208. [Google Scholar] [CrossRef]
- Newman, M.E.; Girvan, M. Finding and Evaluating Community Structure in Networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Van Den Heuvel, M.; Mandl, R.; Hulshoff Pol, H. Normalized Cut Group Clustering of Resting-State FMRI Data. PLoS ONE 2008, 3, e2001. [Google Scholar] [CrossRef]
- She, Q.; Chang, F.; Fan, Y.; Luo, Z. Feature Extraction and Classification of EEG Based on Adjacent Matrix Decomposition. Chin. J. Sens. Actuators 2012, 25, 1204–1209. [Google Scholar]
- Wang, Y.; Li, T.-Q. Analysis of Whole-Brain Resting-State FMRI Data Using Hierarchical Clustering Approach. PLoS ONE 2013, 8, e76315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Girvan, M.; Newman, M.E. Community Structure in Social and Biological Networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E. Fast Algorithm for Detecting Community Structure in Networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef]
- Shchur, O.; Günnemann, S. Overlapping Community Detection with Graph Neural Networks. arXiv 2019, arXiv:1909.12201. [Google Scholar]
- Sun, W.; Shao, S.; Zhao, R.; Yan, R.; Zhang, X.; Chen, X. A Sparse AutoEncoder-Based Deep Neural Network Approach for Induction Motor Faults Classification. Measurement 2016, 89, 171–178. [Google Scholar] [CrossRef]
- Koelstra, S.; Muhl, C.; Soleymani, M.; Lee, J.-S.; Yazdani, A.; Ebrahimi, T.; Pun, T.; Nijholt, A.; Patras, I. Deap: A Database for Emotion Analysis; Using Physiological Signals. IEEE Trans. Affect. Comput. 2011, 3, 18–31. [Google Scholar] [CrossRef]
- Sourina, O.; Liu, Y. A Fractal-Based Algorithm of Emotion Recognition from EEG Using Arousal-Valence Model. Int. Conf. Bio Inspired Syst. Signal Processing 2011, 2, 209–214. [Google Scholar]
- Wang, Z.; Tong, Y.; Heng, X. Phase-Locking Value Based Graph Convolutional Neural Networks for Emotion Recognition. IEEE Access 2019, 7, 93711–93722. [Google Scholar] [CrossRef]
- Hurtado, J.M.; Rubchinsky, L.L.; Sigvardt, K.A. Statistical Method for Detection of Phase-Locking Episodes in Neural Oscillations. J. Neurophysiol. 2004, 91, 1883–1898. [Google Scholar] [CrossRef]
- Langer, N.; Pedroni, A.; Jäncke, L. The Problem of Thresholding in Small-World Network Analysis. PLoS ONE 2013, 8, e53199. [Google Scholar] [CrossRef]
- Lipowski, A.; Lipowska, D. Roulette-Wheel Selection via Stochastic Acceptance. Phys. A Stat. Mech. Its Appl. 2012, 391, 2193–2196. [Google Scholar] [CrossRef]
- Rodríguez-Puente, R.; Lazo-Cortés, M.S. Algorithm for Shortest Path Search in Geographic Information Systems by Using Reduced Graphs. SpringerPlus 2013, 2, 291. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E. Modularity and Community Structure in Networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lancichinetti, A.; Fortunato, S. Consensus Clustering in Complex Networks. Sci. Rep. 2012, 2, 336. [Google Scholar] [CrossRef]
- Lusseau, D. The Emergent Properties of a Dolphin Social Network. Proc. R. Soc. London. Ser. B Biol. Sci. 2003, 270, S186–S188. [Google Scholar] [CrossRef]
- Bolanos, M.; Bernat, E.M.; He, B.; Aviyente, S. A Weighted Small World Network Measure for Assessing Functional Connectivity. J. Neurosci. Methods 2013, 212, 133–142. [Google Scholar] [CrossRef]
- Thorpe, A.; Anders, W.; Rowley, K. The Community Network: An Aboriginal Community Football Club Bringing People Together. Aust. J. Prim. Health 2014, 20, 356–364. [Google Scholar] [CrossRef]
- Schimmack, U.; Derryberry, D.E. Attentional Interference Effects of Emotional Pictures: Threat, Negativity, or Arousal? Emotion 2005, 5, 55. [Google Scholar] [CrossRef]
- Wang, W. Brain Network Features Based on Theta-Gamma Cross-Frequency Coupling Connections in EEG for Emotion Recognition. Neurosci. Lett. 2021, 761, 136106. [Google Scholar] [CrossRef]
- Yang, Z.; Zuo, X.-N.; McMahon, K.L.; Craddock, R.C.; Kelly, C.; de Zubicaray, G.I.; Hickie, I.; Bandettini, P.A.; Castellanos, F.X.; Milham, M.P. Genetic and Environmental Contributions to Functional Connectivity Architecture of the Human Brain. Cereb. Cortex 2016, 26, 2341–2352. [Google Scholar] [CrossRef] [Green Version]
- Claeys, E.H.; Mantingh, T.; Morrens, M.; Yalin, N.; Stokes, P.R. Resting-State FMRI in Depressive and (Hypo) Manic Mood States in Bipolar Disorders: A Systematic Review. Prog. Neuro Psychopharmacol. Biol. Psychiatry 2022, 113, 110465. [Google Scholar]


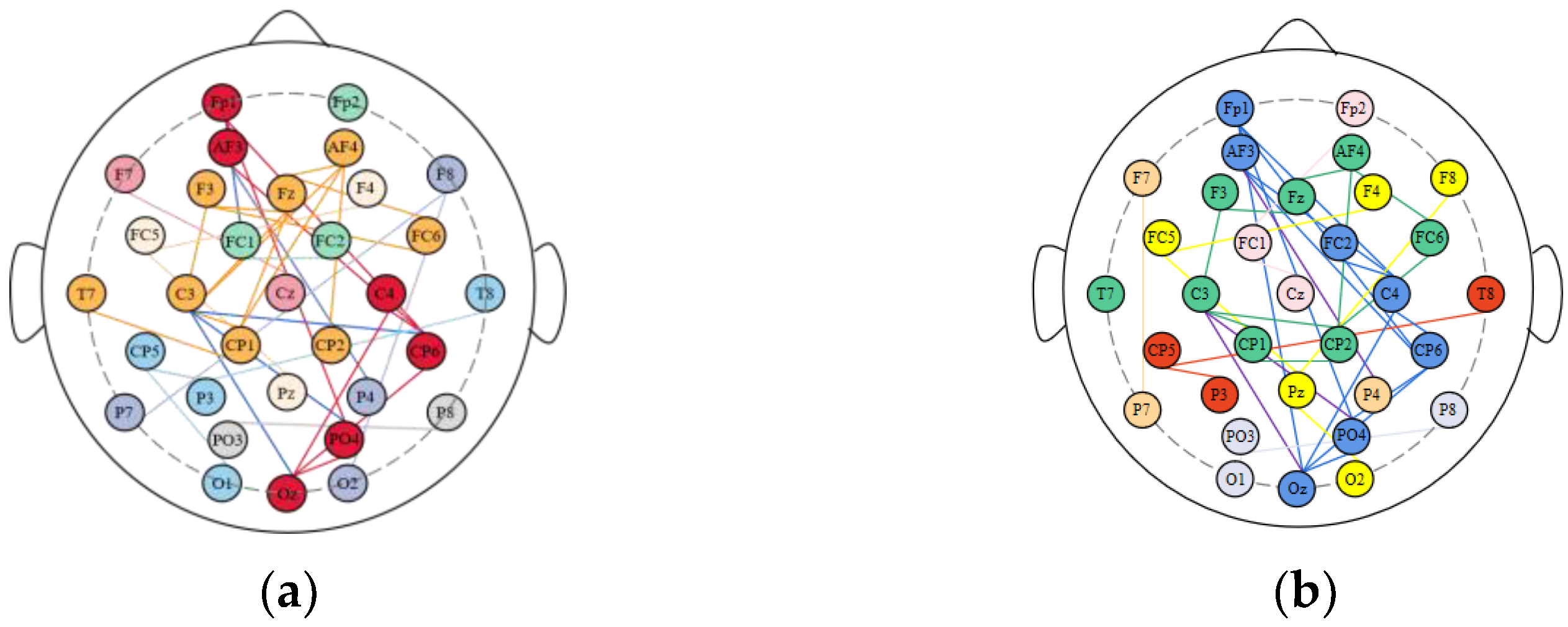
| Nodes in Each Brain Region | Percentage | ||||
|---|---|---|---|---|---|
| Positive State | Negative State | Positive State | Negative State | ||
| Frontal Lobe | Fp1 Fp2 F3 F4 Fz AF3 AF4 | Fp1 AF3 F3 AF4 Fz F4 | Fp1 AF3 F3 AF4 Fz F4 | 85.70% | 85.70% |
| Temporal Lobe | F7 T7 P7 FC5 CP5 F8 T8 P8 FC6 CP6 | CP6 T7 FC6 FC5 | CP6 T7 FC6 F8 FC5 | 40% | 50% |
| Parietal Lobe | P3 P4 Pz | None | None | 0% | 0% |
| Occipital Lobe | O1 O2 Oz PO3 PO4 | Oz PO4 | Oz PO4 O2 | 40% | 60% |
| Central Region | C3 C4 Cz CP1 CP2 FC1 FC2 | C4 C3 CP1 CP2 | C4 FC2 C3 CP1 CP2 | 57.10% | 71.40% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, R.; Zhang, T.; Zhou, S.; Huang, L. Emotional Brain Network Community Division Study Based on an Improved Immunogenetic Algorithm. Brain Sci. 2022, 12, 1159. https://doi.org/10.3390/brainsci12091159
Zhao R, Zhang T, Zhou S, Huang L. Emotional Brain Network Community Division Study Based on an Improved Immunogenetic Algorithm. Brain Sciences. 2022; 12(9):1159. https://doi.org/10.3390/brainsci12091159
Chicago/Turabian StyleZhao, Renjie, Tao Zhang, Shichao Zhou, and Liya Huang. 2022. "Emotional Brain Network Community Division Study Based on an Improved Immunogenetic Algorithm" Brain Sciences 12, no. 9: 1159. https://doi.org/10.3390/brainsci12091159
APA StyleZhao, R., Zhang, T., Zhou, S., & Huang, L. (2022). Emotional Brain Network Community Division Study Based on an Improved Immunogenetic Algorithm. Brain Sciences, 12(9), 1159. https://doi.org/10.3390/brainsci12091159





