Identifying Non-Math Students from Brain MRIs with an Ensemble Classifier Based on Subspace-Enhanced Contrastive Learning
Abstract
:1. Introduction
2. Materials and Methods
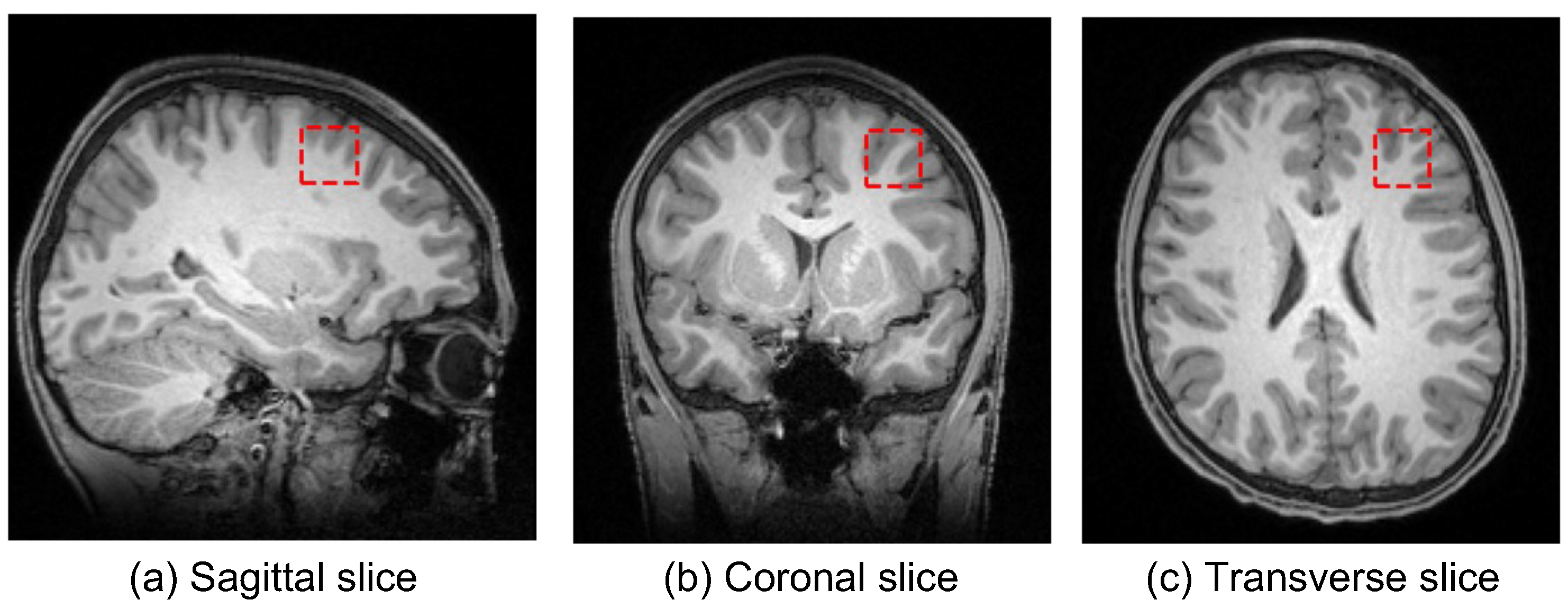
2.1. MRI Data and Preprocessing
2.2. The Proposed Method
2.2.1. Subspace-Enhanced Contrastive Learning
2.2.2. Ensemble Classifier
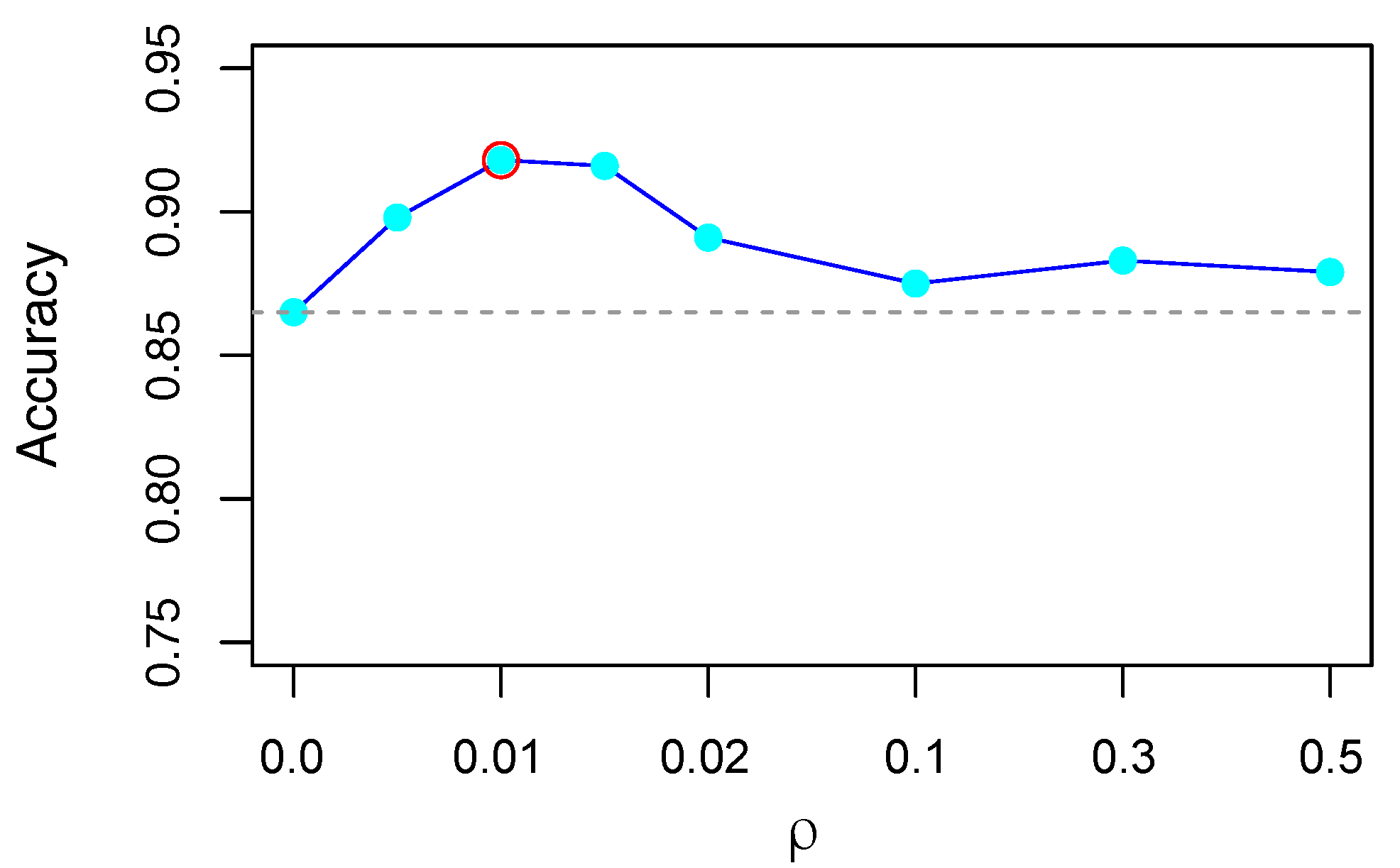
2.3. Model Setting and Evaluation
3. Results
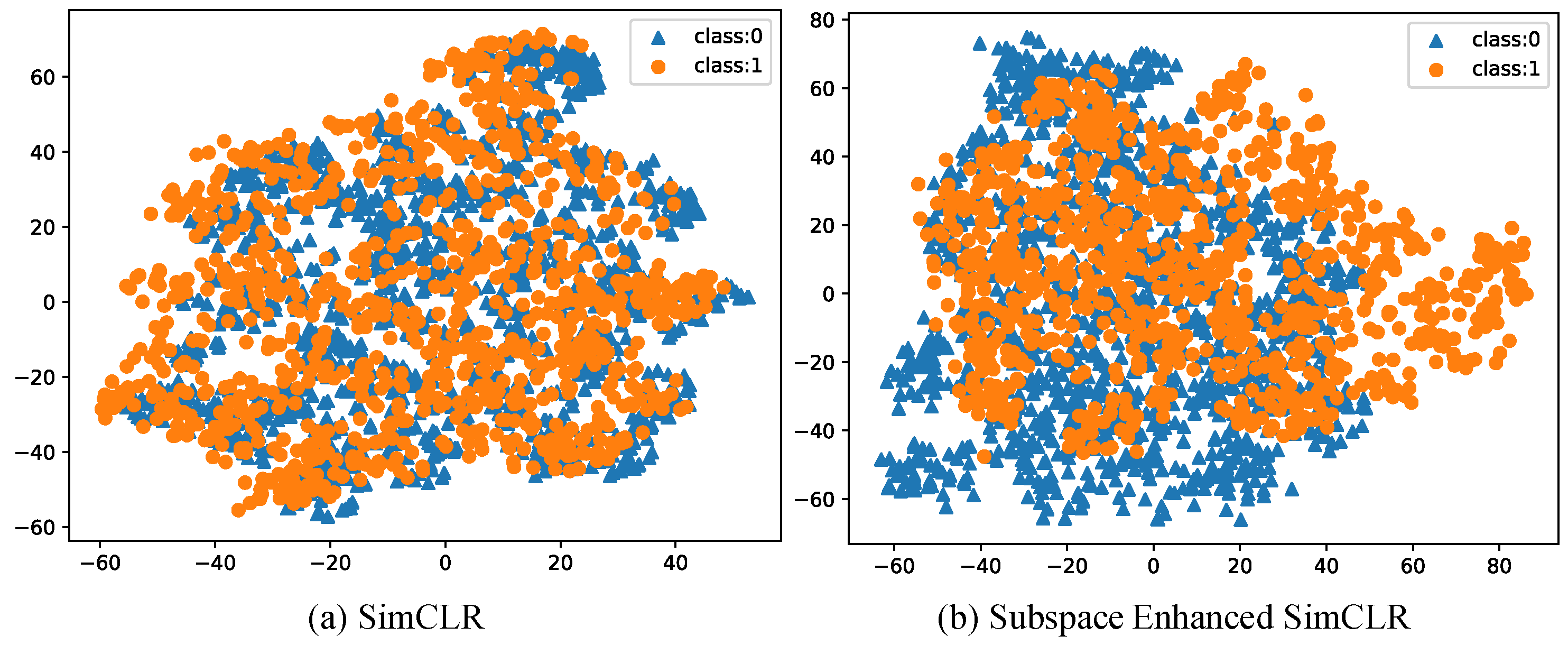
3.1. Feature Visualization
3.2. Overall Evaluation
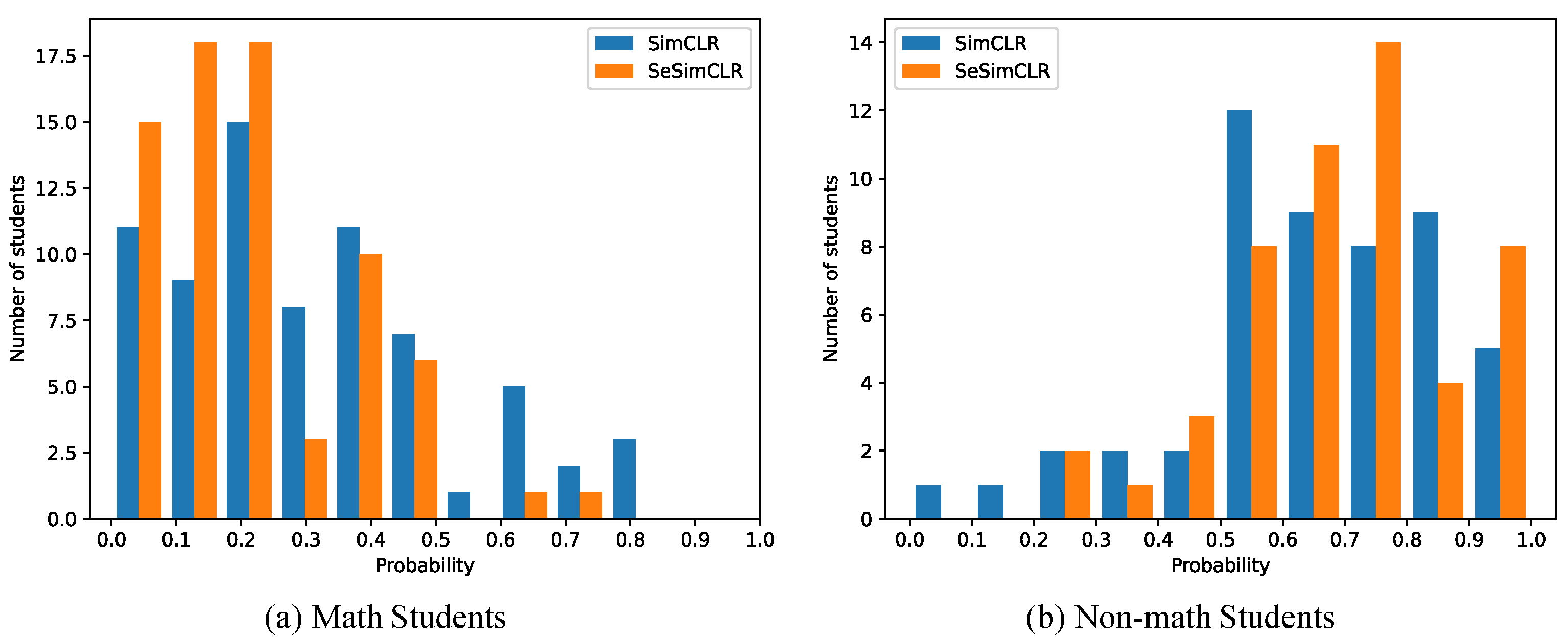
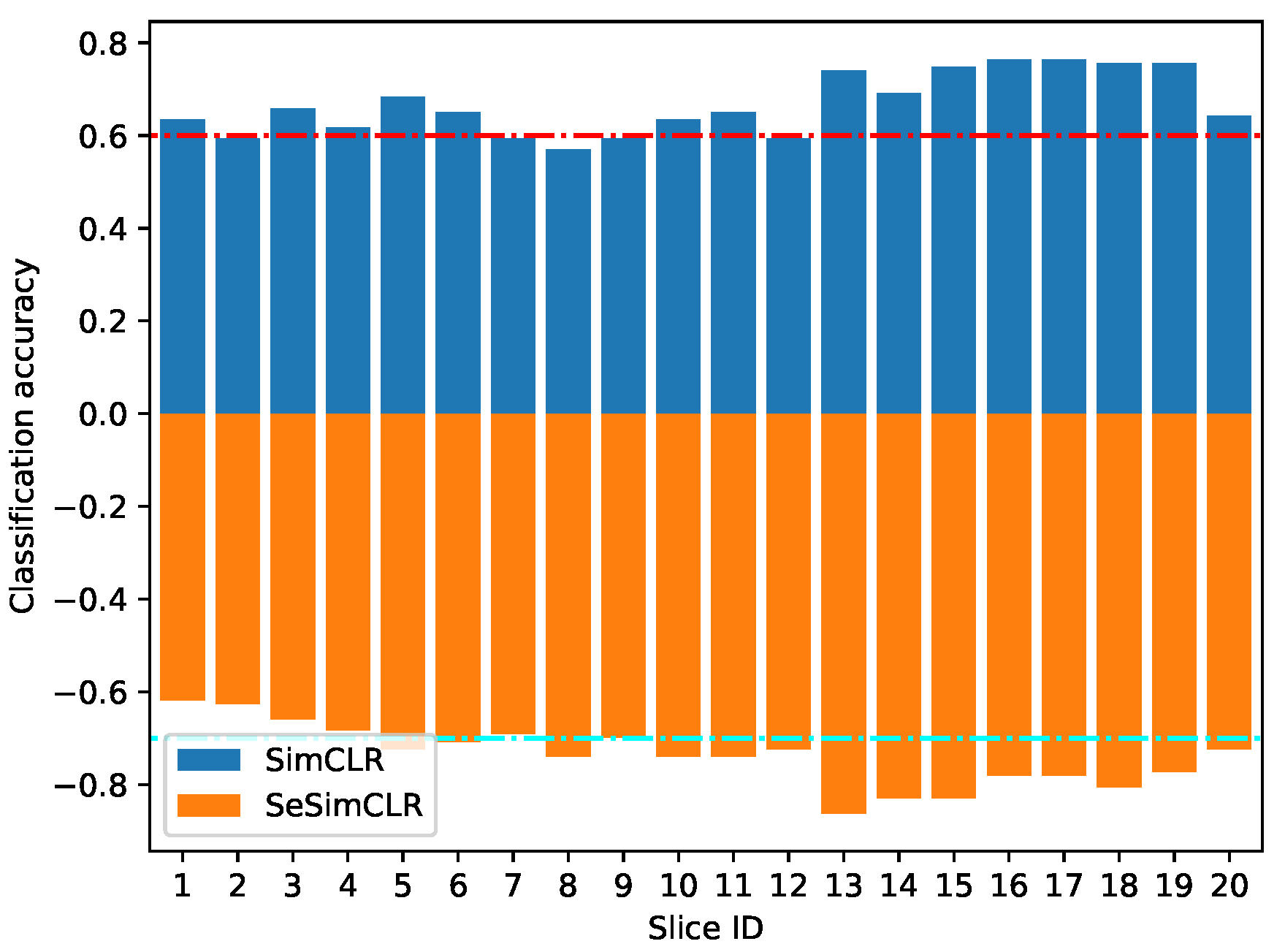
3.3. Detail Evaluation
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Psacharopoulos, G.; Woodhall, M. Education for Development; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Beddington, J.; Cooper, C.L.; Field, J.; Goswami, U.; Huppert, F.A.; Jenkins, R.; Jones, H.S.; Kirkwood, T.B.; Sahakian, B.J.; Thomas, S.M. The mental wealth of nations. Nature 2008, 455, 1057–1060. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zacharopoulos, G.; Sella, F.; Kadosh, R.C. The impact of a lack of mathematical education on brain development and future attainment. Proc. Natl. Acad. Sci. USA 2021, 118, e2013155118. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Dai, H.; Yun, Y.; Liu, S.; Lan, A.; Shang, X. Meta-knowledge dictionary learning on 1-bit response data for student knowledge diagnosis. Knowl.-Based Syst. 2020, 205, 106290. [Google Scholar] [CrossRef]
- Zhang, Y.; An, R.; Cui, J.; Shang, X. Undergraduate grade prediction in Chinese higher education using convolutional neural networks. In Proceedings of the LAK21: 11th International Learning Analytics and Knowledge Conference, Irvine, CA, USA, 12–16 April 2021; pp. 462–468. [Google Scholar]
- Mediouni, M.; Schlatterer, D.R.; Madry, H.; Cucchiarini, M.; Rai, B. A review of translational medicine. The future paradigm: How can we connect the orthopedic dots better? Curr. Med Res. Opin. 2018, 34, 1217–1229. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Y.; Shang, X.; Zhang, Z. ProTICS reveals prognostic impact of tumor infiltrating immune cells in different molecular subtypes. Briefings Bioinform. 2021, 22, bbab164. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Xue, H.; Wei, Z.; Tuncali, I.; Hao, J.; Shang, X. Integrating multi-network topology for gene function prediction using deep neural networks. Briefings Bioinform. 2021, 22, 2096–2105. [Google Scholar] [CrossRef]
- Butterworth, B.; Kovas, Y. Understanding neurocognitive developmental disorders can improve education for all. Science 2013, 340, 300–305. [Google Scholar] [CrossRef] [Green Version]
- Moeller, K.; Willmes, K.; Klein, E. A review on functional and structural brain connectivity in numerical cognition. Front. Hum. Neurosci. 2015, 9, 227. [Google Scholar] [CrossRef] [Green Version]
- Brookman-Byrne, A.; Dumontheil, I. Brain and cognitive development during adolescence: Implications for science and mathematics education. In The ‘BrainCanDo’ Handbook of Teaching and Learning; David Fulton Publishers: London, UK, 2020; pp. 205–221. [Google Scholar]
- Zhang, Y.; Dai, H.; Yun, Y.; Shang, X. Student Knowledge Diagnosis on Response Data via the Model of Sparse Factor Learning. In Proceedings of the 12th International Conference on Educational Data Mining (EDM 2019), Montreal, QC, Canada, 2–5 July 2019. [Google Scholar]
- Lent, R.W.; Lopez, F.G.; Bieschke, K.J. Predicting mathematics-related choice and success behaviors: Test of an expanded social cognitive model. J. Vocat. Behav. 1993, 42, 223–236. [Google Scholar] [CrossRef]
- Steffe, L.P. Psychology in Mathematics Education: Past, Present, and Future. In North American Chapter of the International Group for the Psychology of Mathematics Education; Hoosier Association of Mathematics Teacher Educators: Indianapolis, IN, USA, 2017. [Google Scholar]
- Zhang, Y.; Liu, S. Integrated Sparse Coding with Graph Learning for Robust Data Representation. IEEE Access 2020, 8, 161245–161260. [Google Scholar] [CrossRef]
- Yun, Y.; Dai, H.; Cao, R.; Zhang, Y.; Shang, X. Self-paced Graph Memory Network for Student GPA Prediction and Abnormal Student Detection. In International Conference on Artificial Intelligence in Education; Springer: Berlin/Heidelberg, Germany, 2021; pp. 417–421. [Google Scholar]
- Ayuso, N.; Fillola, E.; Masiá, B.; Murillo, A.C.; Trillo-Lado, R.; Baldassarri, S.; Cerezo, E.; Ruberte, L.; Mariscal, M.D.; Villarroya-Gaudó, M. Gender Gap in STEM: A Cross-Sectional Study of Primary School Students’ Self-Perception and Test Anxiety in Mathematics. IEEE Trans. Educ. 2020, 64, 40–49. [Google Scholar] [CrossRef]
- Arsalidou, M.; Taylor, M.J. Is 2 + 2= 4? Meta-analyses of brain areas needed for numbers and calculations. Neuroimage 2011, 54, 2382–2393. [Google Scholar] [CrossRef] [PubMed]
- Sigman, M.; Peña, M.; Goldin, A.P.; Ribeiro, S. Neuroscience and education: Prime time to build the bridge. Nat. Neurosci. 2014, 17, 497–502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arsalidou, M.; Pawliw-Levac, M.; Sadeghi, M.; Pascual-Leone, J. Brain areas associated with numbers and calculations in children: Meta-analyses of fMRI studies. Dev. Cogn. Neurosci. 2018, 30, 239–250. [Google Scholar] [CrossRef]
- Zhang, Y.; He, X.; Tian, Z.; Jeong, J.J.; Lei, Y.; Wang, T.; Zeng, Q.; Jani, A.B.; Curran, W.J.; Patel, P.; et al. Multi-needle detection in 3D ultrasound images using unsupervised order-graph regularized sparse dictionary learning. IEEE Trans. Med. Imaging 2020, 39, 2302–2315. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Lei, Y.; Lin, M.; Curran, W.; Liu, T.; Yang, X. Region of interest discovery using discriminative concrete autoencoder for COVID-19 lung CT images. In Medical Imaging 2021: Computer-Aided Diagnosis; International Society for Optics and Photonics: Bellingham, WA, USA, 2021; Volume 11597, p. 115970U. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International conference on machine learning, PMLR, Virtual Event, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Lee, K.; Laskin, M.; Srinivas, A.; Abbeel, P. Sunrise: A simple unified framework for ensemble learning in deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual Event, 18–24 July 2021; pp. 6131–6141. [Google Scholar]
- Gao, T.; Yao, X.; Chen, D. SimCSE: Simple Contrastive Learning of Sentence Embeddings. arXiv 2021, arXiv:2104.08821. [Google Scholar]
- Chaitanya, K.; Erdil, E.; Karani, N.; Konukoglu, E. Contrastive learning of global and local features for medical image segmentation with limited annotations. arXiv 2020, arXiv:2006.10511. [Google Scholar]
- Huang, J.; Ling, C.X. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans. Knowl. Data Eng. 2005, 17, 299–310. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Xiang, M.; Yang, B. Hierarchical sparse coding from a Bayesian perspective. Neurocomputing 2018, 272, 279–293. [Google Scholar] [CrossRef]
- Zhang, Y.; An, R.; Liu, S.; Cui, J.; Shang, X. Predicting and Understanding Student Learning Performance Using Multi-source Sparse Attention Convolutional Neural Networks. IEEE Trans. Big Data 2021. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Zhang, Y.; Liu, S.; Shang, X. An MRI Study on Effects of Math Education on Brain Development Using Multi-Instance Contrastive Learning. Front. Psychol. 2021, 12, 765754. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Lysenko, A.; Boroevich, K.A.; Vans, E.; Tsunoda, T. DeepFeature: Feature selection in nonimage data using convolutional neural network. Briefings Bioinform. 2021, 22, bbab297. [Google Scholar] [CrossRef] [PubMed]


| Images | Students | |||
|---|---|---|---|---|
| SimCLR | SeSimCLR | SimCLR | SeSimCLR | |
| ACC | 0.667 | 0.737 | 0.870 | 0.918 |
| Precision | 0.693 | 0.788 | 0.806 | 0.972 |
| Recall | 0.609 | 0.626 | 0.542 | 0.619 |
| F1 | 0.648 | 0.698 | 0.648 | 0.757 |
| AUC | – | – | 0.947 | 0.961 |
| Methods | Student Classification | |
|---|---|---|
| ACC | AUC | |
| SeSimCLR | 0.918 | 0.961 |
| CNN (3D) | 0.772 | 0.857 |
| ResNet (3D) | 0.824 | 0.891 |
| CNN (joint) | 0.809 | 0.887 |
| ResNet (joint) | 0.849 | 0.923 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhang, Y.; Peng, J.; Wang, T.; Shang, X. Identifying Non-Math Students from Brain MRIs with an Ensemble Classifier Based on Subspace-Enhanced Contrastive Learning. Brain Sci. 2022, 12, 908. https://doi.org/10.3390/brainsci12070908
Liu S, Zhang Y, Peng J, Wang T, Shang X. Identifying Non-Math Students from Brain MRIs with an Ensemble Classifier Based on Subspace-Enhanced Contrastive Learning. Brain Sciences. 2022; 12(7):908. https://doi.org/10.3390/brainsci12070908
Chicago/Turabian StyleLiu, Shuhui, Yupei Zhang, Jiajie Peng, Tao Wang, and Xuequn Shang. 2022. "Identifying Non-Math Students from Brain MRIs with an Ensemble Classifier Based on Subspace-Enhanced Contrastive Learning" Brain Sciences 12, no. 7: 908. https://doi.org/10.3390/brainsci12070908
APA StyleLiu, S., Zhang, Y., Peng, J., Wang, T., & Shang, X. (2022). Identifying Non-Math Students from Brain MRIs with an Ensemble Classifier Based on Subspace-Enhanced Contrastive Learning. Brain Sciences, 12(7), 908. https://doi.org/10.3390/brainsci12070908








