Patterns of Attention and Anxiety in Predicting Arithmetic Fluency among School-Aged Children
Abstract
:1. Introduction
1.1. Definition of Sustained Attention
1.2. Relation of Sustained Attention to Math Achievement in Children
1.3. Relation of Anxiety to Math Achievement in Children
1.4. Research Questions in the Present Study
2. Materials and Methods
2.1. Participants
2.2. Procedure
2.3. Materials
2.3.1. Sustained Attention
2.3.2. State Anxiety
2.3.3. General Anxiety
2.3.4. ADHD Self-Rating
2.3.5. Math Achievement
2.4. Data Analysis
3. Results
3.1. Correlation Analysis
3.2. Regression Analysis
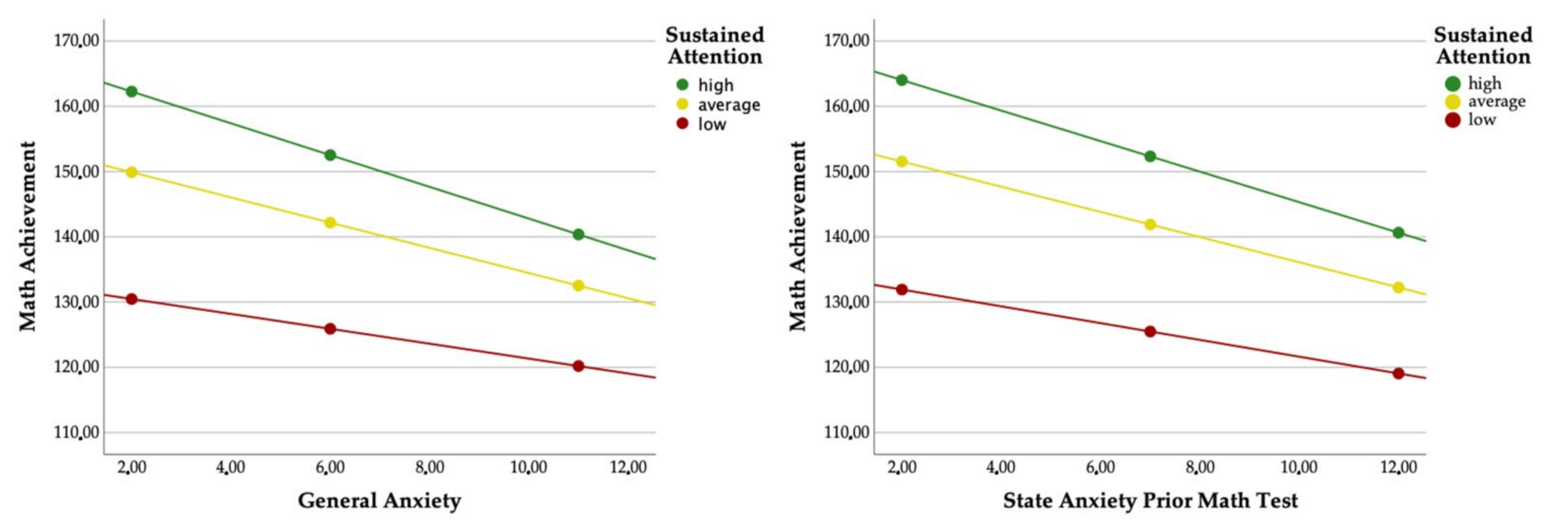
3.3. Moderation Analysis
3.4. Latent Profile Analysis
- Profile 1: Math anxiety subgroup (high state-MA/weak sustained attention). Approximately 7% of the sample were classified to profile 1. Children in this profile reported high state-MA levels, average state anxiety in the presence of the attention test and higher GA. The subgroup showed sustained attention scores and ADHD self-ratings that differ significantly from the sample mean (t(29) = −3.56/6.34, p ≤ 0.001).
- Profile 2: GA subgroup (general high anxiety levels). About 9% of the sample belonged to profile 2, which was characterized by general higher anxiety levels and higher ADHD self-ratings. The sustained attention scores did not differ from the sample mean (t(36) = −1.91, p = 0.065).
- Profile 3: Slight tension subgroup (slightly higher state anxiety/higher sustained attention). Twenty-one percent of the sample was categorized to profile 3. Children in this subgroup reported slightly higher state anxiety levels and had high sustained attention scores. All state anxiety measures (t(83) = 5.04 to 16.81, p ≤ 0.001) and sustained attention (t(83) = 3.02, p = 0.003) differ significantly from the sample mean.
- Profile 4: Attention problems subgroup (higher GA/weak sustained attention). About 14% of the sample belonged to profile 4, which was characterized by low state anxiety measures, higher GA and weaker attention scores. Children in this subgroup exhibited lower sustained attention scores (t(56) = −2.01, p = 0.042) and reported higher ADHS self-rating (t(56) = 6.96, p ≤ 0.001).
- Profile 5: Average subgroup I (average scores). Approximately 15% of the sample was classified to profile 5, which was characterized by average scores on mostly all variables (t(59) = −1.11 to 1.85, p = 0.07 to 0.89). Only ADHD self-ratings (t(59) = −3.09, p = 0.003) differ significantly from the sample mean.
- Profile 6: Average subgroup II (lowest self-ratings). A total of 34% of the sample was categorized to the largest profile 6. Children in this subgroup reported the lowest anxiety and ADHD self-ratings, which also differ significantly from the sample mean (t(134) = −35.61 to −11.50, p ≤ 0.001). Their sustained attention scores were average to slightly higher (t(134) = 1.88, p = 0.063).
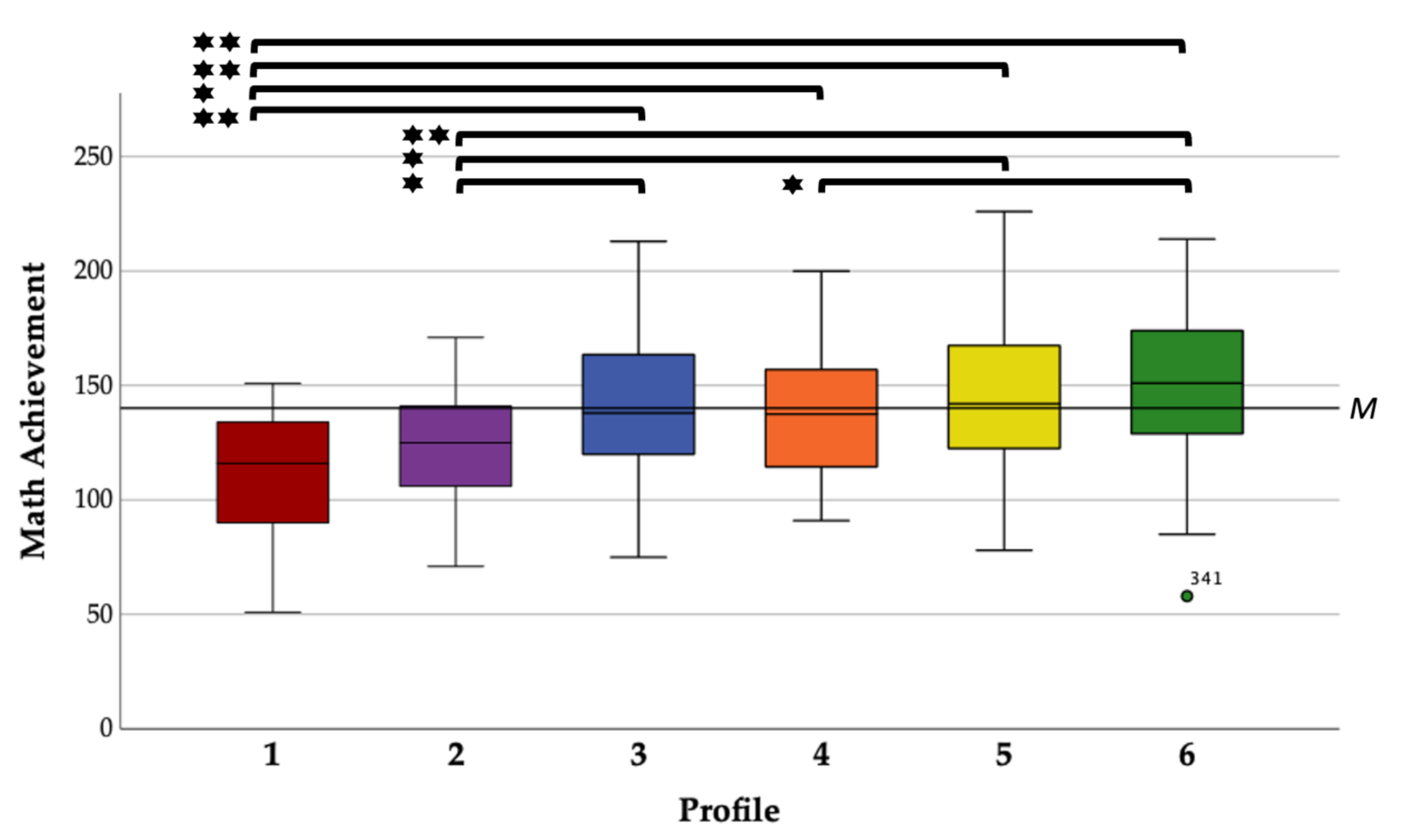
3.5. Profile Comparison of Math Achievement
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Friso-van den Bos, I.; van der Ven, S.H.G.; Kroesbergen, E.H.; van Luit, J.E.H. Working memory and mathematics in primary school children: A meta-analysis. Educ. Res. Rev. 2013, 10, 29–44. [Google Scholar] [CrossRef]
- Peng, P.; Namkung, J.; Barnes, M.; Sun, C. A meta-analysis of mathematics and working memory: Moderating effects of working memory domain, type of mathematics skill, and sample characteristics. J. Educ. Psychol. 2016, 108, 455–473. [Google Scholar] [CrossRef]
- Spiegel, J.A.; Goodrich, J.M.; Morris, B.M.; Osborne, C.M.; Lonigan, C.J. Relations between executive functions and academic outcomes in elementary school children: A meta-analysis. Psychol. Bull. 2021, 147, 329–351. [Google Scholar] [CrossRef] [PubMed]
- Van der Ven, S.H.G.; Kroesbergen, E.H.; Boom, J.; Leseman, P.P.M. The structure of executive functions in children: A closer examination of inhibition, shifting, and updating. Br. J. Dev. Psychol. 2012, 31, 70–87. [Google Scholar] [CrossRef] [PubMed]
- Tosto, M.G.; Momi, S.K.; Asherson, P.; Malki, K. A systematic review of attention deficit hyperactivity disorder (ADHD) and mathematical ability: Current findings and future implications. BMC Med. 2015, 13, 204. [Google Scholar] [CrossRef] [Green Version]
- Steele, A.; Karmiloff-Smith, A.; Cornish, K.; Scerif, G. The Multiple Subfunctions of Attention: Differential Developmental Gateways to Literacy and Numeracy. Child Dev. 2012, 83, 2028–2041. [Google Scholar] [CrossRef]
- Orbach, L.; Herzog, M.; Fritz, A. State- and trait-math anxiety and their relation to math performance in children: The role of core executive functions. Cognition 2020, 200, 104271. [Google Scholar] [CrossRef]
- Schatz, D.B.; Rostain, A.L. ADHD With Comorbid Anxiety. J. Atten. Disord. 2006, 10, 141–149. [Google Scholar] [CrossRef]
- Sorvo, R.; Koponen, T.; Viholainen, H.; Aro, T.; Räikkönen, E.; Peura, P.; Dowker, A.; Aro, M. Math anxiety and its relationship with basic arithmetic skills among primary school children. Br. J. Educ. Psychol. 2017, 87, 309–327. [Google Scholar] [CrossRef] [Green Version]
- Devine, A.; Hill, F.; Carey, E.; Szűcs, D. Cognitive and emotional math problems largely dissociate: Prevalence of developmental dyscalculia and mathematics anxiety. J. Educ. Psychol. 2018, 110, 431–444. [Google Scholar] [CrossRef]
- Eysenck, M.W.; Derakhshan, N.; Santos, R.; Calvo, M. Anxiety and cognitive performance: Attentional control theory. Emotion 2007, 7, 336–353. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baten, E.; Desoete, A. Mathematical (Dis)abilities Within the Opportunity-Propensity Model: The Choice of Math Test Matters. Front. Psychol. 2018, 9, 667. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Passolunghi, M.C.; Cargnelutti, E.; Pellizzoni, S. The relation between cognitive and emotional factors and arithmetic problem-solving. Educ. Stud. Math. 2018, 100, 271–290. [Google Scholar] [CrossRef]
- Nobre, K.; Kastner, S. (Eds.) The Oxford Handbook of Attention; Oxford Library of Psychology; Oxford University Press: Oxford, UK; New York, NY, USA, 2014; ISBN 978-0-19-967511-1. [Google Scholar]
- Posner, M.I.; Petersen, S.E. The Attention System of the Human Brain. Annu. Rev. Neurosci. 1990, 13, 25–42. [Google Scholar] [CrossRef] [PubMed]
- Barkley, R.A. Behavioral inhibition, sustained attention, and executive functions: Constructing a unifying theory of ADHD. Psychol. Bull. 1997, 121, 65–94. [Google Scholar] [CrossRef] [Green Version]
- Petersen, S.E.; Posner, M.I. The Attention System of the Human Brain: 20 Years After. Annu. Rev. Neurosci. 2012, 35, 73–89. [Google Scholar] [CrossRef] [Green Version]
- Posner, M.I. Measuring Alertness. Ann. N. Y. Acad. Sci. 2008, 1129, 193–199. [Google Scholar] [CrossRef] [PubMed]
- Sturm, W.; Willmes, K. On the functional neuroanatomy of intrinsic and phasic alertness. Neuroimage 2001, 14, S74–S84. [Google Scholar] [CrossRef]
- Posner, M.I. Orienting of Attention. Q. J. Exp. Psychol. 1980, 32, 3–25. [Google Scholar] [CrossRef]
- Klein, R.M.; Lawrence, M.A. On the Modes and Domains of Attention. In Cognitive Neuroscience of Attention; Posner, M.I., Ed.; Guilford Press: New York, NY, USA, 2012; pp. 11–28. [Google Scholar]
- Posner, M.I.; DiGirolamo, G.J. Executive Attention: Conflict, Target Detection, and Cognitive Control. In The Attentive Brain; Parasuraman, R., Ed.; The MIT Press: Cambridge, MA, USA, 1998; pp. 401–423. [Google Scholar]
- Merkley, R.; Matusz, P.J.; Scerif, G. The Control of Selective Attention and Emerging Mathematical Cognition. In Heterogeneity of Function in Numerical Cognition; Elsevier: Amsterdam, The Netherlands, 2018; pp. 111–126. ISBN 978-0-12-811529-9. [Google Scholar]
- Miyake, A.; Friedman, N.P.; Emerson, M.J.; Witzki, A.H.; Howerter, A.; Wager, T.D. The Unity and Diversity of Executive Functions and Their Contributions to Complex “Frontal Lobe” Tasks: A Latent Variable Analysis. Cogn. Psychol. 2000, 41, 49–100. [Google Scholar] [CrossRef] [Green Version]
- Diamond, A. Executive Functions. Annu. Rev. Psychol. 2013, 64, 135–168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carone, D.A.; Strauss, E.; Sherman, E.M.S.; Spreen, O. A Compendium of Neuropsychological Tests: Administration, Norms, and Commentary. Appl. Neuropsychol. 2007, 14, 62–63. [Google Scholar] [CrossRef]
- Chan, R.C.K.; Shum, D.; Toulopoulou, T.; Chen, E.Y. Assessment of executive functions: Review of instruments and identification of critical issues. Arch. Clin. Neuropsychol. 2008, 23, 201–216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doyle, A.E. Executive functions in attention-deficit/hyperactivity disorder. J. Clin. Psychiatry 2006, 67, 21–26. [Google Scholar]
- Pennington, B.F.; Ozonoff, S. Executive Functions and Developmental Psychopathology. J. Child Psychol. Psychiatry 1996, 37, 51–87. [Google Scholar] [CrossRef]
- Willcutt, E.G.; Doyle, A.E.; Nigg, J.T.; Faraone, S.V.; Pennington, B.F. Validity of the executive function theory of attention-deficit/hyperactivity disorder: A meta-analytic review. Biol. Psychiatry 2005, 57, 1336–1346. [Google Scholar] [CrossRef]
- Anobile, G.; Stievano, P.; Burr, D. Visual sustained attention and numerosity sensitivity correlate with math achievement in children. J. Exp. Child Psychol. 2013, 116, 380–391. [Google Scholar] [CrossRef]
- Richard, A.E.; Hodges, E.K.; Heinrich, K.P. Visual Attention and Math Performance in Survivors of Childhood Acute Lymphoblastic Leukemia. Arch. Clin. Neuropsychol. 2018, 33, 1015–1023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Szucs, D.; Devine, A.; Soltesz, F.; Nobes, A.; Gabriel, F. Cognitive components of a mathematical processing network in 9-year-old children. Dev. Sci. 2014, 17, 506–524. [Google Scholar] [CrossRef] [Green Version]
- Gold, A.B.; Ewing-Cobbs, L.; Cirino, P.T.; Fuchs, L.S.; Stuebing, K.K.; Fletcher, J.M. Cognitive and behavioral attention in children with math difficulties. Child Neuropsychol. 2013, 19, 420–437. [Google Scholar] [CrossRef]
- DuPaul, G.J.; Anastopoulos, A.D.; Shelton, T.L.; Guevremont, D.C.; Metevia, L. Multimethod Assessment of Attention-Deficit Hyperactivity Disorder: The Diagnostic Utility of Clinic-Based Tests. J. Clin. Child Psychol. 1992, 21, 394–402. [Google Scholar] [CrossRef]
- Toplak, M.E.; West, R.F.; Stanovich, K.E. Practitioner Review: Do performance-based measures and ratings of executive function assess the same construct? J. Child Psychol. Psychiatry 2012, 54, 131–143. [Google Scholar] [CrossRef] [PubMed]
- Nigg, J.T.; Hinshaw, S.P.; Carte, E.T.; Treuting, J.J. Neuropsychological correlates of childhood attention-deficit/hyperactivity disorder: Explainable by comorbid disruptive behavior or reading problems? J. Abnorm. Psychol. 1998, 107, 468–480. [Google Scholar] [CrossRef] [PubMed]
- Nigg, J.T.; Willcutt, E.G.; Doyle, A.E.; Sonuga-Barke, E.J. Causal Heterogeneity in Attention-Deficit/Hyperactivity Disorder: Do We Need Neuropsychologically Impaired Subtypes? Biol. Psychiatry 2005, 57, 1224–1230. [Google Scholar] [CrossRef] [PubMed]
- Thorell, L.B.; Wåhlstedt, C. Executive functioning deficits in relation to symptoms of ADHD and/or ODD in preschool children. Infant Child Dev. 2006, 15, 503–518. [Google Scholar] [CrossRef]
- Hembree, R. Correlates, Causes, Effects, and Treatment of Test Anxiety. Rev. Educ. Res. 1988, 58, 47–77. [Google Scholar] [CrossRef]
- Hembree, R. The Nature, Effects, and Relief of Mathematics Anxiety. J. Res. Math. Educ. 1990, 21, 33. [Google Scholar] [CrossRef]
- Von der Embse, N.; Jester, D.; Roy, D.; Post, J. Test anxiety effects, predictors, and correlates: A 30-year meta-analytic review. J. Affect. Disord. 2018, 227, 483–493. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, N.; Kong, Q.P. The Relationship Between Math Anxiety and Math Performance: A Meta-Analytic Investigation. Front. Psychol. 2019, 10, 1613. [Google Scholar] [CrossRef]
- Namkung, J.M.; Peng, P.; Lin, X. The Relation Between Mathematics Anxiety and Mathematics Performance Among School-Aged Students: A Meta-Analysis. Rev. Educ. Res. 2019, 89, 459–496. [Google Scholar] [CrossRef]
- Barroso, C.; Ganley, C.M.; McGraw, A.L.; Geer, E.A.; Hart, S.A.; Daucourt, M.C. A meta-analysis of the relation between math anxiety and math achievement. Psychol. Bull. 2021, 147, 134–168. [Google Scholar] [CrossRef] [PubMed]
- Caviola, S.; Toffalini, E.; Giofrè, D.; Ruiz, J.M.; Szűcs, D.; Mammarella, I.C. Math Performance and Academic Anxiety Forms, from Sociodemographic to Cognitive Aspects: A Meta-analysis on 906,311 Participants. Educ. Psychol. Rev. 2021, 34, 363–399. [Google Scholar] [CrossRef]
- Ahmed, W.; Minnaert, A.; Kuyper, H.; Van der Werf, M. Reciprocal relationships between math self-concept and math anxiety. Learn. Individ. Differ. 2012, 22, 385–389. [Google Scholar] [CrossRef]
- Brown, M.; Brown, P.; Bibby, T. “I would rather die”: Reasons given by 16-year-olds for not continuing their study of mathematics. Res. Math. Educ. 2008, 10, 3–18. [Google Scholar] [CrossRef] [Green Version]
- Campagna, C.G.; Curtis, G.J. So Worried I Don’t Know What To Be: Anxiety is Associated With Increased Career Indecision and Reduced Career Certainty. Aust. J. Guid. Couns. 2007, 17, 91–96. [Google Scholar] [CrossRef]
- Foley, A.E.; Herts, J.B.; Borgonovi, F.; Guerriero, S.; Levine, S.C.; Beilock, S.L. The Math Anxiety-Performance Link. Curr. Dir. Psychol. Sci. 2017, 26, 52–58. [Google Scholar] [CrossRef]
- Pellicioni, M.S.; Núñez-Peña, M.I.; Colome, A. Math anxiety: A review of its cognitive consequences, psychophysiological correlates, and brain bases. Cogn. Affect. Behav. Neurosci. 2015, 16, 3–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashcraft, M.H. Math Anxiety: Personal, Educational, and Cognitive Consequences. Curr. Dir. Psychol. Sci. 2002, 11, 181–185. [Google Scholar] [CrossRef]
- Choe, K.W.; Jenifer, J.B.; Rozek, C.S.; Berman, M.G.; Beilock, S.L. Calculated avoidance: Math anxiety predicts math avoidance in effort-based decision-making. Sci. Adv. 2019, 5, eaay1062. [Google Scholar] [CrossRef] [Green Version]
- Eysenck, M.W.; Derakshan, N. New perspectives in attentional control theory. Pers. Individ. Differ. 2011, 50, 955–960. [Google Scholar] [CrossRef]
- Robinson, M.D.; Clore, G.L. Belief and feeling: Evidence for an accessibility model of emotional self-report. Psychol. Bull. 2002, 128, 934–960. [Google Scholar] [CrossRef] [Green Version]
- Bieg, M. Trait and State Academic Emotions: Two Sides of the Same Coin? Universität Konstanz: Konstanz, Germany, 2013. [Google Scholar]
- Orbach, L.; Herzog, M.; Fritz, A. Relation of state- and trait-math anxiety to intelligence, math achievement and learning motivation. J. Numer. Cogn. 2019, 5, 371–399. [Google Scholar] [CrossRef] [Green Version]
- Spielberger, C.D. Anxiety Current Trends in Theory and Research; Elsevier Science: Saint Louis, MO, USA, 2014; ISBN 978-1-4832-8921-2. [Google Scholar]
- Buehler, R.; McFarland, C. Intensity Bias in Affective Forecasting: The Role of Temporal Focus. Pers. Soc. Psychol. Bull. 2001, 27, 1480–1493. [Google Scholar] [CrossRef]
- Levine, L.J.; Safer, M.A.; Lench, H.; Levine, L.J.; Safer, M.A.; Lench, H.C. Remembering and Misremembering Emotions. In Judgments over Time: The Interplay of Thoughts, Feelings, and Behaviors; Sanna, L.J., Chang, E.C., Eds.; Oxford University Press: New York, NY, USA, 2006; pp. 271–290. [Google Scholar]
- Faust, M.W. Analysis of Physiological Reactivity in Mathematics Anxiety; Bowling Green State University: Bowling Green, OH, USA, 1992. [Google Scholar]
- Hopko, D.R.; Mahadevan, R.; Bare, R.L.; Hunt, M.K. The Abbreviated Math Anxiety Scale (AMAS). Assessment 2003, 10, 178–182. [Google Scholar] [CrossRef]
- Malanchini, M.; Rimfeld, K.; Shakeshaft, N.G.; Rodic, M.; Schofield, K.; Selzam, S.; Dale, P.S.; Petrill, S.A.; Kovas, Y. The genetic and environmental aetiology of spatial, mathematics and general anxiety. Sci. Rep. 2017, 7, 42218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashcraft, M.H.; Ridley, K.S. Math Anxiety and Its Cognitive Consequences—A Tutorial Review. In Handbook of Mathematical Cognition; Campbell, I.D., Ed.; Psychology Press: New York, NY, USA, 2005; pp. 315–327. [Google Scholar]
- Wang, Z.; Hart, S.A.; Kovas, Y.; Lukowski, S.; Soden, B.; Thompson, L.A.; Plomin, R.; McLoughlin, G.; Bartlett, C.; Lyons, I.M.; et al. Who is afraid of math? Two sources of genetic variance for mathematical anxiety. J. Child Psychol. Psychiatry 2014, 55, 1056–1064. [Google Scholar] [CrossRef]
- Moran, T.P. Anxiety and working memory capacity: A meta-analysis and narrative review. Psychol. Bull. 2016, 142, 831–864. [Google Scholar] [CrossRef]
- Beilock, S.L.; Carr, T.H. When High-Powered People Fail. Psychol. Sci. 2005, 16, 101–105. [Google Scholar] [CrossRef]
- Ramirez, G.; Chang, H.; Maloney, E.A.; Levine, S.C.; Beilock, S.L. On the relationship between math anxiety and math achievement in early elementary school: The role of problem solving strategies. J. Exp. Child Psychol. 2016, 141, 83–100. [Google Scholar] [CrossRef] [Green Version]
- Ramirez, G.; Gunderson, E.A.; Levine, S.C.; Beilock, S.L. Math Anxiety, Working Memory, and Math Achievement in Early Elementary School. J. Cogn. Dev. 2013, 14, 187–202. [Google Scholar] [CrossRef]
- Vukovic, R.K.; Kieffer, M.; Bailey, S.P.; Harari, R.R. Mathematics anxiety in young children: Concurrent and longitudinal associations with mathematical performance. Contemp. Educ. Psychol. 2013, 38, 1–10. [Google Scholar] [CrossRef]
- Ching, B.H.-H. Mathematics anxiety and working memory: Longitudinal associations with mathematical performance in Chinese children. Contemp. Educ. Psychol. 2017, 51, 99–113. [Google Scholar] [CrossRef]
- Beilock, S.L.; DeCaro, M.S. From poor performance to success under stress: Working memory, strategy selection, and mathematical problem solving under pressure. J. Exp. Psychol. Learn. Mem. Cogn. 2007, 33, 983–998. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Shah, P. The effect of pressure on high- and low-working-memory students: An elaboration of the choking under pressure hypothesis. Br. J. Educ. Psychol. 2013, 84, 226–238. [Google Scholar] [CrossRef]
- Geary, D.C.; Hoard, M.K.; Byrd-Craven, J.; DeSoto, M.C. Strategy choices in simple and complex addition: Contributions of working memory and counting knowledge for children with mathematical disability. J. Exp. Child Psychol. 2004, 88, 121–151. [Google Scholar] [CrossRef]
- Owens, M.; Stevenson, J.; Hadwin, J.A.; Norgate, R. When does anxiety help or hinder cognitive test performance? The role of working memory capacity. Br. J. Psychol. 2012, 105, 92–101. [Google Scholar] [CrossRef]
- Soltanlou, M.; Artemenko, C.; Dresler, T.; Fallgatter, A.J.; Ehlis, A.-C.; Nuerk, H.-C. Math Anxiety in Combination With Low Visuospatial Memory Impairs Math Learning in Children. Front. Psychol. 2019, 10, 89. [Google Scholar] [CrossRef] [Green Version]
- Passolunghi, M.C.; Caviola, S.; De Agostini, R.; Perin, C.; Mammarella, I.C. Mathematics Anxiety, Working Memory, and Mathematics Performance in Secondary-School Children. Front. Psychol. 2016, 7, 42. [Google Scholar] [CrossRef] [Green Version]
- Trezise, K.; Reeve, R.A. Worry and working memory influence each other iteratively over time. Cogn. Emot. 2015, 30, 353–368. [Google Scholar] [CrossRef]
- Hickendorff, M.; Edelsbrunner, P.; McMullen, J.; Schneider, M.; Trezise, K. Informative tools for characterizing individual differences in learning: Latent class, latent profile, and latent transition analysis. Learn. Individ. Differ. 2018, 66, 4–15. [Google Scholar] [CrossRef] [Green Version]
- Carr, A. The Handbook of Child and Adolescent Clinical Psychology: A Contextual Approach, 3rd ed.; Routledge: Abingdon, UK, 2016; ISBN 978-1-138-806009. [Google Scholar]
- Ravens-Sieberer, U.; Klasen, F.; Petermann, F. Psychische Kindergesundheit. Kindh. Entwickl. 2016, 25, 4–9. [Google Scholar] [CrossRef]
- Nell, V.; Bretz, J.; Sniehotta, F. Konzentrationstest 3-4 R.; Testzentrale Göttingen: Göttingen, Germany, 2004. [Google Scholar]
- Tewes, A.; Naumann, A. Kinder-Angst-Test III.; Hogrefe: Göttingen, Germany, 2016. [Google Scholar]
- Döpfner, M.; Görtz-Dorten, A.; Lemkuhl, G. Diagnostik-System für Psychische Störungen Nach ICD-10 und DSM-IV für Kinder und Jugendliche-II.; Hogrefe: Göttingen, Germany, 2008. [Google Scholar]
- Haffner, J.; Karin Baro, P.; Parzer, P.; Resch, F. Heidelberger Rechentest 1-4; Hogrefe: Göttingen, Germany, 2005. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; L. Erlbaum Associates: Hillsdale, MI, USA, 1988. [Google Scholar]
- Hayes, A.F. Introduction to Mediation, Moderation, and Conditional Process Analysis: A Regression-Based Approach; The Guilford Press: New York, NY, USA, 2013. [Google Scholar]
- Rosenberg, J. Introduction to TidyLPA. Available online: https://cran.r-project.org/web/packages/tidyLPA/vignettes/Introduction_to_tidyLPA.html (accessed on 26 January 2022).
- Rosenberg, J.; Beymer, P.; Anderson, D.; Van Lissa, C.; Schmidt, J. tidyLPA: An R Package to Easily Carry Out Latent Profile Analysis (LPA) Using Open-Source or Commercial Software. J. Open Source Softw. 2018, 3, 978. [Google Scholar] [CrossRef] [Green Version]
- Nylund, K.L.; Asparouhov, T.; Muthén, B.O. Deciding on the Number of Classes in Latent Class Analysis and Growth Mixture Modeling: A Monte Carlo Simulation Study. Struct. Equ. Model. A Multidiscip. J. 2007, 14, 535–569. [Google Scholar] [CrossRef]
- Tein, J.-Y.; Coxe, S.; Cham, H. Statistical Power to Detect the Correct Number of Classes in Latent Profile Analysis. Struct. Equ. Model. A Multidiscip. J. 2013, 20, 640–657. [Google Scholar] [CrossRef]
- Cohen, J. The earth is round (p < 0.05). Am. Psychol. 1994, 49, 997–1003. [Google Scholar] [CrossRef]
- Emiranda, A.; Colomer, C.; Mercader, J.; Efernández, M.I.; Presentación, M.J. Performance-based tests versus behavioral ratings in the assessment of executive functioning in preschoolers: Associations with ADHD symptoms and reading achievement. Front. Psychol. 2015, 6, 545. [Google Scholar] [CrossRef] [Green Version]
- Devine, A.; Fawcett, K.; Szűcs, D.; Dowker, A. Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behav. Brain Funct. 2012, 8, 33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cargnelutti, E.; Tomasetto, C.; Passolunghi, M.C. The interplay between affective and cognitive factors in shaping early proficiency in mathematics. Trends Neurosci. Educ. 2017, 8-9, 28–36. [Google Scholar] [CrossRef] [Green Version]
- Trezise, K.; Reeve, R.A. Cognition-emotion interactions: Patterns of change and implications for math problem solving. Front. Psychol. 2014, 5, 840. [Google Scholar] [CrossRef] [Green Version]
- Barrouillet, P.; Lépine, R. Working memory and children’s use of retrieval to solve addition problems. J. Exp. Child Psychol. 2005, 91, 183–204. [Google Scholar] [CrossRef]
- Wang, Z.; Lukowski, S.L.; Hart, S.A.; Lyons, I.M.; Thompson, L.A.; Kovas, Y.; Mazzocco, M.M.M.; Plomin, R.; Petrill, S.A. Is Math Anxiety Always Bad for Math Learning? The Role of Math Motivation. Psychol. Sci. 2015, 26, 1863–1876. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Shakeshaft, N.; Schofield, K.; Malanchini, M. Anxiety is not enough to drive me away: A latent profile analysis on math anxiety and math motivation. PLoS ONE 2018, 13, e0192072. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Orbach, L.; Fritz, A. A latent profile analysis of math anxiety and core beliefs toward mathematics among children. Ann. N. Y. Acad. Sci. 2021. [Google Scholar] [CrossRef] [PubMed]
- Dowker, A.; Cheriton, O.; Horton, R.; Mark, W. Relationships between attitudes and performance in young children’s mathematics. Educ. Stud. Math. 2019, 100, 211–230. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Bae, S.R.; Battista, C.; Qin, S.; Chen, T.; Evans, T.M.; Menon, V. Positive Attitude Toward Math Supports Early Academic Success: Behavioral Evidence and Neurocognitive Mechanisms. Psychol. Sci. 2018, 29, 390–402. [Google Scholar] [CrossRef]
- Barry, L.M.; Haraway, D.L. Self-management and ADHD: A literature review. Behav. Anal. Today 2005, 6, 48–64. [Google Scholar] [CrossRef]
- Passolunghi, M.C.; De Vita, C.; Pellizzoni, S. Math anxiety and math achievement: The effects of emotional and math strategy training. Dev. Sci. 2020, 23, e12964. [Google Scholar] [CrossRef]
- Murayama, K.; Pekrun, R.; Lichtenfeld, S.; Hofe, R.V. Predicting Long-Term Growth in Students’ Mathematics Achievement: The Unique Contributions of Motivation and Cognitive Strategies. Child Dev. 2012, 84, 1475–1490. [Google Scholar] [CrossRef]
- Gimbert, F.; Camos, V.; Gentaz, E.; Mazens, K. What predicts mathematics achievement? Developmental change in 5- and 7-year-old children. J. Exp. Child Psychol. 2018, 178, 104–120. [Google Scholar] [CrossRef]
- Geary, D.C. Cognitive predictors of achievement growth in mathematics: A 5-year longitudinal study. Dev. Psychol. 2011, 47, 1539–1552. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Bull, R. Developmental changes in working memory, updating, and math achievement. J. Educ. Psychol. 2016, 108, 869–882. [Google Scholar] [CrossRef] [Green Version]

| Variable | M (SD) | Correlations | ||||||
|---|---|---|---|---|---|---|---|---|
| 2. | 3. | 4. | 5. | 6. | 7. | 8. | ||
| 1. State Anxiety Prior Math Test | 6.86 (4.7) | 0.70 ** | 0.67 ** | 0.56 ** | 0.40 ** | 0.30 ** | −0.07 | −0.30 ** |
| 2. State Anxiety Post Math Test | 7.55 (5.3) | - | 0.65 ** | 0.67 ** | 0.44 ** | 0.30 ** | −0.02 | −0.18 ** |
| 3. State Anxiety Prior Attention Test | 5.19 (4.5) | - | - | 0.78 ** | 0.43 ** | 0.29 ** | −0.06 | −0.25 ** |
| 4. State Anxiety Post Attention Test | 5.17 (5.1) | - | - | - | 0.43 ** | 0.28 ** | −0.03 | −0.15 ** |
| 5. General Anxiety | 6.30 (4.2) | - | - | - | - | 0.57 ** | −0.17 ** | −0.32 ** |
| 6. Self-Rating ADHD | 17.42 (9.9) | - | - | - | - | - | −0.17 ** | −0.31 ** |
| 7. Sustained Attention | 43.06 (19.3) | - | - | - | - | - | - | 0.49 ** |
| 8. Math Achievement | 140.17 (31.4) | - | - | - | - | - | - | - |
| B | SE B | ß | p | R2 | F | |
|---|---|---|---|---|---|---|
| 0.354 | 30.24 | |||||
| 1. State Anxiety Prior Math Test | −1.49 | 0.42 | −0.22 | 0.001 | ||
| 2. State Anxiety Post Math Test | 0.50 | 0.39 | 0.09 | 0.198 | ||
| 3. State Anxiety Prior Attention Test | −0.94 | 0.50 | −0.14 | 0.063 | ||
| 4. State Anxiety Post Attention Test | 0.77 | 0.43 | 0.12 | 0.076 | ||
| 5. General Anxiety | −0.88 | 0.40 | −0.12 | 0.030 | ||
| 6. Self-Rating ADHD | −0.40 | 0.16 | −0.13 | 0.013 | ||
| 7. Sustained Attention | 0.71 | 0.07 | 0.43 | ≤0.001 |
| Model | B | SE B | t | p | R2 |
|---|---|---|---|---|---|
| State Anxiety Prior Math Test × Sustained Attention | −0.03 | 0.02 | −10.99 | 0.048 | 0.31 |
| State Anxiety Post Math Test × Sustained Attention | 0.01 | 0.01 | 0.55 | 0.581 | 0.26 |
| State Anxiety Prior Attention Test × Sustained Attention | −0.01 | 0.02 | −0.88 | 0.377 | 0.29 |
| State Anxiety Post Attention Test × Sustained Attention | 0.01 | 0.01 | 0.35 | 0.730 | 0.26 |
| General Anxiety × Sustained Attention | −0.04 | 0.02 | −20.14 | 0.033 | 0.30 |
| LL | BIC | SABIC | BLRT p-Value | Entropy R2 | |
|---|---|---|---|---|---|
| 1-Profile | −0.3999 | 0.8083 | 0.8038 | ≤0.001 | 1 |
| 2-Profile | −0.3617 | 0.7366 | 0.7296 | ≤0.001 | 0.86 |
| 3-Profile | −0.3443 | 0.7066 | 0.6971 | ≤0.001 | 0.89 |
| 4-Profile | −0.3386 | 0.7001 | 0.6880 | ≤0.001 | 0.85 |
| 5-Profile | −0.3360 | 0.6996 | 0.6850 | ≤0.001 | 0.83 |
| 6-Profile | −0.3339 | 0.7003 | 0.6831 | ≤0.001 | 0.81 |
| 7-Profile | −0.3330 | 0.7032 | 0.6836 | 0.139 | 0.79 |
| Variable | M (SD) | ANOVA | Post-hoc (Scheffé) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Profile 1 n = 30 (7.4%) | Profile 2 n = 37 (9.2%) | Profile 3 n = 84 (20.8%) | Profile 4 n = 57 (14.1%) | Profile 5 n = 60 (14.9%) | Profile 6 n = 135 (33.5%) | Overall n = 403 | F (5, 397) | p | η2 | ||
| 1. State Anxiety Prior Math Test | 12.31 (2.9) | 14.46 (3.4) | 8.90 (3.5) | 4.89 (3.1) | 7.33 (2.8) | 3.24 (2.4) | 6.96 (4.7) | 123.43 | <0.001 | 0.609 | 2 = 1 > 3 = 5 > 4 > 6 |
| 2. State Anxiety Post Math Test | 11.47 (3.2) | 16.24 (3.4) | 10.58 (3.6) | 5.28 (3.3) | 8.42 (3.6) | 2.98 (2.8) | 7.55 (5.3) | 134.72 | <0.001 | 0.629 | 2 > 1 = 3 > 5> 4 > 6 |
| 3. State Anxiety Prior Attention Test | 6.30 (3.1) | 13.86 (4.0) | 8.33 (2.7) | 3.51 (2.2) | 4.98 (2.3) | 1.41 (1.9) | 5.19 (4.5) | 178.95 | <0.001 | 0.693 | 2 > 3 > 1 = 5 = 4 > 6 |
| 4. State Anxiety Post Attention Test | 3.80 (2.5) | 15.78 (2.8) | 9.55 (2.4) | 2.86 (2.4) | 4.85 (2.2) | 0.92 (1.4) | 5.17 (1.4) | 377.80 | <0.001 | 0.827 | 2 > 3 > 5 > 1=5 > 6 |
| 5. General Anxiety | 11.07 (2.6) | 10.89 (3.4) | 7.38 (2.5) | 9.86 (2.8) | 4.02 (2.4) | 2.81 (2.4) | 6.30 (4.2) | 114.78 | <0.001 | 0.591 | 1 = 2 = 4 > 3 > 5 = 6 |
| 6. Self-Rating ADHD | 27.77 (8.9) | 24.03 (10.4) | 19.27 (9.3) | 23.84 (7.0) | 14.25 (8.0) | 10.86 (6.6) | 17.42 (6.6) | 42.75 | <0.001 | 0.350 | 1 = 2 = 4 = 3 > 5 = 6; 1 > 3 |
| 7. Sustained Attention | 31.43 (17.9) | 37.70 (17.1) | 48.55 (16.7) | 37.74 (19.3) | 42.68 (21.2) | 46.12 (18.9) | 43.06 (18.9) | 6.06 | <0.001 | 0.071 | 3 = 6 = 5 = 4 = 2 = 1; 6 > 1; 3 > 4; 3 > 1 |
| Age in months | 127.03 (8.8) | 127.33 (9.0) | 126.57 (12.3) | 128.02 (7.8) | 125.53 (7.2) | 125.92 (8.2) | 126.48 (9.1) | 0.96 | 0.699 | 0.008 | 1 = 2 = 3 = 4 = 5 = 6 |
| Gender ratio (percentage girls) | 60.0% | 75.7% | 60.7% | 56.1% | 45.0% | 51.1% | 55.8% | - | - | - | |
| Math Achievement | 112.13 (26.0) | 122.05 (27.3) | 141.63 (31.8) | 134.79 (25.3) | 144.68 (30.1) | 150.98 (30.3) | 140.17 (31.4) | 12.56 | <0.001 | 0.138 | 1 = 2 = 4 = 3 = 5 = 6; 1 < 3, 4, 5, 6 2 < 3, 5, 6 4 < 6; |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orbach, L.; Fritz, A. Patterns of Attention and Anxiety in Predicting Arithmetic Fluency among School-Aged Children. Brain Sci. 2022, 12, 376. https://doi.org/10.3390/brainsci12030376
Orbach L, Fritz A. Patterns of Attention and Anxiety in Predicting Arithmetic Fluency among School-Aged Children. Brain Sciences. 2022; 12(3):376. https://doi.org/10.3390/brainsci12030376
Chicago/Turabian StyleOrbach, Lars, and Annemarie Fritz. 2022. "Patterns of Attention and Anxiety in Predicting Arithmetic Fluency among School-Aged Children" Brain Sciences 12, no. 3: 376. https://doi.org/10.3390/brainsci12030376
APA StyleOrbach, L., & Fritz, A. (2022). Patterns of Attention and Anxiety in Predicting Arithmetic Fluency among School-Aged Children. Brain Sciences, 12(3), 376. https://doi.org/10.3390/brainsci12030376






