Development of the Mental Number Line Representation of Numbers 0–10 and Its Relationship to Mental Arithmetic
Abstract
1. Introduction
2. Experiment 1
2.1. Method
2.1.1. Participants
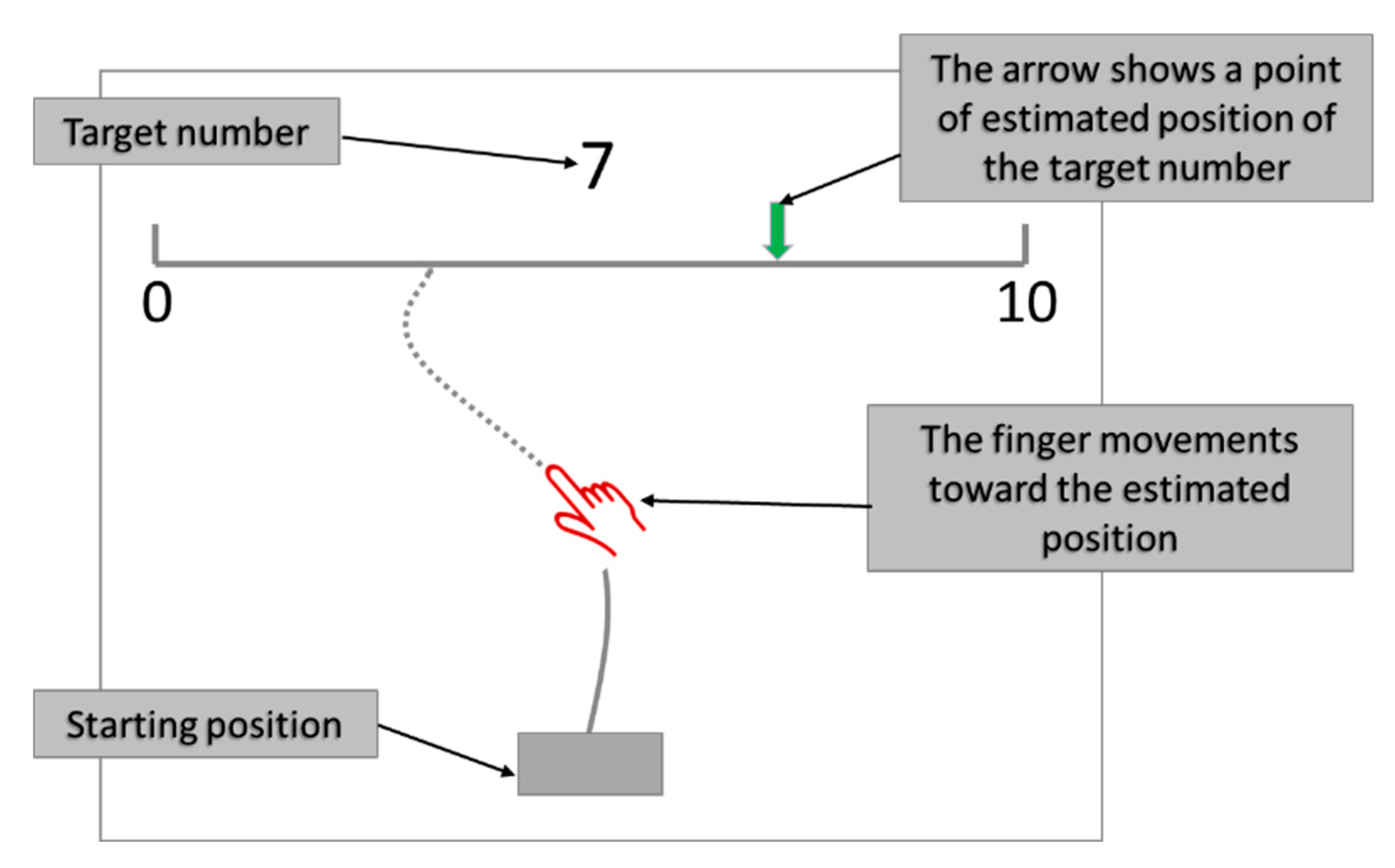
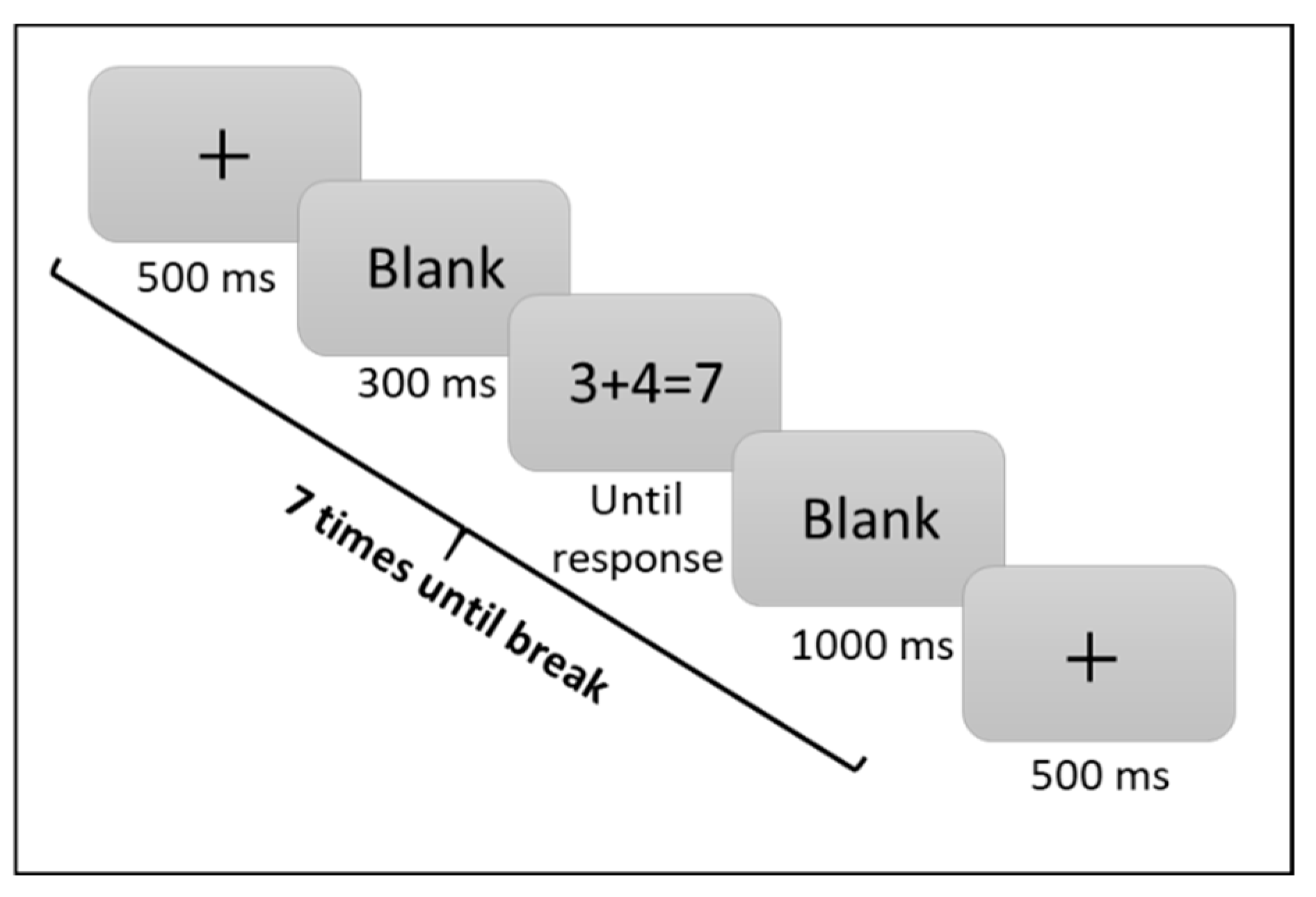
2.1.2. Materials and Procedure
- A task aimed to ensure a minimum level of motor control for the participants. The task was administered like the CNP task, except that each stimulus was not a number but a downward-pointing arrow whose tip touched a random position on the number line. The participants dragged their finger to the location of the arrow. There were 20 trials; no feedback was received.
- Ten training trials in the CNP task were presented to ensure that the participant clearly understood the task. The data set of these trials was not included in the analysis.
2.2. Results
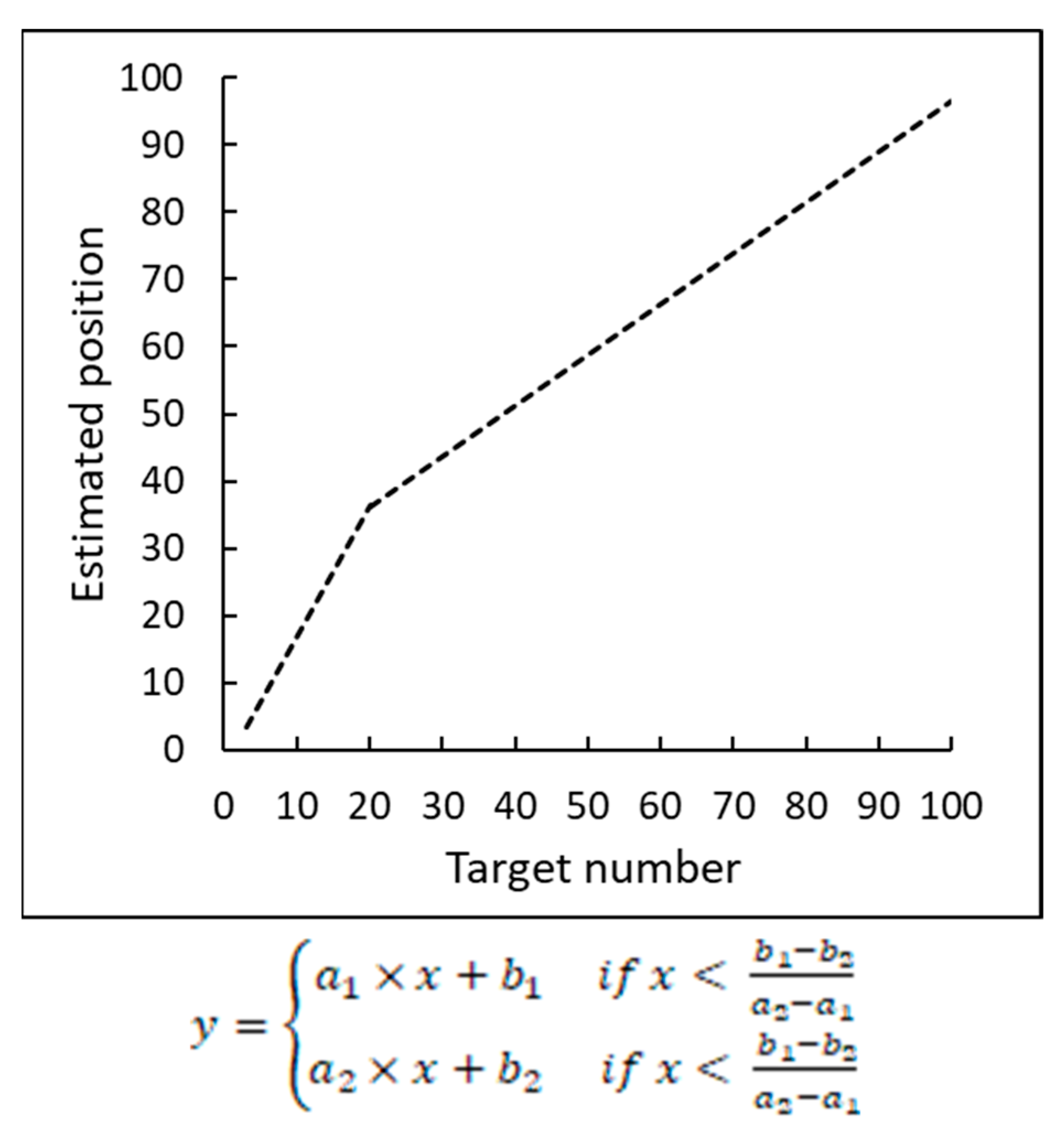
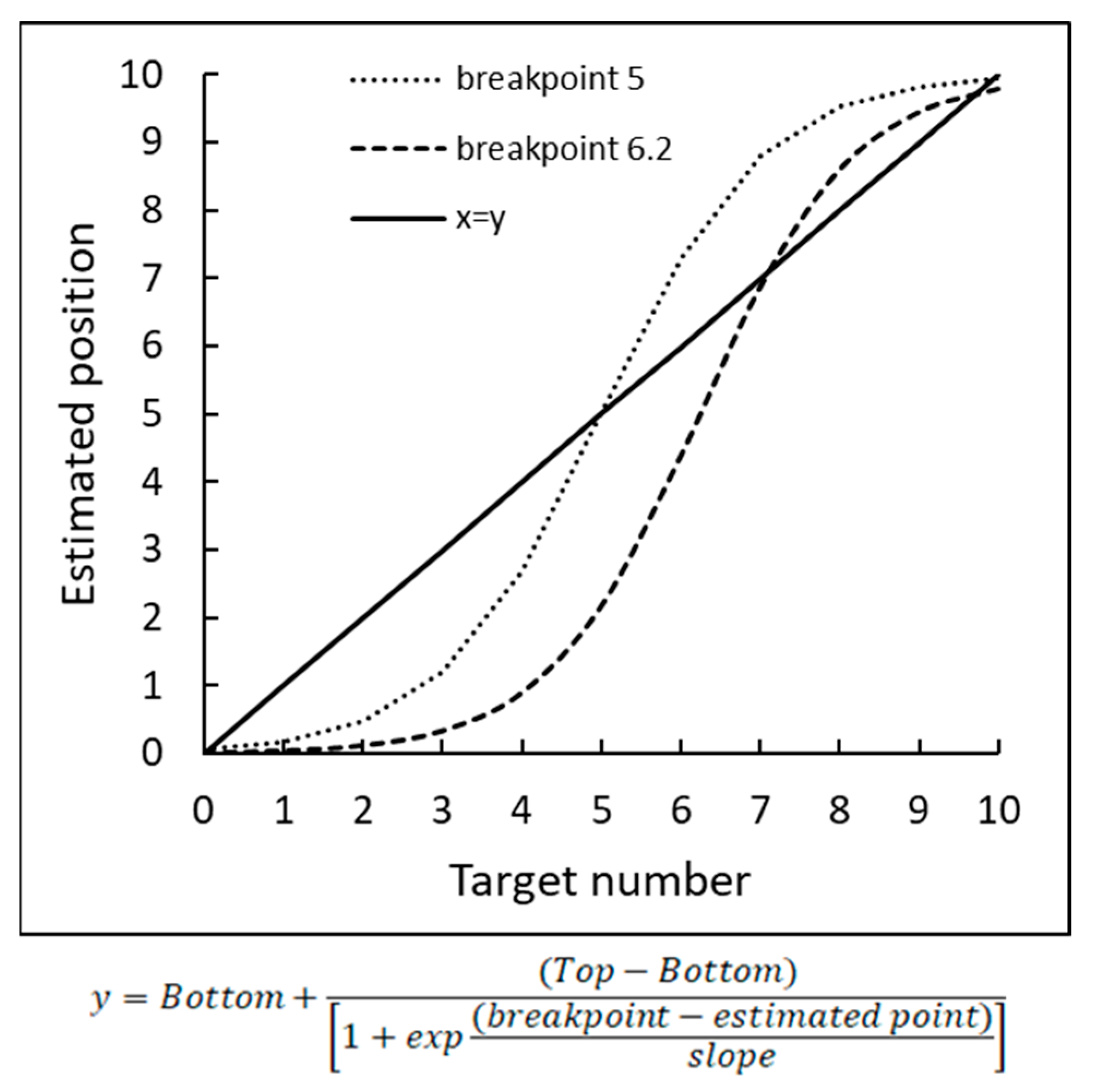
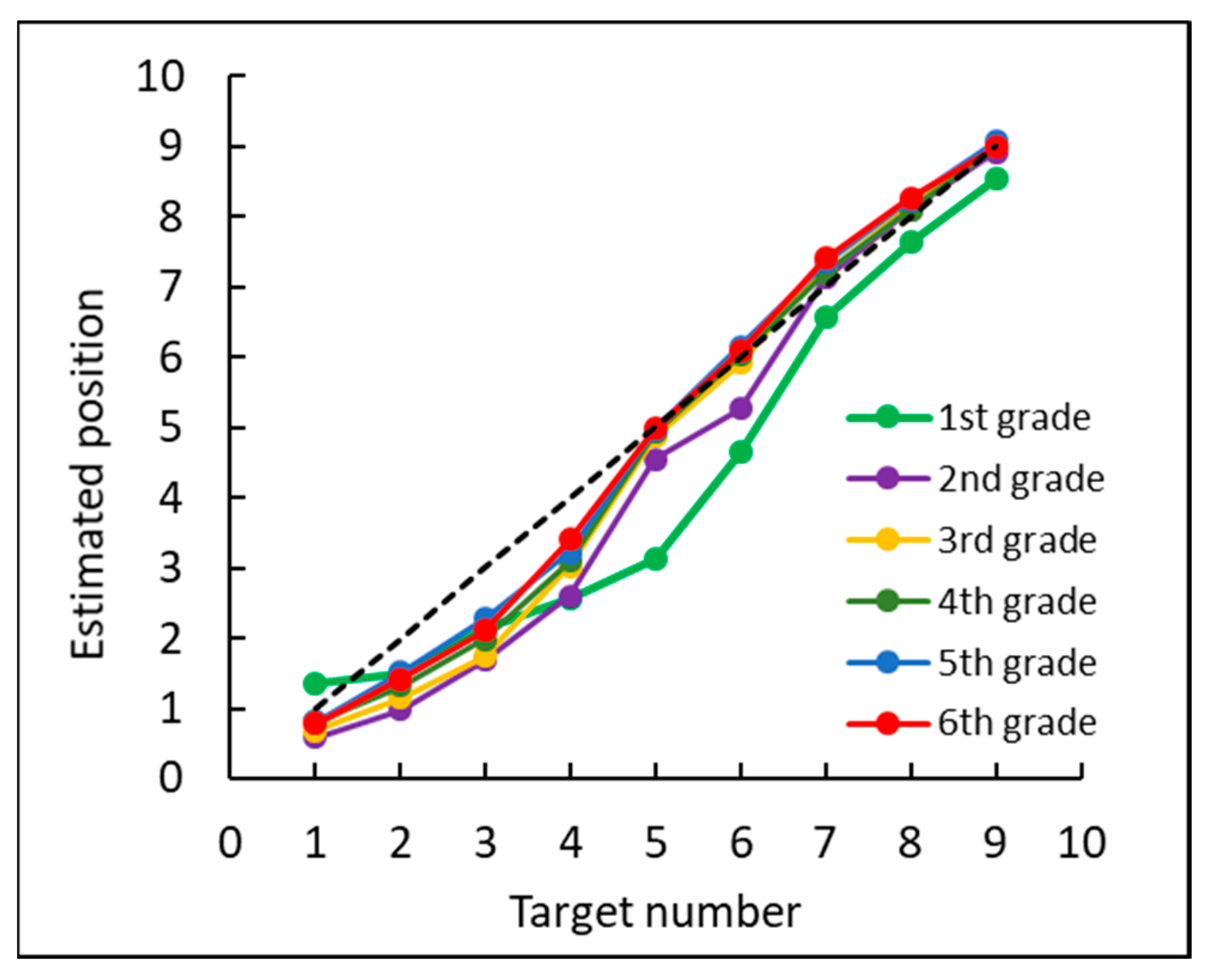
2.2.1. The Estimated Position Pattern Analysis
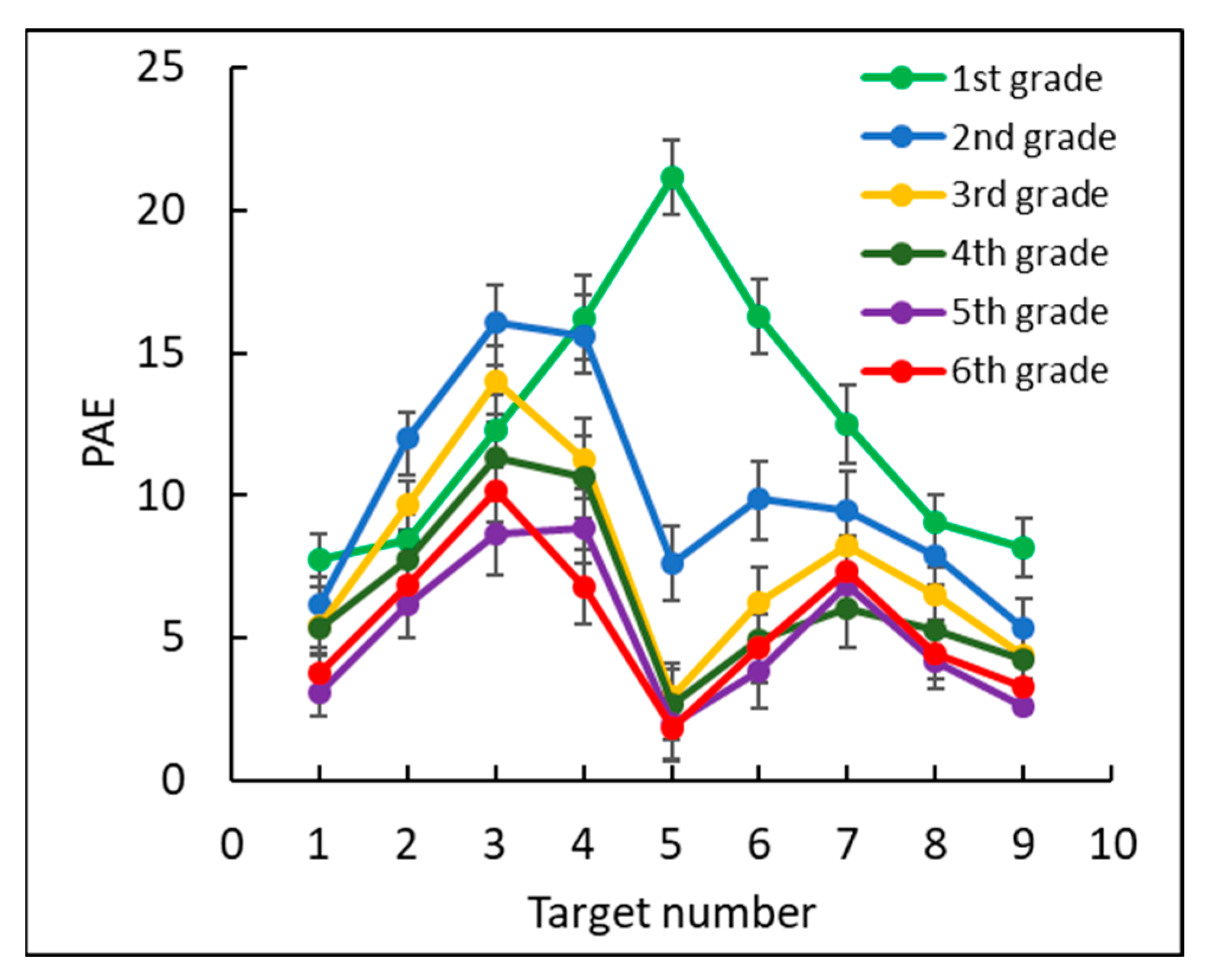
2.2.2. The Estimated Position Accuracy Analysis
2.3. Discussion
3. Experiment 2
3.1. Method
3.1.1. Participants
3.1.2. Materials and Procedure
3.2. Results
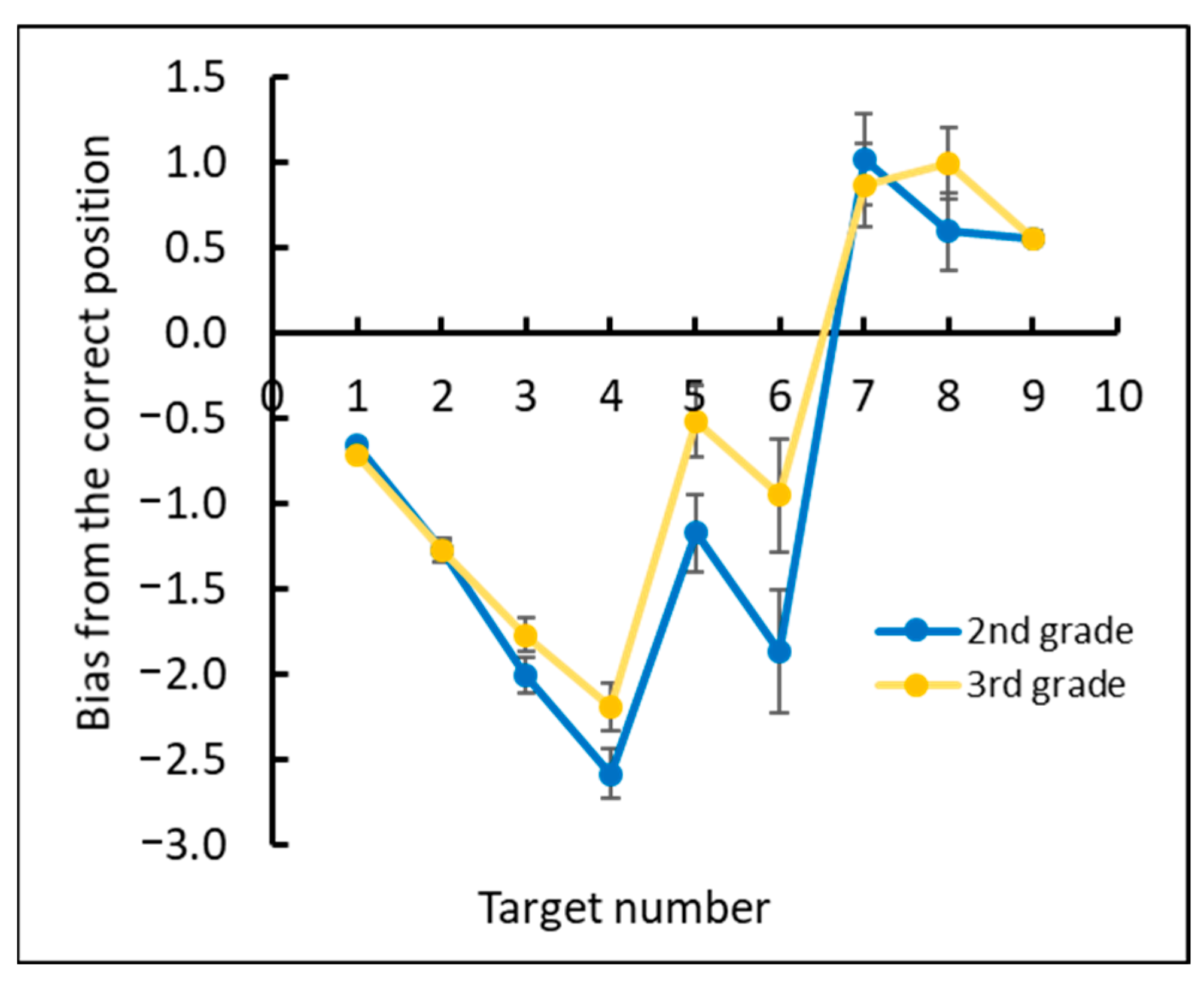
3.3. Discussion
4. Experiment 3
4.1. Method
4.1.1. Participants
4.1.2. Materials and Procedure
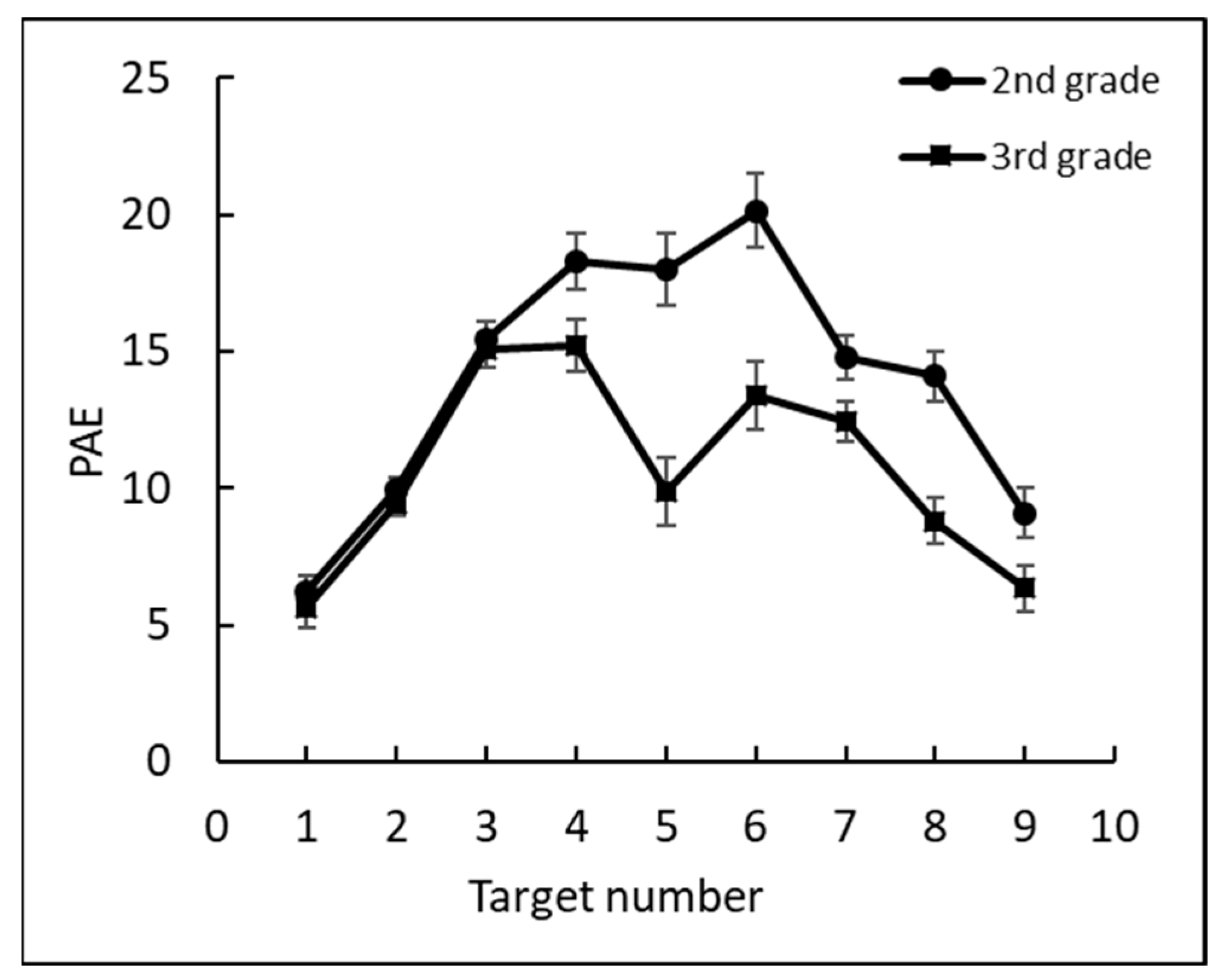
4.2. Results
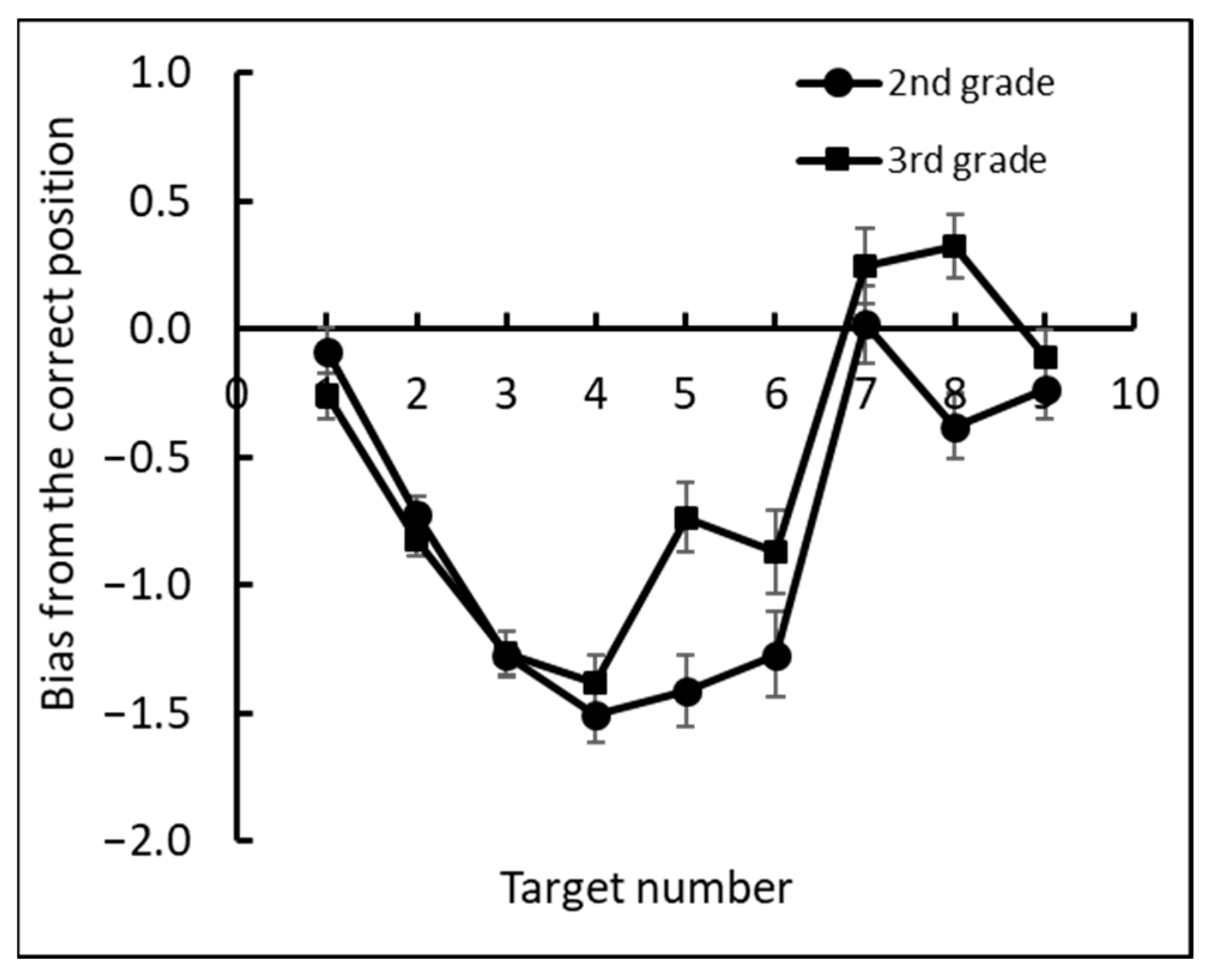
4.2.1. Analysis of the CNP Task
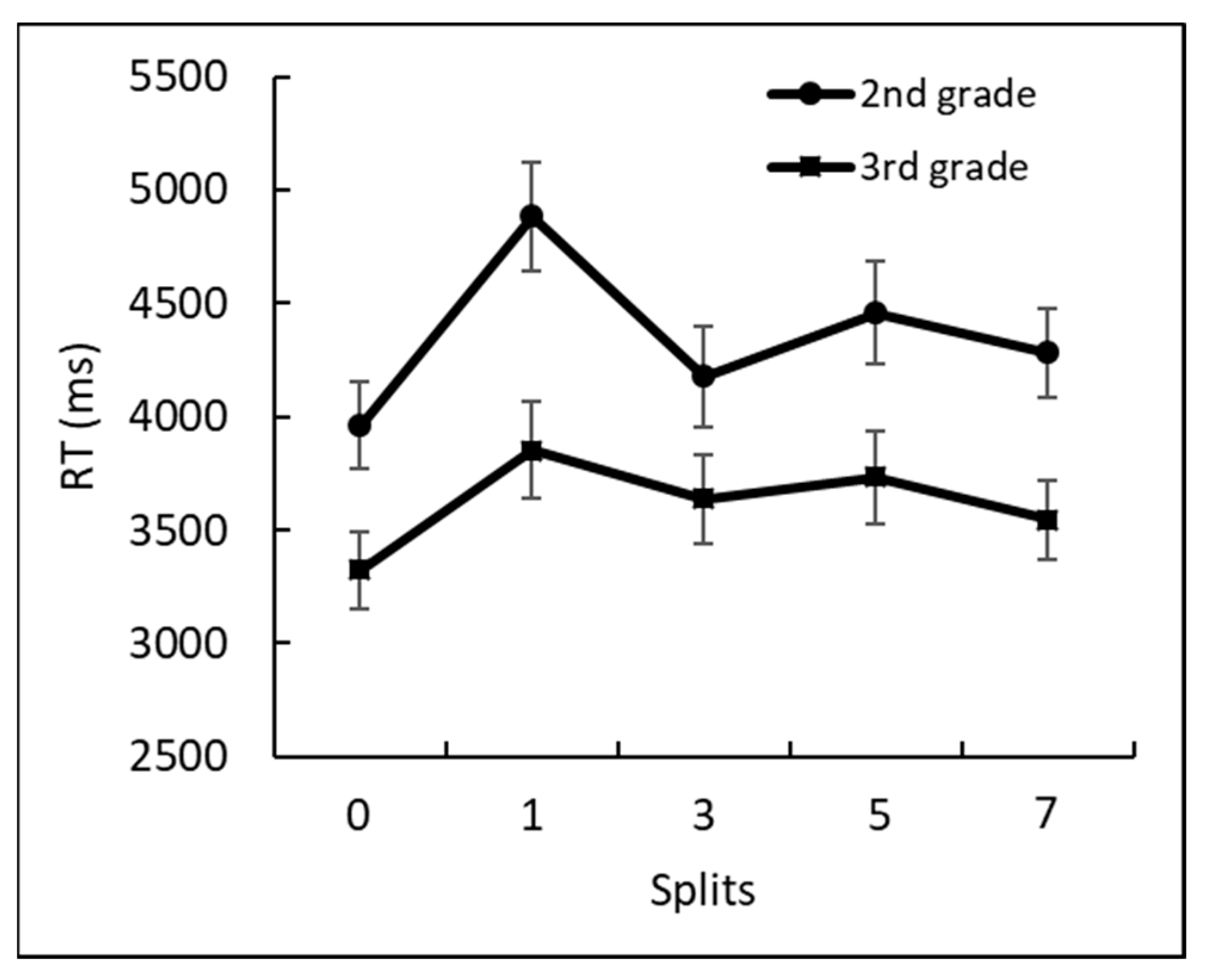
4.2.2. Analysis of the AF Task
4.2.3. Correlation Analysis
4.3. Discussion
5. General Discussion
Implication for Elementary School Math Teachers
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Dehaene, S.; Dupoux, E.; Mehler, J. Is Numerical Comparison Digital? Analogical and Symbolic Effects in Two-Digit Number Comparison. J. Exp. Psychol. Human 1990, 16, 626–641. [Google Scholar] [CrossRef]
- Dehaene, S. Varieties of Numerical Abilities. Cognition 1992, 44, 1–42. [Google Scholar] [CrossRef]
- Dehaene, S.; Piazza, M.; Pinel, P.; Cohen, L. Three Parietal Circuits for Number Processing. Cogn. Neuropsychol. 2003, 20, 487–506. [Google Scholar] [CrossRef] [PubMed]
- Siegler, R.S.; Opfer, J.E. The Development of Numerical Estimation: Evidence for Multiple Representations of Numerical Quantity. Psychol. Sci. 2003, 14, 237–250. [Google Scholar] [CrossRef] [PubMed]
- Siegler, R.S.; Booth, J.L. Development of Numerical Estimation in Young Children. Child Dev. 2004, 75, 428–444. [Google Scholar] [CrossRef] [PubMed]
- Booth, J.L.; Siegler, R.S. Developmental and Individual Differences in Pure Numerical Estimation. Dev. Psychol. 2006, 42, 189–201. [Google Scholar] [CrossRef] [PubMed]
- Laski, E.V.; Siegler, R.S. Is 27 a Big Number? Correlational and Causal Connections Among Numerical Categorization, Number Line Estimation, and Numerical Magnitude Comparison. Child Dev. 2007, 78, 1723–1743. [Google Scholar] [CrossRef] [PubMed]
- Izard, V.; Dehaene, S. Calibrating the Mental Number Line. Cognition 2008, 106, 1221–1247. [Google Scholar] [CrossRef] [PubMed]
- Ebersbach, M.; Luwel, K.; Frick, A.; Onghena, P.; Verschaffel, L. The Relationship Between the Shape of the Mental Number Line and Familiarity with Numbers in 5- to 9-Year Old Children: Evidence for a Segmented Linear Model. J. Exp. Child Psychol. 2008, 99, 1–17. [Google Scholar] [CrossRef]
- Moeller, K.; Pixner, S.; Kaufmann, L.; Nuerk, H.C. Children’s early Mental Number Line: Logarithmic or Decomposed Linear? J. Exp. Child Psychol. 2009, 103, 503–515. [Google Scholar] [CrossRef] [PubMed]
- Barth, H.C.; Paladino, A.M. The Development of Numerical Estimation: Evidence Against a Representational Shift. Dev. Sci. 2011, 14, 125–135. [Google Scholar] [CrossRef] [PubMed]
- Hollands, J.G.; Dyre, B.P. Bias in Proportion Judgments: The Cyclical Power Model. Psychol. Rev. 2000, 107, 500–524. [Google Scholar] [CrossRef] [PubMed]
- Spence, I. Visual Psychophysics of Simple Graphical Elements. J. Exp. Psychol. Human 1990, 16, 683–692. [Google Scholar] [CrossRef]
- Stevens, S.S. On the Theory of Scales of Measurement. Science 1946, 103, 677–680. [Google Scholar] [CrossRef] [PubMed]
- Stevens, S.S. Mathematics, Measurement, and Psychophysics. In Handbook of Experimental Psychology; Stevens, S.S., Ed.; Wiley: New York, NY, USA, 1951; pp. 1–49. [Google Scholar]
- Stevens, S.S. On the Psychophysical Law. Psychol. Rev. 1957, 64, 153–181. [Google Scholar] [CrossRef] [PubMed]
- Slusser, E.B.; Santiago, R.T.; Barth, H.C. Developmental Change in Numerical Estimation. J. Exp. Psychol. Gen. 2013, 142, 193–208. [Google Scholar] [CrossRef]
- Reid, E.E.; Baroody, A.J.; Purpura, D.J. Assessing Young Children’s Number Magnitude Representation: A Comparison Between Novel and Conventional Tasks. J. Cogn. Dev. 2015, 16, 759–779. [Google Scholar] [CrossRef]
- Rouder, J.N.; Geary, D.C. Children’s Cognitive Representation of the Mathematical Number Line. Dev. Sci. 2014, 17, 525–536. [Google Scholar] [CrossRef] [PubMed]
- Zax, A.; Slusser, E.; Barth, H. Spontaneous Partitioning and Proportion Estimation in Children’s Numerical Judgments. J. Exp. Child Psychol. 2019, 185, 71–94. [Google Scholar] [CrossRef]
- Slusser, E.; Barth, H. Intuitive Proportion Judgment in Number-Line Estimation: Converging Evidence from Multiple Tasks. J. Exp. Child Psychol. 2017, 162, 181–198. [Google Scholar] [CrossRef]
- Dackermann, T.; Kroemer, L.; Nuerk, H.C.; Moeller, K.; Huber, S. Influences of Presentation Format and Task Instruction on Children’s Number Line Estimation. Cognitive Dev. 2018, 47, 53–62. [Google Scholar] [CrossRef]
- Campbell, J.I. Handbook of Mathematical Cognition; Psychology Press: New York, NY, USA, 2005. [Google Scholar]
- Nuerk, H.C.; Weger, U.; Willmes, K. A Unit-Decade Compatibility Effect in German Number Words. Curr. Psychol. Lett. Behav. Brain Cogn. 2002, 7, 19–38. [Google Scholar] [CrossRef]
- Dotan, D.; Dehaene, S. How do we convert a number into a finger trajectory? Cognition 2013, 129, 512–529. [Google Scholar] [CrossRef] [PubMed]
- Cipora, K.; Patro, K.; Nuerk, H.C. Are Spatial-Numerical Associations a Cornerstone for Arithmetic Learning? The Lack of Genuine Correlations Suggests No. Mind Brain Edu. 2015, 9, 190–206. [Google Scholar] [CrossRef]
- Cipora, K.; Schroeder, P.A.; Soltanlou, M.; Nuerk, H.C. More Space, Better Mathematics: Is Space a Powerful Tool or a Cornerstone for Understanding Arithmetic? In Visualizing Mathematics: The Role of Spatial Reasoning in Mathematical Thought; Mix, K.S., Battista, M.T., Eds.; Springer: Cham, Switzerland, 2018; pp. 77–116. [Google Scholar]
- Sasanguie, D.; De Smedt, B.; Defever, E.; Reynvoet, B. Association Between Basic Numerical Abilities and Mathematics Achievement. Br. J. Dev. Psychol. 2012, 30, 344–357. [Google Scholar] [CrossRef]
- Link, T.; Moeller, K.; Huber, S.; Fischer, U.; Nuerk, H.C. Walk the Number Line: An Embodied Training of Numerical Concepts. Trends Neurosci. Edu. 2013, 2, 74–84. [Google Scholar] [CrossRef]
- Laski, E.V.; Siegler, R.S. Learning from Number Board Games: You Learn What You Encode. Dev. Psychol. 2014, 50, 853–864. [Google Scholar] [CrossRef]
- Link, T.; Nuerk, H.C.; Moeller, K. On the Relation Between the Mental Number Line and Arithmetic Competencies. Q. J. Exp. Psychol. 2014, 67, 1597–1613. [Google Scholar] [CrossRef]
- Lyons, I.M.; Price, G.; Vaessen, A.; Blomert, L.; Ansari, D. Numerical Predictors of Arithmetic Success in Grades 1–6. Dev. Sci. 2014, 17, 714–726. [Google Scholar] [CrossRef]
- Vanbinst, K.; Ceulemans, E.; Ghesquière, P.; De Smedt, B. Profiles of Children’s Arithmetic Fact Development: A Model-Based Clustering Approach. J. Exp. Child Psychol. 2015, 133, 29–46. [Google Scholar] [CrossRef]
- Siegler, R.S. Magnitude Knowledge: The Common Core of Numerical Development. Dev. Sci. 2016, 19, 341–361. [Google Scholar] [CrossRef] [PubMed]
- Maertens, B.; De Smedt, B.; Sasanguie, D.; Elen, J.; Reynvoet, B. Enhancing Arithmetic in Preschoolers with Comparison or Number Line Estimation Training: Does It Matter? Learn. Instruct. 2016, 46, 1–11. [Google Scholar] [CrossRef]
- Cornu, V.; Hornung, C.; Schiltz, C.; Martin, R. How do Different Aspects of Spatial Skills Relate to Early Arithmetic and Number Line Estimation? J. Num. Cogn. 2017, 3, 309–343. [Google Scholar] [CrossRef]
- Schneider, M.; Merz, S.; Stricker, J.; De Smedt, B.; Torbeyns, J.; Verschaffel, L.; Luwel, K. Associations of Number Line Estimation with Mathematical Competence: A Meta-Analysis. Child Dev. 2018, 89, 1467–1484. [Google Scholar] [CrossRef] [PubMed]
- Geary, D.C.; Widaman, K.F.; Little, T.D. Cognitive Addition and Multiplication: Evidence for a Single Memory Network. Mem. Cognition 1986, 14, 478–487. [Google Scholar] [CrossRef] [PubMed]
- Campbell, J.I.; Fugelsang, J. Strategy Choice for Arithmetic Verification: Effects of Numerical Surface Form. Cognition 2001, 80, B21–B30. [Google Scholar] [CrossRef]
- Hecht, S.A. Counting on Working Memory in Simple Arithmetic When Counting is Used for Problem Solving. Mem. Cogn. 2002, 30, 447–455. [Google Scholar] [CrossRef]
- Webb, N.M.; Shavelson, R.J.; Haertel, E.H. Reliability Coefficients and Generalizability Theory. Handb. Stat. 2006, 26, 81–124. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Automat. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Cohen, D.J.; Blanc-Goldhammer, D. Numerical Bias in Bounded and Unbounded Number Line Tasks. Psychon. B. Rev. 2011, 18, 331–338. [Google Scholar] [CrossRef]
- Dackermann, T.; Huber, S.; Bahnmueller, J.; Nuerk, H.C.; Moeller, K. An Integration of Competing Accounts on Children’s Number Line Estimation. Front. Psychol. 2015, 6, 884. [Google Scholar] [CrossRef] [PubMed]
- Rogers, W.A.; Fisk, A.D.; McLaughlin, A.C.; Pak, R. Touch a Screen or Turn a Knob: Choosing the Best Device for the Job. Hum. Factors 2005, 47, 271–288. [Google Scholar] [CrossRef] [PubMed]
- Lane, J.A. Multimodal Discourse on the Use of Touch Enabled Mobile Devices for Mathematics Education. In Integrating Touch-Enabled and Mobile Devices into Contemporary Mathematics Education; Meletiou-Mavrotheris, M., Ed.; IGI Global: Hershey, PA, USA, 2015; pp. 214–240. [Google Scholar]
- Xu, C.; LeFevre, J.A. Training Young Children on Sequential Relations Among Numbers and Spatial Decomposition: Differential Transfer to Number Line and Mental Transformation Tasks. Dev. Psychol. 2016, 52, 854–866. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Verguts, T. Numerical Proportion Representation: A Neurocomputational Account. Front. Human Neurosci. 2017, 11, 412. [Google Scholar] [CrossRef]
- Huber, S.; Sury, D.; Moeller, K.; Rubinsten, O.; Nuerk, H.C. A General Number-to-Space Mapping Deficit in Developmental Dyscalculia. Res. Dev. Disabil. 2015, 43, 32–42. [Google Scholar] [CrossRef]
- Gilligan, K.A.; Hodgkiss, A.; Thomas, M.S.; Farran, E.K. The Use of Discrimination Scaling Tasks: A Novel Perspective on the Development of Spatial Scaling in Children. Cognitive Dev. 2018, 47, 133–145. [Google Scholar] [CrossRef]
- Huttenlocher, J.; Newcombe, N.; Vasilyeva, M. Spatial Scaling in Young Children. Psychol. Sci. 1999, 10, 393–398. [Google Scholar] [CrossRef]
- Huttenlocher, J.; Vasilyeva, M.; Waterfall, H.R.; Vevea, J.L.; Hedges, L.V. The Varieties of Speech to Young Children. Dev. Psychol. 2007, 43, 1062–1083. [Google Scholar] [CrossRef] [PubMed]
- Spetch, M.L.; Parent, M.B. Age and Sex Differences in Children’s Spatial Search Strategies. Psychon. B Rev. 2006, 13, 807–812. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Uttal, D.H.; Sandstrom, L.B.; Newcombe, N.S. One Hidden Object, Two Spatial Codes: Young Children’s Use of Relational and Vector Coding. J. Cogn. Dev. 2006, 7, 503–525. [Google Scholar] [CrossRef]
- Plumert, J.M.; Hund, A.M.; Recker, K.M. Is Scaling Up Harder Than Scaling Down? How Children and Adults Visually Scale Distance from Memory. Cognition 2019, 185, 39–48. [Google Scholar] [CrossRef] [PubMed]
- Huttenlocher, J.; Newcombe, N.; Sandberg, E.H. The Coding of Spatial Location in Young Children. Cogn. Psychol. 1994, 27, 115–147. [Google Scholar] [CrossRef] [PubMed]
- Domahs, F.; Moeller, K.; Huber, S.; Willmes, K.; Nuerk, H.C. Embodied Numerosity: Implicit Hand-Based Representations Influence Symbolic Number Processing Across Cultures. Cognition 2010, 116, 251–266. [Google Scholar] [CrossRef]
- Overmann, K.A. Finger-Counting in the Upper Palaeolithic. Rock Art Res. 2014, 31, 63–80. [Google Scholar]
- Wiese, H. Numbers, Language, and the Human Mind; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Wiese, H. The Co-Evolution of Number Concepts and Counting Words. Lingua 2007, 117, 758–772. [Google Scholar] [CrossRef]
- Lyons, I.M.; Nuerk, H.-C.; Ansari, D. Rethinking the Implications of Numerical Ratio Effects for Understanding the Development of Representational Precision and Numerical Processing Across Formats. J. Exp. Psychol. Gen. 2015, 144, 1021–1035. [Google Scholar] [CrossRef] [PubMed]
- Vanbinst, K.; Ghesquière, P.; De Smedt, B. Does Numerical Processing Uniquely Predict First Graders’ Future Development of Single-Digit Arithmetic? Learn. Indiv. Differ. 2015, 37, 153–160. [Google Scholar] [CrossRef]
- Iversen, W.; Nuerk, H.-C.; Jäger, L.; Willmes, K. The Influence of an External Symbol System on Number Parity Representation, or What’s Odd About 6? Psychon. B Rev. 2006, 13, 730–736. [Google Scholar] [CrossRef] [PubMed]
- Bobis, J. Early Spatial Thinking and the Development of Number Sense. Aust. Prim. Math. Classr. 2008, 13, 4–9. [Google Scholar]
- Jordan, N.C.; Dyson, N. Catching Math Problems Early: Findings from the Number Sense Intervention Project. In Continuous Issues in Numerical Cognition: How Many or How Much; Henik, A., Ed.; Academic Press: London, UK, 2016; pp. 59–79. [Google Scholar]


| Group | N | The Mean Age in Years (SD) | Males | Females |
|---|---|---|---|---|
| 1st grade | 28 | 6.9 (0.4) | 16 | 12 |
| 2nd grade | 27 | 7.8 (0.3) | 15 | 12 |
| 3rd grade | 31 | 8.9 (0.5) | 14 | 17 |
| 4th grade | 29 | 9.8 (0.3) | 12 | 17 |
| 5th grade | 31 | 11.0 (0.3) | 10 | 21 |
| 6th grade | 35 | 11.9 (0.4) | 21 | 14 |
| Age Group | Model | R2 | Model Comparison | Repeated Contrasts | AIC | |||
|---|---|---|---|---|---|---|---|---|
| F | df | p | ||||||
| 1st grade | 2L | 0.85 | 2L vs. P | 12.13 ** | 1, 27 | <0.001 | 0.31 | 25% |
| P | 0.7 | 2L vs. S | 2.97 | =0.09 | 0.10 | 7% | ||
| S | 0.88 | 68% | ||||||
| 2nd grade | 2L | 0.93 | 2L vs. P | 4.11 * | 1, 26 | =0.053 | 0.14 | 11% |
| P | 0.89 | 2L vs. S | 20.24 ** | <0.001 | 0.44 | 4% | ||
| S | 0.96 | 85% | ||||||
| 3rd grade | 2L | 0.92 | 2L vs. P | 1.46 | 1, 30 | =0.24 | 0.05 | -- |
| P | 0.94 | P vs. S | 15.13 ** | <0.001 | 0.34 | 6% | ||
| S | 0.98 | 94% | ||||||
| 4th grade | 2L | 0.95 | 2L vs. P | 0.11 | 1, 28 | =0.74 | 0.00 | 7% |
| P | 0.95 | P vs. S | 23.31 ** | <0.001 | 0.45 | 7% | ||
| S | 0.97 | 86% | ||||||
| 5th grade | 2L | 0.95 | 2L vs. P | 0.43 | 1, 30 | =0.52 | 0.01 | 13% |
| P | 0.98 | P vs. S | 13.49 ** | <0.001 | 0.31 | 3% | ||
| S | 0.99 | 84% | ||||||
| 6th grade | 2L | 0.97 | 2L vs. P | 0.001 | 1, 34 | =0.97 | 0.00 | 9% |
| P | 0.97 | P vs. S | 8.85 * | <0.01 | 0.21 | 14% | ||
| S | 0.99 | 77% | ||||||
| Age Group | Model | R2 | Model Comparison | Repeated Contrasts | |||
|---|---|---|---|---|---|---|---|
| F | df | p | ƞ2 | ||||
| 2nd grade | 2L | 0.883 | 2L vs. P | 38.58 | 1, 49 | <0.001 | 0.44 |
| P | 0.767 | 2L vs. S | 63.07 | <0.001 | 0.56 | ||
| S | 0.927 | ||||||
| 3rd grade | 2L | 0.936 | 2L vs. P | 7.89 | 1, 60 | <0.001 | 0.31 |
| P | 0.888 | 2L vs. S | 18.8 | <0.001 | 0.66 | ||
| S | 0.998 | ||||||
| Each Number of the CNP Task | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 2nd grade | |||||||||
| Split 0 | −0.326 ** | −0.128 | −0.022 | −0.256 * | −0.153 | −0.004 | −0.096 | −0.440 ** | −0.057 |
| Split 1 | -0.243 * | −0.015 | 0.009 | −0.080 | −0.129 | −0.057 | −0.203 | −0.387 ** | −0.073 |
| Split 3 | −0.308 * | −0.014 | 0.051 | −0.132 | −0.137 | .023 | −0.098 | −0.272 * | −0.112 |
| Split 5 | −0.380 ** | 0.096 | 0.037 | −0.248 * | −0.232 | −0.038 | −0.042 | −0.283 * | −0.063 |
| Split 7 | −0.355 ** | −0.078 | −0.005 | −0.225 | −0.212 | −0.053 | −0.129 | −0.274 * | 0.093 |
| 3rd grade | |||||||||
| Split 0 | −0.133 | −0.178 | −0.144 | −0.026 | −0.326 ** | −0.151 | −0.103 | −0.178 | −0.072 |
| Split 1 | −0.072 | −0.137 | −0.130 | −0.001 | −0.279 * | −0.191 | −0.041 | −0.192 | −0.061 |
| Split 3 | 0.010 | −0.131 | .040 | −0.075 | −0.288 * | −0.184 | 0.041 | 0.046 | −0.064 |
| Split 5 | −0.045 | −0.188 | −0.095 | −0.053 | −0.337 ** | −0.217 * | −0.050 | −0.206 | 0.033 |
| Split 7 | −0.059 | −0.131 | −0.085 | 0.024 | −0.249 * | −0.135 | −0.068 | −0.205 | 0.039 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feldman, A.; Berger, A. Development of the Mental Number Line Representation of Numbers 0–10 and Its Relationship to Mental Arithmetic. Brain Sci. 2022, 12, 335. https://doi.org/10.3390/brainsci12030335
Feldman A, Berger A. Development of the Mental Number Line Representation of Numbers 0–10 and Its Relationship to Mental Arithmetic. Brain Sciences. 2022; 12(3):335. https://doi.org/10.3390/brainsci12030335
Chicago/Turabian StyleFeldman, Anat, and Andrea Berger. 2022. "Development of the Mental Number Line Representation of Numbers 0–10 and Its Relationship to Mental Arithmetic" Brain Sciences 12, no. 3: 335. https://doi.org/10.3390/brainsci12030335
APA StyleFeldman, A., & Berger, A. (2022). Development of the Mental Number Line Representation of Numbers 0–10 and Its Relationship to Mental Arithmetic. Brain Sciences, 12(3), 335. https://doi.org/10.3390/brainsci12030335






