Bayesian Network as a Decision Tool for Predicting ALS Disease
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Bayesian Networks
2.3. Other Machine Learning Methods
2.4. Classification Criteria
3. Results
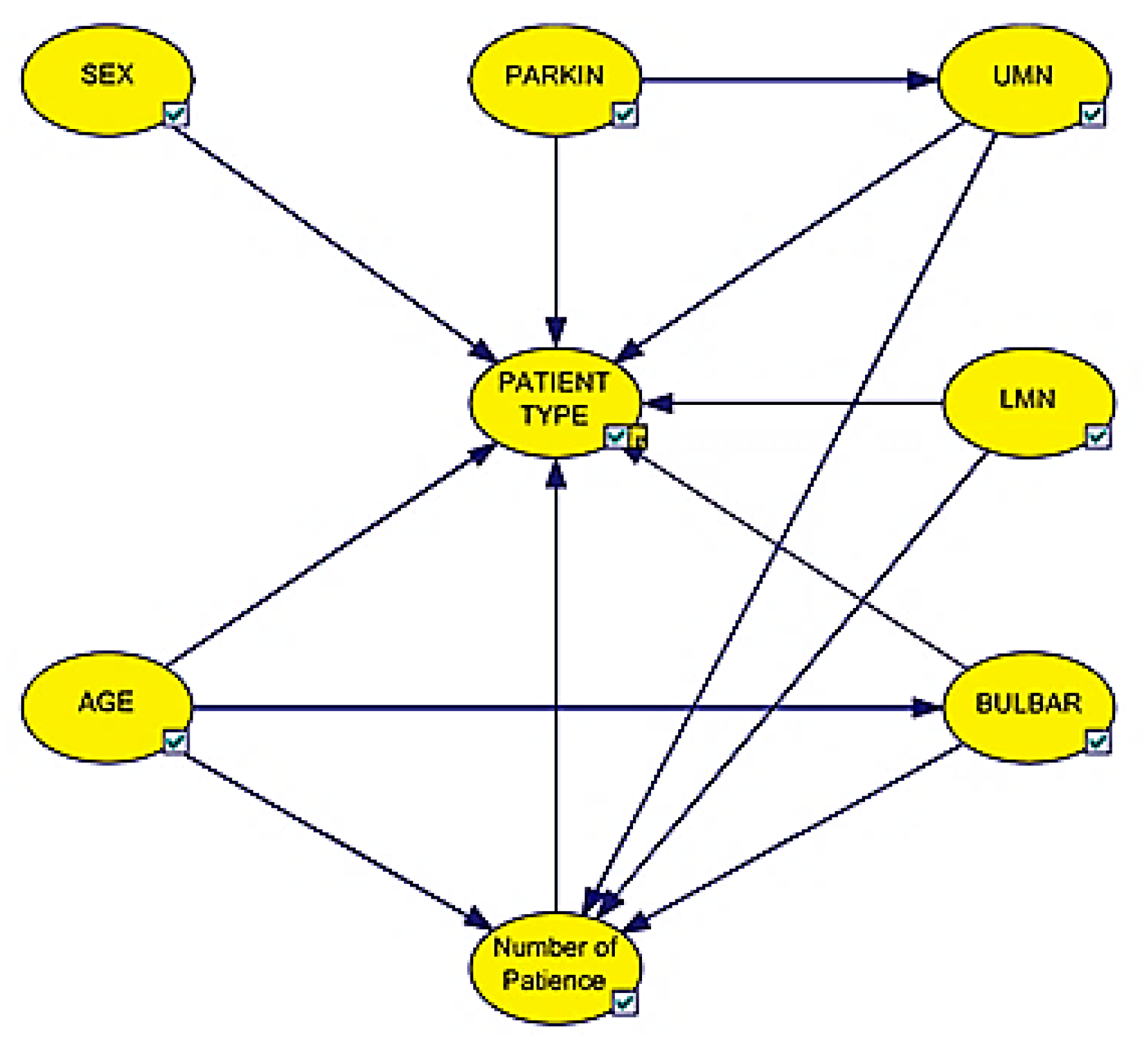
3.1. Bayesian Network Model
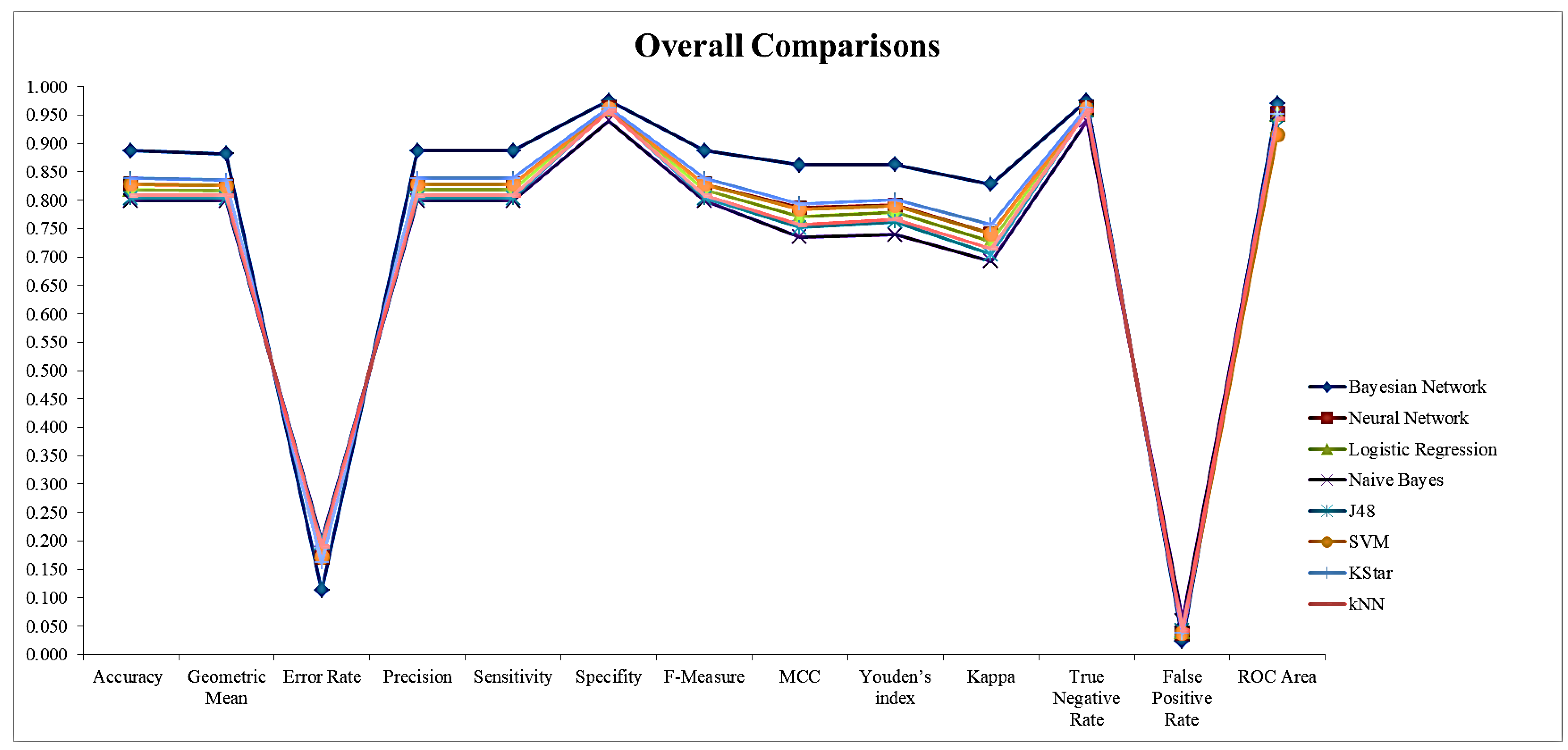
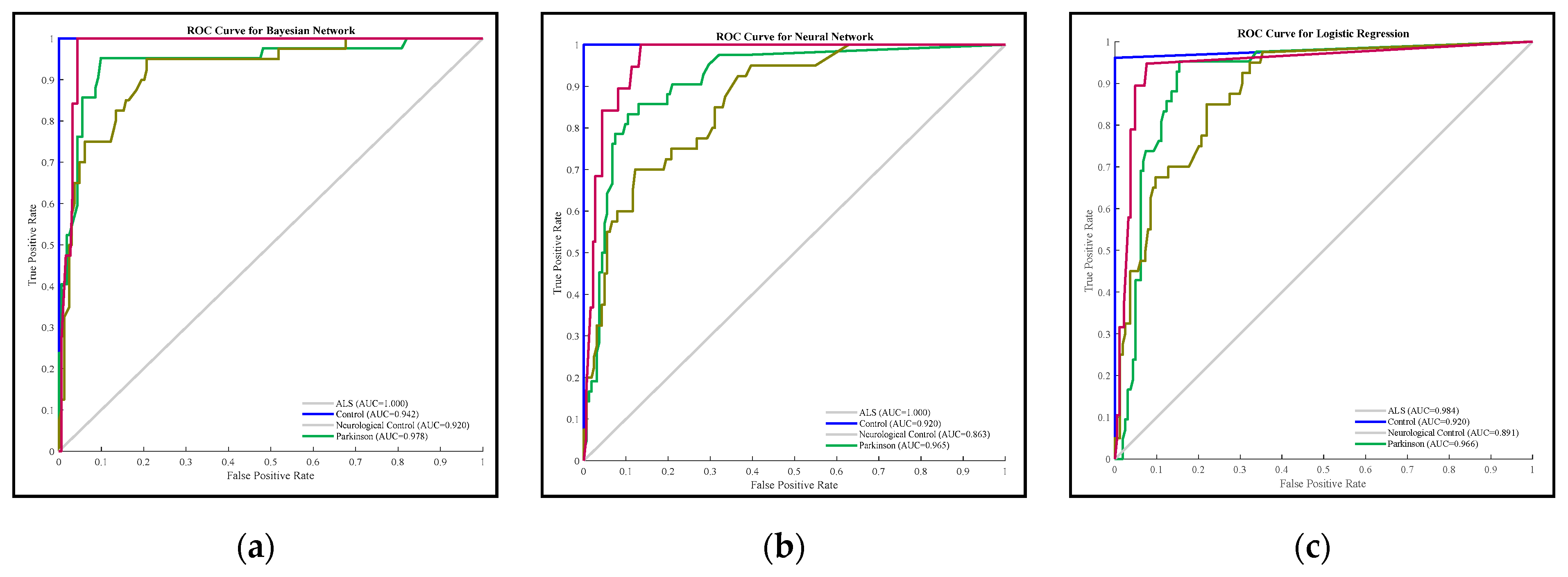
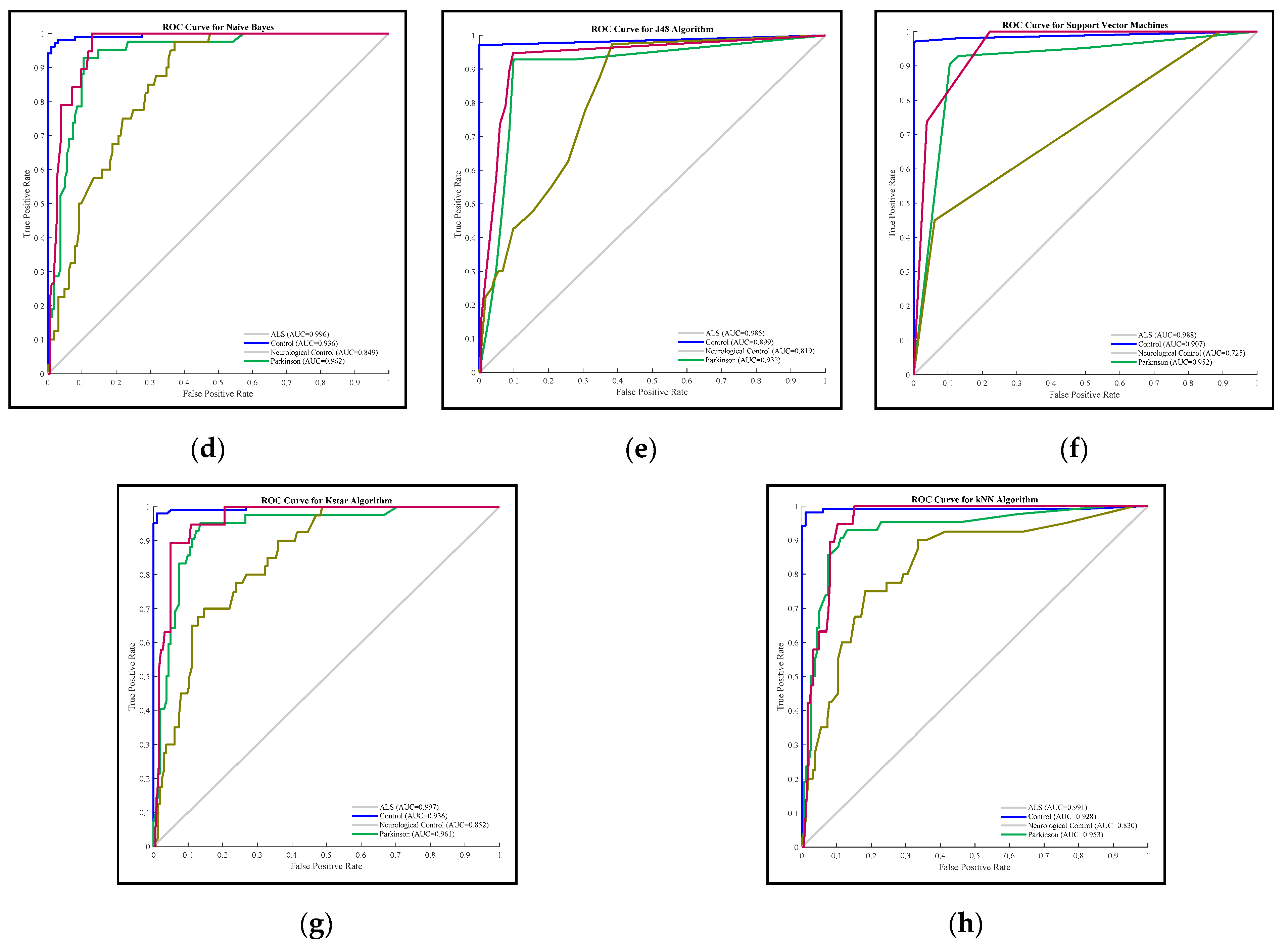
3.2. Comparison Results of Methods
3.3. Queries of Bayesian Network Model
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Rowland, L.P.; Shneider, N.A. Amyotrophic Lateral Sclerosis. N. Engl. J. Med. 2001, 344, 1688–1700. [Google Scholar] [CrossRef] [PubMed]
- Hardiman, O.; van den Berg, L.H.; Kiernan, M.C. Clinical Diagnosis and Management of Amyotrophic Lateral Sclerosis. Nat. Rev. Neurol. 2011, 7, 639–649. [Google Scholar] [CrossRef] [PubMed]
- Swinnen, B.; Robberecht, W. The Phenotypic Variability of Amyotrophic Lateral Sclerosis. Nat. Rev. Neurol. 2014, 10, 661. [Google Scholar] [CrossRef] [PubMed]
- Al-Chalabi, A.; Hardiman, O. The Epidemiology of ALS: A Conspiracy of Genes, Environment and Time. Nat. Rev. Neurol. 2013, 9, 617. [Google Scholar] [CrossRef] [PubMed]
- Filippini, T.; Fiore, M.; Tesauro, M.; Malagoli, C.; Consonni, M.; Violi, F.; Arcolin, E.; Iacuzio, L.; Oliveri Conti, G.; Cristaldi, A.; et al. Clinical and Lifestyle Factors and Risk of Amyotrophic Lateral Sclerosis: A Population-Based Case-Control Study. Int. J. Environ. Res. Public Health 2020, 17, 857. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, D.M.F.; Pizzati, L.; Mostacada, K.; Martins, S.C.D.S.; Higashi, R.; Sá, L.A.; Neto, V.M.; Chimelli, L.; Martinez, A.M.B. Neuroproteomics: An insight into ALS. Neurol. Res. 2012, 34, 937–943. [Google Scholar] [CrossRef]
- Manjaly, Z.R.; Scott, K.M.; Abhinav, K.; Wijesekera, L.; Ganesalingam, J.; Goldstein, L.H.; Janssen, A.; Dougherty, A.; Willey, E.; Stanton, B.R.; et al. The Sex Ratio in Amyotrophic Lateral Sclerosis: A Population Based Study. Amyotroph. Lateral Scler. 2010, 11, 439–442. [Google Scholar] [CrossRef]
- Pape, J.A.; Grose, J.H. The Effects of Diet and Sex in Amyotrophic Lateral Sclerosis. Revue Neurol. 2020, 176, 301–315. [Google Scholar] [CrossRef]
- Longinetti, E.; Fang, F. Epidemiology of Amyotrophic Lateral Sclerosis: An Update of Recent Literature. Curr. Opin. Neurol. 2019, 32, 771. [Google Scholar] [CrossRef]
- Le Gall, L.; Anakor, E.; Connolly, O.; Vijayakumar, U.G.; Duddy, W.J.; Duguez, S. Molecular and Cellular Mechanisms Affected in ALS. J. Pers. Med. 2020, 10, 101. [Google Scholar] [CrossRef]
- Brooks, B.R.; Miller, R.G.; Swash, M.; Munsat, T.L. El Escorial Revisited: Revised Criteria for the Diagnosis of Amyotrophic Lateral Sclerosis. Amyotroph. Lateral Scler. Other Mot. Neuron Disord. 2000, 1, 293–299. [Google Scholar] [CrossRef] [PubMed]
- Vasilopoulou, C.; Morris, A.P.; Giannakopoulos, G.; Duguez, S.; Duddy, W. What Can Machine Learning Approaches in Genomics Tell Us about the Molecular Basis of Amyotrophic Lateral Sclerosis? J. Pers. Med. 2020, 10, 247. [Google Scholar] [CrossRef] [PubMed]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Revised Second Printing; Morgan Kaufmann: San Francisco, CA, USA, 2014; ISBN 978-0-08-051489-5. [Google Scholar]
- Bandyopadhyay, S.; Wolfson, J.; Vock, D.M.; Vazquez-Benitez, G.; Adomavicius, G.; Elidrisi, M.; Johnson, P.E.; OConnor, P.J. Data Mining for Censored Time-to-Event Data: A Bayesian Network Model for Predicting Cardiovascular Risk from Electronic Health Record Data. Data Min. Knowl. Discov. 2015, 29, 1033–1069. [Google Scholar] [CrossRef]
- Kanwar, M.K.; Lohmueller, L.C.; Kormos, R.L.; Teuteberg, J.J.; Rogers, J.G.; Lindenfeld, J.; Bailey, S.H.; McIlvennan, C.K.; Benza, R.; Murali, S.; et al. A Bayesian Model to Predict Survival after Left Ventricular Assist Device Implantation. JACC Heart Fail. 2018, 6, 771–779. [Google Scholar] [CrossRef] [PubMed]
- Kraisangka, J.; Druzdzel, M.J.; Benza, R.L. A Risk Calculator for the Pulmonary Arterial Hypertension Based on a Bayesian Network. In Proceedings of the BMA@ UAI, New York, NY, USA, 29 June 2016; pp. 1–6. [Google Scholar]
- Arora, P.; Boyne, D.; Slater, J.J.; Gupta, A.; Brenner, D.R.; Druzdzel, M.J. Bayesian Networks for Risk Prediction Using Real-World Data: A Tool for Precision Medicine. Value Health 2019, 22, 439–445. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Slater, J.J.; Boyne, D.; Mitsakakis, N.; Béliveau, A.; Druzdzel, M.J.; Brenner, D.R.; Hussain, S.; Arora, P. Probabilistic Graphical Modeling for Estimating Risk of Coronary Artery Disease: Applications of a Flexible Machine-Learning Method. Med. Decis. Mak. 2019, 39, 1032–1044. [Google Scholar] [CrossRef] [PubMed]
- Lam, W.; Bacchus, F. Learning Bayesian Belief Networks: An Approach Based on the Mdl Principle. Comput. Intell. 1994, 10, 269–293. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models. Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Probabilistic Modeling in Bioinformatics and Medical Informatics; Husmeier, D., Dybowski, R., Roberts, S., Eds.; Advanced Information and Knowledge Processing; Springer: London, UK, 2005; ISBN 978-1-85233-778-0. [Google Scholar]
- Senders, J.T.; Staples, P.C.; Karhade, A.V.; Zaki, M.M.; Gormley, W.B.; Broekman, M.L.D.; Smith, T.R.; Arnaout, O. Machine Learning and Neurosurgical Outcome Prediction: A Systematic Review. World Neurosurg. 2018, 109, 476–486. [Google Scholar] [CrossRef]
- Deo Rahul, C. Machine Learning in Medicine. Circulation 2015, 132, 1920–1930. [Google Scholar] [CrossRef]
- Yu, K.-H.; Beam, A.L.; Kohane, I.S. Artificial Intelligence in Healthcare. Nat. Biomed. Eng. 2018, 2, 719–731. [Google Scholar] [CrossRef]
- Dreiseitl, S.; Ohno-Machado, L. Logistic Regression and Artificial Neural Network Classification Models: A Methodology Review. J. Biomed. Inform. 2002, 35, 352–359. [Google Scholar] [CrossRef]
- Gevrey, M.; Dimopoulos, I.; Lek, S. Review and Comparison of Methods to Study the Contribution of Variables in Artificial Neural Network Models. Ecol. Model. 2003, 160, 249–264. [Google Scholar] [CrossRef]
- Christodoulou, E.; Ma, J.; Collins, G.S.; Steyerberg, E.W.; Verbakel, J.Y.; Van Calster, B. A Systematic Review Shows No Performance Benefit of Machine Learning over Logistic Regression for Clinical Prediction Models. J. Clin. Epidemiol. 2019, 110, 12–22. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- Kleinbaum, D.G.; Dietz, K.; Gail, M.; Klein, M.; Klein, M. Logistic Regression; Springer: New York, NY, USA, 2002. [Google Scholar]
- John, G.; Langley, P. Estimating Continuous Distributions in Bayesian Classifiers. In Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence; Morgan Kaufmann: San Mateo, CA, USA, 1995; pp. 338–345. [Google Scholar]
- Wei, W.; Visweswaran, S.; Cooper, G.F. The Application of Naive Bayes Model Averaging to Predict Alzheimer’s Disease from Genome-Wide Data. J. Am. Med. Inform. Assoc. 2011, 18, 370–375. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Shen, Y.; Ding, Y.; Ye, C.; Zheng, Y.; Zhao, P.; Liu, L.; Tong, Z.; Zhou, L.; Sun, S.; et al. A Naive Bayes Algorithm for Tissue Origin Diagnosis (TOD-Bayes) of Synchronous Multifocal Tumors in the Hepatobiliary and Pancreatic System. Int. J. Cancer 2018, 142, 357–368. [Google Scholar] [CrossRef]
- Rokach, L.; Maimon, O. Decision Trees. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer US: Boston, MA, USA, 2005; pp. 165–192. ISBN 978-0-387-25465-4. [Google Scholar]
- Kaur, G.; Chhabra, A. Improved J48 Classification Algorithm for the Prediction of Diabetes. Int. J. Comput. Appl. 2014, 98, 13–17. [Google Scholar] [CrossRef]
- Quinlan, J.R. Improved Use of Continuous Attributes in C4. 5. J. Artif. Intell. Res. 1996, 4, 77–90. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S. Solar Energy Potential Assessment of Western Himalayan Indian State of Himachal Pradesh Using J48 Algorithm of WEKA in ANN Based Prediction Model. Renew. Energy 2015, 75, 675–693. [Google Scholar] [CrossRef]
- bin Othman, M.F.; Yau, T.M.S. Comparison of Different Classification Techniques Using WEKA for Breast Cancer. In Proceedings of the 3rd Kuala Lumpur International Conference on Biomedical Engineering 2006, Kuala Lumpur, Malaysia, 11–14 December 2006; Ibrahim, F., Osman, N.A.A., Usman, J., Kadri, N.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 520–523. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2009; ISBN 0-262-19475-9. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000; ISBN 0-521-78019-5. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques with Java Implementations, 4th ed.; Morgan Kaufmann Publishers: Burlington, MA, USA, 2017; ISBN 1-55860-552-5. [Google Scholar]
- Pinto, D.; Tovar, M.; Vilarino, D.; Beltrán, B.; Jiménez-Salazar, H.; Campos, B. BUAP: Performance of K-Star at the INEX’09 Clustering Task. In Proceedings of the International Workshop of the Initiative for the Evaluation of XML Retrieval, Brisbane, QLD, Australia, 7–9 December 2009; pp. 434–440. [Google Scholar]
- Painuli, S.; Elangovan, M.; Sugumaran, V. Tool Condition Monitoring Using K-Star Algorithm. Expert Syst. Appl. 2014, 41, 2638–2643. [Google Scholar] [CrossRef]
- Wiharto, W.; Kusnanto, H.; Herianto, H. Intelligence System for Diagnosis Level of Coronary Heart Disease with K-Star Algorithm. Healthc. Inform. Res. 2016, 22, 30–38. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, D.; Deng, Z.; Zong, M.; Deng, X. A Novel KNN Algorithm with Data-Driven k Parameter Computation. Pattern Recognit. Lett. 2018, 109, 44–54. [Google Scholar] [CrossRef]
- Filiz, E.; Öz, E. Educational Data Mining Methods For Timss 2015 Mathematics Success: Turkey Case. Sigma J. Eng. Nat. Sci. /Mühendislik ve Fen Bilimleri Dergisi 2020, 38, 963–977. [Google Scholar]
- Ballabio, D.; Grisoni, F.; Todeschini, R. Multivariate Comparison of Classification Performance Measures. Chemom. Intell. Lab. Syst. 2018, 174, 33–44. [Google Scholar] [CrossRef]
- Tharwat, A. Classification Assessment Methods. Appl. Comput. Inform. 2020. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Arnaiz-González, Á.; Díez-Pastor, J.-F.; Gunn, I.A.D. Instance Selection Improves Geometric Mean Accuracy: A Study on Imbalanced Data Classification. Prog. Artif. Intell. 2019, 8, 215–228. [Google Scholar] [CrossRef]
- Marsland, S. Machine Learning: An Algorithmic Perspective, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2015; ISBN 978-1-4665-8333-7. [Google Scholar]
- Sakr, S.; Elshawi, R.; Ahmed, A.M.; Qureshi, W.T.; Brawner, C.A.; Keteyian, S.J.; Blaha, M.J.; Al-Mallah, M.H. Comparison of Machine Learning Techniques to Predict All-Cause Mortality Using Fitness Data: The Henry Ford ExercIse Testing (FIT) Project. BMC Med. Inform. Decis. Mak. 2017, 17, 174. [Google Scholar] [CrossRef]
- Akosa, J. Predictive Accuracy: A Misleading Performance Measure for Highly Imbalanced Data. In Proceedings of the SAS Global Forum, Oklahoma State University, Orlando, FL, USA, 2–5 April 2017; pp. 2–5. [Google Scholar]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- BayesFusion, L. GeNIe Modeler User Manual; BayesFusion, LLC: Pittsburgh, PA, USA, 2017. [Google Scholar]
- Powers, D. Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Viera, A.J.; Garrett, J.M. Understanding Interobserver Agreement: The Kappa Statistic. Fam. Med. 2005, 37, 360–363. [Google Scholar]
- Spiegelhalter, D.J.; Dawid, A.P.; Lauritzen, S.L.; Cowell, R.G. Bayesian Analysis in Expert Systems. Stat. Sci. 1993, 8, 219–247. [Google Scholar] [CrossRef]
- Jensen, F.V.; Nielsen, T.D. Bayesian Networks and Decision Graphs, 2nd ed.; Information Science and Statistics; Springer: New York, NY, USA, 2007; ISBN 978-0-387-68281-5. [Google Scholar]
- Lin, J.-H.; Haug, P.J. Exploiting Missing Clinical Data in Bayesian Network Modeling for Predicting Medical Problems. J. Biomed. Inform. 2008, 41, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Korb, K.B.; Nicholson, A.E. Bayesian Artificial Intelligence; CRC Press: Boca Raton, FL, USA, 2011; p. 479. [Google Scholar]
- Chen, R.; Herskovits, E.H. Clinical Diagnosis Based on Bayesian Classification of Functional Magnetic-Resonance Data. Neuroinformatics 2007, 5, 178–188. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; El Naqa, I.; McShan, D.L.; Ray, D.; Lohse, I.; Matuszak, M.M.; Owen, D.; Jolly, S.; Lawrence, T.S.; Kong, F.-M.; et al. Unraveling Biophysical Interactions of Radiation Pneumonitis in Non-Small-Cell Lung Cancer via Bayesian Network Analysis. Radiother. Oncol. 2017, 123, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Nojavan, A.F.; Qian, S.S.; Stow, C.A. Comparative Analysis of Discretization Methods in Bayesian Networks. Environ. Model. Softw. 2017, 87, 64–71. [Google Scholar] [CrossRef]
- Yang, Y.; Webb, G.I. A Comparative Study of Discretization Methods for Naive-Bayes Classifiers. In Proceedings of the PKAW 2002: The 2002 Pacific Rim Knowledge Acquisition Workshop, Tokyo, Japan, 18–19 August 2002; pp. 159–173. [Google Scholar]
- Rodríguez-López, V.; Cruz-Barbosa, R. Improving Bayesian Networks Breast Mass Diagnosis by Using Clinical Data. In Proceedings of the Pattern Recognition, Mexico City, Mexico, 24–27 June 2015; Carrasco-Ochoa, J.A., Martínez-Trinidad, J.F., Sossa-Azuela, J.H., Olvera López, J.A., Famili, F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 292–301. [Google Scholar]
- Nagarajan, R.; Scutari, M.; Lèbre, S. Bayesian Networks in R: With Applications in Systems Biology; Use R! Springer: New York, NY, USA, 2013; ISBN 978-1-4614-6445-7. [Google Scholar]
- Antal, P.; Fannes, G.; Timmerman, D.; Moreau, Y.; De Moor, B. Using Literature and Data to Learn Bayesian Networks as Clinical Models of Ovarian Tumors. Artif. Intell. Med. 2004, 30, 257–281. [Google Scholar] [CrossRef]
- Khanna, S.; Domingo-Fernández, D.; Iyappan, A.; Emon, M.A.; Hofmann-Apitius, M.; Fröhlich, H. Using Multi-Scale Genetic, Neuroimaging and Clinical Data for Predicting Alzheimer’s Disease and Reconstruction of Relevant Biological Mechanisms. Sci. Rep. 2018, 8, 11173. [Google Scholar] [CrossRef]
- Palmieri, A.; Mento, G.; Calvo, V.; Querin, G.; D’Ascenzo, C.; Volpato, C.; Kleinbub, J.R.; Bisiacchi, P.S.; Sorarù, G. Female Gender Doubles Executive Dysfunction Risk in ALS: A Case-Control Study in 165 Patients. J. Neurol. Neurosurg. Psychiatry 2015, 86, 574–579. [Google Scholar] [CrossRef]
- Trojsi, F.; D’Alvano, G.; Bonavita, S.; Tedeschi, G. Genetics and Sex in the Pathogenesis of Amyotrophic Lateral Sclerosis (ALS): Is There a Link? Int. J. Mol. Sci. 2020, 21, 3647. [Google Scholar] [CrossRef]
- Chiò, A.; Moglia, C.; Canosa, A.; Manera, U.; D’Ovidio, F.; Vasta, R.; Grassano, M.; Brunetti, M.; Barberis, M.; Corrado, L.; et al. ALS Phenotype Is Influenced by Age, Sex, and Genetics: A Population-Based Study. Neurology 2020, 94, e802–e810. [Google Scholar] [CrossRef]
- Ingre, C.; Roos, P.M.; Piehl, F.; Kamel, F.; Fang, F. Risk Factors for Amyotrophic Lateral Sclerosis. Clin. Epidemiol. 2015, 7, 181–193. [Google Scholar] [CrossRef]
- Trojsi, F.; Siciliano, M.; Femiano, C.; Santangelo, G.; Lunetta, C.; Calvo, A.; Moglia, C.; Marinou, K.; Ticozzi, N.; Ferro, C.; et al. Comparative Analysis of C9orf72 and Sporadic Disease in a Large Multicenter ALS Population: The Effect of Male Sex on Survival of C9orf72 Positive Patients. Front. Neurosci. 2019, 13, 485. [Google Scholar] [CrossRef] [PubMed]
- Rooney, J.; Fogh, I.; Westeneng, H.-J.; Vajda, A.; McLaughlin, R.; Heverin, M.; Jones, A.; van Eijk, R.; Calvo, A.; Mazzini, L.; et al. C9orf72 Expansion Differentially Affects Males with Spinal Onset Amyotrophic Lateral Sclerosis. J. Neurol. Neurosurg. Psychiatry 2017, 88, 281. [Google Scholar] [CrossRef] [PubMed]
- Atsuta, N.; Watanabe, H.; Ito, M.; Tanaka, F.; Tamakoshi, A.; Nakano, I.; Aoki, M.; Tsuji, S.; Yuasa, T.; Takano, H.; et al. Age at Onset Influences on Wide-Ranged Clinical Features of Sporadic Amyotrophic Lateral Sclerosis. J. Neurol. Sci. 2009, 276, 163–169. [Google Scholar] [CrossRef] [PubMed]
- Chiò, A.; Calvo, A.; Moglia, C.; Mazzini, L.; Mora, G.; PARALS Study Group. Phenotypic Heterogeneity of Amyotrophic Lateral Sclerosis: A Population Based Study. J. Neurol. Neurosurg. Psychiatry 2011, 82, 740–746. [Google Scholar] [CrossRef] [PubMed]
- Connolly, O.; Le Gall, L.; McCluskey, G.; Donaghy, C.G.; Duddy, W.J.; Duguez, S. A Systematic Review of Genotype–Phenotype Correlation across Cohorts Having Causal Mutations of Different Genes in ALS. J. Pers. Med. 2020, 10, 58. [Google Scholar] [CrossRef]
- van Es, M.A.; Hardiman, O.; Chio, A.; Al-Chalabi, A.; Pasterkamp, R.J.; Veldink, J.H.; van den Berg, L.H. Amyotrophic Lateral Sclerosis. Lancet 2017, 390, 2084–2098. [Google Scholar] [CrossRef]
- Nguyen, H.P.; Van Broeckhoven, C.; van der Zee, J. ALS Genes in the Genomic Era and Their Implications for FTD. Trends Genet. 2018, 34, 404–423. [Google Scholar] [CrossRef]
- Andersen, P.M.; Al-Chalabi, A. Clinical Genetics of Amyotrophic Lateral Sclerosis: What Do We Really Know? Nat. Rev. Neurol. 2011, 7, 603–615. [Google Scholar] [CrossRef]
- Fratello, M.; Caiazzo, G.; Trojsi, F.; Russo, A.; Tedeschi, G.; Tagliaferri, R.; Esposito, F. Multi-View Ensemble Classification of Brain Connectivity Images for Neurodegeneration Type Discrimination. Neuroinform 2017, 15, 199–213. [Google Scholar] [CrossRef]
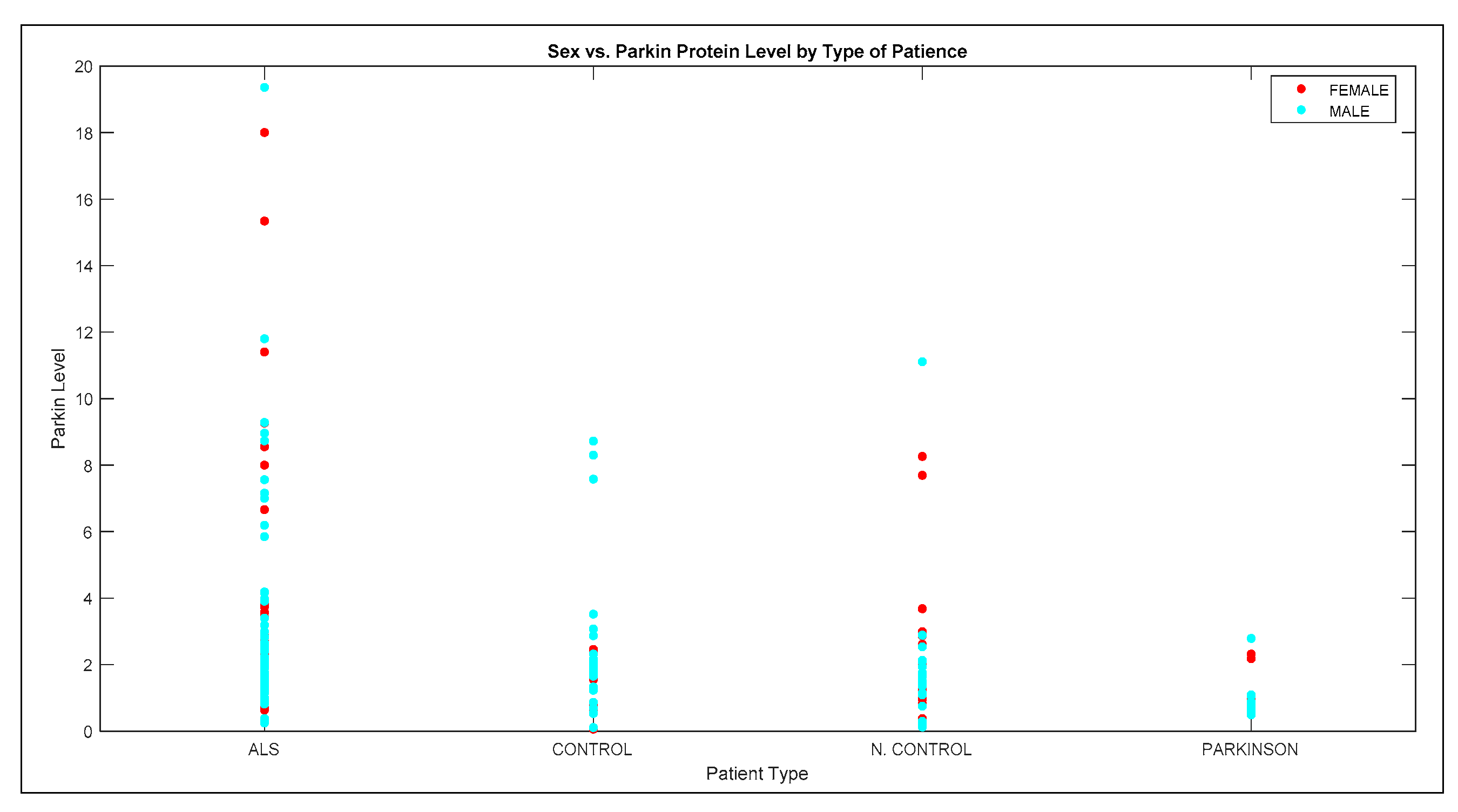
| Feature Name | Feature Value | Freq. | %Value |
|---|---|---|---|
| SEX | Female | 79 | 38.7 |
| Male | 125 | 61.3 | |
| AGE | Below 36 | 29 | 14.2 |
| Between 36–52 | 70 | 34.3 | |
| Between 52–67 | 79 | 38.7 | |
| Upper 67 | 26 | 12.7 | |
| UMN | No | 129 | 63.2 |
| Yes | 75 | 36.8 | |
| LMN | No | 178 | 87.3 |
| Yes | 26 | 12.7 | |
| BULBAR | No | 182 | 89.2 |
| Yes | 22 | 10.8 | |
| Total Number of Chronic Patience | Five | 1 | 0.5 |
| Four | 1 | 0.5 | |
| Three | 12 | 5.9 | |
| Two | 20 | 9.8 | |
| One | 112 | 54.9 | |
| None | 58 | 28.4 | |
| PARKIN Level (ng/mL) | Upper than 3.74 | 31 | 15.2 |
| Between 2.79–3.74 | 17 | 8.3 | |
| Between 2.06–2.79 | 36 | 17.6 | |
| Between 1.36–2.06 | 52 | 25.5 | |
| Lower than 1.36 | 68 | 33.3 | |
| Patient type | ALS | 103 | 50.5 |
| Control | 42 | 20.6 | |
| N-Control | 40 | 19.6 | |
| Parkinson | 19 | 9.3 |
| Criteria | Formula |
|---|---|
| Accuracy | ACC = (TP + TN)/(P + N) |
| Geometric Mean | GM = sqrt ((TP/(TP + FN)) × (TN/(TN + FP))) |
| Error Rate | EER = (FP + FN)/(TP + TN + FP + FN) |
| Precision | PREC = TP/(TP + FP) |
| Sensitivity | SENS = TP/(TP + FN) |
| Specificity | SPEC = TN/(FP + TN) |
| F-Measure | F-Measure = 2 × TP/(2 × TP + FP + FN) |
| Matthews Correlation Coefficient | MCC = TP × TN − FP×FN/sqrt((TP + FP) × (TP + FN) × (TN + FP) × (TN + FN)) |
| Youden’s index | YI = TPR + TNR − 1 |
| Kappa | Kappa = 2 × (TP × TN – FN × FP) / (TP × FN + TP × FP + 2 × TP × TN + FN2 + FN × TN + FP2 + FP × TN) |
| Overall Kappa | Kappa = (p0 − pe)/(1 − pe) |
| p0 = observed accuracy; pe = expected accuracy | |
| False Positive Rate | FPR = FP/(FP + TN) |
| ACC | GM | ERR | SENS | SPEC | F-M | MCC | YI | Kappa | FPR | ROC | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bayesian Network | 0.887 | 0.882 | 0.113 | 0.887 | 0.976 | 0.887 | 0.862 | 0.863 | 0.828 | 0.024 | 0.970 |
| Neural Network | 0.828 | 0.826 | 0.172 | 0.828 | 0.963 | 0.828 | 0.787 | 0.791 | 0.741 | 0.037 | 0.953 |
| Logistic Regression | 0.819 | 0.817 | 0.181 | 0.819 | 0.960 | 0.819 | 0.772 | 0.778 | 0.727 | 0.040 | 0.951 |
| Naive Bayes | 0.799 | 0.800 | 0.201 | 0.799 | 0.940 | 0.799 | 0.736 | 0.739 | 0.693 | 0.060 | 0.951 |
| J48 | 0.804 | 0.804 | 0.196 | 0.804 | 0.958 | 0.804 | 0.752 | 0.762 | 0.705 | 0.042 | 0.930 |
| Support Vector Machine (SVM) | 0.828 | 0.826 | 0.172 | 0.828 | 0.962 | 0.828 | 0.784 | 0.790 | 0.741 | 0.038 | 0.916 |
| KStar | 0.838 | 0.835 | 0.162 | 0.838 | 0.963 | 0.838 | 0.794 | 0.801 | 0.756 | 0.037 | 0.952 |
| k-Nearest Neighbor (k-NN) | 0.809 | 0.808 | 0.191 | 0.809 | 0.958 | 0.809 | 0.756 | 0.766 | 0.715 | 0.042 | 0.943 |
| ACC | GM | ERR | PREC | SENS | SPEC | F-M | MCC | YI | Kappa | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ALS | Bayesian Network | 1.000 | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Neural Network | 0.985 | 0.985 | 0.015 | 1.000 | 0.971 | 1.000 | 0.985 | 0.971 | 0.971 | 0.971 | |
| Logistic Regression | 0.975 | 0.975 | 0.025 | 1.000 | 0.951 | 1.000 | 0.975 | 0.952 | 0.951 | 0.951 | |
| Naive Bayes | 0.971 | 0.970 | 0.029 | 0.962 | 0.981 | 0.960 | 0.971 | 0.941 | 0.941 | 0.941 | |
| J48 | 0.980 | 0.980 | 0.020 | 1.000 | 0.961 | 1.000 | 0.980 | 0.962 | 0.961 | 0.961 | |
| SVM | 0.980 | 0.980 | 0.020 | 1.000 | 0.961 | 1.000 | 0.980 | 0.962 | 0.961 | 0.961 | |
| Kstar | 0.975 | 0.976 | 0.025 | 0.990 | 0.961 | 0.990 | 0.975 | 0.951 | 0.951 | 0.951 | |
| k-NN | 0.956 | 0.956 | 0.044 | 0.990 | 0.922 | 0.990 | 0.955 | 0.914 | 0.912 | 0.912 | |
| Control | Bayesian Network | 0.917 | 0.874 | 0.083 | 0.791 | 0.810 | 0.944 | 0.800 | 0.747 | 0.754 | 0.747 |
| Neural Network | 0.882 | 0.813 | 0.118 | 0.714 | 0.714 | 0.926 | 0.714 | 0.640 | 0.640 | 0.640 | |
| Logistic Regression | 0.868 | 0.845 | 0.132 | 0.642 | 0.810 | 0.883 | 0.716 | 0.638 | 0.692 | 0.631 | |
| Naive Bayes | 0.882 | 0.854 | 0.118 | 0.680 | 0.810 | 0.901 | 0.739 | 0.668 | 0.711 | 0.664 | |
| J48 | 0.887 | 0.902 | 0.113 | 0.661 | 0.929 | 0.877 | 0.772 | 0.718 | 0.805 | 0.700 | |
| SVM | 0.892 | 0.897 | 0.108 | 0.679 | 0.905 | 0.889 | 0.776 | 0.719 | 0.794 | 0.706 | |
| KStar | 0.907 | 0.888 | 0.093 | 0.735 | 0.857 | 0.920 | 0.791 | 0.735 | 0.777 | 0.732 | |
| k-NN | 0.912 | 0.891 | 0.088 | 0.750 | 0.857 | 0.926 | 0.800 | 0.746 | 0.783 | 0.744 | |
| Neurological Control | Bayesian Network | 0.902 | 0.816 | 0.098 | 0.778 | 0.700 | 0.951 | 0.737 | 0.678 | 0.651 | 0.677 |
| Neural Network | 0.848 | 0.738 | 0.152 | 0.615 | 0.600 | 0.909 | 0.608 | 0.513 | 0.509 | 0.513 | |
| Logistic Regression | 0.848 | 0.668 | 0.152 | 0.655 | 0.475 | 0.939 | 0.551 | 0.471 | 0.414 | 0.462 | |
| Naive Bayes | 0.809 | 0.568 | 0.191 | 0.519 | 0.350 | 0.921 | 0.418 | 0.317 | 0.271 | 0.309 | |
| J48 | 0.819 | 0.532 | 0.181 | 0.571 | 0.300 | 0.945 | 0.393 | 0.320 | 0.245 | 0.299 | |
| SVM | 0.843 | 0.650 | 0.157 | 0.643 | 0.450 | 0.939 | 0.529 | 0.449 | 0.389 | 0.439 | |
| KStar | 0.853 | 0.670 | 0.147 | 0.679 | 0.475 | 0.945 | 0.559 | 0.485 | 0.420 | 0.474 | |
| k-NN | 0.833 | 0.661 | 0.167 | 0.594 | 0.475 | 0.921 | 0.528 | 0.432 | 0.396 | 0.428 | |
| Parkinson | Bayesian Network | 0.956 | 0.903 | 0.044 | 0.727 | 0.842 | 0.968 | 0.780 | 0.759 | 0.810 | 0.756 |
| Neural Network | 0.941 | 0.869 | 0.059 | 0.652 | 0.789 | 0.957 | 0.714 | 0.686 | 0.746 | 0.682 | |
| Logistic Regression | 0.946 | 0.898 | 0.054 | 0.667 | 0.842 | 0.957 | 0.744 | 0.721 | 0.799 | 0.715 | |
| Naive Bayes | 0.936 | 0.840 | 0.064 | 0.636 | 0.737 | 0.957 | 0.683 | 0.650 | 0.694 | 0.648 | |
| J48 | 0.922 | 0.832 | 0.078 | 0.560 | 0.737 | 0.941 | 0.636 | 0.600 | 0.677 | 0.593 | |
| SVM | 0.941 | 0.842 | 0.059 | 0.667 | 0.737 | 0.962 | 0.700 | 0.669 | 0.699 | 0.667 | |
| KStar | 0.941 | 0.920 | 0.059 | 0.630 | 0.895 | 0.946 | 0.739 | 0.721 | 0.841 | 0.707 | |
| k-NN | 0.917 | 0.857 | 0.083 | 0.536 | 0.789 | 0.930 | 0.638 | 0.607 | 0.719 | 0.593 |
| Target Node (s) | Target Value | Evidence (Patient Type) | |||
|---|---|---|---|---|---|
| ALS | Control | N-Control | Parkinson | ||
| None | None | 0.340 | 0.252 | 0.257 | 0.151 |
| AGE | Below 36 | 0.119 | 0.249 | 0.106 | 0.078 |
| Between 36–52 | 0.333 | 0.419 | 0.298 | 0.316 | |
| Between 52–67 | 0.437 | 0.232 | 0.449 | 0.430 | |
| Upper 67 | 0.111 | 0.100 | 0.148 | 0.175 | |
| SEX | Female | 0.382 | 0.342 | 0.401 | 0.452 |
| Male | 0.618 | 0.658 | 0.599 | 0.548 | |
| PARKIN Level (ng/mL) | Upper than 3.74 | 0.244 | 0.107 | 0.098 | 0.114 |
| Between 2.79–3.74 | 0.078 | 0.072 | 0.100 | 0.084 | |
| Between 2.06–2.79 | 0.192 | 0.200 | 0.159 | 0.131 | |
| Between 1.36–2.06 | 0.238 | 0.279 | 0.340 | 0.107 | |
| Lower than 1.36 | 0.247 | 0.343 | 0.303 | 0.563 | |
| UMN | No | 0.273 | 0.840 | 0.844 | 0.733 |
| Yes | 0.727 | 0.160 | 0.156 | 0.267 | |
| LMN | No | 0.822 | 0.912 | 0.913 | 0.852 |
| Yes | 0.178 | 0.088 | 0.087 | 0.148 | |
| BULBAR | No | 0.853 | 0.924 | 0.925 | 0.872 |
| Yes | 0.147 | 0.076 | 0.075 | 0.128 | |
| Total Number of Patience | None | 0.040 | 0.696 | 0.288 | 0.075 |
| One | 0.704 | 0.189 | 0.595 | 0.731 | |
| Two | 0.140 | 0.060 | 0.059 | 0.101 | |
| Three | 0.103 | 0.042 | 0.045 | 0.070 | |
| Four | 0.008 | 0.008 | 0.007 | 0.013 | |
| Five | 0.006 | 0.006 | 0.006 | 0.010 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karaboga, H.A.; Gunel, A.; Korkut, S.V.; Demir, I.; Celik, R. Bayesian Network as a Decision Tool for Predicting ALS Disease. Brain Sci. 2021, 11, 150. https://doi.org/10.3390/brainsci11020150
Karaboga HA, Gunel A, Korkut SV, Demir I, Celik R. Bayesian Network as a Decision Tool for Predicting ALS Disease. Brain Sciences. 2021; 11(2):150. https://doi.org/10.3390/brainsci11020150
Chicago/Turabian StyleKaraboga, Hasan Aykut, Aslihan Gunel, Senay Vural Korkut, Ibrahim Demir, and Resit Celik. 2021. "Bayesian Network as a Decision Tool for Predicting ALS Disease" Brain Sciences 11, no. 2: 150. https://doi.org/10.3390/brainsci11020150
APA StyleKaraboga, H. A., Gunel, A., Korkut, S. V., Demir, I., & Celik, R. (2021). Bayesian Network as a Decision Tool for Predicting ALS Disease. Brain Sciences, 11(2), 150. https://doi.org/10.3390/brainsci11020150





