Multiscale Computation and Dynamic Attention in Biological and Artificial Intelligence
Abstract
1. Introduction
2. Bias, Inertia, and Habit Formation in Local Environments
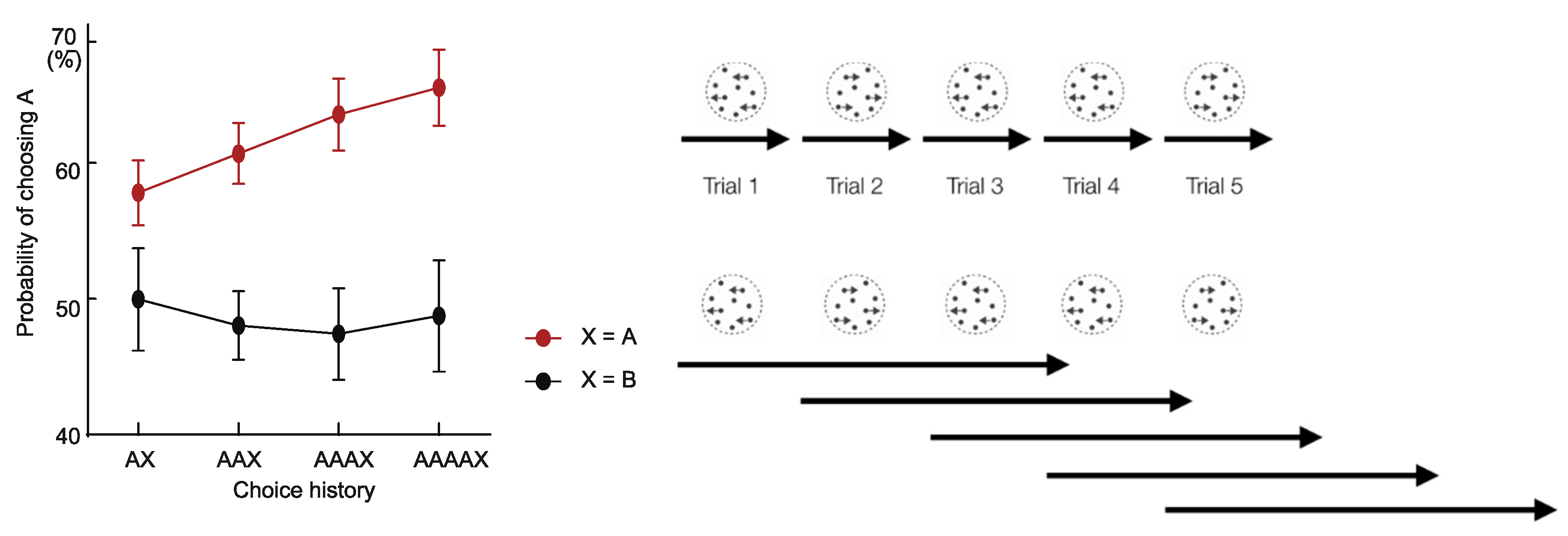
2.1. Decision Inertia
2.2. Habit Formation
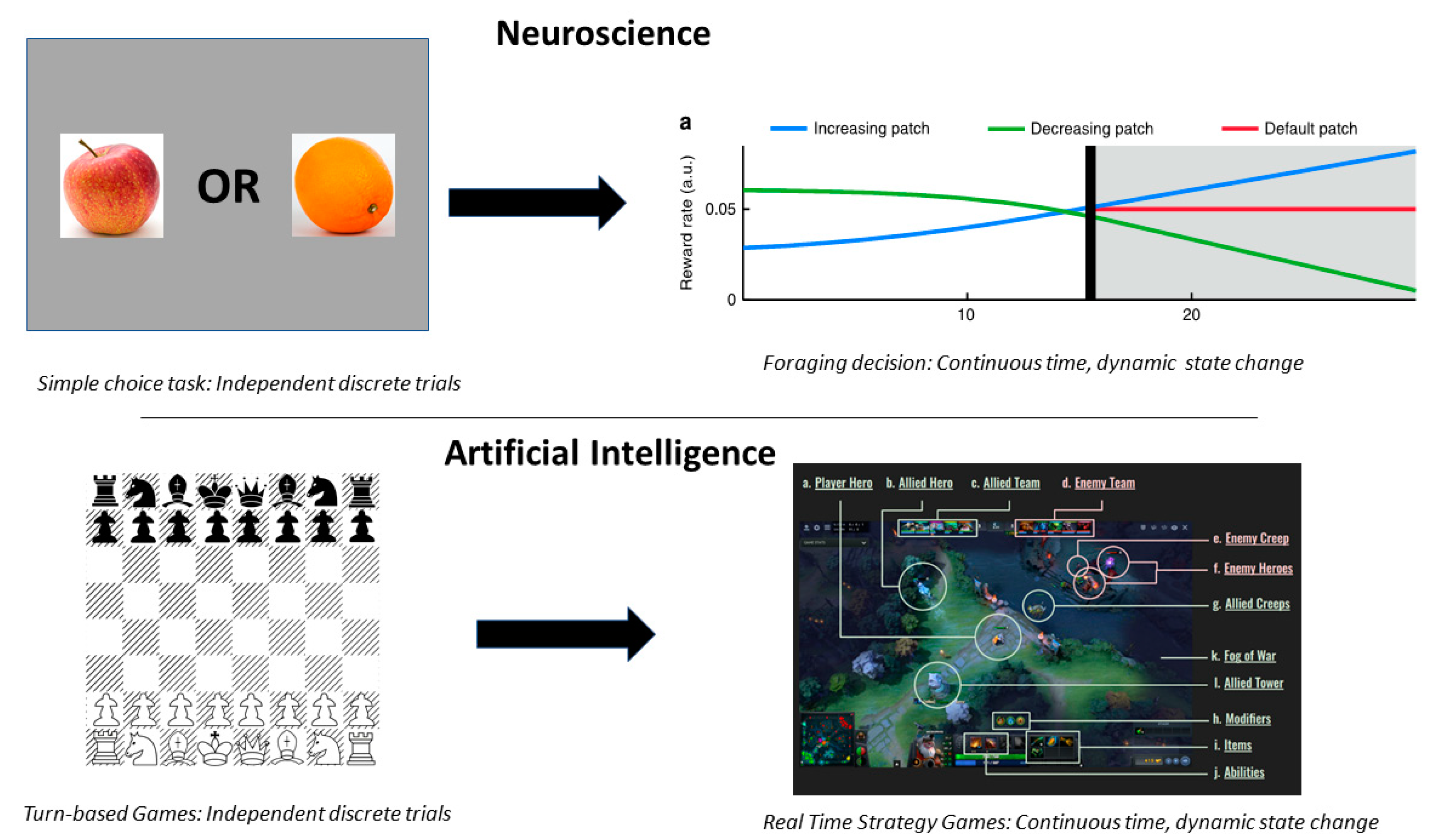
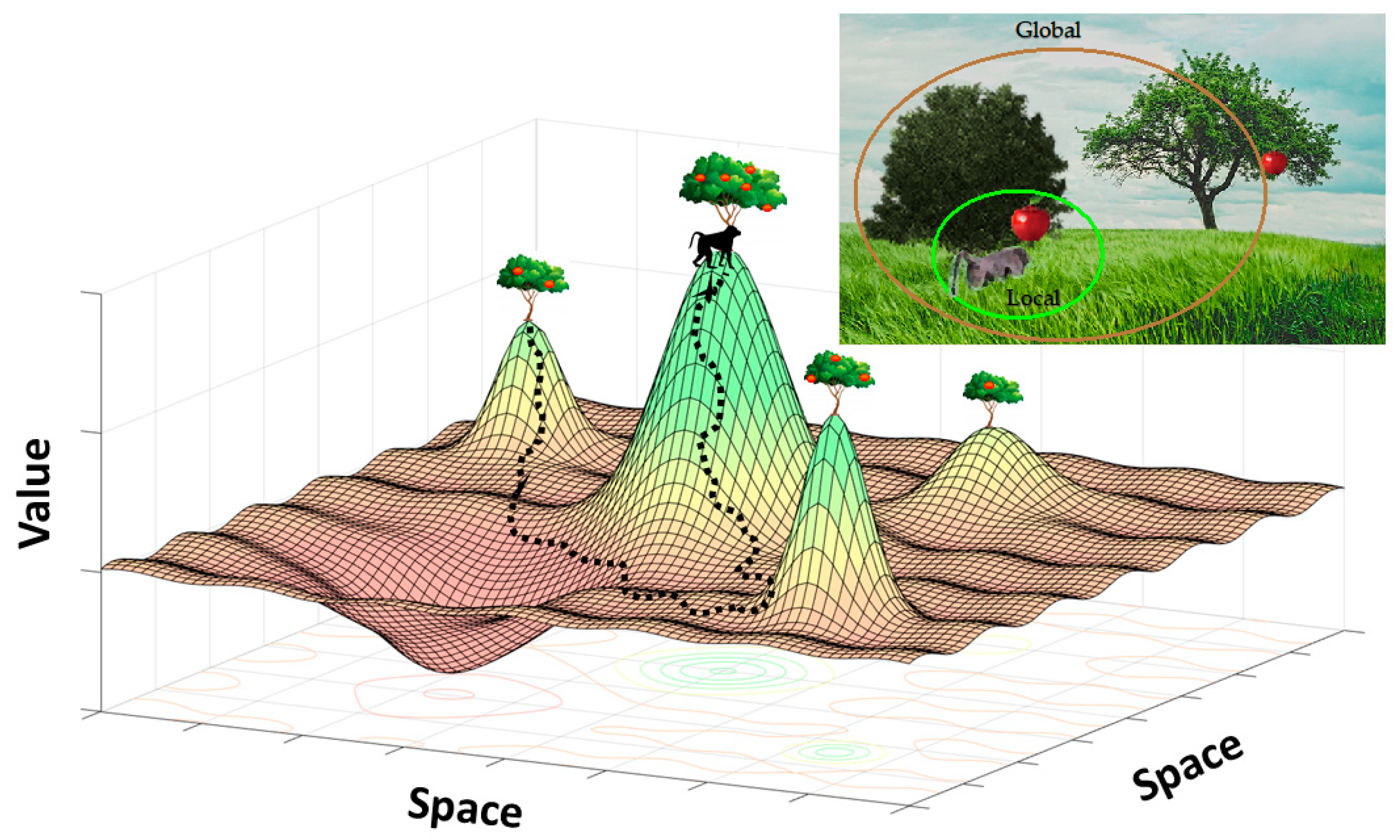
3. Multiscale Decision Making in the Global Environment
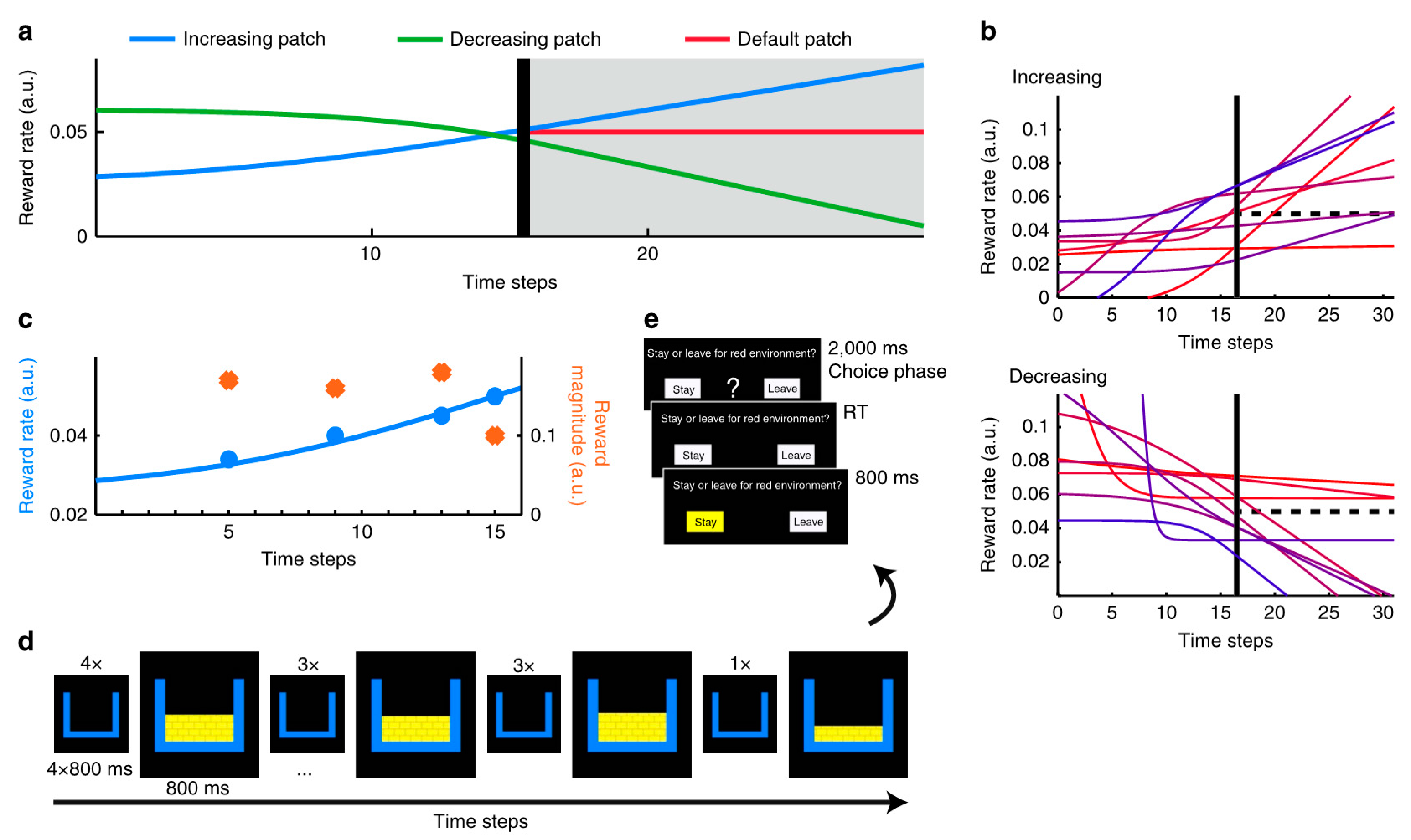
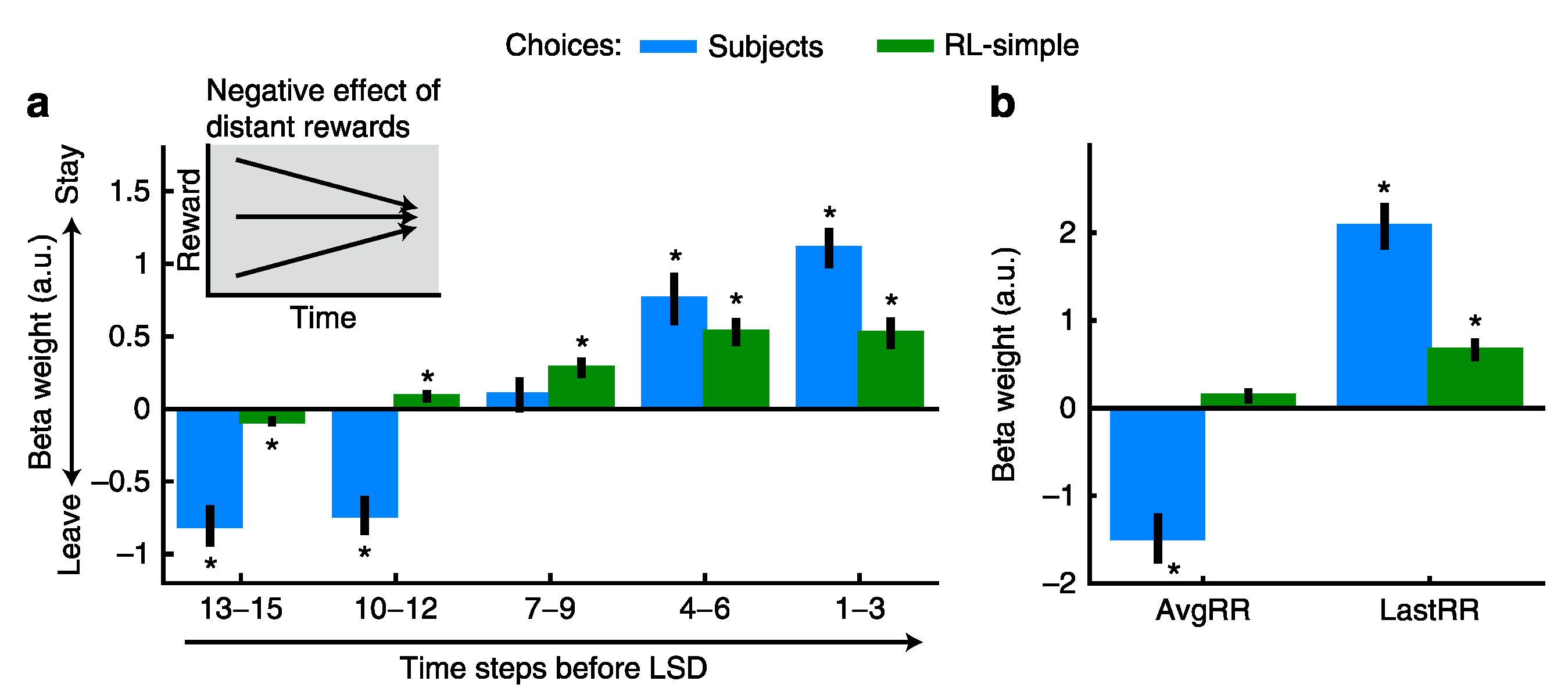
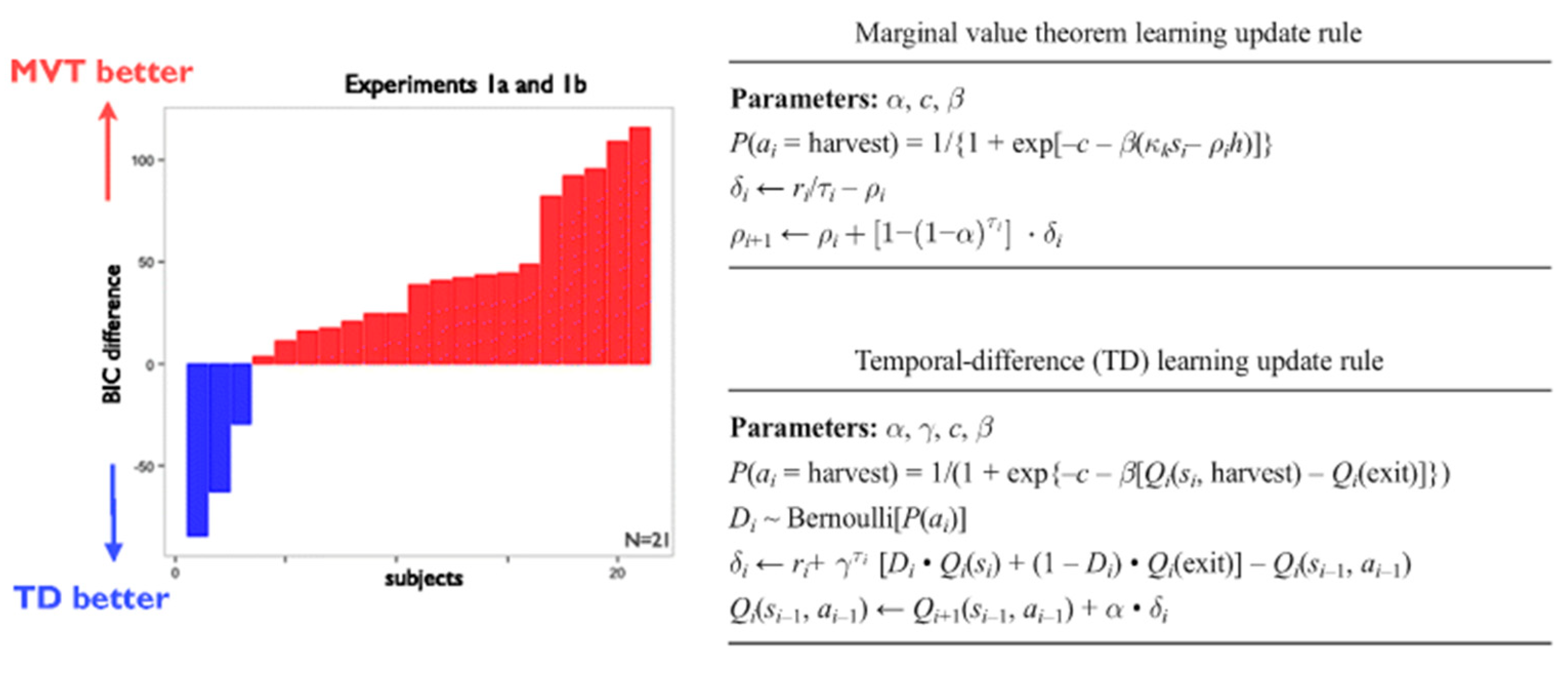
Foraging Decisions
4. Neuronal Bases of Multiscale Computations
4.1. Dorsal and Ventral Medial Prefrontal Cortex
4.2. Lateral Prefrontal Cortex
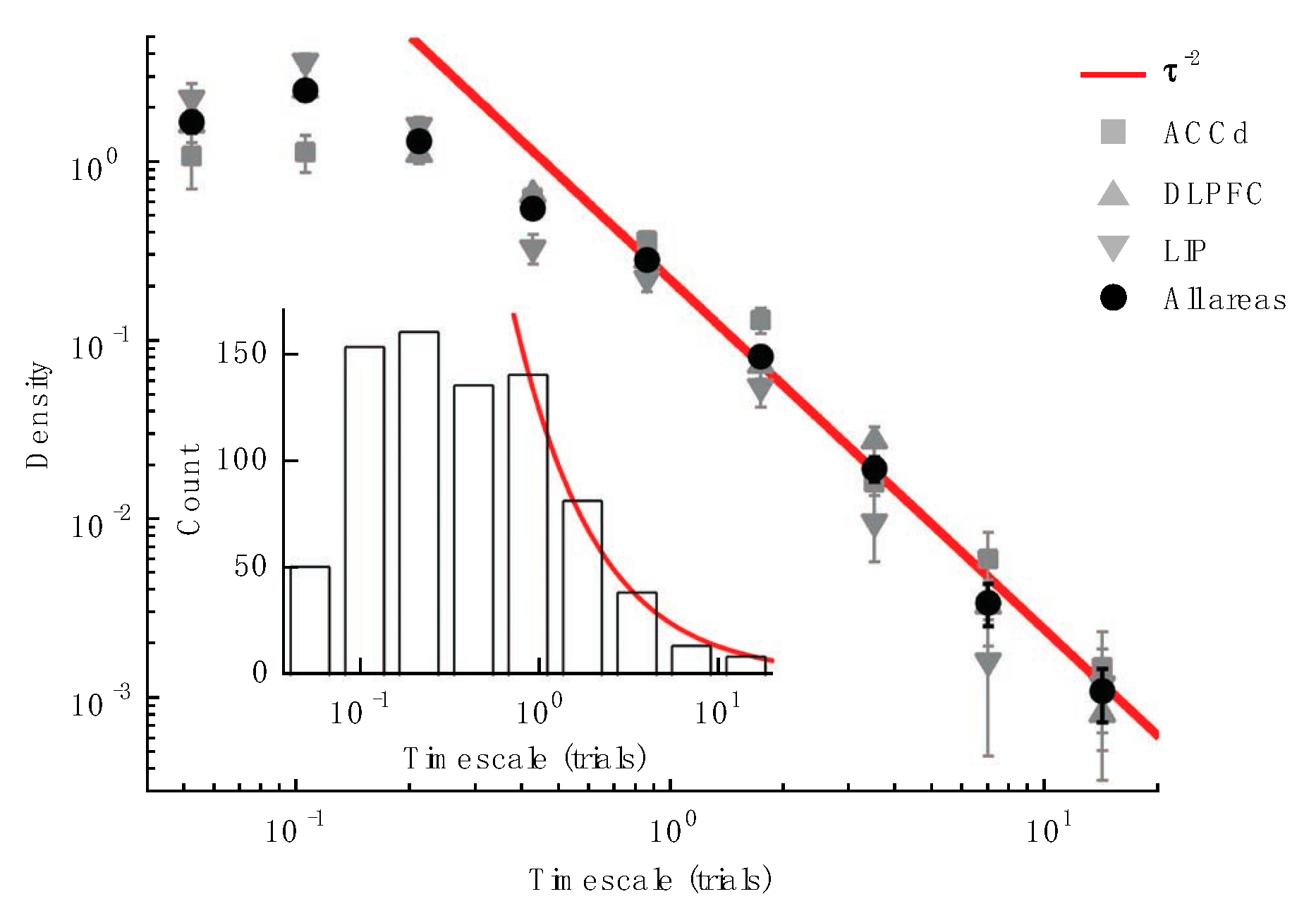
4.3. Cellular Mechanisms
5. Multiscale AI
5.1. Autonomous, Generalizable Robotic Agents for Real World Environments
5.2. Autonomous Game AI for Quasi-Real World Environments
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McClure, S.M.; Laibson, D.I.; Loewenstein, G.; Cohen, J.D. Separate Neural Systems Value Immediate and Delayed Monetary Rewards. Science 2004, 306, 503–507. [Google Scholar] [CrossRef]
- Tanaka, S.C.; Doya, K.; Okada, G.; Ueda, K.; Okamoto, Y.; Yamawaki, S. Prediction of immediate and future rewards differentially recruits cortico-basal ganglia loops. Nat. Neurosci. 2004, 7, 887–893. [Google Scholar] [CrossRef]
- Duncan, J. The multiple-demand (MD) system of the primate brain: Mental programs for intelligent behaviour. Trends Cogn. Sci. 2010, 14, 172–179. [Google Scholar] [CrossRef]
- Kumaran, D.; Hassabis, D.; McClelland, J.L. What Learning Systems do Intelligent Agents Need? Complementary Learning Systems Theory Updated. Trends Cogn. Sci. 2016, 20, 512–534. [Google Scholar] [CrossRef]
- Daw, N.D.; Niv, Y.; Dayan, P. Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nat. Neurosci. 2005, 8, 1704–1711. [Google Scholar] [CrossRef]
- Daw, N.D. Are we of two minds? Nat. Neurosci. 2018, 21, 1497–1499. [Google Scholar] [CrossRef] [PubMed]
- Loewenstein, G.; Prelec, D. Anomalies in Intertemporal Choice: Evidence and an Interpretation. Q. J. Econ. 1992, 107, 573–597. [Google Scholar] [CrossRef]
- Hills, T.T.; Todd, P.M.; Lazer, D.; Redish, A.D.; Couzin, I.D. Exploration versus exploitation in space, mind, and society. Trends Cogn. Sci. 2015, 19, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Hassabis, D.; Kumaran, D.; Summerfield, C.; Botvinick, M. Neuroscience-Inspired Artificial Intelligence. Neuron 2017, 95, 245–258. [Google Scholar] [CrossRef] [PubMed]
- Konar, A. Artificial Intelligence and Soft Computing: Behavioral and Cognitive Modeling of the Human Brain; CRC Press: Boca Raton, FL, USA, 2018; ISBN 978-1-351-83562-6. [Google Scholar]
- Lu, H.; Li, Y.; Chen, M.; Kim, H.; Serikawa, S. Brain Intelligence: Go beyond Artificial Intelligence. Mob. Netw. Appl. 2018, 23, 368–375. [Google Scholar] [CrossRef]
- Legg, S.; Hutter, M. A Collection of Definitions of Intelligence. Advances in Artificial General Intelligence: Concepts, Architectures and Algorithms: Proceedings of the AGI Workshop 2006; IOS Press: Amsterdam, The Netherlands, 2007; pp. 17–24. [Google Scholar]
- Lake, B.M.; Ullman, T.D.; Tenenbaum, J.B.; Gershman, S.J. Building machines that learn and think like people. Behav. Brain Sci. 2017, 40. [Google Scholar] [CrossRef] [PubMed]
- Kriegeskorte, N.; Douglas, P.K. Cognitive computational neuroscience. Nat. Neurosci. 2018, 21, 1148–1160. [Google Scholar] [CrossRef] [PubMed]
- Wu, B. Hierarchical Macro Strategy Model for MOBA Game AI. Proc. AAAI Conf. Artif. Intell. 2019, 33, 1206–1213. [Google Scholar] [CrossRef]
- Behrens, T.E.J.; Muller, T.H.; Whittington, J.C.R.; Mark, S.; Baram, A.B.; Stachenfeld, K.L.; Kurth-Nelson, Z. What Is a Cognitive Map? Organizing Knowledge for Flexible Behavior. Neuron 2018, 100, 490–509. [Google Scholar] [CrossRef]
- Piray, P.; Daw, N.D. A common model explaining flexible decision making, grid fields and cognitive control. bioRxiv 2019, 856849. [Google Scholar] [CrossRef]
- Sallet, J.; Mars, R.B.; Noonan, M.P.; Andersson, J.L.; O’Reilly, J.X.; Jbabdi, S.; Croxson, P.L.; Jenkinson, M.; Miller, K.L.; Rushworth, M.F.S. Social network size affects neural circuits in macaques. Science 2011, 334, 697–700. [Google Scholar] [CrossRef]
- Yamagishi, T.; Takagishi, H.; Fermin, A.d.S.R.; Kanai, R.; Li, Y.; Matsumoto, Y. Cortical thickness of the dorsolateral prefrontal cortex predicts strategic choices in economic games. Proc. Natl. Acad. Sci. USA 2016, 113, 5582–5587. [Google Scholar] [CrossRef]
- Berman, M.G.; Stier, A.J.; Akcelik, G.N. Environmental neuroscience. Am. Psychol. 2019, 74, 1039–1052. [Google Scholar] [CrossRef]
- Berman, M.G.; Kardan, O.; Kotabe, H.P.; Nusbaum, H.C.; London, S.E. The promise of environmental neuroscience. Nat. Hum. Behav. 2019, 3, 414–417. [Google Scholar] [CrossRef]
- Behrens, T.E.J.; Woolrich, M.W.; Walton, M.E.; Rushworth, M.F.S. Learning the value of information in an uncertain world. Nat. Neurosci. 2007, 10, 1214–1221. [Google Scholar] [CrossRef]
- Bernacchia, A.; Seo, H.; Lee, D.; Wang, X.-J. A reservoir of time constants for memory traces in cortical neurons. Nat. Neurosci. 2011, 14, 366–372. [Google Scholar] [CrossRef]
- Collins, A.G.E.; Frank, M.J. How much of reinforcement learning is working memory, not reinforcement learning? A behavioral, computational, and neurogenetic analysis: Working memory in reinforcement learning. Eur. J. Neurosci. 2012, 35, 1024–1035. [Google Scholar] [CrossRef] [PubMed]
- Soltani, A.; Izquierdo, A. Adaptive learning under expected and unexpected uncertainty. Nat. Rev. Neurosci. 2019, 20, 635–644. [Google Scholar] [CrossRef]
- Hills, T.T.; Kalff, C.; Wiener, J.M. Adaptive Lévy Processes and Area-Restricted Search in Human Foraging. PLoS ONE 2013, 8, e60488. [Google Scholar] [CrossRef]
- Cohen, J.D.; McClure, S.M.; Yu, A.J. Should I stay or should I go? How the human brain manages the trade-off between exploitation and exploration. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 933–942. [Google Scholar] [CrossRef] [PubMed]
- Barraclough, D.J.; Conroy, M.L.; Lee, D. Prefrontal cortex and decision making in a mixed-strategy game. Nat. Neurosci. 2004, 7, 404–410. [Google Scholar] [CrossRef] [PubMed]
- Hayden, B.Y.; Nair, A.C.; McCoy, A.N.; Platt, M.L. Posterior Cingulate Cortex Mediates Outcome-Contingent Allocation of Behavior. Neuron 2008, 60, 19–25. [Google Scholar] [CrossRef]
- Pearson, J.M.; Heilbronner, S.R.; Barack, D.L.; Hayden, B.Y.; Platt, M.L. Posterior cingulate cortex: Adapting behavior to a changing world. Trends Cogn. Sci. 2011, 15, 143–151. [Google Scholar] [CrossRef]
- Hills, T.T.; Todd, P.M.; Goldstone, R.L. The central executive as a search process: Priming exploration and exploitation across domains. J. Exp. Psychol. Gen. 2010, 139, 590–609. [Google Scholar] [CrossRef]
- Hills, T.T.; Noguchi, T.; Gibbert, M. Information overload or search-amplified risk? Set size and order effects on decisions from experience. Psychon. Bull. Rev. 2013, 20, 1023–1031. [Google Scholar] [CrossRef]
- Javor, A.; Koller, M.; Lee, N.; Chamberlain, L.; Ransmayr, G. Neuromarketing and consumer neuroscience: Contributions to neurology. BMC Neurol. 2013, 13, 13. [Google Scholar] [CrossRef]
- Wong-Lin, K.; Wang, D.-H.; Moustafa, A.A.; Cohen, J.Y.; Nakamura, K. Toward a multiscale modeling framework for understanding serotonergic function. J. Psychopharmacol. 2017, 31, 1121–1136. [Google Scholar] [CrossRef] [PubMed]
- Akaishi, R.; Hayden, B.Y. A Spotlight on Reward. Neuron 2016, 90, 1148–1150. [Google Scholar] [CrossRef] [PubMed]
- Fyhn, M.; Molden, S.; Witter, M.P.; Moser, E.I.; Moser, M.-B. Spatial Representation in the Entorhinal Cortex. Science 2004, 305, 1258–1264. [Google Scholar] [CrossRef] [PubMed]
- Moser, E.I. Grid cells and the entorhinal map of space. EI Moser/Nobel Prize Physiol. Med. Nobel Lect. 2014, 71214, 401–437. [Google Scholar]
- Moser, E.I.; Moser, M.-B. A metric for space. Hippocampus 2008, 18, 1142–1156. [Google Scholar] [CrossRef]
- La Camera, G.; Rauch, A.; Thurbon, D.; Lüscher, H.-R.; Senn, W.; Fusi, S. Multiple Time Scales of Temporal Response in Pyramidal and Fast Spiking Cortical Neurons. J. Neurophysiol. 2006, 96, 3448–3464. [Google Scholar] [CrossRef]
- Murray, J.D.; Bernacchia, A.; Freedman, D.J.; Romo, R.; Wallis, J.D.; Cai, X.; Padoa-Schioppa, C.; Pasternak, T.; Seo, H.; Lee, D.; et al. A hierarchy of intrinsic timescales across primate cortex. Nat. Neurosci. 2014, 17, 1661–1663. [Google Scholar] [CrossRef]
- Wasmuht, D.F.; Spaak, E.; Buschman, T.J.; Miller, E.K.; Stokes, M.G. Intrinsic neuronal dynamics predict distinct functional roles during working memory. Nat. Commun. 2018, 9, 1–13. [Google Scholar] [CrossRef]
- Gold, J.I.; Shadlen, M.N. The Neural Basis of Decision Making. Annu. Rev. Neurosci. 2007, 30, 535–574. [Google Scholar] [CrossRef]
- Lo, C.-C.; Wang, X.-J. Cortico–basal ganglia circuit mechanism for a decision threshold in reaction time tasks. Nat. Neurosci. 2006, 9, 956–963. [Google Scholar] [CrossRef] [PubMed]
- Krajbich, I.; Armel, C.; Rangel, A. Visual fixations and the computation and comparison of value in simple choice. Nat. Neurosci. 2010, 13, 1292–1298. [Google Scholar] [CrossRef] [PubMed]
- Green, D.M.; Swets, J.A. Signal Detection Theory and Psychophysics; John Wiley: Oxford, UK, 1966. [Google Scholar]
- Green, D.M.; Luce, R.D.; Duncan, J.E. Variability and sequential effects in magnitude production and estimation of auditory intensity. Percept. Psychophys. 1977, 22, 450–456. [Google Scholar] [CrossRef]
- Jesteadt, W.; Luce, R.D.; Green, D.M. Sequential effects in judgments of loudness. J. Exp. Psychol. Hum. Percept. Perform. 1977, 3, 92–104. [Google Scholar] [CrossRef]
- Luce, R.D.; Green, D.M. The response ratio hypothesis for magnitude estimation. J. Math. Psychol. 1974, 11, 1–14. [Google Scholar] [CrossRef]
- Samuelson, W.; Zeckhauser, R. Status quo bias in decision making. J. Risk Uncertain. 1988, 1, 7–59. [Google Scholar] [CrossRef]
- Thaler, R.H. Misbehaving: The Making of Behavioral Economics, 1st ed.; W. W. Norton & Company: New York, NY, USA; London, UK, 2016; ISBN 978-0-393-35279-5. [Google Scholar]
- Wulff, D.U.; Hills, T.T.; Hertwig, R. How short- and long-run aspirations impact search and choice in decisions from experience. Cognition 2015, 144, 29–37. [Google Scholar] [CrossRef]
- Mischel, W.; Shoda, Y.; Rodriguez, M.L. Delay of Gratification in Children. Science 1989, 244, 933–938. [Google Scholar] [CrossRef]
- Hornsby, A.N.; Evans, T.; Riefer, P.S.; Prior, R.; Love, B.C. Conceptual Organization is Revealed by Consumer Activity Patterns. Comput. Brain Behav. 2019. [Google Scholar] [CrossRef]
- Hornsby, A.N.; Love, B.C. How decisions and the desire for coherency shape subjective preferences over time. Cognition 2020, 200, 104244. [Google Scholar] [CrossRef]
- Riefer, P.S.; Prior, R.; Blair, N.; Pavey, G.; Love, B.C. Coherency-maximizing exploration in the supermarket. Nat. Hum. Behav. 2017, 1, 1–4. [Google Scholar] [CrossRef]
- Akrami, A.; Kopec, C.D.; Diamond, M.E.; Brody, C.D. Posterior parietal cortex represents sensory history and mediates its effects on behaviour. Nature 2018, 554, 368–372. [Google Scholar] [CrossRef] [PubMed]
- Fritsche, M.; Mostert, P.; de Lange, F.P. Opposite Effects of Recent History on Perception and Decision. Curr. Biol. 2017, 27, 590–595. [Google Scholar] [CrossRef] [PubMed]
- Hattori, R.; Danskin, B.; Babic, Z.; Mlynaryk, N.; Komiyama, T. Area-Specificity and Plasticity of History-Dependent Value Coding During Learning. Cell 2019, 177, 1858–1872. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.J.; Shenhav, A.; Ludvig, E.A. Habits without values. Psychol. Rev. 2019, 126, 292–311. [Google Scholar] [CrossRef]
- Tsunada, J.; Cohen, Y.; Gold, J.I. Post-Decision Processing in Primate Prefrontal Cortex Influences Subsequent Choices on an Auditory Decision-Making Task. Available online: https://elifesciences.org/articles/46770 (accessed on 14 June 2019).
- Urai, A.E.; Braun, A.; Donner, T.H. Pupil-linked arousal is driven by decision uncertainty and alters serial choice bias. Nat. Commun. 2017, 8, 14637. [Google Scholar] [CrossRef]
- Zhong, L.; Zhang, Y.; Duan, C.A.; Pan, J.; Xu, N. Dynamic and causal contribution of parietal circuits to perceptual decisions during category learning. Nat. Neurosci. 2019, in press. [Google Scholar] [CrossRef]
- Akaishi, R.; Umeda, K.; Nagase, A.; Sakai, K. Autonomous Mechanism of Internal Choice Estimate Underlies Decision Inertia. Neuron 2014, 81, 195–206. [Google Scholar] [CrossRef]
- Kolling, N.; Wittmann, M.; Rushworth, M.F.S. Multiple Neural Mechanisms of Decision Making and Their Competition under Changing Risk Pressure. Neuron 2014, 81, 1190–1202. [Google Scholar] [CrossRef]
- Akaishi, R. Changing Concepts of Decision. Brain Neural Netw. 2015, 22, 30–36. [Google Scholar] [CrossRef][Green Version]
- Wittmann, M.K.; Kolling, N.; Akaishi, R.; Chau, B.K.H.; Brown, J.W.; Nelissen, N.; Rushworth, M.F.S. Predictive decision making driven by multiple time-linked reward representations in the anterior cingulate cortex. Nat. Commun. 2016, 7, 12327. [Google Scholar] [CrossRef] [PubMed]
- Urai, A.E.; de Gee, J.W.; Tsetsos, K.; Donner, T.H. Choice history biases subsequent evidence accumulation. eLife 2019, 8, e46331. [Google Scholar] [CrossRef]
- Sakai, K.; Kitaguchi, K.; Hikosaka, O. Chunking during human visuomotor sequence learning. Exp. Brain Res. 2003, 152, 229–242. [Google Scholar] [CrossRef] [PubMed]
- Botvinick, M.M.; Niv, Y.; Barto, A.C. Hierarchically organized behavior and its neural foundations: A reinforcement learning perspective. Cognition 2009, 113, 262–280. [Google Scholar] [CrossRef]
- Koch, I.; Philipp, A.M.; Gade, M. Chunking in Task Sequences Modulates Task Inhibition. Psychol. Sci. 2006, 17, 346–350. [Google Scholar] [CrossRef] [PubMed]
- Tremblay, P.-L.; Bedard, M.-A.; Levesque, M.; Chebli, M.; Parent, M.; Courtemanche, R.; Blanchet, P.J. Motor sequence learning in primate: Role of the D2 receptor in movement chunking during consolidation. Behav. Brain Res. 2009, 198, 231–239. [Google Scholar] [CrossRef]
- Verwey, W.B.; Abrahamse, E.L. Distinct modes of executing movement sequences: Reacting, associating, and chunking. Acta Psychol. Amst. 2012, 140, 274–282. [Google Scholar] [CrossRef]
- Lu, Q.; Xu, C.; Liu, H. Can chunking reduce syntactic complexity of natural languages? Complexity 2016, 21, 33–41. [Google Scholar] [CrossRef]
- Sakai, K.; Hikosaka, O.; Nakamura, K. Emergence of rhythm during motor learning. Trends Cogn. Sci. 2004, 8, 547–553. [Google Scholar] [CrossRef]
- Nakamura, K.; Sakai, K.; Hikosaka, O. Effects of Local Inactivation of Monkey Medial Frontal Cortex in Learning of Sequential Procedures. J. Neurophysiol. 1999, 82, 1063–1068. [Google Scholar] [CrossRef]
- Hikosaka, O.; Takikawa, Y.; Kawagoe, R. Role of the basal ganglia in the control of purposive saccadic eye movements. Physiol. Rev. 2000, 80, 953–978. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, K.; Sakai, K.; Hikosaka, O. Neuronal Activity in Medial Frontal Cortex during Learning of Sequential Procedures. J. Neurophysiol. 1998, 80, 2671–2687. [Google Scholar] [CrossRef] [PubMed]
- Sakai, K.; Hikosaka, O.; Miyauchi, S.; Takino, R.; Sasaki, Y.; Pütz, B. Transition of Brain Activation from Frontal to Parietal Areas in Visuomotor Sequence Learning. J. Neurosci. 1998, 18, 1827–1840. [Google Scholar] [CrossRef] [PubMed]
- Hikosaka, O.; Kim, H.F.; Yasuda, M.; Yamamoto, S. Basal ganglia circuits for reward value-guided behavior. Annu. Rev. Neurosci. 2014, 37, 289–306. [Google Scholar] [CrossRef]
- Nagase, A.M.; Onoda, K.; Foo, J.C.; Haji, T.; Akaishi, R.; Yamaguchi, S.; Sakai, K.; Morita, K. Neural Mechanisms for Adaptive Learned Avoidance of Mental Effort. J. Neurosci. 2018, 38, 2631–2651. [Google Scholar] [CrossRef] [PubMed]
- Lerner, T.N. Interfacing behavioral and neural circuit models for habit formation. J. Neurosci. Res. 2020, 98, 1031–1045. [Google Scholar] [CrossRef] [PubMed]
- Johnson, A.; Redish, A.D. Neural Ensembles in CA3 Transiently Encode Paths Forward of the Animal at a Decision Point. J. Neurosci. 2007, 27, 12176–12189. [Google Scholar] [CrossRef]
- Redish, A.D. Vicarious trial and error. Nat. Rev. Neurosci. 2016, 17, 147–159. [Google Scholar] [CrossRef]
- Gupta, A.S.; van der Meer, M.A.A.; Touretzky, D.S.; Redish, A.D. Hippocampal Replay Is Not a Simple Function of Experience. Neuron 2010, 65, 695–705. [Google Scholar] [CrossRef]
- Hills, T.T. Animal Foraging and the Evolution of Goal-Directed Cognition. Cogn. Sci. 2006, 30, 3–41. [Google Scholar] [CrossRef]
- Hills, T.T.; Jones, M.N.; Todd, P.M. Optimal foraging in semantic memory. Psychol. Rev. 2012, 119, 431–440. [Google Scholar] [CrossRef] [PubMed]
- Stephens, D.W.; Krebs, J.R. Foraging Theory; Princeton University Press: Princeton, NJ, USA, 1987; ISBN 978-0-691-08442-8. [Google Scholar]
- Charnov, E.L. Optimal foraging, the marginal value theorem. Theor. Popul. Biol. 1976, 9, 129–136. [Google Scholar] [CrossRef]
- Hodos, W.; Trumbule, G.H. Strategies of schedule preference in chimpanzees. J. Exp. Anal. Behav. 1967, 10, 503–514. [Google Scholar] [CrossRef]
- Wanchisen, B.A.; Tatham, T.A.; Hineline, P.N. Pigeons’ choices in situations of diminishing returns: Fixed—Versus progressive-ratio schedules. J. Exp. Anal. Behav. 1988, 50, 375–394. [Google Scholar] [CrossRef] [PubMed]
- Kono, M. Foraging behavior of pigeons (Columba livia) in situations of diminishing returns using a reinforcement schedule that controls the energy expenditure of responses. Learn. Motiv. 2019, 66, 34–45. [Google Scholar] [CrossRef]
- Pirolli, P. Information Foraging Theory: Adaptive Interaction with Information; Oxford University Press: New York, NY, USA, 2007; ISBN 978-0-19-534666-4. [Google Scholar]
- Hayden, B.Y.; Pearson, J.M.; Platt, M.L. Neuronal basis of sequential foraging decisions in a patchy environment. Nat. Neurosci. 2011, 14, 933–939. [Google Scholar] [CrossRef]
- Kolling, N.; Behrens, T.E.J.; Mars, R.B.; Rushworth, M.F.S. Neural Mechanisms of Foraging. Science 2012, 336, 95–98. [Google Scholar] [CrossRef]
- Constantino, S.M.; Daw, N.D. Learning the opportunity cost of time in a patch-foraging task. Cogn. Affect. Behav. Neurosci. 2015, 15, 837–853. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, J.; Glimcher, P.W.; Louie, K. Multiple timescales of normalized value coding underlie adaptive choice behavior. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Hills, T.; Brockie, P.J.; Maricq, A.V. Dopamine and Glutamate Control Area-Restricted Search Behavior in Caenorhabditis elegans. J. Neurosci. 2004, 24, 1217–1225. [Google Scholar] [CrossRef]
- Humphries, N.E.; Weimerskirch, H.; Queiroz, N.; Southall, E.J.; Sims, D.W. Foraging success of biological Lévy flights recorded in situ. Proc. Natl. Acad. Sci. USA 2012, 109, 7169–7174. [Google Scholar] [CrossRef] [PubMed]
- Raichlen, D.A.; Wood, B.M.; Gordon, A.D.; Mabulla, A.Z.P.; Marlowe, F.W.; Pontzer, H. Evidence of Lévy walk foraging patterns in human hunter–gatherers. Proc. Natl. Acad. Sci. USA 2014, 111, 728–733. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, A.; Ceccon, E.; Baldauf, C.; Medeiros, T.K.; Miramontes, O. Lévy foraging patterns of rural humans. PLoS ONE 2018, 13, e0199099. [Google Scholar] [CrossRef] [PubMed]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; Havlin, S.; da Luz, M.G.E.; Raposo, E.P.; Stanley, H.E. Lévy flights in random searches. Phys. Stat. Mech. Its Appl. 2000, 282, 1–12. [Google Scholar] [CrossRef]
- Bartumeus, F.; Catalan, J.; Fulco, U.L.; Lyra, M.L.; Viswanathan, G.M. Optimizing the Encounter Rate in Biological Interactions: Lévy versus Brownian Strategies. Phys. Rev. Lett. 2002, 88, 097901. [Google Scholar] [CrossRef]
- Benhamou, S. How Many Animals Really Do the Lévy Walk? Ecology 2007, 88, 1962–1969. [Google Scholar] [CrossRef]
- Plank, M.J.; James, A. Optimal foraging: Lévy pattern or process? J. R. Soc. Interface 2008, 5, 1077–1086. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; da Luz, M.G.E.; Raposo, E.P.; Stanley, H.E. The Physics of Foraging: An Introduction to Random Searches and Biological Encounters. Available online: https://www.cambridge.org/core/books/physics-of-foraging/B009DE42189D3A39718C2E37EBE256B0 (accessed on 27 February 2020).
- Kolling, N.; O’Reilly, J.X. State-change decisions and dorsomedial prefrontal cortex: The importance of time. Curr. Opin. Behav. Sci. 2018, 22, 152–160. [Google Scholar] [CrossRef]
- Padoa-Schioppa, C. Neurobiology of Economic Choice: A Good-Based Model. Annu. Rev. Neurosci. 2011, 34, 333–359. [Google Scholar] [CrossRef]
- Rushworth, M.F.S.; Noonan, M.P.; Boorman, E.D.; Walton, M.E.; Behrens, T.E. Frontal Cortex and Reward-Guided Learning and Decision-Making. Neuron 2011, 70, 1054–1069. [Google Scholar] [CrossRef]
- Meder, D.; Kolling, N.; Verhagen, L.; Wittmann, M.K.; Scholl, J.; Madsen, K.H.; Hulme, O.J.; Behrens, T.E.J.; Rushworth, M.F.S. Simultaneous representation of a spectrum of dynamically changing value estimates during decision making. Nat. Commun. 2017, 8, 1942. [Google Scholar] [CrossRef] [PubMed]
- Schuck, N.W.; Cai, M.B.; Wilson, R.C.; Niv, Y. Human Orbitofrontal Cortex Represents a Cognitive Map of State Space. Neuron 2016, 91, 1402–1412. [Google Scholar] [CrossRef] [PubMed]
- Camille, N.; Tsuchida, A.; Fellows, L.K. Double Dissociation of Stimulus-Value and Action-Value Learning in Humans with Orbitofrontal or Anterior Cingulate Cortex Damage. J. Neurosci. 2011, 31, 15048–15052. [Google Scholar] [CrossRef] [PubMed]
- Boorman, E.D.; Behrens, T.E.J.; Woolrich, M.W.; Rushworth, M.F.S. How Green Is the Grass on the Other Side? Frontopolar Cortex and the Evidence in Favor of Alternative Courses of Action. Neuron 2009, 62, 733–743. [Google Scholar] [CrossRef]
- Chan, S.C.Y.; Niv, Y.; Norman, K.A. A Probability Distribution over Latent Causes, in the Orbitofrontal Cortex. J. Neurosci. 2016, 36, 7817–7828. [Google Scholar] [CrossRef]
- Miller, E.K.; Cohen, J.D. An Integrative Theory of Prefrontal Cortex Function. Annu. Rev. Neurosci. 2001, 24, 167–202. [Google Scholar] [CrossRef]
- Goldman-Rakic, P.S. Circuitry of Primate Prefrontal Cortex and Regulation of Behavior by Representational Memory. In Comprehensive Physiology; American Cancer Society: New York, NY, USA, 2011; pp. 373–417. ISBN 978-0-470-65071-4. [Google Scholar]
- Moore, T.; Armstrong, K.M. Selective gating of visual signals by microstimulation of frontal cortex. Nature 2003, 421, 370–373. [Google Scholar] [CrossRef]
- Morishima, Y.; Akaishi, R.; Yamada, Y.; Okuda, J.; Toma, K.; Sakai, K. Task-specific signal transmission from prefrontal cortex in visual selective attention. Nat. Neurosci. 2009, 12, 85–91. [Google Scholar] [CrossRef]
- Koechlin, E.; Ody, C.; Kouneiher, F. The Architecture of Cognitive Control in the Human Prefrontal Cortex. Science 2003, 302, 1181–1185. [Google Scholar] [CrossRef]
- Richards, B.A.; Lillicrap, T.P.; Beaudoin, P.; Bengio, Y.; Bogacz, R.; Christensen, A.; Clopath, C.; Costa, R.P.; de Berker, A.; Ganguli, S.; et al. A deep learning framework for neuroscience. Nat. Neurosci. 2019, 22, 1761–1770. [Google Scholar] [CrossRef]
- Russin, J.; O’Reilly, R.C.; Bengio, Y. Deep Learning Needs a Prefrontal Cortex. Available online: https://baicsworkshop.github.io/pdf/BAICS_10.pdf (accessed on 26 April 2020).
- Corbetta, M.; Shulman, G.L. Control of goal-directed and stimulus-driven attention in the brain. Nat. Rev. Neurosci. 2002, 3, 201–215. [Google Scholar] [CrossRef] [PubMed]
- Ruesch, J.; Lopes, M.; Bernardino, A.; Hornstein, J.; Santos-Victor, J.; Pfeifer, R. Multimodal saliency-based bottom-up attention a framework for the humanoid robot iCub. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 962–967. [Google Scholar]
- Tulving, E. Episodic Memory: From Mind to Brain. Annu. Rev. Psychol. 2002, 53, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Baram, A.B.; Muller, T.H.; Whittington, J.C.R.; Behrens, T.E.J. Intuitive planning: Global navigation through cognitive maps based on grid-like codes. Neuroscience 2018. [Google Scholar] [CrossRef]
- Constantinescu, A.O.; O’Reilly, J.X.; Behrens, T.E.J. Organizing conceptual knowledge in humans with a gridlike code. Science 2016, 352, 1464–1468. [Google Scholar] [CrossRef] [PubMed]
- Hills, T.T.; Butterfill, S. From foraging to autonoetic consciousness: The primal self as a consequence of embodied prospective foraging. Curr. Zool. 2015, 61, 368–381. [Google Scholar] [CrossRef]
- Wu, X.; Foster, D.J. Hippocampal Replay Captures the Unique Topological Structure of a Novel Environment. J. Neurosci. 2014, 34, 6459–6469. [Google Scholar] [CrossRef]
- Ólafsdóttir, H.F.; Barry, C.; Saleem, A.B.; Hassabis, D.; Spiers, H.J. Hippocampal place cells construct reward related sequences through unexplored space. eLife 2015, 4, e06063. [Google Scholar] [CrossRef]
- Pfeiffer, B.E.; Foster, D.J. Hippocampal place-cell sequences depict future paths to remembered goals. Nature 2013, 497, 74–79. [Google Scholar] [CrossRef]
- Hills, T.T. Neurocognitive free will. Proc. R. Soc. B Biol. Sci. 2019, 286, 20190510. [Google Scholar] [CrossRef]
- Jacobs, J.; Weidemann, C.T.; Miller, J.F.; Solway, A.; Burke, J.F.; Wei, X.-X.; Suthana, N.; Sperling, M.R.; Sharan, A.D.; Fried, I.; et al. Direct recordings of grid-like neuronal activity in human spatial navigation. Nat. Neurosci. 2013, 16, 1188–1190. [Google Scholar] [CrossRef]
- Doeller, C.F.; Barry, C.; Burgess, N. Evidence for grid cells in a human memory network. Nature 2010, 463, 657–661. [Google Scholar] [CrossRef] [PubMed]
- Stachenfeld, K.L.; Botvinick, M.M.; Gershman, S.J. The hippocampus as a predictive map. Nat. Neurosci. 2017, 20, 1643–1653. [Google Scholar] [CrossRef] [PubMed]
- Momennejad, I. Learning Structures: Predictive Representations, Replay, and Generalization. Curr. Opin. Behav. Sci. 2020, 32, 155–166. [Google Scholar] [CrossRef]
- Chollet, F. On the Measure of Intelligence. arXiv 2019, arXiv:1911.01547. [Google Scholar]
- Ingrand, F.; Ghallab, M. Deliberation for autonomous robots: A survey. Artif. Intell. 2017, 247, 10–44. [Google Scholar] [CrossRef]
- Baranes, A.; Oudeyer, P.-Y. Active learning of inverse models with intrinsically motivated goal exploration in robots. Robot. Auton. Syst. 2013, 61, 49–73. [Google Scholar] [CrossRef]
- Gureckis, T.M.; Markant, D.B. Self-Directed Learning: A Cognitive and Computational Perspective. Perspect. Psychol. Sci. 2012, 7, 464–481. [Google Scholar] [CrossRef]
- Doya, K. Reinforcement learning in continuous time and space. Neural Comput. 2000, 12, 219–245. [Google Scholar] [CrossRef]
- Nodelman, U.; Shelton, C.R.; Koller, D. Continuous Time Bayesian Networks. arXiv 2012, arXiv:1301.0591. [Google Scholar]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional Neural Networks for Large-Scale Remote-Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 645–657. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2019, arXiv:1810.04805. [Google Scholar]
- Xu, J.; Shelton, C.R. Intrusion Detection using Continuous Time Bayesian Networks. J. Artif. Intell. Res. 2010, 39, 745–774. [Google Scholar] [CrossRef]
- Acerbi, E.; Zelante, T.; Narang, V.; Stella, F. Gene network inference using continuous time Bayesian networks: A comparative study and application to Th17 cell differentiation. BMC Bioinform. 2014, 15, 387. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Stella, F.; Hommersom, A.; Lucas, P.J.F.; Boer, L.; Bischoff, E. A comparison between discrete and continuous time Bayesian networks in learning from clinical time series data with irregularity. Artif. Intell. Med. 2019, 95, 104–117. [Google Scholar] [CrossRef]
- Degris, T.; Pilarski, P.M.; Sutton, R.S. Model-Free reinforcement learning with continuous action in practice. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 2177–2182. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All you Need. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 5998–6008. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2016, arXiv:1409.0473. [Google Scholar]
- Xu, K.; Ba, J.L.; Kiros, R.; Cho, K.; Courville, A.; Salakhutdinov, R.; Zemel, R.S.; Bengio, Y. Show, attend and tell: Neural image caption generation with visual attention. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37, pp. 2048–2057. [Google Scholar]
- Wu, F.; Fan, A.; Baevski, A.; Dauphin, Y.N.; Auli, M. Pay Less Attention with Lightweight and Dynamic Convolutions. arXiv 2019, arXiv:1901.10430. [Google Scholar]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language Models are Unsupervised Multitask Learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Bengio, Y. The Consciousness Prior. arXiv 2019, arXiv:1709.08568. [Google Scholar]
- Bresina, J.; Dearden, R.; Meuleau, N.; Ramkrishnan, S.; Smith, D.; Washington, R. Planning under Continuous Time and Resource Uncertainty: A Challenge for AI. Available online: https://arxiv.org/abs/1301.0559 (accessed on 25 May 2020).
- Peng, G.C.Y.; Alber, M.; Tepole, A.B.; Cannon, W.; De, S.; Dura-Bernal, S.; Garikipati, K.; Karniadakis, G.; Lytton, W.W.; Perdikaris, P.; et al. Multiscale modeling meets machine learning: What can we learn? arXiv 2020, arXiv:1911.11958. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, Y.; Gkioxari, G.; Tian, Y. Building Generalizable Agents with a Realistic and Rich 3D Environment. arXiv 2018, arXiv:1801.02209. [Google Scholar]
- Thompson, D.R.; Wettergreen, D.S.; Peralta, F.J.C. Autonomous science during large-scale robotic survey. J. Field Robot. 2011, 28, 542–564. [Google Scholar] [CrossRef]
- Dunbabin, M.; Marques, L. Robots for Environmental Monitoring: Significant Advancements and Applications. IEEE Robot. Autom. Mag. 2012, 19, 24–39. [Google Scholar] [CrossRef]
- Basilico, N.; Amigoni, F. Exploration strategies based on multi-criteria decision making for searching environments in rescue operations. Auton. Robot. 2011, 31, 401. [Google Scholar] [CrossRef]
- Srinivasa, S.S.; Ferguson, D.; Helfrich, C.J.; Berenson, D.; Collet, A.; Diankov, R.; Gallagher, G.; Hollinger, G.; Kuffner, J.; Weghe, M.V. HERB: A home exploring robotic butler. Auton. Robot. 2009, 28, 5. [Google Scholar] [CrossRef]
- Alterovitz, R.; Patil, S.; Derbakova, A. Rapidly-exploring roadmaps: Weighing exploration vs. refinement in optimal motion planning. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3706–3712. [Google Scholar]
- Khamassi, M.; Lallée, S.; Enel, P.; Procyk, E.; Dominey, P.F. Robot Cognitive Control with a Neurophysiologically Inspired Reinforcement Learning Model. Front. Neurorobot. 2011, 5. [Google Scholar] [CrossRef]
- Kober, J.; Bagnell, J.A.; Peters, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef]
- Polydoros, A.S.; Nalpantidis, L. Survey of Model-Based Reinforcement Learning: Applications on Robotics. J. Intell. Robot. Syst. 2017, 86, 153–173. [Google Scholar] [CrossRef]
- Wang, T.; Bao, X.; Clavera, I.; Hoang, J.; Wen, Y.; Langlois, E.; Zhang, S.; Zhang, G.; Abbeel, P.; Ba, J. Benchmarking Model-Based Reinforcement Learning. arXiv 2019, arXiv:1907.02057. [Google Scholar]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep Reinforcement Learning that Matters. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Thrun, S.; Pratt, L. Learning to Learn; Springer Science & Business Media: Berlin, Germany, 2012; ISBN 978-1-4615-5529-2. [Google Scholar]
- Barrett, S.; Taylor, M.E.; Stone, P. Transfer Learning for Reinforcement Learning on a Physical Robot. In Proceedings of the Ninth International Conference on Autonomous Agents and Multiagent Systems-Adaptive Learning Agents Workshop (AAMAS-ALA), Toronto, ON, Canada, 10–14 May 2010. [Google Scholar]
- Fernández, F.; García, J.; Veloso, M. Probabilistic Policy Reuse for inter-task transfer learning. Robot. Auton. Syst. 2010, 58, 866–871. [Google Scholar] [CrossRef]
- Schmidhuber, J. Formal Theory of Creativity, Fun, and Intrinsic Motivation (1990–2010). IEEE Trans. Auton. Ment. Dev. 2010, 2, 230–247. [Google Scholar] [CrossRef]
- Di Domenico, S.I.; Ryan, R.M. The Emerging Neuroscience of Intrinsic Motivation: A New Frontier in Self-Determination Research. Front. Hum. Neurosci. 2017, 11. [Google Scholar] [CrossRef] [PubMed]
- Ha, D.; Schmidhuber, J. World Models. arXiv 2018, arXiv:1803.10122. [Google Scholar]
- AI can Learn Real-World Skills from Playing StarCraft and Minecraft. Science News, 14 May 2019.
- Canaan, R.; Salge, C.; Togelius, J.; Nealen, A. Leveling the playing field: Fairness in AI versus human game benchmarks. In Proceedings of the 14th International Conference on the Foundations of Digital Games, San Luis Obispo, CA, USA, 26–30 August 2019; pp. 1–8. [Google Scholar]
- Palaus, M.; Marron, E.M.; Viejo-Sobera, R.; Redolar-Ripoll, D. Neural Basis of Video Gaming: A Systematic Review. Front. Hum. Neurosci. 2017, 11. [Google Scholar] [CrossRef] [PubMed]
- Preuss, M.; Risi, S. A Games Industry Perspective on Recent Game AI Developments. KI Künstl. Intell. 2020, 34, 81–83. [Google Scholar] [CrossRef]
- Glimcher, P.W.; Fehr, E. Neuroeconomics: Decision Making and the Brain; Academic Press: Cambridge, MA, USA, 2013; ISBN 978-0-12-391469-9. [Google Scholar]
- Huk, A.; Bonnen, K.; He, B.J. Beyond Trial-Based Paradigms: Continuous Behavior, Ongoing Neural Activity, and Natural Stimuli. J. Neurosci. 2018, 38, 7551–7558. [Google Scholar] [CrossRef]
- Hutson, M. AI takes on video games in quest for common sense. Science 2018, 361, 632–633. [Google Scholar] [CrossRef]
- Campbell, M.; Hoane, A.J.; Hsu, F. Deep Blue. Artif. Intell. 2002, 134, 57–83. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Tesauro, G. TD-Gammon, a Self-Teaching Backgammon Program, Achieves Master-Level Play. Neural Comput. 1994, 6, 215–219. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Berner, C.; Brockman, G.; Chan, B.; Cheung, V.; Dębiak, P.; Dennison, C.; Farhi, D.; Fischer, Q.; Hashme, S.; Hesse, C.; et al. Dota 2 with Large Scale Deep Reinforcement Learning. arXiv 2019, arXiv:1912.06680. [Google Scholar]
- Weber, B.G.; Mawhorter, P.; Mateas, M.; Jhala, A. Reactive planning idioms for multi-scale game AI. In Proceedings of the 2010 IEEE Conference on Computational Intelligence and Games, Dublin, Ireland, 18–21 August 2010; pp. 115–122. [Google Scholar]
- Ontañon, S.; Synnaeve, G.; Uriarte, A.; Richoux, F.; Churchill, D.; Preuss, M. A Survey of Real-Time Strategy Game AI Research and Competition in StarCraft. IEEE Trans. Comput. Intell. AI Games 2013, 5, 293–311. [Google Scholar] [CrossRef]
- Font, J.M.; Mahlmann, T. Dota 2 Bot Competition. IEEE Trans. Games 2019, 11, 285–289. [Google Scholar] [CrossRef]
- Botvinick, M.; Ritter, S.; Wang, J.X.; Kurth-Nelson, Z.; Blundell, C.; Hassabis, D. Reinforcement Learning, Fast and Slow. Trends Cogn. Sci. 2019, 23, 408–422. [Google Scholar] [CrossRef]
- Potter, M.C.; Wyble, B.; Hagmann, C.E.; McCourt, E.S. Detecting meaning in RSVP at 13 ms per picture. Atten. Percept. Psychophys. 2014, 76, 270–279. [Google Scholar] [CrossRef]
- Ecoffet, A.; Huizinga, J.; Lehman, J.; Stanley, K.O.; Clune, J. Go-Explore: A New Approach for Hard-Exploration Problems. arXiv 2019, arXiv:1901.10995. [Google Scholar]
- Matheron, G.; Perrin, N.; Sigaud, O. PBCS: Efficient Exploration and Exploitation Using a Synergy between Reinforcement Learning and Motion Planning. arXiv 2020, arXiv:2004.11667. [Google Scholar]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018; ISBN 978-0-262-03924-6. [Google Scholar]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- Hebb, D.O. The Organization of Behavior: A Neuropsychological Theory; Psychology Press: Hove, UK, 2005; ISBN 978-1-135-63191-8. [Google Scholar]
- Jordan, M.I. Serial Order: A Parallel Distributed Processing Approach. Technical Report, June 1985–March 1986; Institute for Cognitive Science, California University: San Diego, CA, USA, 1986. [Google Scholar]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef] [PubMed]
- FeldmanHall, O.; Shenhav, A. Resolving uncertainty in a social world. Nat. Hum. Behav. 2019, 3, 426–435. [Google Scholar] [CrossRef] [PubMed]
- Kappes, A.; Nussberger, A.-M.; Siegel, J.Z.; Rutledge, R.B.; Crockett, M.J. Social uncertainty is heterogeneous and sometimes valuable. Nat. Hum. Behav. 2019, 3, 764. [Google Scholar] [CrossRef] [PubMed]
- Schonberg, T.; Katz, L.N. A Neural Pathway for Nonreinforced Preference Change. Trends Cogn. Sci. 2020, 24, 504–514. [Google Scholar] [CrossRef] [PubMed]
- Chew, B.; Hauser, T.U.; Papoutsi, M.; Magerkurth, J.; Dolan, R.J.; Rutledge, R.B. Endogenous fluctuations in the dopaminergic midbrain drive behavioral choice variability. Proc. Natl. Acad. Sci. USA 2019, 116, 18732–18737. [Google Scholar] [CrossRef]
- Sherman, L.; Steinberg, L.; Chein, J. Connecting brain responsivity and real-world risk taking: Strengths and limitations of current methodological approaches. Dev. Cogn. Neurosci. 2018, 33, 27–41. [Google Scholar] [CrossRef]
- Kidd, C.; Hayden, B.Y. The Psychology and Neuroscience of Curiosity. Neuron 2015, 88, 449–460. [Google Scholar] [CrossRef]
- Oudeyer, P.-Y.; Kaplan, F.; Hafner, V.V. Intrinsic Motivation Systems for Autonomous Mental Development. IEEE Trans. Evol. Comput. 2007, 11, 265–286. [Google Scholar] [CrossRef]
- Oudeyer, P.-Y.; Gottlieb, J.; Lopes, M. Chapter 11—Intrinsic motivation, curiosity, and learning: Theory and applications in educational technologies. In Progress in Brain Research; Studer, B., Knecht, S., Eds.; Motivation; Elsevier: Amsterdam, The Netherlands, 2016; Volume 229, pp. 257–284. [Google Scholar]
- Schilbach, L.; Timmermans, B.; Reddy, V.; Costall, A.; Bente, G.; Schlicht, T.; Vogeley, K. Toward a second-person neuroscience 1. Behav. Brain Sci. 2013, 36, 393–414. [Google Scholar] [CrossRef]
- Ličen, M.; Hartmann, F.; Repovš, G.; Slapničar, S. The Impact of Social Pressure and Monetary Incentive on Cognitive Control. Front. Psychol. 2016, 7. [Google Scholar] [CrossRef]
- Redcay, E.; Schilbach, L. Using second-person neuroscience to elucidate the mechanisms of social interaction. Nat. Rev. Neurosci. 2019, 20, 495–505. [Google Scholar] [CrossRef] [PubMed]
- Shamay-Tsoory, S.G.; Mendelsohn, A. Real-Life Neuroscience: An Ecological Approach to Brain and Behavior Research. Perspect. Psychol. Sci. 2019, 14, 841–859. [Google Scholar] [CrossRef] [PubMed]
- Johnstone, R.A.; Dall, S.R.X.; Franks, N.R.; Pratt, S.C.; Mallon, E.B.; Britton, N.F.; Sumpter, D.J.T. Information flow, opinion polling and collective intelligence in house–hunting social insects. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2002, 357, 1567–1583. [Google Scholar] [CrossRef]
- Berdahl, A.; Torney, C.J.; Ioannou, C.C.; Faria, J.J.; Couzin, I.D. Emergent Sensing of Complex Environments by Mobile Animal Groups. Science 2013, 339, 574–576. [Google Scholar] [CrossRef]
- Rosenberg, L.; Baltaxe, D.; Pescetelli, N. Crowds vs swarms, a comparison of intelligence. In Proceedings of the 2016 Swarm/Human Blended Intelligence Workshop (SHBI), Cleveland, OH, USA, 21–23 October 2016; pp. 1–4. [Google Scholar]
- Rosenberg, L. Artificial Swarm Intelligence vs human experts. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 2547–2551. [Google Scholar]
- Hills, T.T. The Dark Side of Information Proliferation. Perspect. Psychol. Sci. 2018. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badman, R.P.; Hills, T.T.; Akaishi, R. Multiscale Computation and Dynamic Attention in Biological and Artificial Intelligence. Brain Sci. 2020, 10, 396. https://doi.org/10.3390/brainsci10060396
Badman RP, Hills TT, Akaishi R. Multiscale Computation and Dynamic Attention in Biological and Artificial Intelligence. Brain Sciences. 2020; 10(6):396. https://doi.org/10.3390/brainsci10060396
Chicago/Turabian StyleBadman, Ryan Paul, Thomas Trenholm Hills, and Rei Akaishi. 2020. "Multiscale Computation and Dynamic Attention in Biological and Artificial Intelligence" Brain Sciences 10, no. 6: 396. https://doi.org/10.3390/brainsci10060396
APA StyleBadman, R. P., Hills, T. T., & Akaishi, R. (2020). Multiscale Computation and Dynamic Attention in Biological and Artificial Intelligence. Brain Sciences, 10(6), 396. https://doi.org/10.3390/brainsci10060396