Optimal Robust PID Control for First- and Second-Order Plus Dead-Time Processes
Abstract
:1. Introduction
2. Control System and Design Objective
2.1. Plant and Controller
2.2. Performance Function and Constraint
2.3. Normalized Process Model and Controller
3. Unified Optimal PID Tuning with Robust Stability
3.1. Servo Optimization
3.2. Regulation Optimization
4. Numerical Simulation
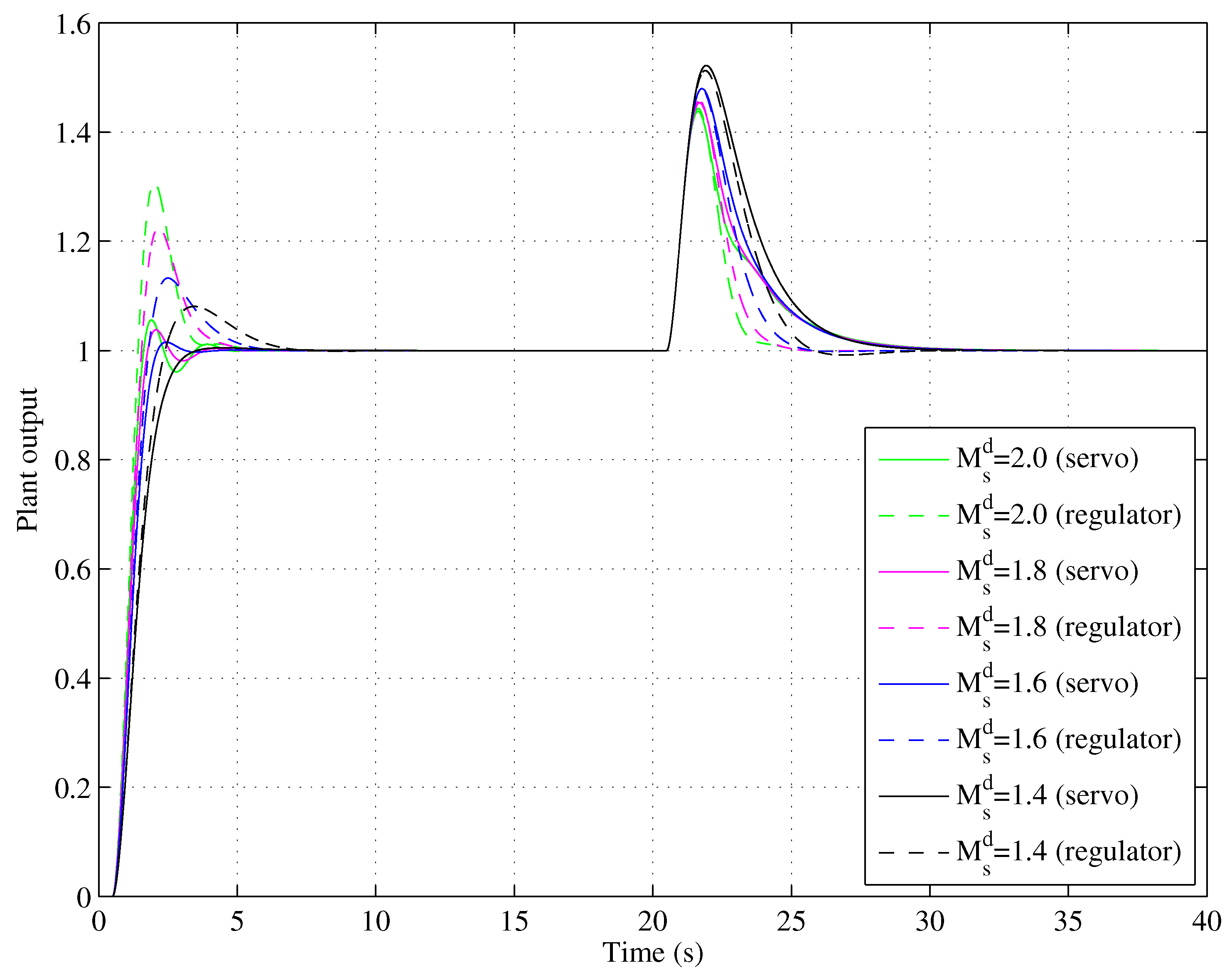
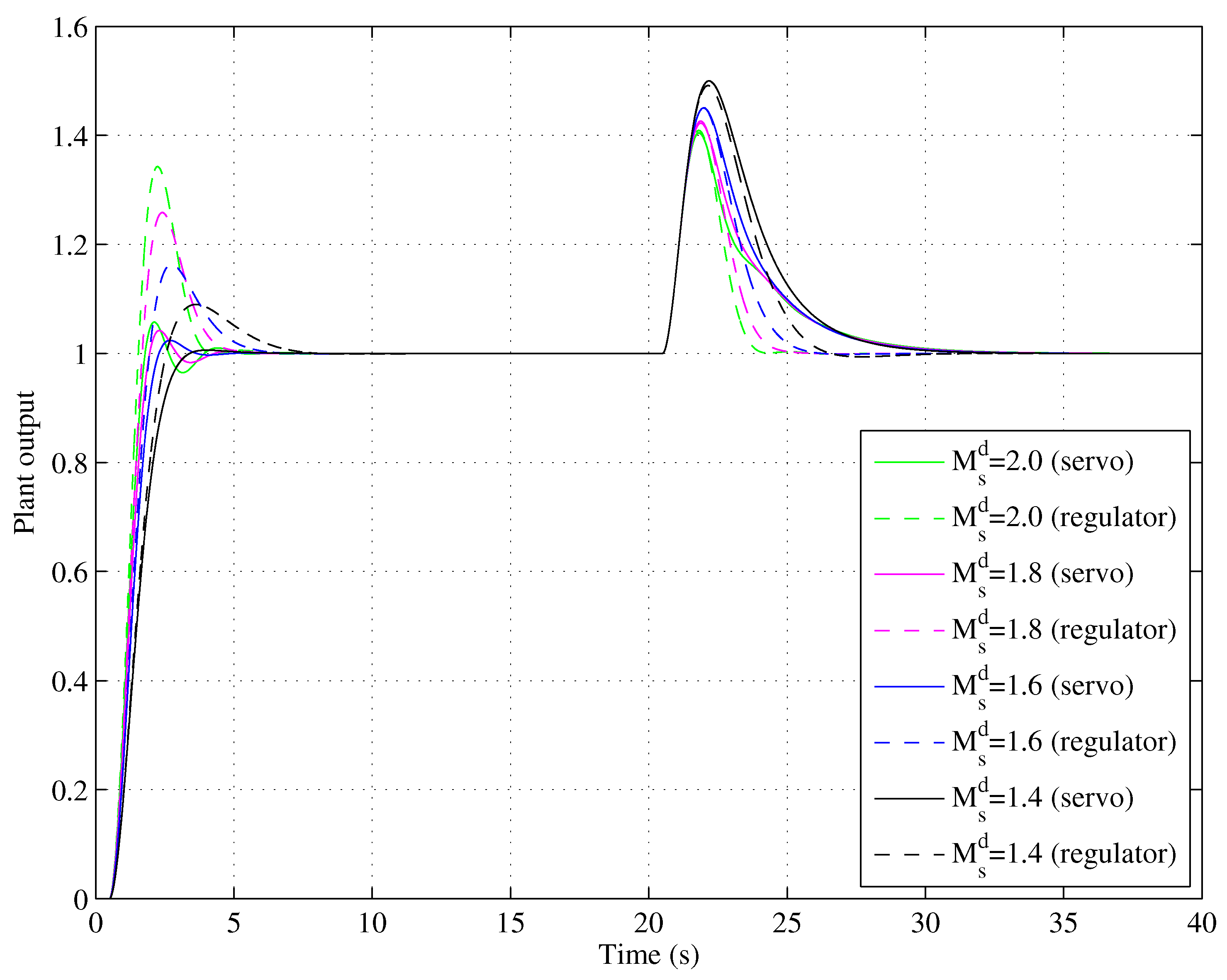
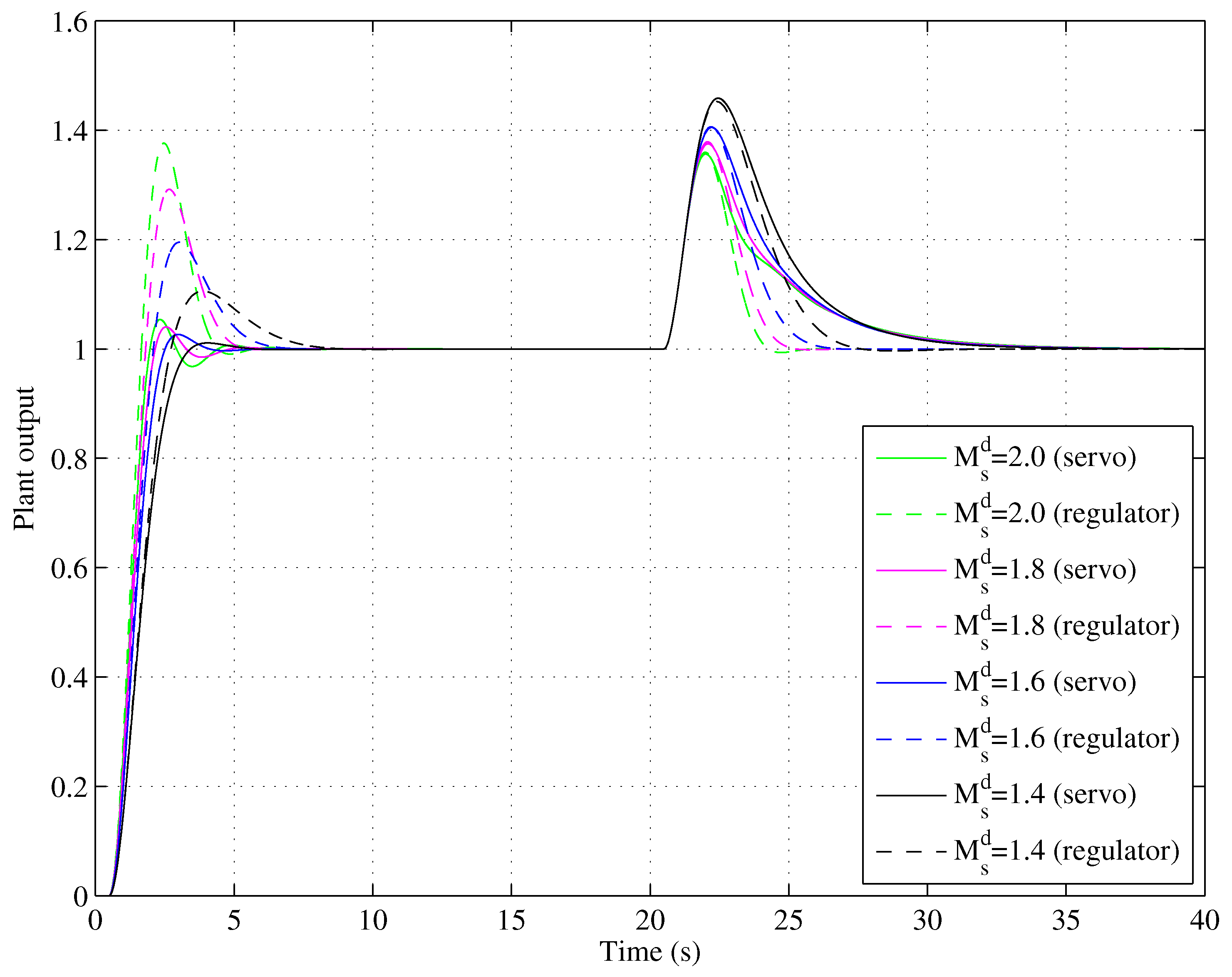
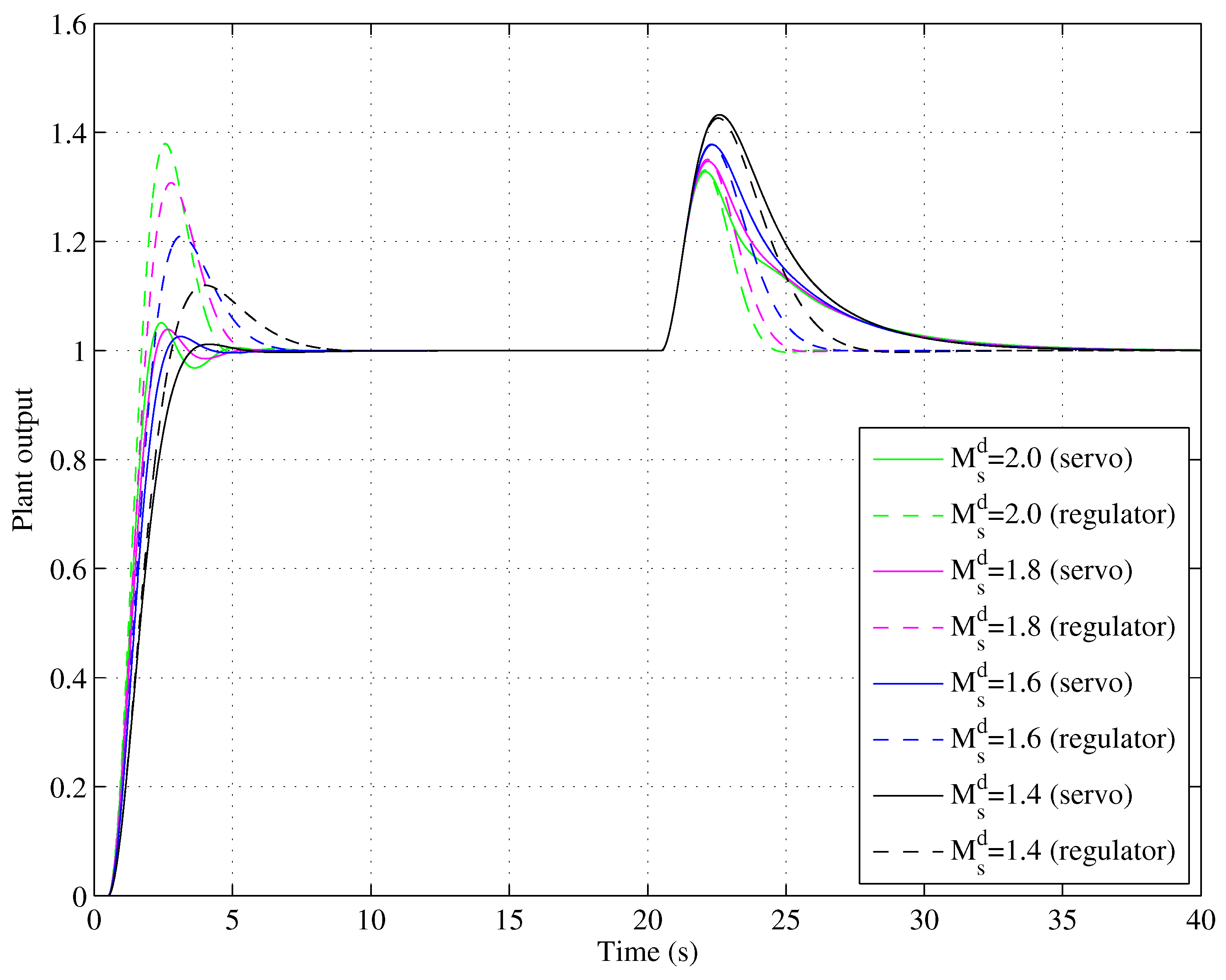
4.1. Servo–Regulation Trade-off Performance for Various SOPDT Systems
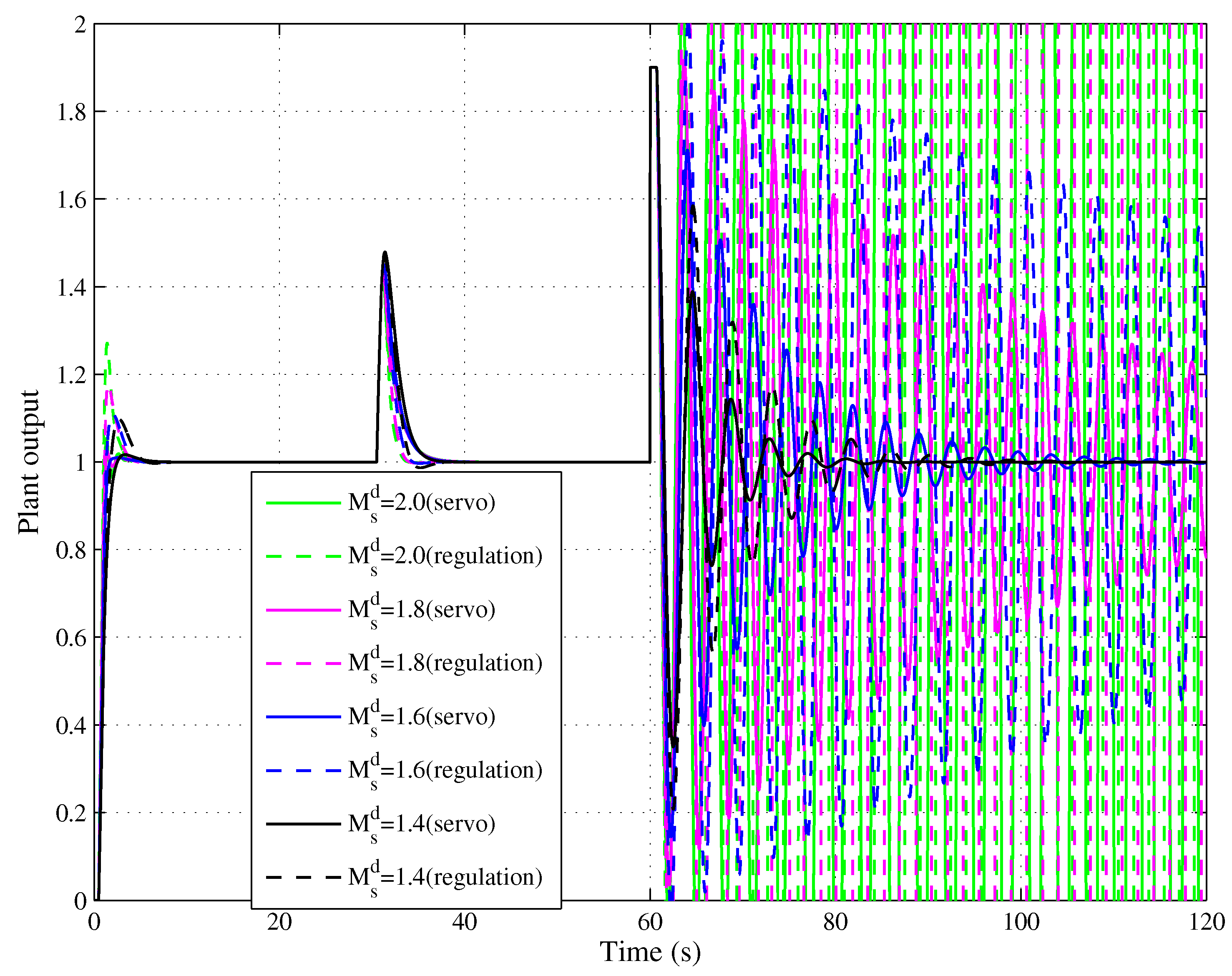
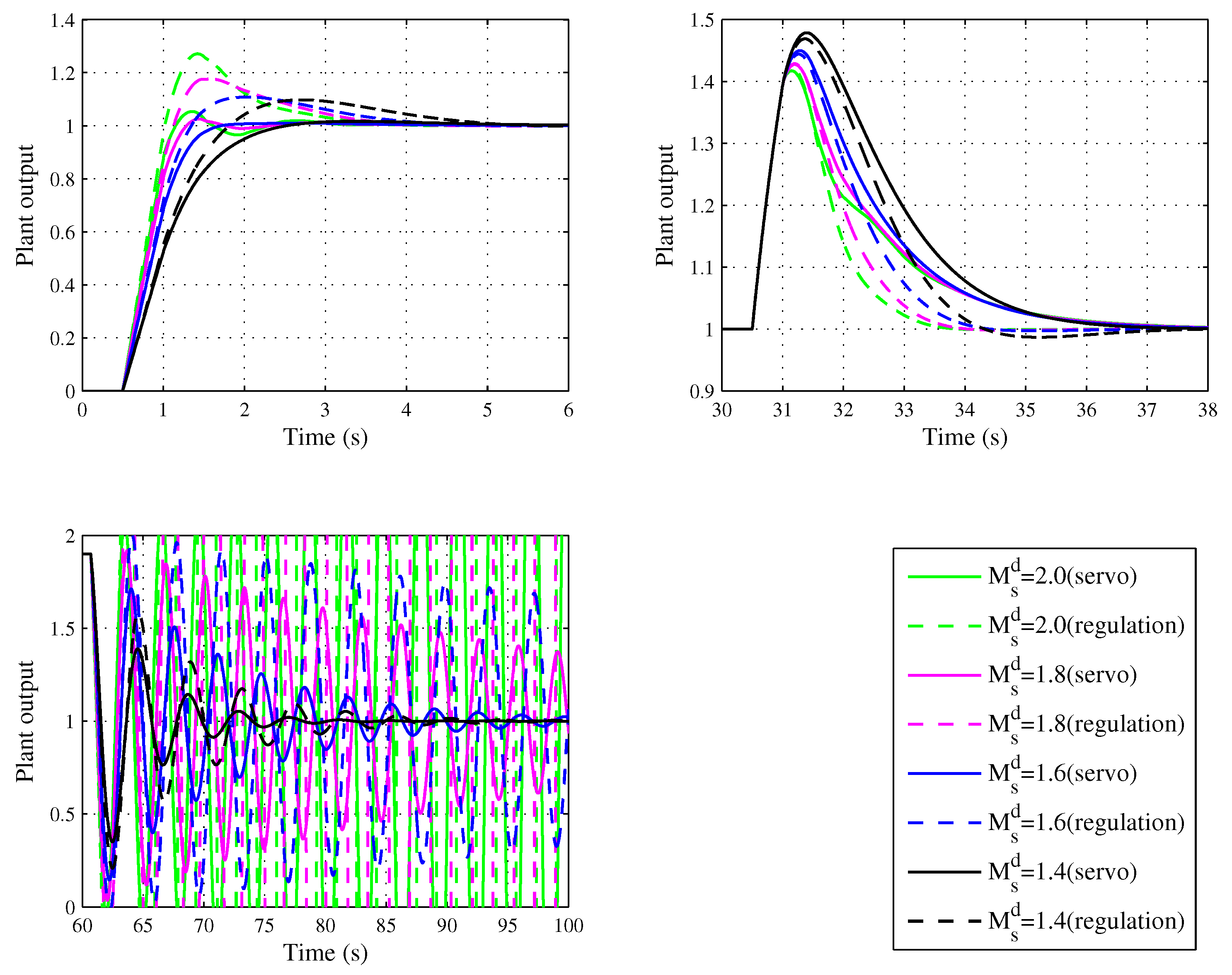
4.2. Tracking–Robustness Trade-Off Performance
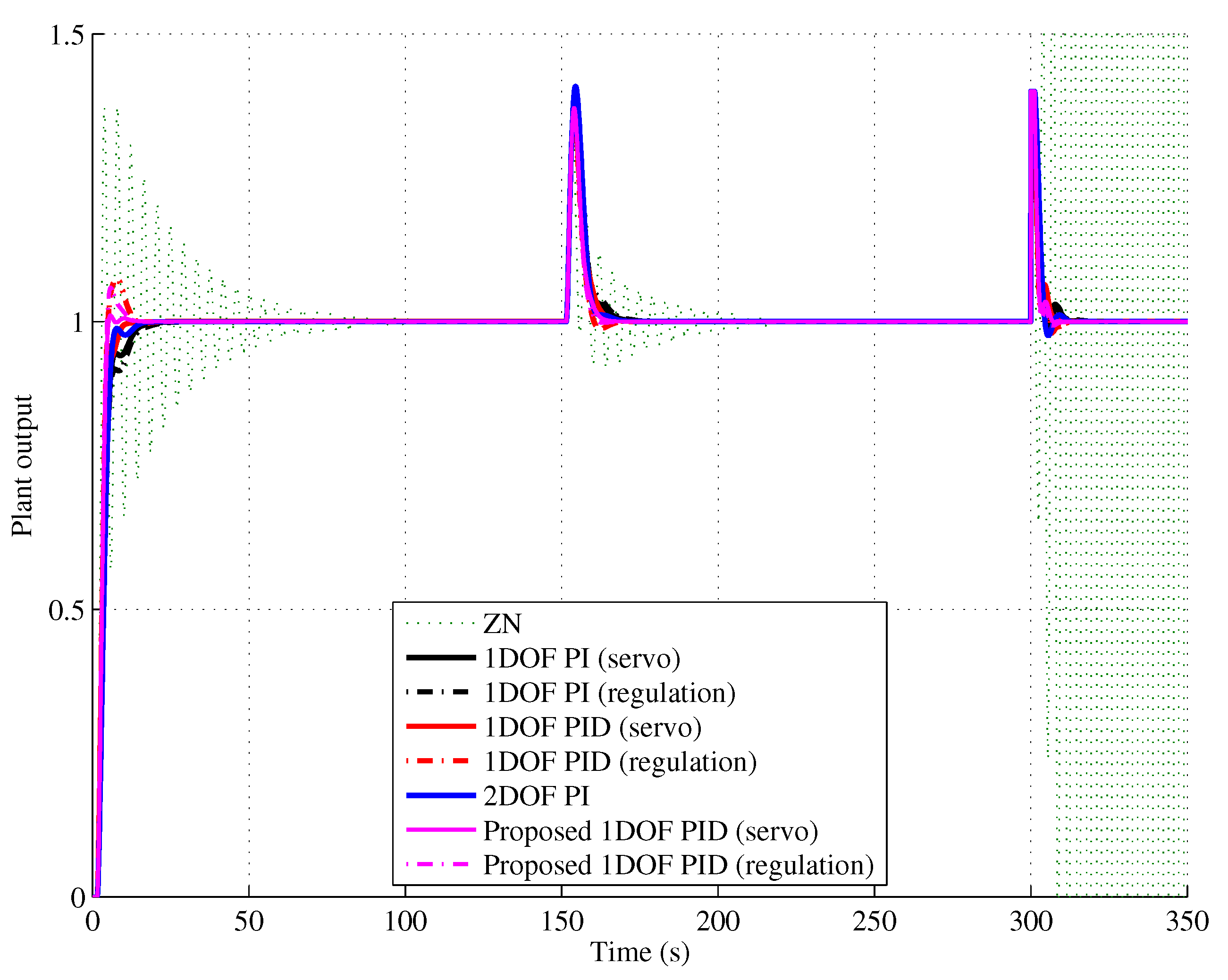
4.3. Comparison with Conventional Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vilanova, R.; Santín, I.; Pedret, C. Control and operation of wastewater treatment plants: Challenges and state of the art. Revista Iberoamericana de Automática e Informática Industrial 2017, 14, 329–345. [Google Scholar] [CrossRef]
- Ziegler, J.; Nichols, N. Optimum Settings for Automatic Controllers. Trans. ASME 1942, 64, 759–768. [Google Scholar] [CrossRef]
- Johnson, M.A.; Moradi, M.H. (Eds.) PID Control: New Identification and Design Methods; Springer: London, UK, 2005. [Google Scholar]
- Åström, K.J.; Hägglund, T. Advanced PID Control; Instrumentation, Systems, and Automation Society: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Visioli, A. Practical PID Control; Springer: London, UK, 2006. [Google Scholar]
- Vilanova, R.; Visioli, A. (Eds.) PID Control in the Third Millennium; Springer: London, UK, 2012. [Google Scholar]
- Saeki, M. Properties of Stabilizing PID Gain Set in Parameter Space. IEEE Trans. Autom. Control 2007, 52, 1710–1715. [Google Scholar] [CrossRef]
- Keel, L.; Bhatacharyya, S.P. Controller synthesis free of Analytical Models: Three Term Controllers. IEEE Trans. Autom. Control 2008, 53, 1353–1369. [Google Scholar] [CrossRef]
- Söylemez, M.; Munro, N.; Baki, H. Fast calculation of stabilizing PID controllers. Automatica 2003, 39, 121–126. [Google Scholar] [CrossRef]
- Tan, N.; Kaya, I.; Yeroglu, C.; Atherton, D. Computation of stabilizing PI and PID controllers using the stability boundary locus. Energy Convers. Manag. 2006, 47, 3045–3058. [Google Scholar] [CrossRef]
- Fang, J.; Ren, D.Z.Z. Computation of stabilizing PI and PID controllers by using Kronecker summation method. Energy Convers. Manag. 2009, 50, 1821–1827. [Google Scholar] [CrossRef]
- Matušů, R.; Prokop, R. Computation of robustly stabilizing PID controllers for interval systems. SpringerPlus 2016, 5, 702. [Google Scholar] [CrossRef] [PubMed]
- Herreros, A.; Baeyens, E.; Peran, J.R. Design of PID-type controllers using multiobjective genetic algorithms. ISA Trans. 2002, 41, 457–472. [Google Scholar] [CrossRef]
- Rosinová, D.; Veselý, V. Robust PID Decentralized Controller Design Using LMI. Int. J. Comput. Commun. Control 2007, 2, 195–204. [Google Scholar] [CrossRef]
- Sahib, M.A.; Ahmed, B.S. A new multiobjective performance criterion used in PID tuning optimization algorithms. J. Adv. Res. 2016, 7, 125–134. [Google Scholar] [CrossRef] [PubMed]
- Alfaro, V.; Vilanova, R.; Méndez, V.; Lafuente, J. Performance/robustness tradeoff analysis of PI/PID servo and regulatory control systems. In Proceedings of the 2010 IEEE International Conference on Industrial Technology (ICIT), Vina del Mar, Chile, 14–17 March 2010; pp. 111–116. [Google Scholar]
- Arrieta, O.; Vilanova, R. Simple PID tuning rules with guaranteed Ms robustness achievement. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011; pp. 12042–12046. [Google Scholar]
- Alfaro, V.; Vilanova, R. Optimal Robust Tuning for 1DOF PI/PID Control Unifying FOPDT/SOPDT Models. In Proceedings of the IFAC Conference on Advances in PID Control, Brescia, Italy, 28–30 March 2012; p. FrA2.2. [Google Scholar]
- Alfaro, V.; Vilanova, R. Model-reference robust tuning of 2DoF PI controllers for first- and second-order plus dead-time controlled processes. J. Process Control 2012, 22, 359–374. [Google Scholar] [CrossRef]
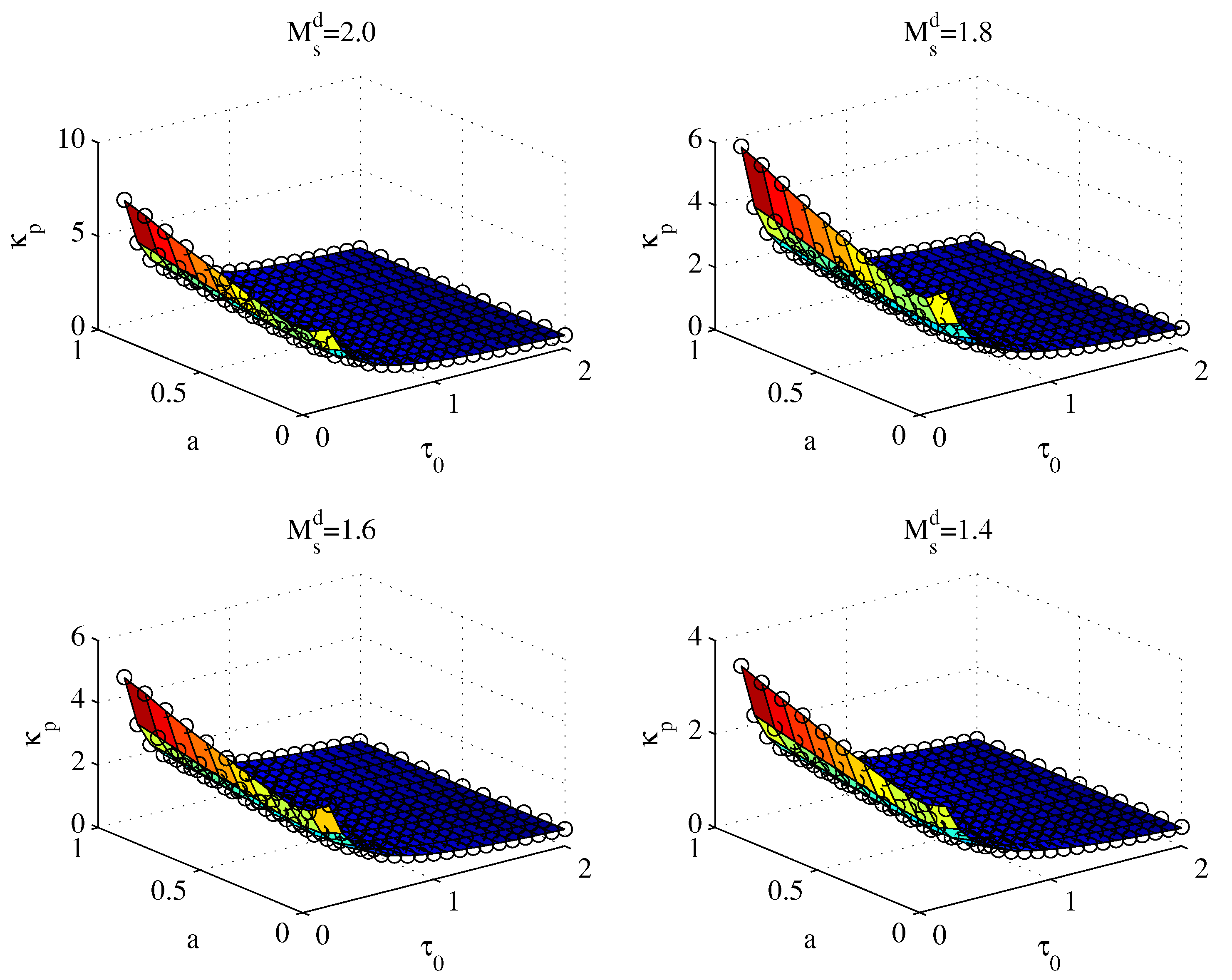
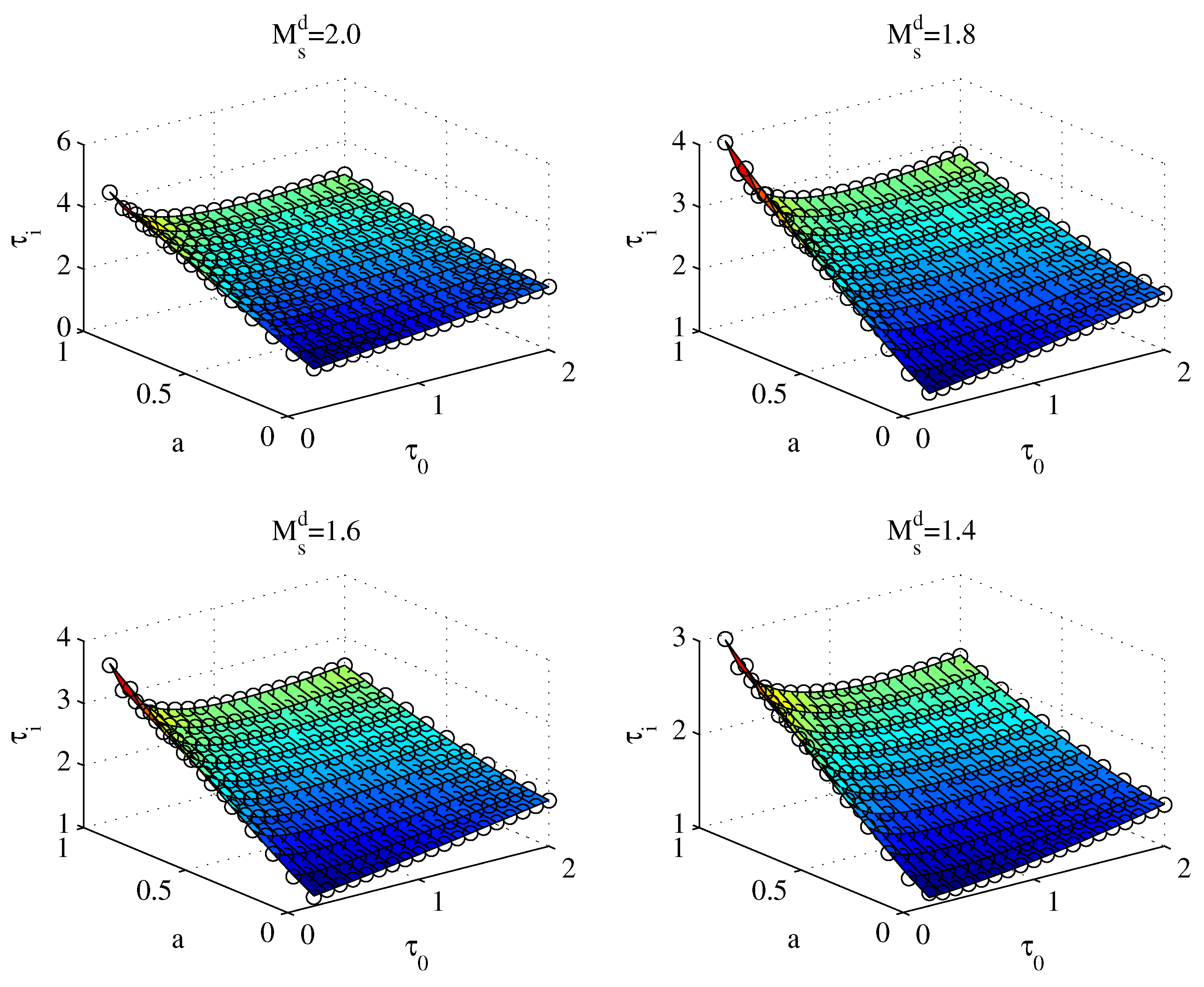
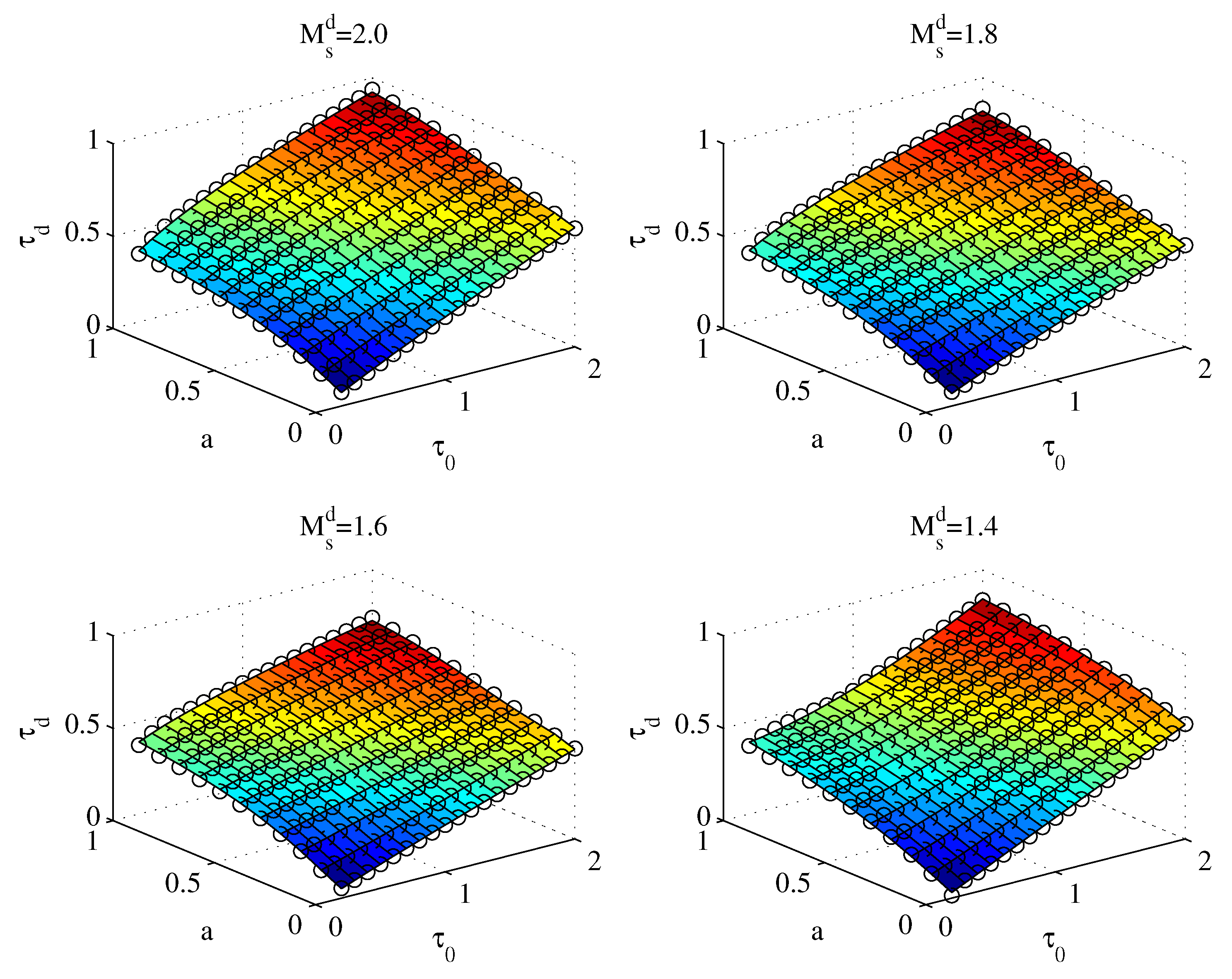
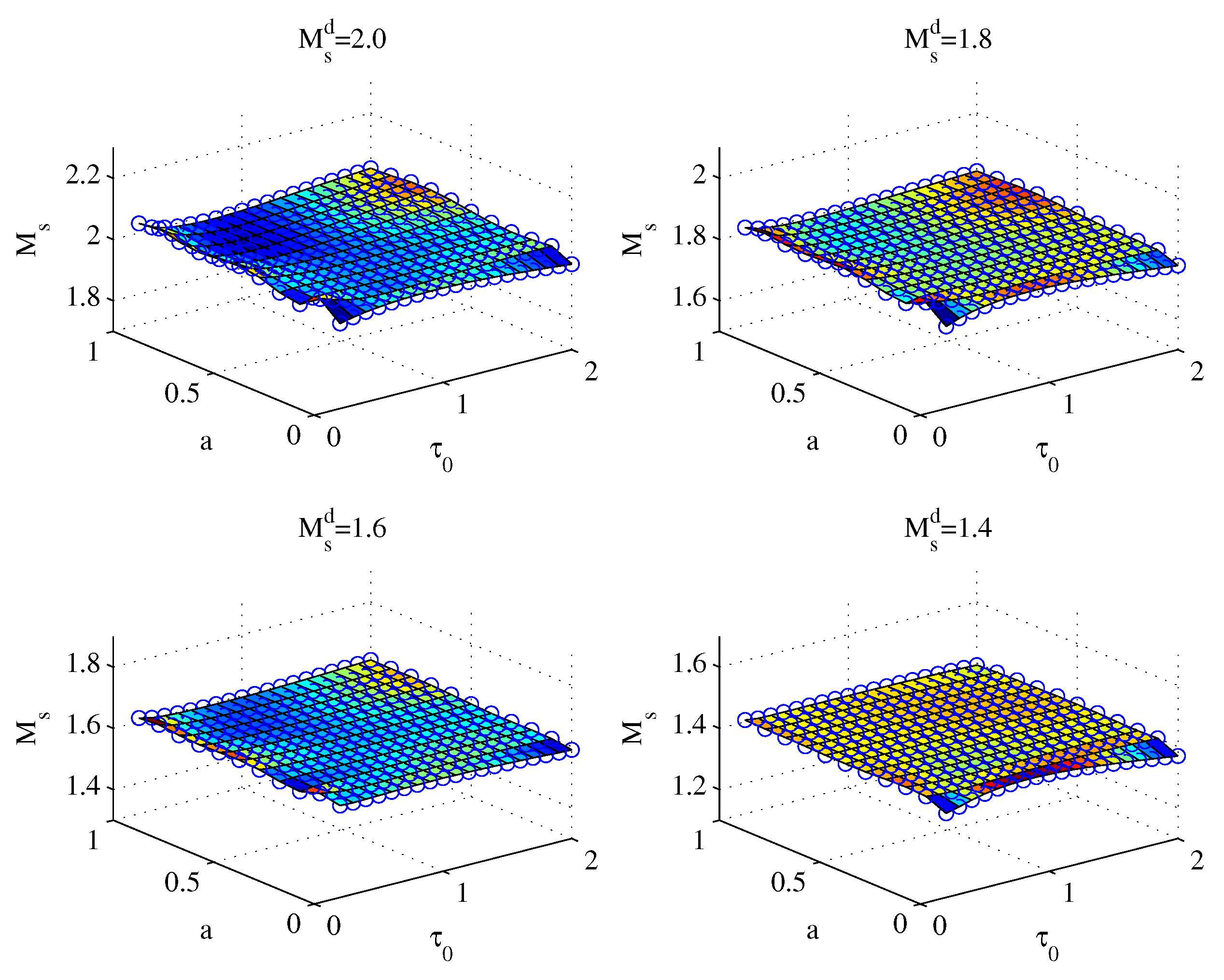
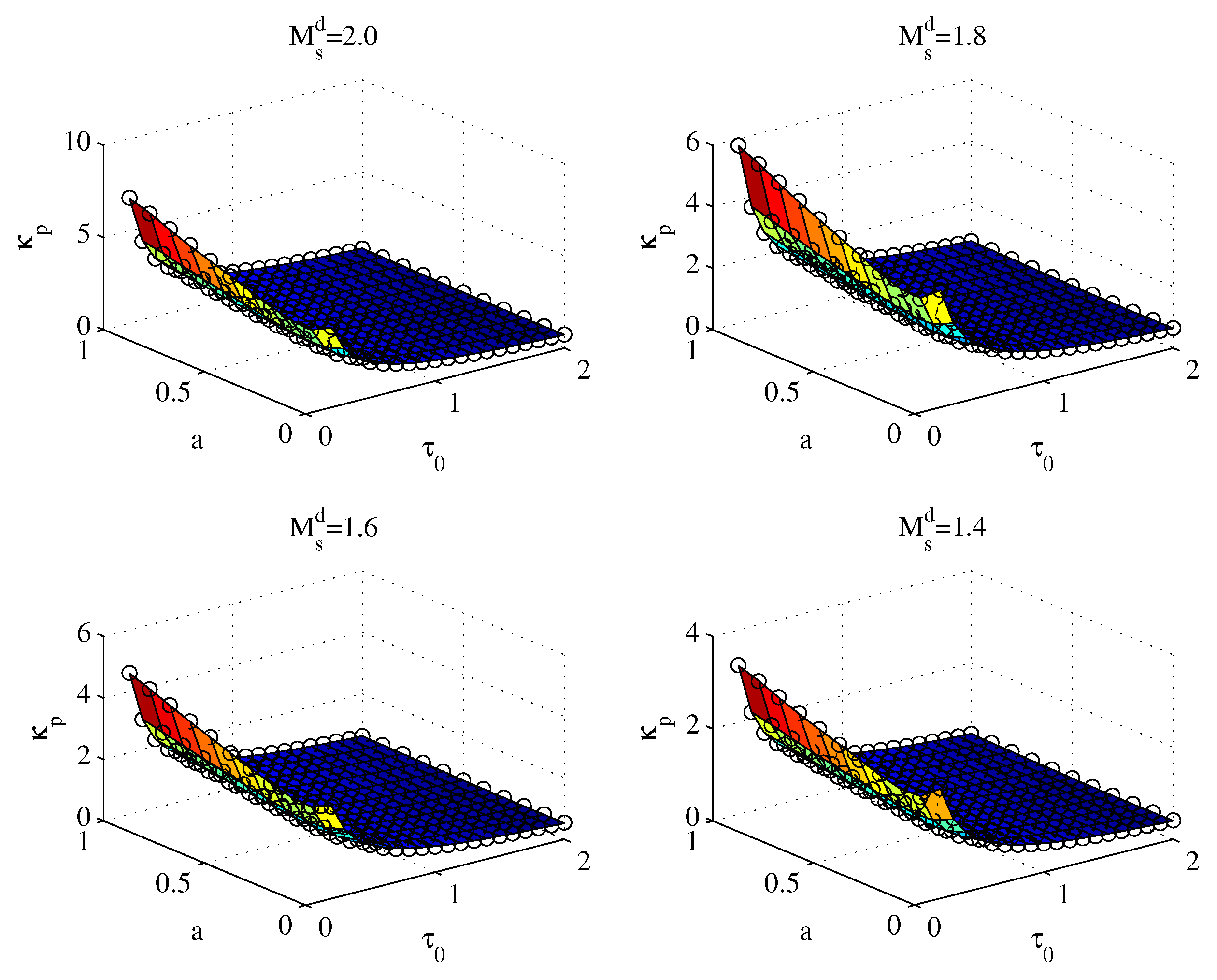

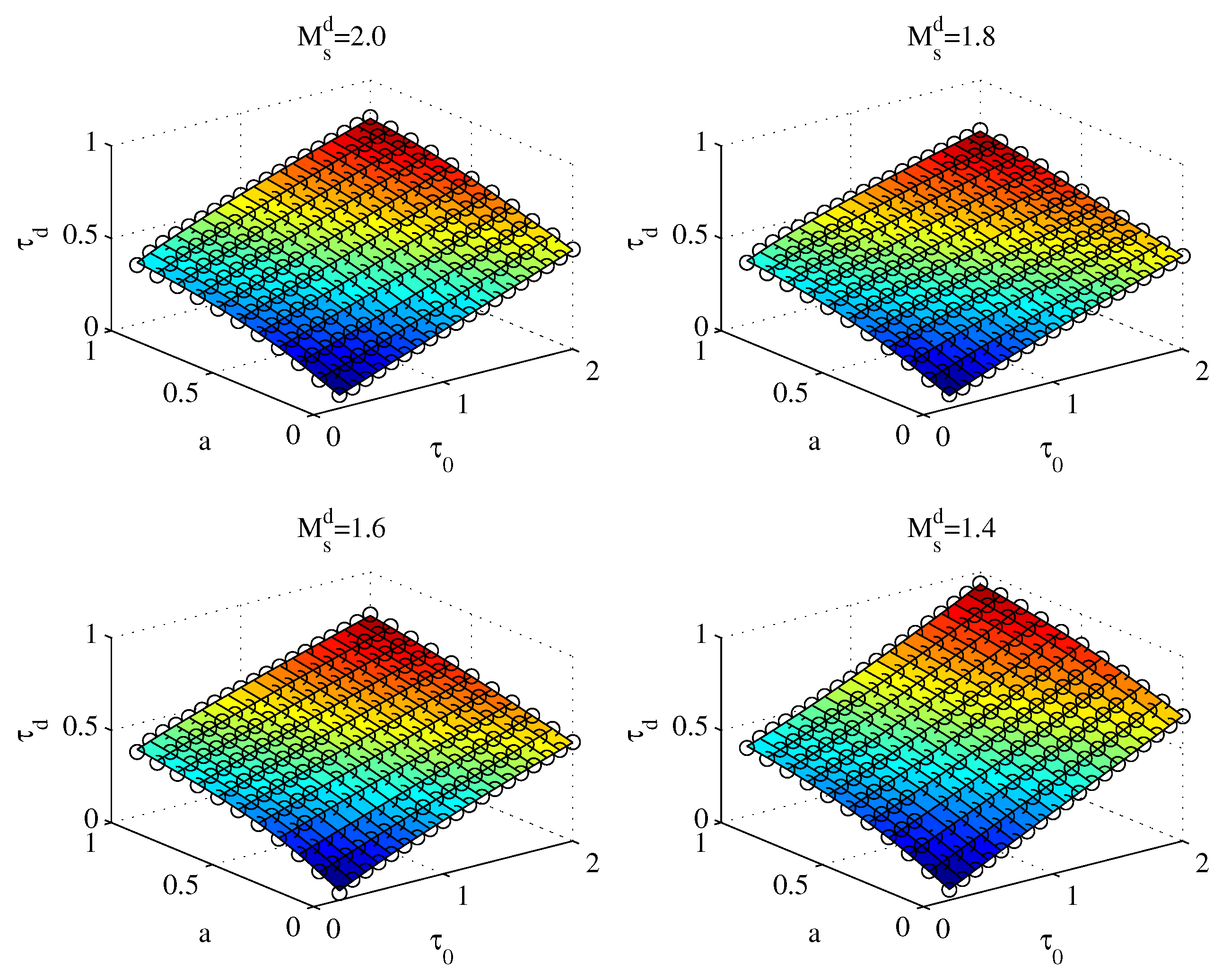
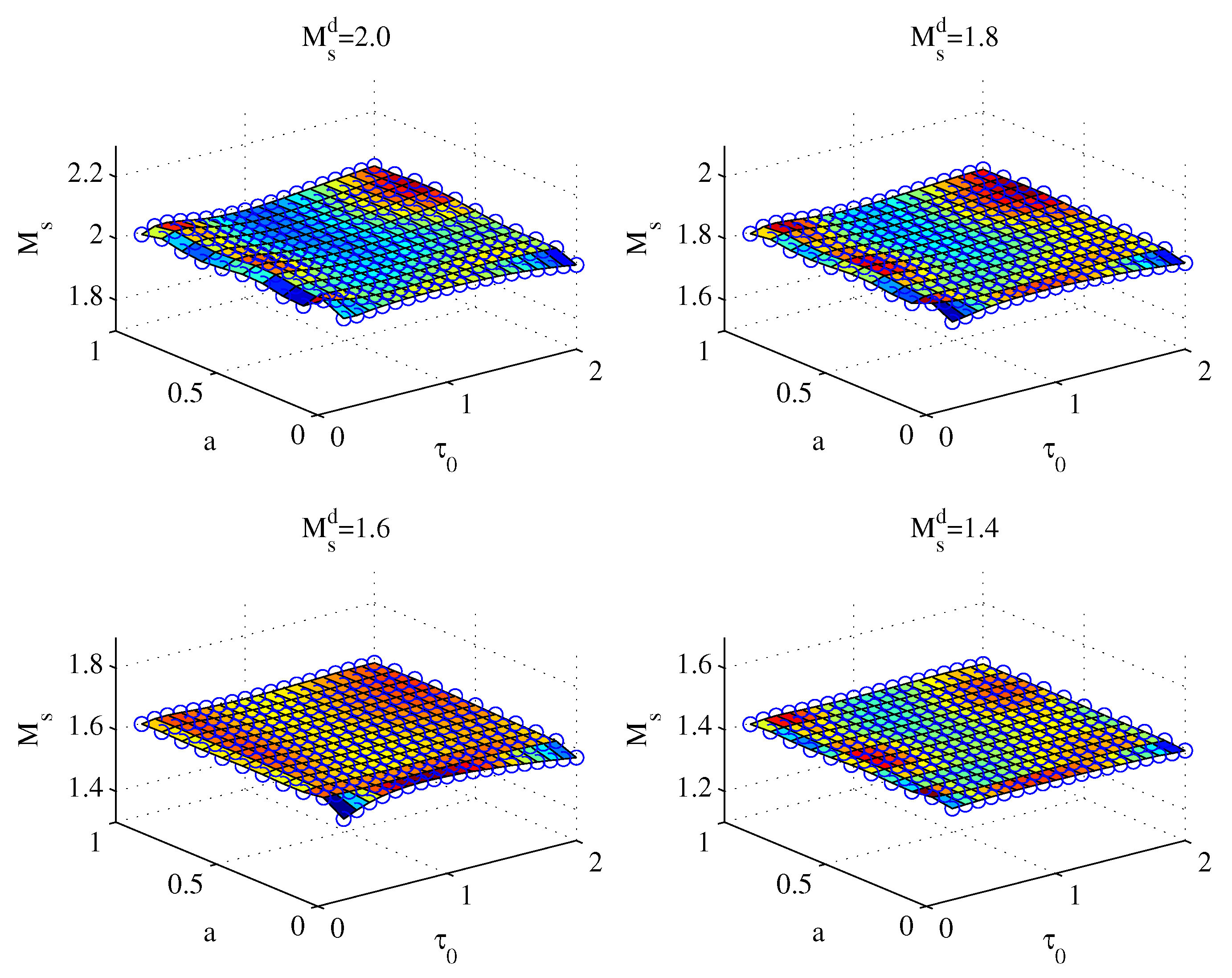
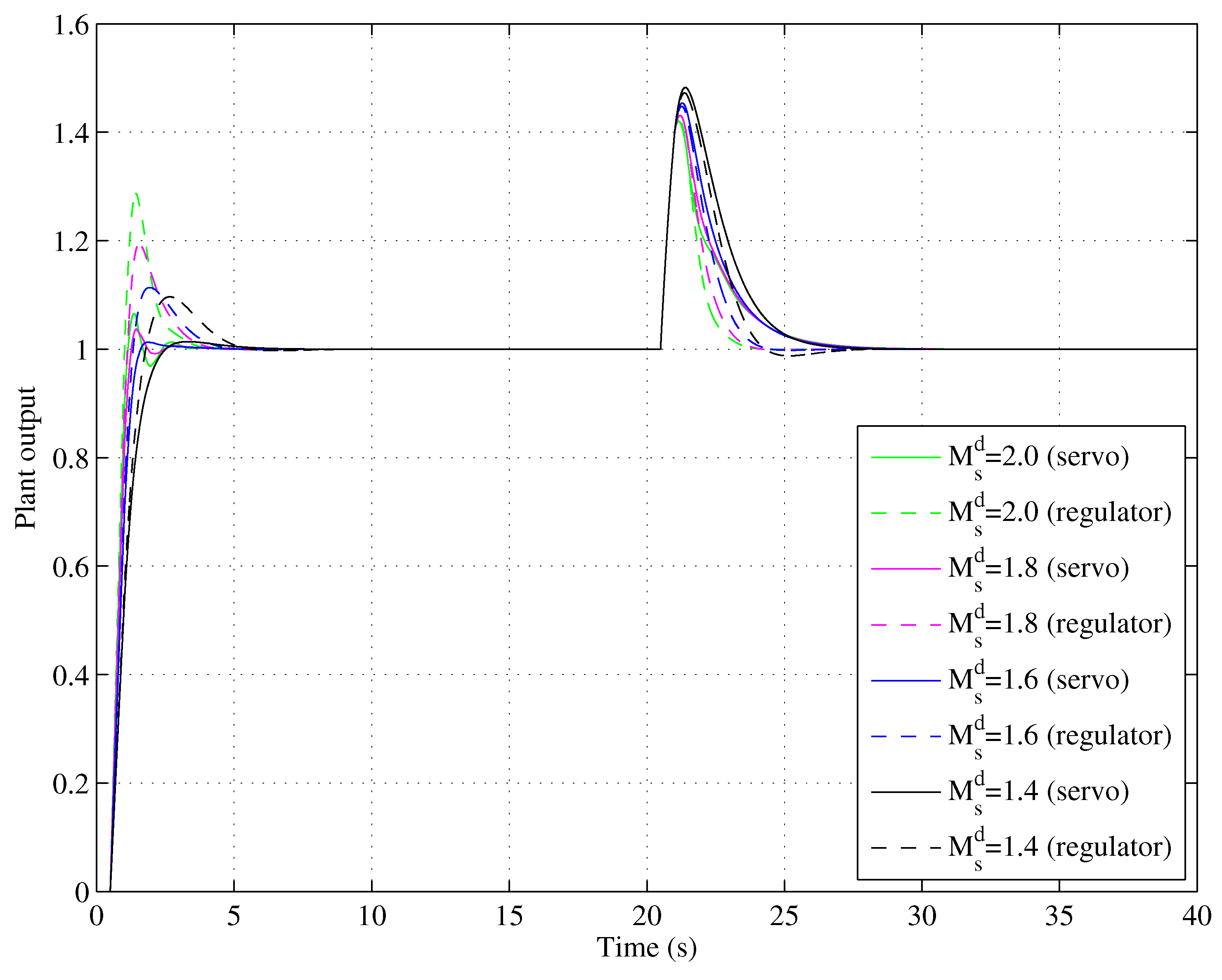

| 1.4 | 1.6 | 1.8 | 2.0 | |
|---|---|---|---|---|
| 1.4 | 1.6 | 1.8 | 2.0 | |
|---|---|---|---|---|
| 1.4 | 1.6 | 1.8 | 2.0 | |
|---|---|---|---|---|
| 1.4 | 1.6 | 1.8 | 2.0 | |
|---|---|---|---|---|
| max | ||||
| ave | ||||
| min |
| max | ||||
| ave | ||||
| min |
| Design Method | ||||
|---|---|---|---|---|
| ZN [2] | 1.52 | 3.44 | 0.859 | – |
| 1DoF PI (servo) [18] | 0.469 | 1.92 | – | – |
| 1DoF PI (reg) [18] | 0.488 | 2.09 | – | – |
| 1DoF PID (servo) [18] | 0.633 | 2.18 | 0.642 | – |
| 1DoF PID (reg) [18] | 0.610 | 1.68 | 0.774 | – |
| 2DoF PI [19] | 0.431 | 1.66 | – | 0.983 |
| Proposed 1DoF PID (servo) | 0.670 | 2.04 | 0.567 | – |
| Proposed 1DoF PID (reg) | 0.665 | 1.87 | 0.582 | – |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sato, T.; Hayashi, I.; Horibe, Y.; Vilanova, R.; Konishi, Y. Optimal Robust PID Control for First- and Second-Order Plus Dead-Time Processes. Appl. Sci. 2019, 9, 1934. https://doi.org/10.3390/app9091934
Sato T, Hayashi I, Horibe Y, Vilanova R, Konishi Y. Optimal Robust PID Control for First- and Second-Order Plus Dead-Time Processes. Applied Sciences. 2019; 9(9):1934. https://doi.org/10.3390/app9091934
Chicago/Turabian StyleSato, Takao, Itaru Hayashi, Yohei Horibe, Ramon Vilanova, and Yasuo Konishi. 2019. "Optimal Robust PID Control for First- and Second-Order Plus Dead-Time Processes" Applied Sciences 9, no. 9: 1934. https://doi.org/10.3390/app9091934
APA StyleSato, T., Hayashi, I., Horibe, Y., Vilanova, R., & Konishi, Y. (2019). Optimal Robust PID Control for First- and Second-Order Plus Dead-Time Processes. Applied Sciences, 9(9), 1934. https://doi.org/10.3390/app9091934






