Improving the Accuracy of Fault Frequency by Means of Local Mean Decomposition and Ratio Correction Method for Rolling Bearing Failure
Abstract
:1. Introduction
2. Materials and Methods
2.1. LMD and Its Improved Algorithm
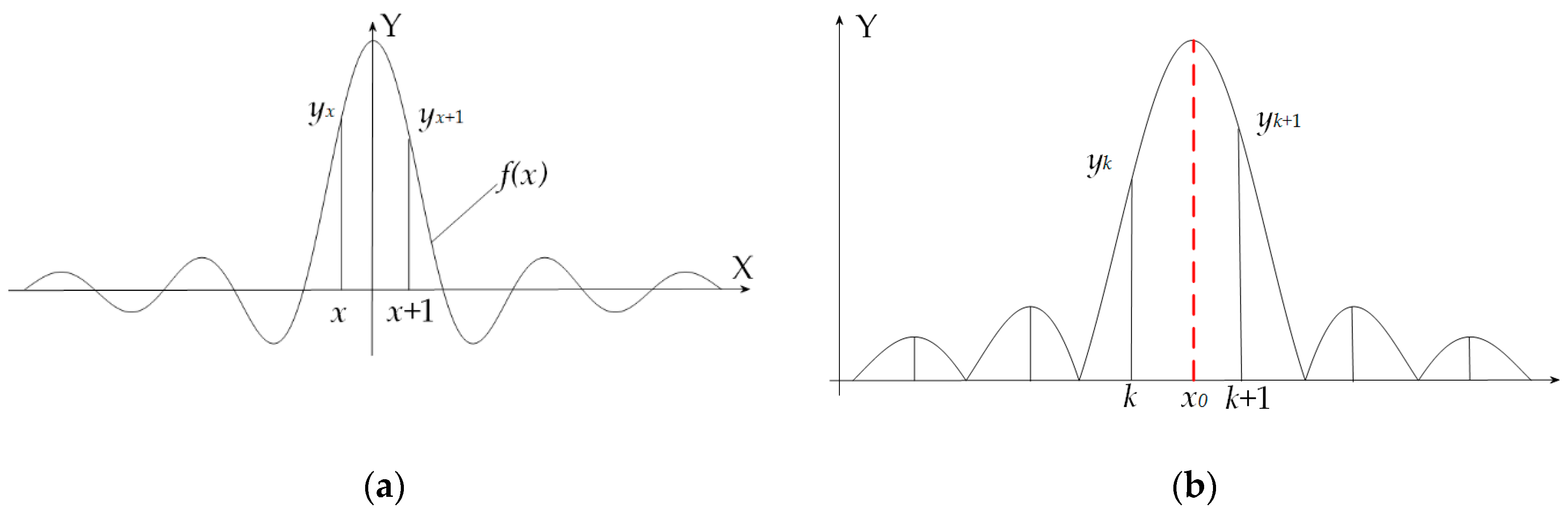
2.2. Ratio Correction Method
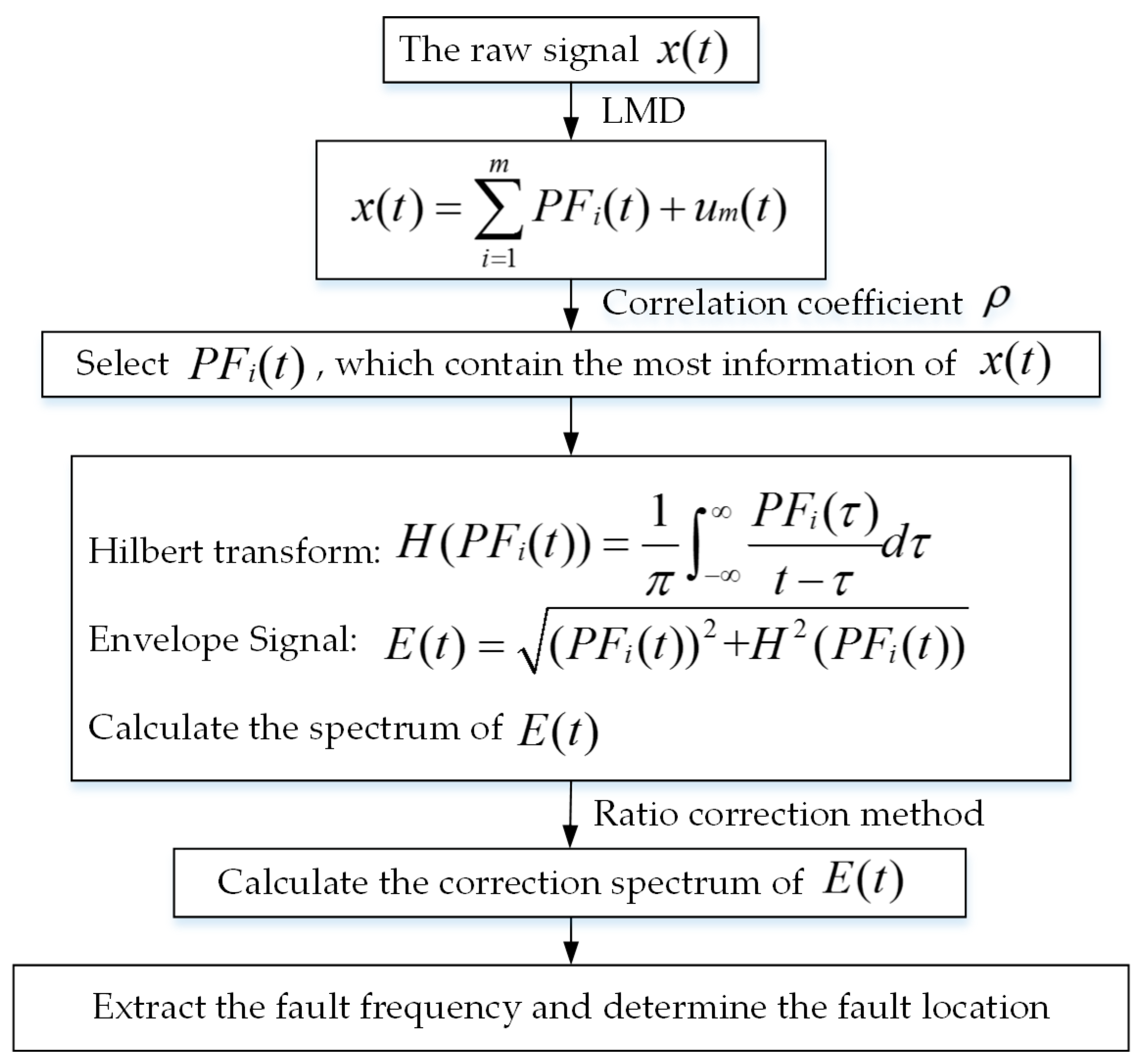
2.3. Diagnostic Method Flow and Simulation Analysis
3. Application and Results
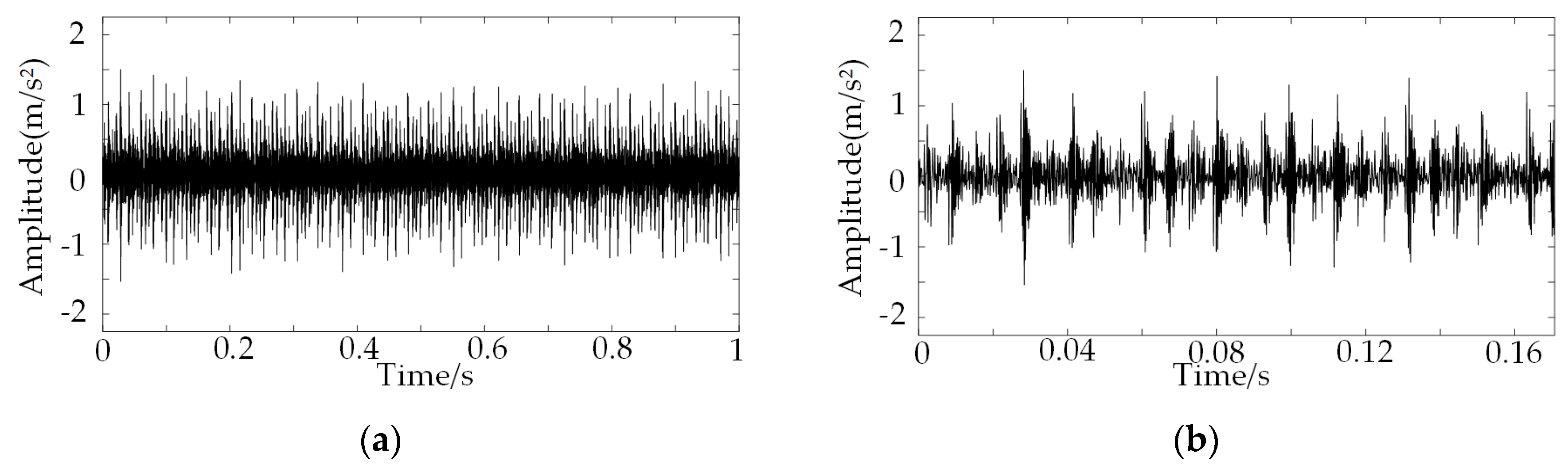
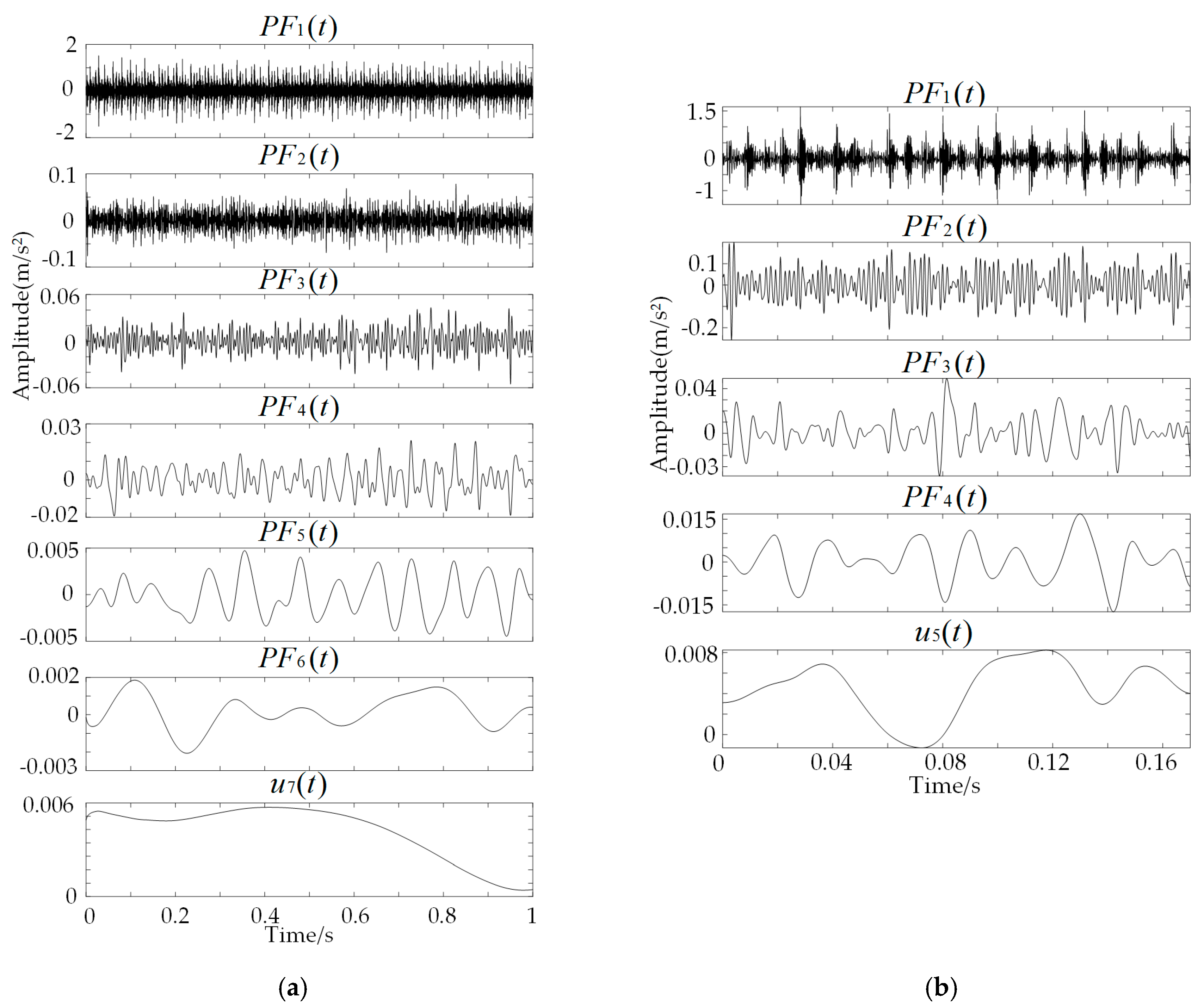
3.1. Fault Diagnosis of Bearing with Fault at the Inner Raceway
3.2. Fault Diagnosis of Bearing with Fault at the Outer Raceway
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cohen, L. Time-frequency distributions-a review. Proc. IEEE 1989, 77, 941–981. [Google Scholar] [CrossRef] [Green Version]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Patt. Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Qin, S.R.; Zhong, Y.M. A new envelope algorithm of Hilbert–Huang Transform. Mech. Syst. Signal Pr. 2006, 20, 1941–1952. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.L.C.; Long, S.R.; Shen, S.S.P.; Qu, W.; Gloersen, P.; Fun, K.L. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis. Proc. A 2003, 459, 2317–2345. [Google Scholar] [CrossRef]
- Deng, Y.J.; Wang, W.; Qian, C.C.; Wang, Z.; Dai, D.J. Boundary-processing-technique in EMD method and Hilbert transform. Chin. Sci. Bull. 2001, 46, 954. [Google Scholar] [CrossRef]
- Cheng, J.S.; Yu, D.J.; Yang, Y. Research on the intrinsic mode function (IMF) criterion in EMD method. Mech. Syst. Signal Pr. 2006, 20, 817–824. [Google Scholar]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [Green Version]
- Pan, H.; He, X.; Tang, S.; Meng, F. An improved bearing fault diagnosis method using one-dimensional CNN and LSTM. J. Mech. Eng. 2018, 64, 443–452. [Google Scholar]
- Jing, L.; Zhao, P.; Li, P.; Xu, X. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox. Measurement 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, Y.; Meng, G.; Lee, J. A hybrid feature selection scheme for unsupervised learning and its application in bearing fault diagnosis. Expert Syst. Appl. 2011, 38, 11311–11320. [Google Scholar] [CrossRef]
- Cheng, J.S.; Zhang, H.; Yang, Y. A comparative study of local mean decomposition and empirical mode decomposition. J. Vibr. Shock 2009, 28, 13–16. [Google Scholar]
- Zhang, F.S.; Geng, Z.X.; Yuan, W. The algorithm of interpolating windowed FFT for harmonic analysis of electric power system. IEEE Trans. Power Deliv. 2001, 16, 160–164. [Google Scholar] [CrossRef]
- Luo, J.F.; Xie, M. Phase difference methods based on asymmetric windows. Mech. Syst. Signal Process. 2015, 54, 52–67. [Google Scholar] [CrossRef]
- Duan, H.M.; Qin, S.R.; Li, N. Review of correction methods for discrete spectrum. J. Vibr. Shock 2007, 26, 138–145. [Google Scholar]
- Xie, M.; Ding, K. A new correction method for discrete spectrum analysis. J. Chongqing Univ. Nat. Sci. Ed. 1995, 18, 48–54. [Google Scholar]
- Grandke, T. Interpolation algorithms for discrete Fourier transforms of weighted signals. IEEE Trans. Instrum. Meas. 1983, 32, 350–355. [Google Scholar] [CrossRef]
- Ding, K.; Jiang, L.Q. Energy centrobaric correction method for discrete spectrum. J. Vibr. Eng. 2001, 14, 354–358. [Google Scholar]
- Lin, H.B.; Ding, K. Energy based signal parameter estimation method and a comparative study of different frequency estimators. Mech. Syst. Signal Process. 2011, 25, 452–464. [Google Scholar]
- Belega, D.; Dallet, D.; Petri, D. Accuracy of the normalized frequency estimation of a discrete-time sine-wave by the energy-based method. IEEE Trans. Instrum. Meas. 2012, 61, 111–121. [Google Scholar] [CrossRef]
- Candan, C. A method for fine resolution frequency estimation from three DFT samples. Signal Process. Lett. IEEE 2011, 18, 351–354. [Google Scholar] [CrossRef]
- Abatzoglou, T.; Candan, C. Analysis and further improvement of fine resolution frequency estimation method from three DFT samples. Signal Process. Lett. IEEE 2013, 20, 913–916. [Google Scholar]
- Macleod, M.D. Fast nearly ML estimation of the parameters of real or complex single tones or resolved multiple tones. IEEE Trans. Signal Process. 1998, 46, 141–148. [Google Scholar] [CrossRef]
- Jacobsen, E.; Kootsookos, P. Fast, accurate frequency estimators. Signal Process. Magaz. IEEE 2007, 24, 123–125. [Google Scholar] [CrossRef]
- Calro, O.; Diaro, P. The influence of windowing on the accuracy of multifrequency signal parameter estimation. IEEE Trans. Instrum. Meas. 1992, 41, 256–261. [Google Scholar]
- Schoukens, J.; Pintelon, R.; Van, H.H. The interpolated fast Fourier transform: A comparative study. IEEE Trans. Instrum. Meas. 1991, 41, 226–232. [Google Scholar] [CrossRef]
- Xie, M.; Ding, K. Corrections for frequency, amplitude and phase in a fast Fourier transform of a harmonic signal. Mech. Syst. Signal Process. 1996, 10, 211–221. [Google Scholar]
- Dishan, H. Phase error in fast Fourier transform analysis. Mech. Syst. Signal Process. 1995, 9, 113–118. [Google Scholar] [CrossRef]
- Xie, M.; Ding, K. Correction method of spectrum analysis. J. Vibr. Eng. 1994, 7, 172–179. [Google Scholar]
- Ding, K.; Xie, M. Method of improving the speed and accuracy of FFT and spectral analysis. J. Chongqing Univ. Nat. Sci. Ed. 1992, 15, 51–57. [Google Scholar]
- Zhang, Y.; Qin, Y.; Xing, Z.Y.; Jia, L.M.; Cheng, X.Q. Roller bearing safety region estimation and state identification based on LMD–PCA–LSSVM. Measurement 2013, 46, 1315–1324. [Google Scholar] [CrossRef]
- Ren, D.Q.; Yang, S.X.; Wu, Z.T.; Yan, G.B. Research on end effect of LMD based time-frequency analysis in rotating machinery fault diagnosis. China Mech. Eng. 2012, 23, 951–956. [Google Scholar]
- Wang, L.; Liu, Z.; Miao, Q. Time-Frequency analysis based on ensemble local mean decomposition and fast kurtogram for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2018, 103, 60–75. [Google Scholar] [CrossRef]
- Liu, Z.L.; Zuo, M.J.; Jin, Y.Q.; Pan, D.; Qin, Y. Improved local mean decomposition for modulation information mining and its application to machinery fault diagnosis. J. Sound Vibr. 2017, 397, 266–281. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 18 October 2018).
- Rife, D.; Boorstyn, R. Single tone parameter estimation from discrete-time observations. IEEE Trans. Inf. Theory 1974, 20, 591–598. [Google Scholar] [CrossRef]
- Xu, C.Y.; Ding, K.; Lin, H.B. Noise influence on amplitude and phase estimation accuracy by interpolation method for discrete spectrum. J. Vibr. Eng. 2011, 24, 633–638. [Google Scholar]
- Chen, K.F.; Jiang, J.T.; Crowsen, S. Against the long-range spectral leakage of the cosine window family. Comput. Phys. Commun. 2009, 180, 904–911. [Google Scholar] [CrossRef]
- Aryan, R.R.; Mehdi, B. Probabilistic Risk-Based Performance Evaluation of Seismically Base-Isolated Steel Structures Subjected to Far-Field Earthquakes. Buildings 2018, 8, 128. [Google Scholar]

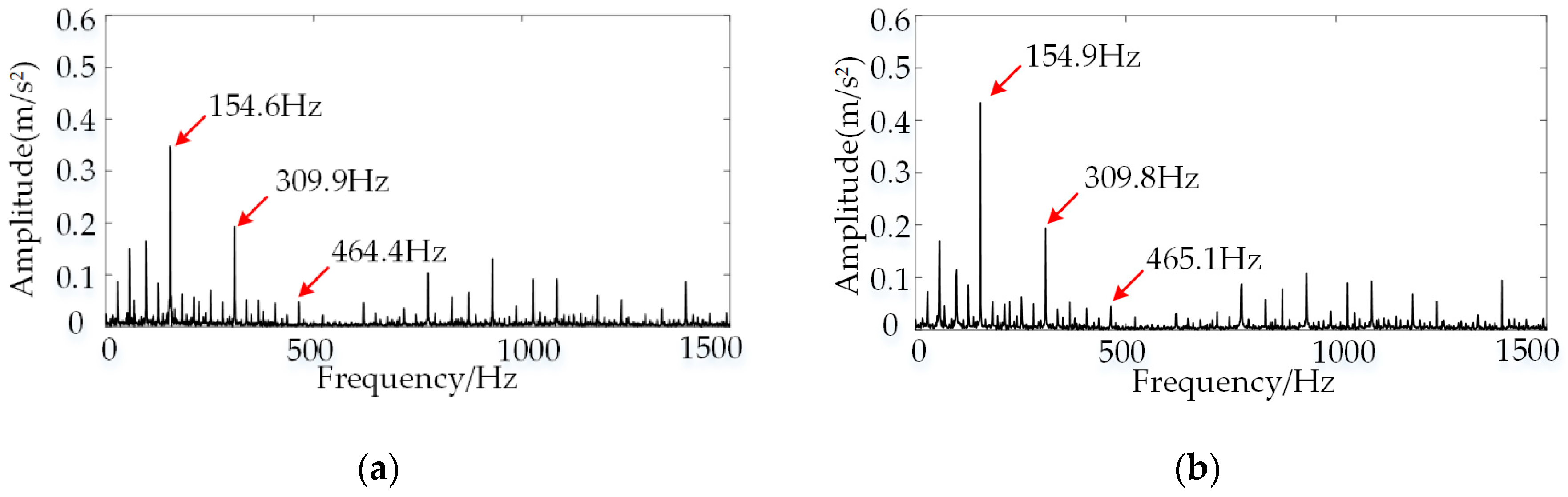


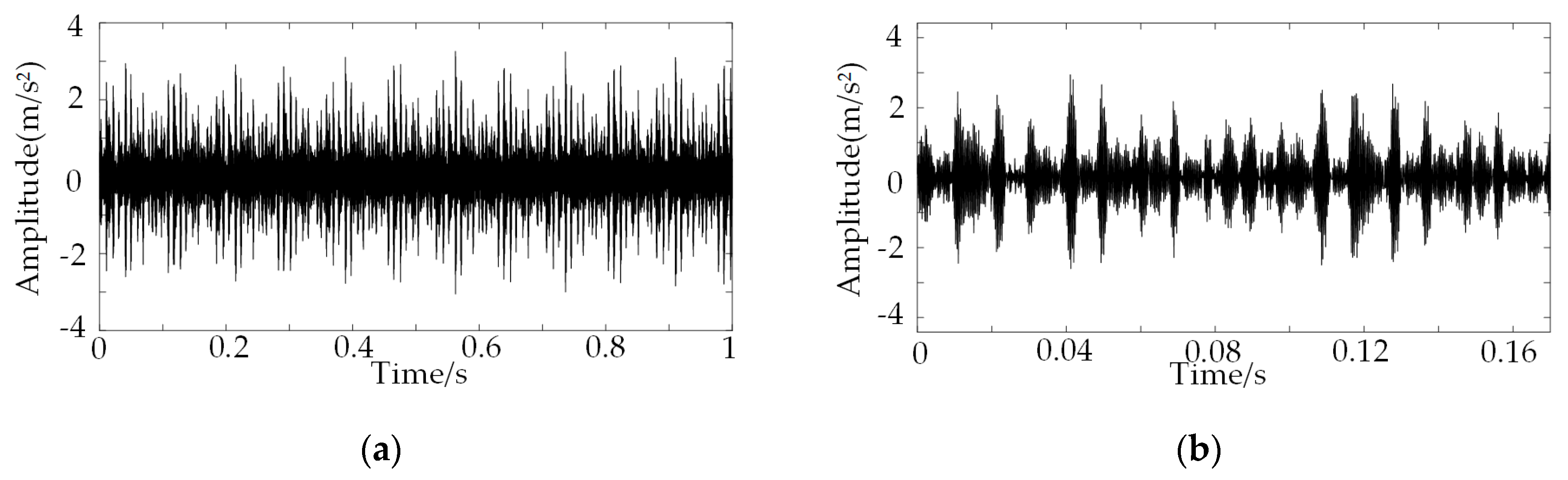
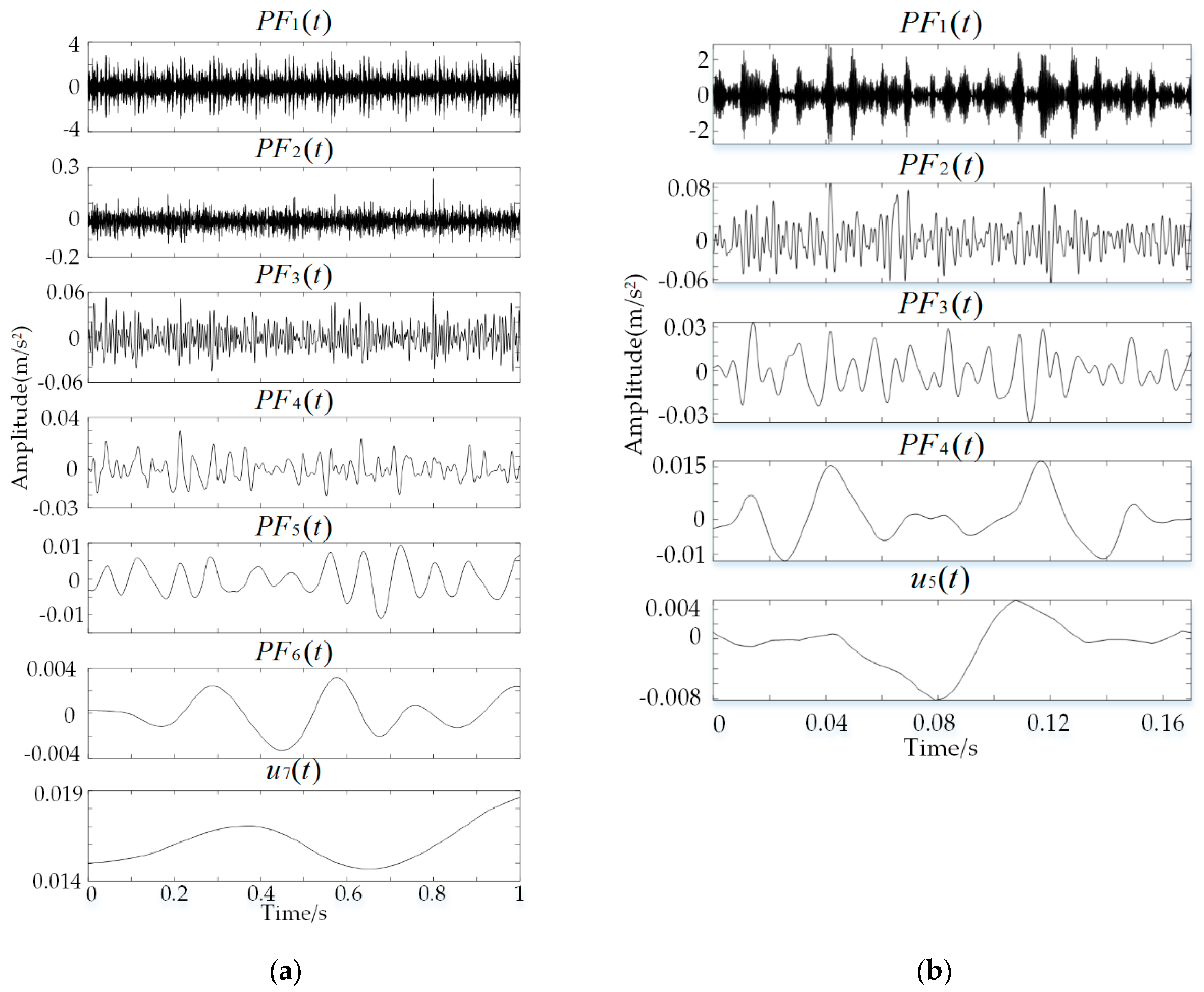
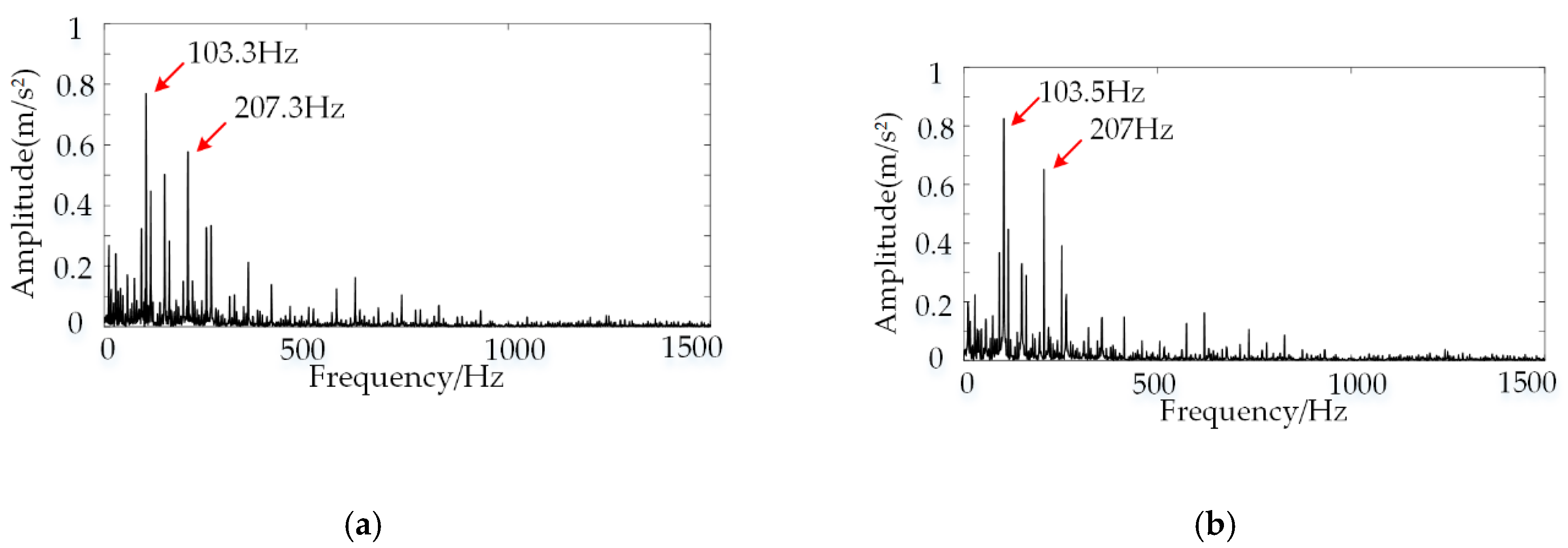
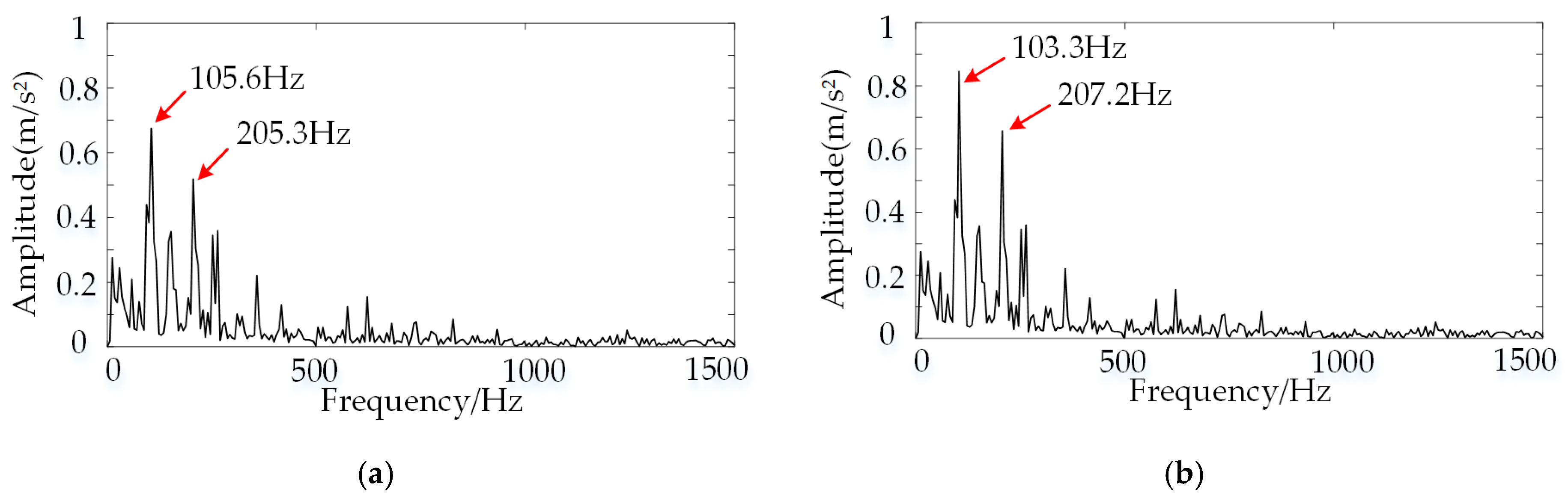
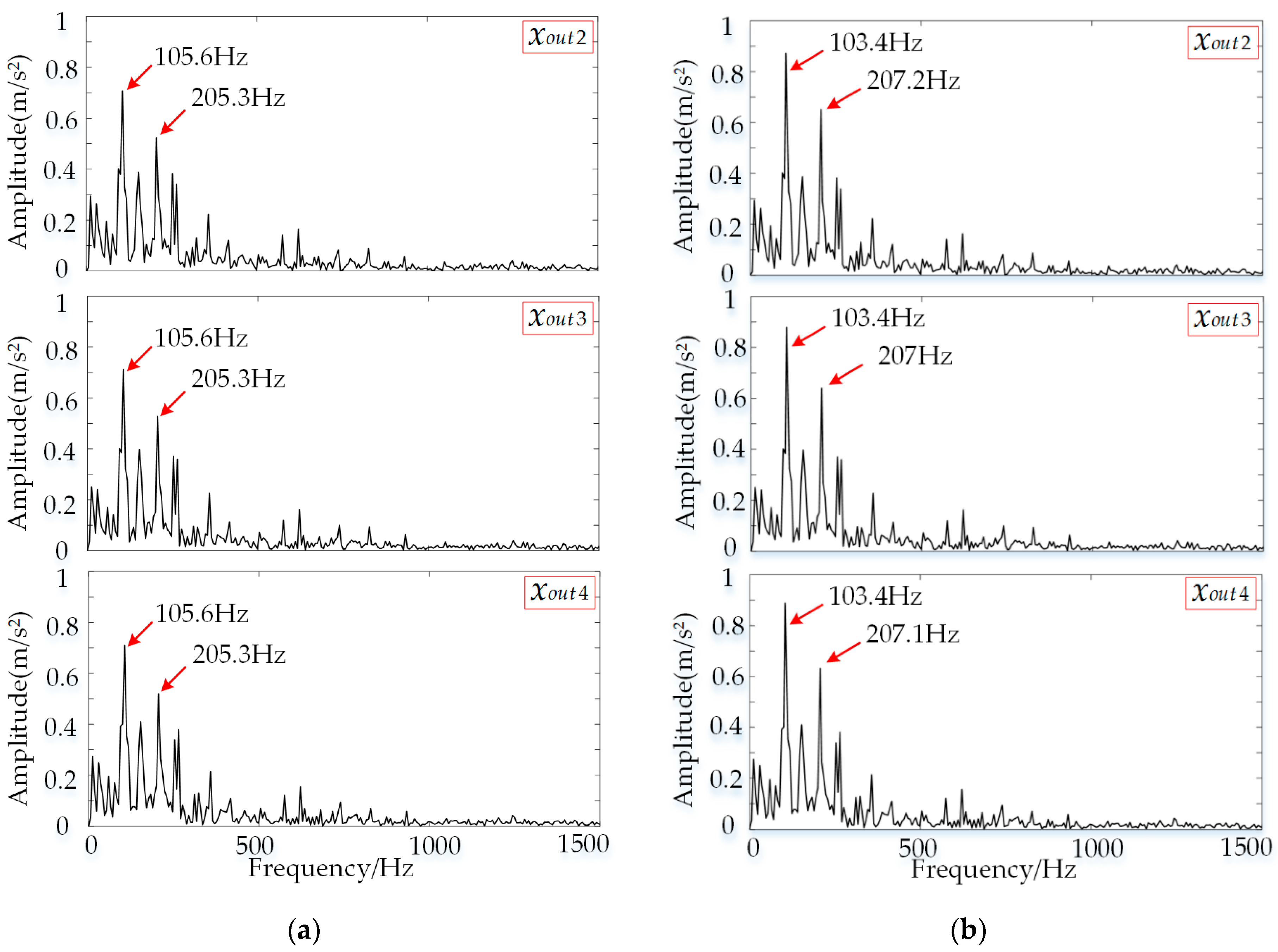
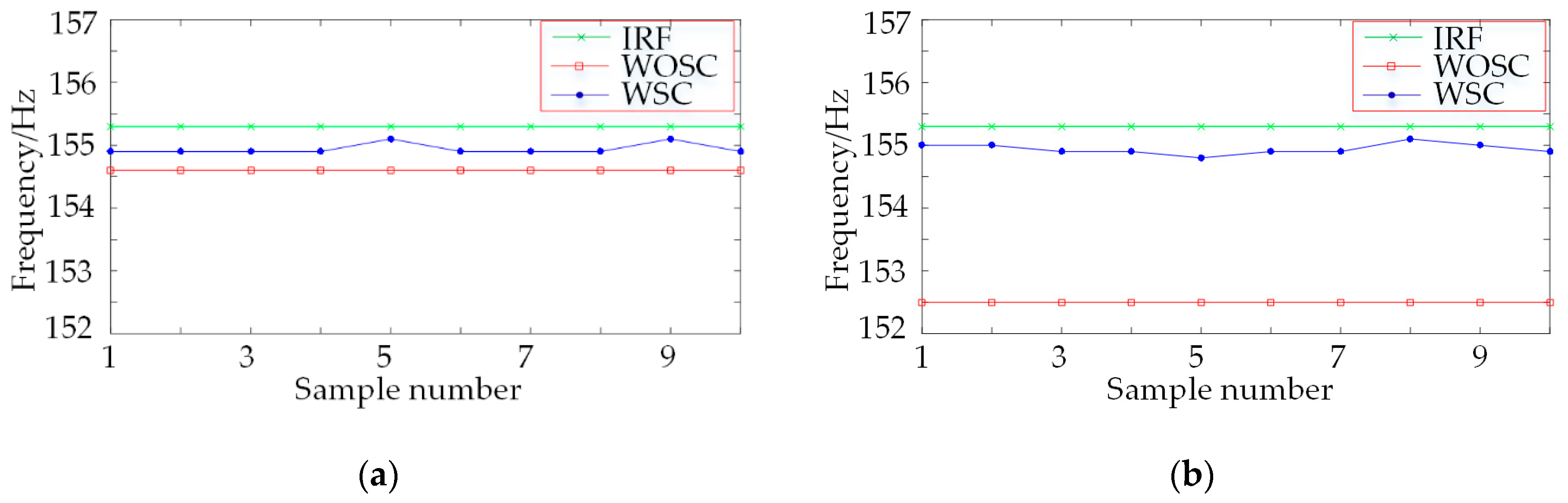
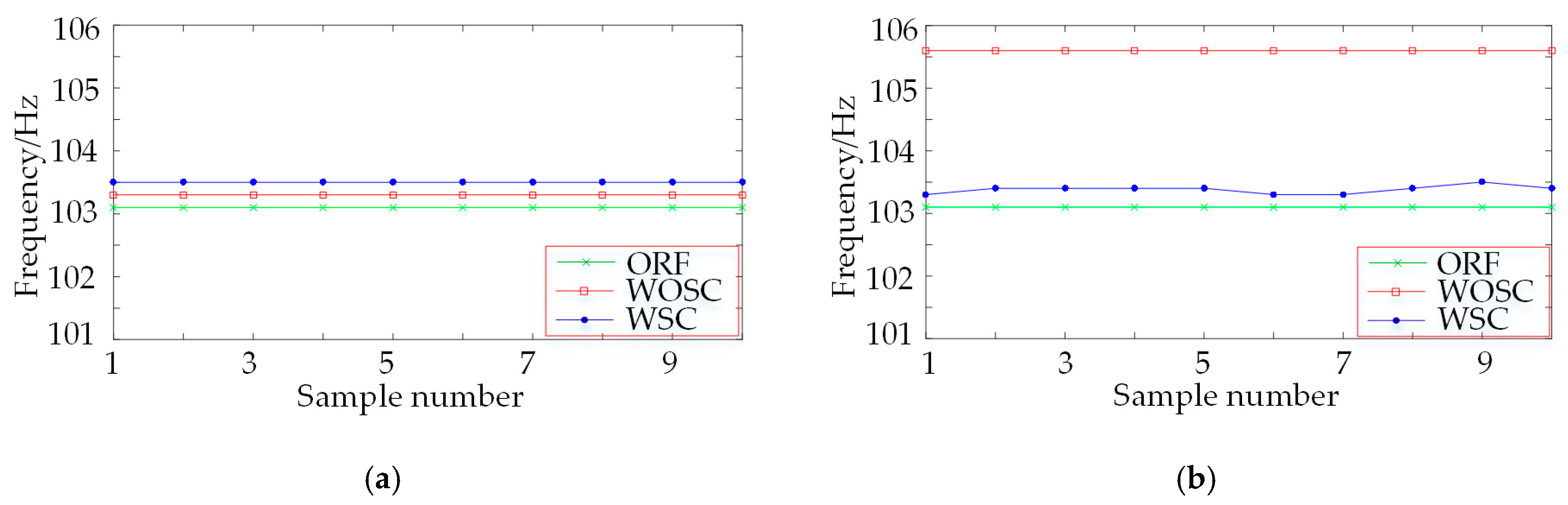
| Data Code | RS | RF | IRF | ORF |
|---|---|---|---|---|
| 1721 r/min | 28.68 Hz | 155.3 Hz | ||
| 1725 r/min | 28.75 Hz | 103.1 Hz |
| 0.9966 | 0.18162 | 0.0202 | 0.0004 | −4.42E−5 | 2.66E−5 | |
| 0.9770 | 0.2096 | 0.0208 | 0.0019 |
| 0.9986 | 0.0602 | 0.0106 | 0.0007 | 0.0001 | 3.605E−5 | |
| 0.9992 | 0.0380 | 0.0090 | 0.0005 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, Y.; Wang, C.; Chen, Y.; Liu, P. Improving the Accuracy of Fault Frequency by Means of Local Mean Decomposition and Ratio Correction Method for Rolling Bearing Failure. Appl. Sci. 2019, 9, 1888. https://doi.org/10.3390/app9091888
Duan Y, Wang C, Chen Y, Liu P. Improving the Accuracy of Fault Frequency by Means of Local Mean Decomposition and Ratio Correction Method for Rolling Bearing Failure. Applied Sciences. 2019; 9(9):1888. https://doi.org/10.3390/app9091888
Chicago/Turabian StyleDuan, Yongqiang, Chengdong Wang, Yong Chen, and Peisen Liu. 2019. "Improving the Accuracy of Fault Frequency by Means of Local Mean Decomposition and Ratio Correction Method for Rolling Bearing Failure" Applied Sciences 9, no. 9: 1888. https://doi.org/10.3390/app9091888
APA StyleDuan, Y., Wang, C., Chen, Y., & Liu, P. (2019). Improving the Accuracy of Fault Frequency by Means of Local Mean Decomposition and Ratio Correction Method for Rolling Bearing Failure. Applied Sciences, 9(9), 1888. https://doi.org/10.3390/app9091888





