Advancement of Individualized Head-Related Transfer Functions (HRTFs) in Perceiving the Spatialization Cues: Case Study for an Integrated HRTF Individualization Method
Abstract
:1. Introduction
2. Database and Characteristics
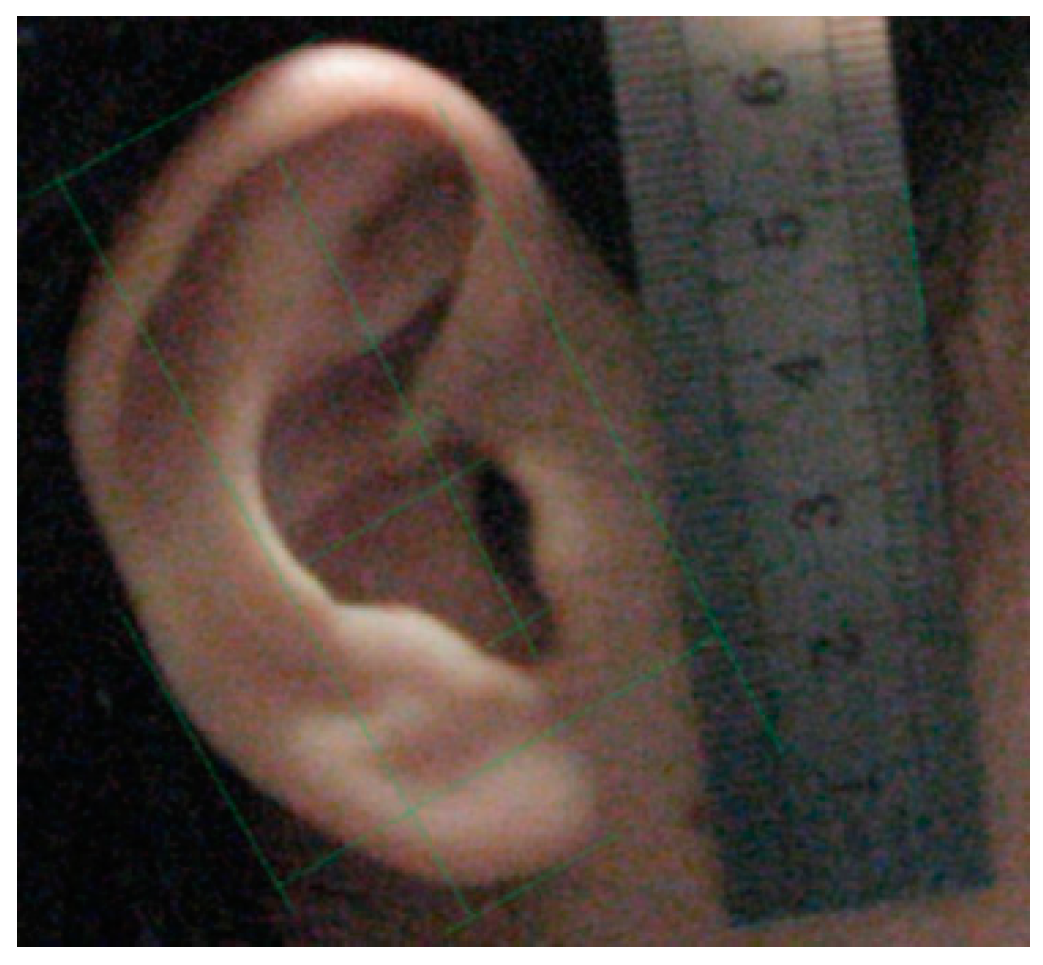
2.1. Database
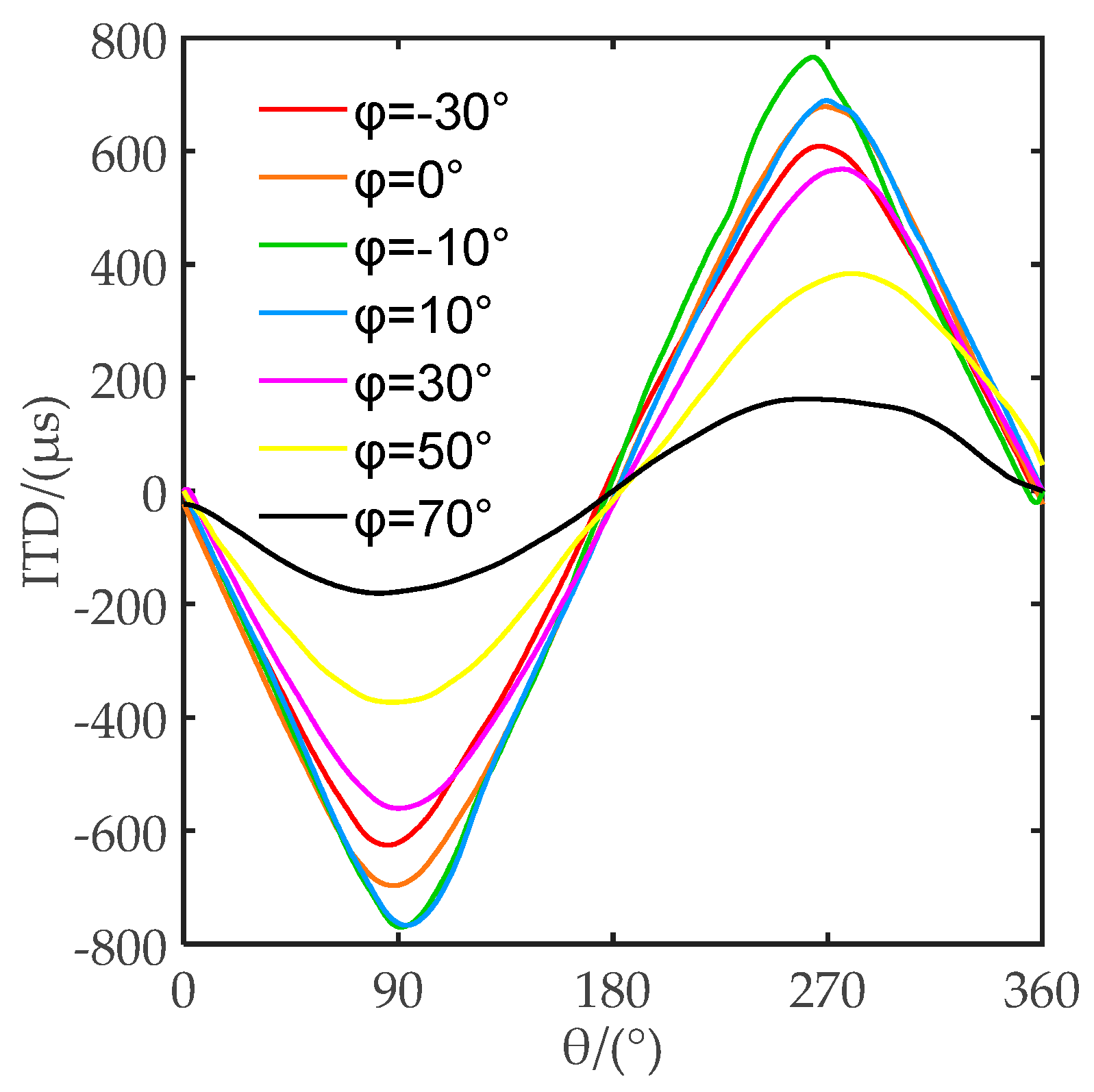
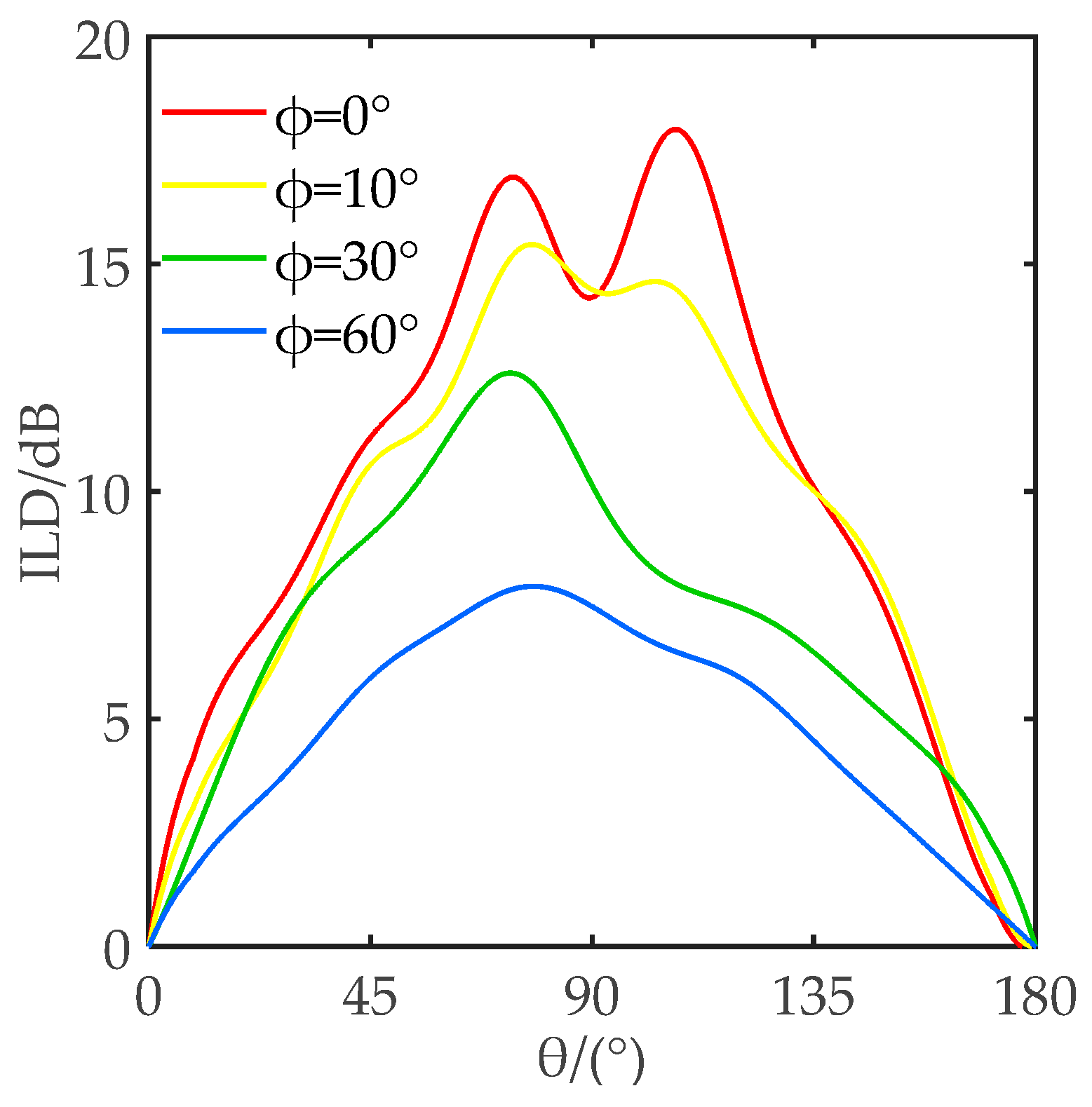
2.2. Characteristics Analysis
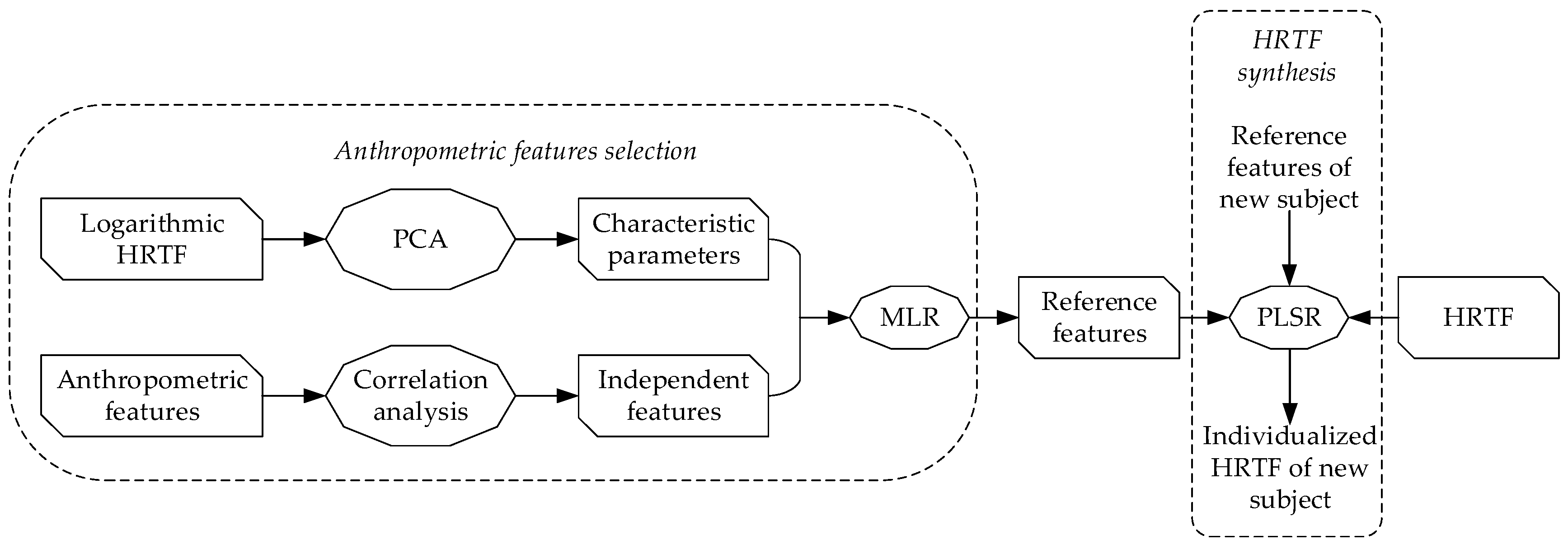
3. Methodology
3.1. Principle Component Analysis for HRTF Characteristics Parameters
3.2. Multiple Linear Regression for Anthropometric Feature Selection
3.3. Partial Least Square Regression for HRTF Synthesis
4. Experimental Investigations
4.1. Objective Experiments
4.1.1. Evaluation Criteria
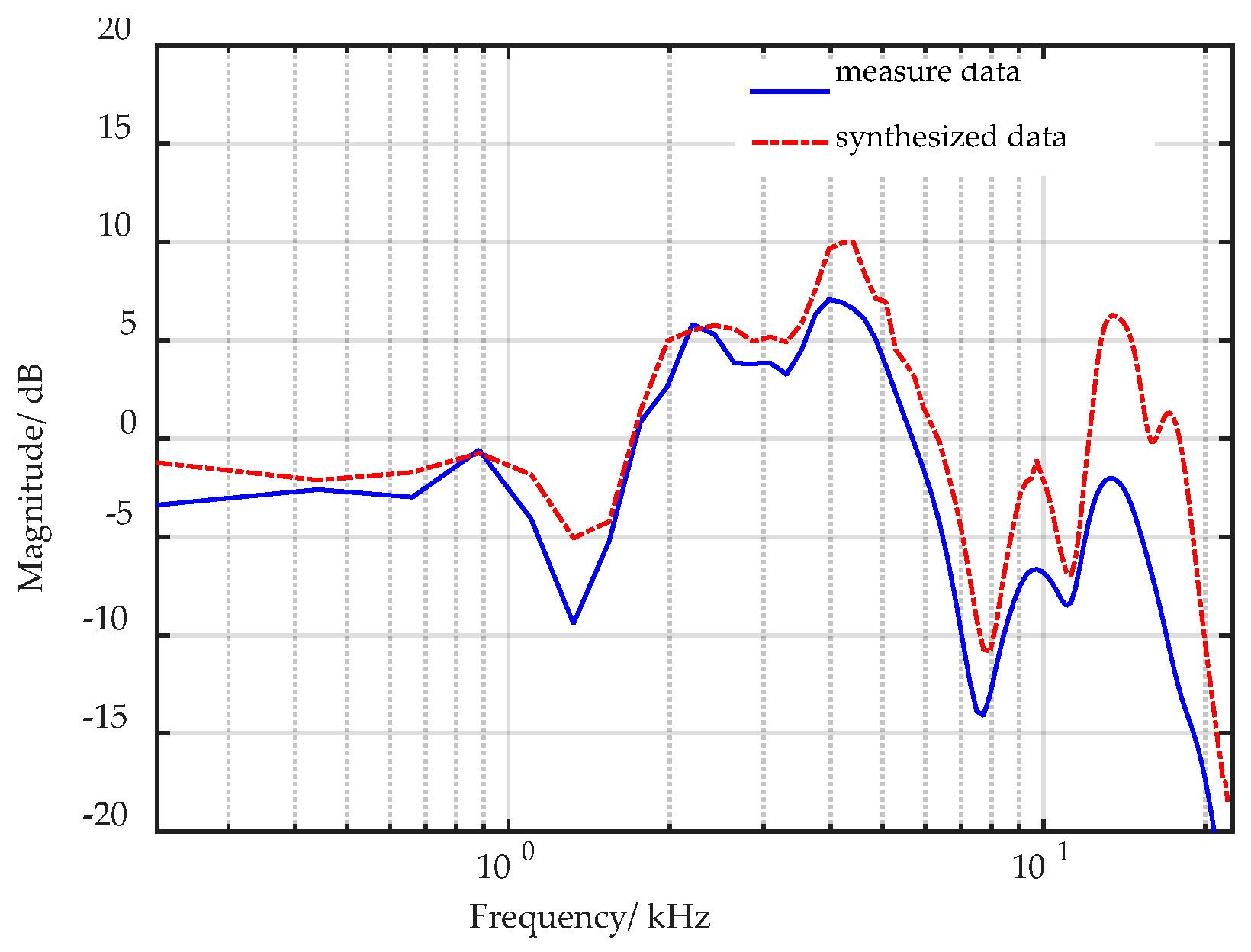
4.1.2. Results
4.2. Subjective Experiments for Discrimination Degree of Given Azimuths
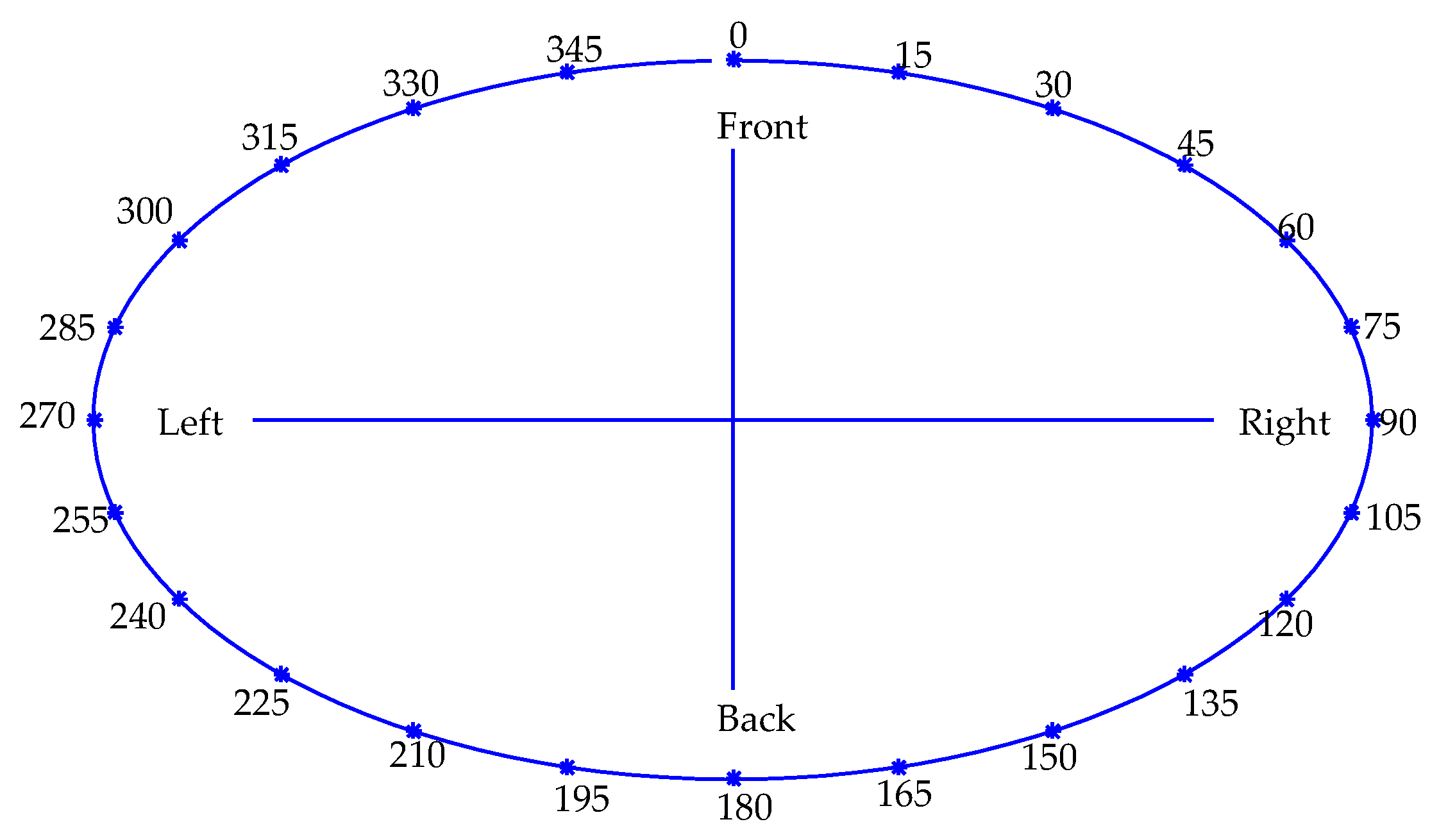
4.2.1. Experimental Protocols
4.2.2. Procedure
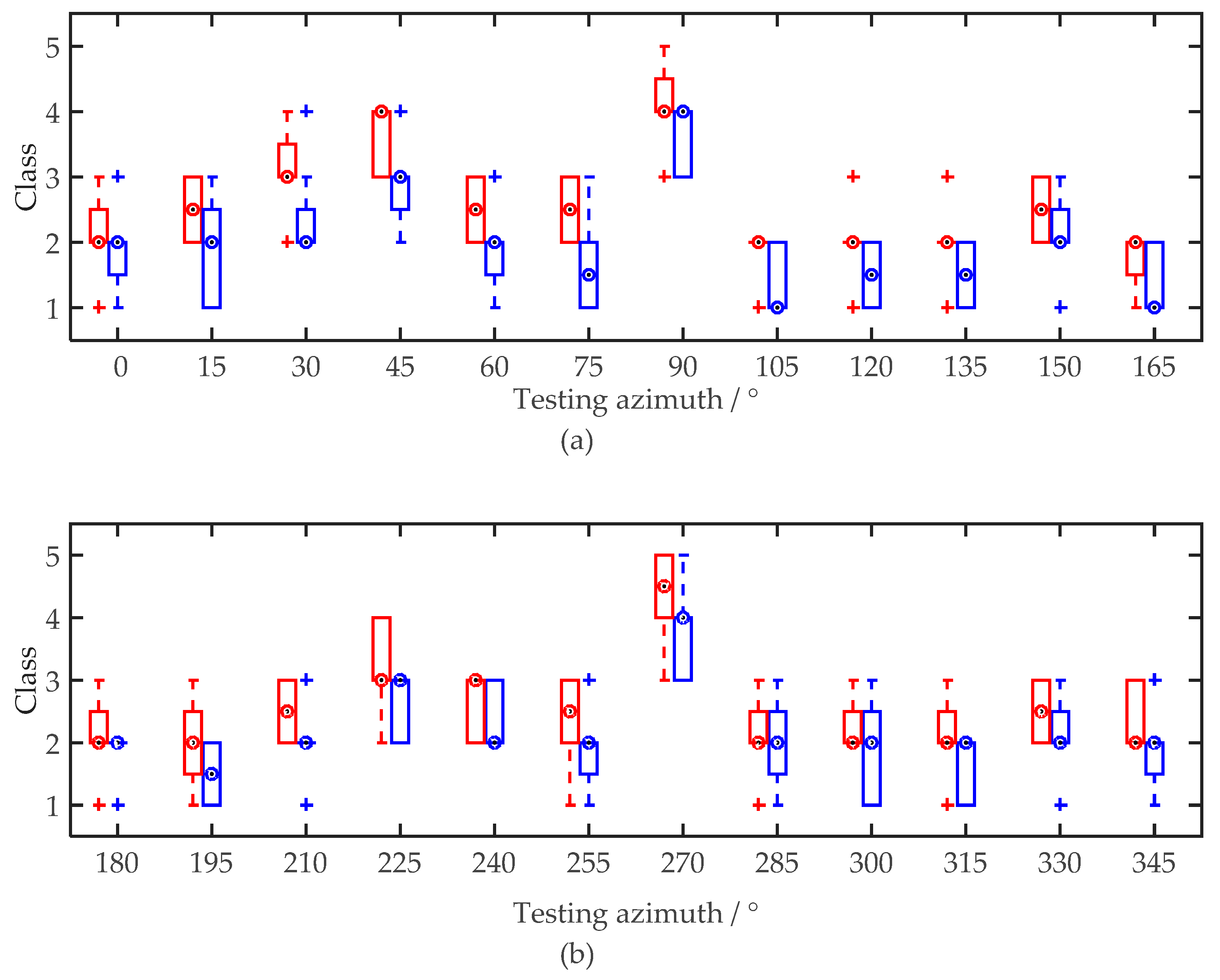
4.2.3. Results and Analysis
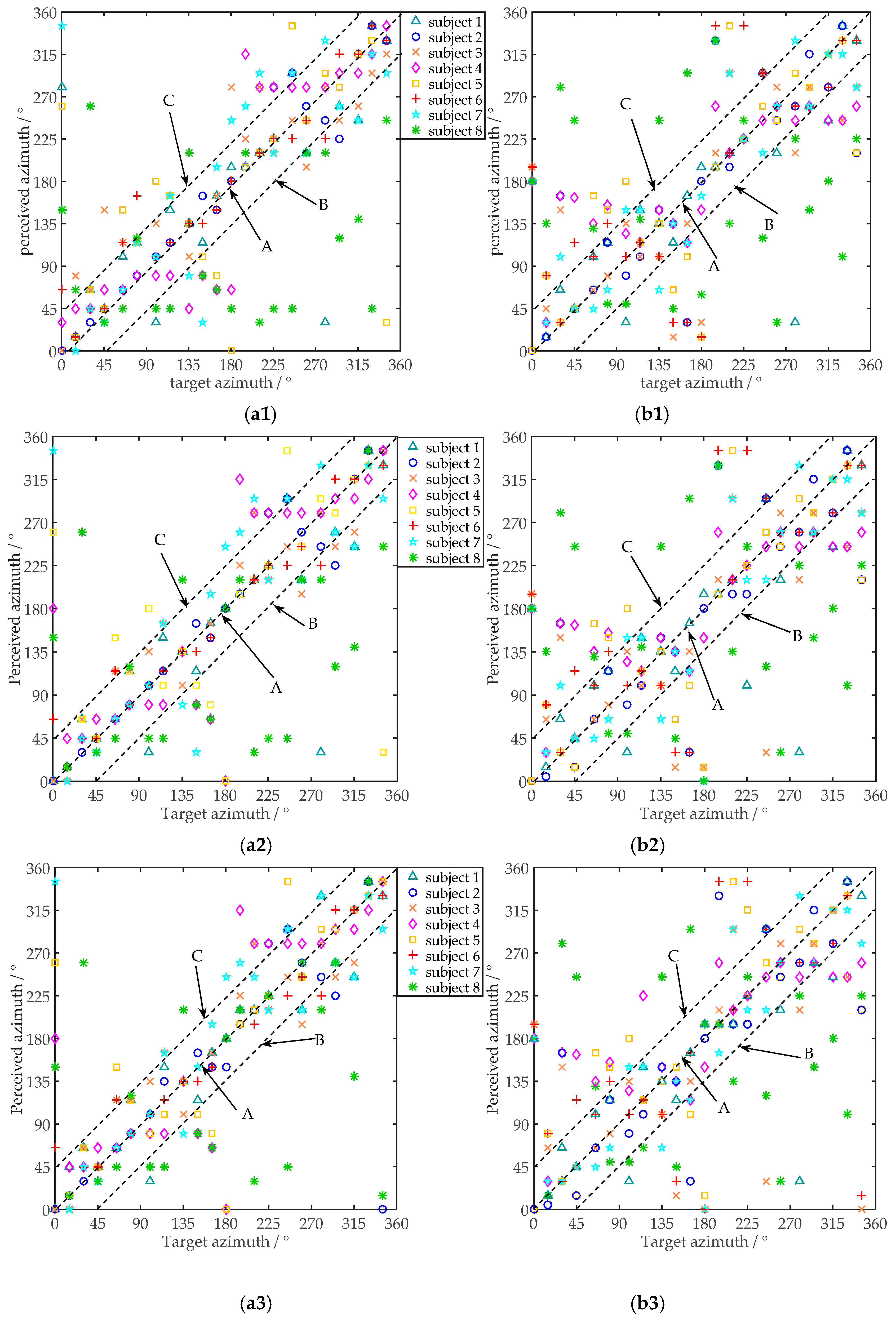
4.3. Subjective Experiment for Auditory Localization
4.3.1. Experimental Protocols
4.3.2. Procedure
4.3.3. Results and Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blauert, J.P. Spatial Hearing; Revised Edition; MIT: Cambridge, MA, USA, 1997. [Google Scholar]
- Algazi, V.R.; Duda, R.O.; Duraiswami, R.; Gumerov, N.A.; Tang, Z. Approximating the head-related transfer function using simple geometric models of the head and torso. J. Acoust. Soc. Am. 2002, 112, 2053–2064. [Google Scholar] [CrossRef] [PubMed]
- Katz, B.F. Boundary element method calculation of individual head-related transfer function. I. Rigid model calculation. J. Acoust. Soc. Am. 2001, 110, 2440–2448. [Google Scholar] [CrossRef] [PubMed]
- Meshram, A.; Mehra, R.; Yang, H.; Dunn, E.; Franm, J.M.; Manocha, D. P-HRTF: Efficient personalized HRTF computation for high-fidelity spatial sound. In Proceedings of the IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Munich, Germany, 10–12 September 2014. [Google Scholar]
- Zeng, X.Y. Customization Methods of Head-related Transfer Function. Audio Eng. 2007, 31, 41–46. [Google Scholar] [CrossRef]
- Zotkin, D.N.; Hwang, J.; Duraiswami, R.; Davis, L.S. HRTF personalization using anthropometric measurements. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 19‒22 October 2003; pp. 157–160. [Google Scholar] [CrossRef]
- Zeng, X.Y.; Wang, S.G.; Gao, L.P. A hybrid algorithm for selecting head-related transfer function based on similarity of anthropometric structures. J. Sound Vib. 2010, 329, 4093–4106. [Google Scholar] [CrossRef]
- Andreopoulou, A.; Roginska, A. Database Matching of Sparsely Measured Head-Related Transfer Functions. J. Audio Eng. Soc. 2017, 65, 552–561. [Google Scholar] [CrossRef]
- Nishino, T.; Inoue, N.; Takeda, K.; Itakura, F. Estimation of HRTFs on the horizontal plane using physical features. J. Acoust. Soc. Am. 2007, 68, 897–908. [Google Scholar] [CrossRef]
- Tang, Y.; Fang, Y.; Huang, Q. Audio personalization using head related transfer function in 3DTV. In Proceedings of the 3dtv Conference: The True Vision-Capture, Antalya, Turkey, 16–18 May 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Hu, H.; Zhou, L.; Ma, H.; Wu, Z. HRTF personalization based on artificial neural network in individual virtual auditory space. J. Appl. Acoust. 2008, 69, 163–172. [Google Scholar] [CrossRef]
- Bilinski, P.T.; Ahrens, J.; Thomas, M.R.; Tashev, I.; Platt, J. HRTF magnitude synthesis via sparse representation of anthropometric features. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 4468–4472. [Google Scholar] [CrossRef]
- Tashev, I. HRTF phase synthesis via sparse representation of anthropometric features. In Proceedings of the Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 9–14 February 2014; pp. 1–5. [Google Scholar] [CrossRef]
- He, J.; Gan, W.; Tan, E. On the preprocessing and postprocessing of HRTF individualization based on sparse representation of anthropometric features. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 639–643. [Google Scholar]
- Zhu, M.; Shahnawaz, M.; Tubaro, S.; Sarti, A. HRTF personalization based on weighted sparse representation of anthropometric features. In Proceedings of the International Conference on 3D Immersion (IC3D), Brussels, Belgium, 11–12 December 2017. [Google Scholar] [CrossRef]
- Spagnol, S.; Geronazzo, M.; Avanzini, F. On the relation between pinna reflection patterns and head-related transfer function features. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 508–519. [Google Scholar] [CrossRef]
- Hugeng, W.W.; Dadang, G. Improved Method for individualization of Head-Related Transfer Functions on Horizontal Plane Using Reduced Number of Anthropometric Measurements. J. Telecommun. 2010, 2, 31–41. [Google Scholar]
- Xie, B.S.; Zhong, X.L.; Rao, D. Head-Related transfer function database and its analysis. Sci. China Ser. G Phys. Mech. Astron. 2007, 50, 267–280. [Google Scholar] [CrossRef]
- Gardner, W.G. 3-D Audio Using Loudspeakers. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1997. [Google Scholar]
- Martens, W.L. Principal components analysis and resynthesis of spectral cues to perceived direction. In Proceedings of the 1987 International Computer Music Conference, San Francisco, CA, USA, 1987; pp. 274–281. [Google Scholar]
- Kistler, D.J.; Wightman, F.L. A model of head-related transfer functions based on principal components analysis and minimum-phase reconstruction. J. Acoust. Soc. Am. 1992, 91, 1637–1647. [Google Scholar] [CrossRef] [PubMed]
- Middlebrooks, J.C.; Green, D.M. Observations on a principal components analysis of head-related transfer functions. J. Acoust. Soc. Am. 1992, 92, 597–599. [Google Scholar] [CrossRef] [PubMed]
- Hoskuldsson, A. PLS regression methods. J. Chemom. 1988, 2, 211–228. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Wang, L.; Zeng, X.Y. New method for synthesizing personalized Head-Related Transfer Function. In Proceedings of the IEEE International Workshop on Acoustic Signal Enhancement (IWAENC), Xi’an, China, 13–16 September 2016. [Google Scholar]
- Huang, H.B.; Huang, X.R.; Li, R.X.; Lim, T.C.; Ding, W.P. Sound quality prediction of vehicle interior noise using deep belief networks. Appl. Acoust. 2016, 113, 149–161. [Google Scholar] [CrossRef]
- Wang, Y.S.; Shen, G.Q.; Xing, Y.F. A sound quality model for objective synthesis evaluation of vehicle interior noise based on artificial neural network. Mech. Syst. Signal Process. 2014, 45, 255–266. [Google Scholar] [CrossRef]
- Han, L.; Kean, C.; Xue, W.; Yan, G.; Weiwei, Y. A perceptual dissimilarities based nonlinear sound quality model for range hood noise. J. Acoust. Soc. Am. 2018, 144, 2300–2311. [Google Scholar] [CrossRef]




| Elevation (ϕ) | Interval of Azimuth | Measured Direction Number |
|---|---|---|
| 0 ° | 5° | 73 |
| ±10° | 5° | 73 |
| ±20° | 5° | 73 |
| ±30° | 6° | 61 |
| ±40° | 6° and 7° by turn | 57 |
| 50° | 8° | 47 |
| 60° | 10° | 37 |
| 70° | 15° | 25 |
| 80° | 30° | 13 |
| Processing Procedure | Anthropometric Features Retained |
|---|---|
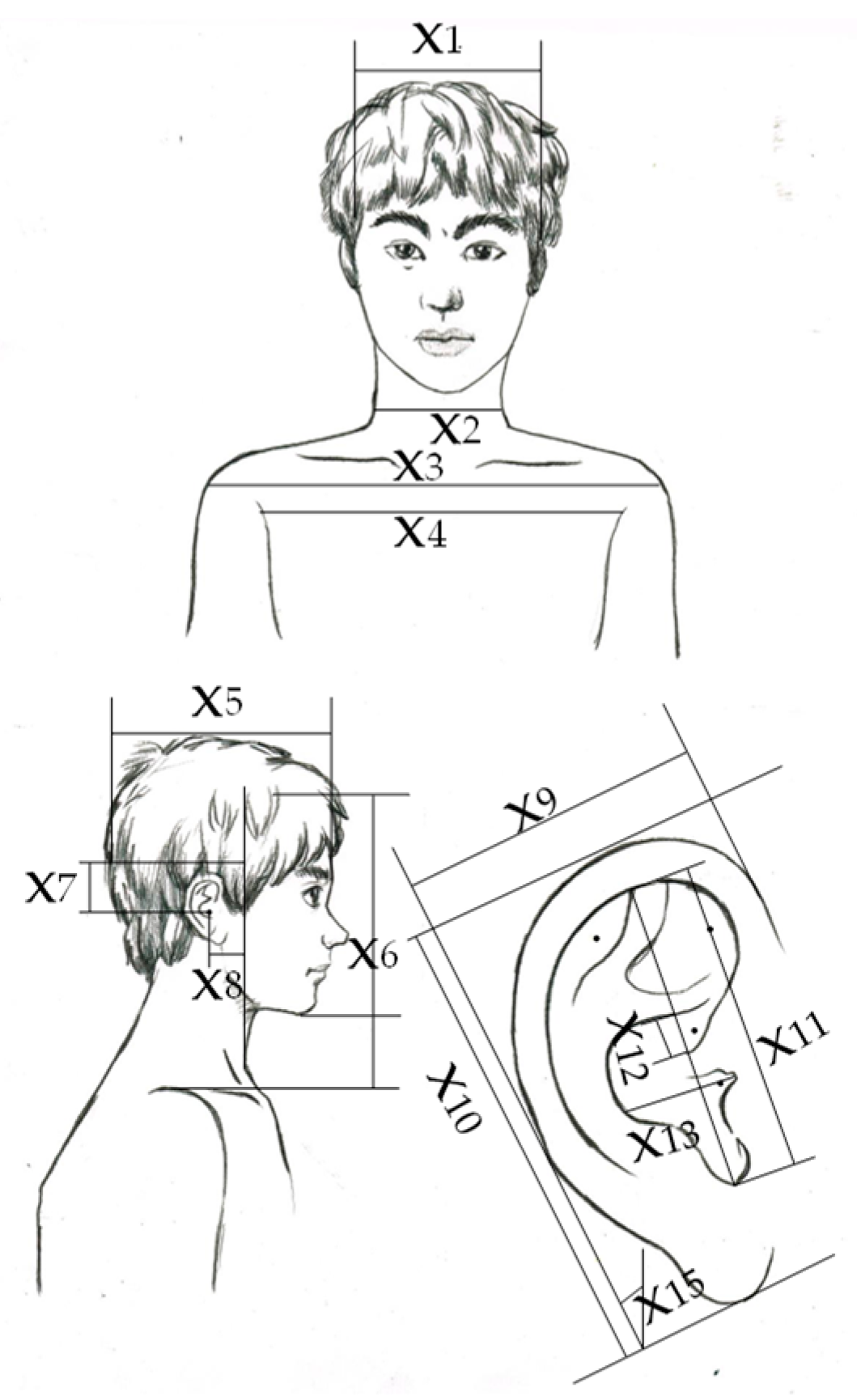
| Correlation analysis between different anthropometric parameters | x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12, x13, x14, x15 |
| Correlation analysis between weight vector and remaining anthropometric parameters | x1, x2, x3, x4, x5, x6, x7, x8, x10, x12, x13, x14 |
| Multiple linear regression | x1, x2, x3, x4, x5, x6, x7, x8, x10, x12, x14 |
| Individualization Method | Left Ear | Right Ear | Average |
|---|---|---|---|
| Proposed method | 7.2537 | 6.9303 | 7.0920 |
| GRNN based method | 7.7385 | 7.1026 | 7.4206 |
| Database-matching method | 7.8314 | 8.2359 | 8.0337 |
| Discrimination Degree | Unconspicuous | Detectable | Obvious | Very Obvious | Extremely Obvious |
|---|---|---|---|---|---|
| Class | 1 | 2 | 3 | 4 | 5 |
| Item | HRTF Species | Azimuth | Interaction |
|---|---|---|---|
| F | 62.7302 | 18.3263 | 0.3395 |
| p | 0 | 0 | 0.9984 |
| H0 | Rejected | Rejected | Kept |
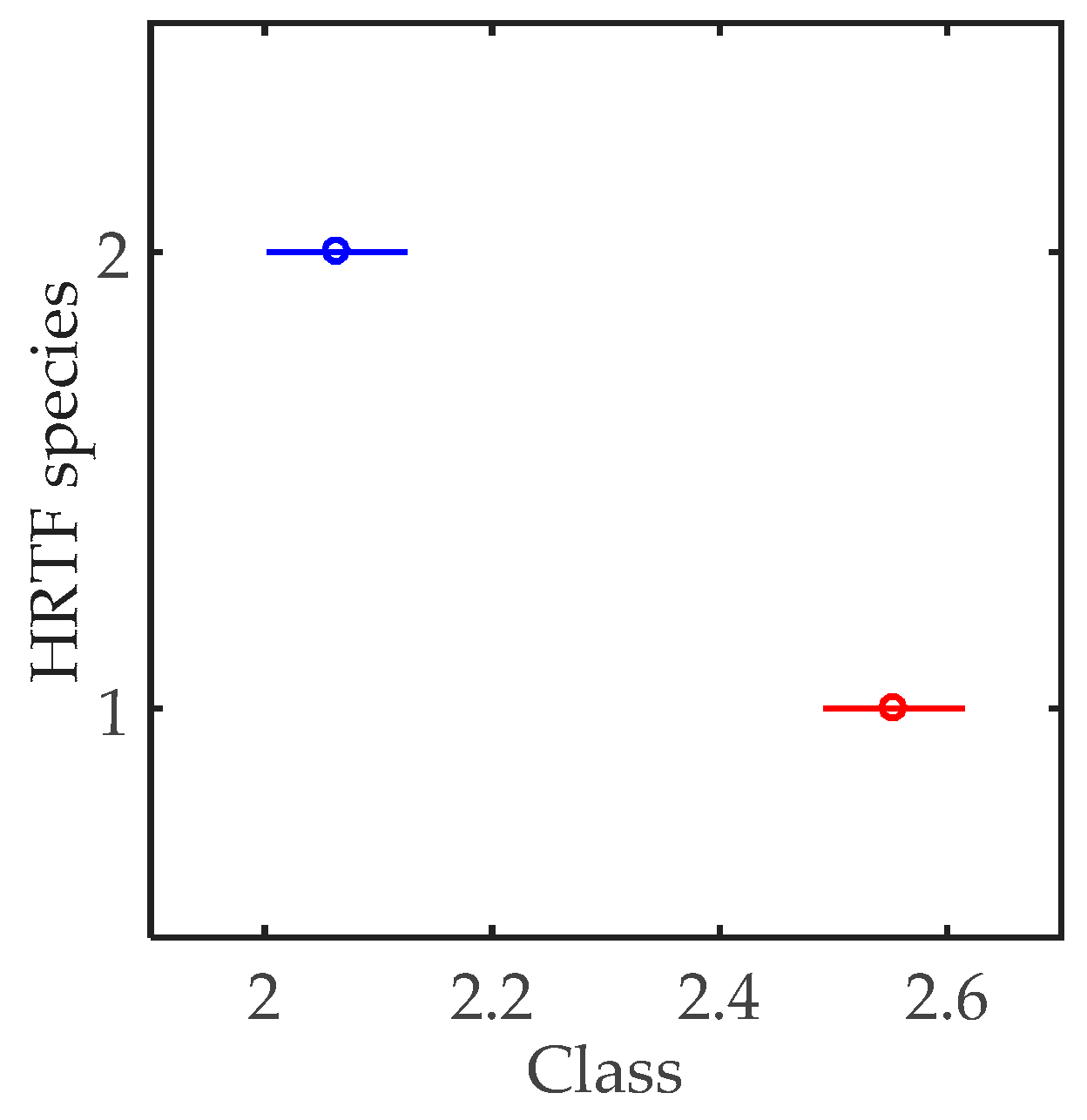
| p | H0 | Mean_ind | Mean_non |
|---|---|---|---|
| 0 | Rejected | 2.5521 | 2.0625 |
| HRTF Species | Item | Subject 1 | Subject 2 | Subject 3 | Subject 4 | Subject 5 | Subject 6 | Subject 7 | Subject 8 |
|---|---|---|---|---|---|---|---|---|---|
| Individualized HRTF | Accuracy rate/(%) | 39.3 | 62.1 | 30.3 | 25.8 | 39.4 | 42.4 | 16.7 | 12.1 |
| Average error/(°) | 26.97 | 12.80 | 32.58 | 42.88 | 37.88 | 15.83 | 28.71 | 81.71 | |
| Standard deviation/(°) | 30.86 | 20.97 | 29.79 | 38.56 | 47.51 | 23.98 | 29.59 | 56.55 | |
| General HRTF | Accuracy rate/(%) | 28.8 | 18.2 | 24.2 | 21.2 | 37.9 | 28.2 | 16.7 | 3.0 |
| Average error/(°) | 37.8 | 38.94 | 53.94 | 51.80 | 44.62 | 56.21 | 46.21 | 80.76 | |
| Standard deviation/(°) | 43.27 | 49.08 | 50.96 | 49.04 | 53.30 | 57.23 | 45.31 | 52.16 |
| Item | HRTF Species | Azimuth | Interaction |
|---|---|---|---|
| F | 41.4313 | 7.4317 | 2.6415 |
| p | 0 | 0 | 0 |
| H0 | Rejected | Rejected | Rejected |
| p | H0 | Mean_ind | Mean_non |
|---|---|---|---|
| 0 | Rejected | 35.9091 | 53.7860 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zeng, X.; Ma, X. Advancement of Individualized Head-Related Transfer Functions (HRTFs) in Perceiving the Spatialization Cues: Case Study for an Integrated HRTF Individualization Method. Appl. Sci. 2019, 9, 1867. https://doi.org/10.3390/app9091867
Wang L, Zeng X, Ma X. Advancement of Individualized Head-Related Transfer Functions (HRTFs) in Perceiving the Spatialization Cues: Case Study for an Integrated HRTF Individualization Method. Applied Sciences. 2019; 9(9):1867. https://doi.org/10.3390/app9091867
Chicago/Turabian StyleWang, Lei, Xiangyang Zeng, and Xiyue Ma. 2019. "Advancement of Individualized Head-Related Transfer Functions (HRTFs) in Perceiving the Spatialization Cues: Case Study for an Integrated HRTF Individualization Method" Applied Sciences 9, no. 9: 1867. https://doi.org/10.3390/app9091867
APA StyleWang, L., Zeng, X., & Ma, X. (2019). Advancement of Individualized Head-Related Transfer Functions (HRTFs) in Perceiving the Spatialization Cues: Case Study for an Integrated HRTF Individualization Method. Applied Sciences, 9(9), 1867. https://doi.org/10.3390/app9091867




