Influence of Shield Attitude Change on Shield–Soil Interaction
Abstract
Featured Application
Abstract
1. Introduction
2. Methodology
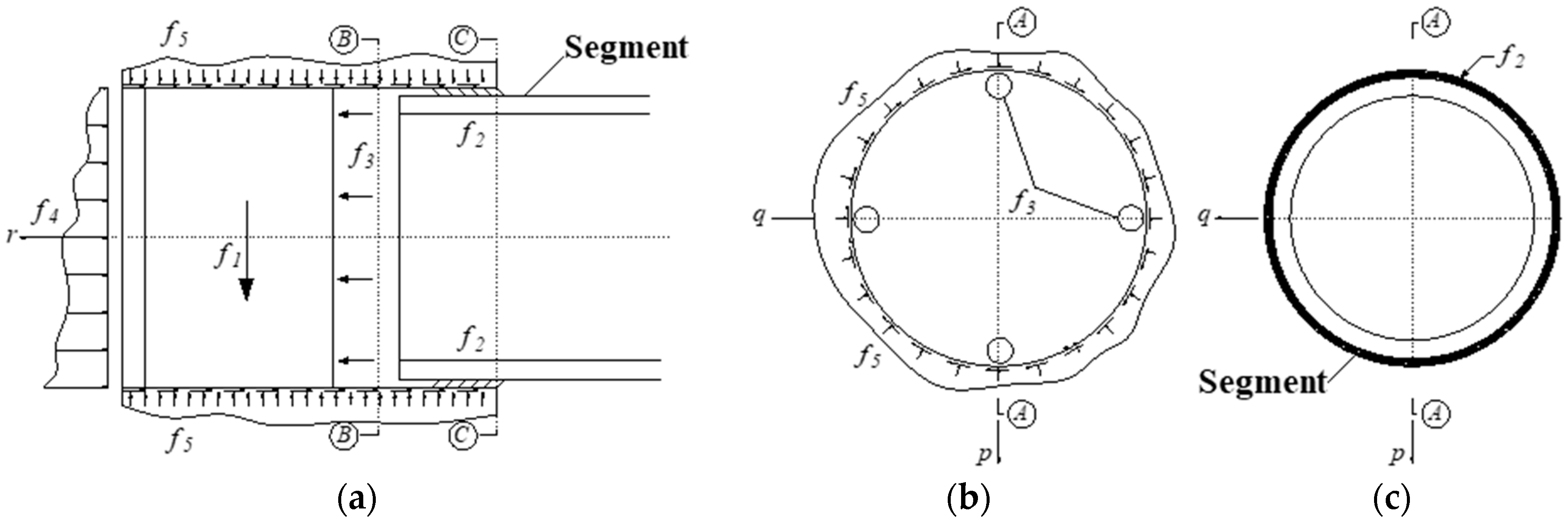
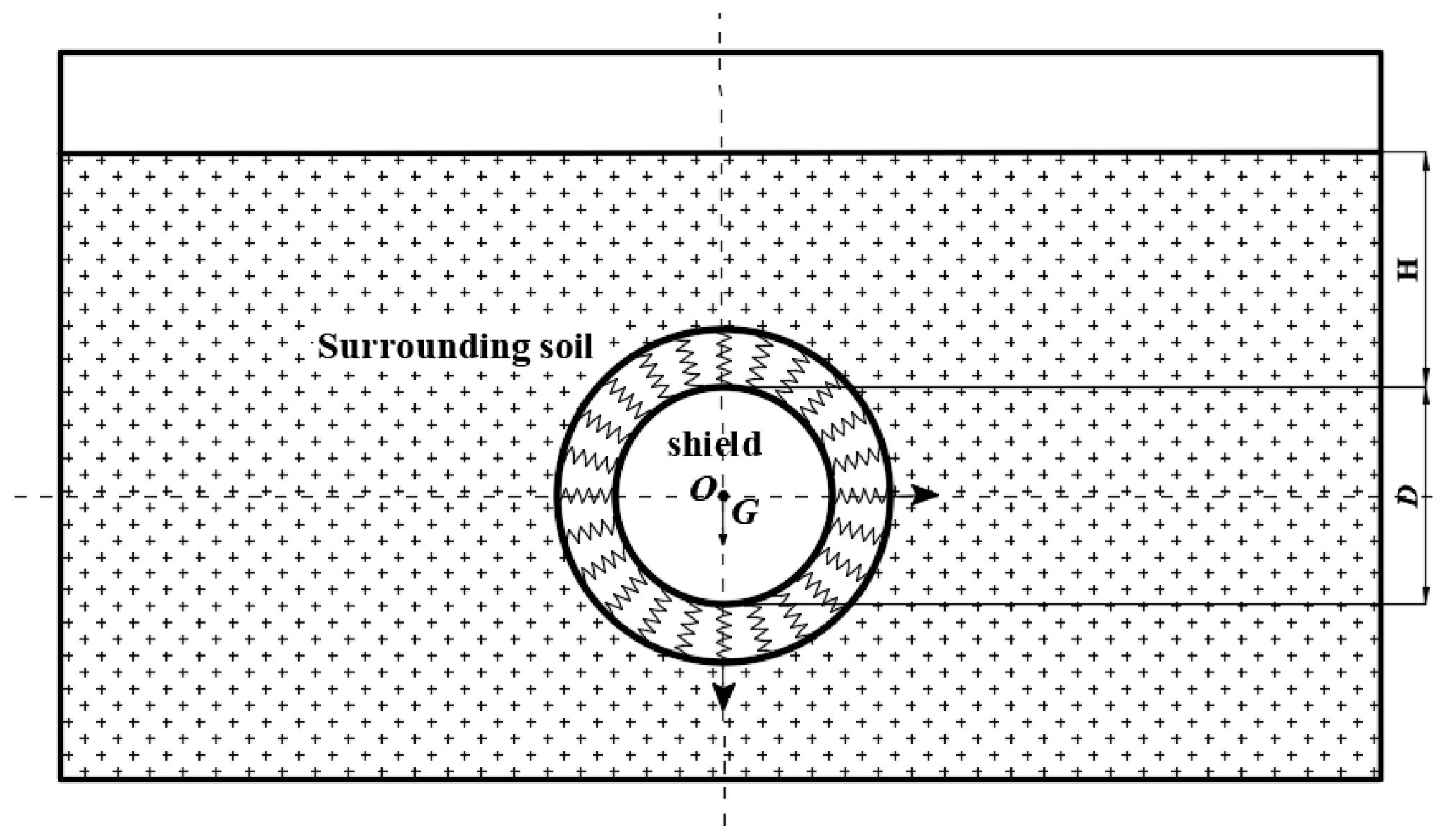
2.1. Model of Load Acting on Shield
2.2. Initial Earth Pressure Calculation
2.2.1. Calculation of Loose Soil Pressure in the Overlaying Soil
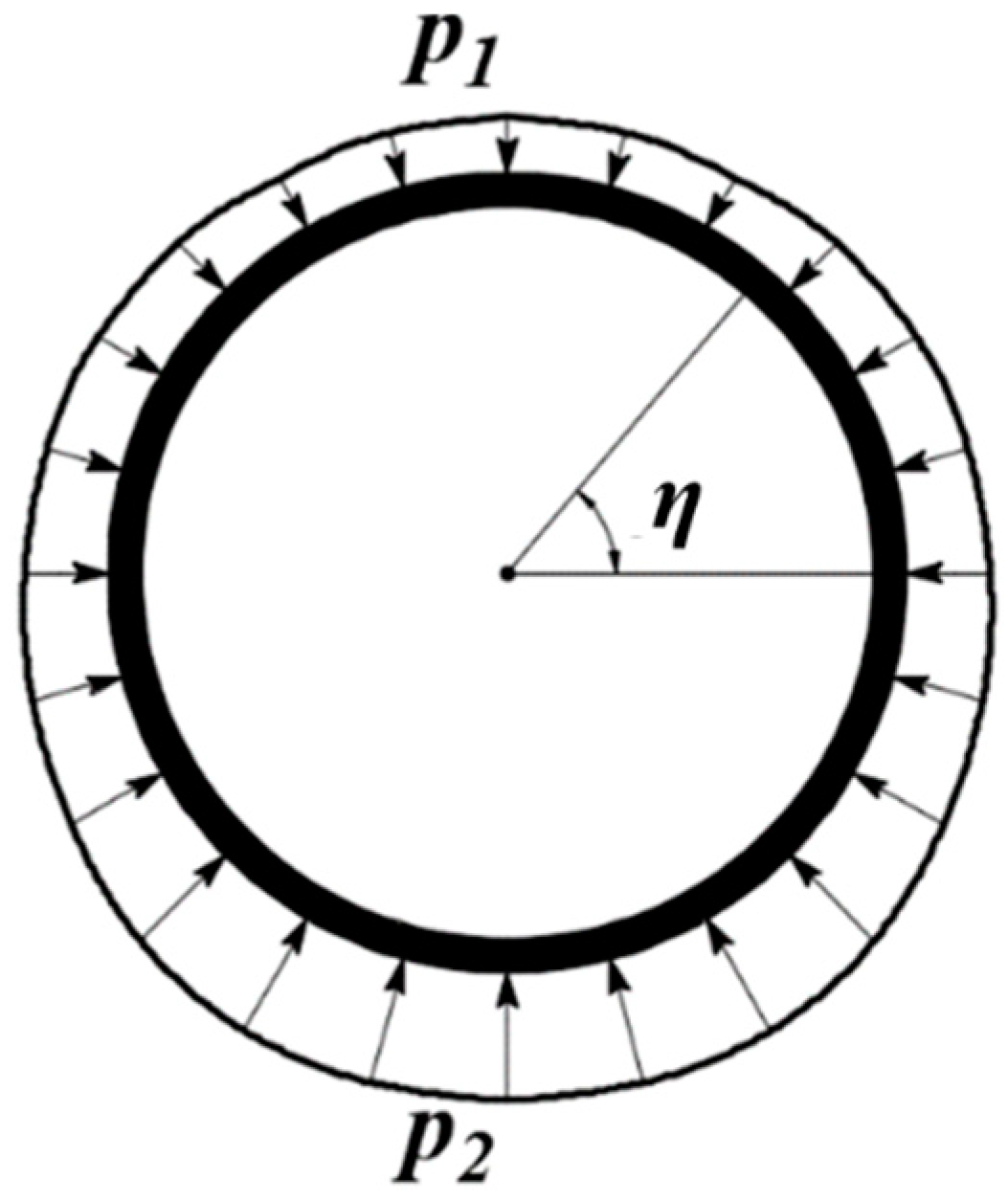
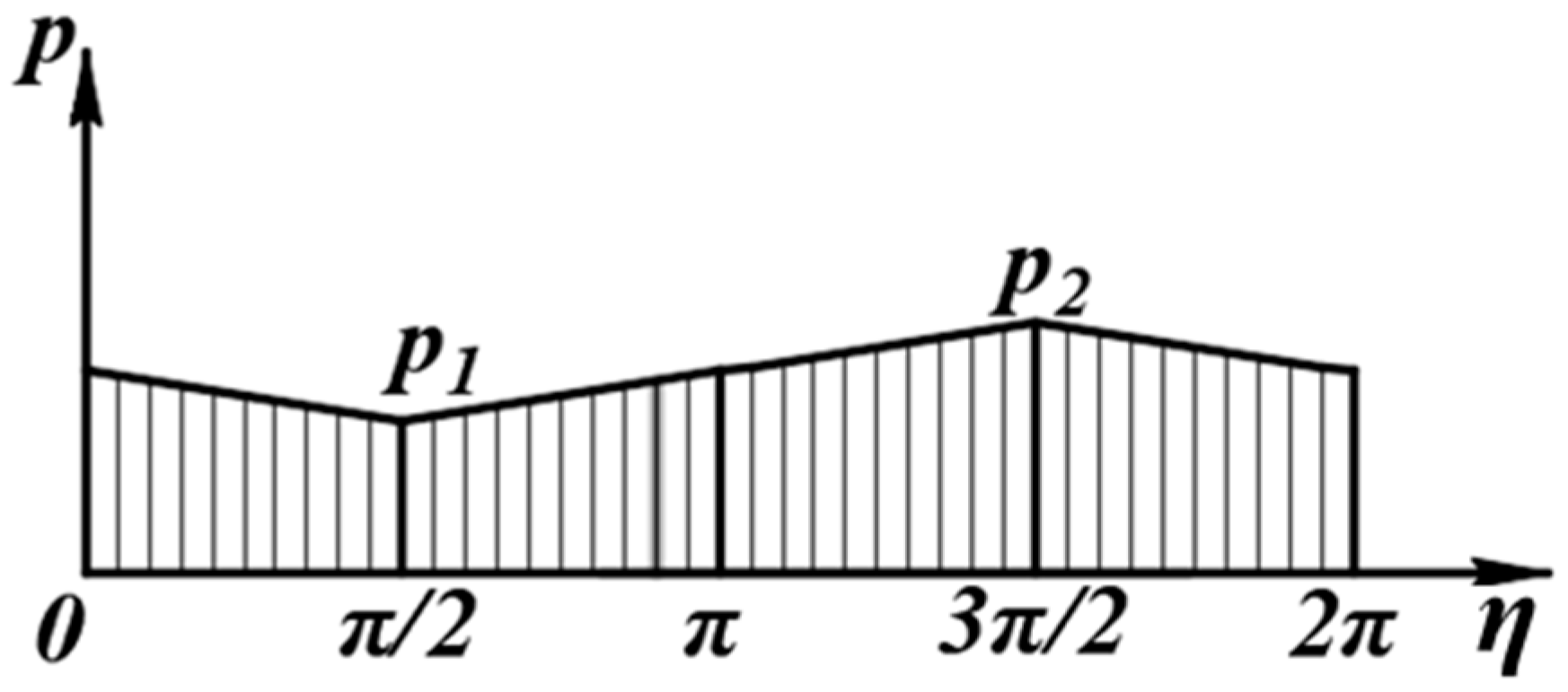
2.2.2. Initial Force Acting on the Shield Periphery
2.3. Shield Shell–Soil Interaction Model
2.3.1. Basic Assumption
- (i)
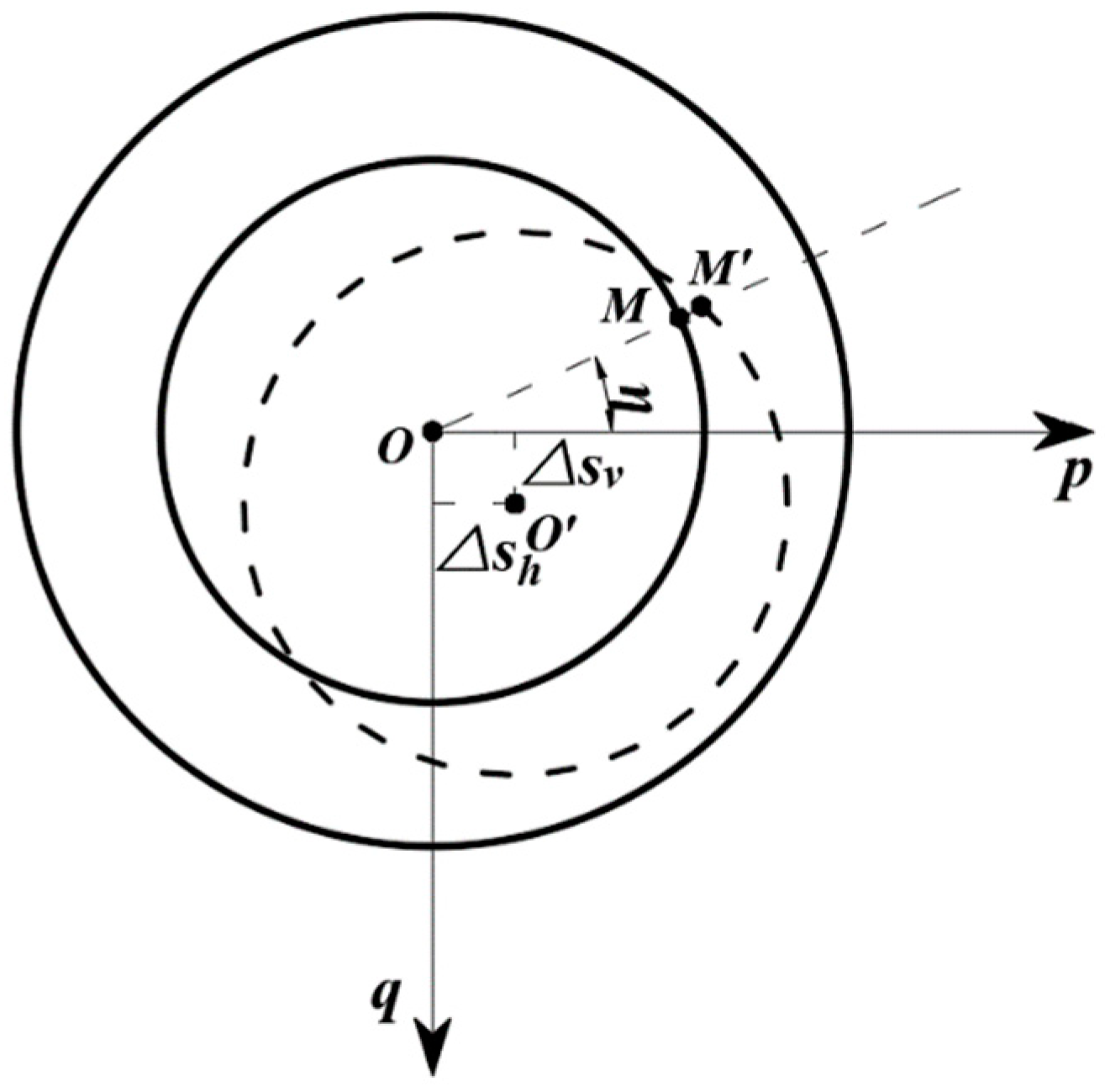
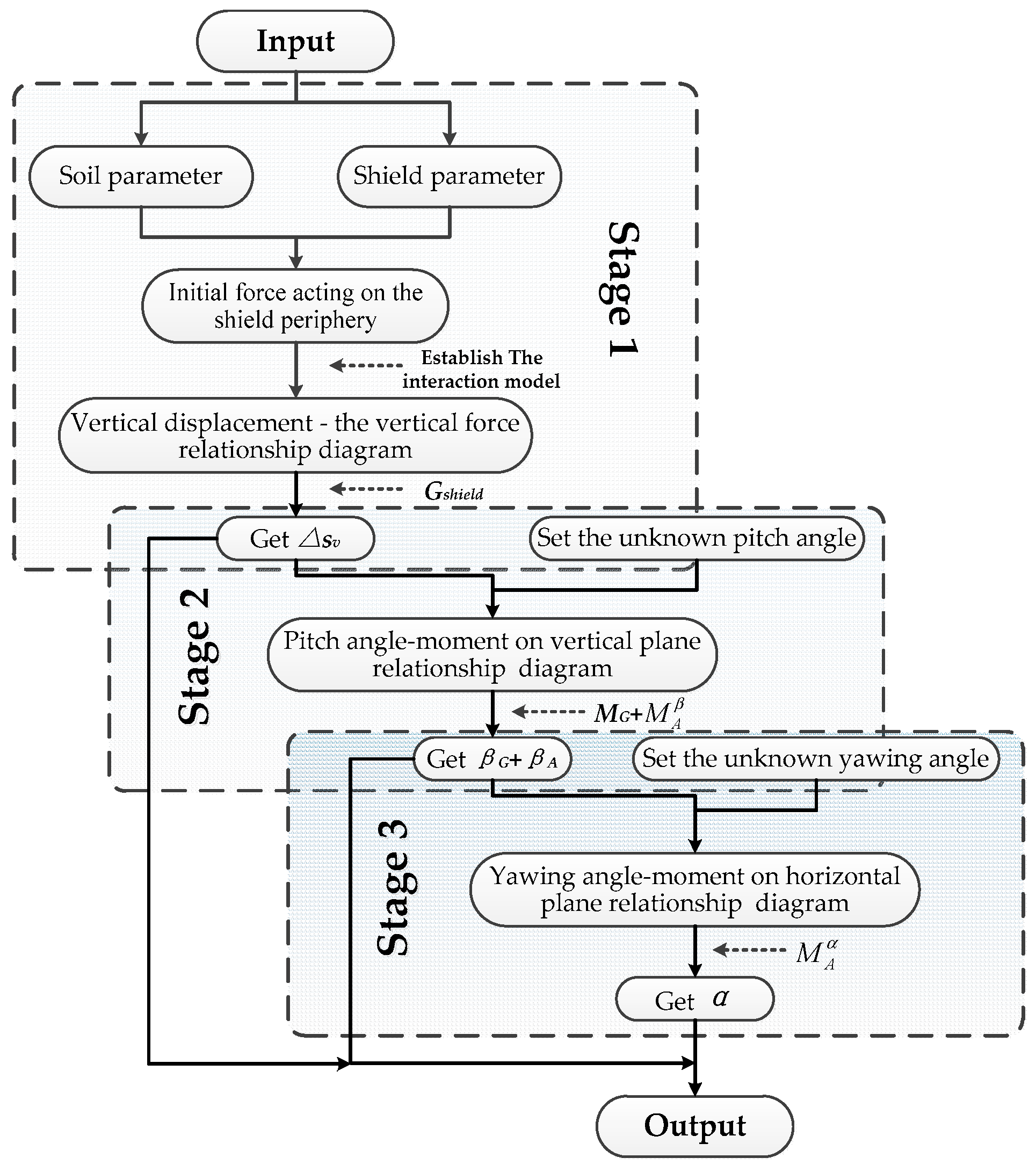
- Stage 1: Gravity stage. The point of gravity action is moved to the geometric centroid while the gravity eccentric moment MG is generated, and only gravity is considered at this stage. Under the action of gravity, the shield machine produces a displacement of Δsv in the vertical direction, and Δsv is positive downward and negative upward, as shown in Figure 7b.
- (ii)
- Stage 2: Gravity eccentric moment stage. The shield deflects due to gravity eccentric bending moment on the vertical plane. The pitch angle caused by the MG is called βG, as shown in Figure 7c. The angle is positive when its direction is counterclockwise, and the angle is negative when its direction is clockwise.
- (iii)
- Stage 3: Vertical bending moment stage. Upper and lower partition jacks produce deflection moments on the vertical plane. The pitch angle caused by the is called βA, as shown in Figure 7c. The angle is positive when its direction is counterclockwise, and the angle is negative when its direction is clockwise.
- (iv)
- Stage 4: Horizontal bending moment stage. Under the action of horizontal deflection bending moment , α which is called yawing angle is generated on the horizontal plane, as shown in Figure 7d. α is positive when its direction is counterclockwise and negative when its direction is clockwise.
2.3.2. Geometric Parameters
2.3.3. Solution of Vertical and Horizontal Forces of Shield–Soil Interaction
2.3.4. Solution of Bending Moment of Shield–Soil Interaction
3. Shield Pitch Angle and Yawing Angle Calculation Method
3.1. Solution Process of Yawing Angle and Pitch Angle
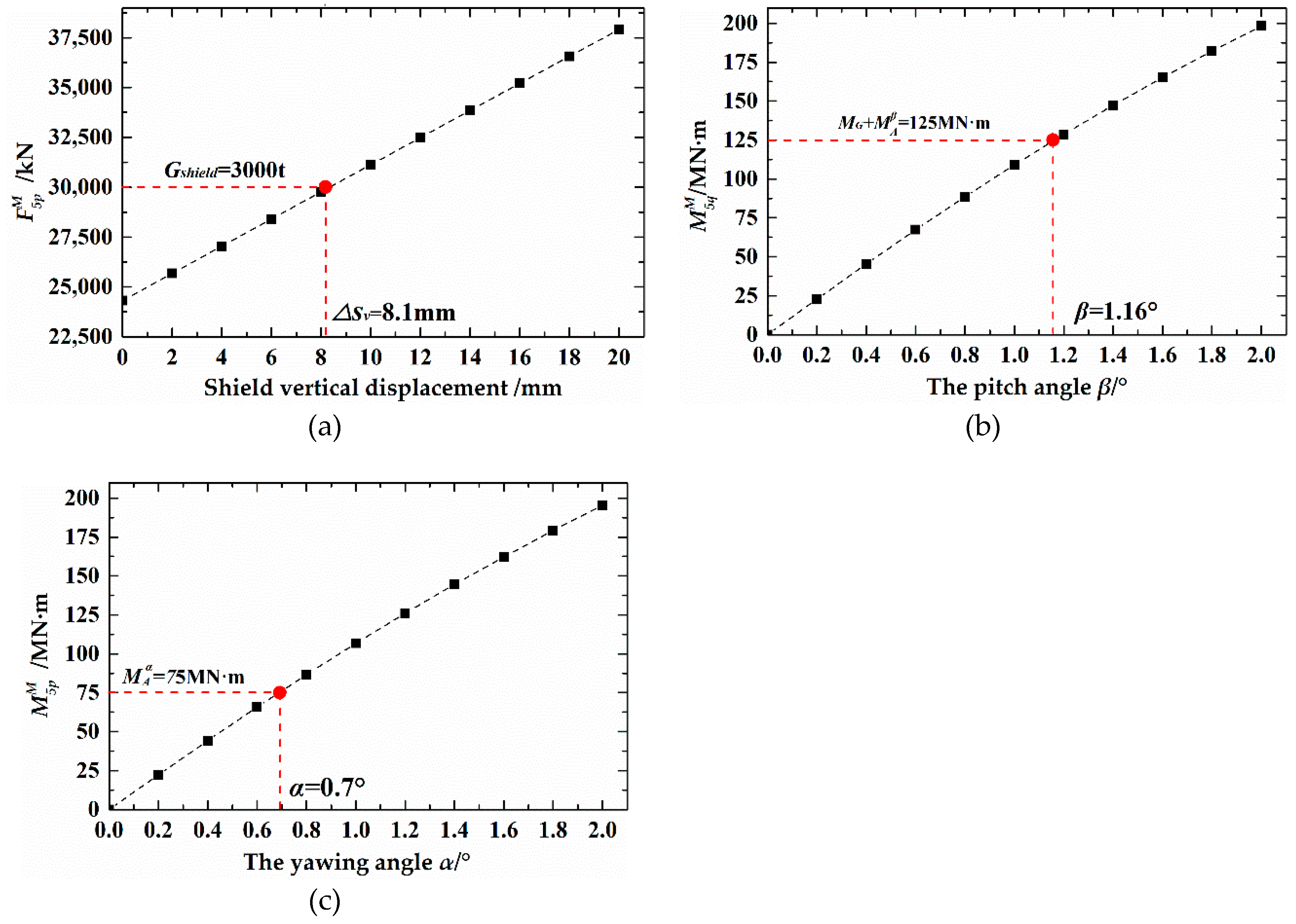
3.2. Calculation Example
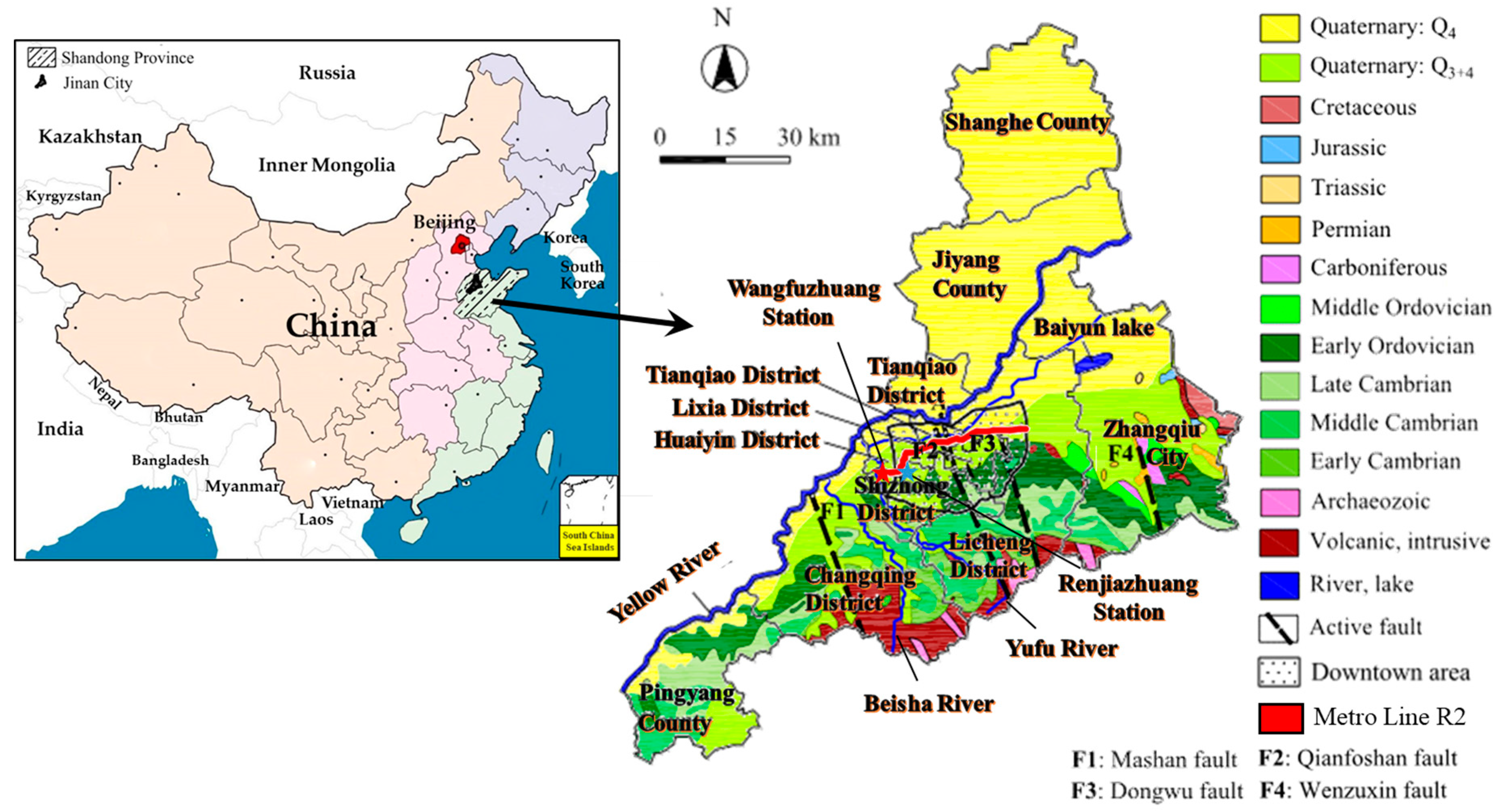
4. Application Engineering
4.1. Engineering Details
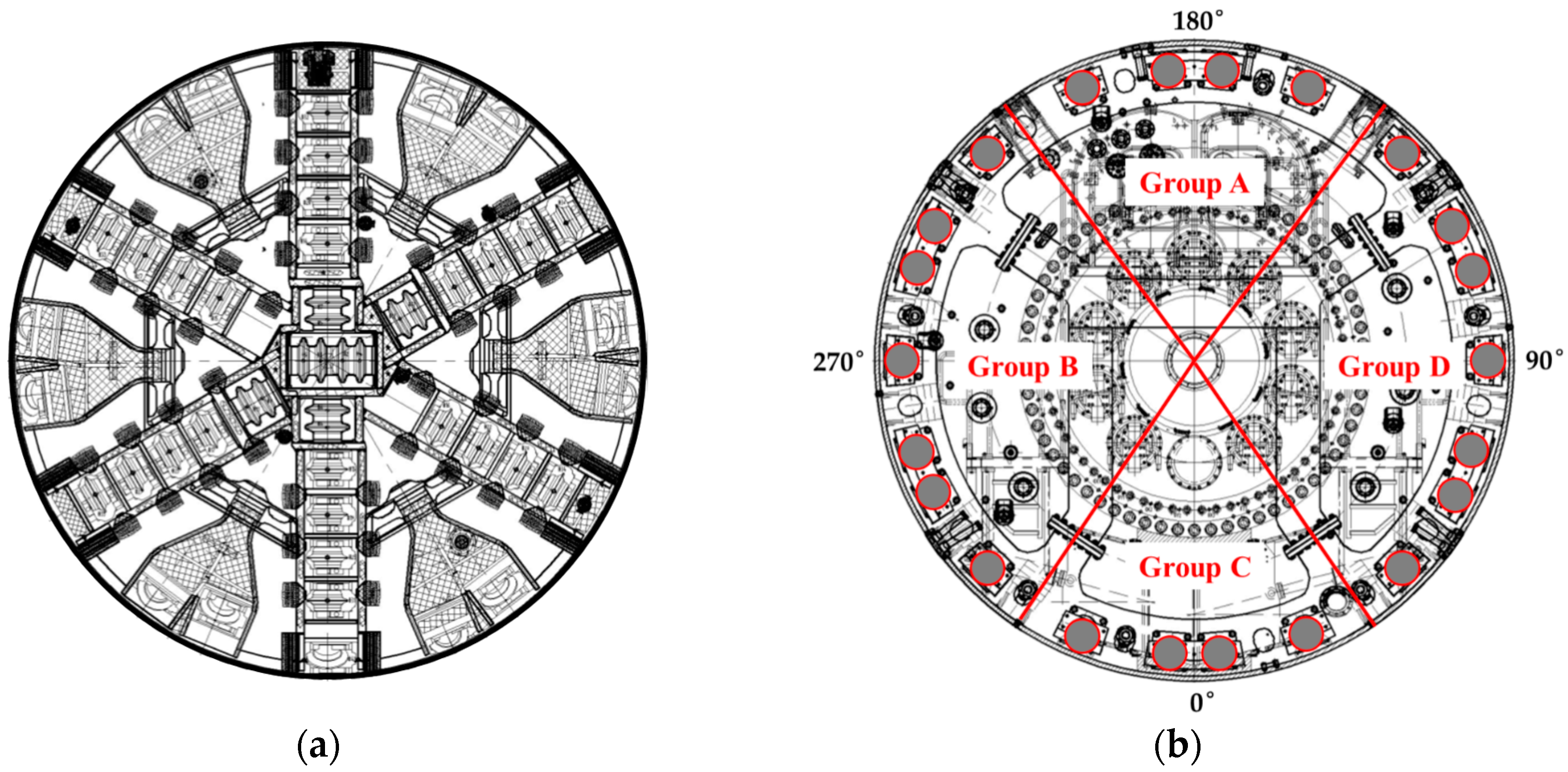
4.2. Shield Details
5. Results and Discussion
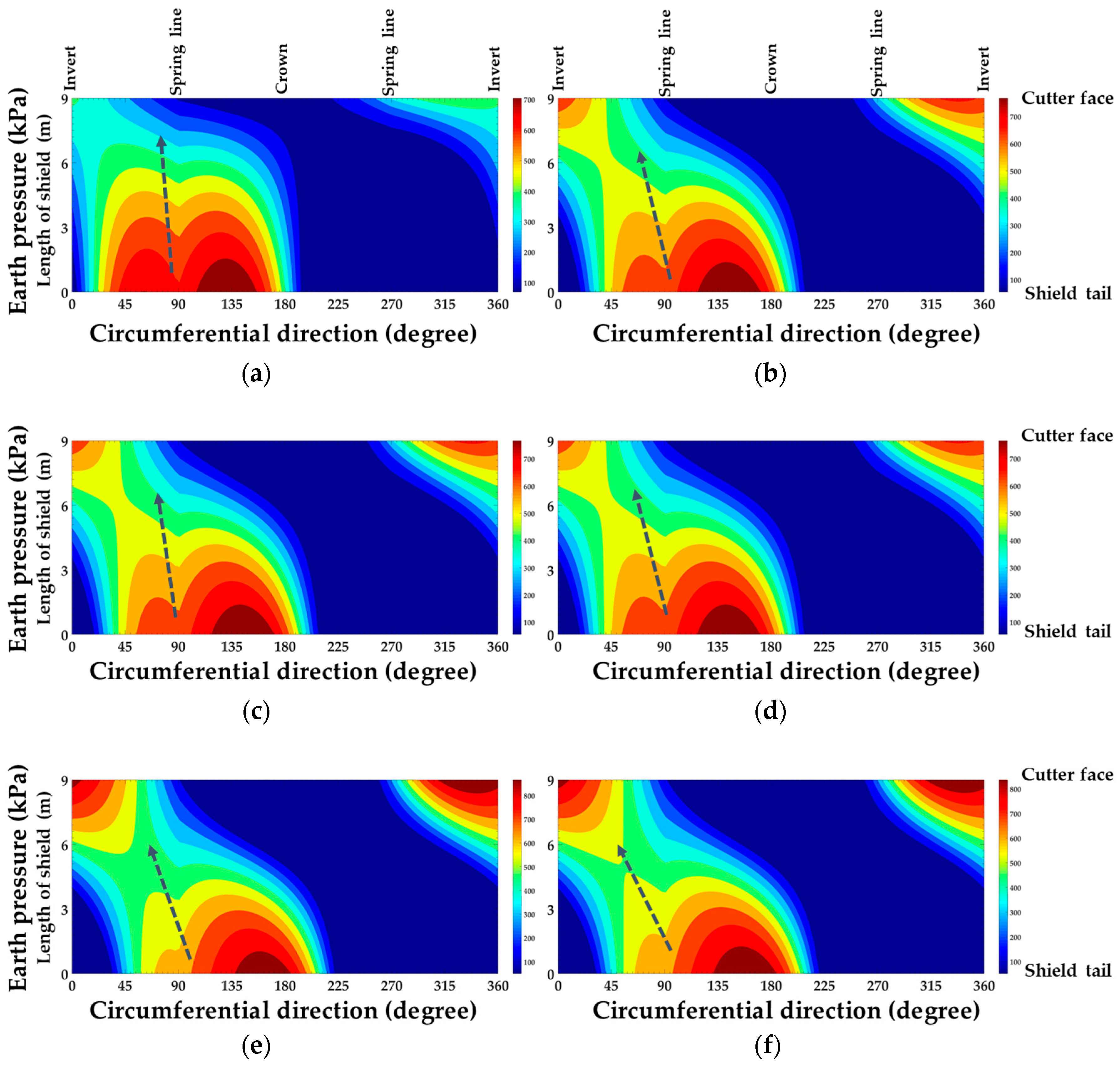
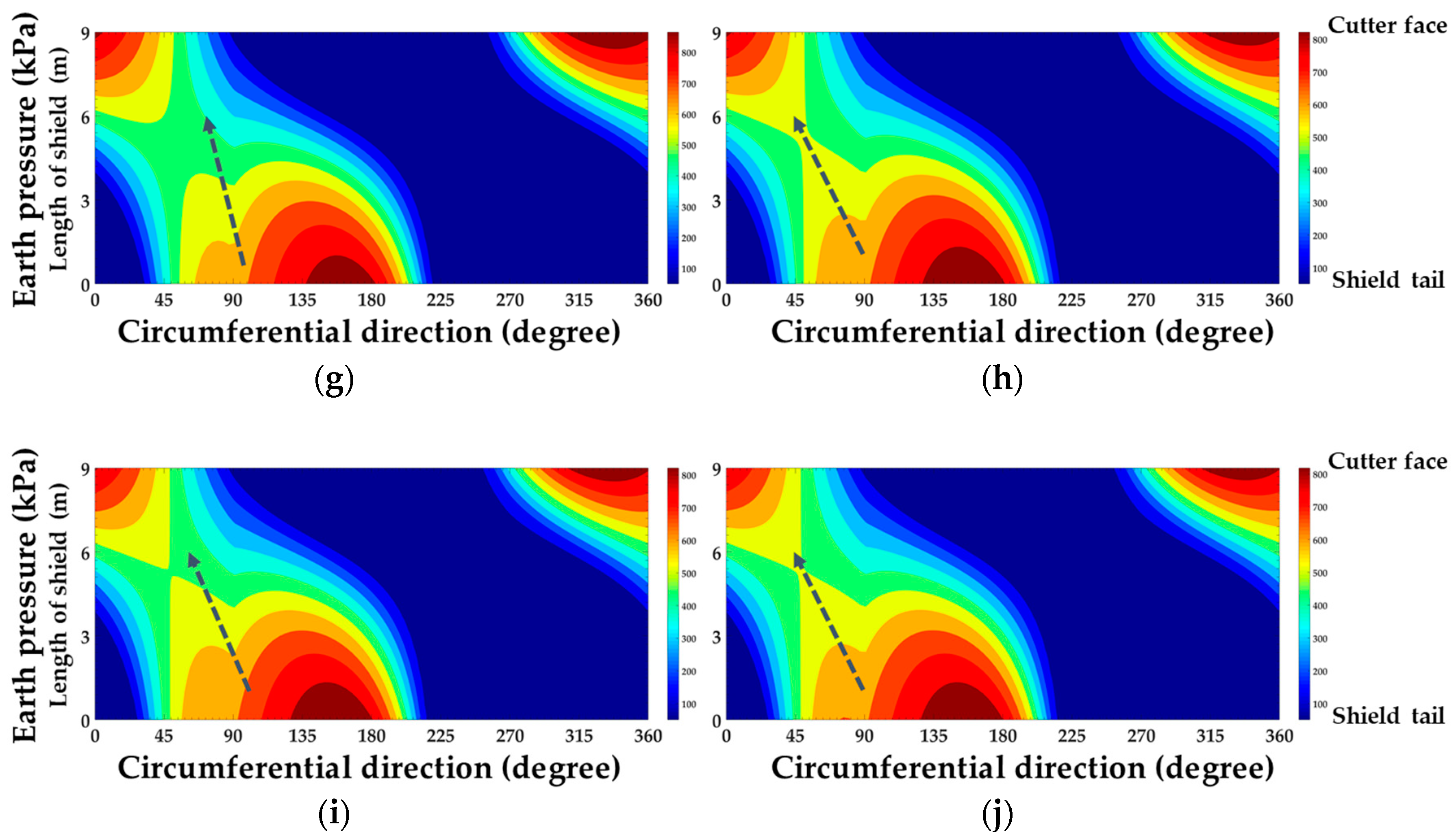
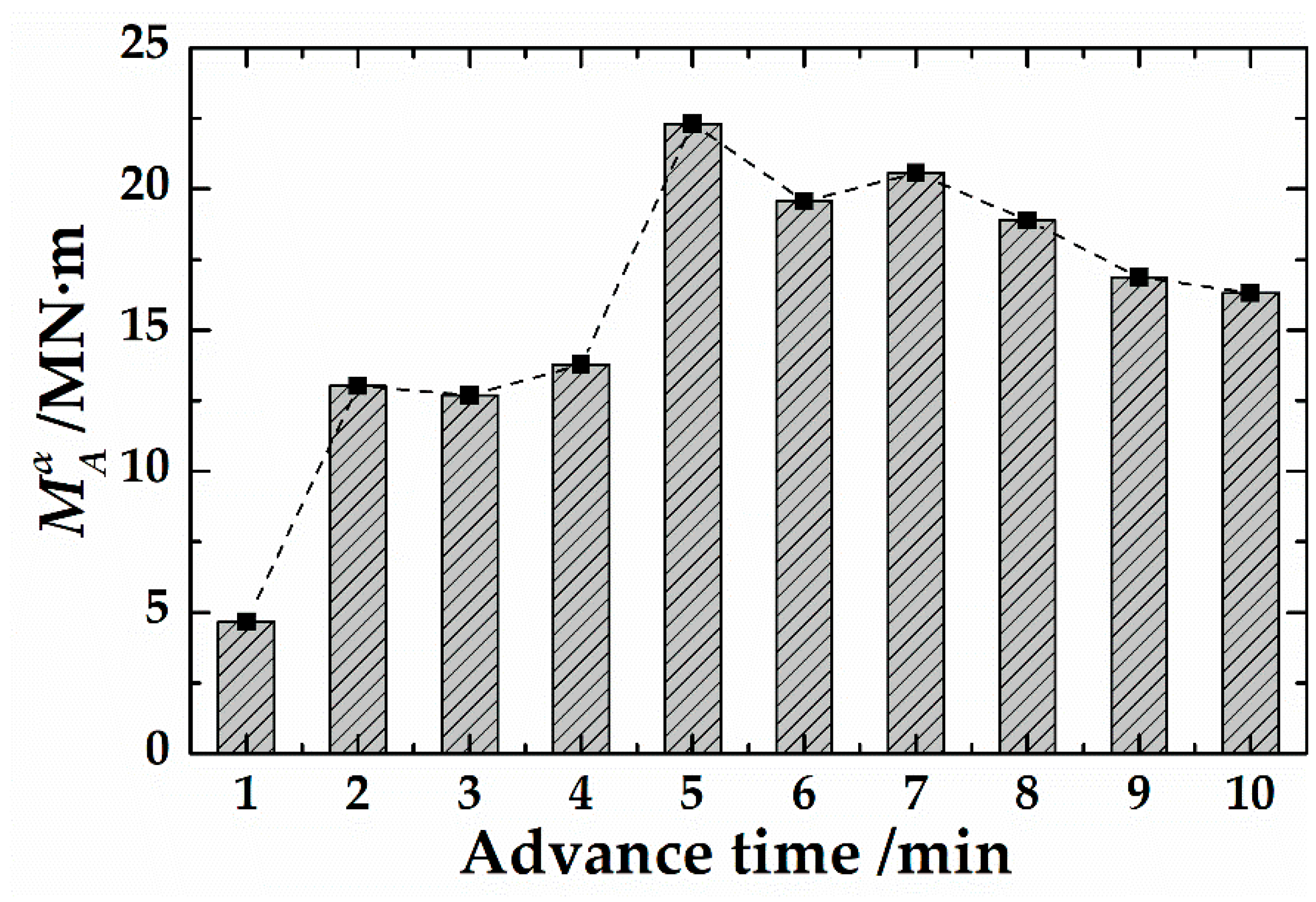
5.1. Engineering Application I: Inversion Calculation of Soil-Shield Interaction Force
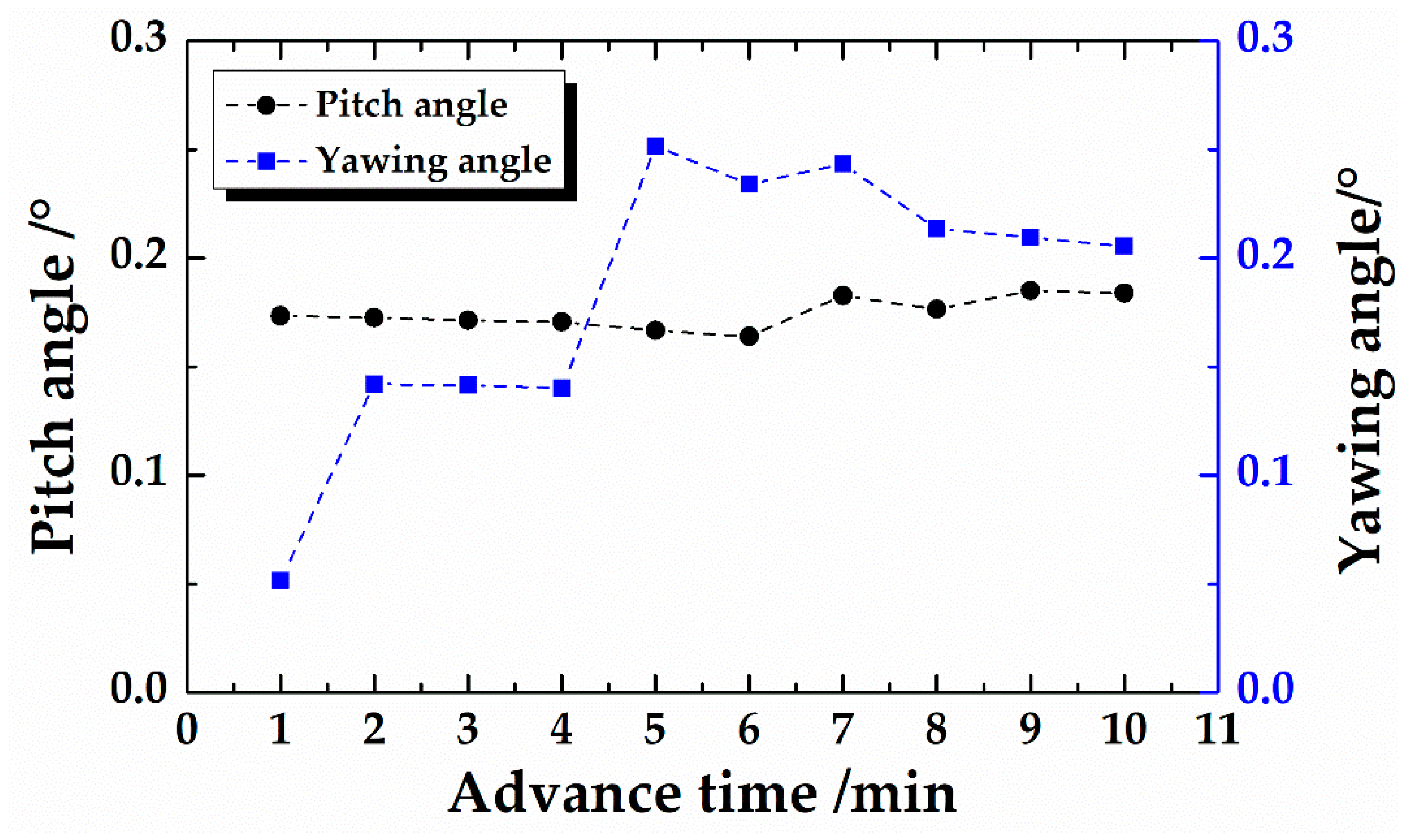
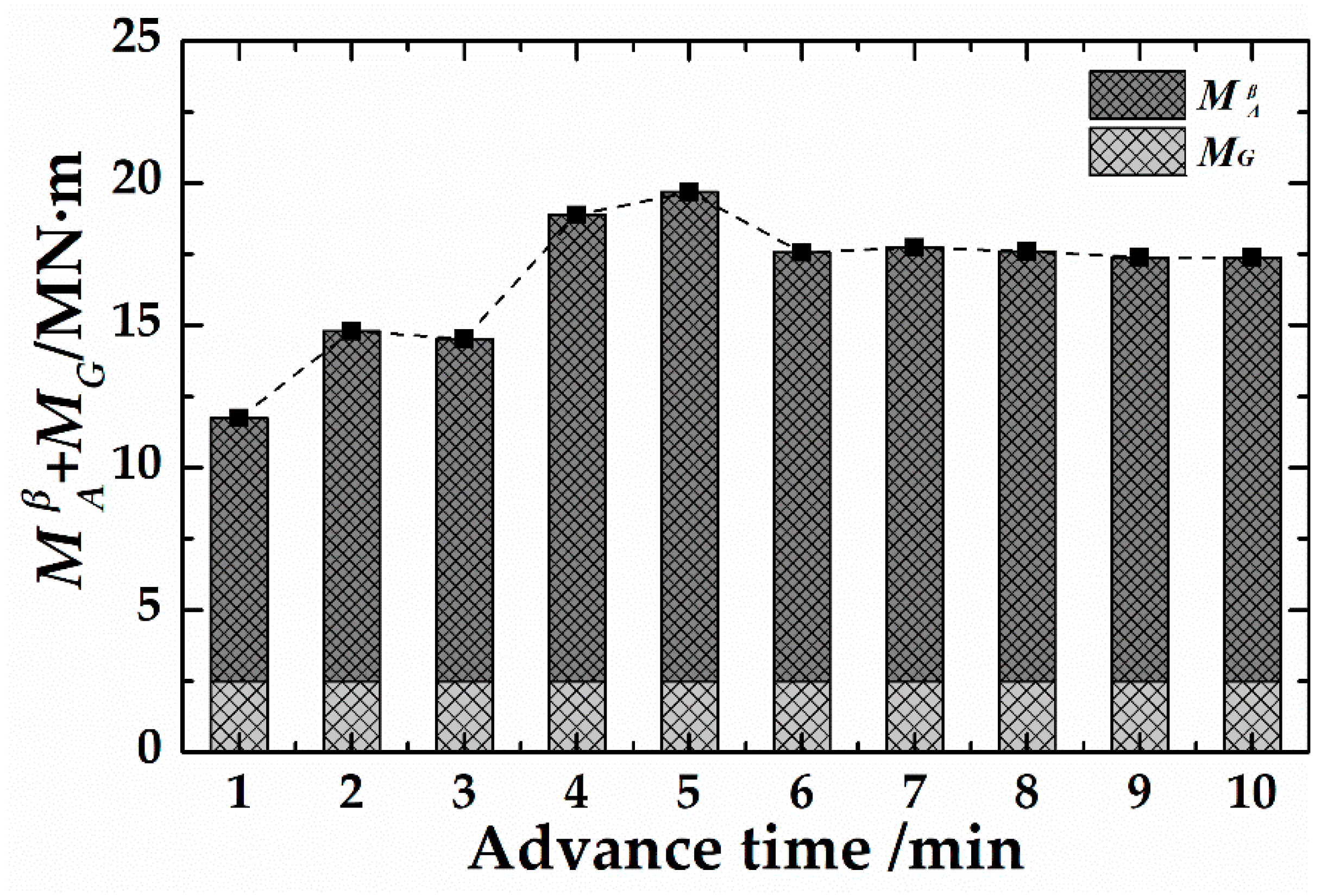
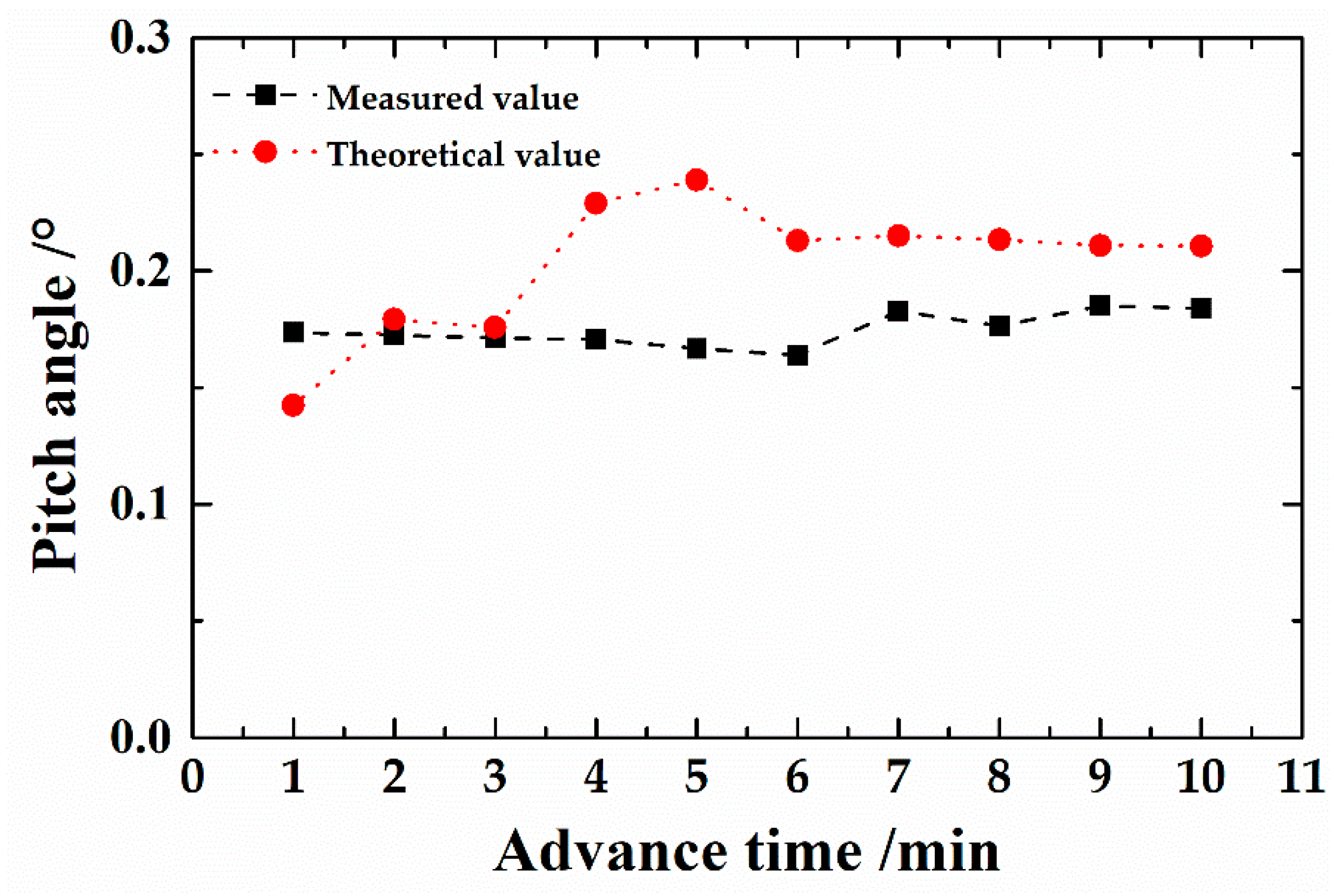
5.2. Engineering Application II: Shield Pitch Angle Prediction
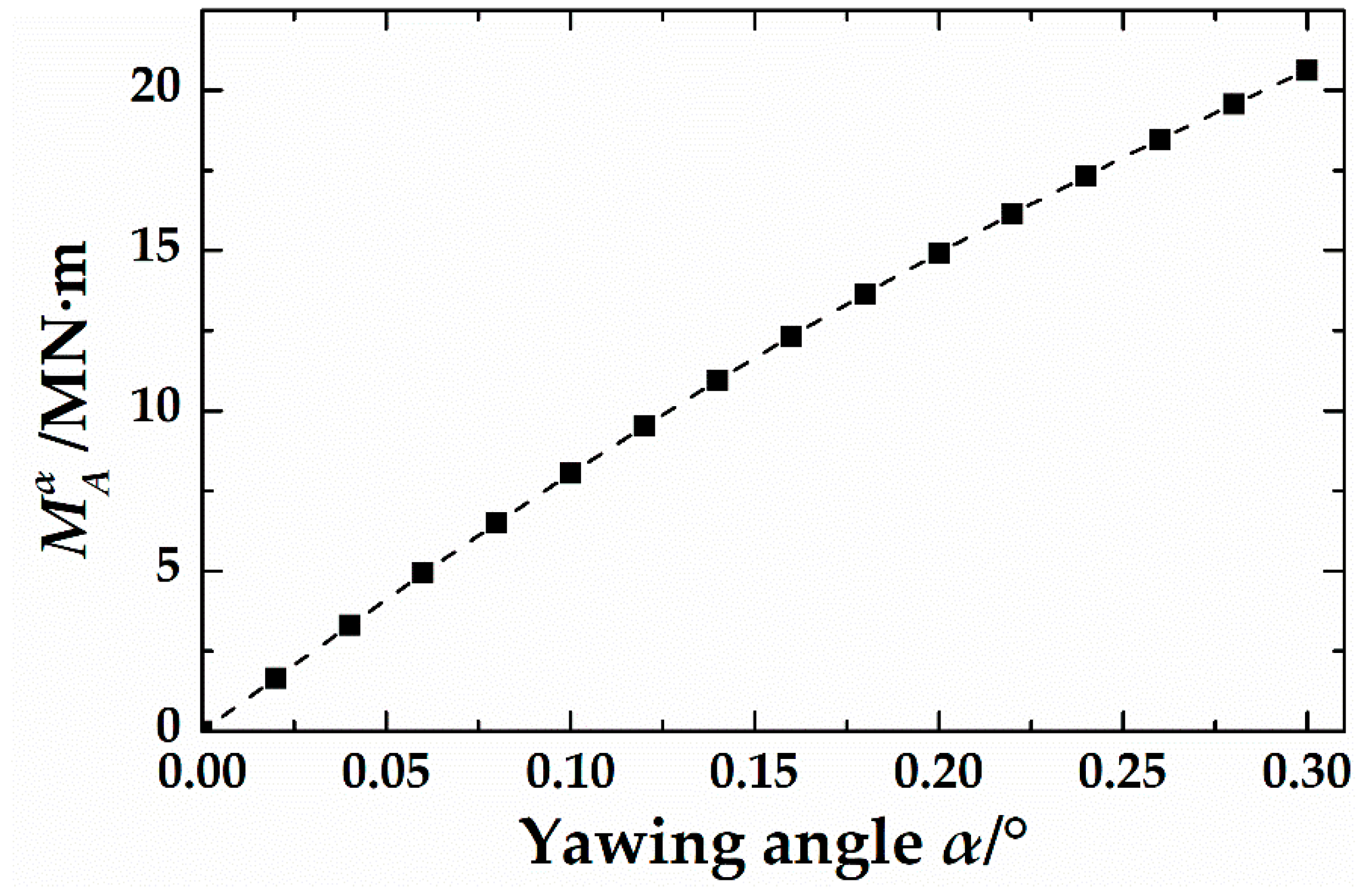
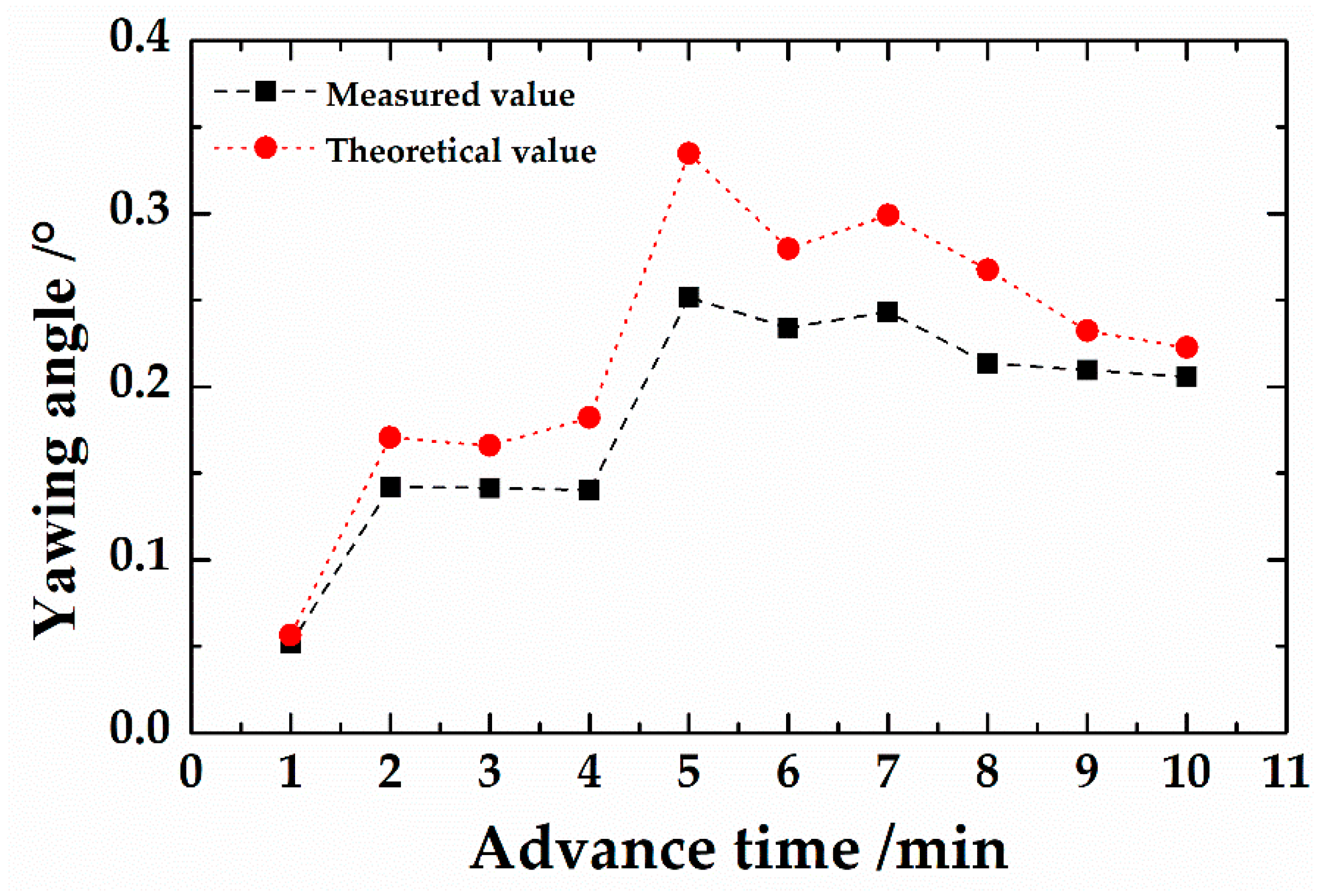
5.3. Engineering Application III: Shield Yawing Angle Prediction
6. Conclusions
- (1)
- Based on the ground reaction force curve, the interaction between the shield and the soil was simulated by the equivalent spring, and the theoretical calculation method of f5 was obtained in the change of the shield attitude.
- (2)
- The improved calculation method of loose earth pressure solved the initial boundary problem of the shield attitude calculation. Combined with the theoretical calculation method of f5, the calculation process of the shield attitude was formed.
- (3)
- Based on the monitoring data of Jinan Metro Line R2, the interaction between the shield and the soil during the construction of the shield was inverted. Through the stress nephogram, the stress concentration area of the shield can be judged to guide the next step of attitude adjustment.
- (4)
- Based on the measured data of the project, the theoretical calculation method of the pitch angle and yawing angle of the shield was verified. The study found that the theoretical value was close to the measured value, but, since the moment generated by the advance cylinders cannot fully act on the shield itself, the theoretical values of the shield attitude angles were generally greater than the measured values.
- (5)
- The model of shield–soil interaction has some benefits for upcoming projects. Firstly, this model can guide the shield operator to perform shield attitude correction. Secondly, it is possible to initially obtain a position where the attitude control of any shield tunnel construction is difficult for upcoming projects.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notations
| Symbol | Description | Unit | Symbol | Description | Unit |
| f1 | Shield self-weight | kPa | f2 | Shield tail load | kPa |
| f3 | Advance load provided by the jacks | kPa | f4 | Load acting on the cutterhead | kPa |
| f5 | Force acting on the shield periphery | kPa | (x0, y0, z0) | cutterhead center coordinates | m |
| α | Yawing angle | ° | β | Pitch angle | ° |
| Ω | Rolling angle | ° | C | Coordinate system | [-] |
| F | Total force | kN | M | Total moment | MN·m |
| σv | Loose earth pressure | kPa | K0 | Later pressure coefficient | [-] |
| H | Overlying soil thickness | m | P0 | Upper load | kPa |
| c | Cohesion | kPa | φ | Internal friction angle | ° |
| γ | Weight density | kN/m3 | B1 | Loose band width | m |
| R | Radius of the tunnel | m | A1 | Characteristic parameters | [-] |
| p1 | Initial soil pressure upper value | kPa | p2 | Initial earth pressure lower value | kPa |
| D | Shield diameter | m | L | Shield length | m |
| ls | Shield eccentricity | m | Δs | Shield displacement | m |
| U | Shield shell unit displacement | m | η | Angle with the p-axis in the CM | ° |
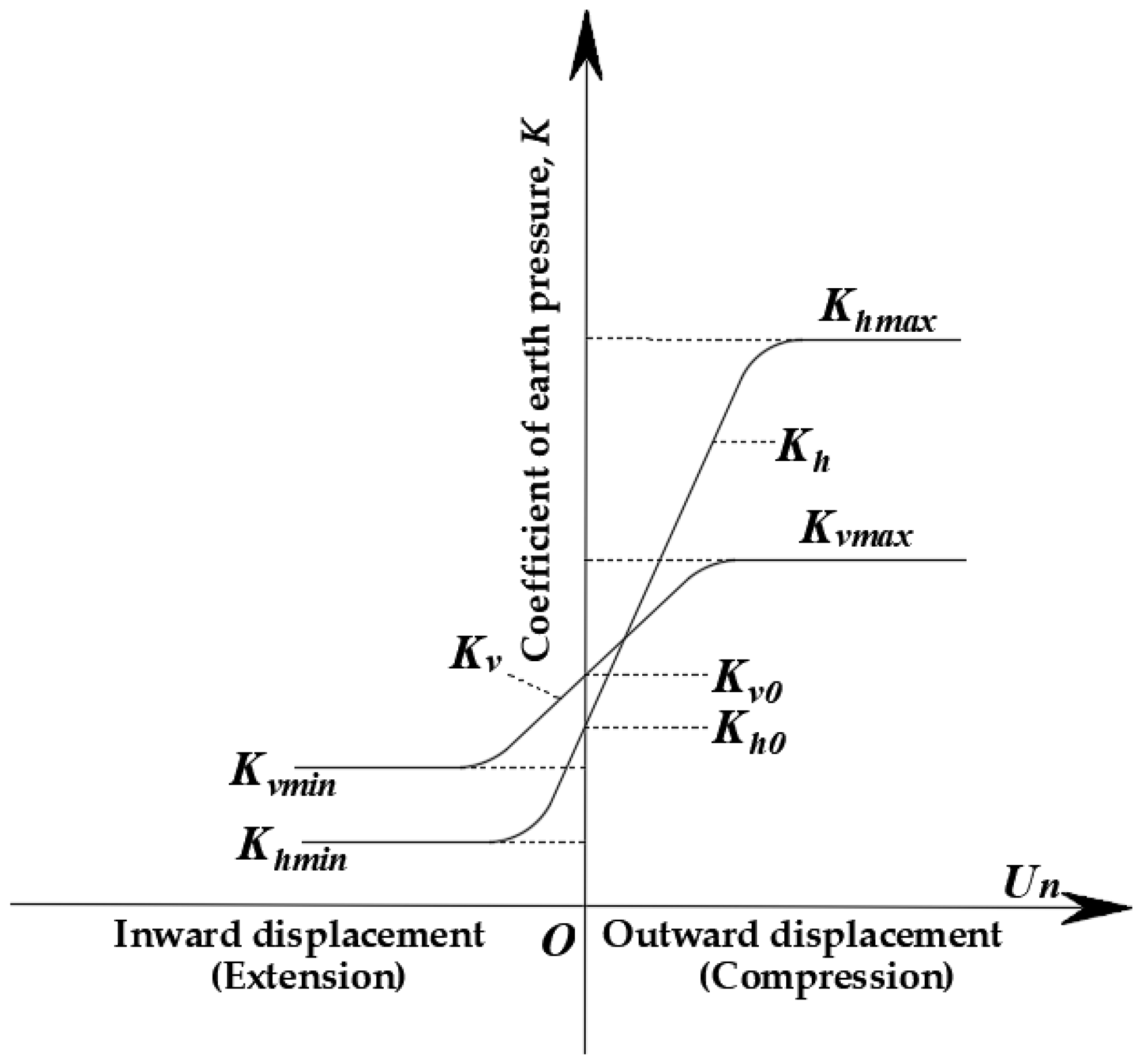
| K | coefficient of earth pressure | [-] | a | the gradient of functions K(U) | [-] |
| σ | Stress | kPa | A | Area | m2 |
| Superscripts | |||||
| E | Global coordinate system | [-] | M | Machine coordinate system | [-] |
| MR | Rotated coordinate system | [-] | b | Different coordinate systems | [-] |
| Subscripts | |||||
| h, v | Horizontal and vertical directions | [-] | e | Different directions of force | [-] |
| A | Shield apply | [-] | max | Maximum | [-] |
| min | Minimum | [-] | o | Origin or initial | [-] |
| i, j | ith and jth calculation points | [-] | s | Final | [-] |
References
- Festa, D.; Broere, W.; Bosch, J.W. Kinematic behaviour of a tunnel boring machine in soft soil: Theory and observations. Tunn. Undergr. Space Technol. 2015, 49, 208–217. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.M. Theoretical algorithm for over-excavated volume and articulation angle during shield tunneling along sharp curves. Chin. J. Highw. Trans. 2017, 30, 66–73. (In Chinese) [Google Scholar]
- Lyu, H.M.; Shen, S.L.; Zhou, A.N.; Yang, J. Perspectives for flood risk assessment and management for mega-city metro system. Tunn. Undergr. Space Technol. 2019, 84, 31–44. [Google Scholar] [CrossRef]
- Ren, D.J.; Shen, S.L.; Arulrajah, A.; Wu, H.N. Evaluation of ground loss ratio with moving trajectories induced in double-O-tube (DOT) tunnelling. Can. Geotech. J. 2018, 55, 894–902. [Google Scholar] [CrossRef]
- Wu, L.; Qu, F.Z. Discrete element simulation of mechanical characteristic of conditioned sands in earth pressure balance shield tunneling. J. Cent. South Univ. Technol. 2009, 16, 1028–1033. [Google Scholar] [CrossRef]
- Koyama, Y. Present status and technology of shield tunneling method in Japan. Tunn. Undergr. Space Technol. 2003, 18, 145–159. [Google Scholar] [CrossRef]
- Xie, H.B.; Duan, X.M.; Yang, H.Y.; Liu, Z.B. Automatic trajectory tracking control of shield tunneling machine under complex stratum working condition. Tunn. Undergr. Space Technol. 2012, 32, 87–97. [Google Scholar] [CrossRef]
- Shimizu, Y.; Isaka, M.; Nishida, S.; Suzuki, M.; Yokogawa, A. Moving characteristics of shield tunneling machine with multi circular face. Trans. Jpn. Soc. Mech. Eng. Ser. C 1994, 60, 144–152. [Google Scholar] [CrossRef][Green Version]
- Shimizu, Y.; Obayashi, M.; Asada, K.; Suzuki, M. Movement of Shield Tunneling Machine of Articulate Type and Model Experiment. Trans. Jpn. Soc. Mech. Eng. Ser. C 1994, 60, 862–868. [Google Scholar] [CrossRef][Green Version]
- Komiya, K.; Soga, K.; Akagi, H.; Hagiwara, T.; Bolton, M.D. Finite element modelling of excavation and advancement processes of a shield tunnelling machine. Soils Found 1999, 39, 37–52. [Google Scholar] [CrossRef]
- Sugimoto, M.; Sramoon, A. Theoretical model of shield behavior during excavation I: Theory. J. Geotech. Geoenviron. Eng. 2002, 128, 138–155. [Google Scholar] [CrossRef]
- Yue, M.; Sun, W.; Wei, J. Sliding mode robust controller for automatic rectification of shield machine. J. Cent. South Univ. Technol. 2011, 18, 536–541. [Google Scholar] [CrossRef]
- Sun, W.; Yue, M.; Wei, J. Relationship between rectification moment and angle of shield based on numerical simulation. J. Cent. South Univ. Technol. 2012, 19, 517–521. [Google Scholar] [CrossRef]
- Ates, U.; Bilgi, N.; Copur, H. Estimating torque, thrust and other design parameters of different type TBMs with some criticism to TBMs used in Turkish tunneling projects. Tunn. Undergr. Space Technol. 2014, 40, 46–63. [Google Scholar] [CrossRef]
- Zhang, Q.; Qu, C.Y.; Cai, Z.X.; Huang, T. Modeling of the thrust and torque acting on shield machines during tunneling. Autom. Constr. 2014, 40, 60–67. [Google Scholar] [CrossRef]
- Hassanpour, J.; Rostami, J.; Zhao, J. A new hard rock TBM performance prediction model for project planning. Tunn. Undergr. Space Technol. 2011, 26, 595–603. [Google Scholar] [CrossRef]
- Acaroglu, O.; Ozdemir, L.; Asbury, B. A fuzzy logic model to predict specific energy requirement for TBM performance prediction. Tunn. Undergr. Space Technol. 2008, 23, 600–608. [Google Scholar] [CrossRef]
- Barton, N. TBM performance estimation in rock using QTBM. Tunn. Tunn. Int. 1999, 31, 30–33. [Google Scholar]
- Yagiz, S. Utilizing rock mass properties for predicting TBM performance in hard rock condition. Tunn. Undergr. Space Technol. 2007, 23, 326–339. [Google Scholar] [CrossRef]
- Sugimoto, M.; Sramoon, A.; Kayukawa, K. Theoretical model of shield behavior during excavation II: Application. J. Geotech. Geoenviron. Eng. 2002, 128, 156–165. [Google Scholar] [CrossRef]
- Sugimoto, M.; Sramoon, A.; Konishi, S.; Sato, Y. Simulation of shield tunneling behavior along a curved alignment in a multilayered Ground. J. Geotech. Geoenviron. Eng. 2007, 133, 684–694. [Google Scholar] [CrossRef]
- Terzaghi, K. Stress distribution in dry and in saturated sand above a yielding trap-door. In Proceedings of the First International Conference on Soil Mechanics and Foundation Engineering, Cambridge, MA, USA, 22–26 June 1936; pp. 307–311. [Google Scholar]
- Li, C.L. Method for calculating loosening earth pressure during construction of shield tunnels. Chin. J. Geotech. Eng. 2014, 36, 1714–1720. (In Chinese) [Google Scholar]
- Sramoon, A.; Sugimoto, M. Development of a ground reaction curve for shield tunneling. In Proceedings of the International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground, Rotterdam, The Netherlands, 19–21 July 1999; pp. 437–442. [Google Scholar]
- Sun, S.Q.; Li, L.P.; Wang, J.; Shi, S.S.; Song, S.G. Karst Development Mechanism and Characteristics Based on Comprehensive Exploration along Jinan Metro, China. Sustainability 2018, 10, 3383. [Google Scholar] [CrossRef]
- Wang, G.F.; Wu, Y.X.; Lu, L.H.; Li, G.; Shen, J.S. Investigation of the geological and hydrogeological environment with relation to metro system construction in Jinan, China. Bull. Eng. Geol. Environ. 2019, 78, 1005–1024. [Google Scholar] [CrossRef]
- Lou, P.J.; Xu, Y. Discussion on “Method for calculating loosening earth pressure during construction of shield tunnels”. Chin. J. Geotech. Eng. 2015, 37, 1353–1354. (In Chinese) [Google Scholar]






| Khmin | Kho | Khmax | Kh | Kvmin | Kvo | Kvmax | Kv |
|---|---|---|---|---|---|---|---|
| 0.3 | 1 | 5 | 3 MN/m3 | 0.3 | 1 | 5 | 3 MN/m3 |
| Shield Type | EPB |
|---|---|
| External diameter (m) | 6.68 |
| The length of shield (m) | 9.0 |
| Shield weight (t) | Approximately 500 |
| Shield eccentricity (m) | Approximately 0.5 |
| Cutter opening ratio (%) | 35 |
| Maximum total thrust (kN) | 40,860 |
| Number of propulsion cylinders | 22 |
| Maximum advance speed (mm/min) | 80 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, X.; Yuan, D.-J.; Jin, D.-L. Influence of Shield Attitude Change on Shield–Soil Interaction. Appl. Sci. 2019, 9, 1812. https://doi.org/10.3390/app9091812
Shen X, Yuan D-J, Jin D-L. Influence of Shield Attitude Change on Shield–Soil Interaction. Applied Sciences. 2019; 9(9):1812. https://doi.org/10.3390/app9091812
Chicago/Turabian StyleShen, Xiang, Da-Jun Yuan, and Da-Long Jin. 2019. "Influence of Shield Attitude Change on Shield–Soil Interaction" Applied Sciences 9, no. 9: 1812. https://doi.org/10.3390/app9091812
APA StyleShen, X., Yuan, D.-J., & Jin, D.-L. (2019). Influence of Shield Attitude Change on Shield–Soil Interaction. Applied Sciences, 9(9), 1812. https://doi.org/10.3390/app9091812






