Smart Obstacle Avoidance Using a Danger Index for a Dynamic Environment
Abstract
1. Introduction
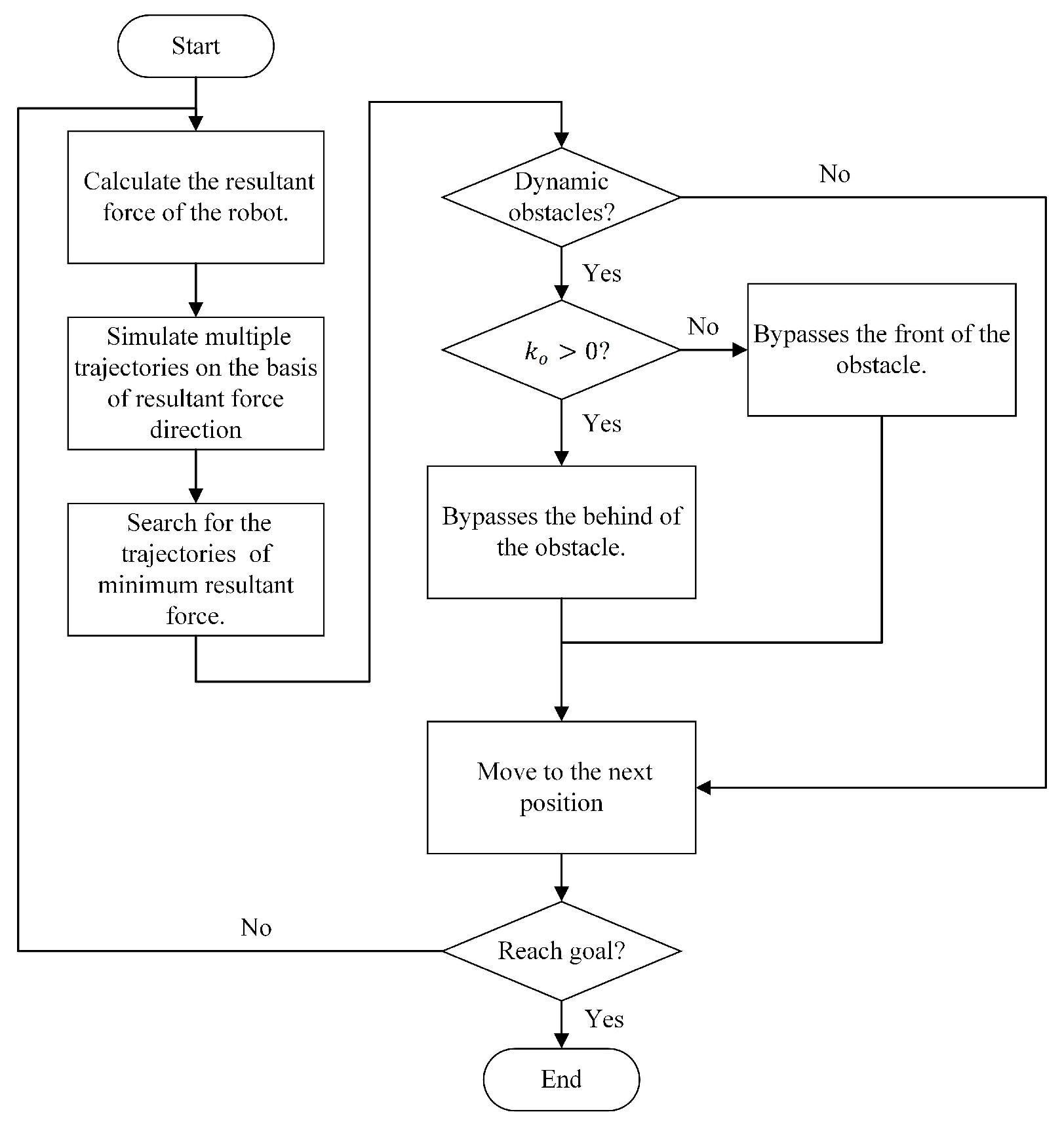
2. The Proposed Method
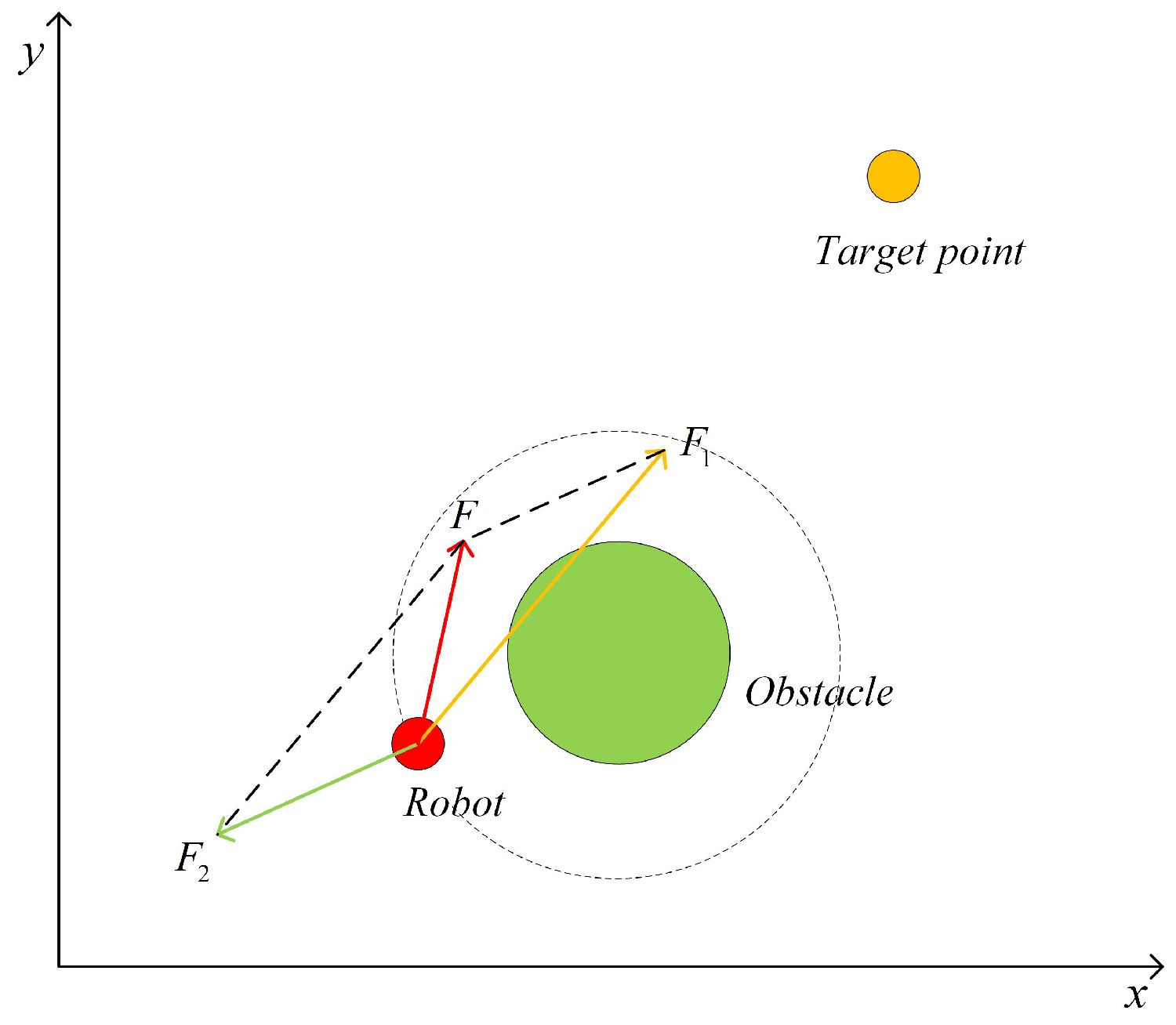
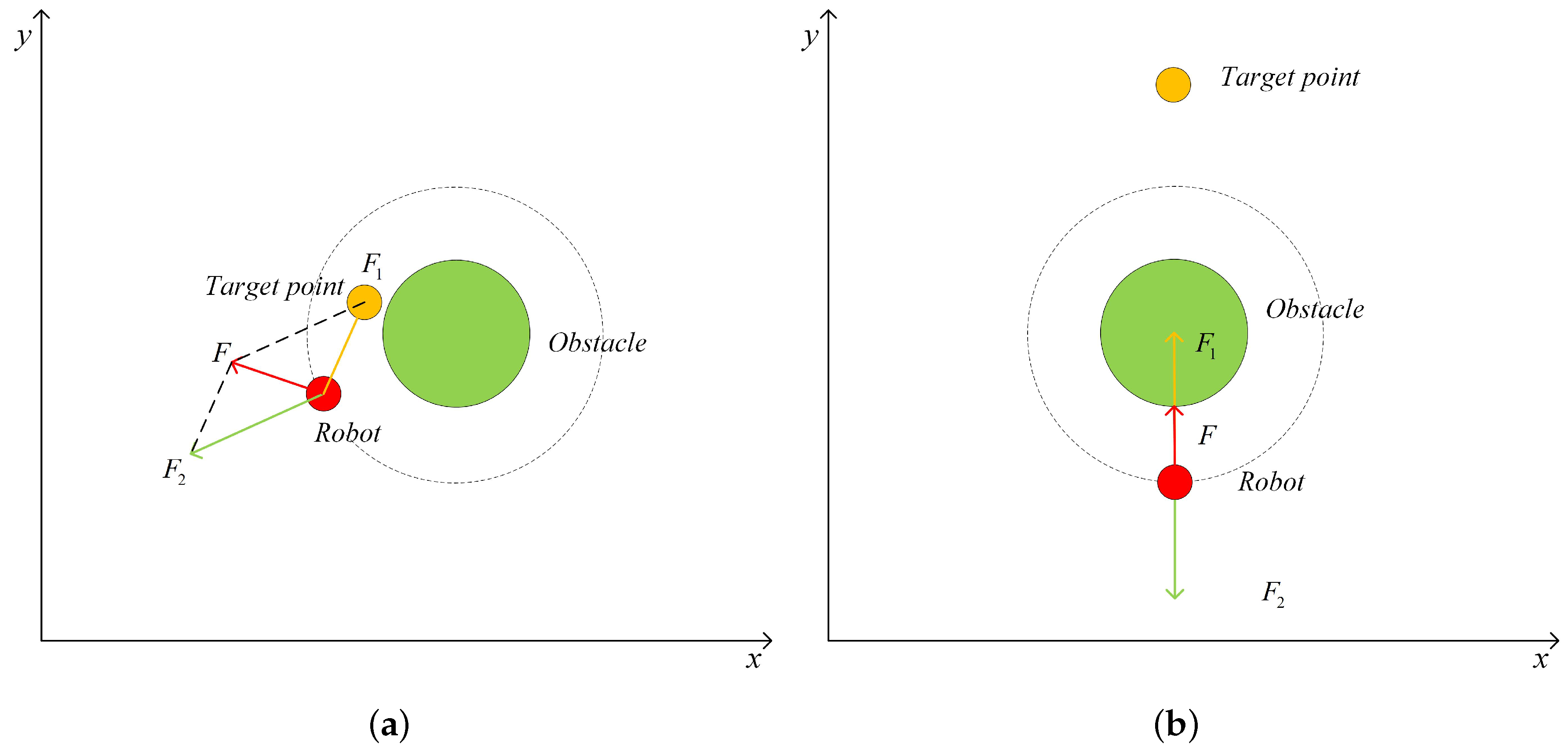
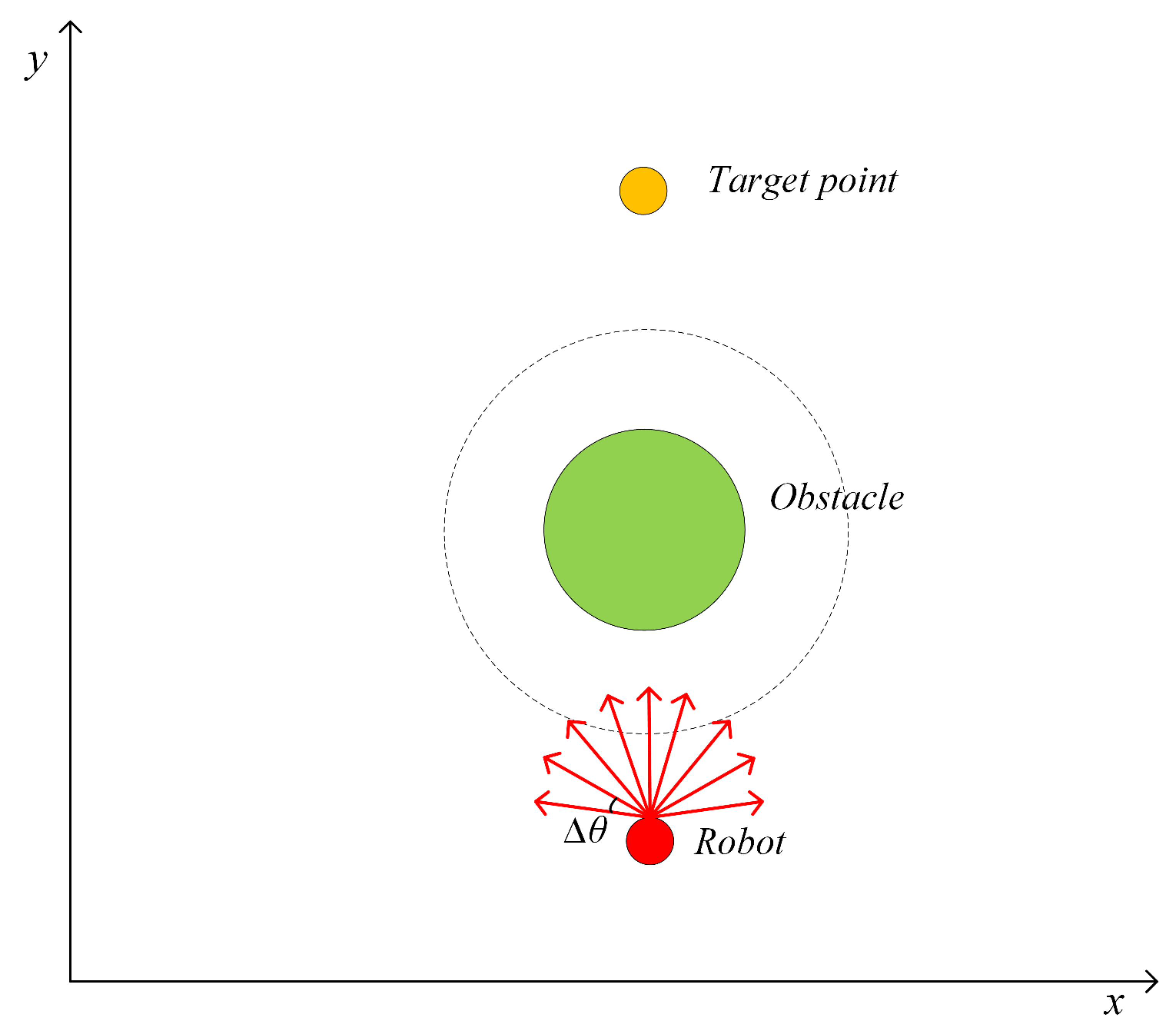
2.1. Dynamic Window Based Artificial Potential Field (DAPF)
2.2. Danger Index Based Artificial Potential Field (DIAPF) for a Dynamic Environment
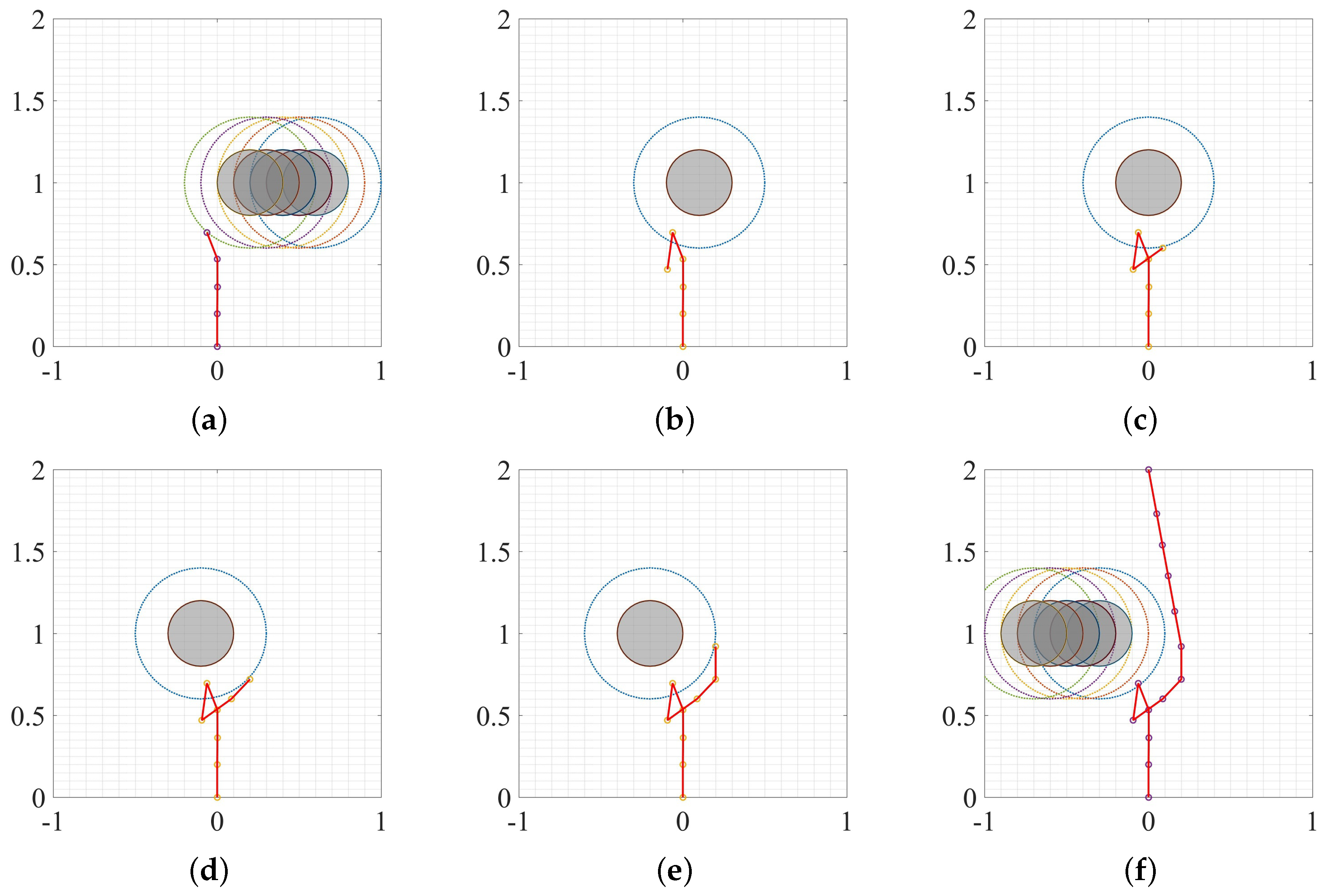
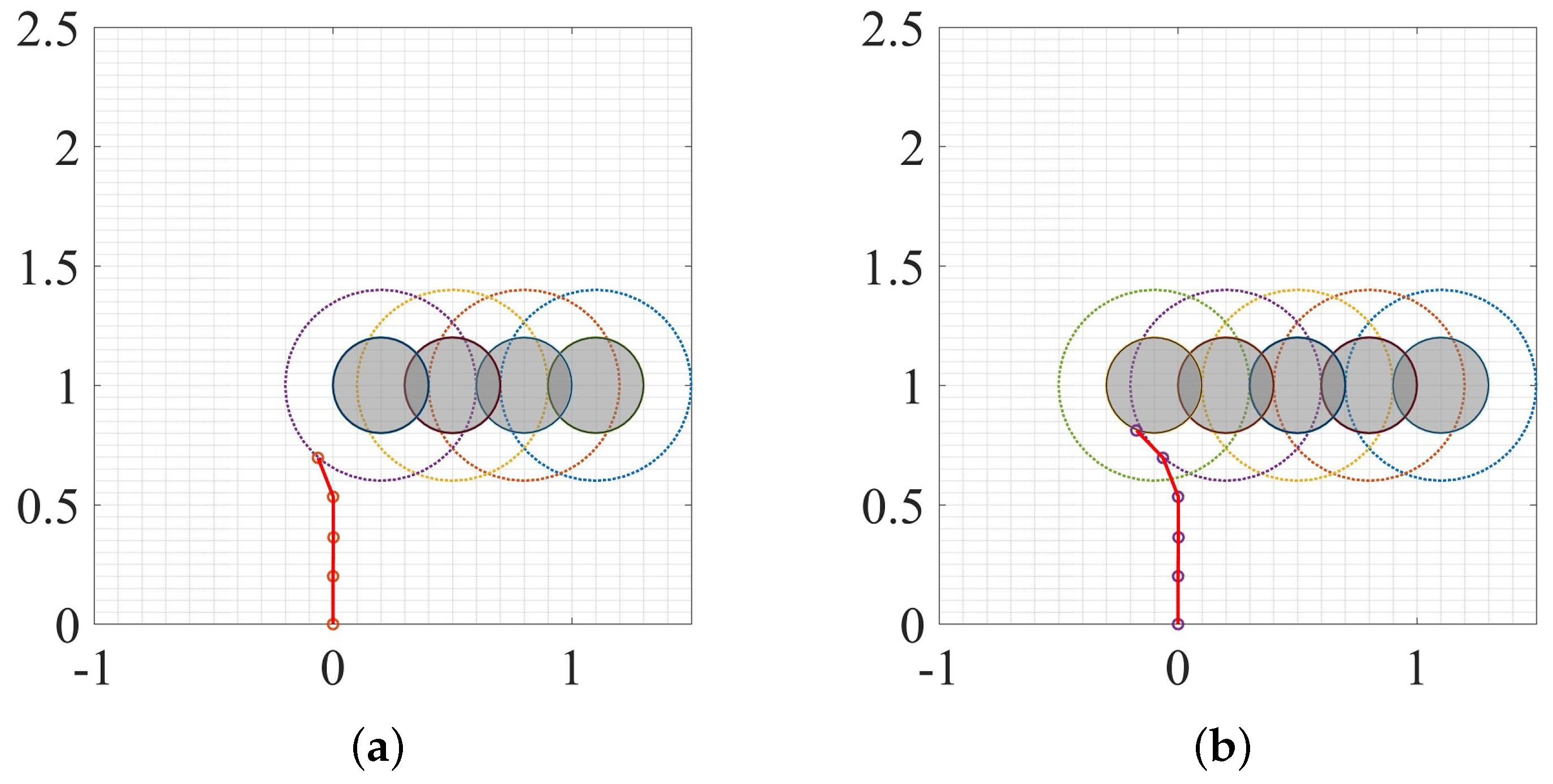
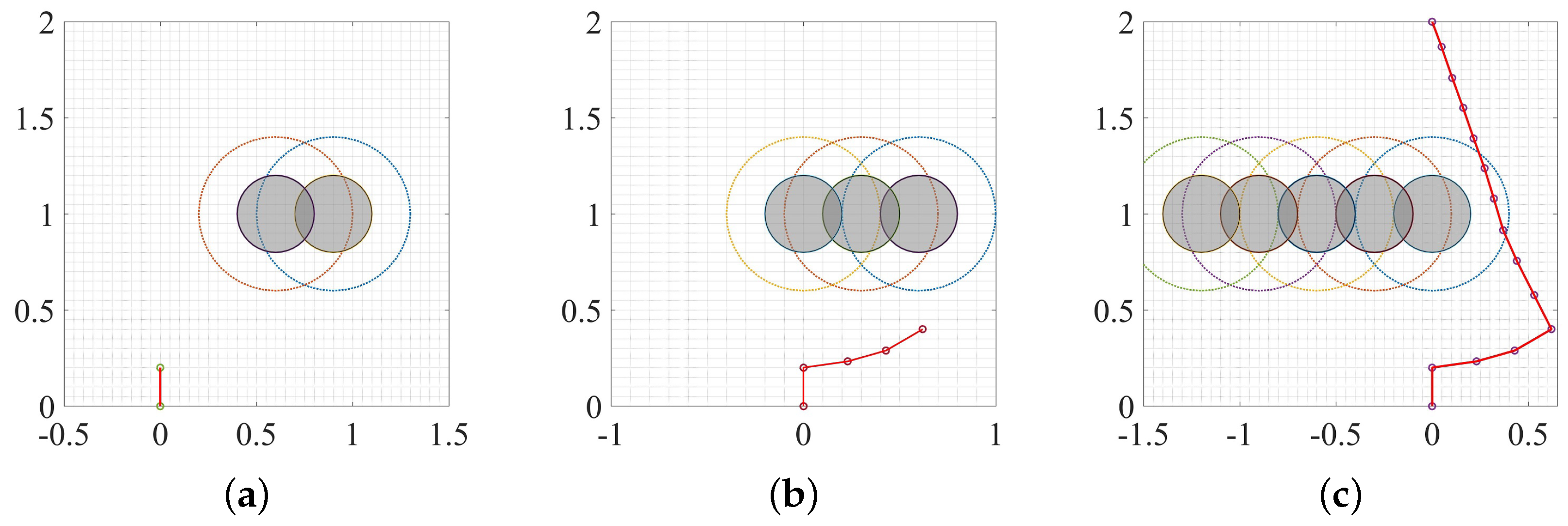
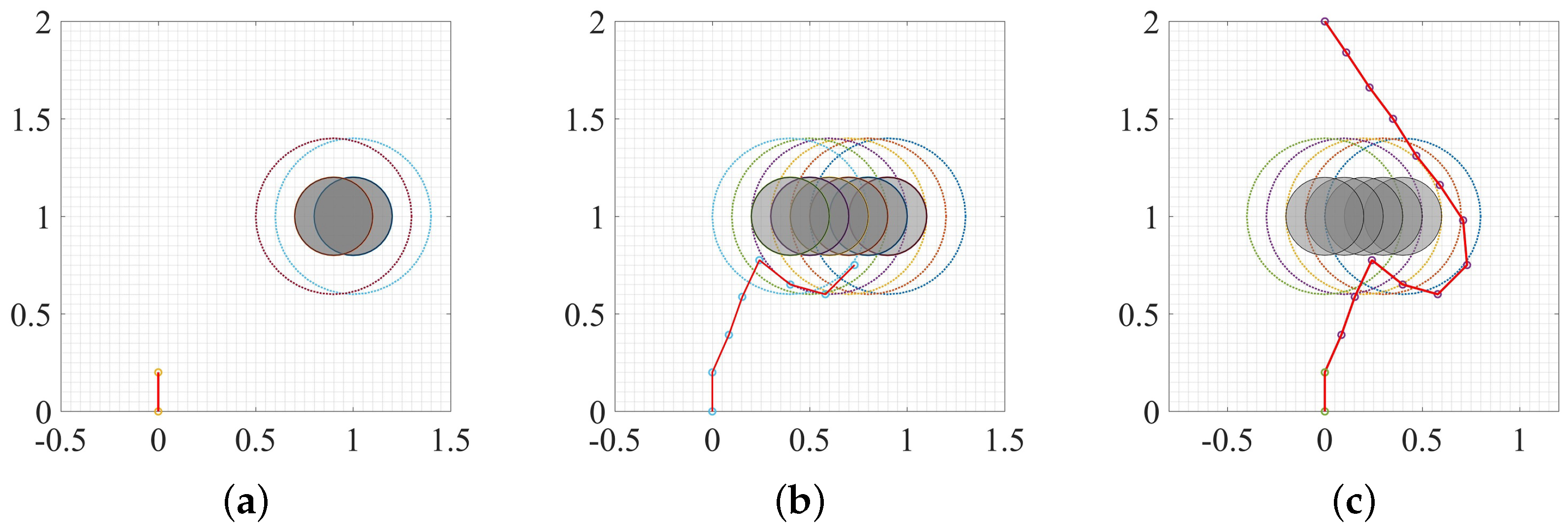
3. Experiment and Analysis
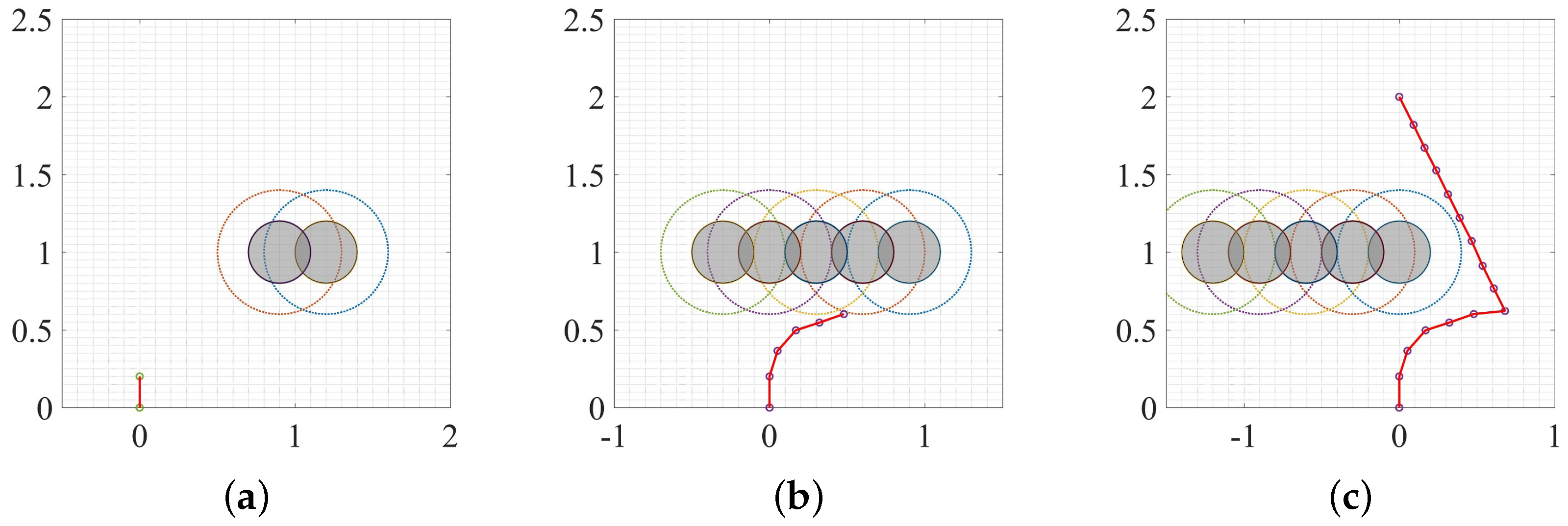
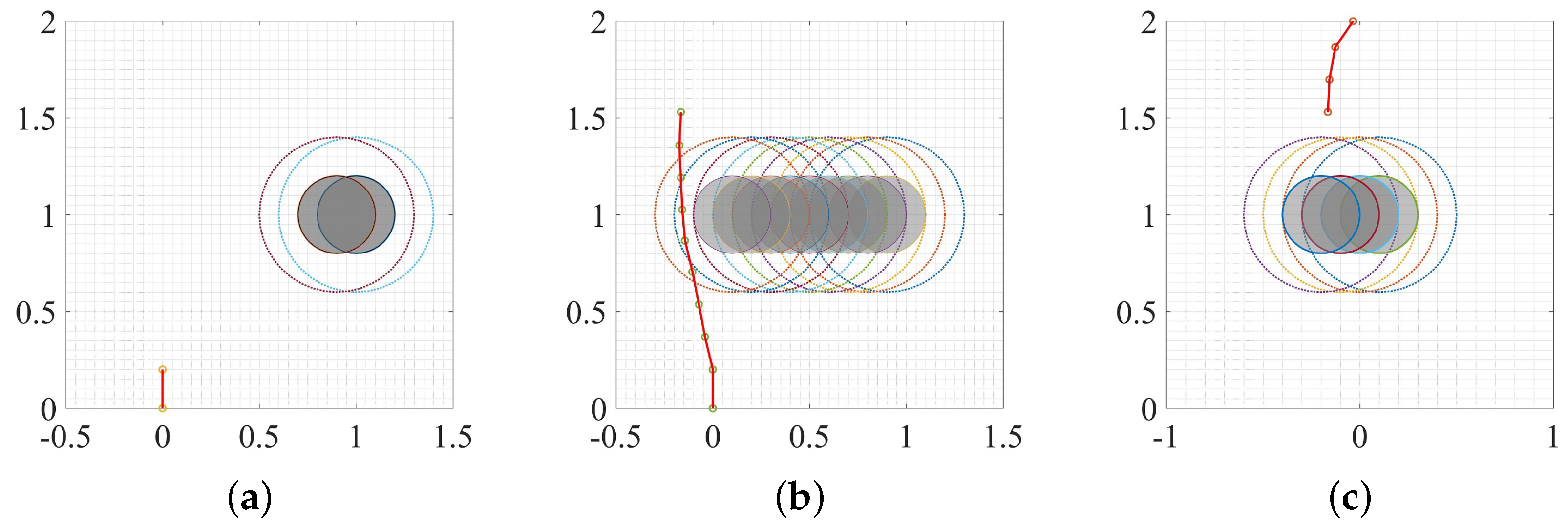
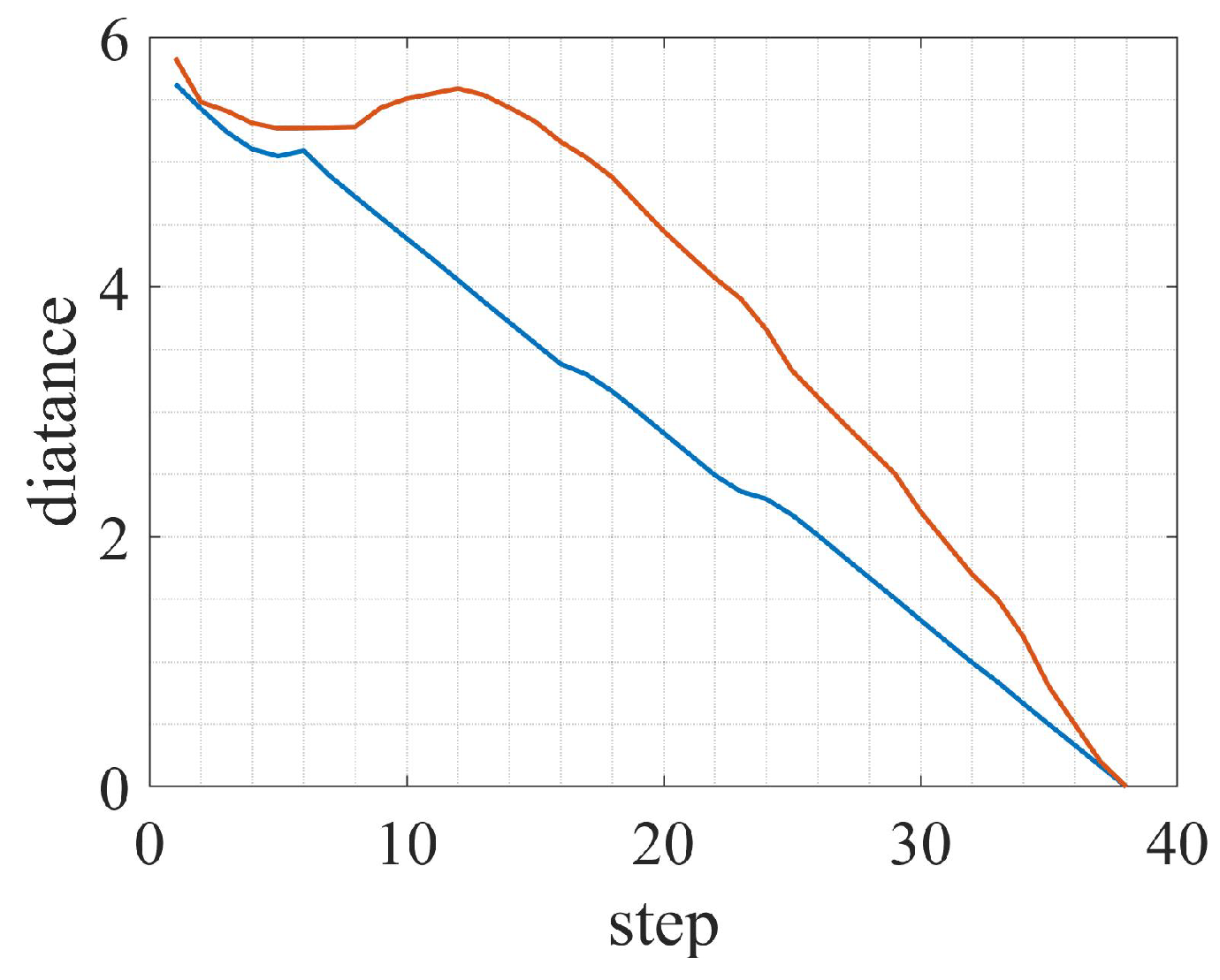
3.1. Static Environment
3.2. Moving Obstacle
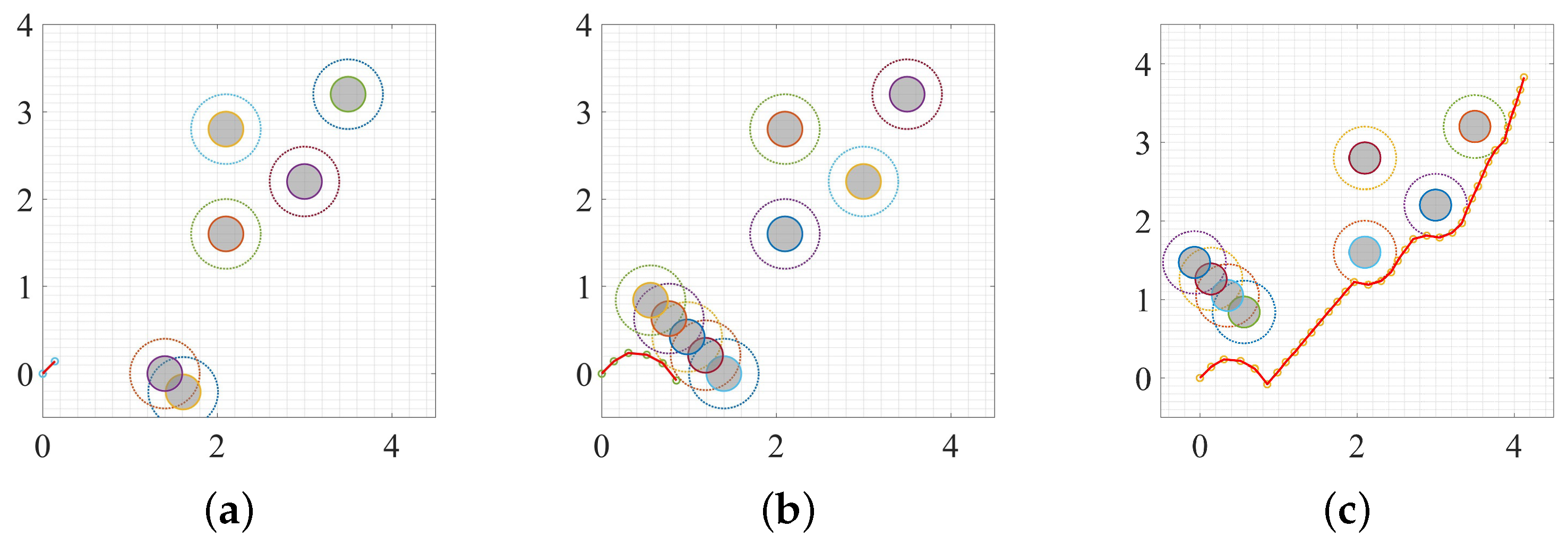
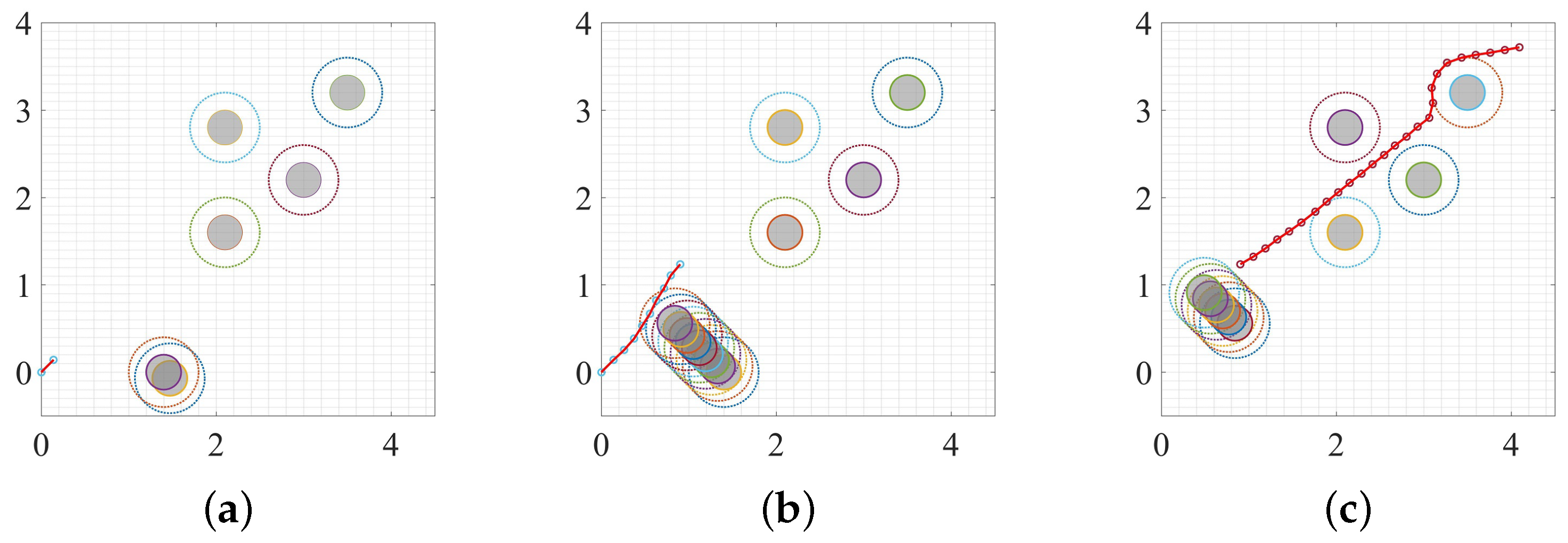
3.3. Dynamic Environment
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rafieisakhaei, M.; Tamjidi, A.; Chakravorty, S.; Kumar, P.R. Feedback motion planning under non-Gaussian uncertainty and non-convex state constraints. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), New York, NY, USA, 15–19 August 2016; pp. 4238–4244. [Google Scholar]
- Al-Sabban, W.H.; Gonzalez, L.F.; Smith, R.N. Wind-energy based path planning for unmanned aerial vehicles using markov decision processes. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 784–789. [Google Scholar]
- Sun, W.; van den Berg, J.; Alterovitz, R. Stochastic extended LQR for optimization-based motion planning under uncertainty. IEEE Trans. Autom. Sci. Eng. 2018, 13, 437–447. [Google Scholar] [CrossRef] [PubMed]
- Chi, W.; Wang, C.; Wang, J.; Meng, M.Q. Risk-DTRRT-Based optimal motion planning algorithm for mobile robots. IEEE Trans. Autom. Sci. Eng. 2008, 142–149. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; TR 98-11, Tech. Rep.; Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Kayraki, L.; Svestka, P.; Latombe, J.C.; Overmars, M. Probabilistic roadmaps for path planning in high-dimensional configurations space. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B.A. Formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Janabi-Sharifi, F.; Vinke, D. Integration of the artificial potential field approach with simulated annealing for robot path planning. In Proceedings of the 8th IEEE International Symposium on Intelligent Control, Chicago, IL, USA, 25–27 August 1993; pp. 539–544. [Google Scholar]
- Lee, S.; Park, J. Cellular robotic collision-free path planning. In Proceedings of the Fifth International Conference on Advanced Robotics’ Robots in Unstructured Environments, Pisa, Italy, 19–22 June 1991; pp. 536–541. [Google Scholar]
- Khatib, O. Real-Time Obstacle Avoidance System for Manipulators and Mobile Robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; pp. 500–505. [Google Scholar]
- Volpe, R.; Khosla, P. Manipulator control with superquadric artificial potential functions: theory and experiments. IEEE Trans. Syst. Man Cybern. 1990, 20, 1423–1436. [Google Scholar] [CrossRef]
- Mohanty, P.K.; Parhi, D.R. A new hybrid intelligent path planner for mobile robot navigation based on adaptive neuro-fuzzy inference system. Aust. J. Mech. Eng. 2015, 13, 195–207. [Google Scholar] [CrossRef]
- Min, G.P.; Jeon, J.H.; Min, C.L. Obstacle avoidance for mobile robots using artificial potential field approach with simulated annealing. In Proceedings of the 2001 IEEE International Symposium on Industrial Electronics Proceedings, Pusan, Korea, 12–16 June 2001; pp. 1530–1535. [Google Scholar]
- Zhu, Q.; Yan, Y.; Xing, Z. Robot path planning based on artificial potential field approach with simulated annealing. In Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications, Jinan, China, 16–18 October 2006; pp. 622–627. [Google Scholar]
- Doria, N.S.F.; Freire, E.O.; Basilio, J.C. An algorithm inspired by the deterministic annealing approach to avoid local minima in artificial potential fields. In Proceedings of the 2013 16th International Conference on Advanced Robotics (ICAR), Montevideo, Uruguay, 25–29 November 2013; pp. 1–6. [Google Scholar]
- Lee, D.; Jeong, J.; Kim, Y.H.; Park, J.B. An improved artificial potential field method with a new point of attractive force for a mobile robot. In Proceedings of the 2017 2nd International Conference on Robotics and Automation Engineering (ICRAE), Shanghai, China, 29–31 December 2017; pp. 63–67. [Google Scholar]
- Weerakoon, T.; Ishii, K.; Nassiraei, A.A.F. An artificial potential field based mobile robot navigation method to prevent from deadlock. J. Artif. Intell. Soft Comput. Res. 2015, 5, 189–203. [Google Scholar] [CrossRef]
- Kim, Y.H.; Son, W.-S.; Park, J.B.; Yoon, T.S. Smooth path planning by fusion of artificial potential field method and collision cone approach. MATEC Web Conf. 2016, 75, 05004. [Google Scholar] [CrossRef]
- Ge, S.S.; Cui, Y.J. Dynamic motion planning for mobile robots using potential field method. Auton. Robots 2002, 13, 207–222. [Google Scholar] [CrossRef]
- Cao, Q.; Huang, Y.; Zhou, J. An evolutionary artificial potential field algorithm for dynamic path planning of mobile robot. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3331–3336. [Google Scholar]
- Montiel, O.; Sepúlveda, R.; Orozco-Rosas, U. Optimal path planning generation for mobile robots using parallel evolutionary artificial potential field. J. Intell. Robot. Syst. 2015, 79, 237–257. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Kulić, D.; Croft, E.A. Safe planning for human-robot interaction. J. Robot. Syst. 2005, 22, 383–396. [Google Scholar] [CrossRef]
- Kulić, D.; Croft, E.A. Affective state estimation for human–robot interaction. IEEE Trans. Robot. 2007, 23, 991–1000. [Google Scholar] [CrossRef]
- Marder-Eppstein, E.; Berger, E.; Foote, T.; Gerkey, B.; Konolige, K. The Office Marathon: Robust Navigation in an Indoor Office Environment. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 300–307. [Google Scholar]



| m | n | Target Point | ||||
|---|---|---|---|---|---|---|
| 0.2 m | 10 | 1 | 1 | 1 | 2 | (2.5, 2.5) |
| (fast) | (slow) | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 1.2 m | 0.3 m | 0.2 m/s | 0.3 m/s | 0.1 m/s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Liu, G.; Tian, G.; Zhang, J. Smart Obstacle Avoidance Using a Danger Index for a Dynamic Environment. Appl. Sci. 2019, 9, 1589. https://doi.org/10.3390/app9081589
Sun J, Liu G, Tian G, Zhang J. Smart Obstacle Avoidance Using a Danger Index for a Dynamic Environment. Applied Sciences. 2019; 9(8):1589. https://doi.org/10.3390/app9081589
Chicago/Turabian StyleSun, Jiubo, Guoliang Liu, Guohui Tian, and Jianhua Zhang. 2019. "Smart Obstacle Avoidance Using a Danger Index for a Dynamic Environment" Applied Sciences 9, no. 8: 1589. https://doi.org/10.3390/app9081589
APA StyleSun, J., Liu, G., Tian, G., & Zhang, J. (2019). Smart Obstacle Avoidance Using a Danger Index for a Dynamic Environment. Applied Sciences, 9(8), 1589. https://doi.org/10.3390/app9081589





