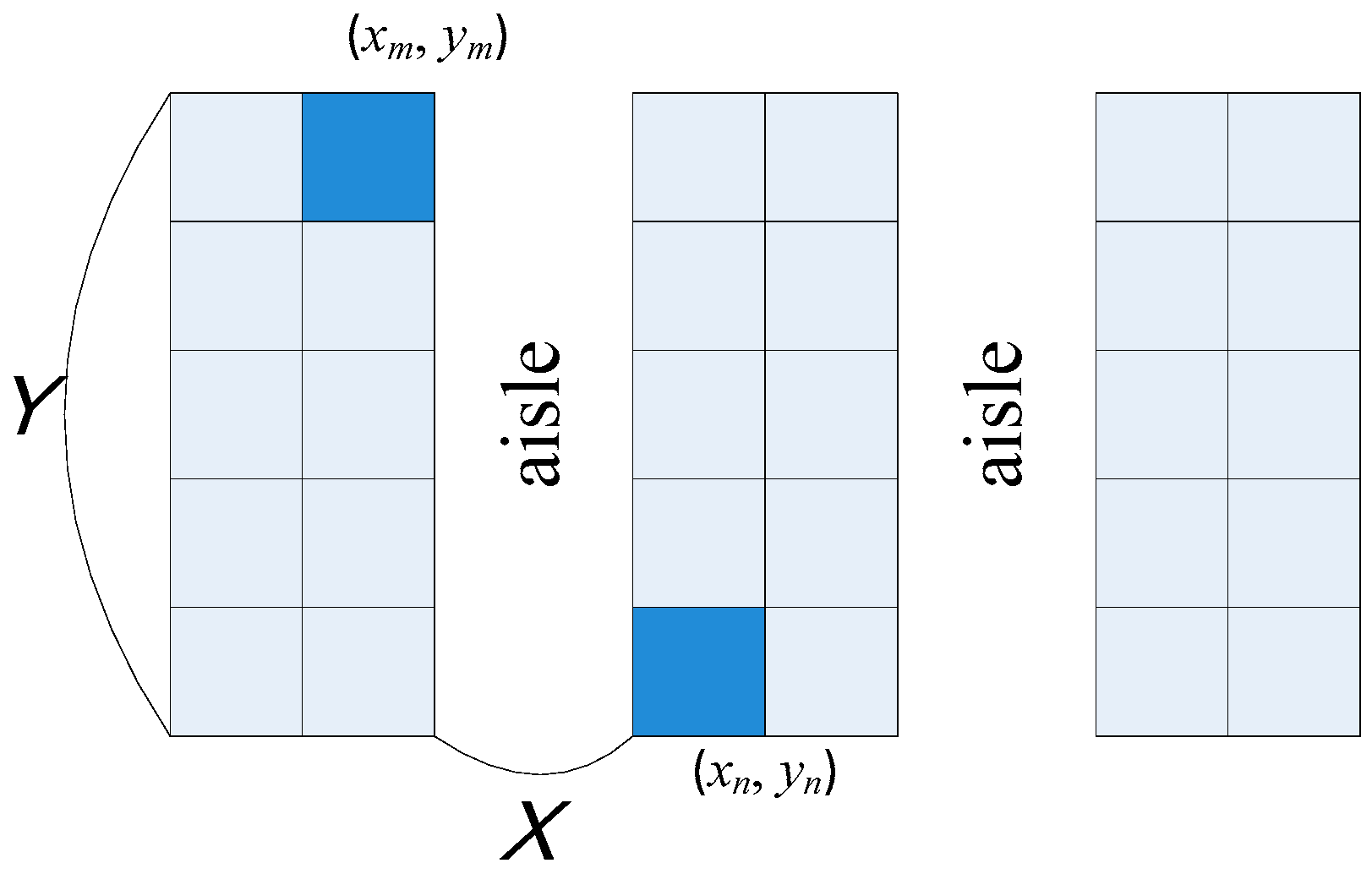1. Introduction
The development of online shopping has created intense competition for traditional retail businesses. These firms have sought to respond by improving their business strategies in terms of ordering, pricing, advertising, shelving, and so on. Effective shelf-space management is a crucial factor in maximizing store profit, minimizing inventories, and building strong relationships with vendors [
1]. Space elasticity has been widely used to estimate the relationship between sales and allocated space [
2,
3,
4], and previous studies have used space elasticity to establish a relationship between shelf space and product demand. However, using space elasticity for shelf-space allocation requires estimating a great number of parameters, resulting in high costs and high error rates in the mathematical models [
5].
Recently, advances in information technology have made it easier for retailers to collect various types of customer data [
6]. Mining this data for insight into customer behavior can help retailers solidify ephemeral relationships with customers into long-term loyalty. As part of this effort, retailers have modified their shelf-space management practices using product association analysis [
7,
8,
9,
10], a powerful data mining tool that can detect significant co-purchase rules underlying a large amount of purchase transaction data. Although previous studies have demonstrated that product association analysis can improve the efficiency of shelf space usage and increase cross-selling possibility, three problems remain to be resolved.
First, most previous studies simply assume that all products in the store can be re-organized based on the outcome of product association analysis. However, moving critical products might disrupt existing customer shopping patterns/rules. In reality, some products are critical to attracting customers and moving them could break existing linkages. Therefore, it might be desirable to analyze the relationships among products before deciding which products are to be re-organized. Second, previous studies have seldom considered the physical proximity of shelf locations when evaluating assignment task. For example, product A and product B are candidates to be assigned to Shelf 1. The original shelf for product A (denoted as Shelf 2) is one foot away from Shelf 1, while the original shelf for product B (denoted as Shelf 3) is ten feet away from Shelf 1. Previous studies might randomly pick a product and assign it to Shelf 1. However, Shelf 1 is much closer to Shelf 2 than to Shelf 3, and failure to consider physical proximity results in some products being reassigned to shelves far from their current locations, which not only incurs a reallocation cost but also increases inconvenience for customers trying to find specific products. Third, previous studies simply assume that products can be reassigned to any locations in the store. In reality, products belong to certain categories and should be grouped with other items within the same category to prevent customer confusion.
To solve these problems, this study proposes a three-stage product-to-shelf assignment method that considers customer purchase behaviors as well as physical and category constraints. The first stage constructs a Product Relationship Network (PRN) that represents the purchase association among product items. Two types of PRNs are studied: Transaction-based networks (TBN) and customer-based networks (CBN), which will be described later in
Section 3.2. The second stage uses network analysis to derive the centrality value of each product item, which reveals the importance of a product item in the network. Based on its centrality value, an item is classified as an attraction item, an opportunity item, or a trivial item (see
Section 3.3.2 for definitions). Opportunity items are those that should be reorganized/re-shelved. The third stage integrates purchase association, geographic relationship, and category constraints to evaluate the location preference of each product. Based on the preference values, a product assignment algorithm is developed to determine the optimal positions/locations for opportunity items.
The remainder of this paper is organized as follows.
Section 2 reviews related research.
Section 3 introduces the proposed method.
Section 4 presents an empirical evaluation and describes a set of experiments. Finally, conclusions and future work directions are discussed in
Section 5.
2. Literature Review
Shelf space is an essential resource in logistics decisions and store management, and well-designed space allocation can attract more consumers and derive increased sales. Corstjens and Doyle [
2] developed a shelf space allocation model which accounts for product space cost elasticity, inter-product cross-elasticity, product profit margins, and product cost. This model was among the first space allocation models to consider interdependencies. A shelf-space allocation problem formulated by Yang and Chen [
3] disregarded cross-elasticities and allowed the profit of each product to vary when allocated to different shelves. Their model was then optimized by Lim et al. [
4] by combining a local search technique with meta-heuristics. However, using space elasticity to determine product assortment and shelf-space allocation requires the estimation of a great quantity of parameters, resulting in increased costs and errors in the mathematical model. In addition, some research used price policy to consider product item location [
11] and explored the product category allocation problem. However, these studies overlooked customer purchase behavior.
Effective shelf-space management can attract consumer attention and encourage additional purchases. Hwang et al. [
12] developed an integrated mathematical model for the shelf space design and item allocation problem and solved it using genetic algorithm. The objective function is composed of the average of an item’s location effect, demand rate, and gross margin. To solve the mathematical problem, they used two types of genetic algorithms: A slicing structure produced by guillotine cuts and horizontal cuts. Cil [
10] used buying association measurements to create a category correlation matrix and applied the multidimensional scale technique to display a set of products in store spaces. Tsafarakis et al. [
13] introduced differential evolution (DE) to assist retailers in adapting their product portfolios in periods of economic recession and facilitate strategic product assortment planning (PAP) decisions. The performance of five different DE implementations was benchmarked against Simulated Annealing. The interrelated issue of assortment adaptation across different retail store formats was also taken into consideration. Flamand et al. [
14] introduced a tactical, store-wide shelf-space management problem where shelves are comprised of smaller, adjacent segments that vary in attractiveness. A product category (e.g., tea or oil) is viewed at an aggregate level. The reward resulting from assigning a product category to a shelf depends on the attractiveness of the shelf segments it is assigned to and its aggregate gross profit. Ghoniem et al. [
15] studied the unclustered variant of the problem, where product categories are taken individually, as a generalized assignment problem with location/allocation considerations for which they develop preprocessing schemes, valid inequalities, and a branch-and-price algorithm that significantly outperforms CPLEX for small- and mid-sized instances. Zhao et al. [
16] developed integrated optimization models with inventory replenishment, shelf display location, and shelf space allocation. The joint optimization models are proposed according to two different situations: (1) Each item is replenished individually; and (2) multiple items are replenished jointly. The results demonstrate that their proposed SA-based hyper-heuristic algorithm is robust and efficient for both joint optimization models. Frontoni et al. [
17] presented a solution to optimally re-allocate shelf space to minimize Out of Stock (OOS) events. The approach uses Shelf Out of Stock (SOOS) data coming in real time from a sensor network technology and an integer linear programming model that integrates a space elastic demand function. Experimental results have proved that the system can efficiently calculate a proper solution able to re-allocate space and reduce OOS events. Flamand et al. [
18] developed a model that jointly examines assortment planning and store-wide shelf space allocation decisions. The model is then solved by a heuristic approach that constructs a high-quality initial solution that is further enhanced using a large-scale neighborhood local search procedure.
Recently, network analysis has been applied to transaction data to provide a better understanding of product relationships from various points of view [
19,
20]. Oestreicher-Singer and Sundararajan [
21] investigated co-purchase networks and demand levels associated with over 250,000 interconnected books over a year. Their results showed that the visibility of co-purchase networks amplifies shared purchasing of complementary products. Raeder and Chawla [
22] used market-basket analysis to evaluate associations between two products, establishing a product network based on history transaction data, followed by community detection. Kim et al. [
23] used product network analysis to extend the market basket analysis with social network analysis. They integrated the centrality concept into product networks and tried to explain the result through social network analysis in actual retail stores. Tsai et al. [
24] proposed a novel shopping behavior prediction system which considers both the quantity and utility of purchased products. A set of frequent shopping patterns, called high-utility mobile sequential patterns (UMSPs), is generated using the UMSPL algorithm. However, the product-to-shelf problem is not addressed in this study.
Grida et al. [
25] introduced a mathematical model to optimize the retail revenue while considering products’ cross-elasticity on demand. The space allocated to each product is considered as a continuous variable that has a lower boundary of one product face. The resulting model, a NP-hard one, is solved using an adaptive meta-heuristic algorithm based on artificial bee colony (ABC). Bianchi-Aguiar et al. [
26] presented a novel mixed integer programming formulation for the shelf space allocation problem considering two innovative features emerging from merchandising rules: Hierarchical product families and display directions. The formulation uses single commodity flow constraints to model product sequencing and explores the product families’ hierarchy to reduce the combinatorial nature of the problem. Reisi et al. [
27] provided a closed-form expression for the approximate solution to the lower-level problem determining the retail prices and the allocated shelf spaces. This solution then is incorporated into the manufacturers’ profit resulting in a single-level optimization problem which is easier to solve.
3. Research Method
3.1. Research Framework and Assumption
Placing products with a high degree of association close to each other raises the likelihood of cross-selling. This paper seeks to develop a method that allocates products to suitable shelves to maximize such associations and thus drive cross-selling.
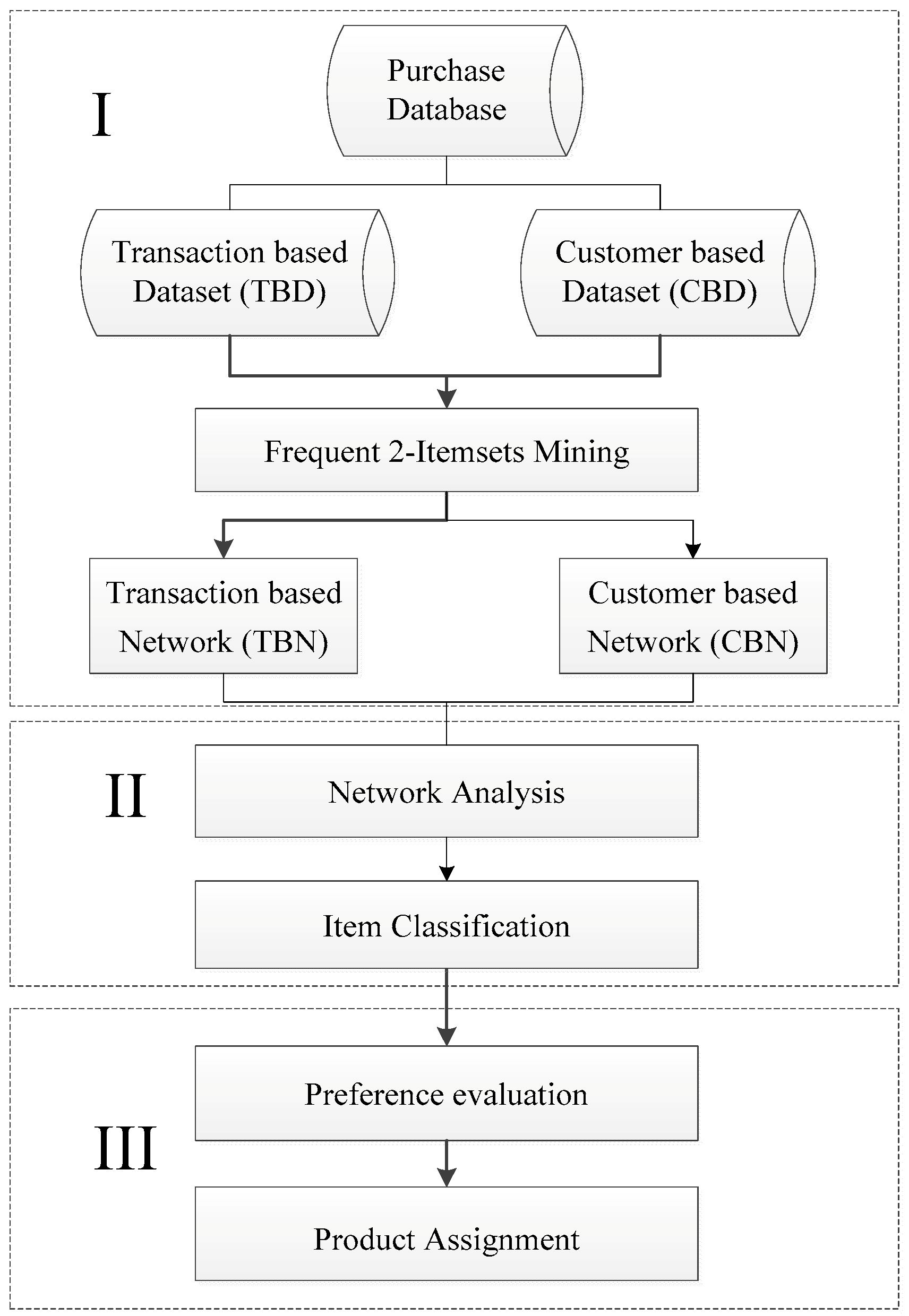
Figure 1 shows the proposed three-stage framework. The first stage constructs a Product Relationship Network (PRN) that represents the purchasing association among the product items. Two types of PRNs—transaction-based networks (TBN) and customer-based networks (CBNs)—are used, depending on how purchasing data are dealt with. The two PRNs will be further defined in
Section 3.2. The second stage uses network analysis to derive the centrality value of each product item, which reveals the importance of the item in its network. Based on the centrality of each product, an item is classified as an attraction item, an opportunity item, or a trivial item. Opportunity items are those to be reorganized/re-shelved. The third stage uses a product assignment algorithm to determine the optimal positions/locations for opportunity items to maximize cross-selling.
The product-to-shelf assignment problem is strongly influenced by a large number of variables that are context specific. Therefore, the following assumptions are made in this study. First, although the type of stores discussed in this study is limited, it is assumed that product volumes are identical and can be smoothly exchanged across the shelves. Second, variables such as the bargaining power of the producers, and setup cost of moving product items are not discussed in this study.
3.2. Product Relationship Networks
Let
I = {
i1,
i2, …,
iP} be the set of product items sold in a store where
P is the total number of product items. A purchase database stores a set of purchase records in which a record consists of a purchase timestamp, a transaction identifier (T_ID), a customer identifier (C_ID), and a product item. Depending on how the product relationship is constructed, product items in the purchase database can be aggregated according to unique T_ID or C_ID. If records are aggregated using T_ID, the dataset is called a transaction-based dataset (TBD). If records are aggregated using C_ID, the dataset is called a customer-based dataset (CBD).
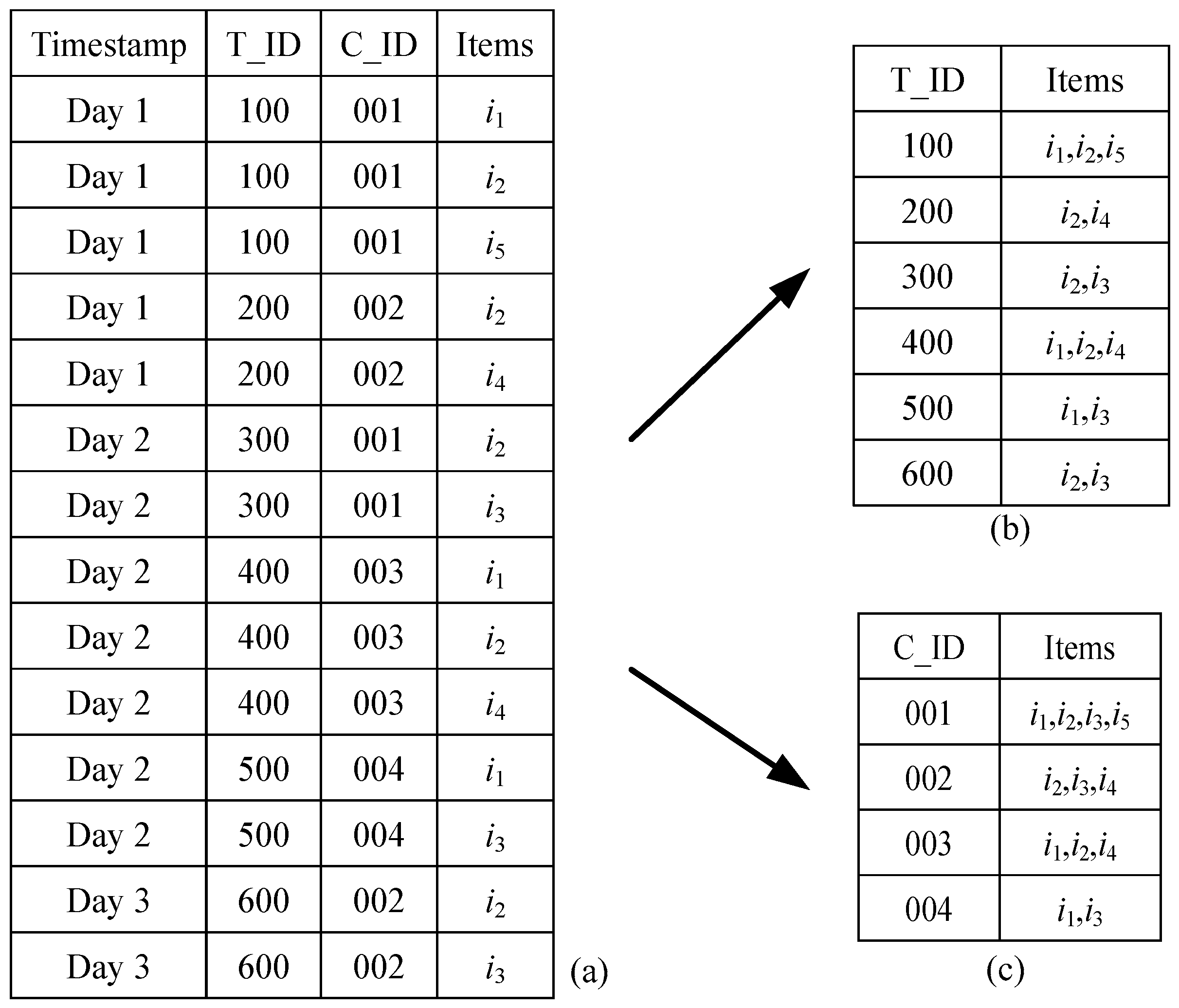
Figure 2 shows a simple aggregation example.
Figure 2a indicates 14 purchase records in a purchase database. After aggregating by T_ID, 6 transaction-based records are generated as shown in
Figure 2b. Similarly, as shown in
Figure 2c, 4 customer-based records are generated if C_ID is used to aggregate the purchase database.
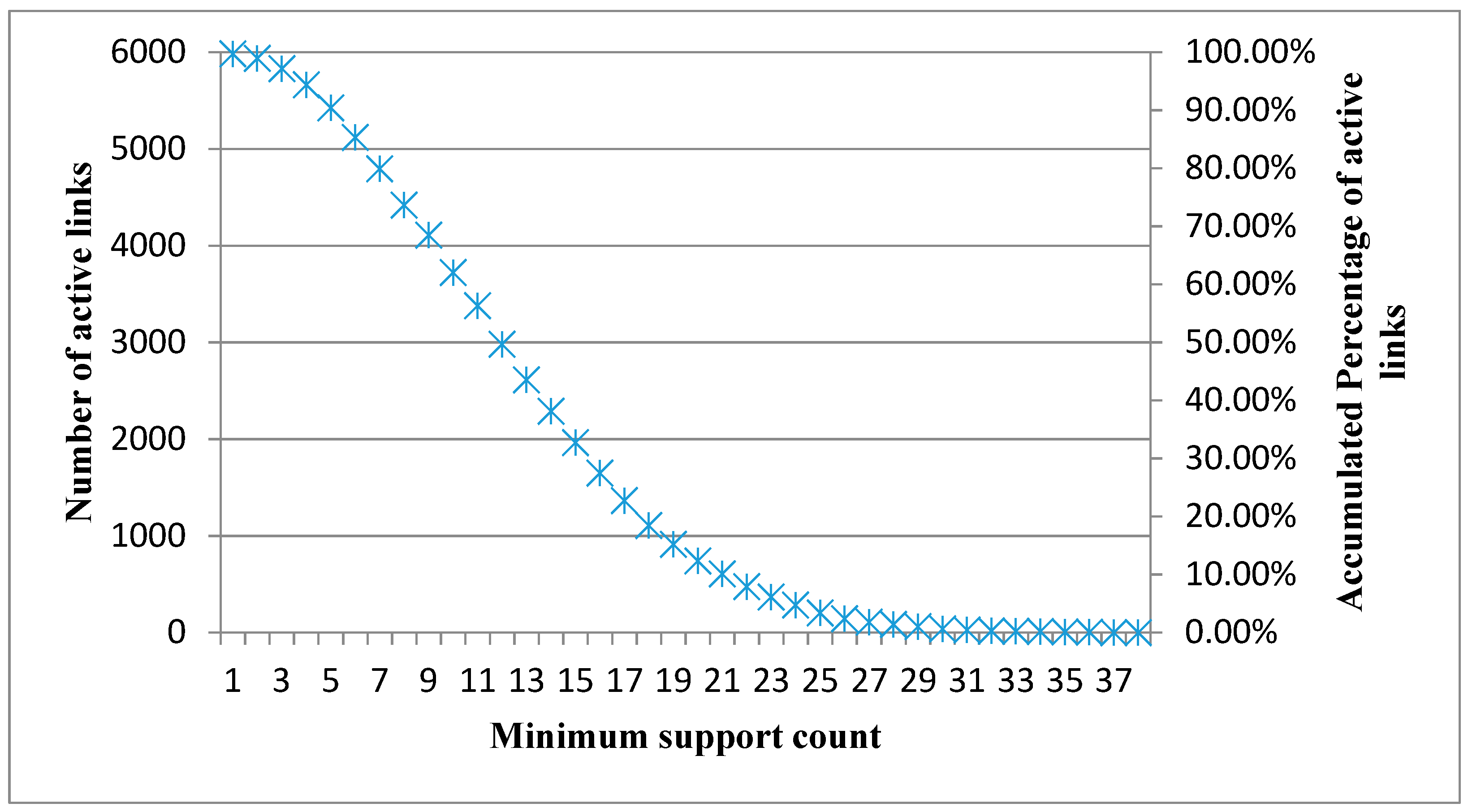
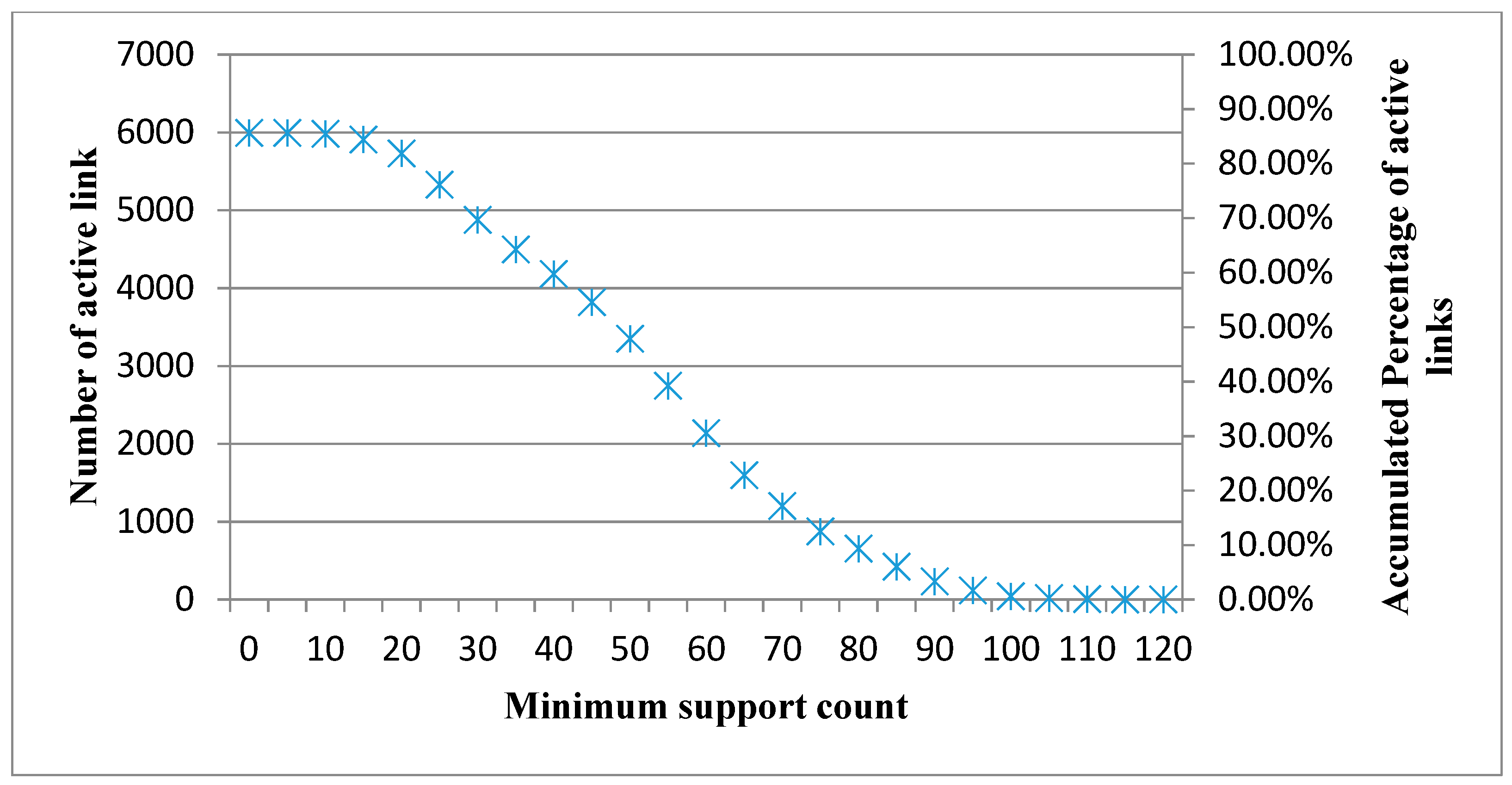
Based on different datasets, two types of Product Relationship Networks (PRNs) are constructed. If the network is constructed using the transaction-based dataset (TBD), the network is called a transaction-based network (TBN). If the network is constructed using the customer-based dataset (CBD), the network is called a customer-based network (CBN). The construction process for both types of PRNs includes the following two phases. The first phase derives all frequent 2-itemsets from an aggregated dataset using the Apriori algorithm under a minimum support count. The second phase builds the product association matrix according to the support values of frequent 2-itemsets.
The Apriori algorithm proposed by Agrawal and Srikant [
7] is a popular method for identifying frequent itemsets. Let
Lk represent the set of all frequent
k-itemsets and
Ck represents the set of candidate
k-itemsets.
k-itemsets may or may not be frequent, but all of the frequent
k-itemsets are included in
Ck. The Apriori algorithm scans the dataset and calculates the count of each candidate in
Ck to determine which
k-itemsets are frequent. All candidates with a count exceeding the minimum support count are frequent and belong to
Lk. Otherwise, the candidates are removed. (
k + 1)-itemsets of
Ck+1, which include frequent
k-itemsets, can be repeatedly generated by
Lk. The algorithm will stop when
Lk = Ø. Note that this algorithm will stop when
k = 2 since only frequent 2-itemsets are required in this study.
After obtaining frequent 2-itemsets, the product association matrix of a PRN can be determined. Let M = [
mi,j] be the product association matrix of size
y × y where
y is the number of individual items which have ever appeared in the frequent 2-itemsets, and
mi,j is defined as:
where
SupCount is the function returning the support count of itemset {
ii,
ij}. If
mij is high, the association between items
ii and
ij is strong. Note that if itemset {
ii,
ij} cannot be found in the frequent 2-itemsets, the support count
mi,j will be marked as “x” in the matrix.
In TBN, records with the same transaction ID are aggregated so that the association value between two items indicates the co-purchase relationship from the viewpoint of transactions. In CBN, records with the same customer ID are aggregated so that the association between items in CBN indicates the co-purchasing relationship from the viewpoint of customers. That is, CBN treats each customer in the store as equally important, while TBN might favor frequent buyers.
3.3. Network Analysis for Item Classification
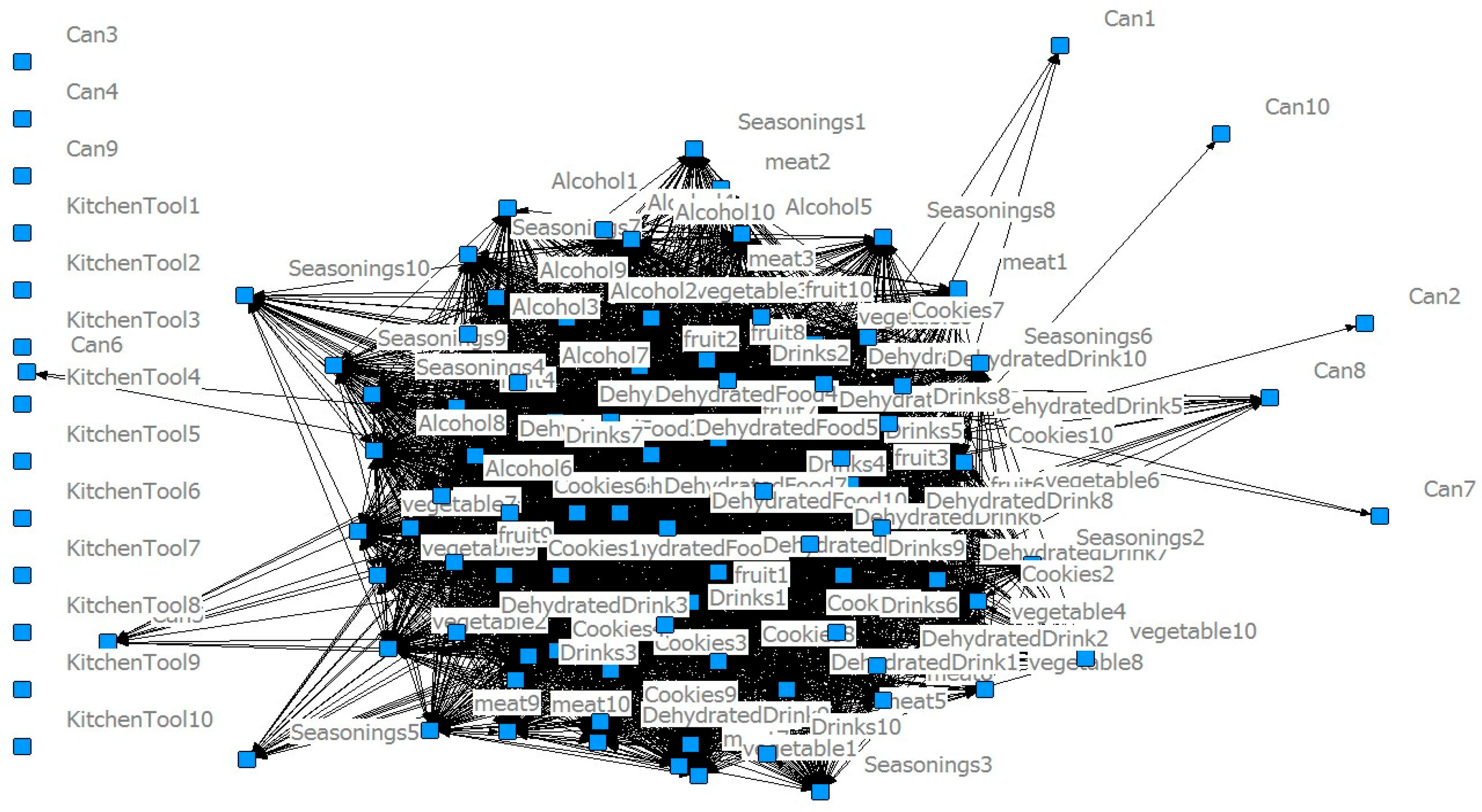
After the product association matrix is obtained, a product item is considered to be a node in a network where a link between two nodes indicates their association strength. In the network, the centrality measure is used to determine the importance of each product item in the store. With this importance, each product is classified as an attraction item, an opportunity item, or a trivial item. Opportunity items are those to be reorganized/re-shelved in the third stage.
3.3.1. Network Analysis
Centrality measure is a popular index used to identify the relative importance of nodes in the network; a higher value indicates the node has a stronger effect in the network. This research uses the two most popular centrality measures, closeness and betweenness [
28]. Closeness centrality measures how close a node is to all other nodes. A node is considered to be central if it can reach all others quickly. Formally, closeness centrality
Cc(
i) is the reciprocal of the sum of the shortest distance from node
i to each other node, which can be formulated as:
where
d(
i,
j) is the distance of the shortest path from node
i to node
j in the network, and
N is the total number of nodes in the network.
Betweenness centrality is a measure of centrality in a network based on shortest paths. For every pair of nodes in a network, there exists at least one shortest path between the nodes such that either the number of edges that the path passes through (for unweighted graphs) or the sum of the weights of the edges (for weighted graphs) is minimized. The betweenness centrality for node
i,
CB(
i), is the number of these shortest paths that pass through node
i. Mathematically, it is defined as:
where
gs,t is the number of shortest paths from node
s to node
t and
gs,t(
i) is the number of the shortest paths from node s to node
t that pass through node
i. In this study, the Dijkstra algorithm [
29] is used to find the shortest path between two nodes.
3.3.2. Item Classification
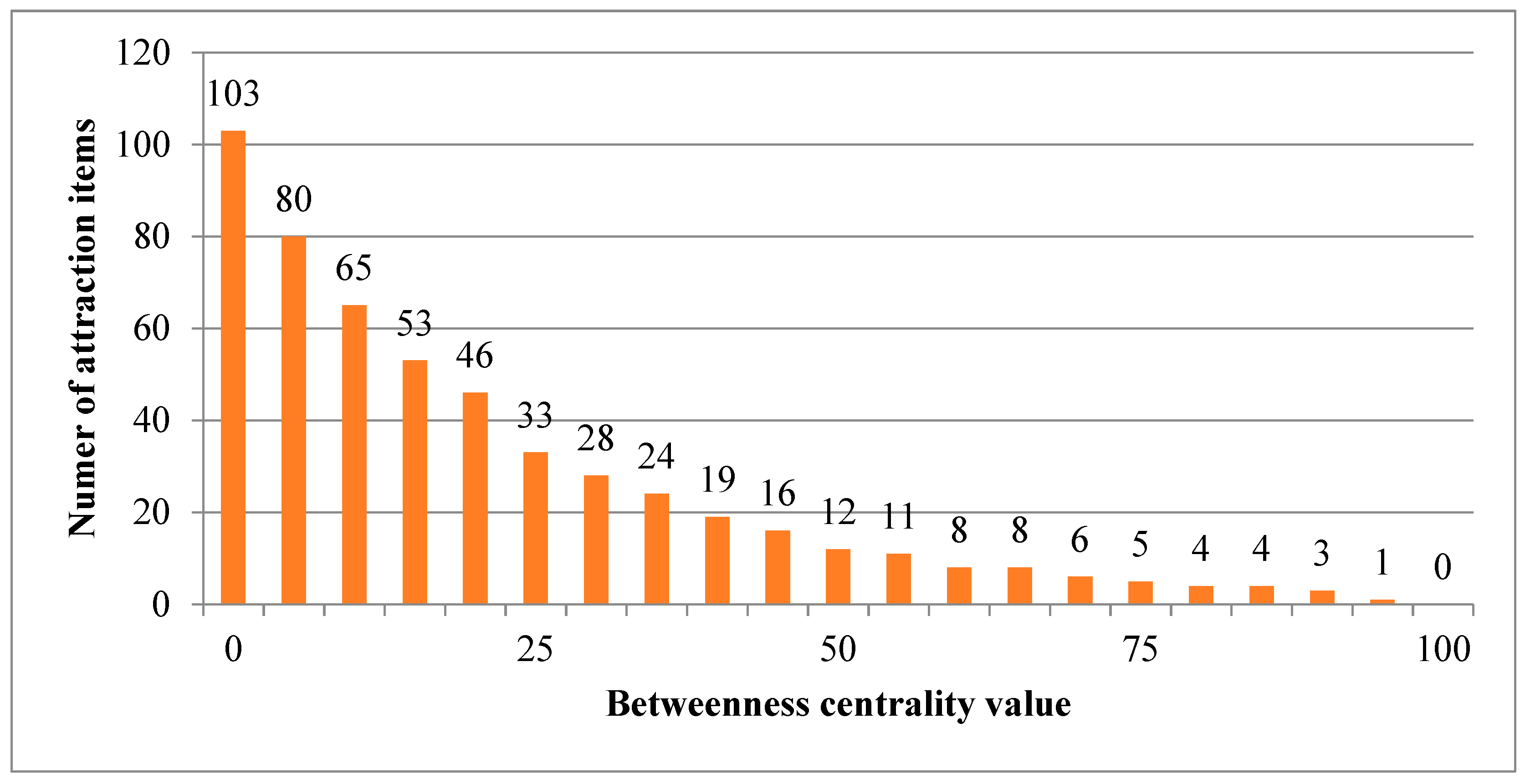
As mentioned in
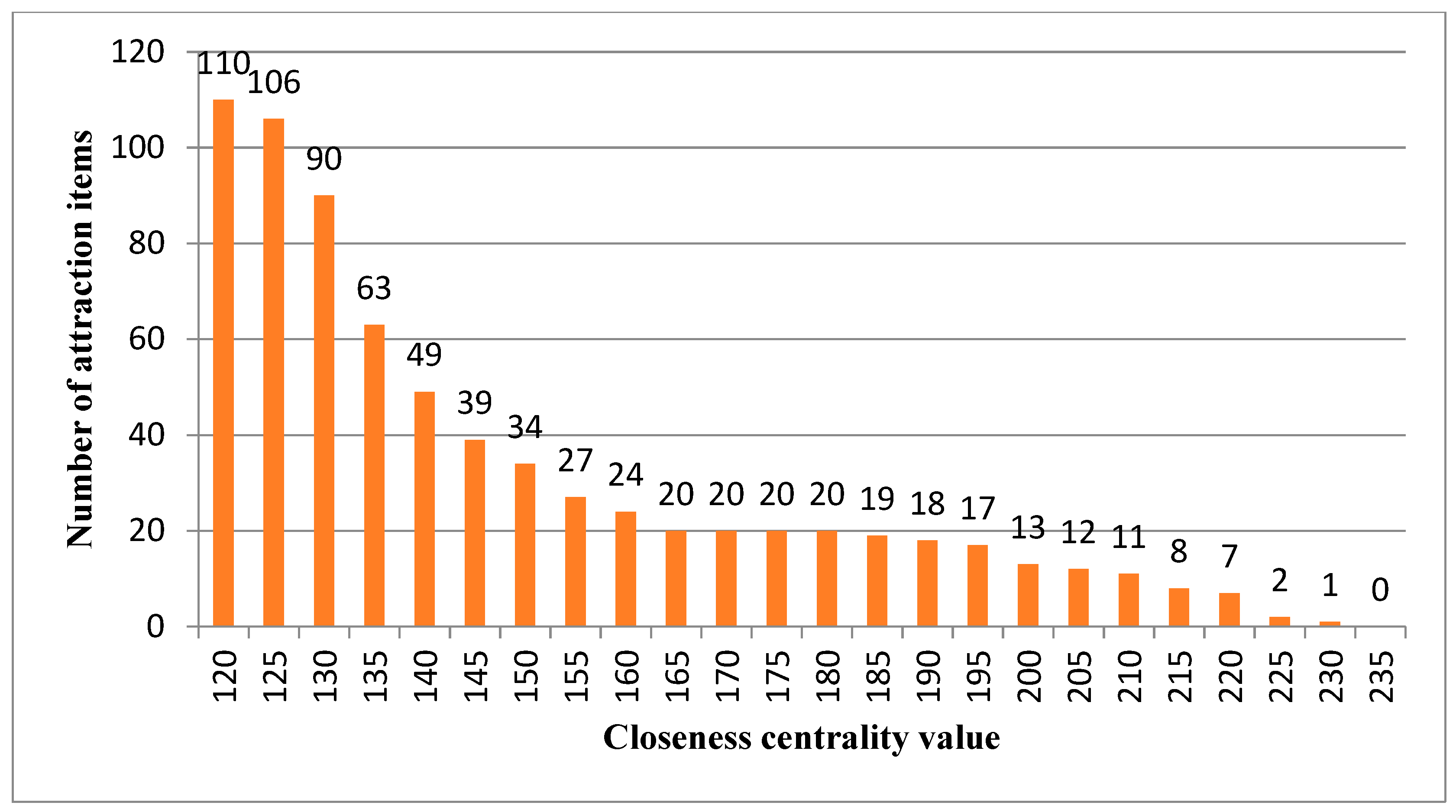
Section 1, not all items are suitable for rearrangement since established shopping behaviors might be disrupted if major attractive items are relocated. To determine item suitability for relocation, this study classifies each product item as an attraction item, an opportunity item, or a trivial item based on its centrality measure.
Definition 1. An attraction item is an item whose centrality value is higher than an upper bound threshold value α in PRN. Attraction items should not be relocated because doing so would disrupt their connection to other products. In the following discussion, the set of attraction items is denoted aswhere C(j) is the centrality for item ij.
Definition 2. An opportunity item is an item whose centrality value is no greater than α but higher than a lower bound threshold value β in PRN. Opportunity items are commodities affiliated with attraction items and might sell better if moved to a more appropriate section/shelf. Therefore, opportunity items are considered to be commodities which should be re-allocated. The set of opportunity items is denoted as.
Definition 3. A trivial item is an item whose centrality value is no greater than β. Trivial items are items which do not show a strong association with other items in PRN. Thus reallocating trivial items might not generate additional sales. The set of trivial items is denoted as.
3.4. Location Preference Evaluation
As mentioned in
Section 3.3.2, opportunity items are those that are re-organized, while attraction items and trivial items are kept in their original locations. To maximize cross-selling, an opportunity item should be moved to a cell close to that of its related attraction items. For example, bottle openers should be placed near bottled beers instead of canned beers. Therefore, the location preference for opportunity items will be evaluated according to purchase association and physical proximity.
Figure 3 illustrates a typical layout consisting of cabinets and aisles in a retail store. A cabinet consists of several cells where a cell is a space used to display a product item. Let (
xm,
ym) and (
xn,
yn) respectively be the center coordinates of cell
m and cell
n. The physical distance between the two cells is defined as:
where
Am is the aisle number of cell
m,
An is the aisle number of cell
n, and
Y is the length of a cabinet. Based on Equation (4), we can derive a physical distance matrix
G = [
gm,n] that shows the physical relationship among all cells.
It is clear that an opportunity item
ii should be placed in a cell close to the set of attraction items,
AI. In addition, if the purchase association between the attraction item
ij and the opportunity item
ii is stronger, items
ij and
ii should be placed closer together. Thus, location preference in which opportunity item
ii is placed to cell
m is defined as:
where
pi,j is the support count for itemset {
ii,
ij} defined in Equation (1),
gm,Cell(j) is the physical distance between cells
m and
Cell(
j), and
Cell(
j) is the function returning the cell to which item
ij belongs.
Product items belong to specific product categories such as beverages, snacks, or fresh food. For management purposes and shopping convenience, a store layout is divided into many zones, each of which is devoted to a single product category. Therefore, the cells to which opportunity items can be moved should be limited by management constraints. Let
ai,m be the likelihood availability that opportunity item
ii is placed in cell
m:
Finally, the final location preference
lpi,m can be derived as:
3.5. Product Assignment
This research assumes that all product items have identical sizes and quantities so that two opportunity items on different shelves can be easily exchanged. The reassignment considers the location preference defined in Equation (7) and reassigns products to the most suitable shelves. Therefore, the objective of product rearrangement is to rearrange opportunity items while minimizing total shelf movement:
subject to:
where opportunity items
i and
j ∈
OI,
Eij = 1 if opportunity item
i is assigned to a shelf which displays opportunity item
j, otherwise
Eij = 0. The item assignment problem shown in Equation (8) is solved using the Hungarian method [
30], a combinatorial optimization algorithm that can solve the assignment problem in polynomial time.
Appendix A shows the computational procedure of the Hungarian method.
5. Discussion and Conclusions
To attract customers and survive in a competitive environment, retailers need to implement appropriate retail-mix strategies including store location, product assortment, pricing, advertising and promotion, store design and shelf display, services, and personal selling. Among these, shelf-space allocation is one of the most important factors in determining customer purchasing decisions. Recently, advances in information technology have made it easier for retailers to collect various types of customer data. Mining this data for insight into customer behavior can help retailers solidify ephemeral relationships with customers into long-term loyalty. As part of this effort, retailers have modified their shelf-space management practices using product association analysis. Previous studies have demonstrated that product association analysis can improve the efficiency of shelf space usage and increase cross-selling.
This study solves the persistent product-to-shelf allocation problem by integrating data mining and network analysis, and makes three major contributions. First, the study compares the effectiveness of transaction-based networks (TBN) and customer-based networks (CBN). Experimental results show that the two network types produce very different association values among products. If store managers want to reduce side effects caused by customers repeatedly purchasing the same products, CBN is a better choice than TBN. Conversely, TBN is more useful if store managers treat all transactions as equally important. Second, this research uses network analysis to evaluate product centrality, and uses the resulting centrality value to classify products as attraction items, opportunity items, or trivial items. Attraction items are popular products which attract customer visits, and should be kept in consistent locations making them easy to find. On the other hand, opportunity items should be relocated to increase cross-selling. Third, this study considers product association along with physical proximity and category constraints when solving the product-to-shelf assignment problem.
Some potential extensions for this research are as follows. First, the proposed method uses closeness and betweenness to measure product centrality in the product relationship network. Different centrality measures give different meanings and future studies should apply a wider range of centrality measures. Second, this study assumes product volumes are identical and can be smoothly exchanged. However, in practice, different products might be displayed in different volumes, and future work should consider this issue. Third, some additional limitations that could be addressed are those concerning restrictions on storage conditions of certain products (e.g. frozen or refrigerated products) or consideration of product relocation costs. Meanwhile, it would be interesting to take the height of positioning within a shelf into consideration. Fourth, this study solves the product-to-shelf assignment using the Hungarian method, which would run too slowly given large quantities of data. Finally, the proposed method is now validated and evaluated using simulated behavior data produced by a transaction sequence generator, and future work should apply authentic store transaction data.