Energy-Aware Online Non-Clairvoyant Scheduling Using Speed Scaling with Arbitrary Power Function
Abstract
1. Introduction
2. Related Work
3. Definitions and Notations
3.1. Scheduling Basics
3.2. Power Function
- Acceptable speeds are a countable collection of disjoint subintervals of
- All the intervals, excluding probably the rightmost, are closed on both ends
- The rightmost interval may be open on the right if the power approaches infinity, as the speed s approaches the rightmost endpoint of that interval
- is non-negative, continuous and differentiable on all but countable many points
- Either there is a maximum allowable speed T, or the limit inferior of as s approaches infinity is not zero Without loss of generality, it can be assumed that [24]:
- P is strictly convex and increasing
- P is unbounded, continuous and differentiable
3.3. Amortized Local Competitive Analysis
4. A 2-Comptitive Scheduling Highest Scaled Importance First (HSIF)
4.1. Scaled Importance-Based Flow Plus Energy
4.1.1. Algorithm HSIF
| Algorithm Highest Scaled Importance First (HSIF) |
| Input: number of active jobs At time t, the importance of all active jobs and the executed time for all active jobs . Output: The speed of all processors and execution sequence of jobs. |
| 1. On arrival of a job 2. If CPU is idle allocate the job to CPU 3. 4. speed of CPU 5. else if CPU is executing some job 6. 7. 8. speed of CPU 9. On completion of a job 10. if 11. 12. select the job with 13. 14. 15. else speed of CPU |
4.1.2. Potential Function
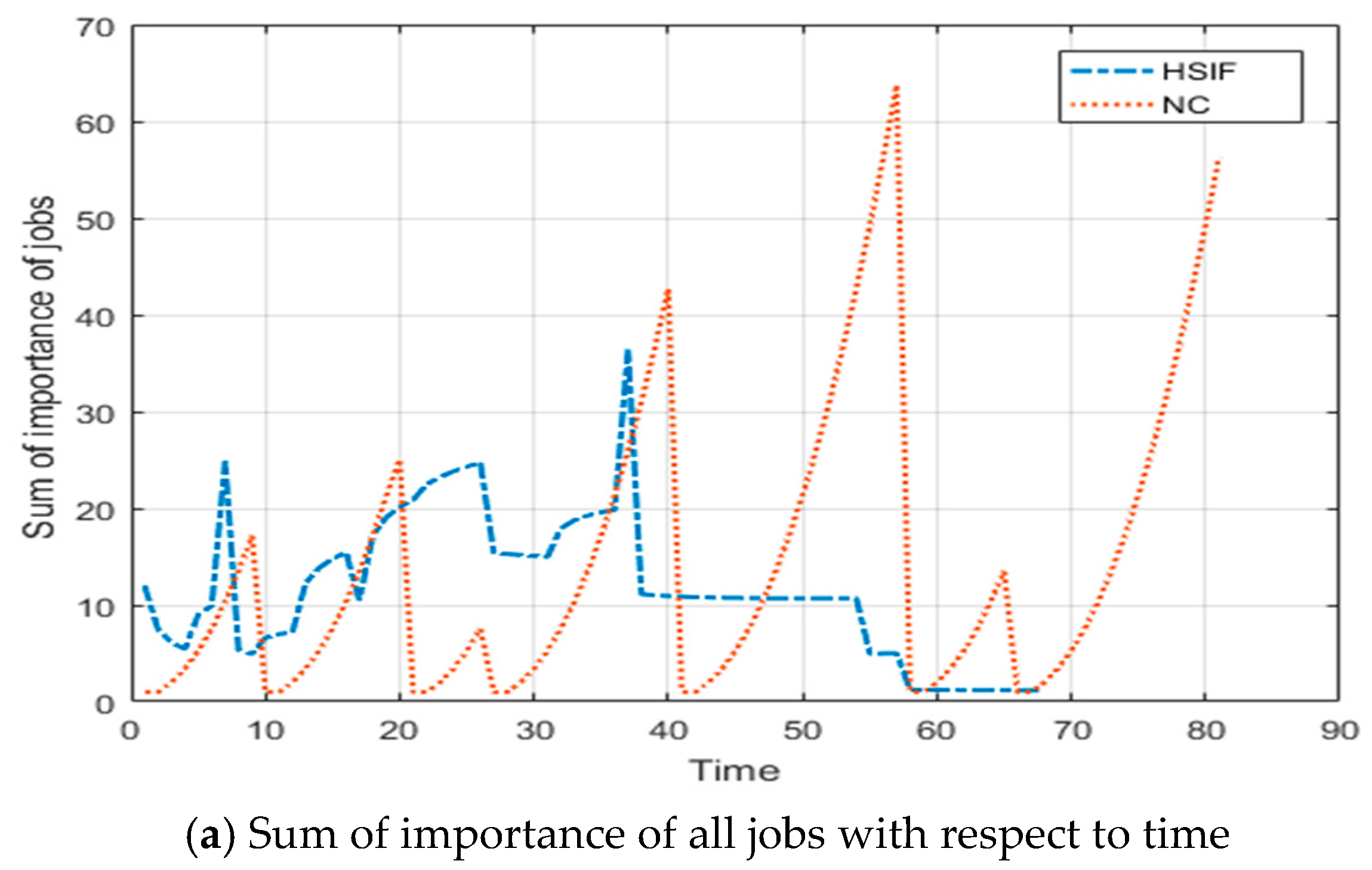
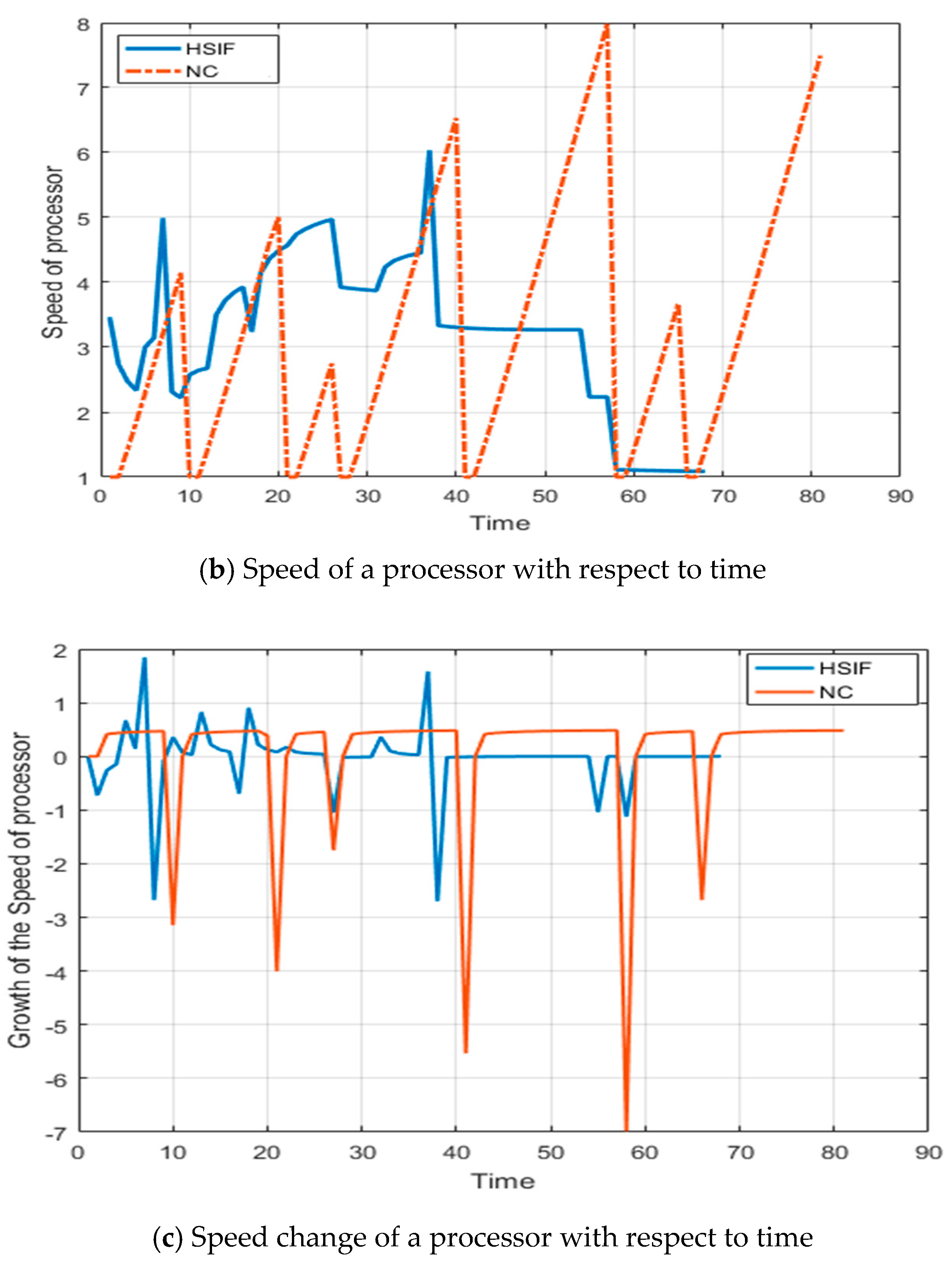
5. Illustrative Example
- For Turnaround Time p-value is less than 0.05 in Levene’s Test for Equality of Variances; therefore, the null hypothesis (the variability of the two groups is equal) is rejected. The lower row of the output (the row labeled “Equal variances not assumed”) is considered. A t test passed to reveal a statistically reliable difference between the mean values of Turnaround Time of HSIF (M = 13.42, s = 12.511366261) and NC (M = 20.6, s = 19.786616792) with t(82.782) = 2.17, p = 0.033.
- The total Turnaround Time for HSIF is 359 time unit lesser than the total Turnaround Time for NC. The average Turnaround Time for HSIF is 7.18 time unit lesser than the average Turnaround Time for NC.
- For Response Time p-value is less than 0.05 in Levene’s Test for Equality of Variances; therefore, the null hypothesis (the variability of the two groups is equal) is rejected. The lower row of the output (the row labeled “Equal variances not assumed”) is considered. A t test passed to reveal a statistically reliable difference between the mean values of Response Time of HSIF (M = 11.72, s = 12.748813) and NC (M = 18.32, s = 19.976966) with t(83.23) = 2.17, p = 0.05.
- The total Response Time for HSIF is 330 time unit lesser than the total Response Time for NC. The average Response Time for HSIF is 6.6 time unit lesser than the average Response Time for NC.
- For Completion Time p-value is greater than 0.05 in Levene’s Test for Equality of Variances; therefore, the null hypothesis (the variability of the two groups is equal) is considered. The upper row of the output (the row labeled “Equal variances assumed”) is considered. A t test failed to reveal a statistically reliable difference between the mean values of Completion Time of HSIF (M = 67.4, s = 30.651431) and NC (M = 74.82, s = 34.902014) with t(98) = 1.13, p = 0.261.
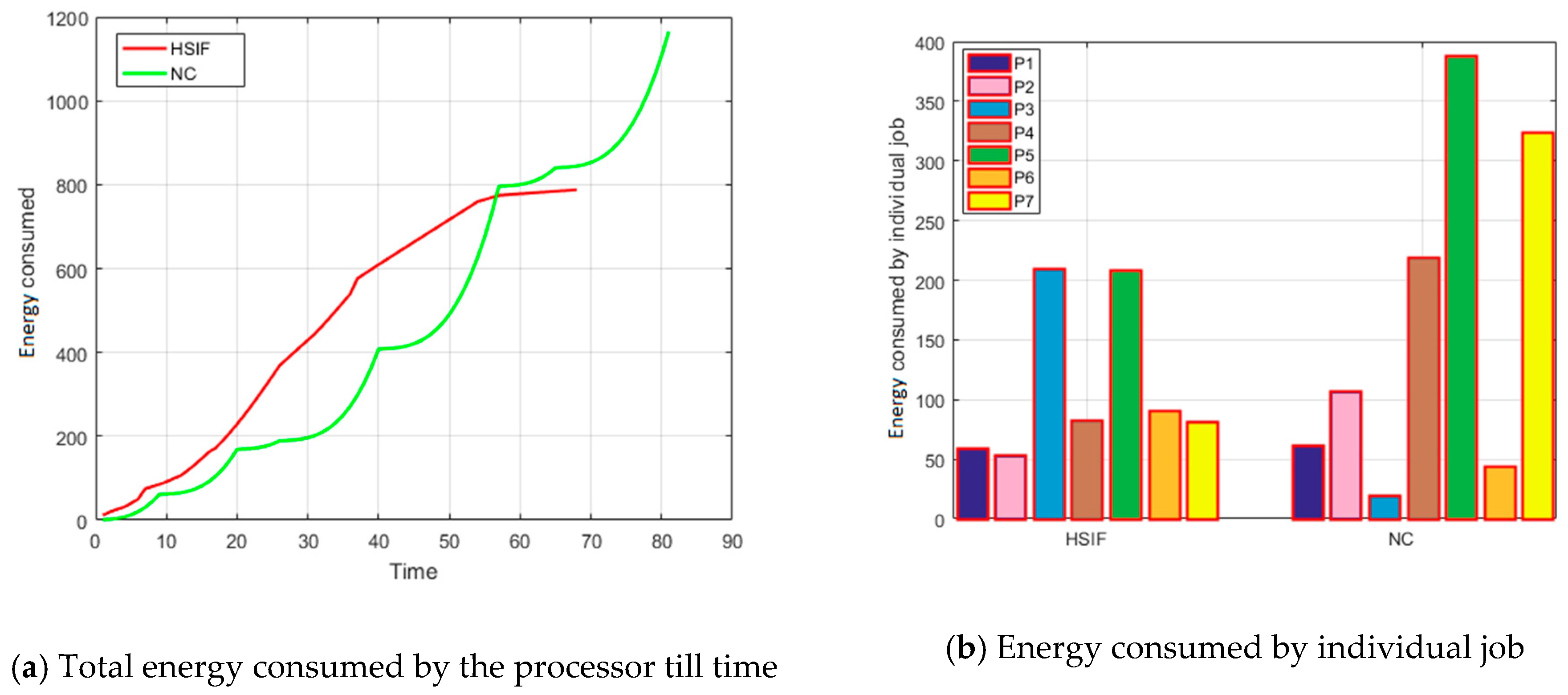
- For Energy Consumed p-value is greater than 0.05 in Levene’s Test for Equality of Variances; therefore, the null hypothesis (the variability of the two groups is equal) is considered. The upper row of the output (the row labeled “Equal variances assumed”) is considered. A t test failed to reveal a statistically reliable difference between the mean values of Energy Consumed of HSIF (M = 196.7, s = 160.31869) and NC (M = 274.778, s = 291.01057) with t(98) = 1.66, p = 0. 1.
- Although, the statistical test failed to identify the difference in HSIF and NC on the basis of energy consumed, the total Energy Consumed for HSIF is 3909.937747 unit lesser than the total Energy Consumed for NC. The average Energy Consumed for HSIF is 78.07875 unit lesser than the average Energy Consumed for NC.
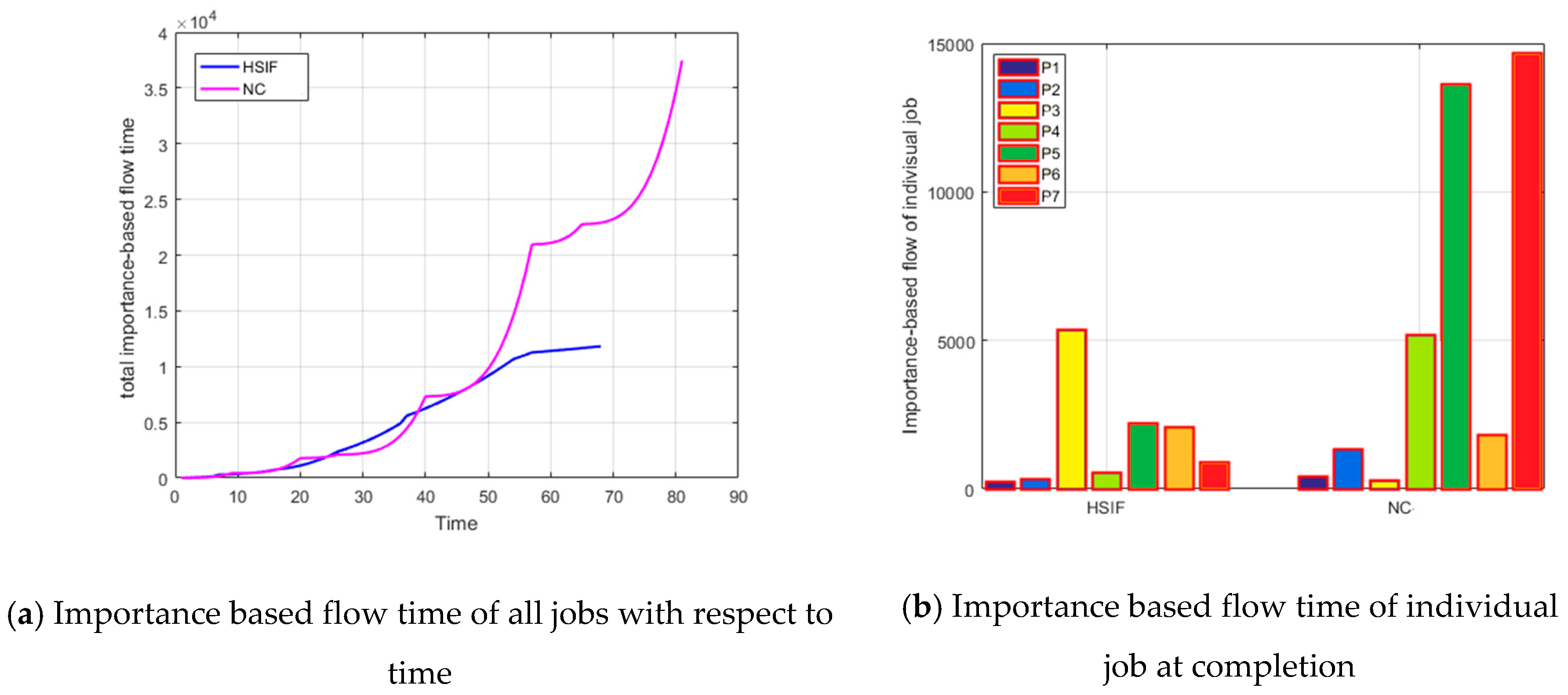
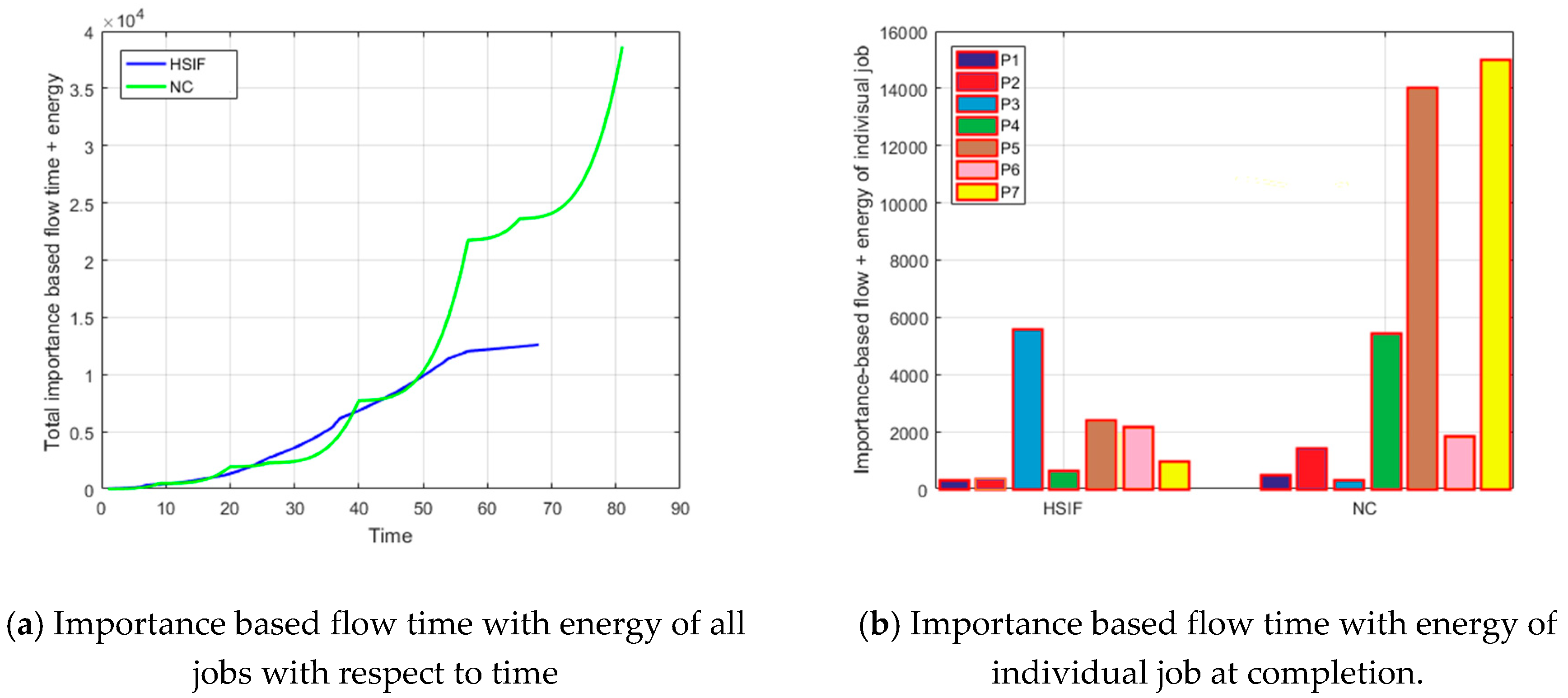
- For Importance-based Flow Time p-value is less than 0.05 in Levene’s Test for Equality of Variances; therefore, the null hypothesis (the variability of the two groups is equal) is rejected. The lower row of the output (the row labeled “Equal variances not assumed”) is considered. A t test passed to reveal a statistically reliable difference between the mean values of Importance-based Flow Time of HSIF (M = 2479.15, s = 3625.2051) and NC (M = 15373.3, s = 21122.893) with t(63.08) = 1.95, p = 0.05.
- The total Importance-based Flow Time for HSIF is 139381.7662 unit lesser than the total Importance-based Flow Time for NC. The average Importance-based Flow Time for HSIF is 2787.635324 unit lesser than the average Importance-based Flow Time for NC.
- For Importance-based Flow Time plus Energy p-value is less than 0.05 in Levene’s Test for Equality of Variances; therefore, the null hypothesis (the variability of the two groups is equal) is rejected. The lower row of the output (the row labeled “Equal variances not assumed”) is considered. A t test passed to reveal a statistically reliable difference between the mean values of Importance-based Flow Time plus Energy of HSIF (M = 2675.83, s = 3774.8105) and NC (M = 5541.57, s = 9740.346) with t(63.39) = 1.94, p = 0.05.
- The total Importance-based Flow Time plus Energy for HSIF is 143286.703 unit lesser than the total Importance-based Flow Time plus Energy for NC. The average Importance-based Flow Time plus Energy for HSIF is 2865.73406 unit lesser than the average Importance-based Flow Time plus Energy for NC.
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Singh, P. Prashast Release Round Robin: R3 an energy-aware non-clairvoyant scheduling on speed bounded processors. Karbala Int. J. Mod. Sci. 2015, 1, 225–236. [Google Scholar] [CrossRef]
- Singh, P.; Wolde-Gabriel, B. Executed-time Round Robin: EtRR an online non-clairvoyant scheduling on speed bounded processor with energy management. J. King Saud Univ. Comput. Inf. Sci. 2016, 29, 74–84. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. EPA Report on server and data centre energy efficiency. Available online: https://www.energystar.gov/index.cfm?c=prod_development.server_efficiency_study (accessed on 10 June 2015).
- Shehabi, A.; Smith, S.J.; Masanet, E.; Koomey, J. Data center growth in the United States: Decoupling the demand for services from electricity use. Environ. Res. Lett. 2018, 13, 1–12. [Google Scholar] [CrossRef]
- Fernández-Cerero, D.; Jakobik, A.; Grzonka, D.; Kołodziej, J.; Fernandez-Montes, A. Security supportive energy-aware scheduling and energy policies for cloud environments. J. Parallel Distrib. Comput. 2018, 119, 191–202. [Google Scholar] [CrossRef]
- Lei, H.; Wang, R.; Zhang, T.; Liu, Y.; Zha, Y. A multi-objective co-evolutionary algorithm for energy-efficient scheduling on a green data center. Comput. Oper. Res. 2016, 75, 103–117. [Google Scholar] [CrossRef]
- Chan, H.-L.; Edmonds, J.; Pruhs, K. Speed Scaling of Processes with Arbitrary Speedup Curves on a Multiprocessor. Theory Comput. Syst. 2011, 49, 817–833. [Google Scholar] [CrossRef][Green Version]
- Bansal, N.; Kimbrel, T.; Pruhs, K. Dynamic speed scaling to manage energy and temperature. J. ACM 2007, 54, 1–39. [Google Scholar] [CrossRef]
- Pruhs, K.; Uthaisombut, P.; Woeginger, G. Getting the best response for your erg. ACM Trans. Algorithms 2008, 4, 1–17. [Google Scholar] [CrossRef]
- Bansal, N.; Chan, H.L.; Pruhs, K. Speed scaling with an arbitrary power function. In Proceedings of the Annual ACM-SIAM Symposium on Discrete Algorithms, New York, NY, USA, 4–6 January 2009; pp. 693–701. [Google Scholar]
- Azar, Y.; Devanur, N.R.; Huang, Z.; Panigrahi, D. Speed Scaling in the Non-clairvoyant Model. In Proceedings of the Annual ACM Symposium on Parallelism in Algorithms and Architectures, Portland, OR, USA, 13–15 June 2015; pp. 133–142. [Google Scholar]
- Bansal, N.; Pruhs, K.; Stein, C. Speed Scaling for Weighted Flow Time. SIAM J. Comput. 2009, 39, 1294–1308. [Google Scholar] [CrossRef]
- Motwani, R.; Phillips, S.; Torng, E. Nonclairvoyant scheduling. Theor. Comput. Sci. 1994, 30, 17–47. [Google Scholar] [CrossRef]
- Bansal, N.; Dhamdhere, K.; Konemann, J.; Sinha, A. Non-clairvoyant Scheduling for Minimizing Mean Slowdown. Algorithmica 2004, 40, 305–318. [Google Scholar] [CrossRef]
- Yao, F.; Demers, A.; Shenker, S. A scheduling model for reduced CPU energy. In Proceedings of the Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 23–25 October 1995; pp. 374–382. [Google Scholar]
- Leonardi, S.; Raz, D. Approximating total flow time on parallel machines. In Proceedings of the ACM Symposium on Theory of Computing, El Paso, TX, USA, 4–6 May 1997; pp. 110–119. [Google Scholar]
- Chekuri, C.; Khanna, S.; Zhu, A. Algorithms for minimizing weighted flow time. In Proceedings of the ACM Symposium on Theory of Computing, Crete, Greece, 6–8 July 2001; pp. 84–93. [Google Scholar]
- Awerbuch, B.; Azar, Y.; Leonardi, S.; Regev, O. Minimizing the Flow Time Without Migration. SIAM J. Comput. 2002, 31, 1370–1382. [Google Scholar] [CrossRef]
- Avrahami, N.; Azar, Y. Minimizing total flow time and total completion time with immediate dispatching. In Proceedings of the ACM Symposium on Parallelism in Algorithms and Architectures, San Diego, CA, USA, 7–9 June 2003; p. 11. [Google Scholar]
- Chekuri, C.; Goel, A.; Khanna, S.; Kumar, A. Multiprocessor scheduling to minimize flow time with epsilon resource augmentation. In Proceedings of the ACM Symposium on Theory of Computing, Chicago, IL, USA, 13–15 June 2004; pp. 363–372. [Google Scholar]
- Pruhs, K.; Sgall, J.; Torng, E. Online Scheduling. In Handbook of Scheduling: Algorithms, Models, and Performance Analysis, 1st ed.; Leung, J.Y.-T., Ed.; CRC Press: Boca Raton, FL, USA, 2004; pp. 15–41. [Google Scholar]
- Becchetti, L.; Leonardi, S.; Marchetti-Spaccamela, A.; Pruhs, K. Online weighted flow time and deadline scheduling. J. Discret. Algorithms 2006, 4, 339–352. [Google Scholar] [CrossRef][Green Version]
- Chadha, J.; Garg, N.; Kumar, A.; Muralidhara, V. A competitive algorithm for minimizing weighted flow time on unrelated processors with speed augmentation. In Proceedings of the Annual ACM Symposium on Theory of Computing, Bethesda, MD, USA, 31 May–2 June 2009; pp. 679–684. [Google Scholar]
- Anand, S.; Garg, N.; Kumar, A. Resource Augmentation for Weighted Flow-time explained by Dual Fitting. In Proceedings of the Twenty-Third Annual ACM-SIAM Symposium on Discrete Algorithms, Kyoto, Japan, 17–19 January 2012; pp. 1228–1241. [Google Scholar]
- Albers, S.; Fujiwara, H. Energy-efficient algorithms for flow time minimization. ACM Trans. Algorithms 2007, 3, 49. [Google Scholar] [CrossRef]
- Chan, S.-H.; Lam, T.-W.; Lee, L.-K. Non-clairvoyant Speed Scaling for Weighted Flow Time. In Proceedings of the Annual European Symposium, Liverpool, UK, 6–8 September 2010; pp. 23–35. [Google Scholar]
- Im, S.; Kulkarni, J.; Munagala, K.; Pruhs, K. SelfishMigrate: A Scalable Algorithm for Non-clairvoyantly Scheduling Heterogeneous Processors. In Proceedings of the 2014 IEEE 55th Annual Symposium on Foundations of Computer Science (FOCS), Philadelphia, PA, USA, 18–21 October 2014; pp. 531–540. [Google Scholar]
- Fernández-Cerero, D.; Fernández-Montes, A.; Ortega, J.A. Energy policies for data-center monolithic schedulers. Expert Syst. Appl. 2018, 110, 170–181. [Google Scholar] [CrossRef]
- Duy, T.V.T.; Sato, Y.; Inoguchi, Y. Performance evaluation of a Green Scheduling Algorithm for energy savings in Cloud computing. In Proceedings of the IEEE international Symposium on Parallel & Distributed Processing, Workshops and Phd Forum (IPDPSW), Atlanta, GA, USA, 19–23 April 2010; pp. 1–8. [Google Scholar]
- Beloglazov, A.; Abawajy, J.; Buyya, R. Energy-aware resource allocation heuristics for efficient management of data centers for Cloud computing. Futur. Gener. Comput. Syst. 2012, 28, 755–768. [Google Scholar] [CrossRef]
- Sohrabi, S.; Tang, A.; Moser, I.; Aleti, A. Adaptive virtual machine migration mechanism for energy efficiency. In Proceedings of the 2016 IEEE/ACM 5th International Workshop on Green and Sustainable Software (GREENS), Austin, TX, USA, 16 May 2016; pp. 8–14. [Google Scholar]
- Juarez, F.; Ejarque, J.; Badia, R.M. Dynamic energy-aware scheduling for parallel task-based application in cloud computing. Futur. Gener. Comput. Syst. 2018, 78, 257–271. [Google Scholar] [CrossRef]
- Gupta, A.; Krishnaswamy, R.; Pruhs, K. Scalably Scheduling Power-Heterogeneous Processors. In Proceedings of the 37th International Colloquium Conference on Automata, Languages and Programming, Bordeaux, France, 6–10 July 2010; pp. 312–323. [Google Scholar]
- Sun, H.; He, Y.; Hsu, W.-J.; Fan, R. Energy-efficient multiprocessor scheduling for flow time and makespan. Theor. Comput. Sci. 2014, 550, 1–20. [Google Scholar] [CrossRef]
| Function Type Used | Algorithms | Competitiveness | Clairvoyant/Non-Clairvoyant | ||
|---|---|---|---|---|---|
| Traditional Power Function | SelMig [27] | 4 | 9 | Non-clairvoyant | |
| NC [11] | 3 | 2.5 | Non-clairvoyant | ||
| ALG [12] | 2 | 2.52 | Clairvoyant | ||
| Arbitrary Power Function | WLAPS [26] | where | >16 | >16 | Non-clairvoyant |
| OCA [10] | 2 | 2 | 2 | Clairvoyant | |
| HSIF [this paper] | 2 | 2 | 2 | Non-clairvoyant | |
| Simulation Parameters | Values |
|---|---|
| CPU | Intel(R) Core(TM) i5-4210U CPU @ 1.70 GHz |
| RAM | 4.00 GB RAM |
| Hard Drive | 1.0 TB |
| Operating System | Red Hat Linux 6.1 |
| Kernel | Linux kernel version 2.2.12 |
| Job | Arrival Time | Importance | Size | Completion Time | Turnaround Time | Response Time | |||
|---|---|---|---|---|---|---|---|---|---|
| HSIF | NC | HSIF | NC | HSIF | NC | ||||
| J1 | 1 | 6 | 17.19 | 7 | 9 | 6 | 8 | 0 | 0 |
| J2 | 5 | 4 | 25.06 | 16 | 20 | 11 | 15 | 3 | 5 |
| J3 | 10 | 2 | 7.55 | 57 | 26 | 47 | 16 | 45 | 11 |
| J4 | 13 | 5 | 42.67 | 26 | 40 | 13 | 27 | 4 | 14 |
| J5 | 18 | 7 | 63.72 | 37 | 57 | 19 | 39 | 9 | 23 |
| J6 | 22 | 1 | 13.51 | 68 | 65 | 46 | 43 | 36 | 36 |
| J7 | 32 | 3 | 56.22 | 54 | 81 | 22 | 49 | 6 | 34 |
| Average values | 23.429 | 28.143 | 14.714 | 17.571 | |||||
| Job | Energy Consumed by Individual Job | Importance Based Flow Time of Individual Job | Importance Based Flow Time Plus Energy of Individual Job | |||
|---|---|---|---|---|---|---|
| HSIF | NC | HSIF | NC | HSIF | NC | |
| J1 | 59.77377 | 62.24247 | 253.36673 | 429.27161 | 313.1405 | 490.5141 |
| J2 | 54.20484 | 107.6397 | 333.41095 | 1348.8623 | 387.6158 | 1456.502 |
| J3 | 209.4849 | 20.23206 | 5397.3745 | 316.85458 | 5606.859 | 337.0866 |
| J4 | 82.46035 | 218.886 | 584.23193 | 5219.856 | 666.6923 | 5438.742 |
| J5 | 208.9329 | 388.0375 | 2226.1519 | 13632.101 | 2435.085 | 14020.14 |
| J6 | 90.82497 | 44.05148 | 2118.0612 | 1816.3544 | 2208.886 | 1860.406 |
| J7 | 82.03271 | 324.3166 | 906.74077 | 14714.469 | 988.7735 | 15038.79 |
| Total | 787.7144 | 1165.406 | 11819.338 | 37477.769 | 12607.05 | 38642.17 |
| Job | Arrival Time | Importance | Size | Completion Time | Turnaround Time | Response Time | |||
|---|---|---|---|---|---|---|---|---|---|
| HSIF | NC | HSIF | NC | HSIF | NC | ||||
| J1 | 1 | 3 | 5 | 4 | 5 | 3 | 4 | 0 | 0 |
| J2 | 3 | 6 | 6 | 7 | 11 | 4 | 8 | 2 | 3 |
| J3 | 7 | 5 | 8 | 10 | 18 | 3 | 11 | 1 | 5 |
| J4 | 9 | 1 | 10 | 15 | 25 | 6 | 16 | 2 | 10 |
| J5 | 10 | 2 | 10 | 44 | 32 | 34 | 22 | 29 | 16 |
| J6 | 15 | 8 | 14 | 19 | 41 | 4 | 26 | 1 | 18 |
| J7 | 15 | 4 | 17 | 38 | 50 | 23 | 35 | 19 | 27 |
| J8 | 18 | 7 | 21 | 23 | 60 | 5 | 42 | 2 | 33 |
| J9 | 20 | 9 | 22 | 28 | 71 | 8 | 51 | 4 | 41 |
| J10 | 28 | 9 | 23 | 33 | 82 | 5 | 54 | 1 | 44 |
| Average values | 9.5 | 26.9 | 6.1 | 19.7 | |||||
| Job | Energy Consumed by Individual Job | Importance Based Flow Time of Individual Job | Importance Based Flow Time Plus Energy of Individual Job | |||
|---|---|---|---|---|---|---|
| HSIF | NC | HSIF | NC | HSIF | NC | |
| J1 | 15.5376 | 11.41421 | 33.58979 | 47.65685 | 49.12738 | 60.07107 |
| J2 | 30.39531 | 18.67619 | 86.8327 | 140.9953 | 117.228 | 159.6715 |
| J3 | 20.89599 | 28.23206 | 50.98298 | 291.4622 | 71.87897 | 319.6943 |
| J4 | 7.883328 | 30.23206 | 30.62239 | 466.6225 | 38.50572 | 496.8546 |
| J5 | 134.5865 | 30.23206 | 2437.376 | 648.0149 | 2571.962 | 678.2469 |
| J6 | 40.10598 | 58.05148 | 114.9347 | 1445.479 | 155.0407 | 1503.531 |
| J7 | 169.0947 | 61.05148 | 2119.993 | 2075.943 | 2289.088 | 2136.994 |
| J8 | 48.41263 | 82.24247 | 166.9621 | 3353.273 | 215.3747 | 3435.516 |
| J9 | 95.6372 | 104.5797 | 452.1316 | 5172.41 | 547.7688 | 5276.99 |
| J10 | 52.16065 | 105.5797 | 171.5501 | 5541.149 | 223.7107 | 5646.729 |
| Total | 614.7099 | 530.2914 | 5664.975 | 19183.01 | 6279.685 | 19714.3 |
| Job | Arrival Time | Importance | Size | Density | Completion Time | Turnaround Time | Response Time | |||
|---|---|---|---|---|---|---|---|---|---|---|
| HSIF | NC | HSIF | NC | HSIF | NC | |||||
| J1 | 1 | 5 | 5.6606 | 1.13212 | 3 | 4 | 2 | 3 | 0 | 0 |
| J2 | 4 | 9 | 11.2292 | 1.2476889 | 7 | 9 | 3 | 5 | 1 | 1 |
| J3 | 6 | 4 | 6.9192 | 1.7298 | 9 | 15 | 3 | 9 | 2 | 8 |
| J4 | 7 | 5 | 20.1173 | 4.02346 | 17 | 13 | 10 | 6 | 7 | 3 |
| J5 | 10 | 10 | 9.6771 | 0.96771 | 12 | 34 | 2 | 24 | 1 | 22 |
| J6 | 12 | 9 | 4.4418 | 0.4935333 | 13 | 42 | 1 | 30 | 1 | 26 |
| J7 | 15 | 19 | 29.5157 | 1.5534579 | 23 | 20 | 8 | 5 | 3 | 1 |
| J8 | 17 | 1 | 10.4579 | 10.4579 | 40 | 22 | 23 | 5 | 19 | 4 |
| J9 | 22 | 2 | 15.2929 | 7.64645 | 33 | 25 | 11 | 3 | 7 | 1 |
| J10 | 23 | 6 | 17.6643 | 2.94405 | 28 | 29 | 5 | 6 | 1 | 3 |
| J11 | 28 | 3 | 5.3368 | 1.7789333 | 35 | 31 | 7 | 3 | 6 | 2 |
| J12 | 35 | 2 | 9.6688 | 4.8344 | 43 | 37 | 8 | 2 | 6 | 0 |
| J13 | 42 | 7 | 13.2021 | 1.8860143 | 74 | 63 | 32 | 21 | 31 | 20 |
| J14 | 43 | 13 | 40.2411 | 3.0954692 | 49 | 49 | 6 | 6 | 1 | 1 |
| J15 | 45 | 14 | 25.5583 | 1.8255929 | 52 | 66 | 7 | 21 | 5 | 19 |
| J16 | 48 | 8 | 40.853 | 5.106625 | 56 | 54 | 8 | 6 | 5 | 2 |
| J17 | 50 | 11 | 12.1269 | 1.1024455 | 66 | 105 | 16 | 55 | 15 | 54 |
| J18 | 52 | 15 | 54.83 | 3.6553333 | 62 | 59 | 10 | 7 | 7 | 3 |
| J19 | 53 | 16 | 26.8655 | 1.6790938 | 58 | 76 | 5 | 23 | 4 | 21 |
| J20 | 55 | 7 | 14.0554 | 2.0079143 | 78 | 61 | 23 | 6 | 22 | 5 |
| J21 | 55 | 9 | 12.1621 | 1.3513444 | 67 | 99 | 12 | 44 | 11 | 43 |
| J22 | 57 | 17 | 10.3702 | 0.6100118 | 65 | 127 | 8 | 70 | 7 | 66 |
| J23 | 57 | 19 | 11.8838 | 0.6254632 | 64 | 122 | 7 | 65 | 6 | 63 |
| J24 | 57 | 20 | 13.2365 | 0.661825 | 63 | 119 | 6 | 62 | 5 | 60 |
| J25 | 57 | 6 | 7.5921 | 1.26535 | 104 | 101 | 47 | 44 | 46 | 43 |
| J26 | 66 | 12 | 11.5422 | 0.96185 | 69 | 110 | 3 | 44 | 2 | 43 |
| J27 | 66 | 7 | 9.5916 | 1.3702286 | 102 | 91 | 48 | 25 | 47 | 24 |
| J28 | 66 | 11 | 37.0895 | 3.3717727 | 72 | 73 | 6 | 7 | 4 | 5 |
| J29 | 66 | 14 | 12.1389 | 0.8670643 | 68 | 114 | 2 | 48 | 1 | 47 |
| J30 | 66 | 8 | 13.9307 | 1.7413375 | 84 | 74 | 18 | 8 | 17 | 7 |
| J31 | 66 | 8 | 40.5456 | 5.0682 | 87 | 69 | 21 | 3 | 18 | 1 |
| J32 | 66 | 11 | 12.1144 | 1.1013091 | 73 | 106 | 7 | 40 | 6 | 39 |
| J33 | 70 | 5 | 5.3607 | 1.07214 | 106 | 108 | 36 | 38 | 35 | 38 |
| J34 | 70 | 6 | 6.5298 | 1.0883 | 105 | 107 | 35 | 37 | 34 | 37 |
| J35 | 70 | 7 | 8.6447 | 1.2349571 | 103 | 103 | 33 | 33 | 32 | 0 |
| J36 | 70 | 8 | 12.6466 | 1.580825 | 93 | 82 | 23 | 12 | 22 | 11 |
| J37 | 73 | 17 | 13.2672 | 0.7804235 | 75 | 116 | 2 | 43 | 1 | 42 |
| J38 | 74 | 19 | 28.4346 | 1.4965579 | 77 | 85 | 3 | 11 | 2 | 9 |
| J39 | 74 | 5 | 8.0565 | 1.6113 | 108 | 80 | 34 | 6 | 32 | 7 |
| J40 | 76 | 9 | 13.8968 | 1.5440889 | 88 | 82 | 12 | 6 | 11 | 7 |
| J41 | 76 | 4 | 2.2268 | 0.5567 | 109 | 131 | 33 | 55 | 32 | 52 |
| J42 | 76 | 8 | 11.3447 | 1.4180875 | 100 | 85 | 24 | 9 | 23 | 10 |
| J43 | 76 | 11 | 29.6523 | 2.6956636 | 82 | 78 | 6 | 2 | 4 | 1 |
| J44 | 77 | 15 | 28.0842 | 1.87228 | 80 | 79 | 3 | 2 | 2 | 3 |
| J45 | 81 | 16 | 14.7864 | 0.92415 | 83 | 112 | 2 | 31 | 1 | 30 |
| J46 | 81 | 9 | 12.1814 | 1.3534889 | 99 | 92 | 18 | 11 | 17 | 10 |
| J47 | 81 | 8 | 10.531 | 1.316375 | 101 | 99 | 20 | 18 | 19 | 19 |
| J48 | 87 | 17 | 54.2747 | 3.1926294 | 92 | 90 | 5 | 3 | 2 | 0 |
| J49 | 93 | 19 | 40.1127 | 2.1111947 | 98 | 95 | 5 | 2 | 2 | 0 |
| J50 | 93 | 20 | 28.3624 | 1.41812 | 95 | 98 | 2 | 5 | 1 | 3 |
| Total | 671 | 1030 | 586 | 916 | ||||||
| Job | Energy Consumed by Individual Job (ECiJ) | Importance Based Flow Time of Individual Job (IbFTiJ) | Importance Based Flow Time Plus Energy of Individual Job (ECiJ+IbFTiJ) | |||
|---|---|---|---|---|---|---|
| HSIF | NC | HSIF | NC | HSIF | NC | |
| J1 | 22.3590357 | 6.770212252 | 37.835144 | 21.78250015 | 59.19418 | 28.55271241 |
| J2 | 46.61278883 | 36.02011586 | 100.76936 | 149.8960335 | 147.3821 | 185.9161493 |
| J3 | 19.25226637 | 40.5746285 | 49.274854 | 228.881385 | 68.52712 | 269.4560135 |
| J4 | 82.78841236 | 64.15138995 | 516.081 | 323.9872543 | 598.8694 | 388.1386443 |
| J5 | 32.71807139 | 229.7936205 | 65.670287 | 2770.892657 | 98.38836 | 3000.686277 |
| J6 | 20.23553431 | 237.102096 | 31.471069 | 3251.6285 | 51.7066 | 3488.730596 |
| J7 | 202.7829624 | 100.2795249 | 983.04991 | 428.7590059 | 1185.833 | 529.0385308 |
| J8 | 42.27367303 | 60.70577844 | 529.99832 | 345.0057207 | 572.272 | 405.7114991 |
| J9 | 33.7634238 | 150.0710023 | 215.89783 | 545.5858599 | 249.6613 | 695.6568622 |
| J10 | 42.07948789 | 114.1502519 | 134.28054 | 647.9364288 | 176.36 | 762.0866808 |
| J11 | 34.33977776 | 14.82308387 | 158.99266 | 43.4028688 | 193.3324 | 58.22595267 |
| J12 | 25.33865247 | 59.42091636 | 102.66566 | 97.67231059 | 128.0043 | 157.093227 |
| J13 | 481.3604361 | 161.075095 | 8793.2476 | 1932.709082 | 9274.608 | 2093.784177 |
| J14 | 85.00788703 | 276.5769064 | 315.44764 | 1565.904674 | 400.4555 | 1842.48158 |
| J15 | 152.3533413 | 341.901121 | 692.16774 | 4081.84265 | 844.5211 | 4423.743771 |
| J16 | 168.7093341 | 444.4016939 | 839.37168 | 2652.137703 | 1008.081 | 3096.539397 |
| J17 | 336.5378155 | 607.6676007 | 3232.0993 | 17099.83442 | 3568.637 | 17707.50202 |
| J18 | 235.6998431 | 431.6038271 | 1408.9237 | 2838.699032 | 1644.624 | 3270.302859 |
| J19 | 127.5172457 | 376.2169431 | 458.29066 | 4628.367088 | 585.8079 | 5004.584031 |
| J20 | 326.6801405 | 58.09137545 | 4373.3849 | 265.635671 | 4700.065 | 323.7270464 |
| J21 | 197.7173871 | 396.6756722 | 1471.3821 | 8940.40525 | 1669.1 | 9337.080922 |
| J22 | 236.5408466 | 1136.468047 | 1249.902 | 38599.64292 | 1486.443 | 39736.11097 |
| J23 | 228.3316502 | 1206.144663 | 1083.7848 | 38904.03481 | 1312.116 | 40110.17947 |
| J24 | 203.5856335 | 1213.137134 | 857.18131 | 37422.77458 | 1060.767 | 38635.91172 |
| J25 | 645.8262181 | 264.632675 | 17000.018 | 5968.470375 | 17645.84 | 6233.10305 |
| J26 | 61.42174437 | 526.4527132 | 160.7368 | 11821.89117 | 222.1585 | 12348.34388 |
| J27 | 551.6457635 | 175.6851143 | 11254.291 | 2292.812971 | 11805.94 | 2468.498086 |
| J28 | 100.7695008 | 196.6953921 | 406.78459 | 1250.246015 | 507.5541 | 1446.941407 |
| J29 | 50.85532029 | 666.0633792 | 106.35154 | 16186.67205 | 157.2069 | 16852.73543 |
| J30 | 280.5938868 | 64.87066875 | 2998.2111 | 295.8360188 | 3278.805 | 360.7066875 |
| J31 | 318.7016553 | 216.3189596 | 3782.0731 | 771.3952677 | 4100.775 | 987.7142273 |
| J32 | 132.192008 | 442.7510756 | 627.45436 | 9143.243446 | 759.6464 | 9585.994522 |
| J33 | 394.0326882 | 190.53607 | 8038.7794 | 3725.90673 | 8432.812 | 3916.4428 |
| J34 | 457.5086268 | 222.54415 | 9087.2176 | 4238.6777 | 9544.726 | 4461.22185 |
| J35 | 498.2490083 | 231.6174786 | 9359.2487 | 3947.994271 | 9857.498 | 4179.61175 |
| J36 | 373.348732 | 96.7904125 | 4998.1542 | 634.2753625 | 5371.503 | 731.065775 |
| J37 | 61.75288892 | 720.4549719 | 129.14116 | 15634.62855 | 190.894 | 16355.08352 |
| J38 | 91.44826525 | 212.2669018 | 234.05556 | 1311.454543 | 325.5038 | 1523.721444 |
| J39 | 362.0526921 | 35.80565 | 6900.7966 | 146.4452 | 7262.849 | 182.25085 |
| J40 | 197.7173871 | 63.77204444 | 1471.3821 | 258.1763556 | 1669.1 | 321.9484 |
| J41 | 284.713719 | 210.1924482 | 5348.1421 | 5632.759218 | 5632.856 | 5842.951667 |
| J42 | 392.3744651 | 80.70904375 | 5464.8046 | 447.7994813 | 5857.179 | 528.508525 |
| J43 | 106.386545 | 53.26049632 | 437.28887 | 136.4336571 | 543.6754 | 189.6941535 |
| J44 | 72.19599888 | 58.38507639 | 184.7807 | 157.6041655 | 256.9767 | 215.9892419 |
| J45 | 58.12036605 | 489.3002581 | 121.54462 | 7737.146183 | 179.665 | 8226.446441 |
| J46 | 315.6681227 | 99.67674444 | 3372.9875 | 602.1209333 | 3688.656 | 701.7976778 |
| J47 | 317.1910961 | 152.6581875 | 3732.1705 | 1533.16375 | 4049.362 | 1685.821938 |
| J48 | 117.5735219 | 291.1073658 | 405.47938 | 974.5465744 | 523.0529 | 1265.65394 |
| J49 | 142.6166731 | 93.38620681 | 503.28556 | 247.963412 | 645.9022 | 341.3496188 |
| J50 | 65.43614279 | 119.1602493 | 131.34057 | 454.3746597 | 196.7767 | 573.534909 |
| Total | 9834.978683 | 13738.91643 | 123957.6903 | 263339.4565 | 133791.6699 | 277078.3729 |
| Group Statistics | |||||
|---|---|---|---|---|---|
| Scheduling | N | Mean (M) | Std. Deviation (s) | Std. Error Mean | |
| Turnaround_time | HSIF | 50 | 13.42 | 12.511366 | 1.7693744 |
| NC | 50 | 20.6 | 19.786617 | 2.7982502 | |
| Responce_time | HSIF | 50 | 11.72 | 12.748813 | 1.8029545 |
| NC | 50 | 18.32 | 19.976966 | 2.8251697 | |
| Completion_time | HSIF | 50 | 67.4 | 30.651431 | 4.3347669 |
| NC | 50 | 74.82 | 34.902014 | 4.9358902 | |
| Energy_consumed | HSIF | 50 | 196.7 | 160.31869 | 22.672486 |
| NC | 50 | 274.778 | 291.01057 | 41.155109 | |
| Importance_based_flow_time | HSIF | 50 | 2479.15 | 3625.2051 | 512.68143 |
| NC | 50 | 15373.3 | 21122.893 | 2987.2282 | |
| Importance_based_flow_time_plus_energy | HSIF | 50 | 2675.83 | 3774.8105 | 533.83883 |
| NC | 50 | 5541.57 | 9740.346 | 1377.4929 | |
| Independent Samples Test | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Objectives | t-Test for Equality of Means | Levene’s Test for Equality of Variances | ||||||||
| t | df | p-Value (2-tailed) | Mean Difference | Std. Error Difference | 95% Confidence Interval of the Difference | F | p-Value | |||
| Lower | Upper | |||||||||
| Turnaround_Time | Equal Variances Assumed | −2.17 | 98 | 0.033 | −7.18 | 3.31072346 | −13.7500229 | −0.60997705 | 14.19 | 0 |
| Equal Variances Not assumed | −2.17 | 82.78 | 0.033 | −7.18 | 3.31072346 | −13.765152 | −0.59484797 | |||
| Responce_Time | Equal Variances Assumed | −1.97 | 98 | 0.05 | −6.6 | 3.35145171 | −13.2508468 | 0.050846846 | 13.27 | 0 |
| Equal Variances Not assumed | −1.97 | 83.23 | 0.05 | −6.6 | 3.35145171 | −13.2656255 | 0.065625546 | |||
| Completion_Time | Equal Variances Assumed | −1.13 | 98 | 0.261 | −7.42 | 6.56911077 | −20.4561865 | 5.616186531 | 1.277 | 0.26 |
| Equal variances Not assumed | −1.13 | 96.39 | 0.261 | −7.42 | 6.56911077 | −20.4589043 | 5.618904335 | |||
| Energy_Consumed | Equal Variances Assumed | −1.66 | 98 | 0.1 | −78.078755 | 46.9870691 | −171.323064 | 15.16555442 | 5.645 | 0.02 |
| Equal Variances Not assumed | −1.66 | 76.23 | 0.101 | −78.078755 | 46.9870691 | −171.656969 | 15.499459 | |||
| Importance_based_flow_time | Equal Variances Assumed | −1.95 | 98 | 0.05 | −2787.635324 | 1432.92269 | −5631.22377 | 55.95311792 | 9.168 | 0 |
| Equal Variances Not assumed | −1.95 | 63.08 | 0.05 | −2787.635324 | 1432.92269 | −5651.02882 | 75.75817343 | |||
| Importance_Based_Flow_time_plus_energy | Equal Variances Assumed | −1.94 | 98 | 0.05 | −2865.734061 | 1477.31876 | −5797.42506 | 65.95693429 | 8.953 | 0 |
| Equal Variances Not assumed | −1.94 | 63.39 | 0.05 | −2865.734061 | 1477.31876 | −5817.56103 | 86.09291177 | |||
| Job | Simple Values | Z Values | Sum (ZHSIF_ECiJ + ZHSIF_IbFTiJ) | Normalized Sum (in range [0 1]) | ||
|---|---|---|---|---|---|---|
| HSIF_ECiJ | HSIF_IbFTiJ | ZHSIF_ECiJ | ZHSIF_IbFTiJ | |||
| J1 | 22.359 | 37.835144 | −1.08746 | −0.67343 | −1.76089 | 0.147822 |
| J2 | 46.6128 | 100.76936 | −0.93618 | −0.65607 | −1.59225 | 0.18155 |
| J3 | 19.2523 | 49.274854 | −1.10684 | −0.67027 | −1.77711 | 0.144578 |
| J4 | 82.7884 | 516.081 | −0.71053 | −0.54151 | −1.25204 | 0.249592 |
| J5 | 32.7181 | 65.670287 | −1.02285 | −0.66575 | −1.6886 | 0.16228 |
| J6 | 20.2355 | 31.471069 | −1.10071 | −0.67518 | −1.77589 | 0.144822 |
| J7 | 202.783 | 983.04991 | 0.03795 | −0.41269 | −0.37474 | 0.425052 |
| J8 | 42.2737 | 529.99832 | −0.96324 | −0.53767 | −1.50091 | 0.199818 |
| J9 | 33.7634 | 215.89783 | −1.01633 | −0.62431 | −1.64064 | 0.171872 |
| J10 | 42.0795 | 134.28054 | −0.96445 | −0.64682 | −1.61127 | 0.177746 |
| J11 | 34.3398 | 158.99266 | −1.01273 | −0.64001 | −1.65274 | 0.169452 |
| J12 | 25.3387 | 102.66566 | −1.06888 | −0.65555 | −1.72443 | 0.155114 |
| J13 | 481.3604 | 8793.2476 | 1.77559 | 1.74172 | 3.51731 | 1.203462 |
| J14 | 85.0079 | 315.44764 | −0.69669 | −0.59685 | −1.29354 | 0.241292 |
| J15 | 152.3533 | 692.16774 | −0.27661 | −0.49293 | −0.76954 | 0.346092 |
| J16 | 168.7093 | 839.37168 | −0.17459 | −0.45233 | −0.62692 | 0.374616 |
| J17 | 336.5378 | 3232.0993 | 0.87225 | 0.2077 | 1.07995 | 0.71599 |
| J18 | 235.6998 | 1408.9237 | 0.24327 | −0.29522 | −0.05195 | 0.48961 |
| J19 | 127.5172 | 458.29066 | −0.43153 | −0.55745 | −0.98898 | 0.302204 |
| J20 | 326.6801 | 4373.3849 | 0.81076 | 0.52252 | 1.33328 | 0.766656 |
| J21 | 197.7174 | 1471.3821 | 0.00635 | −0.27799 | −0.27164 | 0.445672 |
| J22 | 236.5408 | 1249.902 | 0.24851 | −0.33908 | −0.09057 | 0.481886 |
| J23 | 228.3317 | 1083.7848 | 0.19731 | −0.38491 | −0.1876 | 0.46248 |
| J24 | 203.5856 | 857.18131 | 0.04295 | −0.44742 | −0.40447 | 0.419106 |
| J25 | 645.8262 | 17000.018 | 2.80146 | 4.00553 | 6.80699 | 1.861398 |
| J26 | 61.4217 | 160.7368 | −0.84381 | −0.63953 | −1.48334 | 0.203332 |
| J27 | 551.6458 | 11254.291 | 2.214 | 2.42059 | 4.63459 | 1.426918 |
| J28 | 100.7695 | 406.78459 | −0.59837 | −0.57166 | −1.17003 | 0.265994 |
| J29 | 50.8553 | 106.35154 | −0.90971 | −0.65453 | −1.56424 | 0.187152 |
| J30 | 280.5939 | 2998.2111 | 0.5233 | 0.14318 | 0.66648 | 0.633296 |
| J31 | 318.7017 | 3782.0731 | 0.761 | 0.35941 | 1.12041 | 0.724082 |
| J32 | 132.192 | 627.45436 | −0.40237 | −0.51078 | −0.91315 | 0.31737 |
| J33 | 394.0327 | 8038.7794 | 1.23088 | 1.5336 | 2.76448 | 1.052896 |
| J34 | 457.5086 | 9087.2176 | 1.62682 | 1.82281 | 3.44963 | 1.189926 |
| J35 | 498.249 | 9359.2487 | 1.88094 | 1.89785 | 3.77879 | 1.255758 |
| J36 | 373.3487 | 4998.1542 | 1.10186 | 0.69486 | 1.79672 | 0.859344 |
| J37 | 61.7529 | 129.14116 | −0.84174 | −0.64824 | −1.48998 | 0.202004 |
| J38 | 91.4483 | 234.05556 | −0.65651 | −0.6193 | −1.27581 | 0.244838 |
| J39 | 362.0527 | 6900.7966 | 1.0314 | 1.21969 | 2.25109 | 0.950218 |
| J40 | 197.7174 | 1471.3821 | 0.00635 | −0.27799 | −0.27164 | 0.445672 |
| J41 | 284.7137 | 5348.1421 | 0.54899 | 0.7914 | 1.34039 | 0.768078 |
| J42 | 392.3745 | 5464.8046 | 1.22054 | 0.82358 | 2.04412 | 0.908824 |
| J43 | 106.3865 | 437.28887 | −0.56333 | −0.56324 | −1.12657 | 0.274686 |
| J44 | 72.196 | 184.7807 | −0.7766 | −0.63289 | −1.40949 | 0.218102 |
| J45 | 58.1204 | 121.54462 | −0.8644 | −0.65034 | −1.51474 | 0.197052 |
| J46 | 315.6681 | 3372.9875 | 0.74208 | 0.24656 | 0.98864 | 0.697728 |
| J47 | 317.1911 | 3732.1705 | 0.75158 | 0.34564 | 1.09722 | 0.719444 |
| J48 | 117.5735 | 405.47938 | −0.49355 | −0.57202 | −1.06557 | 0.286886 |
| J49 | 142.6167 | 503.28556 | −0.33735 | −0.54504 | −0.88239 | 0.323522 |
| J50 | 65.4361 | 131.34057 | −0.81877 | −0.64764 | −1.46641 | 0.206718 |
| Average | 196.69957 | 2479.153805 | 2 × 10−7 | 8.88178 × 10−18 | 2 × 10−7 | 0.50000004 |
| Total | 9834.9785 | 123957.6903 | 1 × 10−5 | 0 | 1 × 10−5 | 25.000002 |
| Job | Simple Values | Z Values | Sum (ZNC_ECiJ + ZNC_IbFTiJ) | Normalized Sum (in range [0 1]) | ||
|---|---|---|---|---|---|---|
| NC_ECiJ | NC_IbFTiJ | ZNC_ECiJ | ZNC_IbFTiJ | |||
| J1 | 6.7702 | 21.7825 | −0.92096 | −0.55435 | −1.47531 | 0.204938 |
| J2 | 36.0201 | 149.896034 | −0.82045 | −0.54081 | −1.36126 | 0.227748 |
| J3 | 40.5746 | 228.881385 | −0.80479 | −0.53246 | −1.33725 | 0.23255 |
| J4 | 64.1514 | 323.987254 | −0.72378 | −0.52241 | −1.24619 | 0.250762 |
| J5 | 229.7936 | 2770.892657 | −0.15458 | −0.26379 | −0.41837 | 0.416326 |
| J6 | 237.1021 | 3251.6285 | −0.12947 | −0.21298 | −0.34245 | 0.43151 |
| J7 | 100.2795 | 428.759006 | −0.59963 | −0.51133 | −1.11096 | 0.277808 |
| J8 | 60.7058 | 345.005721 | −0.73562 | −0.52019 | −1.25581 | 0.248838 |
| J9 | 150.071 | 545.58586 | −0.42853 | −0.49899 | −0.92752 | 0.314496 |
| J10 | 114.1503 | 647.936429 | −0.55197 | −0.48817 | −1.04014 | 0.291972 |
| J11 | 14.8231 | 43.402869 | −0.89328 | −0.55206 | −1.44534 | 0.210932 |
| J12 | 59.4209 | 97.672311 | −0.74003 | −0.54633 | −1.28636 | 0.242728 |
| J13 | 161.0751 | 1932.709082 | −0.39072 | −0.35238 | −0.7431 | 0.35138 |
| J14 | 276.5769 | 1565.904674 | 0.00618 | −0.39115 | −0.38497 | 0.423006 |
| J15 | 341.9011 | 4081.84265 | 0.23065 | −0.12524 | 0.10541 | 0.521082 |
| J16 | 444.4017 | 2652.137703 | 0.58288 | −0.27634 | 0.30654 | 0.561308 |
| J17 | 607.6676 | 17099.83442 | 1.14391 | 1.25064 | 2.39455 | 0.97891 |
| J18 | 431.6038 | 2838.699032 | 0.5389 | −0.25663 | 0.28227 | 0.556454 |
| J19 | 376.2169 | 4628.367088 | 0.34857 | −0.06748 | 0.28109 | 0.556218 |
| J20 | 58.0914 | 265.635671 | −0.7446 | −0.52858 | −1.27318 | 0.245364 |
| J21 | 396.6757 | 8940.40525 | 0.41888 | 0.38827 | 0.80715 | 0.66143 |
| J22 | 1136.468 | 38599.64292 | 2.96103 | 3.52297 | 6.484 | 1.7968 |
| J23 | 1206.1447 | 38904.03481 | 3.20046 | 3.55515 | 6.75561 | 1.851122 |
| J24 | 1213.1371 | 37422.77458 | 3.22448 | 3.39859 | 6.62307 | 1.824614 |
| J25 | 264.6327 | 5968.470375 | −0.03486 | 0.07416 | 0.0393 | 0.50786 |
| J26 | 526.4527 | 11821.89117 | 0.86483 | 0.69281 | 1.55764 | 0.811528 |
| J27 | 175.6851 | 2292.812971 | −0.34051 | −0.31432 | −0.65483 | 0.369034 |
| J28 | 196.6954 | 1250.246015 | −0.26832 | −0.42451 | −0.69283 | 0.361434 |
| J29 | 666.0634 | 16186.67205 | 1.34457 | 1.15413 | 2.4987 | 0.99974 |
| J30 | 64.8707 | 295.836019 | −0.72131 | −0.52538 | −1.24669 | 0.250662 |
| J31 | 216.319 | 771.395268 | −0.20088 | −0.47512 | −0.676 | 0.3648 |
| J32 | 442.7511 | 9143.243446 | 0.5772 | 0.40971 | 0.98691 | 0.697382 |
| J33 | 190.5361 | 3725.90673 | −0.28948 | −0.16286 | −0.45234 | 0.409532 |
| J34 | 222.5442 | 4238.6777 | −0.17949 | −0.10866 | −0.28815 | 0.44237 |
| J35 | 231.6175 | 3947.994271 | −0.14831 | −0.13938 | −0.28769 | 0.442462 |
| J36 | 96.7904 | 634.275363 | −0.61162 | −0.48961 | −1.10123 | 0.279754 |
| J37 | 720.455 | 15634.62855 | 1.53148 | 1.09578 | 2.62726 | 1.025452 |
| J38 | 212.2669 | 1311.454543 | −0.21481 | −0.41804 | −0.63285 | 0.37343 |
| J39 | 35.8057 | 146.4452 | −0.82118 | −0.54117 | −1.36235 | 0.22753 |
| J40 | 63.772 | 258.176356 | −0.72508 | −0.52936 | −1.25444 | 0.249112 |
| J41 | 210.1924 | 5632.759218 | −0.22194 | 0.03868 | −0.18326 | 0.463348 |
| J42 | 80.709 | 447.799481 | −0.66688 | −0.50932 | −1.1762 | 0.26476 |
| J43 | 53.2605 | 136.433657 | −0.7612 | −0.54223 | −1.30343 | 0.239314 |
| J44 | 58.3851 | 157.604166 | −0.74359 | −0.53999 | −1.28358 | 0.243284 |
| J45 | 489.3003 | 7737.146183 | 0.73716 | 0.26109 | 0.99825 | 0.69965 |
| J46 | 99.6767 | 602.120933 | −0.6017 | −0.49301 | −1.09471 | 0.281058 |
| J47 | 152.6582 | 1533.16375 | −0.41964 | −0.39461 | −0.81425 | 0.33715 |
| J48 | 291.1074 | 974.546574 | 0.05611 | −0.45365 | −0.39754 | 0.420492 |
| J49 | 93.3862 | 247.963412 | −0.62332 | −0.53044 | −1.15376 | 0.269248 |
| J50 | 119.1602 | 454.37466 | −0.53475 | −0.50863 | −1.04338 | 0.291324 |
| Average | 274.77833 | 5266.789129 | 2 × 10−7 | 4 × 10−7 | 6 × 10−7 | 0.50000012 |
| Total | 13738.9165 | 263339.4565 | 1 × 10−5 | 2 × 10−5 | 3 × 10−5 | 25.000006 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, P.; Khan, B.; Vidyarthi, A.; Haes Alhelou, H.; Siano, P. Energy-Aware Online Non-Clairvoyant Scheduling Using Speed Scaling with Arbitrary Power Function. Appl. Sci. 2019, 9, 1467. https://doi.org/10.3390/app9071467
Singh P, Khan B, Vidyarthi A, Haes Alhelou H, Siano P. Energy-Aware Online Non-Clairvoyant Scheduling Using Speed Scaling with Arbitrary Power Function. Applied Sciences. 2019; 9(7):1467. https://doi.org/10.3390/app9071467
Chicago/Turabian StyleSingh, Pawan, Baseem Khan, Ankit Vidyarthi, Hassan Haes Alhelou, and Pierluigi Siano. 2019. "Energy-Aware Online Non-Clairvoyant Scheduling Using Speed Scaling with Arbitrary Power Function" Applied Sciences 9, no. 7: 1467. https://doi.org/10.3390/app9071467
APA StyleSingh, P., Khan, B., Vidyarthi, A., Haes Alhelou, H., & Siano, P. (2019). Energy-Aware Online Non-Clairvoyant Scheduling Using Speed Scaling with Arbitrary Power Function. Applied Sciences, 9(7), 1467. https://doi.org/10.3390/app9071467







