Vibration-Induced Pressures on a Cylindrical Structure Surface in Compressible Fluid
Abstract
Featured Application
Abstract
1. Introduction
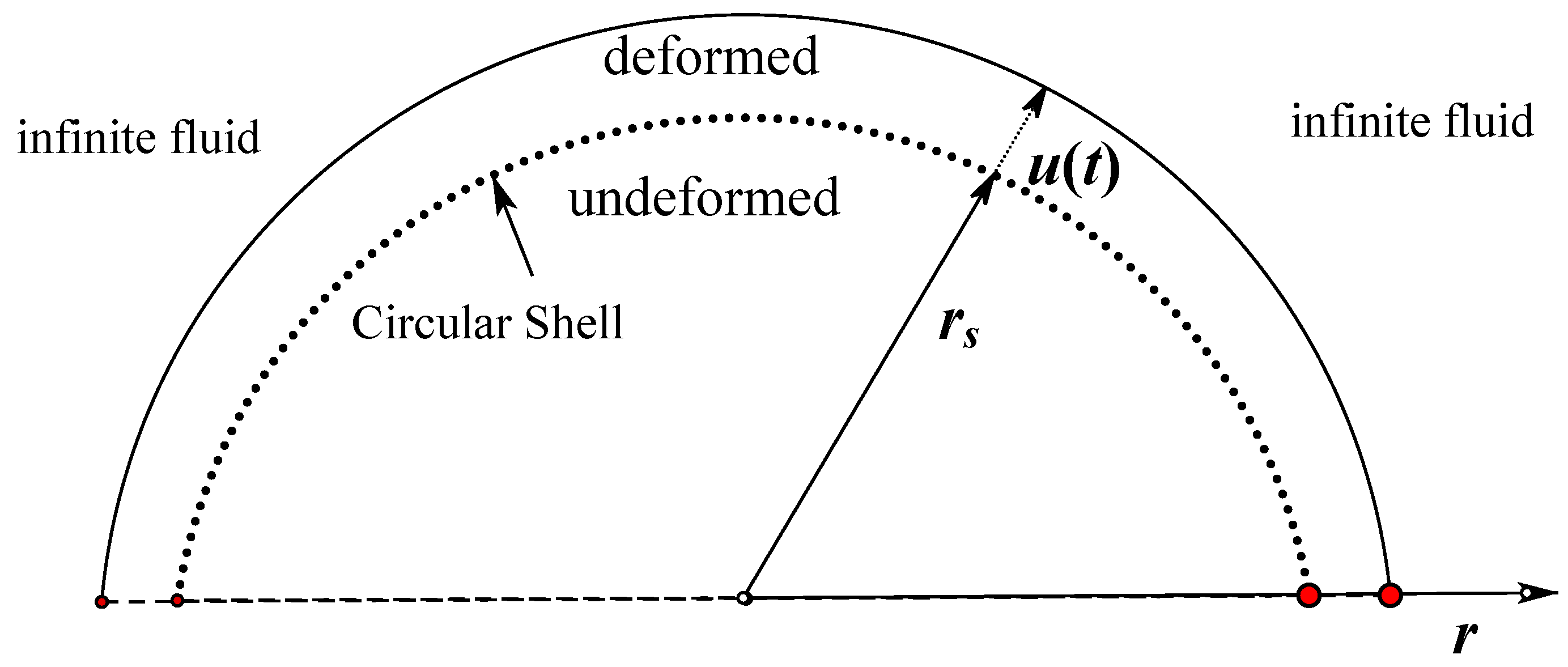
2. Governing Equations
2.1. Solution of the Compressive Fluid
2.2. Analyses of the Velocity
2.3. Analyses of the Pressure
2.4. Incompressible Fluid Solution
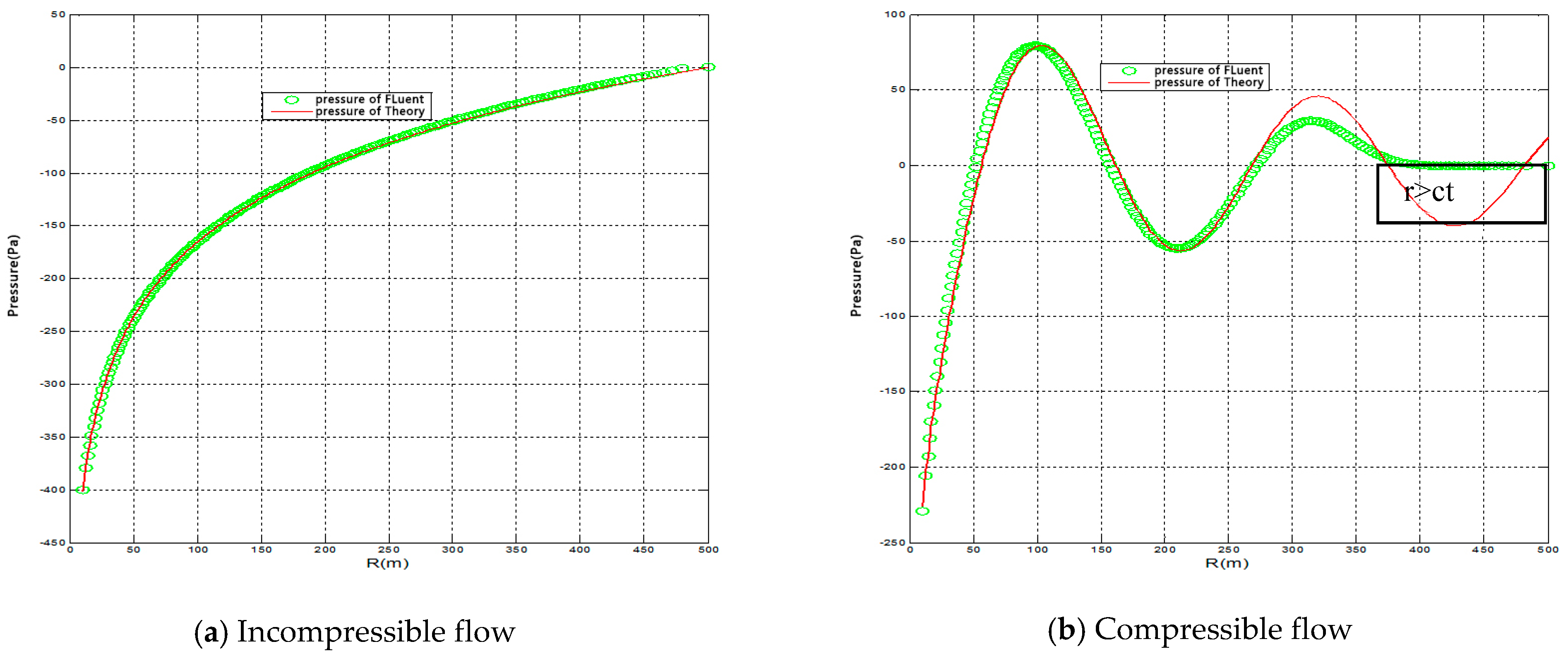
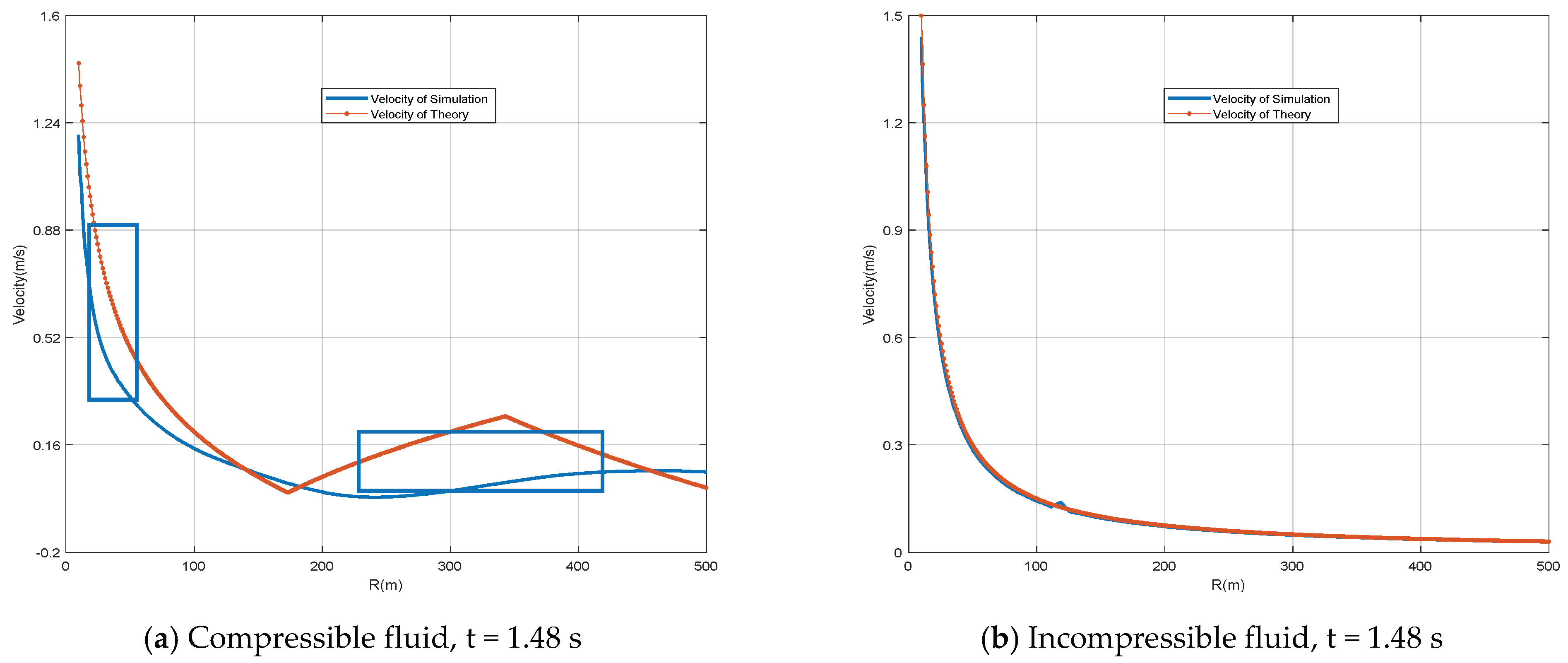
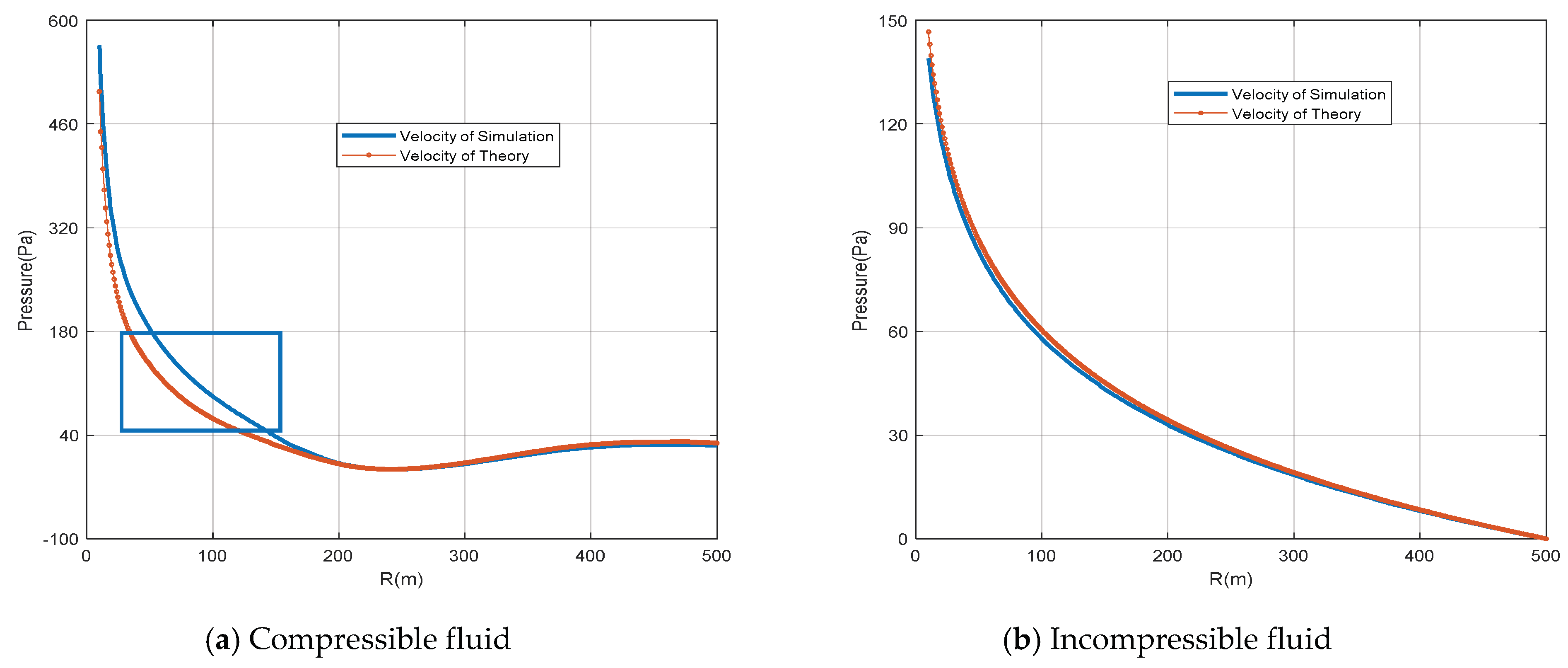
2.5. Discussion
3. Numerical Verification
3.1. Case 1: A Cylindrical Shell
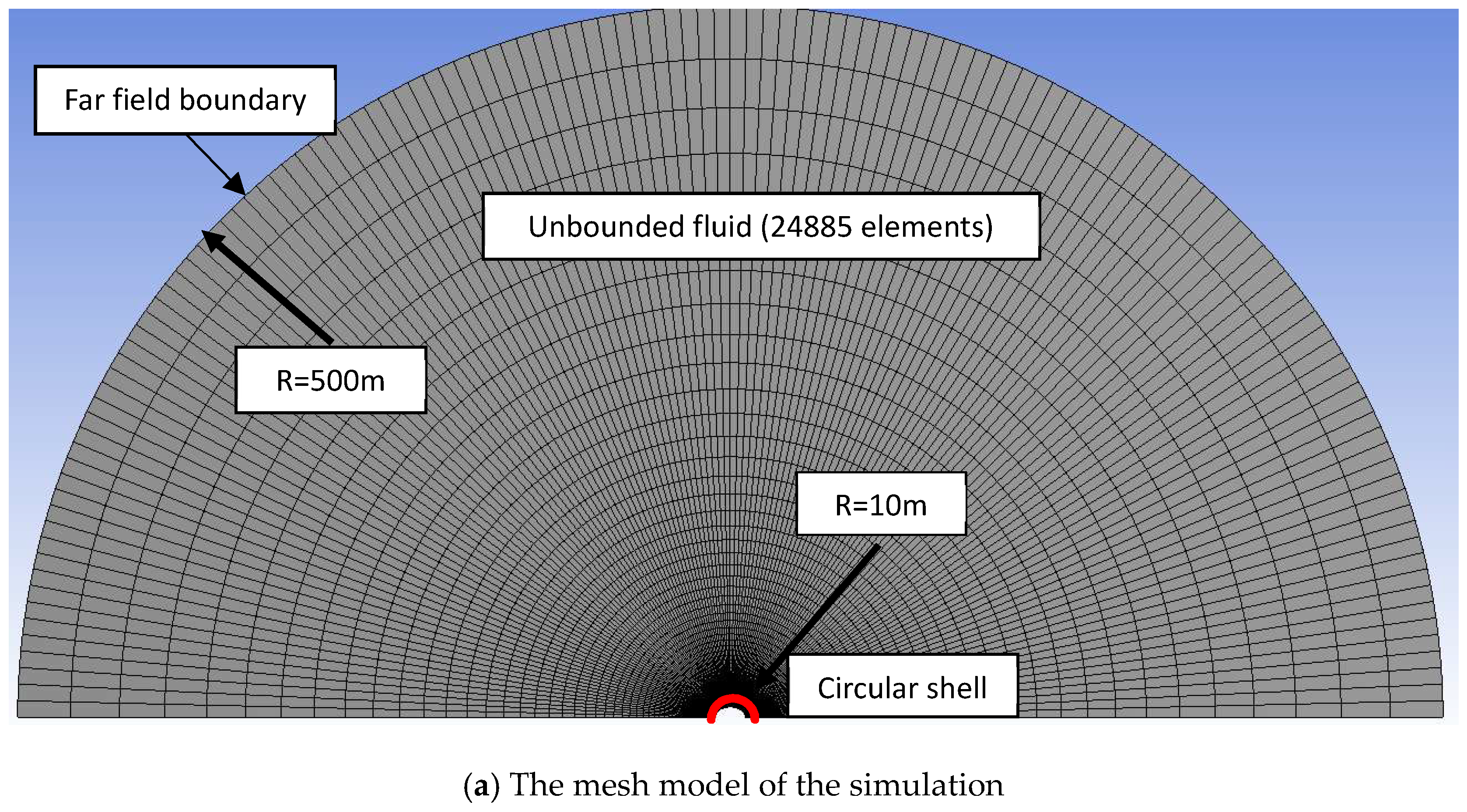
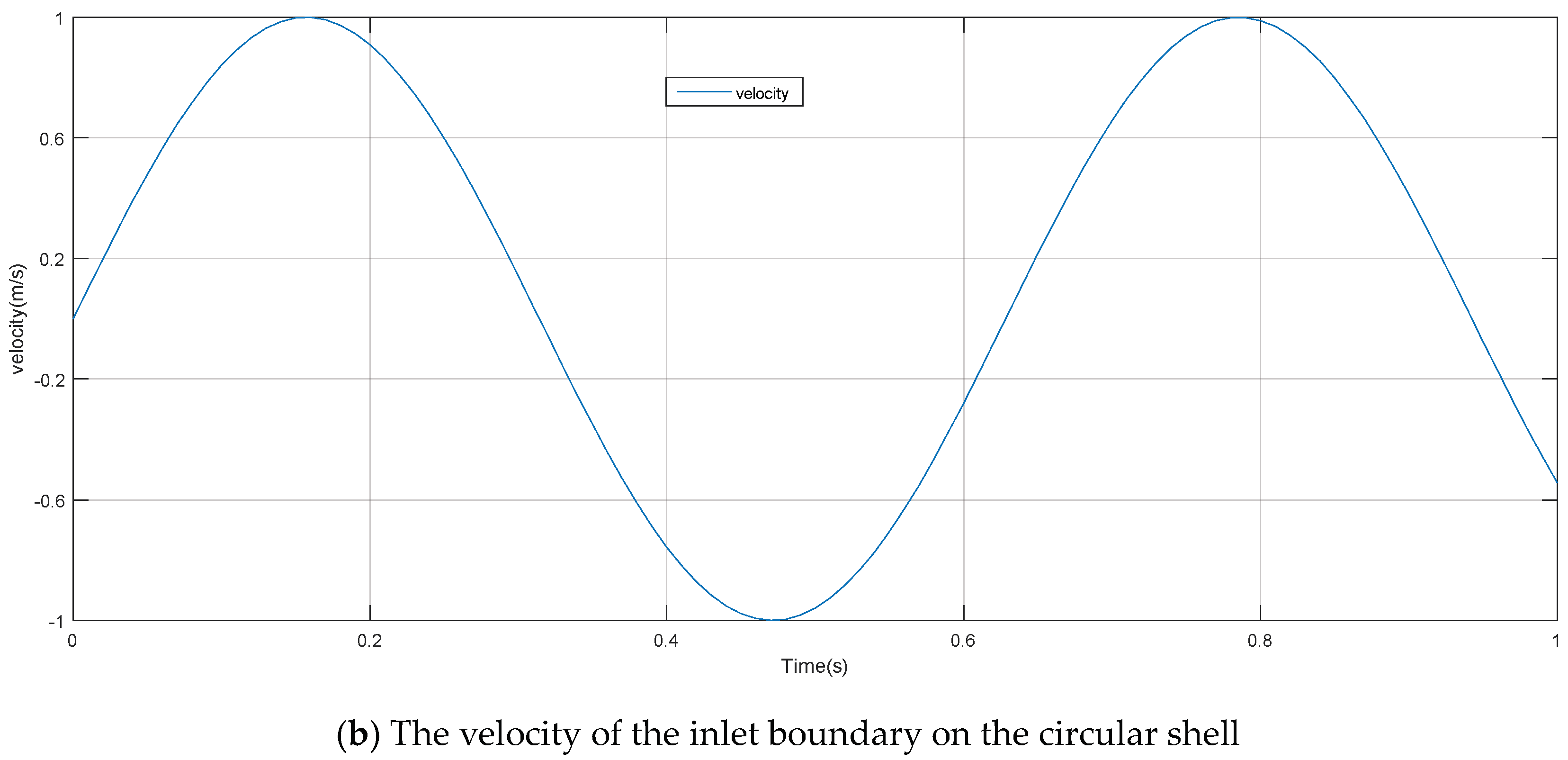
3.1.1. Model Details
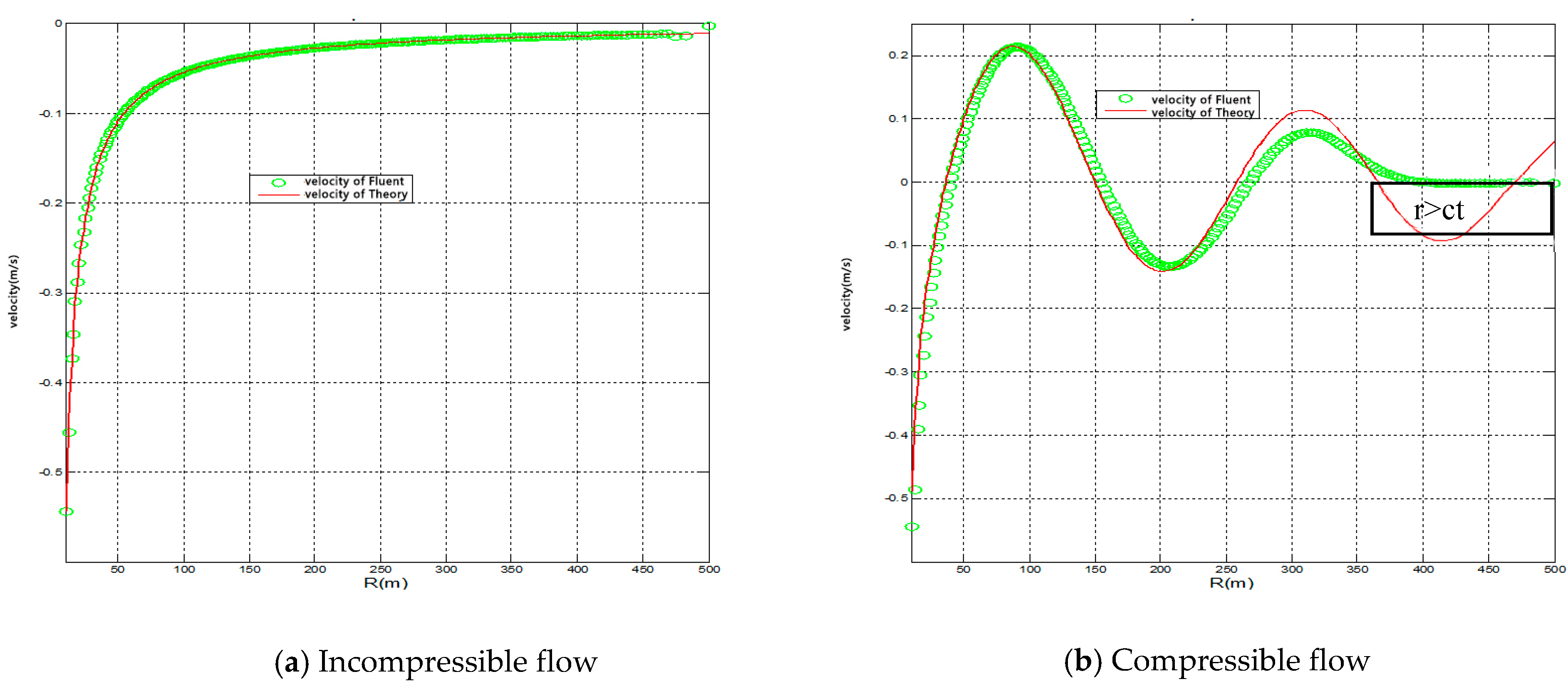
3.1.2. Velocity Analyses
3.1.3. Pressure Analyses
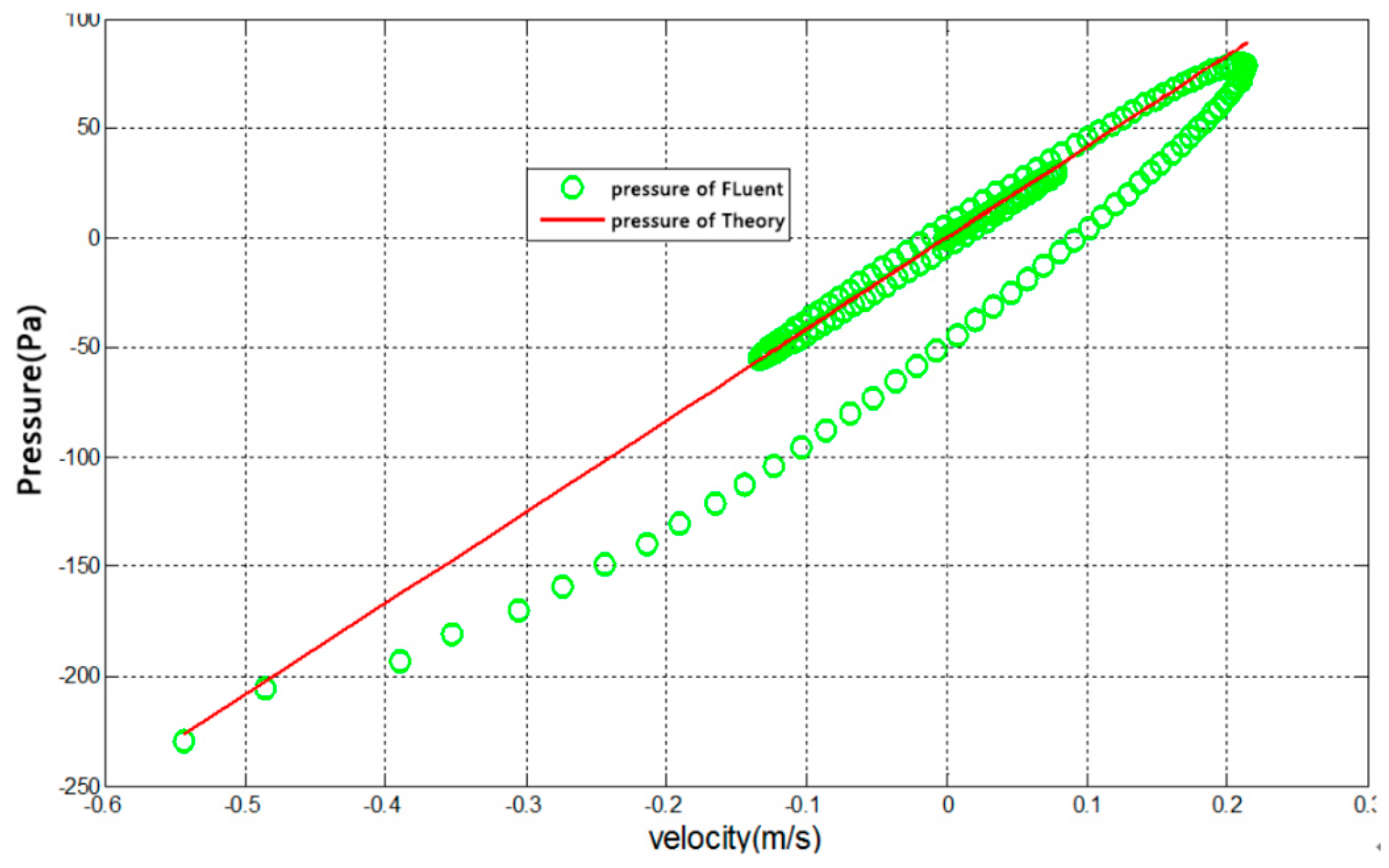
3.1.4. Pressure vs. Velocity
3.2. Case 2: Trigonal Velocity
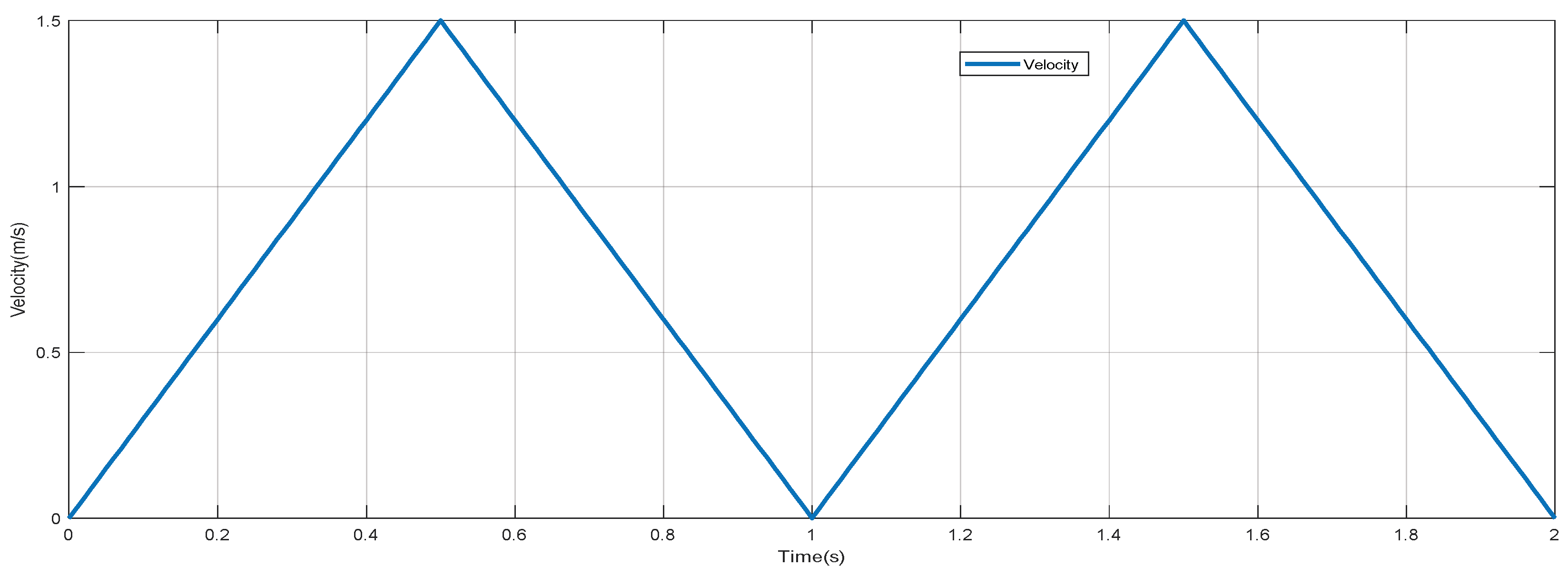
3.2.1. Simulation Model
3.2.2. Velocity Analyses
3.2.3. Pressure Analyses
3.2.4. Pressure vs. Velocity
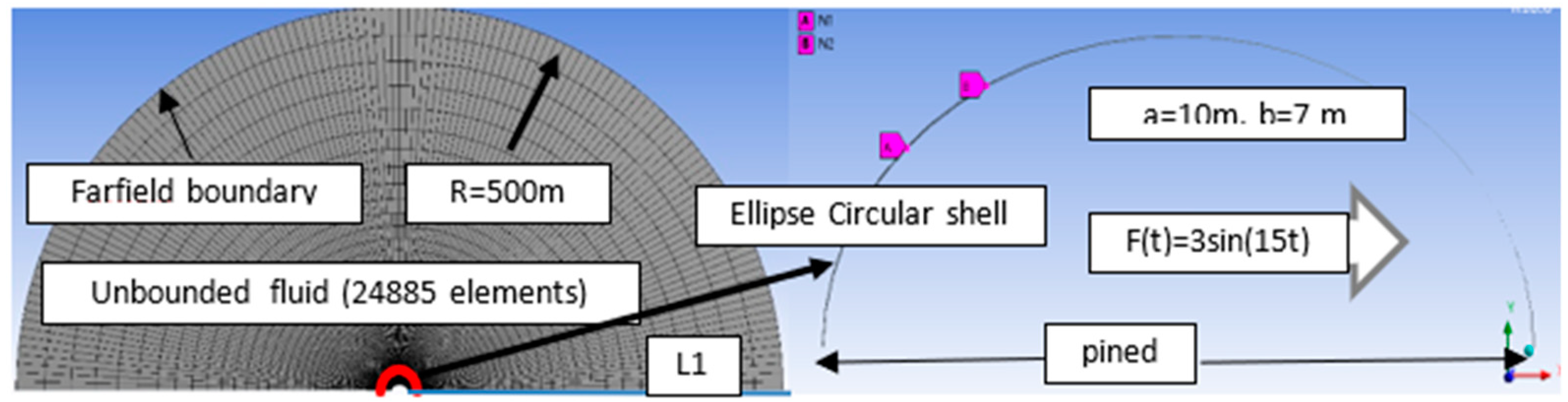
3.3 Case 3: FSI Model of the Elliptical Shell
3.3.1. Model
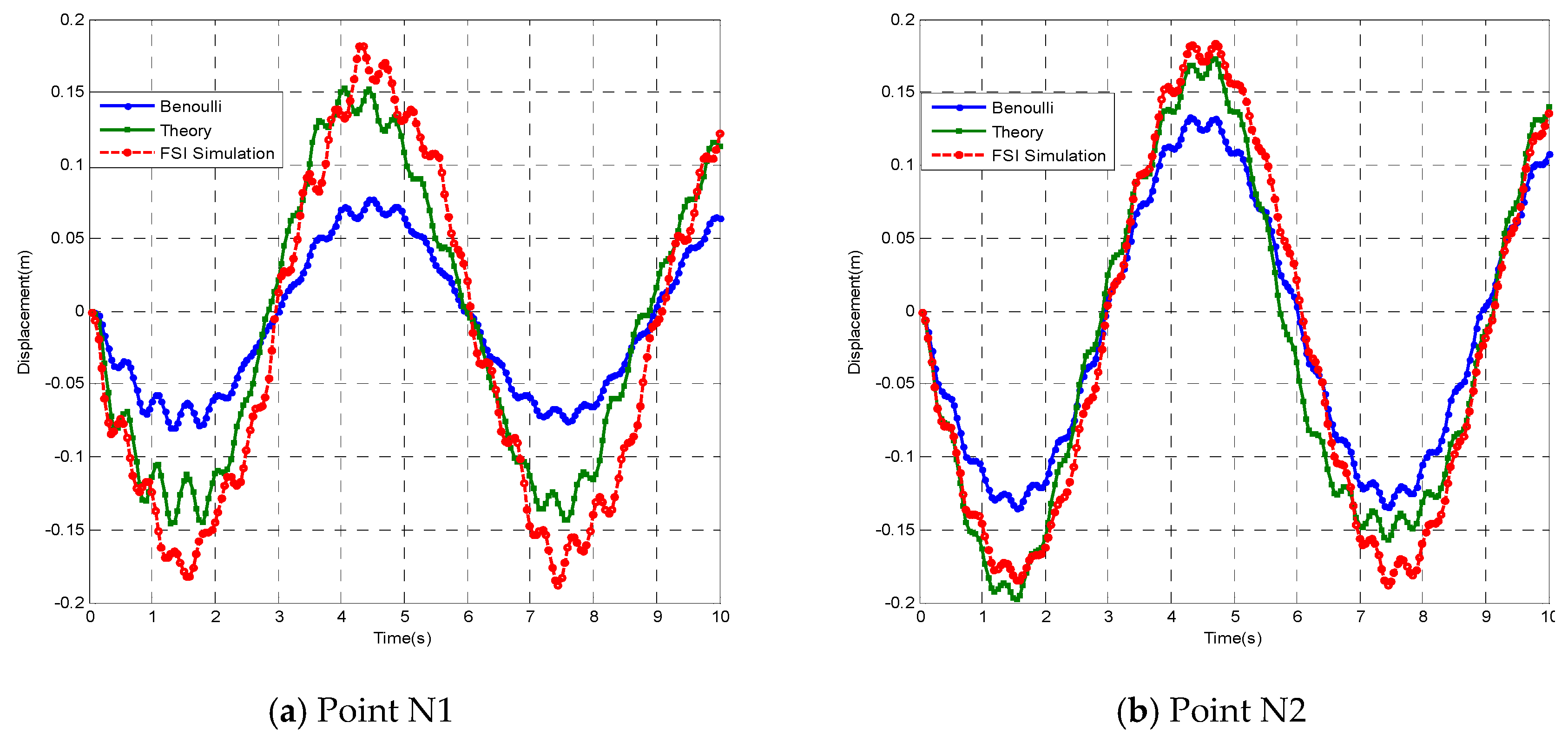
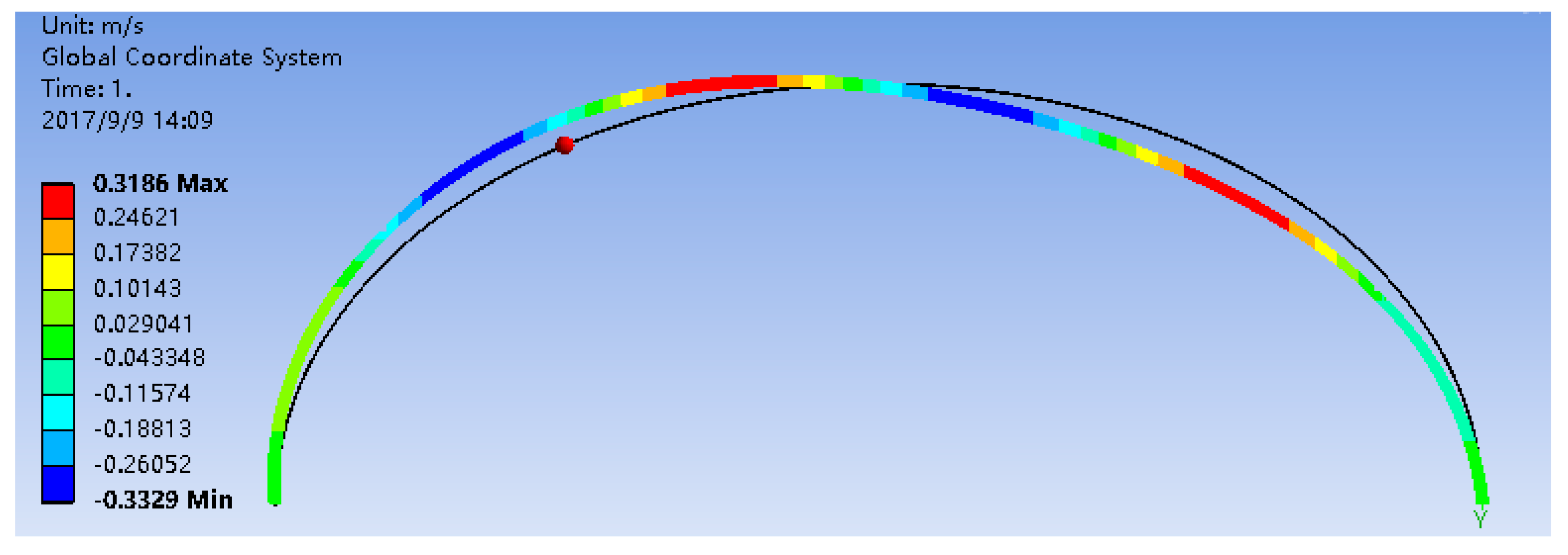
3.3.2. Displacement Results
3.3.3. Pressure Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, P.; Kaewunruen, S.; Zhou, D.; Wang, S.; Zhao, D.C.; Shang, S.W. Investigation of the Dynamic Buckling of Spherical Shell Structures Due to Subsea Collisions. Appl. Sci. 2018, 8, 1148. [Google Scholar] [CrossRef]
- Liu, P.; Kaewunruen, S.; Tang, B. Dynamic Pressure Analysis of Hemispherical Shell Vibrating in Unbounded Compressible Fluid. Appl. Sci. 2018, 8, 1938. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, M.; Cui, W.; Tang, W.; Wang, F.; Pan, B. Elastic-plastic buckling of deep sea spherical pressure hulls. Mar. Struct. 2018, 57, 38–51. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, M.; Cui, W.; Wang, F.; Hua, Z.; Tang, W. Effect of thickness on the buckling strength of egg- shaped pressure hulls. Ships Offshore Struct. 2018, 13, 375–384. [Google Scholar] [CrossRef]
- Zhang, M.; Tang, W.; Wang, F.; Zhang, J.; Cui, W.; Chen, Y. Buckling of bi-segment spherical shells under hydrostatic external pressure. Thin-Walled Struct. 2017, 120, 1–8. [Google Scholar] [CrossRef]
- Chakrabarti, K.; Frampton, R.E. Review of riser analysis techniques. Appl. Ocean Res. 1982, 4, 80–90. [Google Scholar] [CrossRef]
- Pang, S.; Gao, Y.; Choi, S. Flexible and stretchable microbial fuel cells with modified conductive and hydrophilic textile. Biosens. Bioelectron. 2018, 100, 504–511. [Google Scholar] [CrossRef]
- Zhou, X.; Gosling, P.D. Influence of stochastic variations in manufacturing defects on the mechanical performance of textile composites. Compos. Struct. 2018, 194, 226–239. [Google Scholar] [CrossRef]
- Kariou, F.A.; Triantafyllou, S.P.; Bournas, D.A.; Koutas, L.N. Out-of-plane response of masonry walls strengthened using textile-mortar system. Constr. Build. Mater. 2018, 165, 769–781. [Google Scholar] [CrossRef]
- Da Silva Monteiro, L.L.; Netto, T.A.; Da Camara Monteiro, P.C., Jr. On the Dynamic Collapse of Cylindrical Shells Under Impulsive Pressure Loadings. J. Offshore Mech. Arct. 2016, 138, 041101. [Google Scholar] [CrossRef]
- Wu, X.; Ge, F.; Hong, Y. A review of recent studies on vortex-induced vibrations of long slender cylinders. J. Fluid Struct. 2012, 28, 292–308. [Google Scholar] [CrossRef]
- Trivedi, C. A review on fluid structure interaction in hydraulic turbines: A focus on hydrodynamic damping. J. Fluid Dyn. 2016, 35, 333–349. [Google Scholar] [CrossRef]
- Suarez, L.E.; Gaviria, C.A. Equivalent Frequencies and Damping Ratios of Buildings with Viscous Fluid Dampers: A Closed Form Formulation; Earthquake Engineering Research Institute: Anchorage, AK, USA, 2014. [Google Scholar]
- Mattioli, M.; Mancinelli, A.; Brocchini, M. Experimental investigation of the wave-induced flow around a surface-touching cylinder. J. Fluid Struct. 2013, 37, 62–87. [Google Scholar] [CrossRef]
- Minami, H. Added mass of a membrane vibrating at finite amplitude. J. Fluid Struct. 1998, 12, 919–932. [Google Scholar] [CrossRef]
- Kubenko, V.D.; Dzyuba, V.V. Resonance phenomena in cylindrical shell with a spherical inclusion in the presence of an internal compressible liquid and an external elastic medium. J. Fluid Struct. 2006, 22, 577–594. [Google Scholar] [CrossRef]
- Sorokin, S.V.; Terentiev, A.V. Flow-induced vibrations of an elastic cylindrical shell conveying a compressible fluid. J. Sound Vib. 2006, 296, 777–796. [Google Scholar] [CrossRef]
- Chung, M.H. Hydrodynamics of flow over a transversely oscillating circular cylinder beneath a free surface. J. Fluid Struct. 2015, 54, 27–73. [Google Scholar] [CrossRef]
- Calautit, J.K.; O’Connor, D.; Hughes, B.R. Determining the optimum spacing and arrangement for commercial wind towers for ventilation performance. Build. Environ. 2014, 82, 274–287. [Google Scholar] [CrossRef]
- Liberge, E.; Hamdouni, A. Reduced order modelling method via proper orthogonal decomposition (POD) for flow around an oscillating cylinder. J. Fluid Struct. 2010, 26, 292–311. [Google Scholar] [CrossRef]
- Munch, C.; Ausoni, P.; Braun, O.; Farhat, M.; Avellan, F. Fluid-structure coupling for an oscillating hydrofoil. J. Fluid Struct. 2010, 26, 1018–1033. [Google Scholar] [CrossRef]
- Rojratsirikul, P.; Wang, Z.; Gursul, I. Effect of pre-strain and excess length on unsteady fluid-structure interactions of membrane airfoils. J. Fluid Struct. 2010, 26, 359–376. [Google Scholar] [CrossRef]
- Karagiozis, K.; Kamakoti, R.; Cirak, F.; Pantano, C. A computational study of supersonic disk-gap-band parachutes using Large-Eddy Simulation coupled to a structural membrane. J. Fluid Struct. 2011, 27, 175–192. [Google Scholar] [CrossRef]
- Al-Gahtani, H.; Khathlan, A.; Sunar, M.; Naffaa, M. Local Hydrostatic Pressure Test for Cylindrical Vessels. J. Press. Vess.-Technol. ASME 2017, 139, 011601. [Google Scholar] [CrossRef]
- Li, T.Y.; Wang, P.; Zhu, X.; Yang, J.; Ye, W.B. Prediction of Far-Field Sound Pressure of a Semi-submerged Cylindrical Shell with Low-Frequency Excitation. J. Vib Acoust. 2017, 139, 041002. [Google Scholar] [CrossRef]
- Lawrence, V.; Ngamkhanong, C.; Kaewunruen, S. An Investigation to Optimize the Layout of Protective Blast Barriers Using Finite Element Modelling. Mater. Sci. Eng. 2017, 280, 375–383. [Google Scholar] [CrossRef]
- Saadin, B.; Leena, S.; Sakdirat, K.; David, J. Operational Readiness for Climate Change of Malaysia High-Speed Rail; University of Birmingham: Birmingham, UK, 2016. [Google Scholar]
- Kaewunruen, S. Underpinning systems thinking in railway engineering education. Australas. J. Eng. Educ. 2017, 22, 107–114. [Google Scholar] [CrossRef]
- Cholcz, T.P.S.; van Zuijlen, A.H.; Bijl, H. Space-mapping in fluid-structure interaction problems. Comput. Method Appl. Mech. Eng. 2014, 281, 162–183. [Google Scholar] [CrossRef]
- Motiei, P.; Yaghoubi, M.; GoshtashbiRad, E.; Vadiee, A. Two-dimensional unsteady state performance analysis of a hybrid photovoltaic-thermoelectric generator. Renew. Energ. 2018, 2018, 551–565. [Google Scholar] [CrossRef]
- Naccache, G.; Paraschivoiu, M. Parametric study of the dual vertical axis wind turbine using CFD. J. Wind Eng. Ind. Aerodyn. 2018, 2018, 244–255. [Google Scholar] [CrossRef]
- Wua, G.; Qin, Z.; Zhang, L.; Yang, K. Strain response analysis of adhesively bonded extended composite wind turbine blade suffering unsteady aerodynamic loads. Eng. Fail Anal. 2018, 2018, 36–49. [Google Scholar] [CrossRef]
- Wang, S.; Chen, Y.; Liu, Y.Z. Measurement of unsteady flow structures in a low speed wind tunnel using continuous wave laser-based TR-PIV: Near wake behind a circular cylinder. J. Visous 2018, 2018, 73–93. [Google Scholar] [CrossRef]
- Tang, J.; Hu, Y.; Song, B.; Yang, H. An unsteady free wake model for aerodynamic performance of cycloidal propellers. J. Aerosp. Eng. 2018, 223, 290–307. [Google Scholar] [CrossRef]
- Jiang, L.; Li, J.; Li, C. Comparative Study on Non-Gaussian Characteristics of Wind Pressure for Rigid and Flexible Structures. Shock Vib. 2018, 2018, 1–26. [Google Scholar] [CrossRef]
- Basnet, K.; Constantinescu, G. The structure of turbulent flow around vertical plates containing holes and attached to a channel bed. Phys. Fluids 2017, 2017, 1147–1156. [Google Scholar] [CrossRef]
- Li, Q.; Maeda, T.; Kamada, Y.; Hiromori, Y.; Nakai, A.; Kasuya, T. Study on stall behavior of a straight-bladed vertical axis wind turbine with numerical and experimental investigations. J. Wind Eng. Ind. Aerod. 2017, 164, 1–12. [Google Scholar] [CrossRef]
- Mattheij, R.M.M.; Rienstra, S.W.; Boonkkamp, J.H.M.T. Partial Differential Equations: Modeling, Analysis, Computation; Siam: Philadelphia, PA, USA, 2005. [Google Scholar]
- Evans, L.C. Partial Differential Equations, 1st ed.; American Mathematical Society: Providence, RI, USA, 1998. [Google Scholar]
- Ya, L.; Hong, Y.J. The interaction between membrane structure and wind based on the discontinuous boundary element. Sci. China Technol. Sci. 2010, 53, 486–501. [Google Scholar]
- Si, X.H.; Lu, W.X.; Chu, F.L. Modal analysis of circular plates with radial side cracks and in contact with water on one side based on the Rayleigh–Ritz method. J. Sound Vib. 2012, 331, 231–251. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Sussman, J.M.; Matsumoto, A. Grand challenges in transportation and transit systems. Front. Built Environ. 2016, 2, 4. [Google Scholar] [CrossRef]



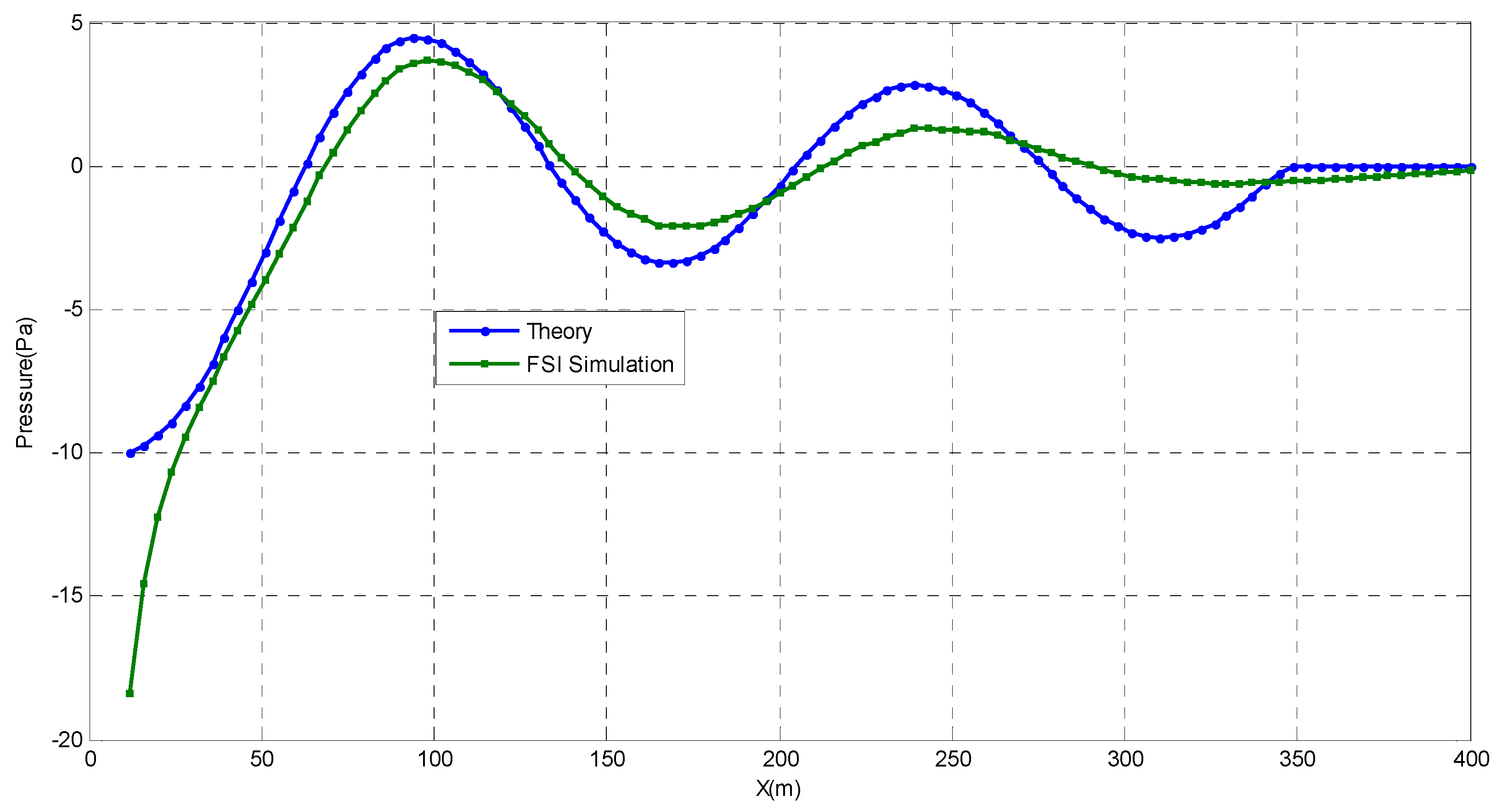
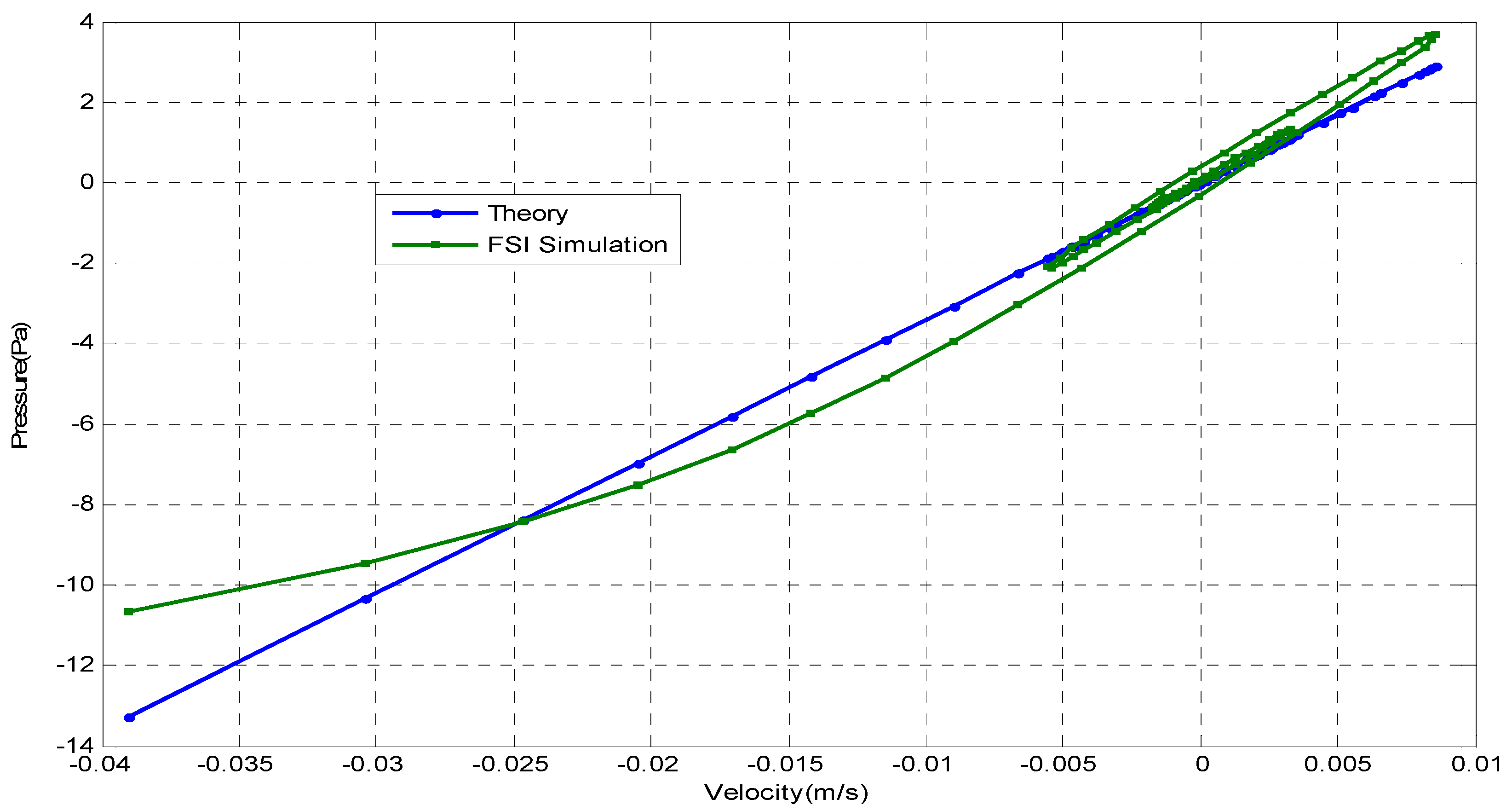
| Density of Shell Mesh (cm) | 2.0 | 1.0 | 0.8 | 0.5 | 0.3 | 0.2 | 0.1 |
| Total energy (104 J) | 4.52 | 4.21 | 3.93 | 3.90 | 3.89 | 3.88 | 3.88 |
| Semi major axles (a) | 10 m | Acceleration load | 3 sin(15 t) | Yang’s module | 210 GPa |
| Semi minor axles (b) | 7 m | Boundary | pined | Poisson’s ratio | 0.3 |
| Thickness of shell | 0.01 m | Total time | 10 s | Delta time | 0.01 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Tang, B.-J.; Kaewunruen, S. Vibration-Induced Pressures on a Cylindrical Structure Surface in Compressible Fluid. Appl. Sci. 2019, 9, 1403. https://doi.org/10.3390/app9071403
Liu P, Tang B-J, Kaewunruen S. Vibration-Induced Pressures on a Cylindrical Structure Surface in Compressible Fluid. Applied Sciences. 2019; 9(7):1403. https://doi.org/10.3390/app9071403
Chicago/Turabian StyleLiu, Ping, Bai-Jian Tang, and Sakdirat Kaewunruen. 2019. "Vibration-Induced Pressures on a Cylindrical Structure Surface in Compressible Fluid" Applied Sciences 9, no. 7: 1403. https://doi.org/10.3390/app9071403
APA StyleLiu, P., Tang, B.-J., & Kaewunruen, S. (2019). Vibration-Induced Pressures on a Cylindrical Structure Surface in Compressible Fluid. Applied Sciences, 9(7), 1403. https://doi.org/10.3390/app9071403






