Recent Developments in the Field of the Metal-Insulator Transition in Two Dimensions
Abstract
:1. Introduction
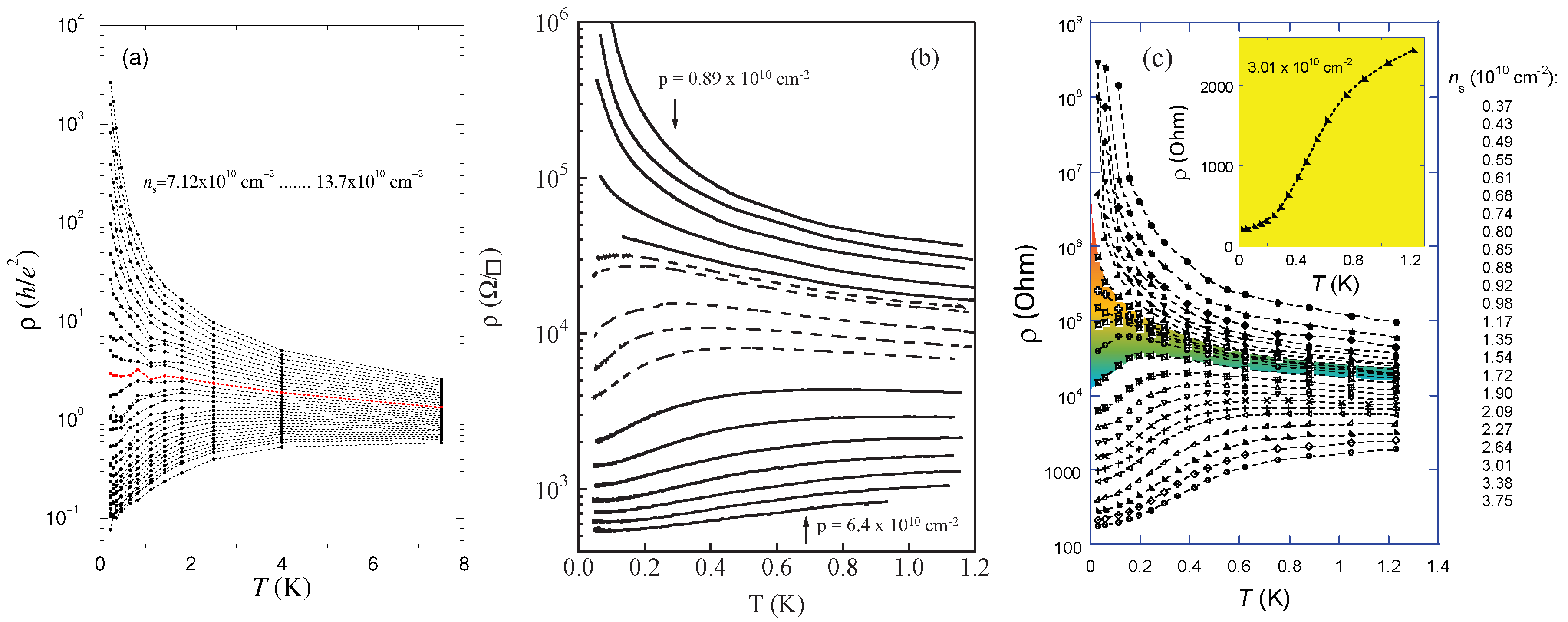
2. Metal-Insulator Transition in Zero Magnetic Field
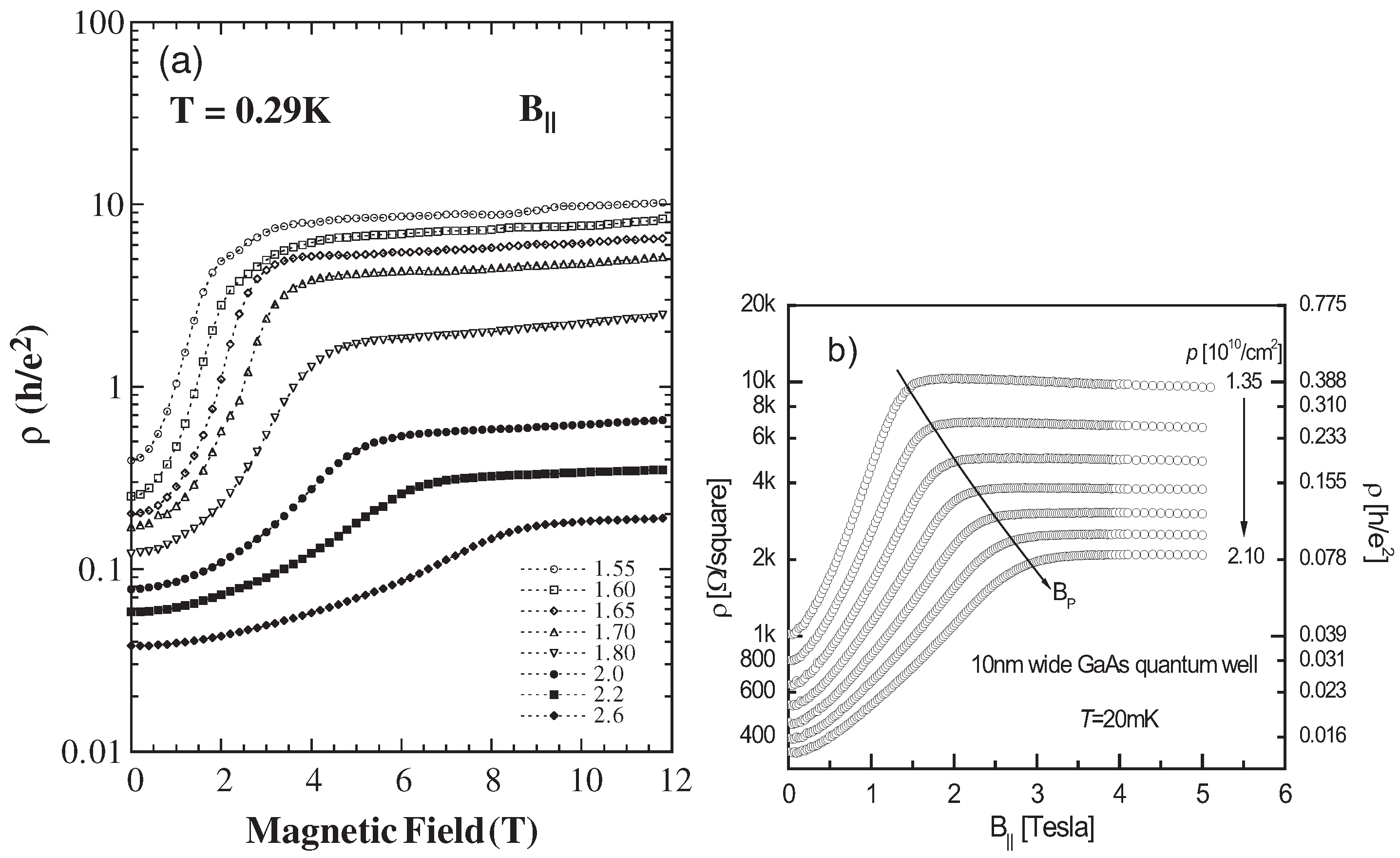
3. Influence of the Magnetic Field Parallel to the 2D Plane
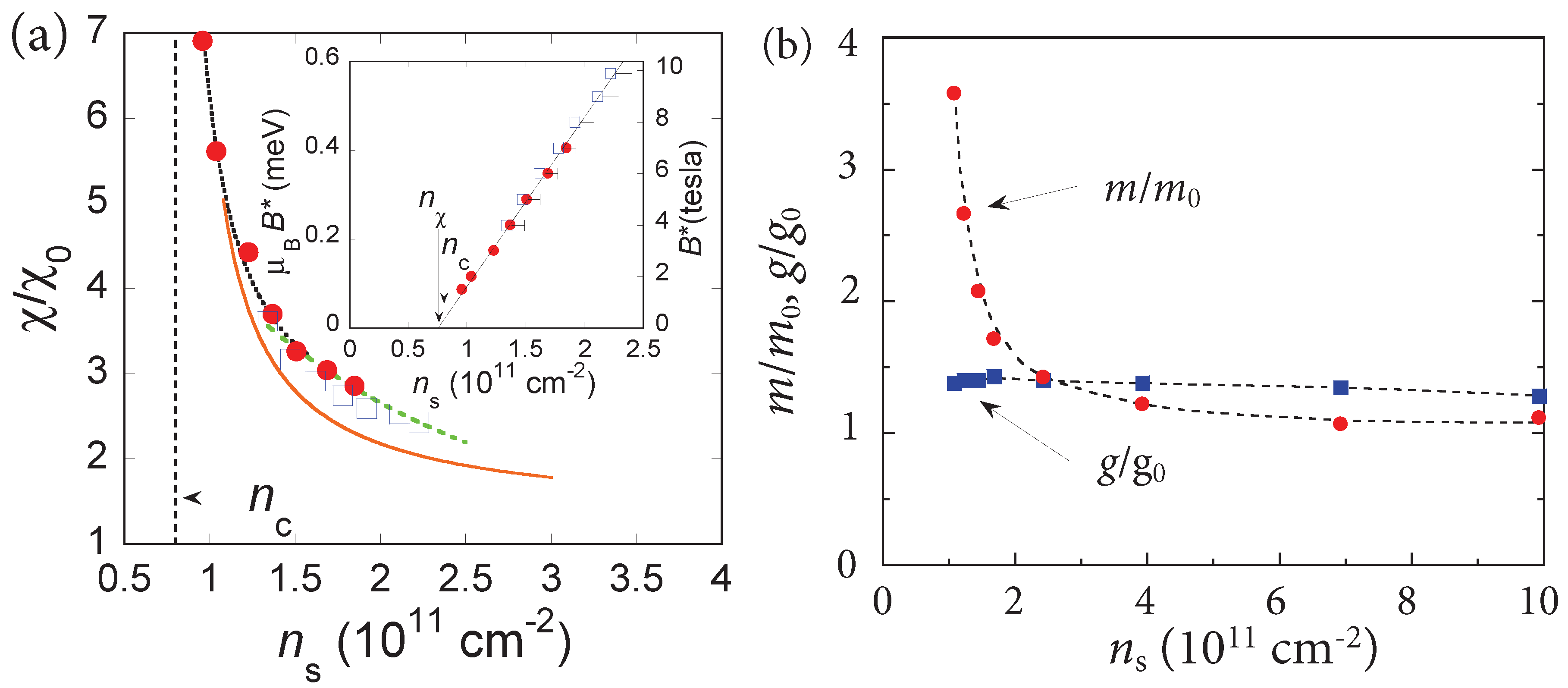
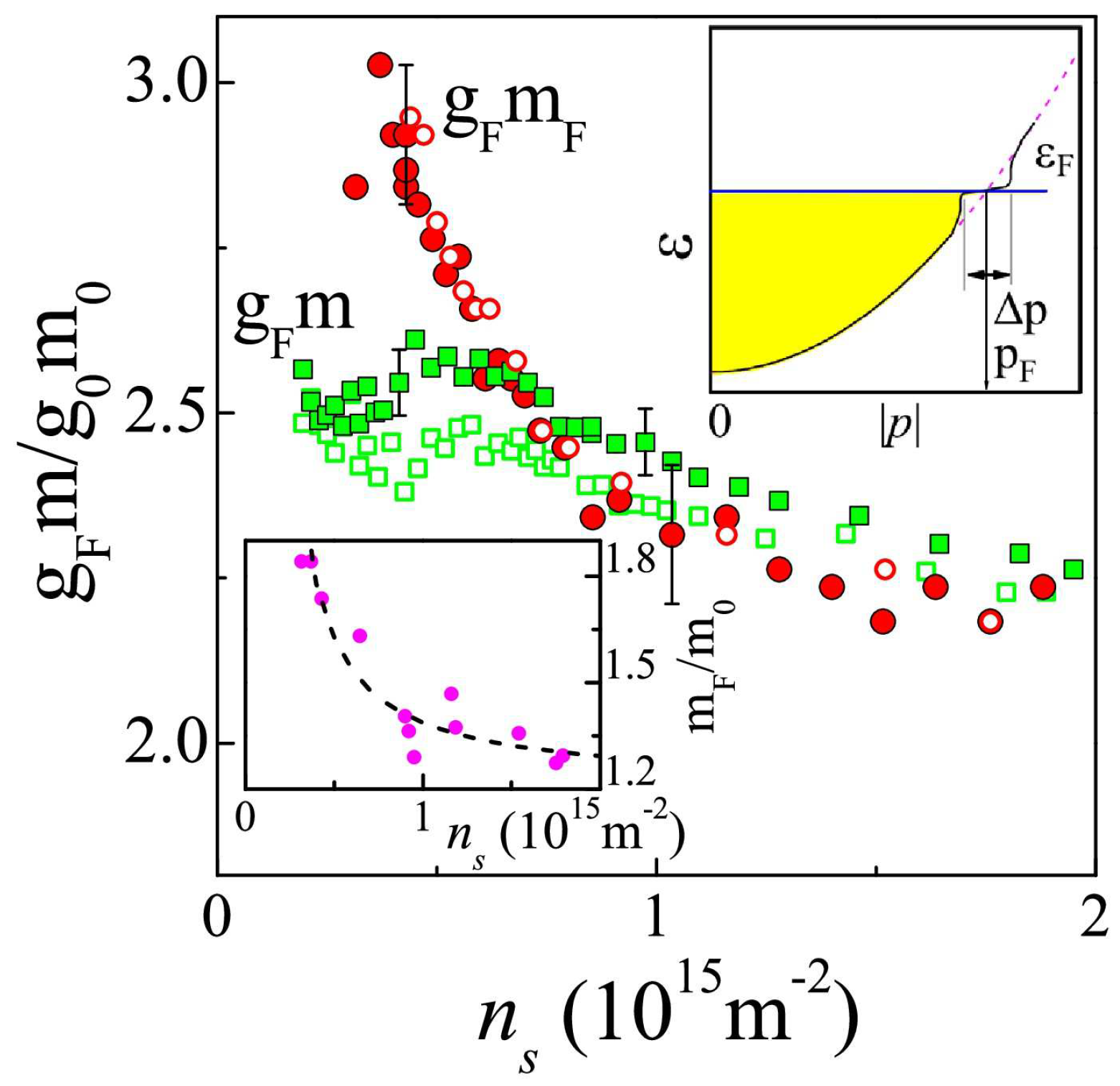
4. Spin Susceptibility; g-Factor; the Effective Mass
5. Band Flattening: Possible Condensation of Fermions
- (a)
- data describing the electron system as a whole, like thermodynamic density of states, magnetization of the electron system, or the magnetic field required to polarize electron spins fully and
- (b)
- data related only to the electrons at the Fermi level, like the amplitude of the Shubnikov–de Haas oscillations. This yields the effective mass and Landé g-factor at the Fermi level.
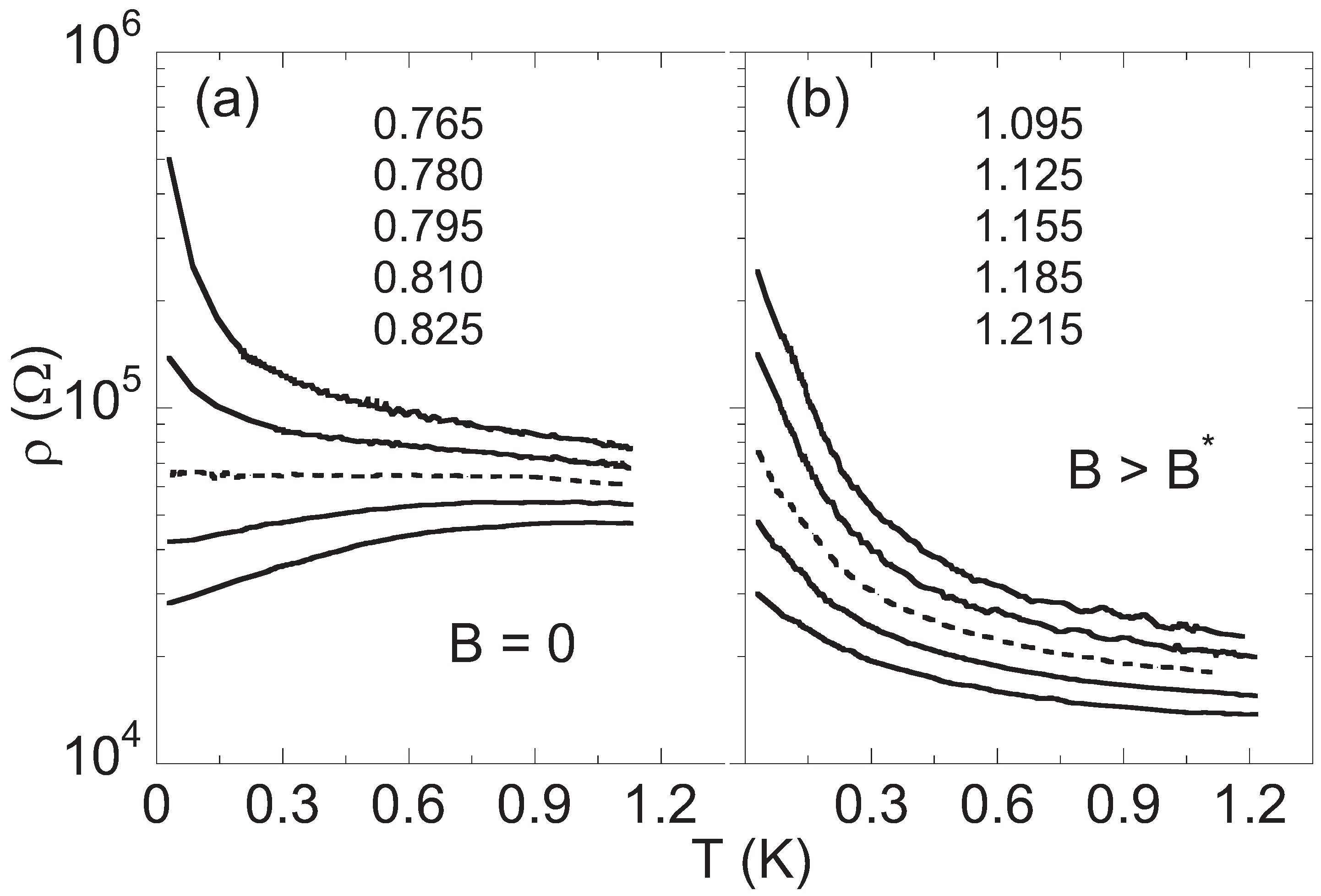
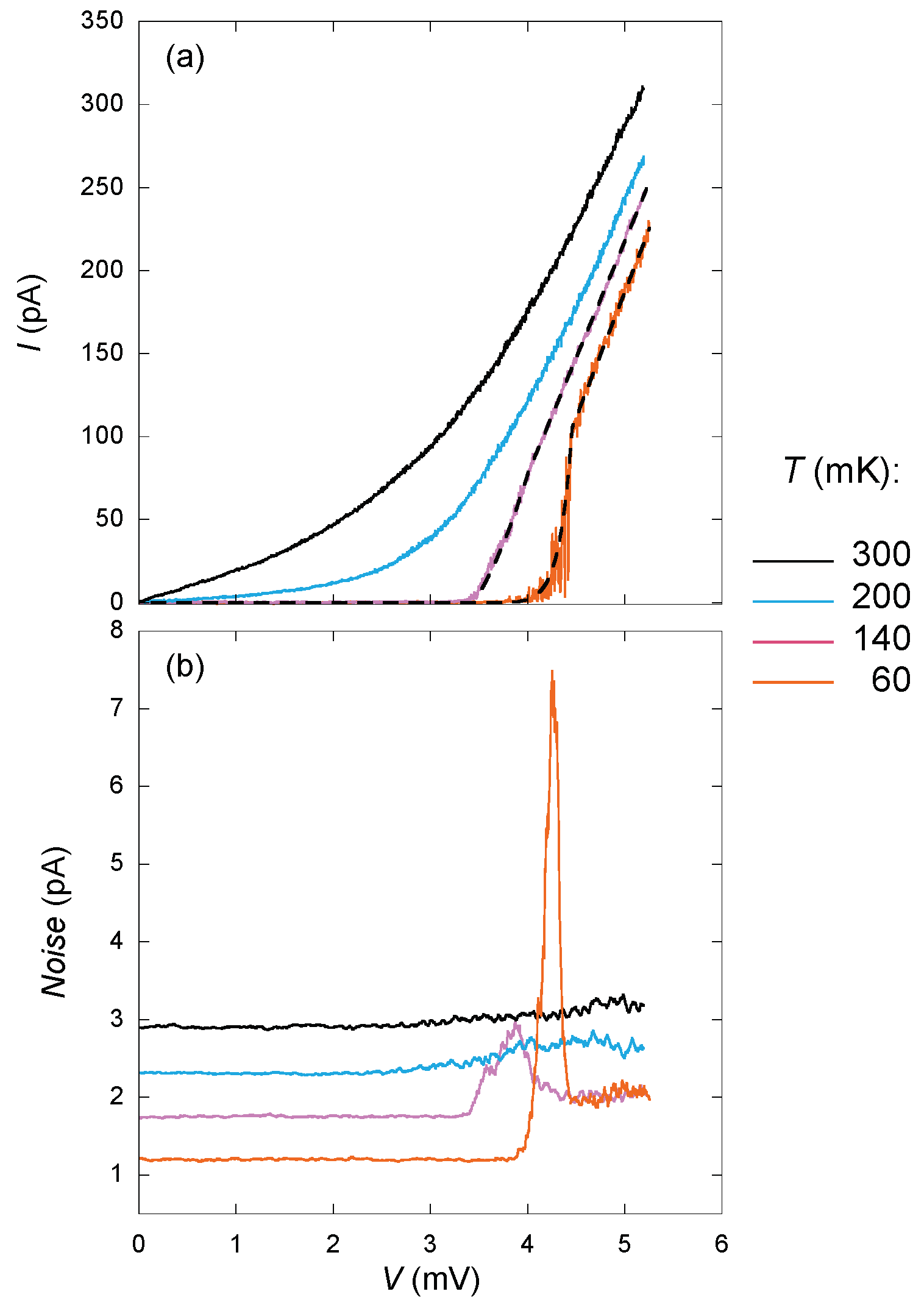
6. Transport Evidence for a Sliding Quantum Electron Solid
7. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Zavaritskaya, T.N.; Zavaritskaya, É.I. Metal-insulator transition in inversion channels of silicon MOS structures. JETP Lett. 1987, 45, 609–613. [Google Scholar]
- Kravchenko, S.V.; Kravchenko, G.V.; Furneaux, J.E.; Pudalov, V.M.; D’Iorio, M. Possible metal-insulator transition at B = 0 in two dimensions. Phys. Rev. B 1994, 50, 8039–8042. [Google Scholar] [CrossRef]
- Popović, D.; Fowler, A.B.; Washburn, S. Metal-insulator transition in two dimensions: Effects of disorder and magnetic field. Phys. Rev. Lett. 1997, 79, 1543–1546. [Google Scholar] [CrossRef]
- Abrahams, E.; Kravchenko, S.V.; Sarachik, M.P. Metallic behavior and related phenomena in two dimensions. Rev. Mod. Phys. 2001, 73, 251–266. [Google Scholar] [CrossRef]
- Kravchenko, S.V.; Sarachik, M.P. Metal-insulator transition in two-dimensional electron systems. Rep. Prog. Phys. 2004, 67, 1–44. [Google Scholar] [CrossRef]
- Shashkin, A.A. Metal-insulator transitions and the effects of electron-electron interactions in two-dimensional electron systems. Phys. Usp. 2005, 48, 129–149. [Google Scholar] [CrossRef]
- Spivak, B.; Kravchenko, S.V.; Kivelson, S.A.; Gao, X.P.A. Transport in strongly correlated two dimensional electron fluids. Rev. Mod. Phys. 2010, 82, 1743–1766. [Google Scholar] [CrossRef]
- Melnikov, M.Y.; Shashkin, A.A.; Dolgopolov, V.T.; Zhu, A.Y.X.; Kravchenko, S.V.; Huang, S.-H.; Liu, C.W. Quantum phase transition in ultrahigh mobility SiGe/Si/SiGe two-dimensional electron system. Phys. Rev. B 2019, 99, 081106(R). [Google Scholar] [CrossRef]
- Punnoose, A.; Finkelstein, A.M. Dilute electron gas near the metal-insulator transition: Role of valleys in silicon inversion layers. Phys. Rev. Lett. 2001, 88, 016802. [Google Scholar] [CrossRef]
- Punnoose, A.; Finkelstein, A.M. Metal-insulator transition in disordered two-dimensional electron systems. Science 2005, 310, 289–291. [Google Scholar] [CrossRef]
- Finkelstein, A.M. Influence of Coulomb interaction on the properties of disordered metals. Sov. Phys. JETP 1983, 57, 97–108. [Google Scholar]
- Finkelstein, A.M. Weak localization and Coulomb interaction in disordered systems. Z. Phys. B 1984, 56, 189–196. [Google Scholar] [CrossRef]
- Castellani, C.; Di Castro, C.; Lee, P.A.; Ma, M. Interaction-driven metal-insulator transitions in disordered fermion systems. Phys. Rev. B 1984, 30, 527–543. [Google Scholar] [CrossRef]
- Castellani, C.; Di Castro, C.; Lee, P.A. Metallic phase and metal-insulator transition in two-dimensional electronic systems. Phys. Rev. B 1998, 57, R9381–R9384. [Google Scholar] [CrossRef]
- Kravchenko, S.V.; Mason, W.E.; Bowker, G.E.; Furneaux, J.E.; Pudalov, V.M.; D’Iorio, M. Scaling of an anomalous metal-insulator transition in a two-dimensional system in silicon at B = 0. Phys. Rev. B 1995, 51, 7038–7045. [Google Scholar] [CrossRef]
- Hanein, Y.; Meirav, U.; Shahar, D.; Li, C.C.; Tsui, D.C.; Shtrikman, H. The metalliclike conductivity of a two-dimensional hole system. Phys. Rev. Lett. 1998, 80, 1288–1291. [Google Scholar] [CrossRef]
- Shashkin, A.A.; Kravchenko, S.V.; Klapwijk, T.M. Metal-insulator transition in a 2D electron gas: Equivalence of two approaches for determining the critical point. Phys. Rev. Lett. 2001, 87, 266402. [Google Scholar] [CrossRef] [PubMed]
- Kravchenko, S.V.; Klapwijk, T.M. Metallic low-temperature resistivity in a 2D electron system over an extended temperature range. Phys. Rev. Lett. 2000, 84, 2909–2912. [Google Scholar] [CrossRef]
- Simonian, D.; Kravchenko, S.V.; Sarachik, M.P.; Pudalov, V.M. Magnetic field suppression of the conducting phase in two dimensions. Phys. Rev. Lett. 1997, 79, 2304–2307. [Google Scholar] [CrossRef]
- Pudalov, V.M.; Brunthaler, G.; Prinz, A.; Bauer, G. Instability of the two-dimensional metallic phase to a parallel magnetic field. JETP Lett. 1997, 65, 932–937. [Google Scholar] [CrossRef]
- Gao, X.P.A.; Boebinger, G.S.; Mills, A.P., Jr.; Ramirez, A.P.; Pfeiffer, L.N.; West, K.W. Spin-polarization-induced tenfold magnetoresistivity of highly metallic two-dimensional holes in a narrow GaAs quantum well. Phys. Rev. B 2006, 73, 241315(R). [Google Scholar] [CrossRef]
- Dolgopolov, V.T.; Gold, A. Magnetoresistance of a two-dimensional electron gas in a parallel magnetic field. JETP Lett. 2000, 71, 27–30. [Google Scholar] [CrossRef]
- Okamoto, T.; Hosoya, K.; Kawaji, S.; Yagi, A. Spin degree of freedom in a two-dimensional electron liquid. Phys. Rev. Lett. 1999, 82, 3875–3878. [Google Scholar] [CrossRef]
- Vitkalov, S.A.; Zheng, H.; Mertes, K.M.; Sarachik, M.P.; Klapwijk, T.M. Small-angle Shubnikov-de Haas measurements in a 2D electron system: The effect of a strong in-plane magnetic field. Phys. Rev. Lett. 2000, 85, 2164–2167. [Google Scholar] [CrossRef] [PubMed]
- Dolgopolov, V.T.; Kravchenko, G.V.; Shashkin, A.A.; Kravchenko, S.V. Properties of electron insulating phase in Si inversion layers at low-temperatures. JETP Lett. 1992, 55, 733–737. [Google Scholar]
- Dolgopolov, V.T.; Shashkin, A.A.; Kravchenko, S.V. Spin polarization and exchange-correlation effects in transport properties of two-dimensional electron systems in silicon. Phys. Rev. B 2017, 96, 075307. [Google Scholar] [CrossRef]
- Li, S.; Sarachik, M.P. Resistivity of the insulating phase approaching the two-dimensional metal-insulator transition: The effect of spin polarization. Phys. Rev. B 2017, 95, 041301(R). [Google Scholar] [CrossRef]
- Kravchenko, S.V.; Shashkin, A.A.; Bloore, D.A.; Klapwijk, T.M. Shubnikov-de Haas oscillations near the metal-insulator transition in a two-dimensional electron system in silicon. Solid State Commun. 2000, 116, 495–499. [Google Scholar] [CrossRef]
- Shashkin, A.A.; Kravchenko, S.V.; Dolgopolov, V.T.; Klapwijk, T.M. Indication of the ferromagnetic instability in a dilute two-dimensional electron system. Phys. Rev. Lett. 2001, 87, 086801. [Google Scholar] [CrossRef]
- Shashkin, A.A.; Anissimova, S.; Sakr, M.R.; Kravchenko, S.V.; Dolgopolov, V.T.; Klapwijk, T.M. Pauli spin susceptibility of a strongly correlated two-dimensional electron liquid. Phys. Rev. Lett. 2006, 96, 036403. [Google Scholar] [CrossRef]
- Kozuka, Y.; Tsukazaki, A.; Kawasaki, M. Challenges and opportunities of ZnO-related single crystalline heterostructures. Appl. Phys. Rev. 2014, 1, 011303. [Google Scholar] [CrossRef]
- Shashkin, A.A.; Kravchenko, S.V.; Dolgopolov, V.T.; Klapwijk, T.M. Sharp increase of the effective mass near the critical density in a metallic two-dimensional electron system. Phys. Rev. B 2002, 66, 073303. [Google Scholar] [CrossRef]
- Shashkin, A.A.; Rahimi, M.; Anissimova, S.; Kravchenko, S.V.; Dolgopolov, V.T.; Klapwijk, T.M. Spin-independent origin of the strongly enhanced effective mass in a dilute 2D electron system. Phys. Rev. Lett. 2003, 91, 046403. [Google Scholar] [CrossRef] [PubMed]
- Anissimova, S.; Venkatesan, A.; Shashkin, A.A.; Sakr, M.R.; Kravchenko, S.V.; Klapwijk, T.M. Magnetization of a strongly interacting two-dimensional electron system in perpendicular magnetic fields. Phys. Rev. Lett. 2006, 96, 046409. [Google Scholar] [CrossRef] [PubMed]
- Mokashi, A.; Li, S.; Wen, B.; Kravchenko, S.V.; Shashkin, A.A.; Dolgopolov, V.T.; Sarachik, M.P. Critical behavior of a strongly interacting 2D electron system. Phys. Rev. Lett. 2012, 109, 096405. [Google Scholar] [CrossRef]
- Heikkila, T.T.; Kopnin, N.B.; Volovik, G.E. Flat bands in topological media. JETP Lett. 2011, 94, 233–239. [Google Scholar] [CrossRef]
- Bennemann, K.-H.; Ketterson, J.B. Novel Superfluids; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Peotta, S.; Torma, P. Superfluidity in topologically nontrivial flat bands. Nat. Commun. 2015, 6, 8944. [Google Scholar] [CrossRef]
- Volovik, G.E. From standard model of particle physics to room-temperature superconductivity. Phys. Scr. 2015, T164, 014014. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Popov, K.G.; Shaginyan, V.R.; Stephanovich, V.A. Theory of Heavy Fermion Compounds; Springer: Berlin, Germany, 2014. [Google Scholar]
- Camjayi, A.; Haule, K.; Dobrosavljević, V.; Kotliar, G. Coulomb correlations and the Wigner-Mott transition. Nat. Phys. 2008, 4, 932–935. [Google Scholar] [CrossRef]
- Yudin, D.; Hirschmeier, D.; Hafermann, H.; Eriksson, O.; Lichtenstein, A.I.; Katsnelson, M.I. Fermi condensation near van Hove singularities within the Hubbard model on the triangular lattice. Phys. Rev. Lett. 2014, 112, 070403. [Google Scholar] [CrossRef] [PubMed]
- Melnikov, M.Y.; Shashkin, A.A.; Dolgopolov, V.T.; Huan, S.-H.; Liu, C.W.; Kravchenko, S.V. Indication of band flattening at the Fermi level in a strongly correlated electron system. Sci. Rep. 2017, 7, 14539. [Google Scholar] [CrossRef] [PubMed]
- Melnikov, M.Y.; Shashkin, A.A.; Dolgopolov, V.T.; Huan, S.-H.; Liu, C.W.; Kravchenko, S.V. Ultra-high mobility two-dimensional electron gas in a SiGe/Si/SiGe quantum well. Appl. Phys. Lett. 2015, 106, 092102. [Google Scholar] [CrossRef]
- Melnikov, M.Y.; Shashkin, A.A.; Dolgopolov, V.T.; Kravchenko, S.V.; Huan, S.-H.; Liu, C.W. Effective electron mass in high-mobility SiGe/Si/SiGe quantum wells. JETP Lett. 2014, 100, 114–119. [Google Scholar] [CrossRef]
- Khodel, V.A.; Shaginyan, V.R. Superfluidity in system with fermion condensate. JETP Lett. 1990, 51, 553–555. [Google Scholar]
- Nozières, P. Properties of Fermi liquids with a finite range interaction. J. Phys. I 1992, 2, 443–458. [Google Scholar] [CrossRef]
- Zverev, M.V.; Khodel, V.A.; Pankratov, S.S. Microscopic theory of a strongly correlated two-dimensional electron gas. JETP Lett. 2012, 96, 192–202. [Google Scholar] [CrossRef]
- Andrei, E.Y.; Deville, G.; Glattli, D.C.; Williams, F.I.B.; Paris, E.; Etienne, B. Observation of a magnetically induced Wigner solid. Phys. Rev. Lett. 1988, 60, 2765–2768. [Google Scholar] [CrossRef]
- Goldman, V.J.; Santos, M.; Shayegan, M.; Cunningham, J.E. Evidence for two-dimensional quantum Wigner crystal. Phys. Rev. Lett. 1990, 65, 2189–2192. [Google Scholar] [CrossRef] [PubMed]
- Kravchenko, S.V.; Pudalov, V.M.; Campbell, J.; D’Iorio, M. Electron solid at the Si surface in zero magnetic field? JETP Lett. 1991, 54, 532–536. [Google Scholar]
- Pudalov, V.M.; D’Iorio, M.; Kravchenko, S.V.; Campbell, J.W. Zero-magnetic-field collective insulator phase in a dilute 2D electron system. Phys. Rev. Lett. 1993, 70, 1866–1869. [Google Scholar] [CrossRef] [PubMed]
- Knighton, T.; Wu, Z.; Huang, J.; Serafin, A.; Xia, J.S.; Pfeiffer, L.N.; West, K.W. Evidence of two-stage melting of Wigner solids. Phys. Rev. B 2018, 97, 085135. [Google Scholar] [CrossRef]
- Williams, F.I.B.; Wright, P.A.; Clark, R.G.; Andrei, E.Y.; Deville, G.; Glattli, D.C.; Probst, O.; Etienne, B.; Dorin, C.; Foxon, C.T.; et al. Conduction threshold and pinning frequency of magnetically induced Wigner solid. Phys. Rev. Lett. 1991, 66, 3285–3288. [Google Scholar] [CrossRef] [PubMed]
- Chitra, R.; Giamarchi, T. Zero field Wigner crystal. Eur. Phys. J. B 2005, 44, 455–467. [Google Scholar] [CrossRef]
- Marianer, S.; Shklovskii, B.I. Effective temperature of hopping electrons in a strong electric field. Phys. Rev. B 1992, 46, 13100–13103. [Google Scholar] [CrossRef]
- Jiang, H.W.; Stormer, H.L.; Tsui, D.C.; Pfeiffer, L.N.; West, K.W. Magnetotransport studies of the insulating phase around ν=1/5 Landau-level filling. Phys. Rev. B 1991, 44, 8107–8114. [Google Scholar] [CrossRef]
- D’Iorio, M.; Pudalov, V.M.; Semenchinsky, S.G. Magnetic field induced transitions between quantized Hall and insulator states in a dilute 2D electron gas. Phys. Lett. A 1990, 150, 422–426. [Google Scholar] [CrossRef]
- D’Iorio, M.; Pudalov, V.M.; Semenchinsky, S.G. Reentrant insulating phase in Si inversion layers in low magnetic fields. Phys. Rev. B 1992, 46, 15992–16004. [Google Scholar] [CrossRef]
- Qiu, R.L.J.; Gao, X.P.A.; Pfeiffer, L.N.; West, K.W. Connecting the reentrant insulating phase and the zero-field metal-insulator transition in a 2D hole system. Phys. Rev. Lett. 2012, 108, 106404. [Google Scholar] [CrossRef] [PubMed]
- Qiu, R.L.J.; Liu, C.W.; Liu, S.; Gao, X.P.A. New reentrant insulating phases in strongly interacting 2D systems with low disorder. Appl. Sci. 2018, 8, 1909. [Google Scholar] [CrossRef]
- Wigner, E. On the interaction of electrons in metals. Phys. Rev. 1934, 46, 1002–1011. [Google Scholar] [CrossRef]
- Chaplik, A.V. Possible crystallization of charge carriers in low-density inversion layers. Sov. Phys. JETP 1972, 35, 395–398. [Google Scholar]
- Tanatar, B.; Ceperley, D.M. Ground state of the two-dimensional electron gas. Phys. Rev. B 1989, 39, 5005–5016. [Google Scholar] [CrossRef]
- Attaccalite, C.; Moroni, S.; Gori-Giorgi, P.; Bachelet, G.B. Correlation energy and spin polarization in the 2D electron gas. Phys. Rev. Lett. 2002, 88, 256601. [Google Scholar] [CrossRef]
- Dolgopolov, V.T. Quantum melting of a two-dimensional Wigner crystal. Phys. Usp. 2017, 60, 731–742. [Google Scholar] [CrossRef]
- Brussarski, P.; Li, S.; Kravchenko, S.V.; Shashkin, A.A.; Sarachik, M.P. Transport evidence for a sliding two-dimensional quantum electron solid. Nat. Commun. 2018, 9, 3803. [Google Scholar] [CrossRef]
- Blatter, G.; Feigel’man, M.Y.; Geshkenbein, Y.B.; Larkin, A.I.; Vinokur, V.M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 1994, 66, 1125–1388. [Google Scholar] [CrossRef]
- Ovadia, M.; Sacepe, B.; Shahar, D. Electron-phonon decoupling in disordered insulators. Phys. Rev. Lett. 2009, 102, 176802. [Google Scholar] [CrossRef] [PubMed]
- Altshuler, B.L.; Kravtsov, V.E.; Lerner, I.V.; Aleiner, I.L. Jumps in current-voltage characteristics in disordered films. Phys. Rev. Lett. 2009, 102, 176803. [Google Scholar] [CrossRef]
- Chui, S.T.; Tanatar, B. Impurity effect on the two-dimensional-electron fluid-solid transition in zero field. Phys. Rev. Lett. 1995, 74, 458–461. [Google Scholar] [CrossRef] [PubMed]
- Spivak, B.; Kivelson, S.A. Phases intermediate between a two-dimensional electron liquid and Wigner crystal. Phys. Rev. B 2004, 70, 155114. [Google Scholar] [CrossRef]
- Reichhardt, C.; Olson, C.J.; Grønbech-Jensen, N.; Nori, F. Moving Wigner glasses and smectics: Dynamics of disordered Wigner crystals. Phys. Rev. Lett. 2001, 86, 4354–4357. [Google Scholar] [CrossRef]
- Reichhardt, C.; Olson Reichhardt, C.J. Depinning and nonequilibrium dynamic phases of particle assemblies driven over random and ordered substrates: A review. Rep. Prog. Phys. 2017, 80, 026501. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shashkin, A.A.; Kravchenko, S.V. Recent Developments in the Field of the Metal-Insulator Transition in Two Dimensions. Appl. Sci. 2019, 9, 1169. https://doi.org/10.3390/app9061169
Shashkin AA, Kravchenko SV. Recent Developments in the Field of the Metal-Insulator Transition in Two Dimensions. Applied Sciences. 2019; 9(6):1169. https://doi.org/10.3390/app9061169
Chicago/Turabian StyleShashkin, Alexander A., and Sergey V. Kravchenko. 2019. "Recent Developments in the Field of the Metal-Insulator Transition in Two Dimensions" Applied Sciences 9, no. 6: 1169. https://doi.org/10.3390/app9061169
APA StyleShashkin, A. A., & Kravchenko, S. V. (2019). Recent Developments in the Field of the Metal-Insulator Transition in Two Dimensions. Applied Sciences, 9(6), 1169. https://doi.org/10.3390/app9061169




