Abstract
The continuous uninterrupted supply of Natural Gas (NG) is crucial to today’s economy, with issues in key infrastructure, e.g., Baumgarten hub in Austria in 2017, highlighting the importance of the NG infrastructure for the supply of primary energy. The balancing of gas supply from a wide range of sources with various end users can be challenging due to the unique and different behaviours of the end users, which in some cases span across a continent. Further complicating the management of the NG network is its role in supporting the electrical network. The fast response times of NG power plants and the potential to store energy in the network play a key role in adding flexibility across other energy systems. Traditionally, modelling the NG network relies on nonlinear pipe flow equations that incorporate the demand (load), flow rate, and physical network parameters including topography and NG properties. It is crucial that the simulations produce accurate results quickly. This paper seeks to provide a novel method to solve gas flow equations through a network under steady-state conditions. Firstly, the model is reformulated into non-linear matrix equations, then the equations separated into their linear and nonlinear components, and thirdly, the non-linear system is solved approximately by providing a linear system with similar solutions to the non-linear one. The non-linear equations of the NG transport system include the main variables and characteristics of a gas network, focusing on pressure drop in the gas network. Two simplified models, both of the Irish gas network (1. A gas network with 13 nodes, 2. A gas network with 109 nodes) are used as a case study for comparison of the solutions. Results are generated by using the novel method, and they are compared to the outputs of two numerical methods, the Newton–Raphson solution using MATLAB and SAINT, a commercial software that is used for the simulation of the gas network and electrical grids.
1. Introduction
The continuous uninterrupted supply of Natural Gas (NG) is crucial to today’s economy. The balancing of gas supply from a wide range of sources with various end users can be challenging due to the unique and different behaviours of the end users, which in some cases span across a continent [1,2]. NG is one of the strategic primary sources of energy in the world, supplying approximately 24% of the world’s primary energy in 2016 [3]. This increases to 30% in Ireland, where on occasion, 80% of peak power demand is provided by NG [4], and in Singapore, where generated electricity can be up to 95% [5] from NG. Transport of NG via pipeline is the most efficient and economic and has the lowest carbon footprint [6,7,8], and in many instances, the gas network is capable of supplying NG from gas fields directly to the end users (from Well to Wheels; WtW is a common expression for the life cycle of a product). A gas network includes both transmission and distribution pipelines, compressor stations to bring the transmission network to its operating pressure and City Gas reduction Stations (CGS) and Town Break Stations (TBS) to reduce the NG pressure so that it can be provided safely into homes and business [9]. Gas systems need a reliable design to ensure effective operation, and due to the important role of natural gas of supplying primary energy and the significant investment in the network infrastructure, using a reliable and fast method for solving the gas flow calculations is essential. Gas network simulation allows for the understanding and forecast of the behaviour of the gas network under different conditions, and it is useful for decision makers for installing an optimal system. For the simulation of a gas network, the pipe flow equations that describe the flow, pressure, compressibility, line-pack capacity, and density of the compressible gas in the pipelines need to be solved. These equations include variables dependant on the gas composition, temperature, pipe length and diameter, gas constant, and pipe inclination, along with unknown variables such as pressure and flow rate. The pressure and flow rate are the most important variables from all points of view including financial/trading, technical, environmental, and health and safety. Gas network simulation helps the Transmission System Operator (TSO) understand how the individual components work together as a system. It is crucial in planning for the development and expansion of the network, the prevention of faults due to system changes in supply or demand nodes [2], and in managing crisis events that occur due to catastrophic component failures. Furthermore, deviations between accurate simulations and measured parameters can be an indication of leakage, which is important not just due to lost revenue point of view, but also from an environmental [10,11] and worker safety point of view. Therefore, accuracy is hugely important for simulations, where it can be the difference between making a profit or loss for both the TSO and the retailer [12]. Validation of the simulations requires reliable data, and robust reliable metering devices are key to ensuring this; they are also crucial in custody transfer, which is becoming more important as gas markets are opening up.
Multiple variables affect gas flow through a pipeline, all of which must be accounted for in the modelling of the gas network; these are pressure, flow rate, density, comparability, friction factors, inclination of the pipe, the Reynolds number, gas velocity, and pipe length and diameter. The most important variable in a gas network is pressure, which is the driving force for the transport of the NG through the pipe. When gas flows, the pressure decreases due to the frictional interaction between the gas and the pipe wall, exerting a shear force on the gas [2,13,14,15,16,17].
The modelling of the network topology also needs to be accounted for as it affects the gas pressure and has a major impact on the energy required to pump gas through the network. Each network has its unique particular distribution/transmission characteristics, and changes at a node (supplier or demand) will have consequences throughout the NG transport system [18]. In most countries, gas is distributed by pipeline networks over a vast range of pressures [19]; these are mainly divided into two, high pressure and low pressure systems, which are specified for transmission and distribution lines, respectively. However, in some research simulations, e.g., [18], middle-pressure pipelines are also investigated. Very large users of NG, such as power stations, are supplied directly from the transmission network, while other users including residential users receive NG via the distribution network [20]. A gas network is generally represented by a diagram involving branches (pipelines) and nodes (pipe connections). Facilities and equipment can be divided two groups: active and/or passive [21]. An active node or branch represents a actively-controlled facility, which is controlled during operation, e.g., compressors, regulator valves, and town gate stations. On the other side, the passive equipment will exert an influence on the network; however, its impact is due to the flow conditions, and the device is not adjusted or controlled. The prime example of passive equipment is the pipes [13].
Gas networks are large infrastructures with significant interconnection to the other networks, mainly electrical grids. Therefore, the security of gas supply is important to ensure continuing electricity supply. The challenge in gas networks is to balance the supply from different sources, with the changing demand. By controlling the pressure of the network, the TSO can ensure that sufficient gas is available to supply the end users with sufficient quantities. In this paper, a novel method is used to solve the non-linear system of algebraic equations. It provides a matrix formulation of the non-linear system describing the model, and by using matrix algebra, an alternative linear system is created. The solution of the alternative linear system can be used as a smooth approximation of the solutions of the non-linear system. This formulation is ready for software implementation and may also be used in atomic scale models as an alternative to existing empirical approaches with pair and cohesive potentials. An illustrative example, analysing a local region of a node, is presented to demonstrate the model performance.
In this study, two simplified gas networks were created, each based on the Irish Gas Network. Network 1 is A gas network with 13 nodes and 14 pipes, and a bigger network, Network 2, has 109 nodes and 112 pipes. Both networks are used for comparison of the novel approach with numerical solutions. Having a new reliable method for gas network modelling with fast calculation and precise results can be an option to replace numerical solutions, especially for large gas networks, such as those in continental Europe or North America, which contain several hundred nodes and pipelines and where large computation power is required. This new approach is a computational method that helps in producing faster results, and when the modelling of NG networks is coupled with other energy systems, for example the electrical network, faster and less computationally-demanding results are of key importance.
2. Literature Review
Various methods have been published to model a gas network and solve the governing equations of gas flow through the pipelines, with the vast majority applying numerical methods due to the non-linearity of the equations. In the literature, a Steady-State Model (SSM) is frequently used where the pressure (the driving force) and flow rate at the inlet and outlet of the pipeline are assumed constant. The steady-state equations of gas flow are non-linear algebraic, and in most cases, for solving this type of equation, numerical solutions are employed. Some valuable studies of SSM have been published. The principles and fundamentals of graph theory can be used to model a network along with the empirical flow equations for low-, medium-, and high-pressure flow. Various different empirical flow equations have been proposed such as Lacey’s equation, the Polyflo equation, the Panhandle equation, and the Weymouth equation (for high-pressure networks). Osiadacz [19] applied the Newton–Raphson method to deal with the non-linear equations. In this work, a step-by-step, Newton–Raphson method using a Jacobian matrix in graph theory was presented to model a horizontal gas pipe network. The essence of the work is the presentation of a computational method based on physical and mathematical laws for simplification of fundamental equations. While this work is one of the leading references in the modelling of gas networks, no specified example for a pipeline with inclination was presented. Many authors for simplification neglect the inclination term; however, Matko, Kwabena, and Iterran-Gonzales [22,23,24,25] are some authors who have considered inclination in the pipe flow equation, because of its importance for the validation of models with real-world data. Simulation of a natural gas network focusing on gas quality using a numerical-iteration method was carried out by Abeysekera [26]. An important point of this literature is the inclusion of gases with different density in the network. Varying gas composition will impact gas pipeline system characteristics such as pressure and flow rate. With a move to decarbonise the NG network, this is vital in the evaluation of the networks’ ability to store synthetic natural gas or hydrogen. Szoplik [18], after describing three different gas networks, low, middle, and high pressure, indicated two methods to run the gas system model, which are the nodal method and loop method. In the nodal method, the flow rate is the dependent variable, and the pressure drop (differential pressures between two nodes of a pipe/branch) through each branch is the independent variable , while the loop method describes that pressure is a function of flow rate (Equation (1)). The article investigates the impact of ambient temperature on the flow rate.
Debebe’s [27] paper focused on simulation of transmission pipelines in a gas network focusing on compressor stations. The equations are mainly based on the mass balance, flow principles, and compression characteristics of gas in pipes. The Newton–Raphson method has been applied to solve the equation using C++. The model evaluated the energy consumption for various configurations in order to optimize the transmission pipeline flow and pressure. There are a number of papers that have implemented the MATLAB-Simulink tool to simulate pipelines: Behbahani and Bagheri [28] and Herran-Gonzalez in [24] applied the Simulink toolbox in MATLAB to model the gas network. Behbahani and Bagheri [28] have manipulated the Simulink model of a gas system, and in order to verify the accuracy, the results have been compared with outputs from the finite difference scheme (FSM) and experimental test cases. The proposed model can predict the transient response of the dependent variable (pressure) with a good correlation with the nonlinear finite difference models. Herran [24] has implemented two models, the characteristic method and Crank–Nicholson, both using the MATLAB-Simulink library for solving the partial differential equations. The results for a simple triangle gas network (including two demand nodes and one supplier node) for both models produced similar results to the Osiadacz model [19]. Mohring [29] applied a numerical method to run the simplified loop model of a gas network. In this study, the inclination term has been neglected, and during simplification, the compressibility term was held constant. Matko [25] discussed the non-linear equations and presented a solution by linearizing the unsteady-state equations where density, viscosity, and temperature (in adiabatic flow) are constant, but in reality, the non-linear flow equation consists of a number of interdependent variables, e.g., flow through a pipeline gas flow rate relates the squares of the inlet and outlet pressures [30].
Yue-Wu [31] believed there were two important aspects in the modelling of gas systems; numerical solutions and optimization, where a numerical solution is applied to determine the actual behaviour of gas flow in the pipe. However, it is highlighted that the disadvantage of the numerical method is that it is not able to put constraints on the system to find minimal cost, which is necessary for optimization. Furthermore, due to the fact that sizing of pipe diameters depends on the users’ demand, optimization could lead to significant operational advantages. The aim of optimization is to find the best set of control variables within a single optimization run. For some recent optimization methods useful for this we refer to [32,33,34].
Along with the equation parameters, the solving of non-linear equations is dependent on both the initial conditions and tolerance level chosen by the programmers, which can increase the computational time required and impact the convergence of the model (accuracy of the solution). Alternative methods of solving the pipe flow equations such as the one presented in this work are therefore of interest, as when a large-scale network is modelled, the numerical iteration method will take more time to solve the equations.
In recent years, there has been a significant development in using matrix theory to study networks related to engineering problems [35,36,37,38] and the solutions of non-linear algebraic systems [39,40,41,42,43,44,45]. The idea is to provide new techniques and methods ready for software implementation in order to solve non-linear equations, similar to those for modelling gas pipelines.
This paper presents a novel method for solving the equations governing flow and pressure in a natural gas network using matrix theory to derive a unique theorem.
3. Modelling of a Gas Network
A large amount of NG is transported long distances through the high-pressure pipeline network. Therefore, modelling/simulating of a gas transmission system with sufficient accuracy and fast calculations methods is beneficial in understanding how the system will behave. Evaluation of the feasibility of networks to cope with new customers, as well as the ability to determine the capacity of the current network, or to forecast the response of the system to any changes in supplying nodes (decrease/outage), as well as designing new gas network systems are areas where modelling can be used. The differential equations are used depending on the working pressure of the network and the operational conditions [19]. The major equations that must be satisfied in modelling gas flow in a pipeline are:
- Mass conservation equation (equation of continuity).
- Newton’s second law of motion (conservation of momentum).
- Energy equation (thermodynamic first law) and the equation of state.
According to forces’ directions in a pipe, the governing equation has been extracted, which is shown in Figure 1 and from Newton’s second law of motion-momentum Equation (3).
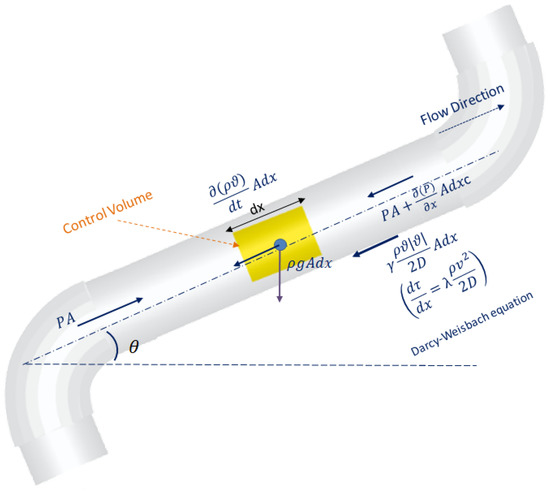
Figure 1.
Forces effective on a specific volume of gas flow through a pipeline.
The common equation for the steady-state flow of gas through a pipe is derived from Bernoulli’s equation of fluid flow, including changing density of gas due to the pressure drop along the pipe in the direction of flow. The equation of mass conservation from inlet Point (1) to outlet Point (2) is shown in Equation (2).
where is density and represents flow velocity.
Newton’s second law of motion (conservation of momentum) in Equation (4):
where the following terms describe each portion of Equation (4):
: inertia force (acting against the flow direction through the pipe)
: convective term
: pressure force
: shear force
: force of gravity
The variable pressure, p, and displacement, x, have been changed to and , respectively, which have been identified in Bernoulli’s Equation (5):
where “” is the head losses, i and j are sending and receiving nodes, respectively, and “z” is pipe elevation. The first law of thermodynamics expresses the conservation of energy and for a system may be written as:
where “” is the heat added to the system, “W” is the work done by the system, and “E” is the change in energy of the system. Energy associated with the mass of the system is customarily separated into three parts:
where “U” is the internal energy associated with molecular and atomic behaviour, “” the kinetic energy, and “” the potential energy associated with the height. If the rate of work on the flow is zero, Equation (6) can be written as [46]:
The final energy equation for gas flow in a pipeline can be expressed in two cases: firstly, an adiabatic flow (d = 0); secondly, an isothermal flow. In adiabatic flow, the rate of heat change will be zero, and in the isothermal flow, temperature will remain constant (T = constant and d) [47]. The change of temperature within the gas due to heat conduction between the pipe and the ground (if it is constructed as an underground pipeline) is sufficiently slow to be neglected [48]. This means, due to the slow flowing gas, it has sufficient time to exchange heat with the ground and its temperature with the ground temperature (for underground pipes) and for aboveground pipes, with the surrounding temperature. Therefore, temperature changes can be neglected and assumed a constant temperature equal to the ground/environment temperature [19,23,24].
where “” and “Q” are the density at standard conditions and flow rate of the NG. “A” and “D” are the cross-sectional area and inner diameter of the pipe, and “p” in Equation (9) is the average pressure between two nodes. “” is the efficiency of pipe friction factor to convert theoretical friction to actual friction factor (Equation (10)).
Another significant and effective term in a pipe network equation is the compressibility factor, “Z”. This is a correction factor in the state of gas equations for real gases, which accounts for the deviation from ideal gas behaviour. “Z” depends on pressure and temperature of gas and can be calculated using correlations such as Peng–Robinson, Redlich–Kwong, Soave-RK, the cubic equation, etc. [49]. In this research “Z” has been approximated by the PAPAY equation, which is applicable for high-pressure networks [50].
Due to slow changes of the variable in gas network pipelines, the focus of this study is a steady-state model. At steady state, outlet flow equals inlet flow, and the first term of Equation (9) is neglected. The equation then becomes:
By integrating from Equation (12), the final steady-state equation is presented in Equation (13), where pressure drop depends on inertia force, frictional force of the pipe, and different elevations of the pipeline in a gas network.
where:
In the next section only the modelling of the Irish gas network with 13 nodes and 14 branches is explained step-by-step using the matrix approach, see Figure 2. Due to massive matrices associated with the larger Network 2, details are shown in Appendix D. Boundary conditions and network details can be seen in Table 1 and Table A1.
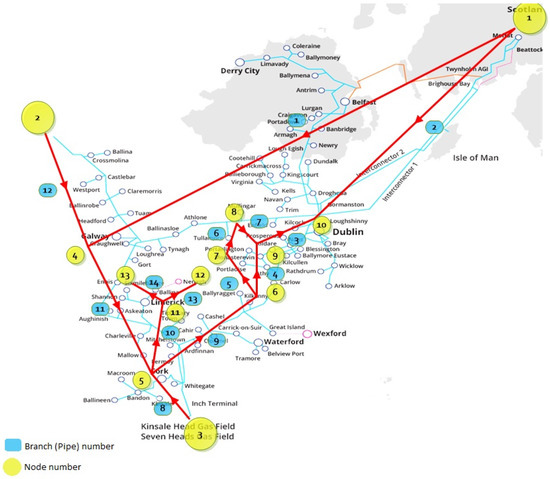
Figure 2.
A simplified gas network of Ireland with 13 nodes and 14 branches.

Table 1.
Parameters of the gas flow equation in the small network with 13 nodes and 14 branches.
4. Solving the Non-Linear System
In this section we will focus on the case of the Irish gas network of 13 nodes and 14 branches, see Figure 2. This model consists of two sets of equations. The first set includes the equations for pressure drop in (13) which are non-linear. Analytically in the case of the under study model, these non-linear equations are given by (A1). The second set describes the connectivity of the network in Figure 2 and consists of the linear equations (A2). These two sets of linear and non-linear equations can be written in the following matrix form:
where: , with:
Furthermore, , with:
and: , with:
and:
By setting with:
The subsystem (17) can take the form:
There exists , which satisfies the solution of (16) and can be found through a standard numerical method like the Newton–Raphson, such that:
Then, by replacing (19) in the above expression:
or, equivalently,
where , and . The system (21) with the system (18) will provide a solution for the non-linear system (16).
The following Theorem is provided.
5. Numerical Example Results
Both of the gas networks modelled include three supplier nodes of natural gas at a 70-barg pressure set point, which are shown in Figure 2 and Figure A1 (Nodes 1, 2, and 3). No constraint was placed on the flow of gas, which can be supplied from any of the supply nodes. Details and the boundary conditions of Network 1 and Network 2 are presented in Table 1 and Appendix D. The load at the demand nodes was weighted according to approximated town populations at the given node. These networks were then modelled as isothermal systems at 288.15 K using MATLAB (modelling the pipe flow equation using the Newton–Raphson method), SAINT (an energy system modelling software), and the new approach proposed in this paper. Results for Network 1 are presented in Tables 3 and 4, while those for Network 2 can be found in Appendix D. In both networks, there are three supply nodes, which represent the current sources of NG for the Island of Ireland Node 1, Moffat the Irish-Great Britain Interconnector, Node 2 the Corrib Gas field, and Node 3 the Kinsale Gas Field. Using the estimated gas consumption for each demand node, along with reported NG supplies [4], with the ZRT term representing the isothermal squared speed of sound in a pipeline, which was nearly 341 m/s in this case, the model was solved for pressure at each node and flow rate in each pipe. Using Equations (14) and (15), the parameters and for each pipe have been calculated, for which relates to the friction factor, pipe length, ZRT, normal density of gas, and diameter, while relates to the pipe angle, pipe length, and ZRT. The numbers shown in Table 2 for the smaller network and for the bigger network can be found in the Appendix D. In the pipe flow Equation (13), is a secondary important term.

Table 2.
Parameters and , which come from Equations (13) and (14).
To supply the estimated overall demand of Network 1, the Moffat interconnectors supply nearly 53.5 m3/s, and gas flows from Nodes 2 and 3 are 38 m3/s and 88 m3/s, respectively. Based on the picture of Ireland’s gas network (Figure 2), distributing this flow among the demand nodes resulted in an maximum pressure drop of 4 barg at Node 10 and and minimum pressure drop of 0.6 barg at Node 4 when the inlet pressure was 70 barg using SAINT. It is important to note that the maximum and minimum pressures did not occur at the minimum and maximum elevations, which was 130 m at Node 1 and 25 m at Node 11, respectively; therefore, the major source of pressure loss in the system was due to gas flow in the pipelines.
A summary of the results from the numerical solutions is shown in Table 3 and Table 4, and the results of Network 2 are shown in Appendix D. The pipelines’ and nodes’ details including pipe diameter, length, and inclination are shown. In Figure 2, the designed network is illustrated.

Table 3.
Demand and supply nodes’ details with pressure results from SAINT, MATLAB, and the novel approach at each node.

Table 4.
Pipelines’ details with flow rate outputs through the pipes from SAINT, MATLAB, and the novel approach models.
6. The Novel Approach Results and Discussion
By applying Theorem 1 (see Appendix C), the following outputs are shown in Table 3 and Table 4 for the results generated for Network 1. The outputs’ tables of the smaller network are presented in this section; however, all outputs for the bigger gas network are shown in Appendix D. The two variables of pressure and flow rate are the main outputs from the three models and used for the benchmarking of the proposed method. As can be observed from Table 3 and Table 4, there was a slight deviation between the results generated using the MATLAB and SAINT model for Network 1. Applying initial approximations for the non-linear part (F(X)) of linearized Equation (16) provided the outputs of the novel method of pressure and flow rate, which can be compared with the results from the SAINT and MATLAB models and the novel approach. As an example, the pressures at Node 5 from different solution methods were 68.32, 68.28, and 67.93 barg from SAINT, MATLAB, and the novel approach, respectively. The comparison between flow rates from the numerical methods and the novel method is shown in Table 4. As a result, The explored flow rates of Pipe Number 5 were 16.38, 16.73, and 16.22 sm3/s using SAINT, MATLAB, and the novel approach, respectively.
The comparison of outputs between the new method calculations and numerical solution using MATLAB for Network 1 showed 0.32% deviation of pressures and 1.38% deviation between flow rates in Table 5 and 0.3% and 2.95% average deviations of pressure and flow rate from the outputs of SAINT. Furthermore, for the bigger network with 109 nodes, the average deviations of pressure and flow rate were 0.07% and 1.23%, respectively, using MATLAB, and the average deviations between the novel approach and SAINT software for pressure and flow rates were 0.77% and 3.48%. The comparisons are shown in Appendix D, Table A2. Along with accuracy, the time taken for each of the simulations was measured for both modelled networks. The proposed new method was significantly faster, taking 0.31 s, while 1 s was taken for the solution in SAINT and 2.80 for the MATLAB solution of the bigger network. This time is even less for the smaller network, with 0.058 s, shown in the Table 6. This method can be used for much bigger networks at continental scales with fast calculations.

Table 5.
Deviations of the novel method from the MATLAB and SAINT outputs.

Table 6.
Elapsed for calculations in seconds for each model.
7. Conclusions
Currently, there are several numerical methods along with commercially-available software to solve the non-linear equations describing the compressible gas flow through the gas network. In this paper, a novel, unique mathematical method has been developed for simulating a steady-state non-linear gas network to quantify the main characteristics, pressure and flow rate through the transmission pipeline system.
Using two approximate models of the Irish natural gas transmission network as a case study the novel method was compared and benchmarked against a numerical modelling solution using the Newton–Raphson method carried out in MATLAB and the commercial software SAINT. The comparison of the results from all solutions showed that the new model is much faster than the alternative methods, and the average deviation between the methods was less than 0.31% (0.3% and 0.32%) for pressure and less than 2.1% (2.95% and 1.38%) for flow rate. Based on these key findings, the new method can be applied as a reliable fast method to model various conditions in a gas network even when there is a large number of nodes and branches. The method also lends its self ideally to the modelling of integrated energy systems as it is fast, simple, and can be easily integrated with linear models of electrical networks. The networks presented here only contain boundary conditions associated with pressure for supply nodes and load for demand nodes; in reality, there may be other real-world constraints that impact gas supply or demand. These constraints need to be included when modelling real-world systems, so that in the future, the results from the novel method can be validated with accurate data from a real gas network.
Author Contributions
I.D.; methodology, I.D., A.E. and M.L.; software, I.D. and A.E.; formal analysis, I.D., and A.E.; original draft preparation, A.E., and M.L.; data curation, I.D., E.S. and A.E.; editing.
Funding
This work is supported by the Science Foundation Ireland, by funding Ioannis Dassios and Muyang Liu under Investigator Programme Grant No. SFI/15/IA/3074; and Ali Ekhtiari and Eoin Syron under Strategic Partnership Programme Grant No. SFI/15/SPP/3125.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CBI | Cross Border Import |
| CGS | City Gas Station |
| ODE | Ordinary Differential Equation |
| PDE | Partial Differential Equation |
| SSM | Steady-State Model |
| TBS | Town Board Station |
| A | cross-sectional area of the pipe |
| A | matrix system of variables |
| D | pipe inner diameter |
| E | energy |
| f | friction factor |
| theoretical friction factor | |
| g | gravitational acceleration |
| head losses | |
| i | sender note punctuation |
| j | receiver node punctuation |
| L | nodal load (demand) |
| l | pipe length |
| p | nodal pressure |
| basic pressure | |
| critical pressure | |
| dp | differential pressure |
| p | pressure drop |
| U | internal energy |
| x | pipeline coordinate |
| pressure variable matrix | |
| flow rate variable matrix | |
| z | elevation |
| Z | compressibility factor |
| inclination | |
| normal density | |
| density | |
| pipe efficiency | |
| shear stress | |
| velocity | |
| heat energy | |
| volume | |
| W | work |
| Q | flow rate |
| R | gas constant |
| Re | Reynold’s number |
| t | time |
| T | Temperature |
| basic temperature | |
| critical temperature |
Appendix A. Non-Linear Equations
The non-linear equations of the model are the following:
Appendix B. Linear Equations
The linear equations of the model are the following:
Appendix C. Matrices and Tools for the Numerical Example
Substituting the data in the model as described in the matrix equations in Theorem 1, we have:
where −54,730,788,737.1; −137,782,182,351; −17,806,184,141.6; and = −21,014,390,336.9.
With the above result, we arrive at the results in Table 5.
Appendix D. Table of Outputs

Table A1.
Parameters of the gas flow equation in the bigger network with 109 nodes and 112 branches.
Table A1.
Parameters of the gas flow equation in the bigger network with 109 nodes and 112 branches.
| Pipe Number | From Node | To Node | Pipe Length, km | Diameter, m |
|---|---|---|---|---|
| 1 | 1 | 89 | 75 | 0.9 |
| 2 | 89 | 88 | 5 | 0.7 |
| 3 | 89 | 86 | 150 | 0.7 |
| 4 | 88 | 87 | 80 | 0.8 |
| 5 | 87 | 90 | 70 | 0.8 |
| 6 | 90 | 91 | 5 | 0.8 |
| 7 | 86 | 51 | 70 | 0.7 |
| 8 | 51 | 52 | 5 | 0.7 |
| 9 | 51 | 49 | 20 | 0.7 |
| 10 | 49 | 50 | 5 | 0.7 |
| 11 | 49 | 47 | 10 | 0.7 |
| 12 | 47 | 48 | 10 | 0.7 |
| 13 | 47 | 46 | 15 | 0.7 |
| 14 | 46 | 45 | 15 | 0.7 |
| 15 | 45 | 43 | 10 | 0.7 |
| 16 | 43 | 44 | 5 | 0.7 |
| 17 | 43 | 30 | 10 | 0.7 |
| 18 | 2 | 41 | 20 | 0.8 |
| 19 | 41 | 42 | 10 | 0.7 |
| 20 | 41 | 39 | 15 | 0.7 |
| 21 | 39 | 40 | 10 | 0.7 |
| 22 | 39 | 36 | 15 | 0.7 |
| 23 | 36 | 37 | 10 | 0.7 |
| 24 | 36 | 38 | 5 | 0.7 |
| 25 | 36 | 33 | 10 | 0.7 |
| 26 | 33 | 34 | 5 | 0.7 |
| 27 | 33 | 35 | 5 | 0.7 |
| 28 | 33 | 31 | 15 | 0.7 |
| 29 | 31 | 32 | 5 | 0.7 |
| 30 | 31 | 30 | 3 | 0.7 |
| 31 | 30 | 28 | 5 | 0.7 |
| 32 | 28 | 29 | 5 | 0.7 |
| 33 | 28 | 26 | 5 | 0.7 |
| 34 | 26 | 27 | 3 | 0.7 |
| 35 | 26 | 25 | 10 | 0.7 |
| 36 | 25 | 24 | 15 | 0.7 |
| 37 | 24 | 22 | 5 | 0.7 |
| 38 | 22 | 23 | 3 | 0.7 |
| 39 | 22 | 14 | 10 | 0.7 |
| 40 | 14 | 17 | 10 | 0.7 |
| 41 | 17 | 21 | 10 | 0.7 |
| 42 | 17 | 20 | 10 | 0.7 |
| 43 | 17 | 18 | 10 | 0.7 |
| 44 | 18 | 19 | 10 | 0.7 |
| 45 | 14 | 15 | 5 | 0.7 |
| 46 | 15 | 16 | 10 | 0.7 |
| 47 | 3 | 4 | 20 | 0.7 |
| 48 | 4 | 5 | 3 | 0.7 |
| 49 | 4 | 6 | 5 | 0.7 |
| 50 | 6 | 8 | 10 | 0.7 |
| 51 | 8 | 7 | 10 | 0.7 |
| 52 | 8 | 9 | 10 | 0.7 |
| 53 | 8 | 10 | 10 | 0.7 |
| 54 | 4 | 11 | 20 | 0.7 |
| 55 | 11 | 12 | 10 | 0.7 |
| 56 | 12 | 13 | 10 | 0.7 |
| 57 | 12 | 14 | 8 | 0.7 |
| 58 | 53 | 54 | 5 | 0.8 |
| 59 | 54 | 55 | 3 | 0.7 |
| 60 | 54 | 60 | 5 | 0.7 |
| 61 | 60 | 56 | 10 | 0.7 |
| 62 | 56 | 57 | 15 | 0.7 |
| 63 | 57 | 59 | 5 | 0.7 |
| 64 | 57 | 58 | 10 | 0.7 |
| 65 | 11 | 82 | 15 | 0.7 |
| 66 | 82 | 83 | 5 | 0.7 |
| 67 | 82 | 84 | 10 | 0.7 |
| 68 | 84 | 85 | 10 | 0.7 |
| 69 | 82 | 78 | 15 | 0.7 |
| 70 | 78 | 81 | 5 | 0.7 |
| 71 | 78 | 79 | 15 | 0.7 |
| 72 | 79 | 80 | 15 | 0.7 |
| 73 | 78 | 76 | 3 | 0.7 |
| 74 | 76 | 77 | 3 | 0.7 |
| 75 | 76 | 75 | 5 | 0.7 |
| 76 | 75 | 74 | 10 | 0.7 |
| 77 | 74 | 73 | 5 | 0.8 |
| 78 | 73 | 72 | 5 | 0.7 |
| 79 | 72 | 71 | 10 | 0.7 |
| 80 | 71 | 70 | 5 | 0.7 |
| 81 | 70 | 69 | 5 | 0.7 |
| 82 | 72 | 69 | 5 | 0.7 |
| 83 | 69 | 68 | 5 | 0.7 |
| 84 | 68 | 66 | 5 | 0.7 |
| 85 | 66 | 67 | 3 | 0.7 |
| 86 | 73 | 61 | 10 | 0.7 |
| 87 | 61 | 62 | 3 | 0.7 |
| 88 | 62 | 63 | 3 | 0.7 |
| 89 | 62 | 64 | 3 | 0.7 |
| 90 | 62 | 65 | 3 | 0.7 |
| 91 | 61 | 60 | 3 | 0.8 |
| 92 | 61 | 66 | 2 | 0.7 |
| 93 | 60 | 55 | 3 | 0.7 |
| 94 | 90 | 53 | 5 | 0.8 |
| 95 | 53 | 92 | 10 | 0.8 |
| 96 | 92 | 94 | 10 | 0.8 |
| 97 | 94 | 95 | 3 | 0.8 |
| 98 | 92 | 93 | 3 | 0.7 |
| 99 | 93 | 97 | 10 | 0.7 |
| 100 | 97 | 98 | 10 | 0.7 |
| 101 | 93 | 96 | 10 | 0.7 |
| 102 | 91 | 99 | 20 | 0.7 |
| 103 | 99 | 100 | 20 | 0.8 |
| 104 | 100 | 101 | 15 | 0.8 |
| 105 | 101 | 102 | 3 | 0.7 |
| 106 | 101 | 103 | 5 | 0.8 |
| 107 | 103 | 104 | 5 | 0.8 |
| 108 | 103 | 105 | 5 | 0.8 |
| 109 | 105 | 106 | 10 | 0.8 |
| 110 | 106 | 107 | 5 | 0.8 |
| 111 | 106 | 108 | 15 | 0.8 |
| 112 | 108 | 109 | 15 | 0.8 |

Table A2.
SAINT, MATLAB, and the novel method outputs for a 109-node network.
Table A2.
SAINT, MATLAB, and the novel method outputs for a 109-node network.
| Pressure, barg | Flow Rate, sm3/s | ||||||
|---|---|---|---|---|---|---|---|
| Node Number | SAINT | MATLAB | Novel Approach | Pipe Number | SAINT | MATLAB | Novel Approach |
| 1 | 85 | 85 | 85 | 1 | 152.27 | 142.83 | 142.83 |
| 2 | 85 | 85 | 85 | 2 | 113.33 | 107.67 | 107.49 |
| 3 | 85 | 85 | 85 | 3 | 38.93 | 35.17 | 35.09 |
| 4 | 82.15 | 82.24 | 82.22 | 4 | 113.33 | 107.67 | 107.21 |
| 5 | 82.22 | 82.22 | 82.21 | 5 | 113.33 | 107.67 | 107.21 |
| 6 | 81.86 | 82.14 | 82.10 | 6 | 65.00 | 65.00 | 64.98 |
| 7 | 81.69 | 82.13 | 82.09 | 7 | 38.93 | 35.17 | 35.01 |
| 8 | 81.68 | 82.13 | 82.09 | 8 | 5.00 | 5.00 | 5.00 |
| 9 | 81.66 | 82.13 | 82.09 | 9 | 33.93 | 30.16 | 30.13 |
| 10 | 82.06 | 82.13 | 82.09 | 10 | 5.00 | 5.00 | 5.00 |
| 11 | 81.23 | 81.16 | 81.11 | 11 | 28.93 | 25.16 | 25.13 |
| 12 | 81.19 | 81.16 | 81.12 | 12 | 5.00 | 5.00 | 5.00 |
| 13 | 80.70 | 81.16 | 81.09 | 13 | 23.93 | 20.16 | 20.09 |
| 14 | 80.77 | 81.17 | 81.16 | 14 | 23.93 | 20.16 | 20.00 |
| 15 | 80.84 | 81.17 | 81.13 | 15 | 23.93 | 20.16 | 20.00 |
| 16 | 80.84 | 81.17 | 81.19 | 16 | 5.00 | 5.00 | 5.00 |
| 17 | 80.81 | 81.13 | 81.12 | 17 | 18.93 | 15.16 | 15.11 |
| 18 | 80.80 | 81.12 | 81.13 | 18 | 115.71 | 119.14 | 119.00 |
| 19 | 80.77 | 81.12 | 81.12 | 19 | 5.00 | 5.00 | 5.00 |
| 20 | 81.05 | 81.12 | 81.11 | 20 | 110.71 | 114.14 | 113.23 |
| 21 | 81.12 | 81.12 | 81.12 | 21 | 5.00 | 5.00 | 5.00 |
| 22 | 81.32 | 81.29 | 81.28 | 22 | 105.71 | 109.14 | 109.01 |
| 23 | 81.32 | 81.29 | 81.29 | 23 | 5.00 | 5.00 | 5.00 |
| 24 | 81.39 | 81.36 | 81.35 | 24 | 5.00 | 5.00 | 5.00 |
| 25 | 81.60 | 81.55 | 81.55 | 25 | 95.71 | 99.14 | 99.00 |
| 26 | 81.73 | 81.69 | 81.67 | 26 | 5.00 | 5.00 | 5.00 |
| 27 | 81.73 | 81.69 | 81.68 | 27 | 2.00 | 2.00 | 2.00 |
| 28 | 81.81 | 81.76 | 81.74 | 28 | 88.71 | 92.14 | 92.12 |
| 29 | 81.81 | 81.75 | 81.74 | 29 | 50.00 | 50.00 | 50.00 |
| 30 | 81.89 | 81.84 | 81.82 | 30 | 38.71 | 42.14 | 42.12 |
| 31 | 81.92 | 81.87 | 81.80 | 31 | 57.64 | 57.30 | 57.27 |
| 32 | 81.89 | 81.82 | 81.80 | 32 | 5.00 | 5.00 | 5.00 |
| 33 | 82.56 | 82.42 | 82.42 | 33 | 52.64 | 52.30 | 52.01 |
| 34 | 82.56 | 82.42 | 82.41 | 34 | 2.00 | 2.00 | 2.00 |
| 35 | 82.56 | 82.42 | 82.41 | 35 | 50.64 | 50.30 | 50.30 |
| 36 | 83.02 | 82.85 | 82.83 | 36 | 50.64 | 50.30 | 50.28 |
| 37 | 83.02 | 82.85 | 82.84 | 37 | 50.64 | 50.30 | 50.23 |
| 38 | 83.02 | 82.85 | 82.84 | 38 | 2.00 | 2.00 | 2.00 |
| 39 | 83.86 | 83.60 | 83.60 | 39 | 48.64 | 48.30 | 48.25 |
| 40 | 83.86 | 83.60 | 83.57 | 40 | 35.00 | 35.00 | 35.00 |
| 41 | 84.77 | 84.41 | 84.40 | 41 | 5.00 | 5.00 | 5.00 |
| 42 | 84.77 | 84.41 | 84.39 | 42 | 5.00 | 5.00 | 5.00 |
| 43 | 81.95 | 81.85 | 81.79 | 43 | 5.00 | 5.00 | 5.00 |
| 44 | 81.95 | 81.84 | 81.81 | 44 | 5.00 | 5.00 | 5.00 |
| 45 | 81.98 | 81.86 | 81.85 | 45 | 7.00 | 7.00 | 7.00 |
| 46 | 82.03 | 81.88 | 81.87 | 46 | 5.00 | 5.00 | 5.00 |
| 47 | 82.08 | 81.91 | 81.90 | 47 | 175.03 | 181.03 | 181.00 |
| 48 | 82.08 | 81.91 | 81.89 | 48 | 0.00 | 0.00 | 0.00 |
| 49 | 82.16 | 81.93 | 81.90 | 49 | 75.00 | 75.00 | 75.00 |
| 50 | 82.16 | 81.93 | 81.90 | 50 | 15.00 | 15.00 | 15.00 |
| 51 | 82.29 | 82.00 | 81.98 | 51 | 5.00 | 5.00 | 5.00 |
| 52 | 82.29 | 82.00 | 81.98 | 52 | 5.00 | 5.00 | 5.00 |
| 53 | 78.89 | 78.09 | 78.00 | 53 | 5.00 | 5.00 | 5.00 |
| 54 | 78.87 | 78.09 | 78.00 | 54 | 100.03 | 106.03 | 106.04 |
| 55 | 78.84 | 78.08 | 78.00 | 55 | 1.64 | 1.30 | 1.29 |
| 56 | 78.85 | 78.09 | 78.00 | 56 | 5.00 | 5.00 | 5.00 |
| 57 | 78.83 | 78.08 | 78.00 | 57 | 6.00 | 6.30 | 6.20 |
| 58 | 78.97 | 78.08 | 78.09 | 58 | 42.33 | 36.67 | 36.99 |
| 59 | 78.83 | 78.08 | 78.04 | 59 | 40.08 | 39.89 | 39.89 |
| 60 | 78.87 | 78.10 | 78.01 | 60 | 2.25 | 3.23 | 3.21 |
| 61 | 78.89 | 78.14 | 78.00 | 61 | 15.00 | 15.00 | 15.00 |
| 62 | 78.88 | 78.14 | 78.01 | 62 | 15.00 | 15.00 | 15.00 |
| 63 | 78.88 | 78.14 | 78.11 | 63 | 5.00 | 5.00 | 5.00 |
| 64 | 78.88 | 78.14 | 78.11 | 64 | 5.00 | 5.00 | 5.00 |
| 65 | 78.88 | 78.14 | 78.11 | 65 | 101.67 | 107.34 | 106.23 |
| 66 | 78.89 | 78.15 | 78.09 | 66 | 2.00 | 2.00 | 2.00 |
| 67 | 78.89 | 78.15 | 78.09 | 67 | 5.00 | 5.00 | 5.00 |
| 68 | 78.92 | 78.19 | 78.29 | 68 | 5.00 | 5.00 | 5.00 |
| 69 | 78.94 | 78.22 | 78.30 | 69 | 94.67 | 100.34 | 100.12 |
| 70 | 78.94 | 78.22 | 78.19 | 70 | 5.00 | 5.00 | 5.00 |
| 71 | 78.94 | 78.22 | 78.22 | 71 | 5.00 | 5.00 | 5.00 |
| 72 | 78.96 | 78.24 | 78.20 | 72 | 5.00 | 5.00 | 5.00 |
| 73 | 79.00 | 78.29 | 78.20 | 73 | 84.67 | 90.34 | 90.32 |
| 74 | 79.09 | 78.41 | 78.39 | 74 | 2.00 | 2.00 | 2.00 |
| 75 | 79.45 | 78.90 | 78.89 | 75 | 82.67 | 88.34 | 88.30 |
| 76 | 79.64 | 79.15 | 79.09 | 76 | 82.67 | 88.34 | 88.30 |
| 77 | 79.64 | 79.15 | 79.06 | 77 | 82.67 | 88.34 | 88.30 |
| 78 | 79.79 | 79.30 | 78.93 | 78 | 38.20 | 40.93 | 40.90 |
| 79 | 79.78 | 79.30 | 79.12 | 79 | 14.44 | 15.68 | 15.23 |
| 80 | 79.78 | 79.30 | 79.13 | 80 | 9.44 | 10.68 | 10.00 |
| 81 | 79.89 | 79.30 | 79.03 | 81 | 4.44 | 5.68 | 5.52 |
| 82 | 80.49 | 80.18 | 80.00 | 82 | 23.76 | 25.25 | 24.56 |
| 83 | 80.49 | 80.18 | 80.03 | 83 | 28.20 | 30.93 | 30.89 |
| 84 | 80.49 | 80.18 | 80.00 | 84 | 28.20 | 30.93 | 30.89 |
| 85 | 80.49 | 80.18 | 80.12 | 85 | 5.00 | 5.00 | 5.00 |
| 86 | 82.90 | 82.32 | 82.29 | 86 | 44.47 | 47.41 | 47.30 |
| 87 | 81.25 | 80.28 | 80.16 | 87 | 15.00 | 15.00 | 15.00 |
| 88 | 83.78 | 82.71 | 82.68 | 88 | 5.00 | 5.00 | 5.00 |
| 89 | 84.10 | 83.00 | 82.97 | 89 | 5.00 | 5.00 | 5.00 |
| 90 | 78.96 | 78.09 | 78.09 | 90 | 5.00 | 5.00 | 5.00 |
| 91 | 78.90 | 77.98 | 77.89 | 91 | 52.67 | 58.33 | 57.23 |
| 92 | 78.92 | 78.09 | 78.00 | 92 | 23.20 | 25.93 | 24.54 |
| 93 | 78.92 | 78.09 | 78.00 | 93 | 39.92 | 40.11 | 40.01 |
| 94 | 78.92 | 78.09 | 78.03 | 94 | 48.33 | 42.67 | 42.62 |
| 95 | 78.92 | 78.09 | 78.01 | 95 | 6.00 | 6.00 | 6.00 |
| 96 | 78.92 | 78.09 | 78.02 | 96 | 2.00 | 2.00 | 2.00 |
| 97 | 78.92 | 78.09 | 78.02 | 97 | 2.00 | 2.00 | 2.00 |
| 98 | 78.92 | 78.09 | 78.05 | 98 | 4.00 | 4.00 | 4.00 |
| 99 | 78.47 | 77.05 | 77.00 | 99 | 2.00 | 2.00 | 2.00 |
| 100 | 78.30 | 76.57 | 76.56 | 100 | 2.00 | 2.00 | 2.00 |
| 101 | 78.23 | 76.20 | 76.15 | 101 | 2.00 | 2.00 | 2.00 |
| 102 | 78.12 | 76.17 | 76.16 | 102 | 65.00 | 65.00 | 65.00 |
| 103 | 78.16 | 76.17 | 76.16 | 103 | 65.00 | 65.00 | 65.00 |
| 104 | 78.16 | 76.14 | 76.09 | 104 | 65.00 | 65.00 | 65.00 |
| 105 | 78.16 | 76.17 | 76.09 | 105 | 50.00 | 50.00 | 50.00 |
| 106 | 78.16 | 76.16 | 76.18 | 106 | 15.00 | 15.00 | 15.00 |
| 107 | 78.16 | 76.16 | 76.14 | 107 | 5.00 | 5.00 | 5.00 |
| 108 | 78.15 | 76.16 | 76.15 | 108 | 10.00 | 10.00 | 10.00 |
| 109 | 78.15 | 76.16 | 76.11 | 109 | 10.00 | 10.00 | 10.00 |
| 110 | 5.00 | 5.00 | 5.00 | ||||
| 111 | 5.00 | 5.00 | 5.00 | ||||
| 112 | 5.00 | 5.00 | 5.00 | ||||
Appendix E. Figures
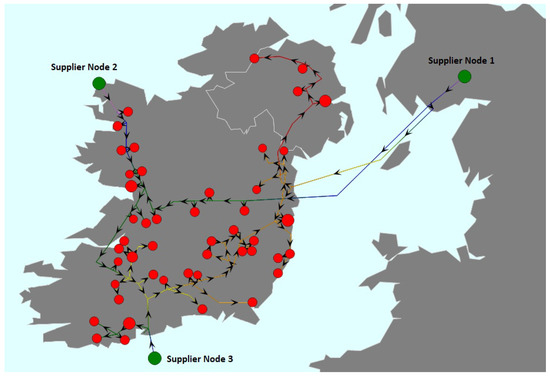
Figure A1.
The 109-node map of Ireland’s gas network.
References
- Sircar, A.; Sahajpal, S.; Yadav, K. Challenges & Issues in Natural Gas Distribution Industry. STM J. 2017, 7, 1–8. [Google Scholar]
- Ekhtiari, A.; Syron, E. Moffat Constraints to supply Ireland’s Gas Network. Eng. J. (Irel. Soc. Eng.) 2018. Available online: http://www.engineersjournal.ie/2018/05/15/irelands-future-natural-gas-supply-wellconnected-island/ (accessed on 1 July 2018).
- Global, B.P. Bp Statistical Review of World Energy. 2017. Available online: http://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy (accessed on 1 July 2018).
- Gas Network Ireland. Delivering a Reliable and Secure Gas Supply. 2016. Available online: https://www.gasnetworks.ie/corporate/company/our-network/18048_GNI_GasNetwork_ReliabilityCapacity_Doc_Update.pdf (accessed on 1 July 2018).
- Electrify. Electricity Generation in Singapore. Available online: https://electrify.sg/content/articles/electricity-generation-singapore/ (accessed on 5 November 2018).
- Thomas, S.; Dawe, R.A. Review of ways to transport natural gas energy from countries which do not need the gas for domestic use. Energy 2003, 28, 1461–1477. [Google Scholar] [CrossRef]
- Jaramillo, P.; Griffin, W.M.; Matthews, H.S. Comparative life-cycle air emissions of coal, domestic natural gas, LNG, and SNG for electricity generation. Environ. Sci. Technol. 2007, 41, 6290–6296. [Google Scholar] [CrossRef] [PubMed]
- Natgas. The Transportation of Natural Gas. Available online: http://naturalgas.org/naturalgas/transport/ (accessed on 5 November 2018).
- Ardali, E.K.; Heybatian, E. Energy regeneration in natural gas pressure reduction stations by use of gas turbo expander; evaluation of available potential in Iran. In Proceedings of the 24th World Gas Conference, Buenos Aires, Argentina, 5–9 October 2009. [Google Scholar]
- Brandt, A.R.; Heath, G.; Kort, E.; O’sullivan, F.; P’etron, G.; Jordaan, S.; Tans, P.; Wilcox, J.; Gopstein, A.; Arent, D.; et al. Methane leaks from North American natural gas systems. Science 2014, 343, 733–735. [Google Scholar] [CrossRef]
- Karion, A.; Sweeney, C.; P’etron, G.; Frost, G.; Hardesty, R.M.; Kofler, J.; Miller, B.R.; Newberger, T.; Wolter, S.; Banta, R. Methane emissions estimate from airborne measurements over a western United States natural gas field. Geophys. Res. Lett. 2013, 40, 4393–4397. [Google Scholar] [CrossRef]
- Buck, A.; (Coriolis Product Manager). The Importance of Mass Flow Measurement and the Relevance of Coriolis Technology. 2014. Available online: https://www.bronkhorst.com/blog/the-importance-of-mass-flow-measurement-and-the-relevance-of-coriolis-technology-en/ (accessed on 1 July 2018).
- Pambour, K.A.; Bolado-Lavin, R.; Dijkema, G.P. An integrated transient model for simulating the operation of natural gas transport systems. Nat. Gas Sci. Eng. 2016, 28, 672–690. [Google Scholar] [CrossRef]
- Wu, S.; Rios-Mercado, R.Z.; Boyd, E.A.; Scott, L.R. Model relaxations for the fuel cost minimization of steady-state gas pipeline networks. Math. Comput. Model. 2000, 31, 197–220. [Google Scholar] [CrossRef]
- Askari, S.; Montazerin, N.; Zarandi, M.F. Gas networks simulation from disaggregation of low frequency nodal gas consumption. Energy 2016, 112, 1286–1298. [Google Scholar] [CrossRef]
- Menon, E.S. Pressure Required to Transport. In Gas Pipeline Hydraulics; Forn, T.D., Hecht, M., Eds.; Taylor & Francis: New York, NY, USA, 2005; pp. 85–137. ISBN 0-8493-2785-7. [Google Scholar]
- Carvalho, R.; Buzna, L.; Bono, F.; Guti’errez, E.; Just, W.; Arrowsmit, D. Robustness of trans-European gas networks. Phys. Rev. E 2009, 80, 016106. [Google Scholar] [CrossRef]
- Szoplik, J. The Gas Transportation in a Pipeline Network. In Advances in Natural Gas Technology; Al-Megren, H., Ed.; InTech: Rijeka, Croatia, 2012; ISBN 978-953-51-0507-7. [Google Scholar]
- Osiadacz, A.J. Simulation and Analysis of Gas Networks; Taylor & Francis: London, UK, 1987. [Google Scholar]
- DCCAE. Energy, Gas. Department of Communications, Climate Action and Environment (DCCAE). 2016. Available online: https://www.dccae.gov.ie/en-ie/energy/topics/gas/Pages/default.aspx (accessed on 1 July 2018).
- Pambour, K.A.; Erdener, B.C.; Bolado-Lavin, R.; Dijkema, G.P. Development of a simulation framework for analysing security of supply in integrated gas and electric power systems. Appl. Sci. 2017, 7, 47. [Google Scholar] [CrossRef]
- Pambour, K.A.; Erdener, B.C.; Bolado-Lavin, R.; Dijkema, G.P. SAInt—A novel quasi-dynamic model for assessing security of supply in coupled gas and electricity transmission networks. Appl. Energy 2017, 203, 829–857. [Google Scholar] [CrossRef]
- Pambour, K.A.; Erdener, B.C.; Bolado-Lavin, R.; Dijkema, G.P. An integrated simulation tool for analysing the operation and interdependency of natural gas and electric power systems. In Proceedings of the PSIG Annual Meeting, Vancouver, BC, Canada, 10–13 May 2016. [Google Scholar]
- Herr’an-Gonz’alez, A.; de la Cruz, J.; de Andr’es-Toro, B.; Risco-Martin, J. Modeling and simulation of a gas distribution pipeline network. Appl. Math. Model. 2009, 33, 1584–1600. [Google Scholar] [CrossRef]
- Matko, D.; Geiger, G.; Gregoritza, W. Pipeline simulation techniques. Math. Comput. Simul. 2000, 52, 211–230. [Google Scholar] [CrossRef]
- Abeysekera, M.; Wu, J.; Jenkins, N.; Rees, M. Steady state analysis of gas networks with distributed injection of alternative gas. Appl. Energy 2016, 164, 991–1002. [Google Scholar] [CrossRef]
- Woldeyohannes, A.D.; Majid, M.A.A. Simulation model for natural gas transmission pipeline network system. Simul. Model. Pract. Theory 2011, 19, 196–212. [Google Scholar] [CrossRef]
- Woldeyohannes, A.D.; Majid, M.A.A. The accuracy and efficiency of a MATLAB-Simulink library for transient flow simulation of gas pipelines and networks. Pet. Sci. Eng. 2010, 70, 256–265. [Google Scholar]
- Mohring, J.; Hoffmann, J.; Halfmann, T.; Zemitis, A.; Basso, G.; Lagoni, P. Automated model reduction of complex gas pipeline networks. In Proceedings of the PSIG Annual Meeting, Vancouver, BC, Canada, 10–13 May 2004. [Google Scholar]
- Van der Hoeven, T. Math in Gas and the Art of Linearization; Energy Delta Institute, Universty of Groningen: Groningen, The Netherlands, 2004; ISBN 90-367-1990-9. [Google Scholar]
- Wu, Y.; Lai, K.K.; Liu, Y. Deterministic global optimization approach to steady-state distribution gas pipeline networks. Optim. Eng. 2007, 8, 259–275. [Google Scholar] [CrossRef]
- Dassios, I.; Baleanu, D. Optimal solutions for singular linear systems of Caputo fractional differential equations. Math. Methods Appl. Sci. 2018. [Google Scholar] [CrossRef]
- Dassios, I.; Fountoulakis, K.; Gondzio, J. A Preconditioner for a Primal-Dual Newton Conjugate Gradients Method for Compressed Sensing Problems. SIAM J. Sci. Comput. 2015, 37, A2783–A2812. [Google Scholar] [CrossRef]
- Dassios, I. Optimal solutions for non-consistent singular linear systems of fractional nabla difference equations. Circuits Syst. Signal Process. 2015, 34, 1769–1797. [Google Scholar] [CrossRef]
- Cuffe, P.; Dassios, I.; Keane, A. Analytic Loss Minimization: A Proof. IEEE Trans. Power Syst. 2016, 31, 3322–3323. [Google Scholar] [CrossRef]
- Dassios, I. Analytic Loss Minimization: Theoretical Framework of a Second Order Optimization Method. Symmetry 2019, 11, 136. [Google Scholar] [CrossRef]
- Dassios, I.; Cuffe, P.; Keane, A. Calculating Nodal Voltages Using the Admittance Matrix Spectrum of an Electrical Network. Mathematics 2019, 7, 106. [Google Scholar] [CrossRef]
- Dassios, I.; Cuffe, P.; Keane, A. Visualizing Voltage Relationships Using The Unity Row Summation and Real Valued Properties of the FLG Matrix. Electr. Power Syst. Res. 2016, 140, 611–618. [Google Scholar] [CrossRef]
- Boutarfa, B.; Dassios, I. A stability result for a network of two triple junctions on the plane. Math. Methods Appl. Sci. 2017, 40, 6076–6084. [Google Scholar] [CrossRef]
- Dassios, I.; Jivkov, A.; Abu-Muharib, A.; James, P. A mathematical model for plasticity and damage: A discrete calculus formulation. Comput. Appl. Math. 2017, 312, 27–38. [Google Scholar] [CrossRef]
- Dassios, I.; O’Keeffe, G.; Jivkov, A. A mathematical model for elasticity using calculus on discrete manifolds. Math. Methods Appl. Sci. 2018, 41, 9057–9070. [Google Scholar] [CrossRef]
- Dassios, I. Stability of Bounded Dynamical Networks with Symmetry. Symmetry 2018, 10, 121. [Google Scholar] [CrossRef]
- Dassios, I. Stability of basic steady states of networks in bounded domains. Comput. Math. Appl. 2015, 70, 2177–2196. [Google Scholar] [CrossRef]
- Esqueda, H.; Herrera, R.; Botello, S.; Moreles, M.A. A geometric description of Discrete Exterior Calculus for general. arXiv, 2018; arXiv:1802.01158. [Google Scholar]
- Woldeyohannes, A.D.; Majid, M.A.A. Portfolio Implementation Risk Management Using Evolutionary Multiobjective Optimization. Appl. Sci. 2011, 7, 1079. [Google Scholar]
- Moayeri, M. Fluid Mechanics, 3rd ed.; Shiraz University: Shiraz, Iran, 2008; ISBN 978-964-462-282-3. [Google Scholar]
- Van Wylen, G.J.; Sonntag, R.E. Fundamentals of Classical Thermodynamics; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Ames, W.F. Numerical Methods for Partial Differential Equations; Elsevier: New York, NY, USA, 2014. [Google Scholar]
- Ramdharee, S.; Muzenda, E.; Belaid, M. A review of the equations of state and their applicability in phase equilibrium modelling. In Proceedings of the International Conference on Chemical and Environmental Engineering, New Delhi, India, 14–15 September 2013. [Google Scholar]
- Heidaryan, E.; Salarabadi, A.; Moghadasi, J. A novel correlation approach for prediction of natural gas compressibility factor. Nat. Gas Chem. 2010, 19, 189–192. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).