Abstract
The cognitive radio network (CRN) is vulnerable to various newly-arising attacks targeting the weaknesses of cognitive radio (CR) communication and networking. In this paper, we focus on improving the secrecy performance of CR communications in a decentralized, multiple-channel manner while various eavesdroppers (EVs) try to listen to their private information. By choosing the best channel, the secondary user (SU) aims at mitigating the effects of eavesdropping and other SUs that compete for the same channel. Accordingly, the problem of finding the best channel that maximizes the secrecy rate for the SU is formulated as the framework of multiple repeated games where both the SU and the EVs try to maximize their own performance. In this case, the secrecy rate of an SU is defined based on the expected rewards of the SUs and the EVs. In the paper, we propose a repeated games-based scheme that can provide the best channel for the SU to avoid eavesdropping attacks and also minimize interference from other SUs that compete for the same channel. The simulation results demonstrate that the proposed scheme can combat a physical layer attack from EVs quite well and can provide much better performance, in comparison with other conventional channel selection schemes.
1. Introduction
Over the past few years, due to the rapid growth of mobile devices, there has been a dramatic increase in the number of wireless services and applications. Consequently, the demand for spectrum resources has increased, and spectrum scarcity has become a more and more serious problem. To address these emerging issues, researchers have been developing new paradigms in network design. Hence, emerging wireless technologies, such as cognitive radio networks (CRNs) [1,2], were introduced to improve the efficiency in the spatial utilization of the radio spectrum [3,4,5,6,7,8,9]. The basic idea of a CR network is to allow unlicensed radio users, called secondary users (SUs), to share frequencies assigned to licensed users, called the primary users (PUs). In order to avoid interfering with the operations of the licensed user, the SU is allowed to be active when the frequency is not used by the corresponding PU. However, when the presence of the PU is detected, the SU has to vacate the occupied frequency.
Due to the development of data sharing among wireless communications networks and the broadcast nature of the wireless medium, the sensitivity of the data being sent through wireless networks is vulnerable to security threats. These threats are not only in hostile environments such as national defense and national security, but also in covert commercial networks handling private and sensitive information [10]. These increasing threats have caught the attention of service providers, who have recently introduced new security measures to target these problems [10].
Because of the dynamic access manner in CR communications, the issues of information safety and security require significant consideration due to many threats in the operating environments [11,12,13,14]. In particular, the physical layer of CR networks is supposed to have the ability to perform spectrum sensing and learn the surrounding radio frequency (RF) environment, and then, the CR network can dynamically access a frequency band that was assigned to a PU [15,16,17,18]. However, it is also a critical weakness that can be exploited by an adversary for launching attack activities [19,20,21,22,23,24]. The most common attacker in the physical layer is an eavesdropper because of the simple process, but high efficiency. In addition, there is no doubt that eavesdroppers become more challenging when the SU must monitor various parameters, such as PUs’ activity and any potential or suspected eavesdropping, before deciding on its own operations. Subsequently, the threat from eavesdroppers is becoming a major concern for CR communications.
Many aspects of security in cognitive radio have been investigated [19]. However, the influence of eavesdroppers on SU secrecy rates and the spectrum sharing process has had little consideration. Previous research such as [25,26] proposed beamforming, optimal power allocation, and artificial jamming (AJ) to protect secret communications against eavesdroppers. In [27], the authors investigated physical layer security against eavesdropping attacks in CRNs by introducing a multiuser scheduling scheme to achieve multiuser diversity while improving the security level of cognitive transmissions with a PU quality-of-service (QoS) constraint. Most researchers considered power allocation and AJ in which all SUs cooperate to defend against eavesdroppers.
For efficient spectrum utilization in CR networks, many channel selection mechanisms have been extensively studied in the existing literature [28,29,30,31,32,33]. Most of these mechanisms consider only the remaining idle duration of the channel. For instance, Zhai et al. [28] used the availability of the spectrum and the idle channel duration to decide whether the SU will access the primary channel or not. Ali et al. [29] proposed a rank-based channel selection scheme for efficient license bands’ exploitation. A learning strategy for distributed channel selection in cognitive radio networks was proposed in [30], by which the QoS of competing SUs converges to their rank-optimal channels to avoid the collision on their own orthogonal channels. The authors of [31,32] performed channel ranking based on the channel state prediction, which is related to the duration of the channel availability. Aslam et al. [33] proposed the dynamic channel selection and parameter adaptation scheme based on the genetic algorithm to provide better QoS for the CR such that the best channel can be selected in terms of the quality, the power, and the PU activity. The CSPA deals with the problem of channel switchings, and it provides better QoS to the CR user. These techniques rank the channel using some parameters, perform well under specific settings, consider parameters separately in the ranking, and exclude critical parameters, which cannot lead to the selection of the best channel. To address these issues, Arjoune et al. [34] proposed a multiple attributes utility-based model to rank the frequency channels, which associates a weight to each parameter involved in the ranking mechanism. The weights corresponding to these parameters are determined using a nonlinear regression algorithm. In short, even though the proposed schemes utilize the spectrum efficiently and perform channel selection well, they do not jointly consider threats such as eavesdroppers and jammers that can attack the channel. Consequently, the channel quality is degraded. Thus, the channel selection mechanism combined with the security on the physical layer remains a significant open issue in CR networks.
In this paper, we investigate physical layer security in a multiuser and multiple eavesdropper cognitive radio system where multiple SUs are transmitting their private data to a common data center (DC), while multiple eavesdroppers execute independent eavesdropping on SU-DC transmissions. Each eavesdropper randomly chooses a channel of interest for an attack. Each SU shares its access strategy, but makes decisions independently. To optimize the PHY security for a CR network, in the paper, we propose an anti-eavesdropping scheme based on multiple games. In the proposed scheme, the interactions of SUs and EVs are formulated as the framework for multiple repeated games in order to choose the best action that provides the best channel selection for the SU. By accessing the best channel, the SU can achieve the maximum secrecy rate that mitigates the effects from eavesdropping and from other SUs that compete for the same channel. For performance evaluation of the proposed scheme, we utilize the secrecy rate of the SU in terms of the expected reward (i.e., throughput) of both SUs and EVs.
2. System Model
We consider the operations of a CR network where N SUs try to transmit data to a data center (DC) through K unlicensed channels. Let and denote the sets of SUs and channels, respectively. Primary users (PUs) that are licensed to use channels are assumed to operate in a time-slotted model. In this paper, we assume that the operation of a PU in channel k follows the Markov chain model. The operation can be expressed by the state transition probability between two states of the PU as and where the symbols (P) and (A) represent the presence and absence of the PU, as shown in Figure 1. The transition probabilities of the PU from state P to state A and from state A to itself are defined as and , respectively, where s is the state of the PU on channel k, and t is the index of the time slot. In the network, E eavesdroppers will try to overhear data from the SUs as shown in Figure 2. Let denote the set of eavesdroppers in the network.
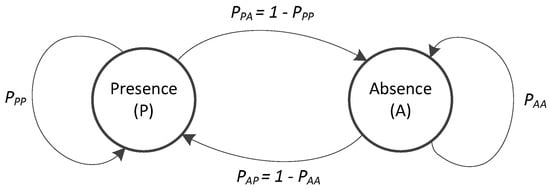
Figure 1.
Markov chain states of the PU.
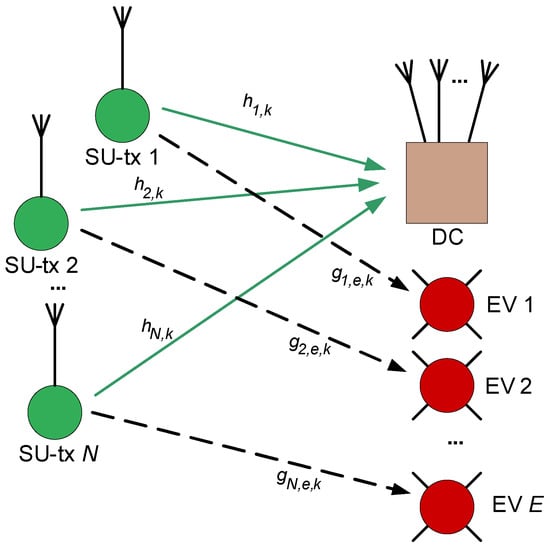
Figure 2.
The system model.
At the beginning of each time slot, the SU selects a channel for sensing where energy detection is used, and then, if the channel is free, the SU will transmit data over the channel, which is assumed as an additive white Gaussian noise (AWGN) channel; otherwise, the SU is not allowed to access the channel, then it will wait for the next time slot and repeat the process.
When SU i transmits data over available channel k, the received signal-to-noise ratio (SNR) can be given as:
where is the noise variance, is the channel gain of SU i on channel k, is the transmission power of SU i over channel k, and is the set of SUs that transmit data over channel k.
Accordingly, let us define the achievement of SU i over channel k as follows:
While SU i transmits data over channel k, an eavesdropper may try to listen to the data over the channel. Then, the received SNR at the EV can be given as follows:
where is the channel gain at eavesdropper e when it hears the data of SU i over channel k.
The achievement of eavesdropper e can also be given as follows:
The goal of the SU is to maximize its own achievement and minimize the achievement of eavesdroppers. To measure the performance of the proposed scheme, in the paper, we utilize the secrecy rate of the SU, defined as the difference between the expected reward (i.e., throughput) of both the SU and that of EVs, since the secrecy rate is often used as the main performance metric for anti-eavesdropping schemes [25,26]. The secrecy rate of SU i can be given as follows:
where the function is given as .
Local Spectrum Sensing
The considered a CR network that is assumed to be composed of N SUs. Each SU performs spectrum sensing independently by using an energy detection method and then sends the outcome to the DC. The hypothesis test statistics for local spectrum sensing at SU i can be formulated as follows [35]:
where is the received signal by the SU in time slot t, denotes the channel gain of the link between the PU and the SU, denotes the PU signal, and is zero mean and unit variance AWGN. Regarding energy detection, the observed energy at the SU is expressed as follows [36]:
where is the sample of the received PU signal at the SU and is the number of sensing samples during each sensing period. For simplicity, we assume that the number of sensing samples collected by each SU is the same for all the SUs. When is relatively large (e.g., ), can be approximated as a Gaussian random variable under the two hypotheses (P and A) with mean and variance given as follows [37]:
where is the signal-to-noise ratio (SNR) of the sensing channel between the PU and the SU. The decision about the state of the PU can be made as follows:
where 1 and 0 are single-bit data that correspond to the states P and A of the PU, respectively; and is a predefined decision energy threshold.
3. Game Models for Channel Selection
3.1. Game Formulation
In this section, we use a repeated-game framework to formulate the interaction between SUs and EVs. There are () players who join the game, where N is the number of SUs and E is the number of eavesdroppers. All players join the game intending to maximize their achievements as defined in Equations (2) and (4).
Let us define the state of the CR system as,
where . is defined as the belief of the system about channel k that represents the probability that channel k is in state A (i.e., the channel is free), and is the probability that SU i uses channel k.
According to the states of the system, in each time slot, each player (SU or EV) should choose its own suitable action. The action set for the SUs is defined as:
where is the selected channel of SU i and .
The payoff of SU i that chooses action is determined as:
where is the action of other users.
The action of an eavesdropper is defined as:
where is the selected channel of EV e and .
The payoff of the EV e, when it chooses action , is given as:
Because both types of players will join the game, we define the mixed players of the game as , which includes members.
The strategy of player is defined as:
where is the probability that player m chooses channel k.
The mixed action of the game can be shown as:
According to the mixed strategy and action, we can estimate the expected payoff for player m as follows:
where is the strategy of a remaining player other than player m.
The optimization problem can be formulated as:
3.2. Game Solution
In order to solve the problem in Equation (18), we need to compute the expected payoffs of user m for its action space. For each action in the action space of user m, we can determine possible action combinations of users, except user m. Therefore, the complexity of the proposed scheme can be given as . Based on the access strategy of users in the network, we can approximate that percentage that an action combination can happen. Then, the expected payoff of user m for its action space can be achieved. Following this analysis, the solution for the game in Equation (18) can be achieved by using a dynamic program, as shown in Algorithm 1.
| Algorithm 1 Solve the game problem in Equation (18). |
| Output of the algorithm: the optimal action of user m, . 1: for 2: Calculate expected payoff of player m 3: Initial value 4: Define as a combination action of users, except user m. 5: 6: The total number of possible combination actions : 7: All combination actions of users except m are: 8: for 9: Calculate 10: 11: with 12: is calculated with Equation (12) 13: end for 14: end for 15: Find the optimal action of the game, : |
4. An Anti-Eavesdropper Scheme for the Multiple-Channel Communications of Cognitive Radio Users
In this section, we present an anti-eavesdropper scheme based on multiple games for a cognitive radio network. The flowchart of the proposed scheme is shown in Figure 3. The first game determines pre-selected channel for the SU by solving the problem in Equation (18). The SU will perform spectrum sensing on the pre-selected channel to collect information about the status of the PU on the channel. According to the sensing results, the belief of the system about the pre-selected channel will be estimated as follows.
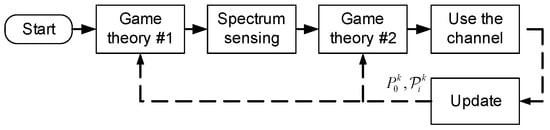
Figure 3.
Flowchart of the proposed scheme.
If the sensing result is state A for the PU signal (i.e., the channel is free), then is given as:
If the sensing result is state P for the PU signal (i.e., the channel is busy), then is given as:
The estimated belief of the system in Equation (19) or Equation (20) will be used to determine the updated state of the system, , which is defined as in Equation (10). According to the updated state , the payoffs for the players in the system will be updated by using Equations (12) and (14). The updated payoffs will be used as input for the second game where the problem in Equation (18) (with the updated payoffs) will be solved to determine optimal action for the SU.
Optimal action is the output of the multiple-game algorithm that provides the user m with the best channel in order to defend against an attack from an eavesdropper and to maximize its secrecy rate.
The SU will access the selected channel to achieve its reward. According to the observation on the status of the channel , the state of the system will be updated for utilization in the next time slot.
In addition, the parameters of state , the belief of the system, , and the access strategy of SU i, , will be updated. If communication over channel is successful, this means the channel is free, and belief will be updated as follows:
Otherwise, if communications fails, this means the channel is busy (i.e., the channel was accessed by the PU), and the belief will be updated as:
On the other hand, the strategies of the players who assessed the channel are changed. Then, the strategy will be updated as:
where and are the strategies of the SU in channel and of the SUs in channels other than channel , respectively, and D is the window time used to adapt the dynamics of the SUs in the network.
The updated , and will be used to update state of the game in Equation (10) for use in the next time slot.
Finally, the proposed anti-eavesdropper scheme is summarized in Algorithm 2.
| Algorithm 2 An anti-eavesdropper scheme based on multiple games for SUs. |
| Output of the algorithm: the optimal channel for user m. Given the state of the system: as defined in Equation (10), where . 1: The first game: We determine pre-selected channel by solving Equation (18) with the state where Equation (18) can be solved with Algorithm 1. 2: The user m will perform spectrum sensing on the pre-selected channel ; according to the sensing result in the channel, we update belief as Equation (19) or (20). 3: According to the updated belief , we determine the updated state of the system, , as defined in Equation (10). 4: The second game: The updated state will be used to compute the payoff of player m, as shown in Equation (17), which is the object function for the problem in Equation (18). The problem in Equation (18) will be solved to find optimal action for the user m according to Algorithm 1. 5: The user m will access channel to achieve its reward. According to the observation of the communications link in the channel, the state of the system will be updated for use in the next time slot as Equations (21)–(24). |
5. Simulation Results
In this section, we present simulation results to show the efficiency of the proposed scheme. In the simulation, the proposed Scheme 1 in which multiple games are used, the proposed scheme 2 in which a single game is used, and a random scheme are provided for comparison. The multiple-game scheme is the proposed scheme utilizing the proposed Algorithm 1 and the proposed Algorithm 2 in all figures and is denoted as “PPScheme 1: multiple games” in all figures. The single game scheme is the scheme that only uses the proposed Algorithm 1 to select the channel and is denoted as “PP Scheme 2: single games”. The random scheme does not consider the operation of the eavesdroppers and other SUs that randomly choose a channel in each time slot and is denoted as the “random scheme”. In addition, the EVs in all simulations randomly chose a channel for eavesdropping. For performance comparison among the considered schemes, the secrecy rate was used.
Figure 4 shows the secrecy rate of the considered schemes according to the number of SUs in the network. When the number of SUs increased, the multiuser diversity of the network improved, and the secrecy rate was also improved. However, more SUs created stronger interference in the network, so the secrecy rate improved very slightly. The proposed scheme with multiple games achieved the best performance, while the random scheme provided a limited performance. The reason is as follows: the proposed scheme with multiple games can estimate the immediate state of the CR system. On the other hand, the scheme with a single game utilized the estimated average state of the system only, so it provided slightly lower performance than the proposed scheme with multiple games.
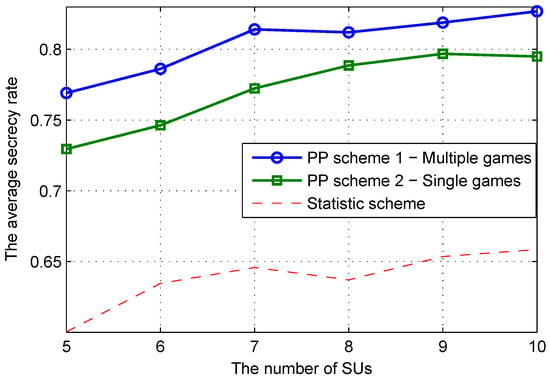
Figure 4.
Secrecy rate of the CR system versus the number SUs when the number of EVs is six and the number of channels is 10.
Figure 5 illustrates the secrecy rate according to the number of EVs in the network. It was observed that a higher number of EVs made the eavesdropping attack more serious, and then, the secrecy rate dropped. However, in all cases, the proposed scheme with multiple games provided the best defense to the network.
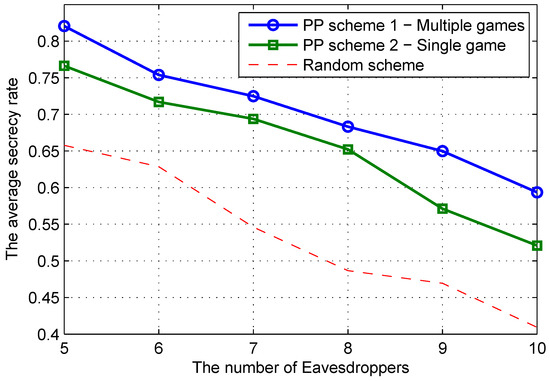
Figure 5.
Secrecy rate of the CR system versus the number EVs when the number of SUs is five and number of channels is 10.
The effect of the number of channels on the performance of the considered schemes is shown in Figure 6. Because more channels made it more difficult for the EVs to capture data from CR communications, all the schemes achieved a higher secrecy rate with an increase in the number of channels.
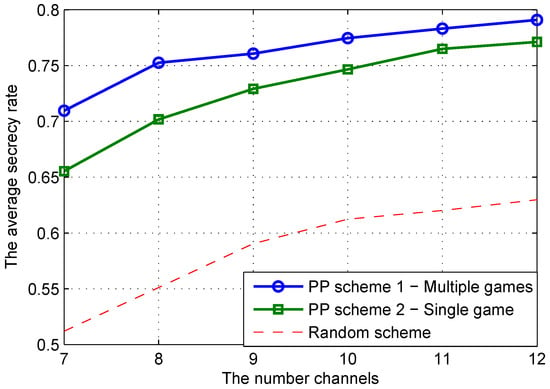
Figure 6.
Secrecy rate of the CR system versus the number channels when the number of EVs is six and the number of SUs is five.
In summary, the simulation results shown in all the figures prove that the proposed scheme can protect CR communications against eavesdropping attacks. By using game theory, the proposed scheme can choose the best channel for the SU. In addition, the multiple-game scheme shows a greater advantage than the single-game scheme.
6. Conclusions
In this paper, we formulated and solved an optimization problem aiming at maximizing the achievable secrecy rates on the SU. We also proposed an anti-eavesdropping scheme based on multiple games to optimize the PHY security for a CR network, in which the SUs work in a multiple-channel communications manner and various eavesdroppers randomly capture data from SU-DC communications. In particular, the first game determines the pre-selected channel for the SU by solving the problem of maximizing the expected payoff for the players, which are composed of SUs and EVs. Then, the SU will perform spectrum sensing on the selected channel to collect information about the status of the PU on the channel and update the payoff that is used as input for the second game. After that, the second game determines the optimal action that provides the user with the best channel in order to defend against an attack from an eavesdropper and to maximize its secrecy rate. In the game model, all SUs in the network share information about their access strategy, but they independently make access decisions (i.e., selected channels). Through the proposed scheme, the SU can choose the best channel that can avoid eavesdropping attacks, minimize interference from other SUs that compete for the same channel, and significantly improve the secrecy rates of CR networks.
Author Contributions
All authors conceived of and proposed the research idea. V.-H.V. made the formulation and performed the simulations under the supervision of I.K.; I.K. analyzed the simulation results; H.T.T. wrote the draft of the paper; H.T.T. and I.K. reviewed and edited the paper.
Funding
This research received no external funding.
Acknowledgments
This work has supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT)(NRF-2018R1A2B6001714.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liang, Y.C.; Chen, K.C.; Li, G.Y.; Mahonen, P. Cognitive Radio Networking and Communications: An Overview. IEEE Trans. Veh. Technol. 2011, 60, 3386–3407. [Google Scholar] [CrossRef]
- Mitola, J.; Maguire, G.Q. Cognitive Radio: Making Software Radios More Personal. IEEE Pers. Commun. 1999, 6, 13–18. [Google Scholar] [CrossRef]
- Haykin, S. Cognitive Radio: Brain-Empowered Wireless Communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar] [CrossRef]
- Ghasemi, A.; Sousa, E.S. Collaborative Spectrum Sensing for Opportunistic Access in Fading Environments. In Proceedings of the First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN), Baltimore, MD, USA, 8–11 November 2005; pp. 131–136. [Google Scholar]
- Letaief, K.B.; Zhang, W. Cooperative Spectrum Sensing. In Cognitive Wireless Communication Networks; Springer: Boston, MA, USA, 2007; pp. 115–138. [Google Scholar]
- Sun, C.; Zhang, W.; Letaief, K.B. Cluster-Based Cooperative Spectrum Sensing in Cognitive Radio Systems. In Proceedings of the IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 2511–2515. [Google Scholar]
- Lee, C.H.; Wolf, W. Energy Efficient Techniques for Cooperative Spectrum Sensing in Cognitive Radios. In Proceedings of the IEEE Consumer Communications and Networking Conference, Las Vegas, NV, USA, 10–12 January 2008; pp. 968–972. [Google Scholar]
- Ghurumuruhan, G.; Li, Y.G. Cooperative Spectrum Sensing in Cognitive Radio: Part I: Two User Networks. IEEE Trans. Wirel. Commun. 2007, 6, 2204–2213. [Google Scholar]
- Ghurumuruhan, G.; Li, Y.G. Cooperative Spectrum Sensing in Cognitive Radio: Part II: Multiuser Networks. IEEE Trans. Wirel. Commun. 2007, 6, 2214–2222. [Google Scholar]
- Networks, A. Worldwide Infrastructure Security Report. 2015. Available online: https://pages.arbornetworks.com/rs/082-kna-087/images/12th_worldwide_infrastructure_security_report.pdf (accessed on 20 November 2019).
- Gao, Q.; Huo, Y.; Ma, L.; Xing, X.; Cheng, X.; Jing, T.; Liu, H. Optimal Stopping Theory Based Jammer Selection for Securing Cooperative Cognitive Radio Networks. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 265–270. [Google Scholar]
- Lou, L.; Fan, J.H. An Anti-Jamming Routing Selection Criteria Based on The Cross-Layer Constraints of Channel State Information for Manets. In Proceedings of the 2015 IEEE Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 19–20 December 2015; pp. 1000–1004. [Google Scholar]
- Wang, B.; Wu, Y.; Liu, K.J.R.; Clancy, T.C. An Anti-Jamming Stochastic Game for Cognitive Radio Networks. IEEE J. Sel. Areas Commun. 2011, 29, 877–889. [Google Scholar] [CrossRef]
- Slimeni, F.; Scheers, B.; Nir, V.L.; Chtourou, Z.; Attia, R. Learning Multi-Channel Power Allocation Against Smart Jammer in Cognitive Radio Networks. In Proceedings of the 2016 International Conference on Military Communications and Information Systems (ICMCIS), Brussels, Belgium, 23–24 May 2016; pp. 1–7. [Google Scholar]
- Xu, X.; He, B.; Yang, W.; Zhou, X.; Cai, Y. Secure transmission design for cognitive radio networks with poisson distributed eavesdroppers. IEEE Trans. Inf. Forensics Secur. 2016, 11, 373–387. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, T.; Song, L.; Han, Z. Interference improves PHY security for cognitive radio networks. IEEE Trans. Inf. Forensics Secur. 2016, 11, 609–620. [Google Scholar] [CrossRef]
- Al-Talabani, A.; Deng, Y.; Nallanathan, A.; Nguyen, H.X. Enhancing secrecy rate in cognitive radio networks via multilevel stackelberg game. IEEE Commun. Lett. 2016, 20, 1112–1115. [Google Scholar] [CrossRef]
- Zhu, F.; Yao, M. Improving physical-layer security for CRNs using SINR-based cooperative beamforming. IEEE Trans. Veh. Technol. 2016, 65, 1835–1841. [Google Scholar] [CrossRef]
- Clancy, T.; Goergen, N. Security in Cognitive Radio Networks: Threats and Mitigation. In Proceedings of the 3rd International Conference on Cognitive Radio Oriented Wireless Networks and Communications (CrownCom), Singapore, 15–17 May 2008; pp. 1–8. [Google Scholar]
- Aggarwal, V.; Sankar, L.; Calderbank, A.; Poor, H. Information Secrecy from Multiple Eavesdroppers in Orthogonal Relay Channels. In Proceedings of the IEEE International Symposium on Information Theory, Seoul, Korea, 28 June–3 July 2009; pp. 2607–2611. [Google Scholar]
- Bian, K.; Park, J.M. Security Vulnerabilities in IEEE 802.22. In Proceedings of the Fourth International Wireless Internet Conference (WICON2008), Maui, HI, USA, 17–19 November 2008. [Google Scholar]
- Chen, R.; Park, J.M.; Bian, K. Robust Distributed Spectrum Sensing in Cognitive Radio Networks. In Proceedings of the IEEE Infocom 2008 Conference on Computer Communications, Phoenix, AZ, USA, 13–18 April 2008; pp. 1876–1884. [Google Scholar]
- Wang, W.; Li, H.; Sun, Y.; Han, Z. Attack-Proof Collaborative Spectrum Sensing in Cognitive Radio Systems. In Proceedings of the Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 18–20 March 2009; pp. 130–134. [Google Scholar]
- Chen, R.; Park, J.-M.; Reed, J.H. Defense Against Primary User Emulation Attacks in Cognitive Radio Networks. IEEE J. Sel. Areas Commun. 2007, 26, 1. [Google Scholar] [CrossRef]
- Goel, S.; Negi, R. Guaranteeing Secrecy Using Artificial Noise. IEEE Trans. Wirel. Commun. 2008, 7, 2180–2189. [Google Scholar] [CrossRef]
- Zhou, X.; McKay, M.R. Physical Layer Security with Artificial Noise: Secrecy Capacity and Optimal Power Allocation. In Proceedings of the 3rd International Conference on Signal Processing and Communication Systems, Omaha, NE, USA, 28–30 September 2009; pp. 1–5. [Google Scholar]
- Zou, Y.; Wang, X.; Shen, W. Physical Layer Security with Multiuser Scheduling in Cognitive Radio Networks. IEEE Trans. Commun. 2013, 61, 5103–5113. [Google Scholar] [CrossRef]
- Zhai, Y.B.; Wu, X.; Huang, X.L.; Wu, J. Channel Quality Ranking in Cognitive Radio Networks. In Proceedings of the Wireless Communications, Networking and Mobile Computing Conference, Beijing, China, 26–28 September 2014; pp. 191–194. [Google Scholar]
- Ali, A.; Sakhare, M.; Hwang, K.; Suh, D.Y. A novel channel indexing-based channel selection algorithm for cognitive radio networks. In Proceedings of the ICT Convergence (ICTC), Jeju, Korea, 14–16 October 2013; pp. 682–687. [Google Scholar]
- Torabi, N.; Rostamzadeh, K.; Leung, V.C. Rank-optimal channel selection strategy in cognitive networks. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 410–415. [Google Scholar]
- Xing, X.; Jing, T.; Huo, Y.; Li, H.; Cheng, X. Channel quality prediction based on Bayesian inference in cognitive radio networks. In Proceedings of the INFOCOM 2013, Turin, Italy, 14–19 April 2013; pp. 1465–1473. [Google Scholar]
- Sengottuvelan, S.; Ansari, J.; Mähönen, P.; Venkatesh, T.G.; Petrova, M. Channel selection algorithm for cognitive radio networks with heavy-tailed idle times. IEEE Trans. Mob. Comput. 2017, 16, 1258–1271. [Google Scholar] [CrossRef]
- Aslam, S.; Lee, K.G. CSPA: Channel selection and parameter adaptation scheme based on genetic algorithm for cognitive radio ad hoc networks. EURASIP J. Wirel. Commun. Netw. 2012, 2012, 349. [Google Scholar] [CrossRef]
- Arjoune, Y.; Mrabet, Z.E.; Kaabouch, N. Multi-Attributes, Utility-Based, Channel Quality Ranking Mechanism for Cognitive Radio Networks. Appl. Sci. 2018, 8, 628. [Google Scholar] [CrossRef]
- Zhang, W.; Mallik, R.K.; Letaief, K.B. Optimization of cooperative spectrum sensing with energy detection in cognitive radio networks. IEEE Trans. Wirel. Commun. 2009, 8, 5761–5766. [Google Scholar] [CrossRef]
- Atapattu, S.; Tellambura, C.; Jiang, H. Energy Detection for Spectrum Sensing in Cognitive Radio; Springer: New York, NY, USA, 2014; pp. 11–27. [Google Scholar]
- Quan, Z.; Cui, S.; Sayed, A.H. Optimal linear cooperation for spectrum sensing in cognitive radio networks. IEEE J. Sel. Top. Signal Process. 2008, 2, 28–40. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).