Abstract
More and more huge embedded foundations are used in large-span bridges, such as caisson foundations and anchorage open caisson foundations. Most of the embedded foundations are undergoing horizontal vibration forces, that is, wind and wave forces or other types of dynamic forces. The embedded foundations are regarded as rigid due to its high stiffness and small deformation during the forcing process. The performance of a rigid, massive, cylindrical foundation embedded in a poroelastic half-space is investigated by an analytical method developed in this paper. The mixed boundary problem is solved by reducing the dual integral equations to a pair of Fredholm integral equations of the second kind. The numerical results are compared with existing solutions in order to assess the accuracy of the presented method. To further demonstrate the applicability of this method, parametric studies are performed to evaluate the dynamic response of the embedded foundation under horizontal vibration. The horizontal dynamic impedance and response factor of the embedded foundation are examined based on different embedment ratio, foundation mass ratio, relative stiffness, and poroelastic material properties versus nondimensional frequency. The results of this study can be adapted to investigate the horizontal vibration responses of a foundation embedded in poroelastic half-space.
1. Introduction
The analytical solution of the dynamic response of surface foundation in a poroelastic medium under horizontal, vertical, and torsional vibration is widely studied by many researchers [1,2,3]. Generally, the foundation is embedded in a certain depth and the horizontal force from wind, earthquake ground motion, and mechanical vibrations that governs the dynamic response of embedded foundations. A great deal of research has been done in order to study the dynamic response of surface foundation under horizontal vibration. Apsel et al. [4] presented the impedance of foundation resting on an elastic soil medium. Numerical methods, that is, the finite element method and boundary element method were employed in order to investigate the dynamic response of embedded footings. Ahmad et al. [5] presented an extensive investigation on the horizontal impedance of square footing in layered soil using a boundary element method. Latini [1] investigated the dynamic response of suction caissons by 3D element models in the frequency domain. Wang and Rajapakse [6] studied the dynamic response of rigid strip footing foundations using the indirect boundary integral equation method. The soil is treated as a single-phase linear elastic material in most of the existing studies. Generally, the majority of the foundations are embedded in two-phase soils consisting of a solid skeleton and pores full of groundwater, which is so-called poroelastic medium. Biot [7,8] first derived the wave propagation equations in poroelastic material. Then, many of the researchers studied the dynamic responses of a disk resting on or embedded in a poroelastic medium [2,9,10,11,12,13,14]. Rizzo et al. [15] studied the dynamic response of embedded foundation resting on a uniform half-space under torsional vibration. Aspel and Luco [4] presented an integration technique to calculate the dynamic response of embedded foundations subjected to external forces and moments. Different embedment ratios were also studied. Senjuntichai and Sapsathiarn [16] presented the dynamic response of forced vertical vibrations of an elastic circular plate embedded in poroelastic soils. The dynamic response of an arbitrary buried load was also studied by virtue of Green’s function by Chen et al. [17]. Indirect boundary integral equation method was adopted to investigate the vertical vibration of the massless foundation embedded in a homogeneous poroelastic medium by Senjuntichai et al. [18]. Cai et al. [19] studied the vertical vibration of embedded massive foundation resting in a poroelastic medium using a simplified analytical method. Cai and Hu [20] also extended their research to the finite thickness of poroelastic soil. Bilotta et al. [21] had done an excellent exploration on addressing the importance of seismic site response and soil-structure interaction of a tall building in Italy. Fabozzi and Bilotta [22] further conducted the feasibility study of a loss-driven earthquake early warning and rapid response systems for tunnels in Italy high-speed railway network. Di Laora et al. [23] investigated the effect of the rotational component of motion induced by the interaction between a pile group. An application highlighting the rotational component of input motion is important for tall structures on small pile groups. In conclusion, with the rapid development of underground structures in recent years, the dynamic response of embedded foundations is still a matter of great concern. Seismic vibration, ground shaking due to machine or high-speed train can easily induce damages to the infrastructure which may cause great economic losses. Soil-structure interaction has been an important issue in the assessment of the seismic vulnerability of a building. Considering the great risk of structures under seismic risk, a number of techniques have been developed to deal with this problem. Note that the above solutions indicate that the analytical solution of embedded foundations under horizontal vibration is still not reported in the literature.
The aim of the current study is to provide an analytical solution of embedded footing resting in a poroelastic medium under horizontal vibration. The soil medium is divided into two parts, that is, the soil under the foundation and the soil around the foundation. The soil medium is modeled as an isotropic homogeneous poroelastic medium under the footing while the soil around the footing is divided into infinitesimal thin layers. The soil and the foundation contact surface are fully permeable. Biot’s poroelastic theory is adopted, and the governing equation is solved by the Hankel transform. The mixed boundary problem is solved by reducing the dual integral equations to a pair of Fredholm integral equations of the second kind. The accuracy of the present analytical solution is compared with existing solutions by degenerating existing solutions to previous situations. The horizontal impedance and dynamic response factor of the embedded foundation are delineated. The influence of foundation embedment ratio, foundation mass ratio, relative stiffness, and poroelastic material properties is discussed separately.
2. Problem Definition and Governing Equations
2.1. Problem Statement
The foundations are subjected to time-harmonic loading as shown in Figure 1. The cylindrical foundation is bonded with soil medium with the same displacement, and the contact between foundation and soil is totally permeable. The exact solution for an embedded foundation under dynamic vibration is hard to obtain due to complex mathematics. Thin layer theory by Novak and Beredugo [24,25] is adopted to separate the soil medium into two independent parts. The soil underlying the foundation base is assumed to be a homogeneous poroelastic half-space while the soil along the side of the foundation is assumed to be a series of infinitesimally thin layers [20]. The total reaction force consists of the reaction force at the foundation side and foundation base. The vertical and torsional displacement of the foundation is neglected.
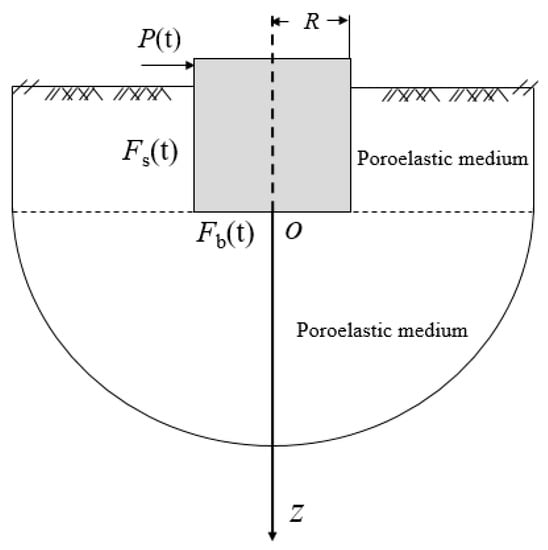
Figure 1.
Rigid cylindrical foundation embedded in a poroelastic half-space.
2.2. Governing Equations of Poroelastic Soil
The motion of vibration P(t) is assumed to be time-harmonic with a time factor of eiωt, where ω is the circular frequency and . The time factor of eiωt is canceled henceforth from all expressions for simplicity.
The equilibrium governing equation of foundation motion is:
where m is the mass of the cylindrical foundation, is the time-harmonic horizontal displacement of the foundation. When equals to 0, means the dynamic acceleration of foundation is zero, the dynamic motion equation can degenerate to static equilibrium function. is the excitation force. is the horizontal dynamic reaction force at the foundation base, is the horizontal dynamic reaction force along the foundation side.
The governing differential equations for the poroelastic medium are expressed under cylindrical coordinates system o (r, θ, z), shown as follows [7,8],
The seepage function under cylindrical coordinates is expressed as follows under the assumption of soil grain, and the fluid is incompressible.
where uz, ur, uθ is the vertical, radial, and tangential displacement of the solid matrix, wz, wr, wθ is the average fluid displacement of the solid matrix in the vertical radial and tangential direction. . ρ is the mass density of the bulk material, and ρ = (1 − n)ρs + nρf, where ρf is the density of the fluid, ρs is the density of solid mass. b is defined as the ratio between the fluid viscosity and the intrinsic permeability of the porous medium (s·Pa/m2). The ratio of fluid density ρf over the porosity n is defined as a. λ, G are the Lame parameter. g is the acceleration of gravity. α, M are the Biot’s parameters accounting for compressibility of the poroelastic material. pf is the pore water pressure. e is the dilatation of the solid matrix, ▽2 is the Laplace operator, which are defined as , .
2.3. General Solutions of Horizontal Vibration of Embedded Foundation
2.3.1. Reaction Force at the Side of the Embedded Foundation
Thin layer theory is adapted to conduct the reaction force along the height of the embedded foundation (L). The integration of force along the foundation side can be conducted to calculate the reaction force along the foundation side. The horizontal displacement of foundation under horizontal excitation is uh (at θ = 0 direction), the foundation is under time-harmonic vibration. The normal stress on the ground surface is zero. There’s no displacement at the bottom of the foundation. The model of motion is purely horizontal vibration, and the vertical and torsional displacement is neglected. Displacement at tangential and radial direction is not zero, that is, ur, uθ ≠ 0, wr, wθ ≠ 0, uz, wz = 0. With the radiation condition, the boundary condition of the model of motion can be written as,
The rigid footing is fully bonded with the surrounding soil, and the contact surface is assumed to be fully permeable. The consistent boundary condition can be expressed as:
Potential function method is a powerful and physical meaningful method for solving coupled partial differential equations. The displacement potential function of solid and fluid φs, ψs, φf, ψf are introduced by Yu [26] to solve the coupled differential equations. The potential functions of solid and fluid in poroelastic materials can be expressed as follows:
E = es = ▽2φs and ef = ▽2φf, the following equations can be obtained by substituting Equations (5) and (6) to Equations (2) and (3),
The following equations can be derived by substituting the potential functions to the fluid constitutive relations after some manipulations.
After divergence and curl operation of Equations (13) and (14), the following equation set can be obtained:
Equations (15) and (16) can be compiled as
where , , ,
Equations (17) and (18) can be written as
with , , is assumed as in order to separate variables. The following equation can be obtained:
The solution of Equation (20) is:
The formulation of and can be obtained as follows,
where In1, In2, Kn1, Kn2 denote modified Bessel function of the first and second kind. With the property of Bessel function and the odevity of e, Sb = Sbb = 0, Sc = Scc = 0,
By substituting the expression of Equations (24) and (25) to Equations (13) and (14),
where
By substituting the expression of to the potential function and using the boundary condition of , , wr (r0,θ,z) = 0, the following equations can be obtained,
The roots of S1, S11, S3 can be obtained by solving a 3 × 3 matrix. The force resultant around the foundation side is qh. The horizontal resultant of reaction stress can be obtained by direct integration of the horizontal stress. With the negative pore water pressure considered, .
The expression of qh can be obtained as follows by a series of substitution of normal stress, shear stress, and pore water pressure.
The reaction force along the foundation side is:
where , .
2.3.2. Reaction Force at the Base of the Embedded Foundation
The dynamic reaction at the base of the foundation is independent of the depth of embedment. The reaction force at the base of embedded foundation can be solved by considering the foundation base as a surface foundation.
As it is delineated above, it is convenient to substitute the expression of stress, displacement, and pore water pressure to the solid function, and after some manipulations, the following equations can be derived.
where , , , ,
Dimensionless variables are defined with a hat “-” on it. a0 is the dimensionless excitation frequency.
Equations (32)–(37) can be derived as follows:
where , , , .
With the stress-strain relationships and soil constitutive models, we can define,
denotes the Hankel transforms of . With the properties of Hankel transforms, the solutions of Equations (41) to (46) can be derived as follows,
where , , ,
In order to solve the mixed boundary-value problem of horizontal vibration of the base of embedded foundation resting on poroelastic medium, the following dual integral equations can be obtained under the given boundary conditions.
where
- , ,
The dual integral equations can be solved by reducing to the Fredholm integral equations of the second kind. With the aid of Sonine’s integrals in Noble [27], combining with the Heaviside functions as defined by Pak and Saphores [28], and the properties of Bessel functions, with a series of manipulations, the dual integral equations can be reduced to a pair of Fredholm integral equations of the second kind.
where
The force resultant of the foundation base can be obtained by the integration of contact stress on the foundation base,
After substituting the expression of stress into Equation (63) and several manipulations, the force at the foundation base can be obtained:
where , , is regarded as the dynamic compliance coefficient of foundation base.
2.4. Dynamic Response of Embedded Foundation under Horizontal Vibration
By substituting Equations (31) and (64) to Equation (1), the equivalent equation can be derived:
The nondimensional equivalent horizontal dynamic impedance Kh can be expressed as
where
The horizontal dynamic response factor is given as Ah, proposed by Lysmer and Richart [29,30]:
3. Results and Discussion
3.1. Verification of the Analytical Solutions with Existing Results
The solutions of the dynamic response of embedded foundation under horizontal vibration are programmed by Matlab code. The results by the proposed method are verified by comparing similar conclusions reported by Yu [26] and Jin [31]. The solution scheme in the preceding sections is conducted to verify the accuracy of this solution. The real and imaginary part of nondimensional horizontal dynamic impedance can degenrate to the side, and bottom vibration of an embedded foundation which can be found by different combinations of L/R, the radius of the foundation is selected as a unit of length R.
3.1.1. Verification of the Base of the Embedded Foundation
Solutions corresponding to present analysis are reduced to a surface foundation problem by setting the embedment from 5 m to 0 m. The real part and imaginary part are separated under different nondimensional frequency. The solutions derived from the present study are compared with the analytical solution of horizontal vibration of a disk on the poroelastic half-space by Jin [31], with a nondimensional frequency range of 0 < a0 ≤ 5 using the same material parameters. fbss and fbds are the dynamic impedance of surface footing presented by Jin [31]. As it is indicated in Figure 2, the real and imaginary part of the present solution is gradually close to the solution of a surface foundation by reducing the embedment ratio. The present solution shows a very close agreement with Jin’s solution when the embedment depth goes to zero.
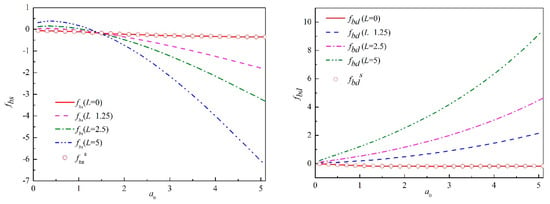
Figure 2.
Verification of the foundation base.
3.1.2. Verification of the Side of the Embedded Foundation
Figure 3 shows a comparison of nondimensional results of dynamic stiffness and damping at the embedded foundation side by varying the embedment from 0 m to 5 m. The dynamic impedance along the foundation side is investigated by comparing the results with Yu’s results [26] (fssp and fsdp) by adopting the same material parameters. As indicated in Figure 3, the dynamic impedance side agrees excellently, both in the real and imaginary part of dynamic impedance, as the foundation embedment increases. The real part increases when a0 < 2 and then decreases throughout the considered frequency range. The imaginary part shows a linear increase with increasing a0. Comparisons of the dynamic impedance of the present solution with Yu’s results (fssp and fsdp) proves that the accuracy of the present solution is confirmed.
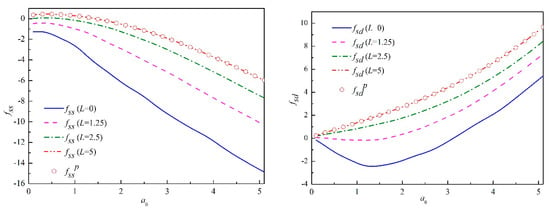
Figure 3.
Verification of the foundation side.
In this paper, the soil is considered as drained condition (high permeability) with a soil permeability larger than 10−4, that is, 0.1. Selected key parameters, such as the ratio of embedment, the variation of foundation mass, etc., of a rigid, massive, cylindrical foundation embedded under horizontal vibration, are investigated by varying the nondimensional excitation frequency. The effect of Poisson’s ratio v on the horizontal dynamic impedance of embedded foundation can be ignored through verification. The nondimensional frequency of excitation is defined as 0 ≤ a0 ≤ 5 from lower frequency range to moderate frequency range. The nondimensional horizontal impedance Kh are studied by its real part (kh) and imaginary part (ch), respectively. The dynamic response factor is also demonstrated with nondimensional frequency.
The key parameters are studied, including:
- (1)
- The ratio of embedment over foundation radius, that is, L/R from 0 to two.
- (2)
- The effect of the mass ratio (the variation of foundation mass) from one to four.
- (3)
- The effect of poroelastic material property M from 10 to 300.
- (4)
- The relative stiffness of the soil layer around the foundation and under the foundation, that is, Gs/Gb from 0.1 to two.
3.2. Effect of the Footing Embedment Ratio
The embedment of a foundation is crucial to the stiffness of the foundation because the stiffness can significantly increase with the embedment. The foundation stiffness increases because part of the load is transmitted into the soil through shear and normal traction acting on the side-walls [5]. With uniformly distributed soil around the foundation and under the foundation, the effect of embedment ratio L/R = 0, 0.5, 1, 2 is investigated. The dynamic response of the depth ratio under horizontal excitations is presented by varying the nondimensional frequency of excitation. Figure 4 indicates the real part (kh) and the imaginary part (ch) of Kh, respectively. As we can see from Figure 4, the dynamic impedance increases significantly with increasing foundation embedment ratio. However, the variation of kh and ch with the frequency a0 shows a different trend for all the values of foundation embedment. In the case of the real part, the stiffness of the foundation for horizontal vibration increases with increasing a0. The spring coefficient increases remarkably with the embedment ratio at a higher frequency. For the imaginary part, the damping of foundation decreases a0 < 2 and reach a minimum value at about a0 = 1.5 and then increases with increasing frequency. It is noted that both components of the dynamic impedance vary for different embedment ratios. The real part of dynamic impedance is small at low frequency and then increases linearly with frequency thereafter which result from little wave propagates at these low frequencies. Different from this trend, the imaginary part decreases with the interested frequency range and then increases slowly, indicating wave propagation throughout the frequency [32]. The magnitudes of the real part (kh) and the imaginary part(ch) of Kh increases with increasing embedment. The influence of embedment has a relatively smaller influence on the imaginary part when compared to the real part.
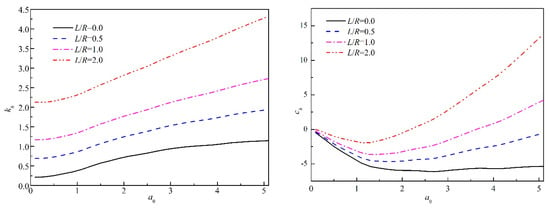
Figure 4.
Horizontal dynamic impedance of embedded foundation under different embedment ratio.
Figure 5 indicates the effect of the depth ratio on the dynamic response factor. It is clear that the embedment of the foundation has a significant effect on the magnitude and shape of the dynamic response factor. It is noticed that the foundation becomes stiffer as the dynamic response factor decreases with increasing embedment ratio. This effect can be explained with the restriction of the movement of the embedded foundation by the normal stress and shear stress from the overlying soil. The foundation’s response factor also decreases with increasing a0, as expected. However, the dynamic response factor is dependent on high frequency (a0 > 2). In addition, the larger the embedment ratio, the steeper is the corresponding response factor curve. Therefore, at high frequencies away from 2, the dynamic response factor keeps steady.
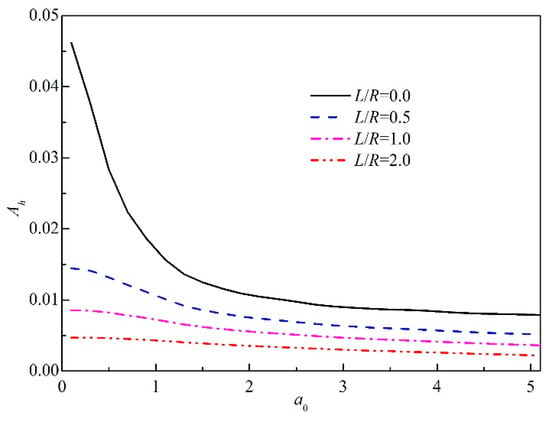
Figure 5.
Dynamic response factor of embedded foundation under different embedment ratio.
3.3. Effect of the Footing Mass Ratio
The mass ratio can significantly affect the dynamic response of embedded foundation. Figure 6 shows the dynamic response of embedded foundation in order to investigate the effect of the mass ratio of the foundation under horizontal vibration with a depth ratio L/R = 1.0. In general, the dynamic impedance of the embedded foundation increases by increasing the mass ratio. The initial density of embedded foundation is set to be one, and the density of massive foundation varies from one to four in order to examine the mass ratio of the embedded foundation. It is obvious that an increase in the mass ratio can definitely increase the stiffness of foundation, as shown in Figure 6. The foundation stiffness increases almost linearly with the increasing value of a0 when the mass ratio (RM) is 1:4, with almost the same speed. The increasing trend tends to be gentle when a0 > 1.5. The mass ratio has little effect on the imaginary part of Kh. The reason for this phenomenon is that the soil mass ratio has no influence on the contact with the surrounding soil. The imaginary part increases first to a maximum value at about a0 = 1.5 and then decreases for a larger value of frequency. The imaginary part of horizontal impedance Kh is nearly independent of the mass ratio when compared to the real part. The imaginary part shows a gradual increase when a0 < 1.5, which shows a near linear variation with a0. The mass ratio is more significant on the real part of the horizontal impedance and relatively smaller on the imaginary part of Kh. The parametric study indicates that the imaginary part of horizontal impedance is less affected by the mass ratio than the real part.
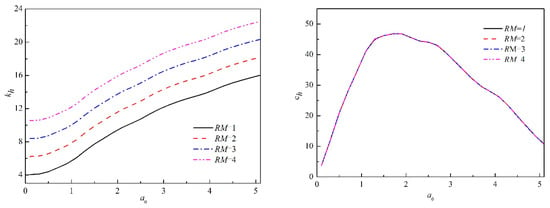
Figure 6.
Horizontal dynamic impedance of embedded foundation under different mass ratio.
Figure 7 shows the influence of mass ratio on the horizontal dynamic response factor Ah for an embedment ratio L/R = 1. It can be concluded that the mass ratio of the embedded foundation has a significant influence on the dynamic response factor. The peak value of the dynamic response factor is at zero frequency, and the foundation stiffness is the maximum at this state. By increasing the value of the mass ratio, the dynamic response factor decreases, and the foundation stiffness increases. In addition, the dynamic response factor decreases sharply with the lower value of the mass ratio. The dynamic response of foundation also decreases with the increase in nondimensional frequency a0. The value of Ah is close to each other at any mass ratio when the frequency is larger than 3. It is noted that a significant decrease occurs when a0 < 1.5, and then the dynamic response factor decreases slowly as a0 increases. As expected, the response factor decreases with increasing foundation mass. However, at high frequencies away from 1.5, the response factor shows little dependence on the mass ratio.
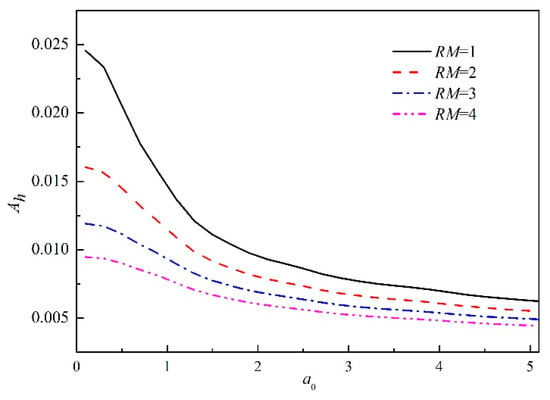
Figure 7.
Dynamic response factor of embedded foundation under different mass ratio.
3.4. Effect of Poroelastic Material Parameters
In order to investigate the effect of poroelastic material parameters under horizontal dynamic interaction, Figure 8 shows the dynamic impedance of embedded foundation versus a0 for L/R = 1. The only difference is the poroelastic material parameter. As it is indicated, the real part of dynamic impedance increases with the increasing poroelastic material parameters. As we proved, the increasing speed of the real part decreases when the relative value is larger than 100. The real part of dynamic impedance seems overlapped when a0 is smaller than 1.5, and the increasing speed differs when a0 is larger than 3. The imaginary part of dynamic impedance decreases with the increasing poroelastic material parameters when the poroelastic material parameters are smaller than 5 and then increases at a larger relative ratio. The imaginary part seems to increase to a maximum value at about a0 = 1.5 and then decreases for higher frequencies. As expected, both the real and imaginary part of all impedance shows the strong influence of the poroelastic material and the influence of excitation especially when 10 < M < 100 and a0 > 1.5. The parametric study indicates that both the real and imaginary part of the horizontal impedance component are independent when a0 < 1.5. However, it is affected by the poroelastic material properties significantly when a0 > 1.5.
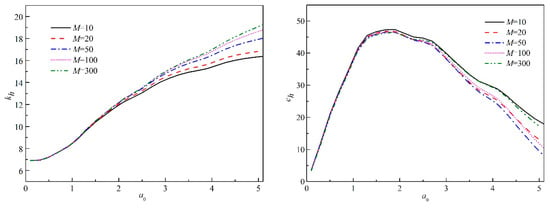
Figure 8.
Horizontal dynamic impedance of embedded foundation under different poroelastic material properties.
The dynamic response factor of embedded foundation affected by the poroelastic material properties versus a0 is depicted in Figure 9. It can be noticed that the dynamic response factor decreases with the increasing poroelastic material properties modulus. By increasing the poroelastic material properties, the dynamic response factor decreases obviously when the relative ratio is lower than 50. This decrease in value is very small when the relative ratio is larger than 100. The dynamic response factor decreases with the increase in frequency. In the case of frequency a0 < 1.5, the dynamic response factor for different poroelastic material properties are the same. The effect of poroelastic material properties pronounced for higher frequency. The dynamic response factor shows little dependence on M and when a0 > 1.5, the dynamic response factor decreases with the increasing M. Moreover, the dynamic response factor decreases with the increase in frequency.
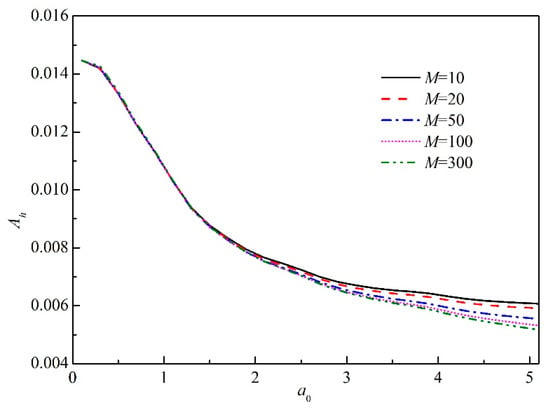
Figure 9.
Dynamic response factor of embedded foundation under different poroelastic material properties.
3.5. Effect of the Relative Stiffness
The effect of relative stiffness on the horizontal dynamic impedance of embedded footing in poroelastic soil medium are investigated to demonstrate the influence of nondimensional frequency. Figure 10 shows that the dynamic impedance Kh varies with frequency a0 with a different value of the relative soil stiffness. It is noted that the horizontal dynamic impedance depends on the relative soil stiffness with other fixed parameters. The real part of Kh increases with the increasing Gs/Gb which is due to the embedded foundation. The foundation stiffness enhances with larger soil stiffness around the foundation. The foundation stiffness also increases with the increasing frequency, especially for a frequency higher than 1. In general, the imaginary part of dynamic impedance increases with the increasing Gs/Gb, while this trend reverses when a0 > 4. The damping of foundation increases to a maximum value at about a0 = 2 and then decreases at the same speed for different Gs/Gb with the increasing a0. Figure 10 also indicates that the relative stiffness of the foundation soil has a noticeable influence on the value of dynamic impedance. Both foundation stiffness and damping increase as the Gs/Gb increases. The results from Figure 10 also show that the relative stiffness of the subsoil has a strong effect on the magnitude of the horizontal impedance Kh, which is investigated by discussing the real and imaginary part separately. Another important conclusion revealed from Figure 10 is the rising difference of the dynamic impedance between the undisturbed soil and disturbed soil which has also been proved by Cai et al [20].
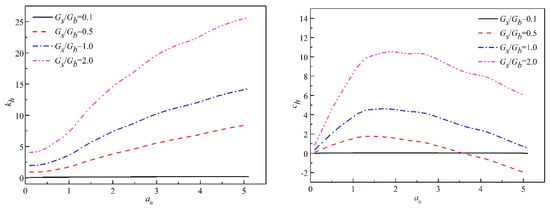
Figure 10.
Horizontal dynamic impedance of embedded foundation under different soil stiffness.
The dynamic response factor of embedded foundation under horizontal excitation under different relative stiffness is investigated by varying a0. It is indicated that the response factor decreases with the increasing Gs/Gb, especially when Gs/Gb increases from 0.1 to 0.5. As expected, the foundation stiffness increases with the increasing Gs/Gb because of the side-wall effect of embedded foundations. The dynamic response factor decreases with the increasing frequency at the range of 0 to five. Note that Ah decreases significantly at a lower frequency, a0 < 1.5, while the dynamic response factor shows little dependence on a0 when a0 > 1.5. It is evident that the horizontal dynamic response factor depends significantly on the frequency and the relative stiffness of subsoil and backfill. The dynamic response factor shows a similar trend for different values of Gs/Gb. Another important conclusion revealed in Figure 11 is the independence of the dynamic response factor on high frequency.
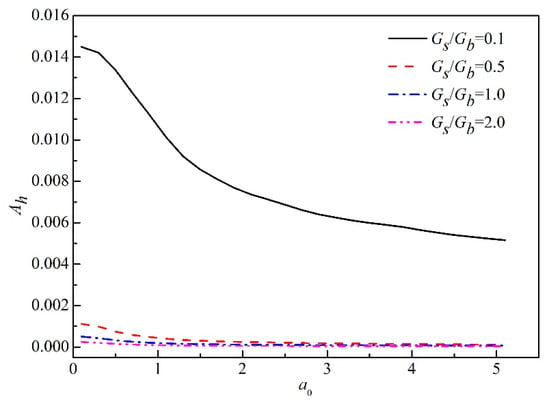
Figure 11.
Dynamic response factor of embedded foundation under different soil stiffness.
4. Conclusions
A simplified analytical method was performed to investigate the dynamic response of embedded foundation under horizontal vibration in the poroelastic soil medium. Biot’s theory was used to solve the dynamic behavior of soil. The mixed boundary value problem was analyzed by adopting a simplified analytical method. The proposed method in this study was confirmed by comparing the results with the existing literature. Analytical expressions were developed for predicting the dynamic impedance of embedded foundation under horizontal vibration. Furthermore, a comprehensive parametric analysis was performed in order to assess the applicability of this method. The dynamic impedance and dynamic response factor versus frequency were depicted in the dimensionless scale, respectively. Some conclusions are drawn below:
- (1)
- Results illustrated in this paper show that the embedment ratio of the foundation, mass ratio of the foundation, relative stiffness, and poroelastic properties of the backfill has a significant influence on the horizontal dynamic response of embedded foundation for the frequency range of 0 ≤ a0 ≤ 5.
- (2)
- The horizontal dynamic impedance of embedded foundation increases while the dynamic response factor decreases with the increasing embedment ratio. There’s an increase in dynamic impedance and a decrease in dynamic response factor with the increasing frequency.
- (3)
- It should be noted that the real part of dynamic impedance increases with the increasing mass ratio while the imaginary part is independent of the mass ratio. The dynamic response factor decreases with increasing mass ratio. An increase in the dynamic impedance and a decrease in the dynamic response factor are described with the increasing frequency.
- (4)
- By increasing the poroelastic material properties, the real part of dynamic impedance increases while the imaginary part, as well as the dynamic response factor, decreases. The larger the frequency, the larger is the dynamic impedance and the smaller the dynamic response factor.
- (5)
- The dynamic impedance increases significantly, especially for a frequency smaller than 1.5. The real part keeps increasing while the imaginary part decreases when the frequency is larger than 1.5. A considerable decrease in the dynamic response factor is noted due to the presence of relative backfill modulus. The effect of Poisson’s ratio v on the horizontal dynamic impedance of embedded foundation can be ignored.
With the aid of simplified analytical solutions proposed in this study, the expressions of dynamic impedance and dynamic response factor are formulated. The method proposed in this paper can be used to evaluate the dynamic response of embedded foundation subjected to horizontal dynamic loading. The comprehensive parametric study can provide versatile guidance to civil engineering and other dynamic construction. However, the proposed method is limited by the perfect smooth contact between the foundation and soil interface. The analytical solution of the horizontal impedance of embedded foundation with rigid underlying bedrock also remains unclear.
Author Contributions
Concepts and designs: Y.C. and W.Z.; Data analysis and numerical results: P.J. and J.H.; Examination of the simulation results: Y.G.
Funding
The research described in this paper was supported by the National Science Foundation of China (No. 51578116, No. 51878127) and the China Scholarship Council (No. 201706080075).
Acknowledgments
The authors would like to thank Northeastern University in providing access to the software and other facilities. The research described in this paper was supported by the National Science Foundation of China (No. 51578116, No. 51878127) and the China Scholarship Council (No. 201706080075). These supports are gratefully acknowledged. And the data is available for the journal.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Latini, C.; Zania, V. Dynamic lateral response of suction caissons. Soil Dyn. Earthq. Eng. 2017, 100, 59–71. [Google Scholar] [CrossRef]
- Eskandari-Ghadi, M.; Fallahi, M.; Ardeshir-Behrestaghi, A. Forced vertical vibration of rigid circular disc on a transversely isotropic half-space. J. Eng. Mech. 2009, 136, 913–922. [Google Scholar] [CrossRef]
- Reissner, E.; Sagoci, H.F. Forced torsional oscillations of an elastic half-space. Int. J. Appl. Phys. 1944, 15, 652–654. [Google Scholar] [CrossRef]
- Apsel, R.J.; Luco, J.E. Impedance functions for foundations embedded in a layered medium: An integral equation approach. Earthq. Eng. Struct. Dyn. 1987, 15, 213–231. [Google Scholar] [CrossRef]
- Ahmad, S.; Rupani, A.K. Horizontal impedance of square foundation in layered soil. Soil Dyn. Earthq. Eng. 1999, 18, 59–69. [Google Scholar] [CrossRef]
- Rajapakse, R.K.N.D.; Wang, Y. Elastodynamic Green’s functions of orthotropic half plane. J. Eng. Mech. 1991, 117, 588–604. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Halpern, M.R.; Christiano, P. Steady-state harmonic response of a rigid plate bearing on a liquid-saturated poroelastic halfspace. Earthq. Eng. Struct. Dyn. 1986, 14, 439–454. [Google Scholar] [CrossRef]
- Pak, R.Y.S.; Saphores, J.D. Rocking rotation of a rigid disc in a half-space. Int. J. Solids Struct. 1991, 28, 389–401. [Google Scholar] [CrossRef]
- Dargush, G.F.; Chopra, M.B. Dynamic analysis of axisymmetric foundations on poroelastic media. J. Eng. Mech. 1996, 122, 623–632. [Google Scholar] [CrossRef]
- Jin, B.; Zhou, D.; Zhong, Z. Lateral dynamic compliance of pile embedded in poroelastic half space. Soil Dyn. Earthq. Eng. 2001, 21, 519–525. [Google Scholar] [CrossRef]
- He, R.; Wang, L.Z. Horizontal vibration of a rigid disk buried in a poroelastic half-space in contact with a fluid half-space. Soil Dyn. Earthq. Eng. 2013, 44, 38–41. [Google Scholar] [CrossRef]
- Ni, P.; Song, L.; Mei, G.; Zhao, Y. Predicting excavation-induced settlement for embedded footing: Case study. Int. J. Geomech. 2018, 18, 05018001. [Google Scholar] [CrossRef]
- Rizzo, F.J.; Shippy, D.J.; Rezayat, M. Boundary Integral Equation Analysis for a Class of Earth-Structure Interaction Problems; Department of Engineering Mechanics, College of Engineering, University of Kentucky: Kentucky, OH, USA, 1985. [Google Scholar]
- Senjuntichai, T.; Sapsathiarn, Y. Forced vertical vibration of circular plate in multilayered poroelastic medium. J. Eng. Mech. 2003, 129, 1330–1341. [Google Scholar] [CrossRef]
- Chen, S.L.; Chen, L.Z.; Pan, E. Three-dimensional time-harmonic Green’s functions of saturated soil under buried loading. Soil Dyn. Earthq. Eng. 2007, 27, 448–462. [Google Scholar] [CrossRef]
- Senjuntichai, T.; Mani, S.; Rajapakse, R.K.N.D. Vertical vibration of an embedded rigid foundation in a poroelastic soil. Soil Dyn. Earthq. Eng. 2006, 26, 626–636. [Google Scholar] [CrossRef]
- Cai, Y.; Hu, X. Vertical vibrations of a rigid foundation embedded in a poroelastic half space. J. Eng. Mech. 2010, 136, 390–398. [Google Scholar] [CrossRef]
- Cai, Y.Q.; Hu, X.Q.; Xu, C.J.; Hong, Z.S. Vertical dynamic response of a rigid foundation embedded in a poroelastic soil layer. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 1363–1388. [Google Scholar] [CrossRef]
- Bilotta, E.; De Sanctis, L.; Di Laora, R.; D’Onofrio, A.; Silvesti, F. Importance of seismic site response and soil–structure interaction in dynamic behaviour of a tall building. Géotechnique 2015, 65, 391–400. [Google Scholar] [CrossRef]
- Fabozzi, S.; Bilotta, E.; Picozzi, M.; Zollo, A. Feasibility study of a loss-driven earthquake early warning and rapid response systems for tunnels of the Italian high-speed railway network. Soil Dyn. Earthq. Eng. 2018, 112, 232–242. [Google Scholar] [CrossRef]
- Di Laora, R.; Grossi, Y.; De Sancist, L.; Viggiani, G.M.B. An analytical solution for the rotational component of the Foundation Input Motion induced by a pile group. Soil Dyn. Earthq. Eng. 2017, 97, 424–438. [Google Scholar] [CrossRef]
- Novak, M. Dynamic stiffness and damping of piles. Can. Geotech. J. 1974, 11, 574–598. [Google Scholar] [CrossRef]
- Beredugo, Y.O.; Novak, M. Coupled horizontal and rocking vibration of embedded footings. Can. Geotech. J. 1972, 9, 477–497. [Google Scholar] [CrossRef]
- Yu, J. Theoretical Analysis and Test Research on Saturated Soil-Pile-Structure Dynamic Interaction; Central South University: Changsha, China, 2007. [Google Scholar]
- Noble, B. The Solution of Bessel Function Dual Integral Equations by a Multiplying-Factor Method. In Mathematical Proceedings of the Cambridge Philosophical Society; No. 2; Cambridge University Press: Cambridge, UK, 1963; Volume 59, pp. 351–362. [Google Scholar]
- Pak, R.Y.S.; Saphores, J.-D.M. Lateral translation of a rigid disk in a semi-infinite solid. Quart. J. Mech. Appl. Math. 1992, 45, 435–449. [Google Scholar] [CrossRef]
- Lysmer, J.; Richart, F.E. Dynamic response of footings to vertical loading. J. Soil Mech. Found. Div. 1966, 921, 65–91. [Google Scholar]
- Lysmer, J.; Kuhlemeyer, R.L. Finite dynamic model for infinite media. J. Eng. Mech. Div. 1969, 95, 859–878. [Google Scholar]
- Jin, B.; Liu, H. Horizontal vibrations of a disk on a poroelastic half-space. Soil Dyn. Earthq. Eng. 2000, 19, 269–275. [Google Scholar] [CrossRef]
- Nogami, T.; Chen, H.S. Dynamic soil stiffnesses at side of embedded structures with rectangular base. J. Eng. Mech. 2003, 129, 963–973. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).