A Static-loop-current Attack Against the Kirchhoff-Law-Johnson-Noise (KLJN) Secure Key Exchange System

Abstract

In this study, a new attack against the Kirchhoff-Law-Johnson-Noise (KLJN) key distribution system is explored. The attack is based on utilizing a parasitic voltage-source in the loop. Relevant situations often exist in the low-frequency limit in practical systems, especially when the communication is over a distance, or between different units within an instrument, due to a ground loop and/or electromagnetic interference (EMI). Our present study investigates the DC ground loop situation when no AC or EMI effects are present. Surprisingly, the usual current/voltage comparison-based defense method that exposes active attacks or parasitic features (such as wire resistance allowing information leaks) does not function here. The attack is successfully demonstrated and proposed defense methods against the attack are shown.

1. Introduction

1.1. On Secure Communications

Communications systems, standards, and technologies have been developed since ancient times. Today we have the internet, Internet-of-Things (IoT), operating fourth generation wireless networks (LTE), and the expected fifth generation wireless networks. An important requirement of any communication paradigm between these devices is to accomplish secure communication, i.e., to protect the privacy and integrity of users’ data that is transferred over the network. To achieve the security of transferred data which can contain sensitive information (e.g., bank account credentials, social security number, etc.) it is of utmost importance to defend against attacks. These attacks might be launched by an eavesdropper (Eve) who has access to the information channel between the communicating parties A (Alice) and B (Bob). The attack is passive if it eavesdrops without disturbing the channel. The attack is active (invasive) if Eve disturbs or changes the channel, such as with a man-in-the-middle attack. In the present paper, we introduce a new passive attack against the Kirchhoff-Law-Johnson-Noise (KLJN) secure key exchange scheme.

1.1.1. Secure Key Exchange

Secure communication systems employ ciphers to encrypt messages (plaintext) and to decrypt encrypted messages (cyphertext). While the creation of a secure and efficient cipher is a complex problem, this problem may be solved simply. Ciphers operate with secure keys that form a momentary shared secret between Alice and Bob. Sharing (exchanging) the key securely is the difficult task. A communicator system cannot be more secure than its key. The security of the key exchange can be conditional or information-theoretic (unconditional).

1.1.2. Conditional Security

Conditionally secure key exchange systems are the ones used generally nowadays. They are software protocols installed at Alice and Bob. Such algorithms utilize computational complexity and achieve only (computationally) conditional security (see e.g., [1,2]). The system is temporarily secure provided the adversary has limited computational resources. A major goal of quantum computer developments is to crack these types of key exchange systems (e.g., the Shor algorithm). From an information-theoretic point of view, security is non-existent because Eve has all the information to crack the encryption, but she needs a long time to do that unless she has a quantum computer or a yet-to-be-discovered classical algorithm that can do the job in a short time. The security is not future-proof.

1.1.3. Unconditional (Information-Theoretic) Security

In order to achieve unconditional (information-theoretic) security at the key exchange, proper laws of physics with a special hardware are utilized. Two major classes of physics-based schemes have emerged for unconditional security:

(i) Quantum key distribution (QKD) [3,4] concepts assume single photons and utilize quantum physics. The underlying laws of physics are Heisenberg’s uncertainty principle and the related quantum no-cloning theorem [5]. Even though there are serious debates about the actual level of unconditional security a practical QKD can offer (see e.g., [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]), most scientists agree that QKD is unique in its offering information-theoretic security via (a dark) optical fiber and also through air at night, provided the visibility is good.

(ii) The Kirchhoff-Law-Johnson-Noise key distribution method that is based on the statistical physical features of the thermal noise of resistors [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56]. The related law of physics is the fluctuation-dissipation-theorem (FDT). Some of its advantages are: It works via wire connections including power, phone, and internet lines, which can be used as information channels [31,32] to connect all homes and other establishments. It can be integrated on a chip, which implies excellent robustness, low price, and applicability in bankcards, computers, instruments, and physical unclonable function (PUF) hardware keys [33,34]. Its low price allows general applications such as unconditional security for the control of autonomous vehicular networks [35,36].

1.2. On the KLJN Secure Key Distribution

The KLJN scheme [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52] utilizes the thermal noise of resistors (or the emulation of that by a specific hardware). In the core scheme Alice and Bob have two identical pairs of resistors, $R_{\mathrm{L}}$ and $R_{\mathrm{H}}$ ($R_{\mathrm{L}}<R_{\mathrm{H}}$), respectively (see Figure 1).

The key exchange protocol of a single secure bit is as follows: Alice and Bob randomly pick one of their resistors ($R_{\mathrm{L}}$ or $R_{\mathrm{H}}$), connect it to the wire channel, and keep them there during the bit exchange period while they execute voltage and/or current measurements to learn the resistor value at the other end (see below).

The noise voltage generators shown in Figure 1 with each resistor can be the resistors’ own thermal noise, or an external noise generator emulating a much higher, common noise-temperature that is publicly agreed. The power density spectra of the voltage and current in the channel are given by the Johnson-Nyquist formulas [11]

$$S_u(f)=\frac{4kT{R}_{\mathrm{A}}{R}_{\mathrm{B}}}{R_{\mathrm{A}}+R_{\mathrm{B}}},$$

(1)

$$S_i(f)=\frac{4kT}{R_{\mathrm{A}}+R_{\mathrm{B}}}$$

(2)

where $k$ is the Boltzmann’s constant, $T$ is the common temperature, and $R_{\mathrm{A}}$ and $R_{\mathrm{B}}$ are the actually connected resistances at Alice’s and Bob’s ends, respectively, with $R_{\mathrm{A}},R_{\mathrm{B}}\in \left\{R_{\mathrm{L}},R_{\mathrm{H}}\right\}$. After the measurement and spectral analysis, Equations (1) and (2) have two unknown variables, namely, the values of $R_{\mathrm{A}}$ and $R_{\mathrm{B}}$, and thus Eve can find the values of the connected resistors, but not necessarily their locations, by solving these equations.

We can represent the four different situations of the connected resistors ($R_{\mathrm{L}}$ and/or $R_{\mathrm{H}}$) at Alice’s and Bob’s ends by the indices of the connected resistors, LL, LH, HL, and HH, respectively. As all the resistors have the same (noise) temperature, the ideal system is in thermal equilibrium, where the second law of thermodynamics guarantees zero net power-flow. Hence, Eve cannot use the evaluation of power flow to determine the locations of the momentarily connected resistors unless they have the same resistance values. On the other hand, Alice and Bob can determine the connected resistor values by using Equations (1) or (2) since they know the value of their own connected resistors. When $R_{\mathrm{A}}=R_{\mathrm{B}}$, which happens at 50% of the bit exchange attempts, the results are discarded.

On Former Attacks Against the KLJN Secure Key Distribution

Several attacks have been proposed but no attack has been able to compromise the unconditional security of the KLJN scheme because each known attack can efficiently be nullified by a corresponding defense scheme.

The attacks can be categorized into two classes:

(i) Passive attacks that utilize the non-ideal or parasitic features in a practical KLJN system for information leaks. Non-zero wire resistance (see [37,38]) poses the greatest known threat, and the most efficient attack is power balance measurement (Second Law Attack) [39]. An efficient defense is based on a proper temperature-offset [39,40]. Temperature-inaccuracies [41] and resistance-inaccuracies [42] can also cause information leaks. On the other hand, these inaccuracies can compensate for each other [43] if used in a creative way. Non-zero cable capacitance [44] or cable inductance can also yield information leaks that can be fixed by specific designs including the proper choice of frequency range and privacy amplification. Transients can also be utilized for attack [45] but there are various means of defense against these [46,47]. The newest KLJN system, the random-resistor-random-temperature KLJN (RRRT-KLJN) scheme [48], is robust against the above vulnerabilities, or at least, no known attack exists against it yet.

(ii) Active attacks, where Eve either modifies the information channel or she injects an extra current into it. Current injection attacks [30,49] and man-in-the-middle attacks [50] are examples which have been explored [56]. Due to the current and voltage comparison [50] feature and its more advanced cable-modeling version [49], active attacks are, so far, the least efficient attacks against the KLJN scheme.

(iii) Flawed attacks. There are some proposed attack methods that are based on misconceptions and they do not work. See their brief summary and criticism in, for example, papers [51,52,53,54,55] and the book [56].

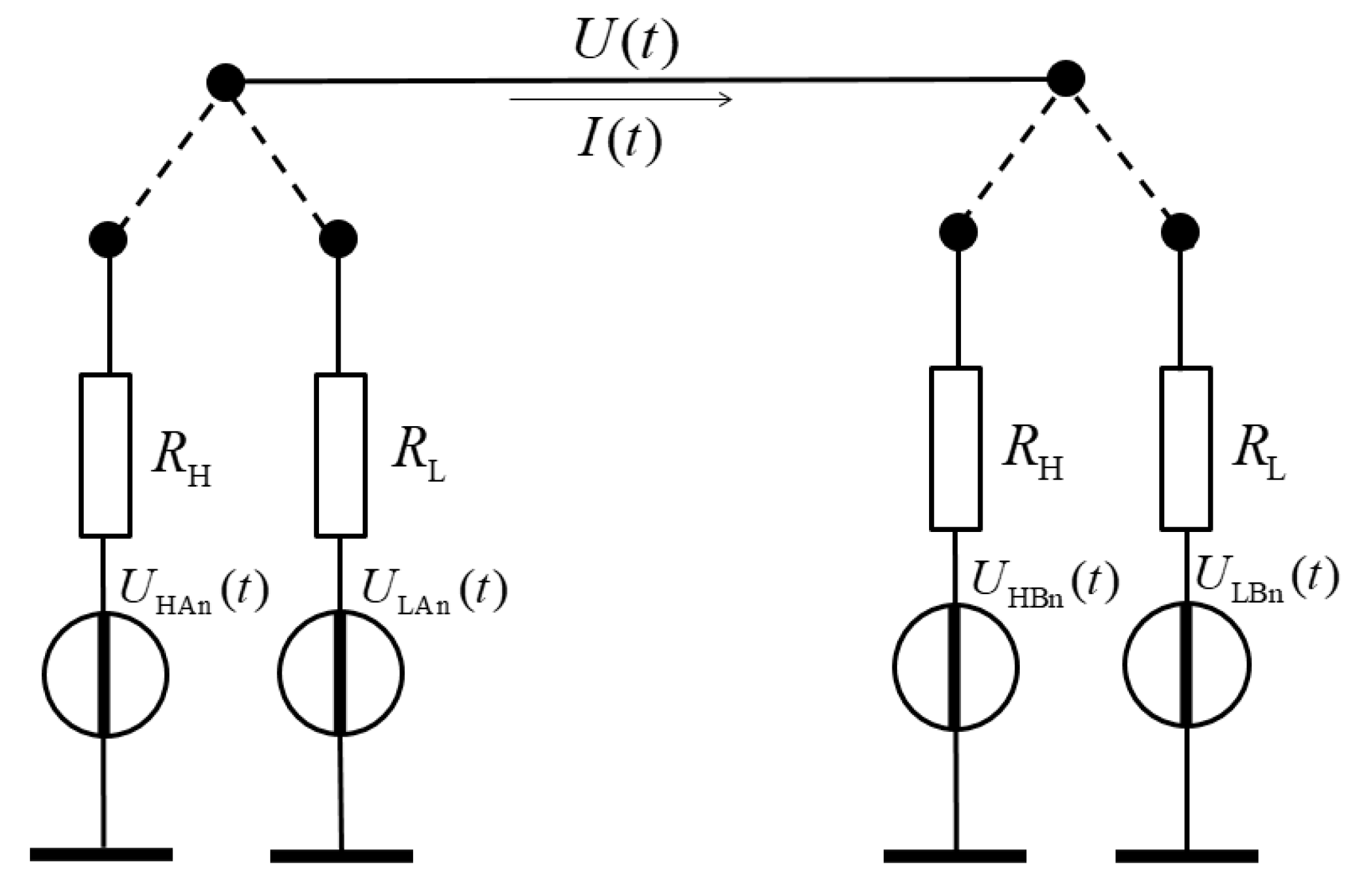
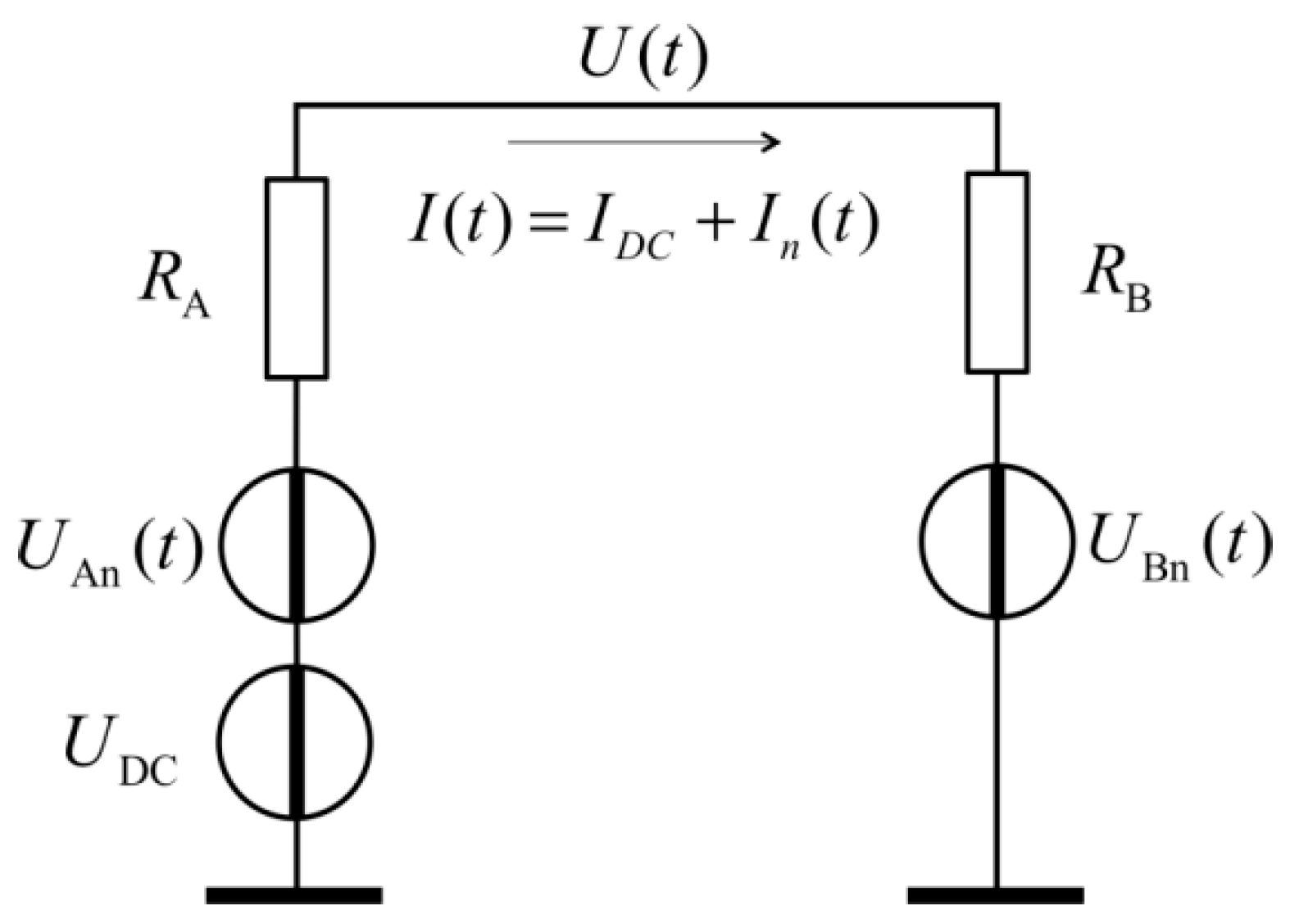
2. The New Attack Scheme Utilizing Deterministic Loop Currents

2.1. The Situation that Eve Utilizes for the Attack

In practical KLJN systems, in order to save a wire, the common end of the resistors (see Figure 1) is often connected to the ground. In practical situations there is often an imbalance, a voltage difference between various locations of the ground that is due, for example, to ground loop currents or electromagnetic interference (EMI) [53]. This potential information leak was pointed out in [53] as a potential source of information leaks in the case of significant cable resistance. However, it was not realized in [53] that information leaks can exist even at zero cable resistance. The present study is directly relevant for DC current-based ground loops (such as during secure communication between different units in instruments [33,34]). For EMI-induced ground loops, our DC-limited study is only a first step in addressing a more general situation (which should be investigated in future works).

In this paper, we explore this new information leak in the DC parasitic voltage limit. Hence, consideration was given to situations where during the bit exchange period, the relative change in the parasitic voltage is small. For the sake of simplicity but without the limitation of generality, we assume that the imperfection is represented by a positive DC voltage generator located at Alice’s end (see Figure 2).

Due to Kerckhoffs’s principle of security, that is, the assumption that the enemy knows everything except the momentary key, we must assume that Eve knows the polarity and value of this DC voltage (if she does not know it at first, she will be able to extract it via long-time averaging). The direction of the current I(t) is assumed to point from Alice to Bob. The voltage U(t) and current I(t) in the wire contain the sum of a DC component and an AC (stochastic, that is, noise) component.

Let us analyze the resulting voltages and currents. The current in the wire is

$$I(t)=I_{\mathrm{DC}}+I_{\mathrm{n}}(t)$$

(3)

where I_DC is its DC component

$$I_{\mathrm{DC}}=\frac{U_{\mathrm{DC}}}{R_{\mathrm{A}}+R_{\mathrm{B}}}$$

(4)

and $I_{\mathrm{n}}(t)$ is its AC (noise) component

$$I_{\mathrm{n}}(t)=\frac{U_{\mathrm{An}}(t)-U_{\mathrm{Bn}}(t)}{R_{\mathrm{A}}+R_{\mathrm{B}}}$$

(5)

in which $U_{\mathrm{An}}$ and $U_{\mathrm{Bn}}$, with $U_{\mathrm{An}}\in \{U_{\mathrm{LAn}};U_{\mathrm{HAn}}\}$ and $U_{\mathrm{Bn}}\in \{U_{\mathrm{LBn}};U_{\mathrm{HBn}}\}$, are the voltage noise sources of the chosen resistors, $R_{\mathrm{A}}$ and $R_{\mathrm{B}}$, respectively.

The voltage on the wire is

$$U(t)=I(t)R_{\mathrm{B}}+U_{\mathrm{Bn}}(t).$$

(6)

From Equations (3) and (6) we obtain

$$U(t)=U_{\mathrm{DCw}}+U_{\mathrm{ACw}}(t)=I_{\mathrm{DC}}{R}_{\mathrm{B}}+I_{\mathrm{n}}(t)R_{\mathrm{B}}+U_{\mathrm{Bn}}(t)$$

(7)

where U_DCw and U_ACw(t) represent the DC and AC voltage components in the wire, respectively. The DC component can be written as

$$U_{\mathrm{DCw}}=I_{\mathrm{DC}}{R}_{\mathrm{B}}=\frac{U_{\mathrm{DC}}}{R_{\mathrm{A}}+R_{\mathrm{B}}}{R}_{\mathrm{B}}.$$

(8)

The DC component is different during Alice’s and Bob’s LH and HL bit situations of secure bit exchange, which yields information leaks. In the LH situation, that is, when $R_{\mathrm{A}}=R_{\mathrm{L}}$ and $R_{\mathrm{B}}=R_{\mathrm{H}}$, the DC component of the voltage on the wire is

$$U_{\mathrm{DCw}}\equiv U_{\mathrm{LH}}=U_{DC}\frac{R_{\mathrm{H}}}{R_{\mathrm{H}}+R_{\mathrm{L}}}$$

(9)

and, in the HL bit situation,

$$U_{\mathrm{DCw}}\equiv U_{\mathrm{HL}}=U_{\mathrm{DC}}\frac{R_{\mathrm{L}}}{R_{\mathrm{H}}+R_{\mathrm{L}}}.$$

(10)

Note that as we have been assuming that in the given KLJN setup R_H > R_L, in this particular situation

$$U_{\mathrm{HL}}<U_{\mathrm{LH}}.$$

(11)

For later usage, we evaluate the average of $U_{\mathrm{LH}}$ and $U_{\mathrm{HL}}$ and call this quantity the threshold voltage, $U_{\mathrm{th}}$, where

$$U_{\mathrm{th}}=\frac{U_{\mathrm{LH}}+U_{\mathrm{HL}}}{2}=\frac{U_{\mathrm{DC}}}{2}.$$

(12)

The effective (RMS) amplitude $U_{\mathrm{ACw}}$ of the noise voltage on the wire is identical in both the LH and HL cases:

$$U_{\mathrm{ACw}}=\sqrt{4kT{B}_W\frac{R_{\mathrm{L}}{R}_{\mathrm{H}}}{R_{\mathrm{L}}+R_{\mathrm{H}}}}.$$

(13)

Note that the voltage and current noises in the wire follow a normal distribution since the addition of normally distributed signals results in a signal that has normal (Gaussian) distribution with a corresponding mean (see Equation (10)) and variance.

For an illustration of the information leak, see Figure 3. The DC component, that is, the mean value of the resulting (AC + DC) Gaussian depends on the bit situation during the secure key exchange. This dependence poses as a source of information for Eve about the secret key. This feature will be exploited below for the new attack scheme.

2.2. The Attack Scheme

The attack consists of three steps: measurement, evaluation, and guessing.

(i) Measurement: During a single secure bit exchange, Eve measures N independent samples of the wire voltage.

(ii) Evaluation: She evaluates the fraction γ of these N samples that are above $U_{\mathrm{th}}$, which is

$$\gamma =\frac{N^{+}}{N}$$

(14)

where $N^{+}$ is the number of samples that are above $U_{\mathrm{th}}$.

(iii) Guessing (based on Equations (9)–(14)): For $0.5<\gamma$ and $\gamma <0.5$, Eve’s guesses are the $\mathrm{LH}$ and $\mathrm{HL}$ bit situations, respectively. For $\gamma =0.5$ her decision is undetermined and carries no useful information.

(iv) Eve’s correct guessing probability p is given as

$$p=\underset{n_{\mathrm{tot}}\to \infty }{\lim }\frac{n_{\mathrm{cor}}}{n_{\mathrm{tot}}}$$

(15)

where $n_{\mathrm{tot}}$ is the total number of guess bits and $n_{\mathrm{cor}}$ is the number of correctly guessed bits. The situation $p=0.5$ indicates perfect security against Eve’s attack.

In the next section, we demonstrate the attack method via computer simulation.

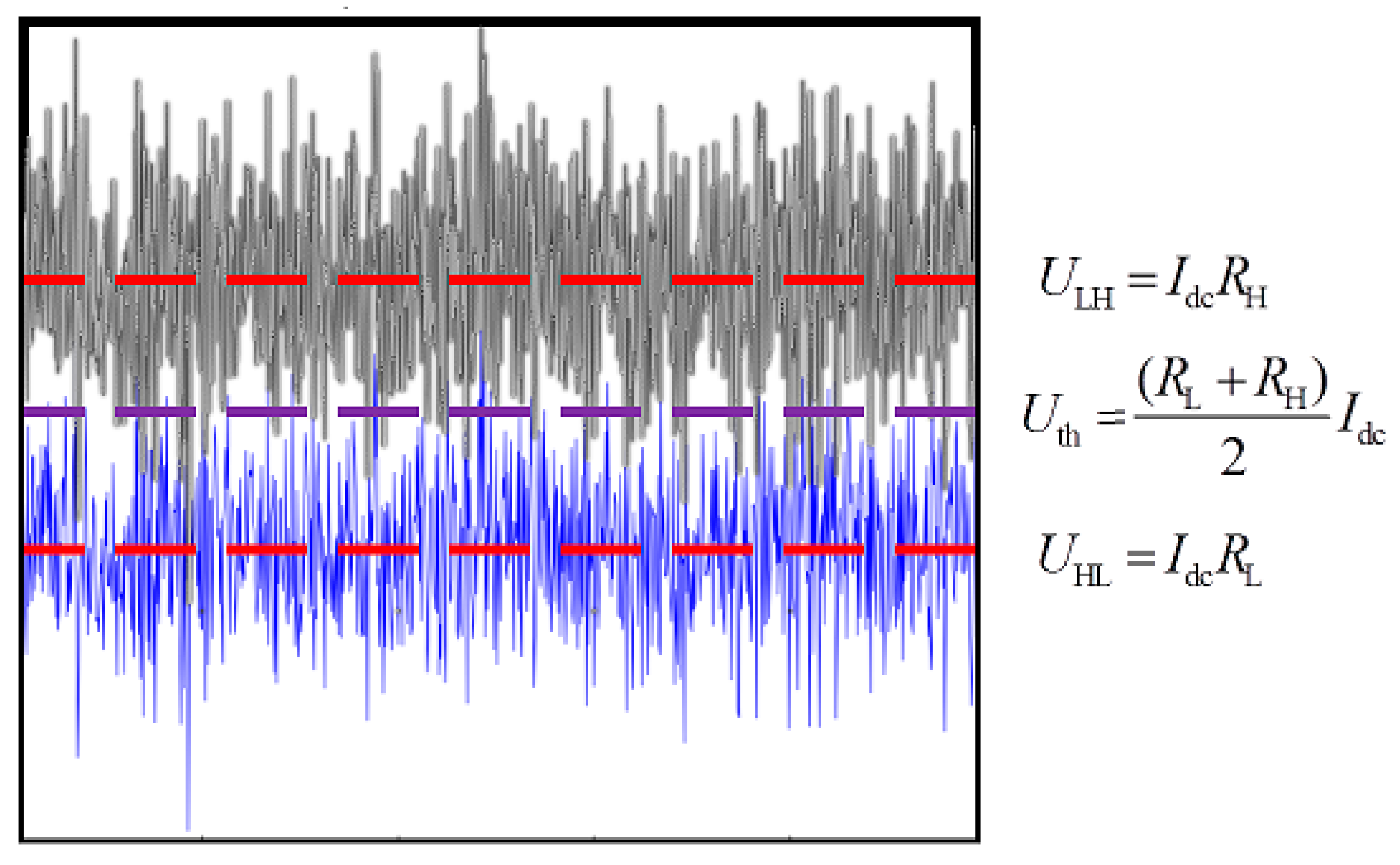
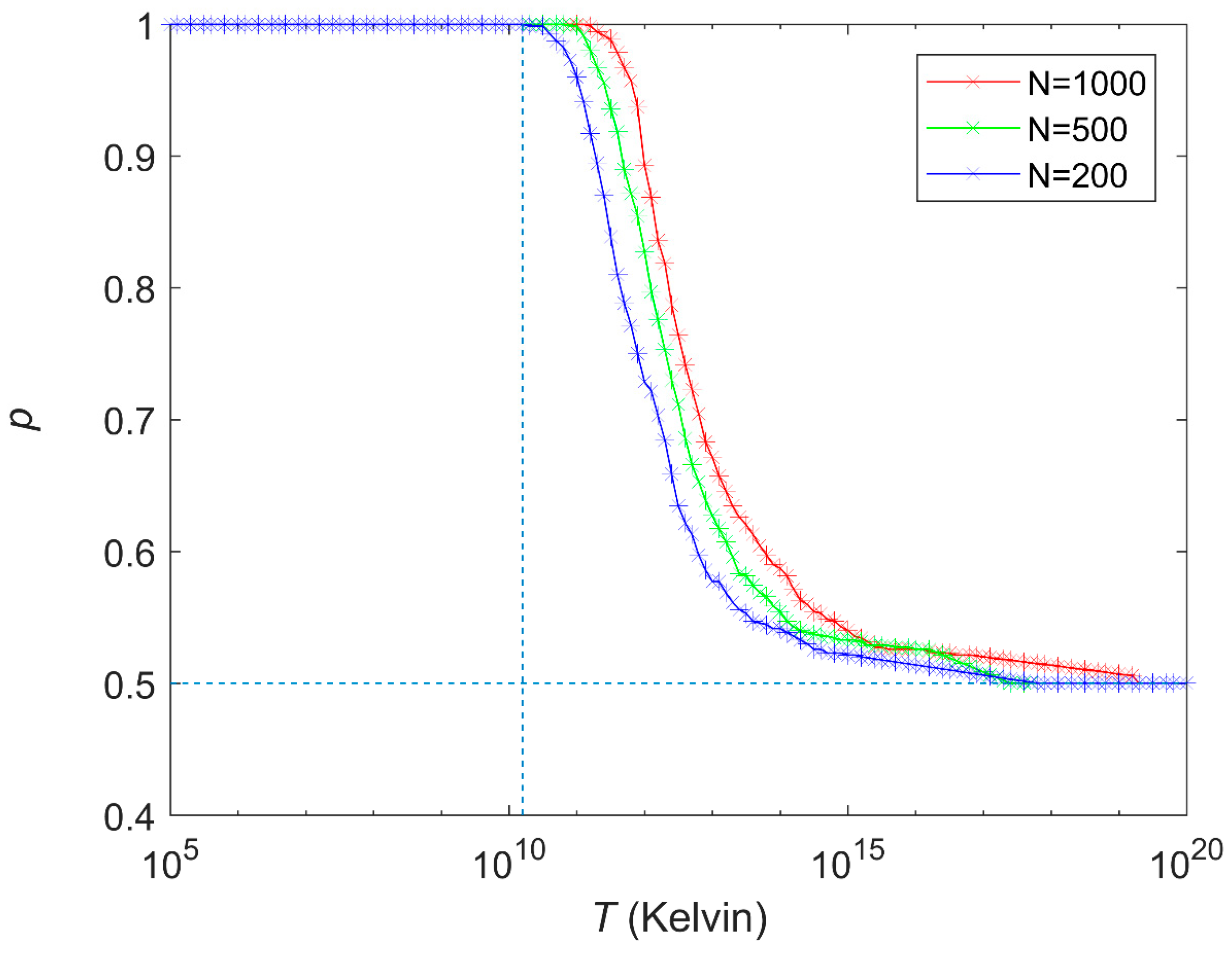
3. Simulation Results

To test Eve’s correct guessing probability $p$ for the LH situation, we assumed that Alice and Bob selected $R_{\mathrm{L}}=1\mathrm{k}\mathsf{\Omega }$ and $R_{\mathrm{H}}=10\mathrm{k}\mathsf{\Omega }$. During these experiments, the DC voltage was kept at a constant level of 0.1 V (see Figure 2 and Figure 3). To generate noise, we used the white Gaussian noise function (wgn) from the Matlab communication system toolbox to test the success statistics of the attack scheme while varying the temperature. The effective bandwidth $\Delta f$ and the range of temperatures were 1 MHz and ${10}^8<T<{10}^{18}\mathrm{K}$, respectively. At lower temperatures $p$ was 1, within the statistical inaccuracy of simulations; at the high-temperature limit it converged to 0.5. The duration of the secure bit exchange period was characterized by the number N of independent noise samples used during the exchange of the particular bit.

We tested secure key length M = 700 bits at different bit exchange durations represented by sample/bit numbers N = 1000, 500, and 200, respectively. Figure 4 shows Eve’s correct guessing probability ($p$) of a key bit versus temperature. With temperature approaching infinity, the effective noise voltage on the wire also approaches infinity and the Gaussian density function is symmetrically distributed around the threshold voltage $U_{\mathrm{th}}$. Thus, the probabilities of finding the noise amplitude above or below $U_{\mathrm{th}}$ are identical (0.5) Therefore, Eve’s correct guessing probability represents the perfect security limit, p = 0.5.

The observed dependence can be interpreted by the behavior of the error function (see also Equations (8) and (12))

$$p\left\{U\left(t\right)\ge U_{\mathrm{th}}\right\}=0.5\left[1-erf\left(\frac{U_{\mathrm{th}}-U_{\mathrm{DCw}}}{U_{\mathrm{eff}}\sqrt{2}}\right)\right]$$

(16)

where U(t) is the instantaneous voltage amplitude in the wire and the error function is

$$erf(x)=\frac{1}{\sqrt{\pi }}{\displaystyle \underset{-x}{\overset{x}{\int }}\exp \left(-y^2\right)}dy.$$

(17)

The noise in the KLJN scheme is a bandlimited white noise, and thus, in accordance with the Johnson formula, the effective noise voltage scales as

$$U_{\mathrm{eff}}\propto \sqrt{T\Delta f}$$

(18)

Therefore, when temperature T is converging towards infinity, p converges to the perfect security limit of 0.5 (see Figure 4).

4. Some of the Possible Defense Techniques Against the Attack

Based on the considerations above, the impact of the attack can be eliminated by various means. The most natural ways are:

(i) Cancelling the effect of the DC-voltage sources. For example, Bob can use a variable DC source that compensates for its effect. Similarly, eliminating ground loops is also beneficial.

(ii) Alice and Bob can increase the effective temperature, that is, the amplitudes of their noise generators (see Equation (18) and Figure 4).

(iii) Alice and Bob can increase the bandwidth to increase the effective value of the noise (see Equations (18) and (20)). However, the bandwidth must stay below the wave limit [54] to avoid information leaks due to reflection, and thus the applicability of this tool is strongly limited.

5. Conclusions

The KLJN secure key exchange scheme is a statistical physical system that offers unconditional (information-theoretic) security. For a detailed survey and its history, see the recent book [56].

In this paper a novel attack against the KLJN protocol is shown which has revealed that uses a frequently occurring parasitic feature, namely the imbalance of voltages between the ground points at the two ends. We showed that, in the DC limit, such parasite voltages and currents could cause information leaks. The present study is directly relevant for DC current-based ground loops (for example, during secure communication between different units in instruments [33,34]). The attack was demonstrated via computer simulation and proper defense protocols were shown to eliminate the information leak. For AC-type ground loops, our DC-limited study is only a first step in addressing a more general situation (which should be investigated in future works).