Bayesian Game-Theoretic Bidding Optimization for Aggregators Considering the Breach of Demand Response Resource
Abstract
:1. Introduction
- A DR framework is proposed to optimize the bidding strategy of DR resource for community operators considering the risk of DR resource’s breach.
- A Bayesian game based approach is formulated for the proposed scenario with incomplete information to promote the participants’ profit, and then an iterative algorithm is designed to obtain the bidding equilibrium among community operators.
- A case study is carried out to verify the performance and effectiveness of the proposed Bayesian game approach by simulating the bidding strategy optimization of 3 community operators.
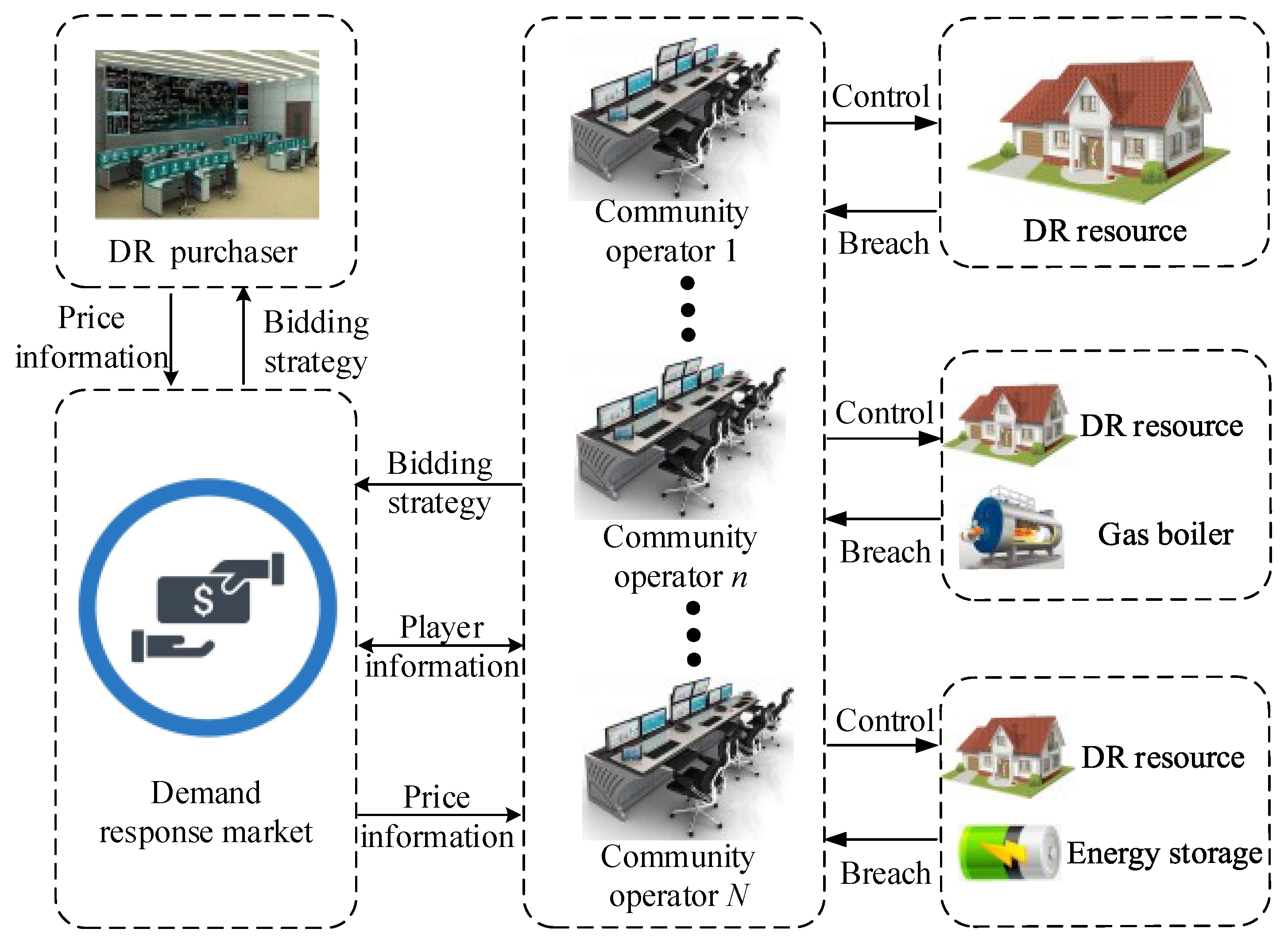
2. Proposed DR Framework
3. System Model
3.1. Gas Boiler Model
3.2. Energy Storage Model
3.3. Bidding Price Model
3.4. DR Resource’s Breach Model
4. Bayesian Game among Community Operators
4.1. Community Operator’s Profit Model
- Profit from DR purchaserFrom DR purchaser, community operator’s income is the earning for selling DR resource, and cost is the punishment for DR resource’s breach. According to the bidding price, when DR resource of community operator n is the ith grade, then the profit from DR purchaser can be expressed aswhere is the punishment for ith grade of DR resource’s breach, is the price paid to consumers.
- Profit from gas boilerFrom gas boiler, community operator’s income is the earning for providing heat to users, and cost is the energy cost for natural gas, investment and maintenance cost. Accordingly, profit from gas boiler can be expressed aswhere is heat price charged from users; is natural gas price; is the investment and maintenance of gas boiler with the following formulawhere and are investment price and maintenance price, respectively; r is the discount rate; is the lifetime of gas boiler; is the capacity of gas boiler.
- Profit from energy storageFrom energy storage, community operator’s income is the earning for providing electricity to users, and cost is the electricity cost for charging storage, investment and maintenance cost. Accordingly, profit from energy storage can be expressed aswhere is electricity price charged from users; is electricity price charged by public grid; is the investment and maintenance of energy storage with the following formulawhere and are investment price and maintenance price, respectively; is the lifetime of energy storage; is the capacity of energy storage.
4.2. Game Formulation with Complete Information
- Players: All community operators who willing to participating in the bidding market.
- Strategies: each community changes its bidding strategy to maximize its payoff.
- Payoffs: the payoff of each community operator is defined aswhere is the bidding strategy set of community operator n and is the bidding strategy set of all community operators except operator n; and represent community operator n has equipped gas boiler and energy storage, otherwise and .
4.3. Bayesian Game Formulation
- DR resource’s grade constraintCommunity operators employ gas boiler and energy storage to promote the grade of DR resource. In which, gas boiler can reduce breach amount by substituting electrical heating appliance; while energy storage can compensate breach amount via providing electricity for users. When community operator equips gas boiler or energy storage, its expected breach amount can be expressed aswhere is the compensation amount by gas boiler and energy storage, which is equal towhere is the energy efficiency ratio of electrical heating appliance. Based on formulaes (17) and (18), the breach amount will be reduced to from the perspective of DR purchaser. Therefore, the breach percentage changes to . When community operator n wants to participate in the bidding of ith grade of DR resource, then breach percentage must satisfy the upper limit
- Device output constraintEnergy output of gas boiler and energy storage have to be less than the maximal energy output of devicewhere and are the maximal energy output of energy storage and gas boiler. Additionally, the state of energy storage has to satisfywhere is the maximal discharge depth of energy storage.
- Bidding amount constraintEach community operator makes bidding strategy according to the DR resource level in its native users. Since flexible loads only take a certain percentage of all users’ loads, the bidding amount must satisfy
4.4. Distribution Algorithm
- Community operator n with type initializes its bidding strategy;
- Community operator n will optimize the bidding strategy of its opponents;
- On basis of the optimal strategy of opponents, community operator n will optimize its own bidding strategy;
- Repeat step 2 and 3 until all operators’ strategies is unchanged.
| Algorithm 1: Executed by each community operator |
 |
5. Case Study
5.1. Simulation Parameters
5.2. Equilibrium Solution
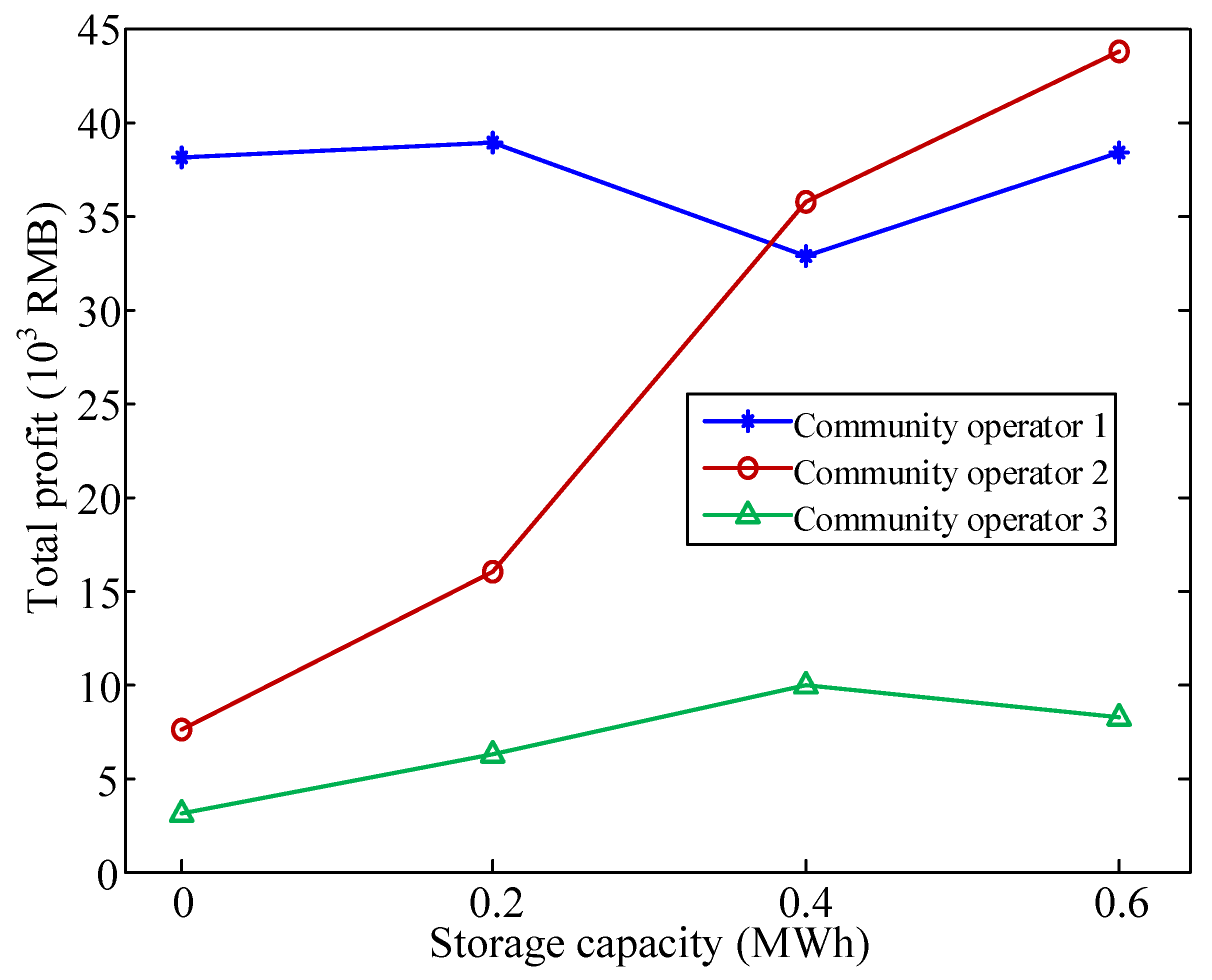
5.3. Impact of Energy Storage Capacity
5.4. Benefit of Auxiliary Equipment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zeng, B.; Wu, G.; Wang, J. Impact of behavior-driven demand response on supply adequacy in smart distribution systems. Appl. Energy 2017, 202, 125–137. [Google Scholar] [CrossRef]
- Bao, Z.; Zhou, Q.; Yang, Z. A multi time-scale and multi energy-type coordinated microgrid scheduling solution-Part I: Model and methodology. IEEE Trans. Power Syst. 2015, 30, 2257–2266. [Google Scholar] [CrossRef]
- Rodrlguez, L.R.; Ramos, J.S.; Domlnguez, S.A. Contributions of heat pumps to demand response: A case study of a plus-energy dwelling. Appl. Energy 2018, 214, 191–204. [Google Scholar]
- Alamaniotis, M.; Gatsis, N.; Tsoukalas, L.H. Virtual Budget: Integration of electricity load and price anticipation for load morphing in price-directed energy utilization. Electr. Power Syst. Res. 2018, 158, 284–296. [Google Scholar] [CrossRef]
- Jacquot, P.; Beaude, O.; Gaubert, S. Analysis and implementation of an hourly billing mechanism for demand response management. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Nehrir, M.H.; Sheppard, J.W. Agent-based modeling of retail electrical energy markets with demand response. IEEE Trans. Smart Grid 2018, 9, 3465–3475. [Google Scholar] [CrossRef]
- Menniti, D.; Costanzo, F.; Scordino, N. Purchase-bidding strategies of an energy coalition with demand-response capabilities. IEEE Trans. Power Syst. 2009, 24, 1241–1255. [Google Scholar] [CrossRef]
- Chen, S.; Chen, Q.; Xu, Y. Strategic bidding and compensation mechanism for a load aggregator with direct thermostat control capabilities. IEEE Trans. Smart Grid 2018, 9, 2327–2336. [Google Scholar] [CrossRef]
- Kardakos, E.G.; Simoglou, C.K.; Bakirtzis, A.G. Optimal offering strategy of a virtual power plant: A stochastic bi-level approach. IEEE Trans. Smart Grid 2016, 7, 794–806. [Google Scholar] [CrossRef]
- Henriquez, R.; Wenzel, G.; Olivares, D.E. Participation of demand response aggregators in electricity markets: Optimal portfolio management. IEEE Trans. Smart Grid 2018, 9, 4861–4871. [Google Scholar] [CrossRef]
- Marialaura, D.; Giorgio, G.; Pierluigi, S. Optimal bidding strategy for a DER aggregator in the day-ahead market in the presence of demand flexibility. IEEE Trans. Ind. Electron. 2019, 66, 1509–1519. [Google Scholar]
- Jia, Y.; Mi, Z.; Yu, Y. A bilevel model for optimal bidding and offering of flexible load aggregator in day-ahead energy and reserve markets. IEEE Access 2018, 6, 67799–67808. [Google Scholar] [CrossRef]
- Parvania, M.; Fotuhi-Firuzabad, M.; Shahidehpour, M. Optimal demand response aggregation in wholesale electricity markets. IEEE Trans. Smart Grid 2013, 4, 1957–1965. [Google Scholar] [CrossRef]
- Calvillo, C.F.; Sanchez-Miralles, A.; Villar, J. Optimal planning and operation of aggregated distributed energy resources with market participation. Appl. Energy 2016, 182, 340–357. [Google Scholar] [CrossRef]
- Mnatsakanyan, A.; Kennedy, S.W. A novel demand response model with an application for a virtual power plant. IEEE Trans. Smart Grid 2015, 6, 230–237. [Google Scholar] [CrossRef]
- Pourghaderi, N.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. Commercial demand response programs in bidding of a technical virtual power plant. Ind. Inf. 2018, 14, 5100–5111. [Google Scholar] [CrossRef]
- Mashhour, E.; Moghaddas-Tafreshi, S.M. Bidding strategy of virtual power plant for participating in energy and spinning reserve markets-Part I: Problem formulation. IEEE Trans. Power Syst. 2011, 26, 949–956. [Google Scholar] [CrossRef]
- Mashhour, E.; Moghaddas-Tafreshi, S.M. Bidding strategy of virtual power plant for participating in energy and spinning reserve markets-Part II: Numerical analysis. IEEE Trans. Power Syst. 2011, 26, 957–964. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.H.; Wong, V.W.S.; Jatskevich, J. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid. IEEE Trans. Smart Grid 2010, 1, 320–331. [Google Scholar] [CrossRef]
- Gao, B.; Liu, X.; Zhang, W. Autonomous household energy management based on a double cooperative game approach in the smart grid. Energies 2015, 8, 7326–7343. [Google Scholar] [CrossRef]
- Baharlouei, Z.; Hashemi, M.; Narimani, H. Achieving optimality and fairness in autonomous demand response: Benchmarks and billing mechanisms. IEEE Trans. Smart Grid 2013, 4, 968–975. [Google Scholar] [CrossRef]
- Maharjan, S.; Zhu, Q.; Zhang, Y. Dependable demand response management in the smart grid: A Stackelberg game approach. IEEE Trans. Smart Grid 2013, 4, 120–132. [Google Scholar] [CrossRef]
- Contreras-Ocana, J.E.; Ortega-Vazquez, M.A.; Zhang, B. Participation of an energy storage aggregator in electricity markets. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Liu, X.; Gao, B.; Luo, J. Non-cooperative game based hierarchical dispatch model of residential loads. Autom. Electr. Power Syst. 2017, 41, 54–60. [Google Scholar]
- Guo, D.; Zheng, R.; Lin, Z. A game-theoretic approach to decentralized control of heterogeneous load population. Electr. Power Syst. Res. 2016, 140, 552–559. [Google Scholar] [CrossRef]
- Nekouei, E.; Alpcan, T.; Chattopadhyay, D. Game-theoretic frameworks for demand response in electricity markets. IEEE Trans. Smart Grid 2015, 6, 748–758. [Google Scholar] [CrossRef]
- Gao, B.; Liu, X.; Chen, C. Economic optimization for distributed energy network with cooperative game. J. Renew. Sustain. Energy 2018, 10, 055101. [Google Scholar] [CrossRef]
- Atzeni, I.; Ordonez, L.; Scutari, G. Demand-side management via distributed energy generation and storage optimization. IEEE Trans. Smart Grid 2013, 4, 866–876. [Google Scholar] [CrossRef]
- Pender, J. The truncated normal distribution: Applications to queues with impatient customers. Oper. Res. Lett. 2015, 43, 40–45. [Google Scholar] [CrossRef]
- Samadi, P.; Mohsenian-Rad, H.; Schober, R. Advanced demand side management for the future smart grid using mechanism design. IEEE Trans. Smart Grid 2012, 3, 1170–1180. [Google Scholar] [CrossRef]
- Harsanyi, J.C. Games with incomplete information played by Bayesian players, I–III: Part I. The basic model. Manag Sci. 1967, 14, 159–182. [Google Scholar] [CrossRef]
- Zhang, K.; Song, Y.; Yan, Z. Energy storage capacity optimization for load aggregrators considerring probability of demand response resources’ breach. Autom. Electr. Power Syst. 2015, 39, 127–133. [Google Scholar]
- Li, T.; Shahidehpour, M. Strategic bidding of transmission-constrained GENCOs with incomplete information. IEEE Trans. Power Syst. 2005, 20, 437–447. [Google Scholar] [CrossRef]
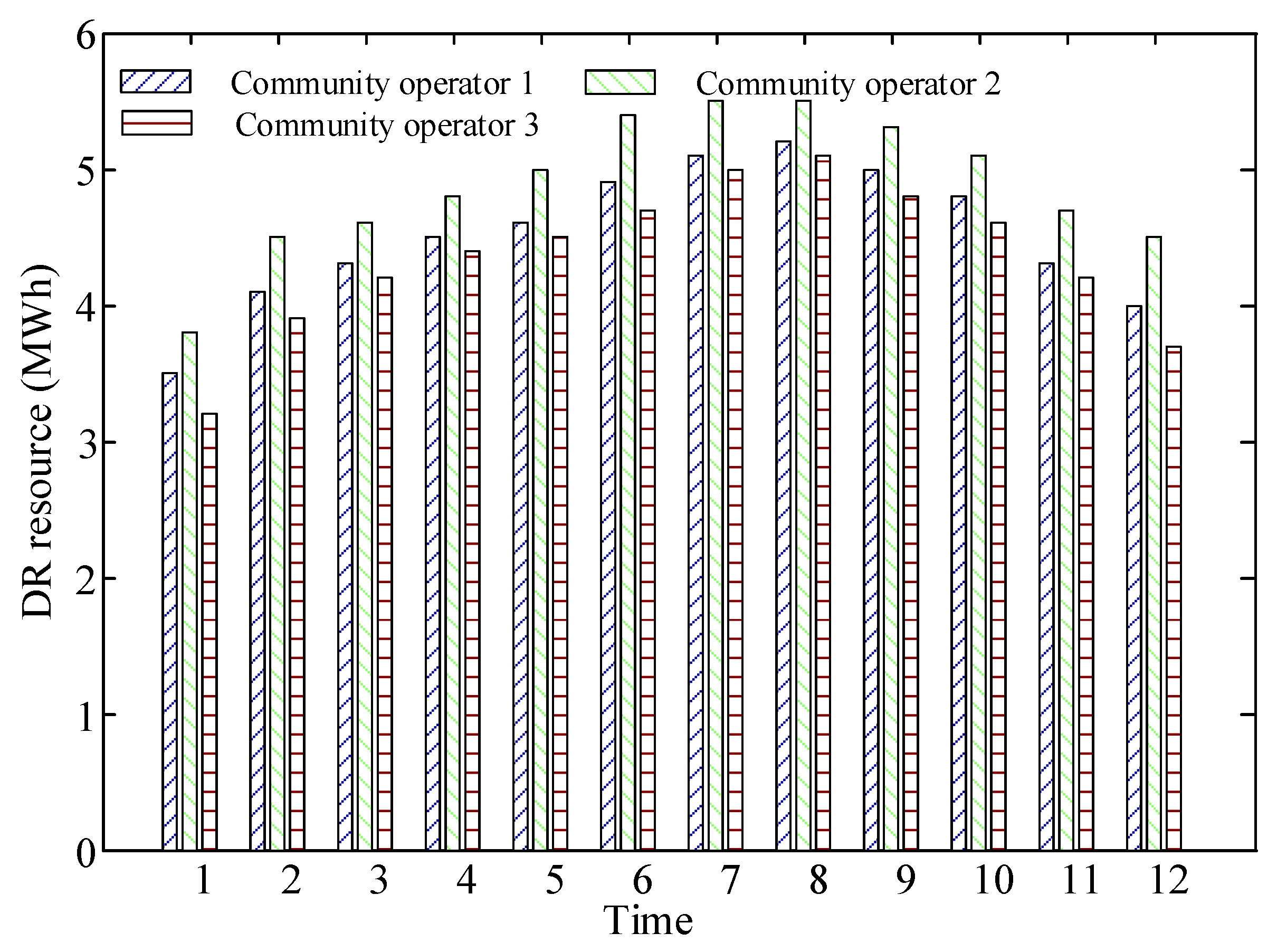
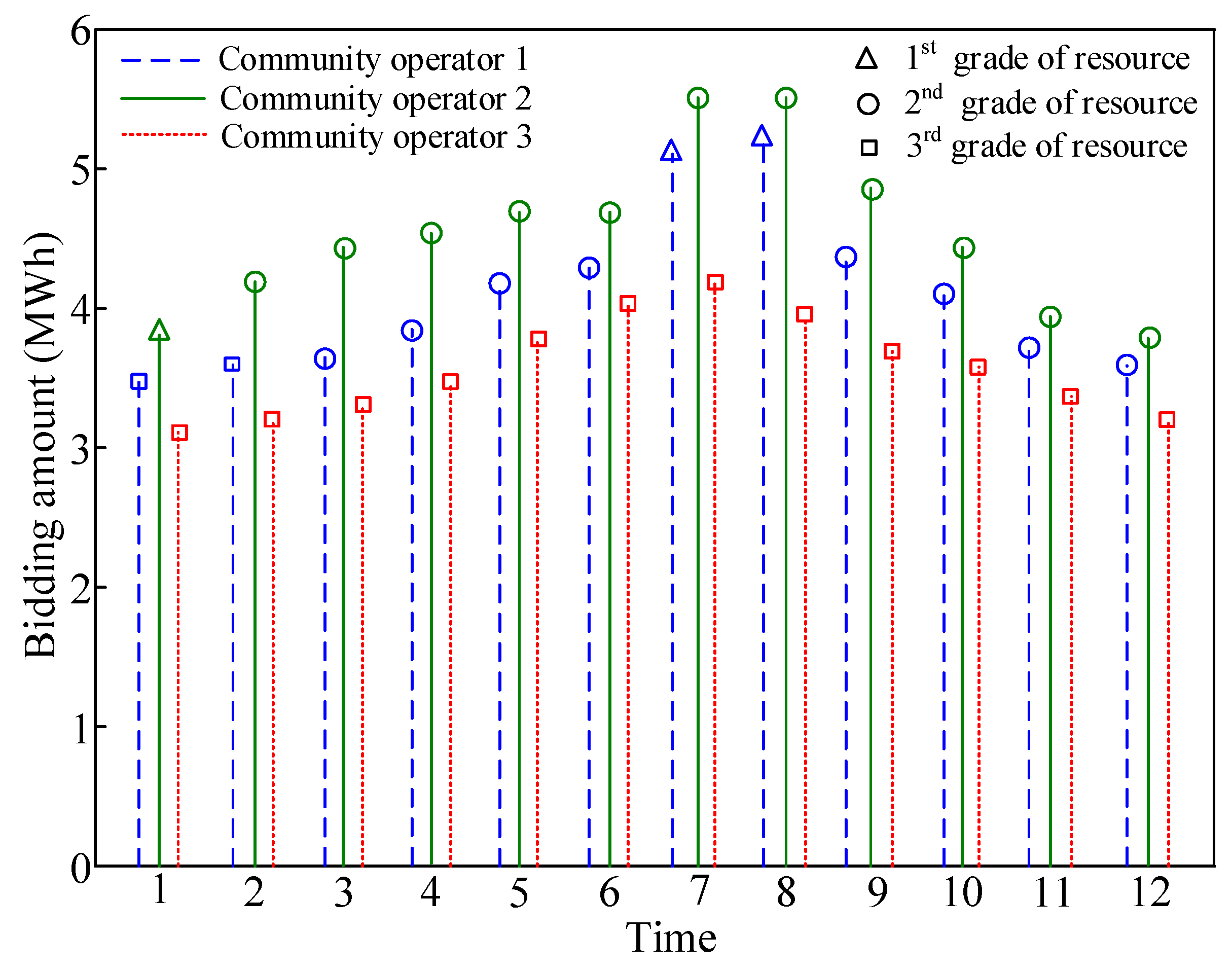
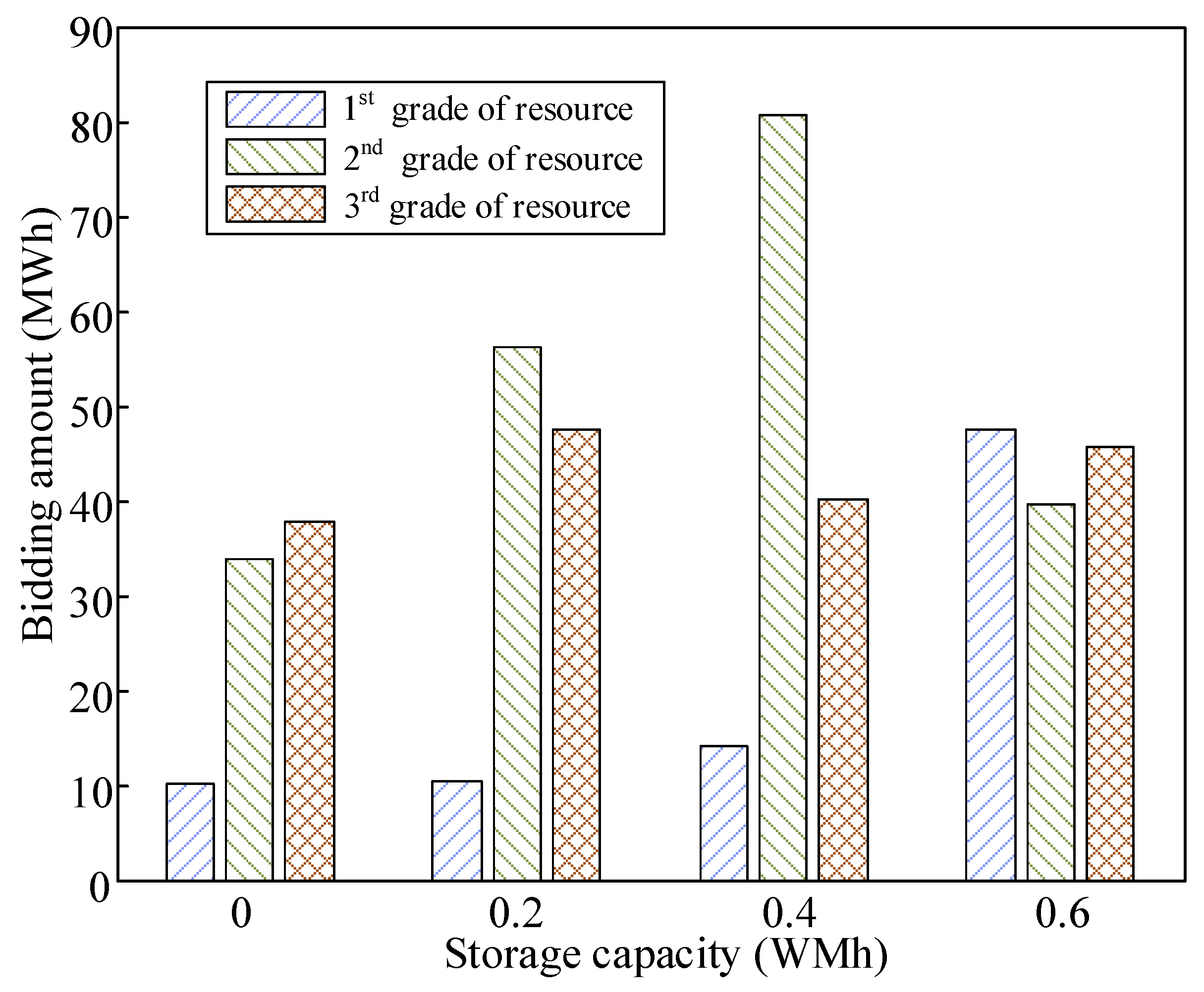
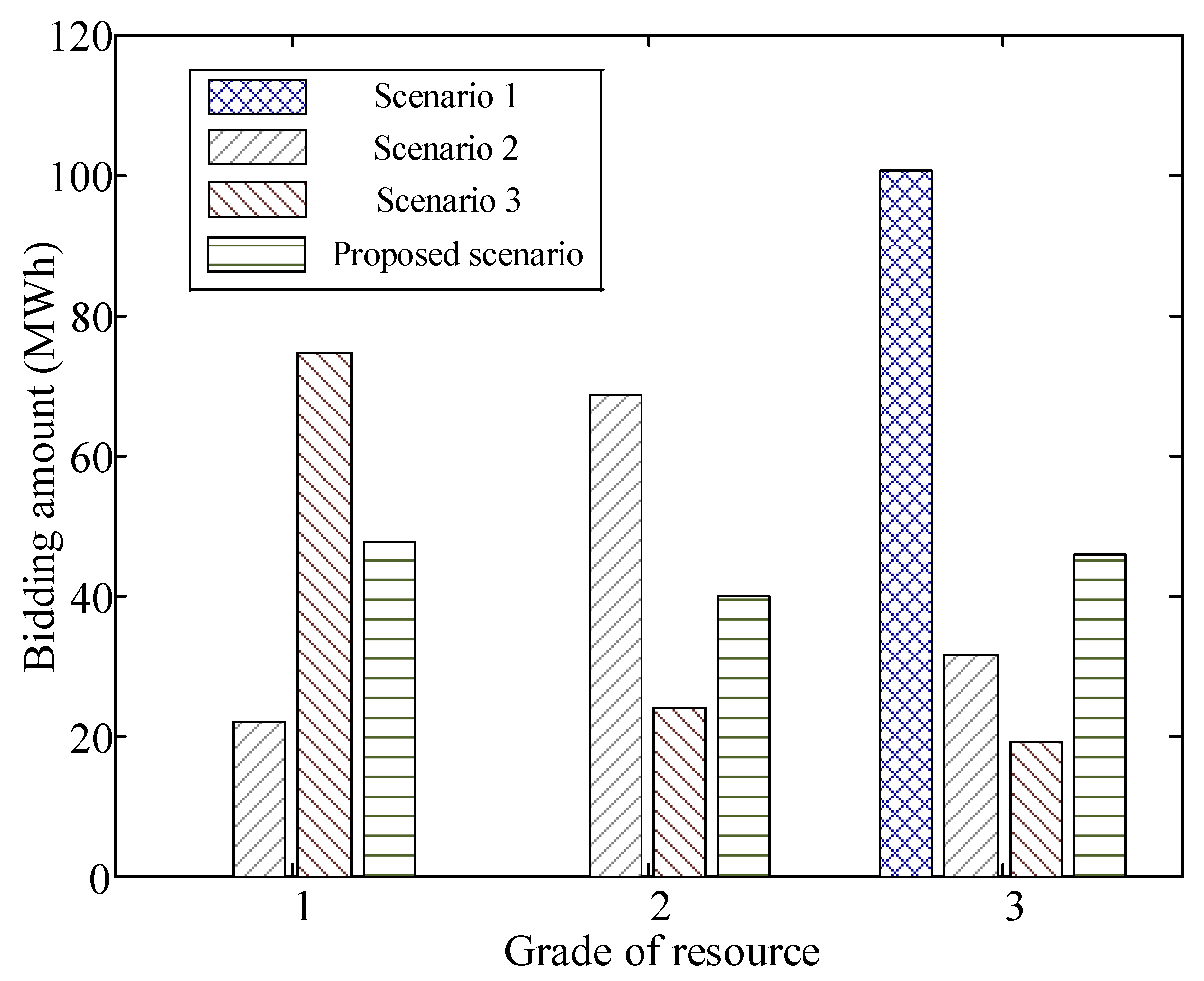
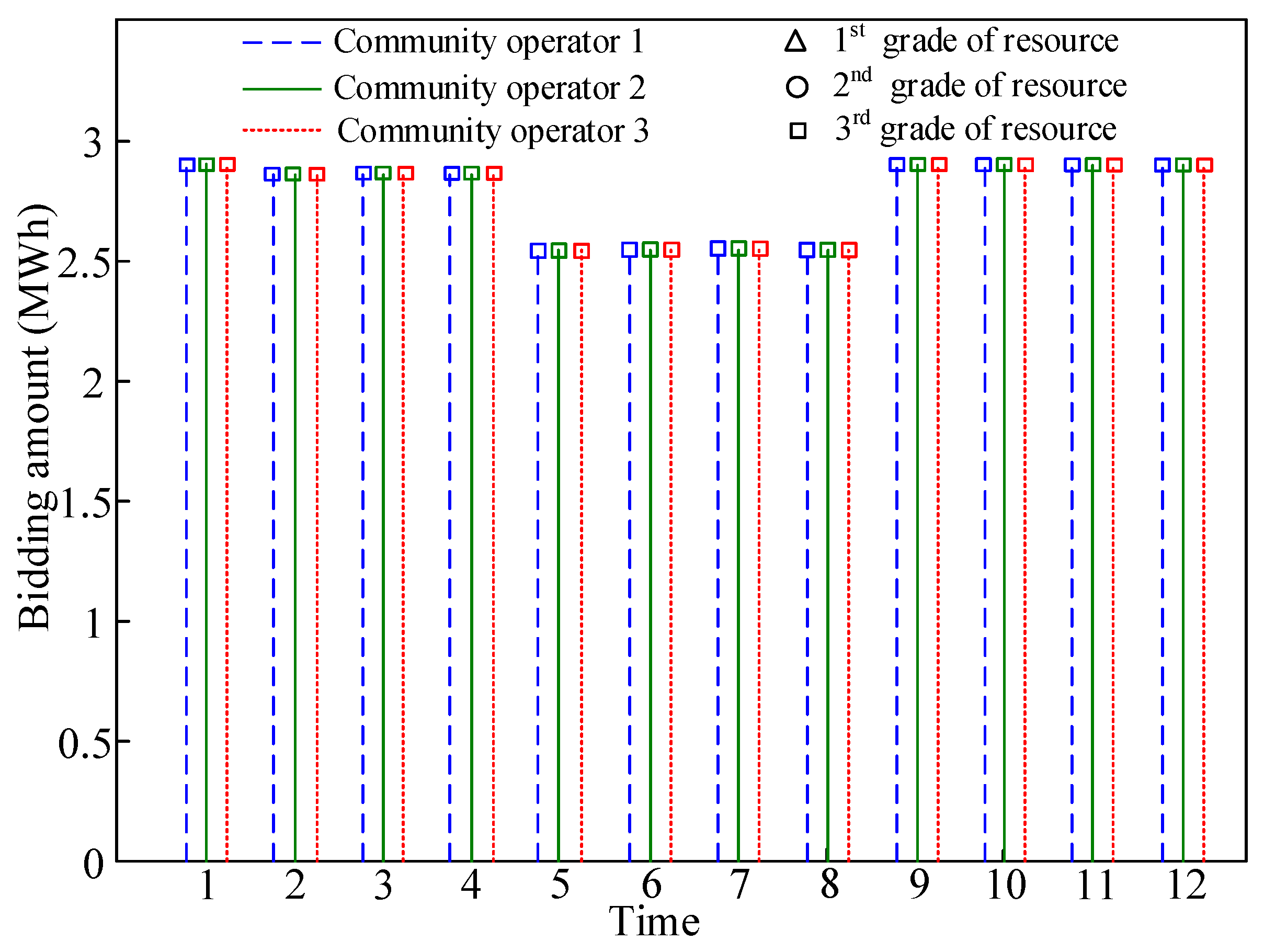
| DR Resource | 18:00–19:00 (t = 1–4) | 19:00–20:00 (t = 5–8) | 20:00–21:00 (t = 9–12) |
|---|---|---|---|
| Grade 1 | |||
| Grade 2 | |||
| Grade 3 | |||
| Community Operator | Operator 1 | Operator 2 | Operator 3 |
|---|---|---|---|
| Profit from DR purchaser | 31.54 | 36.41 | 9.97 |
| Profit from gas boiler | 1.23 | 0 | 0 |
| Profit from energy storage | 0 | −0.63 | 0 |
| Total profit | 32.77 | 35.78 | 9.97 |
| Community Operator | Operator 1 | Operator 2 | Operator 3 |
|---|---|---|---|
| Scenario 1 | 3.55 | 3.55 | 3.55 |
| Scenario 2 | 29.68 | 31.27 | 28.93 |
| Scenario 3 | 31.67 | 33.10 | 30.78 |
| Proposed scenario | 38.34 | 43.69 | 8.28 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Gao, B.; Li, Y. Bayesian Game-Theoretic Bidding Optimization for Aggregators Considering the Breach of Demand Response Resource. Appl. Sci. 2019, 9, 576. https://doi.org/10.3390/app9030576
Liu X, Gao B, Li Y. Bayesian Game-Theoretic Bidding Optimization for Aggregators Considering the Breach of Demand Response Resource. Applied Sciences. 2019; 9(3):576. https://doi.org/10.3390/app9030576
Chicago/Turabian StyleLiu, Xiaofeng, Bingtuan Gao, and Yuanmei Li. 2019. "Bayesian Game-Theoretic Bidding Optimization for Aggregators Considering the Breach of Demand Response Resource" Applied Sciences 9, no. 3: 576. https://doi.org/10.3390/app9030576
APA StyleLiu, X., Gao, B., & Li, Y. (2019). Bayesian Game-Theoretic Bidding Optimization for Aggregators Considering the Breach of Demand Response Resource. Applied Sciences, 9(3), 576. https://doi.org/10.3390/app9030576





