Kinetics of a Phonon-Mediated Laser-Driven Structural Phase Transition in Sn2P2Se6
Abstract
:1. Introduction
2. Materials and Methods
3. Results
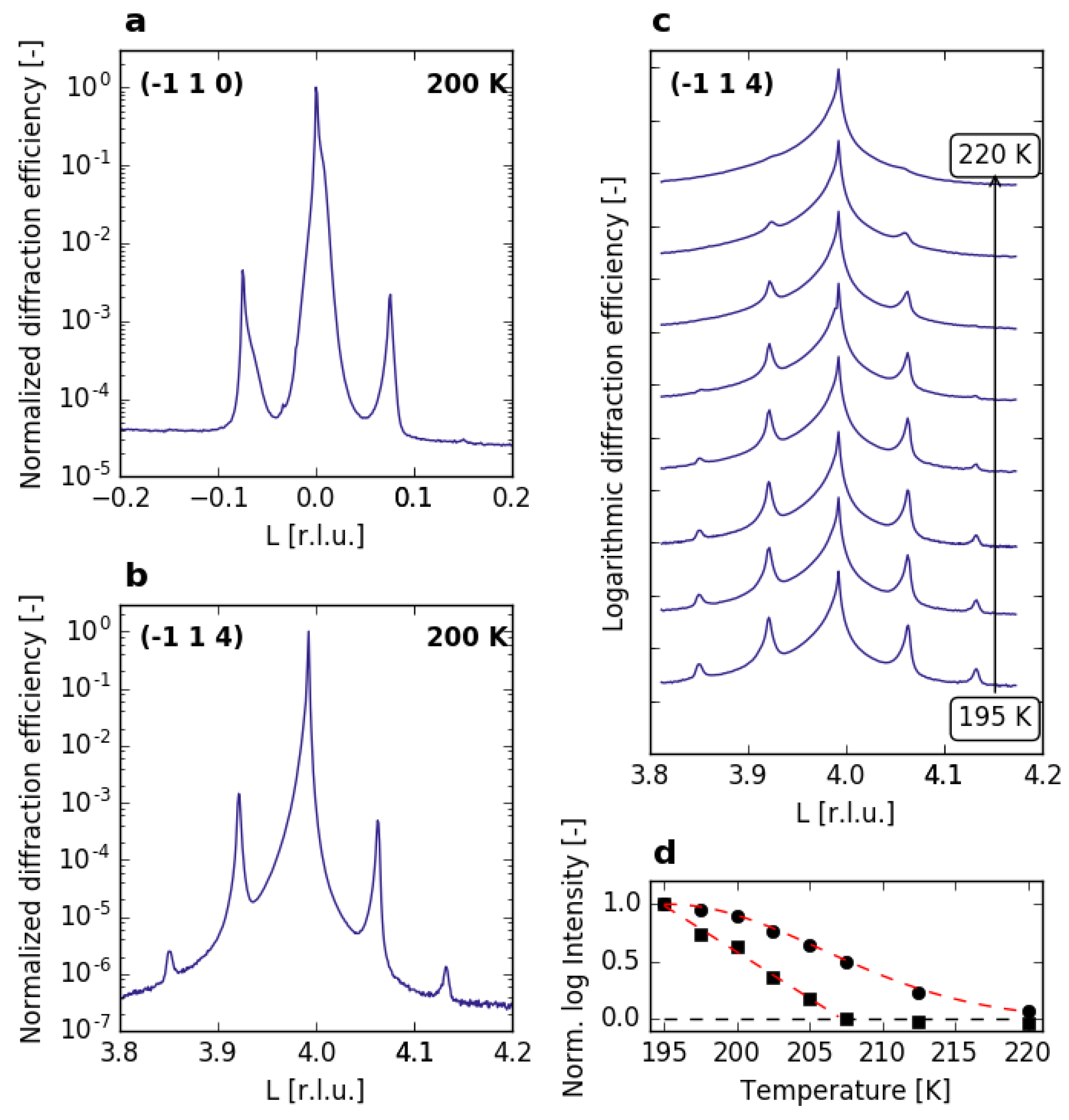
3.1. Equilibrium Structure of SnPSe
3.2. Time-Resolved Experiments
4. Discussion
4.1. Equilibrium Structure
4.2. Time-Dependent Response
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cowley, R. Structural phase transitions I. Landau theory. Adv. Phys. 1980, 29, 1–110. [Google Scholar] [CrossRef]
- Johnson, S.L.; Savoini, M.; Beaud, P.; Ingold, G.; Staub, U.; Carbone, F.; Castiglioni, L.; Hengsberger, M.; Osterwalder, J. Watching ultrafast responses of structure and magnetism in condensed matter with momentum-resolved probes. Struct. Dyn. 2017, 4, 061506–061526. [Google Scholar] [CrossRef] [PubMed]
- Buzzi, M.; Först, M.; Mankowsky, R.; Cavalleri, A. Probing dynamics in quantum materials with femtosecond X-rays. Nat. Rev. Mater. 2018, 3, 299–311. [Google Scholar] [CrossRef]
- Koopmans, B.; Malinowski, G.; Dalla Longa, F.; Steiauf, D.; Fähnle, M.; Roth, T.; Cinchetti, M.; Aeschlimann, M. Explaining the paradoxical diversity of ultrafast laser-induced demagnetization. Nat. Mater. 2010, 9, 259–265. [Google Scholar] [CrossRef] [PubMed]
- Beaud, P.; Caviezel, A.; Mariager, S.O.; Rettig, L.; Ingold, G.; Dornes, C.; Huang, S.W.; Johnson, J.A.; Radovic, M.; Huber, T.; et al. A time-dependent order parameter for ultrafast photoinduced phase transitions. Nat. Mater. 2014, 13, 923–927. [Google Scholar] [CrossRef]
- Porer, M.; Fechner, M.; Bothschafter, E.M.; Rettig, L.; Savoini, M.; Esposito, V.; Rittmann, J.; Kubli, M.; Neugebauer, M.J.; Abreu, E.; et al. Ultrafast Relaxation Dynamics of the Antiferrodistortive Phase in Ca Doped SrTiO3. Phys. Rev. Lett. 2018, 121, 55701. [Google Scholar] [CrossRef]
- Israël, R.; de Gelder, R.; Smits, J.M.M.; Beurskens, P.T.; Eijt, S.W.H.; Rasing, T.; van Kempen, H.; Maior, M.M.; Motrija, S.F. Crystal structures of di-tin-hexa(seleno)hypodiphosphate, Sn2P2Se6, in the ferroelectric and paraelectric phase. Z. Kristallog. Cryst. Mater. 1998, 213, 34–41. [Google Scholar] [CrossRef]
- Blinc, R.; Z̆eks̆, B.; Prelovs̆ek, P.; Levstik, A.; Filipic̆, C.; Carlsson, T.; Mus̆evic̆, I. Incommensurate-Commensurate Transitions in Solid and Liquid Crystalline Ferroelectrics in External Fields. Jpn. J. Appl. Phys. 1985, 24, 65–69. [Google Scholar] [CrossRef]
- Shiozaki, Y. Satellite X-ray scattering and structural modulation of thiourea. Ferroelectrics 1971, 2, 245–260. [Google Scholar] [CrossRef]
- McKenzie, D.R. The antiferroelectric transition in thiourea studied by thermal neutron scattering. J. Phys. C Solid State Phys. 1975, 8, 1607–1619. [Google Scholar] [CrossRef]
- Hirota, R.; Tsujimoto, S. Conserved Quantities of a Class of Nonlinear Difference-Difference Equations. J. Phys. Soc. Jpn. 1995, 64, 3125–3127. [Google Scholar] [CrossRef]
- Moriya, K.; Yamada, T.; Sakai, K.; Yano, S.; Baluja, S.; Matsuo, T.; Pritz, I.; Vysochanskii, Y.M. Ferroelectric phase transitions in Pb2xSn2(1−x)P2Se6 system. J. Therm. Anal. Calorim. 2002, 70, 321–328. [Google Scholar] [CrossRef]
- Enjalbert, R.; Galy, J.; Vysochanskii, Y.M.; Ouedraogo, A.; Saint-Gregoire, P. Structural study of the ferroelectric instability in Sn2P2Se6. Eur. Phys. J. B 1999, 5, 169–177. [Google Scholar] [CrossRef]
- van Loosdrecht, P.H.M.; Maior, M.M.; Molnar, S.B.; Vysochanskii, Y.M.; van Bentum, P.J.M.; van Kempen, H. Raman study of the ferroelectric semiconductor Sn2P2Se6. Phys. Rev. B 1993, 48, 6014–6018. [Google Scholar] [CrossRef]
- Eijt, S.W.H.; Maior, M. Raman and infrared hard mode spectroscopy of the internal vibrations in Sn2P2Se6. J. Phys. Chem. Solids 1999, 60, 631–643. [Google Scholar] [CrossRef]
- Eijt, S.W.H.; Currat, R.; Lorenzo, J.E. Soft modes and phonon interactions in Sn2P2S6 studied by neutron scattering. Eur. Phys. J. B 1998, 178, 169–178. [Google Scholar] [CrossRef]
- Eijt, S.W.H.; Currat, R.; Lorenzo, J.E.; Katano, S.; Saint-Gregoire, P.; Hennion, B.; Vysochanskii, Y.M. Soft mode behaviour of incommensurate Sn2P2Se6: An inelastic neutron scattering study. Ferroelectrics 1997, 202, 121–129. [Google Scholar] [CrossRef]
- Vysochanskii, Y.M.; Drobnich, A.V. Lattice dynamics and relaxation effects in ferroelectrics of (Sn,Pb)2P2(S,Se)6 system. Ferroelectrics 2000, 236, 105–116. [Google Scholar] [CrossRef]
- Van Benthem, K.; Elsässer, C.; French, R.H. Bulk electronic structure of SrTiO3: Experiment and theory. J. Appl. Phys. 2001, 90, 6156–6164. [Google Scholar] [CrossRef]
- Nitsche, R.; Wild, P. Crystal growth of metal-phosphorus-sulfur compounds by vapor transport. Mater. Res. Bull. 1970, 5, 419–423. [Google Scholar] [CrossRef]
- Willmott, P.R.; Meister, D.; Leake, S.J.; Lange, M.; Bergamaschi, A.; Böge, M.; Calvi, M.; Cancellieri, C.; Casati, N.; Cervellino, A.; et al. The Materials Science beamline upgrade at the Swiss Light Source. J. Synchrotron Radiat. 2013, 20, 667–682. [Google Scholar] [CrossRef] [PubMed]
- Kraft, P.; Bergamaschi, A.; Broennimann, C.; Dinapoli, R.; Eikenberry, E.F.; Henrich, B.; Johnson, I.; Mozzanica, A.; Schlepütz, C.M.; Willmott, P.R.; et al. Performance of single-photon-counting PILATUS detector modules. J. Synchrotron Radiat. 2009, 16, 368–375. [Google Scholar] [CrossRef]
- Beaud, P.; Johnson, S.L.; Streun, A.; Abela, R.; Abramsohn, D.; Grolimund, D.; Krasniqi, F.; Schmidt, T.; Schlott, V.; Ingold, G. Spatiotemporal stability of a femtosecond hard-X-ray undulator source studied by control of coherent optical phonons. Phys. Rev. Lett. 2007, 99, 174801. [Google Scholar] [CrossRef] [PubMed]
- Yabashi, M.; Tanaka, H.; Ishikawa, T. Overview of the SACLA facility. J. Synchrotron Radiat. 2015, 22, 477–484. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat. Photonics 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Tono, K.; Togashi, T.; Inubushi, Y.; Sato, T.; Katayama, T.; Ogawa, K.; Ohashi, H.; Kimura, H.; Takahashi, S.; Takeshita, K.; et al. Beamline, experimental stations and photon beam diagnostics for the hard X-ray free electron laser of SACLA. New J. Phys. 2013, 15, 083035. [Google Scholar] [CrossRef]
- Henke, B.; Gullikson, E.; Davis, J. X-Ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50–30,000 eV, Z = 1–92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Lipavičius, J.; Čijauskas, E.; Audzijonis, A. The Fundamental Absorption Edge Tail of Sn2P2Se6. Phys. Status Solidi B 1988, 148, K97–K100. [Google Scholar] [CrossRef]
- Li, Y.; Singh, D.J. Properties of the ferroelectric visible light absorbing semiconductors: Sn2P2S6 and Sn2P2Se6. Phys. Rev. Mater. 2017, 1, 075402. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- Johnson, S.L.; Beaud, P.; Milne, C.J.; Krasniqi, F.S.; Zijlstra, E.S.; Garcia, M.E.; Kaiser, M.; Grolimund, D.; Abela, R.; Ingold, G. Nanoscale depth-resolved coherent femtosecond motion in laser-excited bismuth. Phys. Rev. Lett. 2008, 100, 155501. [Google Scholar] [CrossRef]
- Barsamian, T.K.; Khasanov, S.S.; Shekhtman, V.S. Diffraction analysis of incommensurate phases in crystals of quasi-binary system Sn2P2(S1−xSex)6. Ferroelectrics 1993, 138, 63–77. [Google Scholar] [CrossRef]
- Barsamian, T.K.; Khasanov, S.S.; Shekhtman, V.S.; Vysochanskii, Y.M.; Slivka, V.Y. Incommensurate phase in proper ferroelectric Sn2P2Se6. Ferroelectrics 1986, 67, 47–54. [Google Scholar] [CrossRef]
- Yamamoto, A. Modulated structure of thiourea [SC(NH2)2]. Phys. Rev. B 1980, 22, 373–379. [Google Scholar] [CrossRef]
- Bruce, A.D.; Cowley, R.A.; Murray, A.F. The theory of structurally incommensurate systems. II. Commensurate-incommensurate phase transitions. J. Phys. C Solid State Phys. 1978, 11, 3591–3608. [Google Scholar] [CrossRef]
- Moriya, K.; Kuniyoshi, H.; Tashita, K.; Ozaki, Y.; Yano, S.; Matsuo, T. Ferroelectric Phase Transitions in Sn2P2S6 and Sn2P2Se6 Crystals. J. Phys. Soc. Jpn. 1998, 67, 3505–3511. [Google Scholar] [CrossRef]
- Maior, M.M.; van Loosdrecht, P.H.M.; van Kempen, H.; Rasing, T.; Molnar, S.B.; Motrij, S.F. Fluctuation effects on the thermal expansion of the incommensurate crystal Sn2P2Se6. J. Phys. Condens. Matter 1993, 5, 6023–6028. [Google Scholar] [CrossRef]
- Valyavichyus, V.D.; Samulenis, V.I.; Vysochanskii, Y.M.; Maior, M.M.; Gurzan, M.I. Ultrasound velocity and attenuation in Sn2P2Se6 ferroelectric with incommensurate phase. Sov. Phys. Solid State 1989, 31, 1180. [Google Scholar]
- Johnson, J.A.; Maznev, A.A.; Cuffe, J.; Eliason, J.K.; Minnich, A.J.; Kehoe, T.; Torres, C.M.; Chen, G.; Nelson, K.A. Direct measurement of room-temperature nondiffusive thermal transport over micron distances in a silicon membrane. Phys. Rev. Lett. 2013, 110, 025901. [Google Scholar] [CrossRef]
- Van Der Veen, J.F.; Frenken, J.W.M. Dynamics and melting of surfaces. Surf. Sci. 1986, 178, 382–395. [Google Scholar] [CrossRef]
- Cummins, H.Z. Experimental studies of structurally incommensurate crystal phases. Phys. Rep. 1990, 185, 211–409. [Google Scholar] [CrossRef]
- Mashiyama, H.; Kasatani, H. Relaxation of the Modulated Structure near the Lock-in Transition in K2ZnCl4. Jpn. J. Appl. Phys. 1985, 24, 802–804. [Google Scholar] [CrossRef]

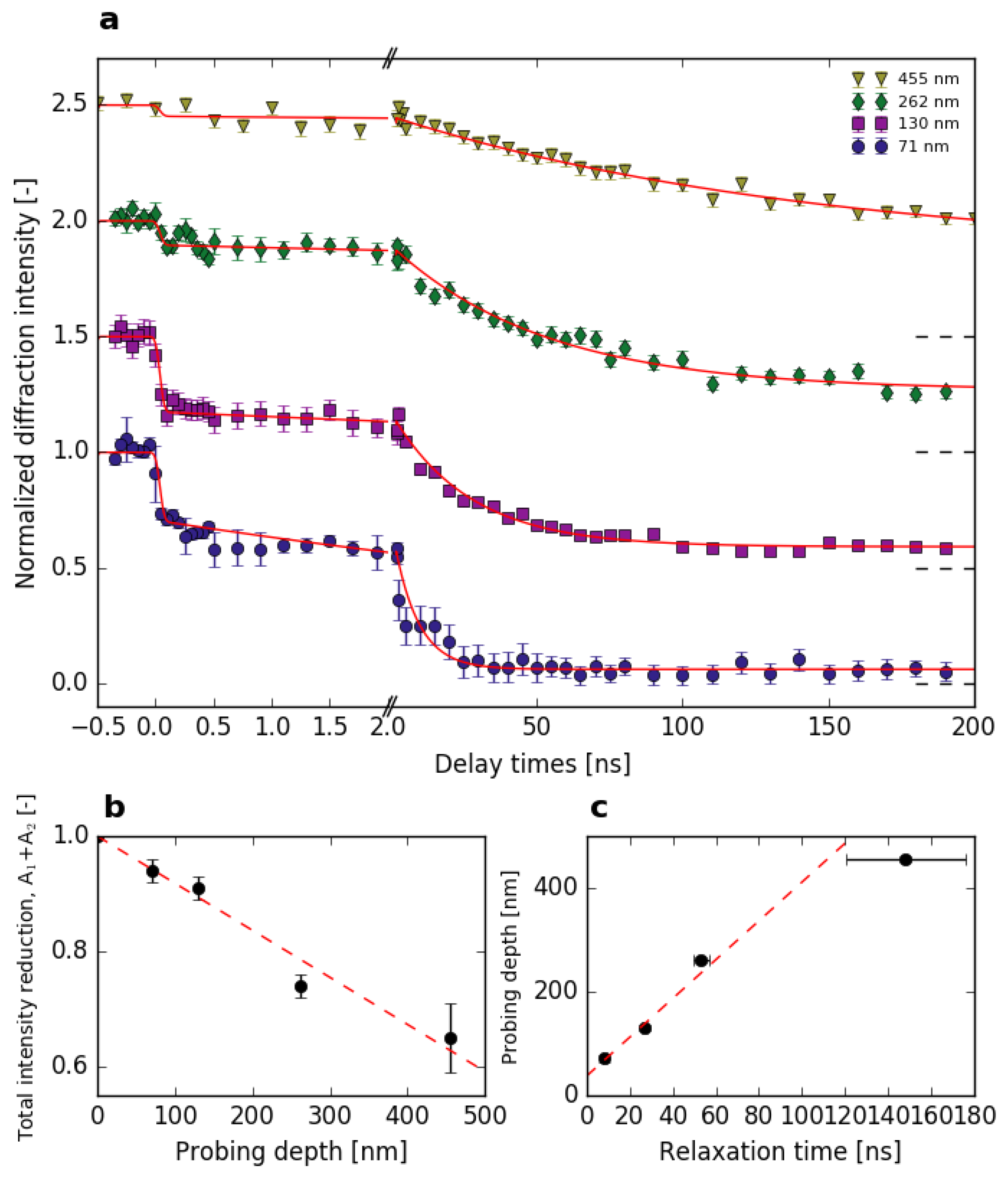
| Fluence | Probing Depth | |||
|---|---|---|---|---|
| [mJ/cm] | [nm] | [-] | [-] | [ns] |
| 3.5 | 71 | 0.30 ± 0.01 | 0.64 ± 0.01 | 8.25 ± 0.94 |
| 3.5 | 130 | 0.33 ± 0.01 | 0.58 ± 0.01 | 26.74 ± 1.21 |
| 3.5 | 262 | 0.11 ± 0.01 | 0.63 ± 0.02 | 53.04 ± 3.73 |
| 3.5 | 455 | 0.05 ± 0.01 | 0.60 ± 0.06 | 148.1 ± 27.7 |
| 1.0 | 130 | 0.08 ± 0.02 | 0.47 ± 0.02 | 11.59 ± 2.07 |
| 2.0 | 130 | 0.16 ± 0.01 | 0.60 ± 0.01 | 15.90 ± 1.89 |
| 3.5 | 130 | 0.33 ± 0.01 | 0.58 ± 0.01 | 26.74 ± 1.21 |
| 7.0 | 130 | 0.33 ± 0.02 | 0.61 ± 0.02 | 20.75 ± 2.42 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubli, M.; Savoini, M.; Abreu, E.; Burganov, B.; Lantz, G.; Huber, L.; Neugebauer, M.J.; Boie, L.; Esposito, V.; Bothschafter, E.M.; et al. Kinetics of a Phonon-Mediated Laser-Driven Structural Phase Transition in Sn2P2Se6. Appl. Sci. 2019, 9, 525. https://doi.org/10.3390/app9030525
Kubli M, Savoini M, Abreu E, Burganov B, Lantz G, Huber L, Neugebauer MJ, Boie L, Esposito V, Bothschafter EM, et al. Kinetics of a Phonon-Mediated Laser-Driven Structural Phase Transition in Sn2P2Se6. Applied Sciences. 2019; 9(3):525. https://doi.org/10.3390/app9030525
Chicago/Turabian StyleKubli, Martin, Matteo Savoini, Elsa Abreu, Bulat Burganov, Gabriel Lantz, Lucas Huber, Martin J. Neugebauer, Larissa Boie, Vincent Esposito, Elisabeth M. Bothschafter, and et al. 2019. "Kinetics of a Phonon-Mediated Laser-Driven Structural Phase Transition in Sn2P2Se6" Applied Sciences 9, no. 3: 525. https://doi.org/10.3390/app9030525
APA StyleKubli, M., Savoini, M., Abreu, E., Burganov, B., Lantz, G., Huber, L., Neugebauer, M. J., Boie, L., Esposito, V., Bothschafter, E. M., Parchenko, S., Grübel, S., Porer, M., Rittmann, J., Beaud, P., Staub, U., Yabashi, M., Tanaka, Y., Katayama, T., ... Johnson, S. L. (2019). Kinetics of a Phonon-Mediated Laser-Driven Structural Phase Transition in Sn2P2Se6. Applied Sciences, 9(3), 525. https://doi.org/10.3390/app9030525





