A Real-Time BOD Estimation Method in Wastewater Treatment Process Based on an Optimized Extreme Learning Machine
Abstract
:1. Introduction
2. Materials and Methods
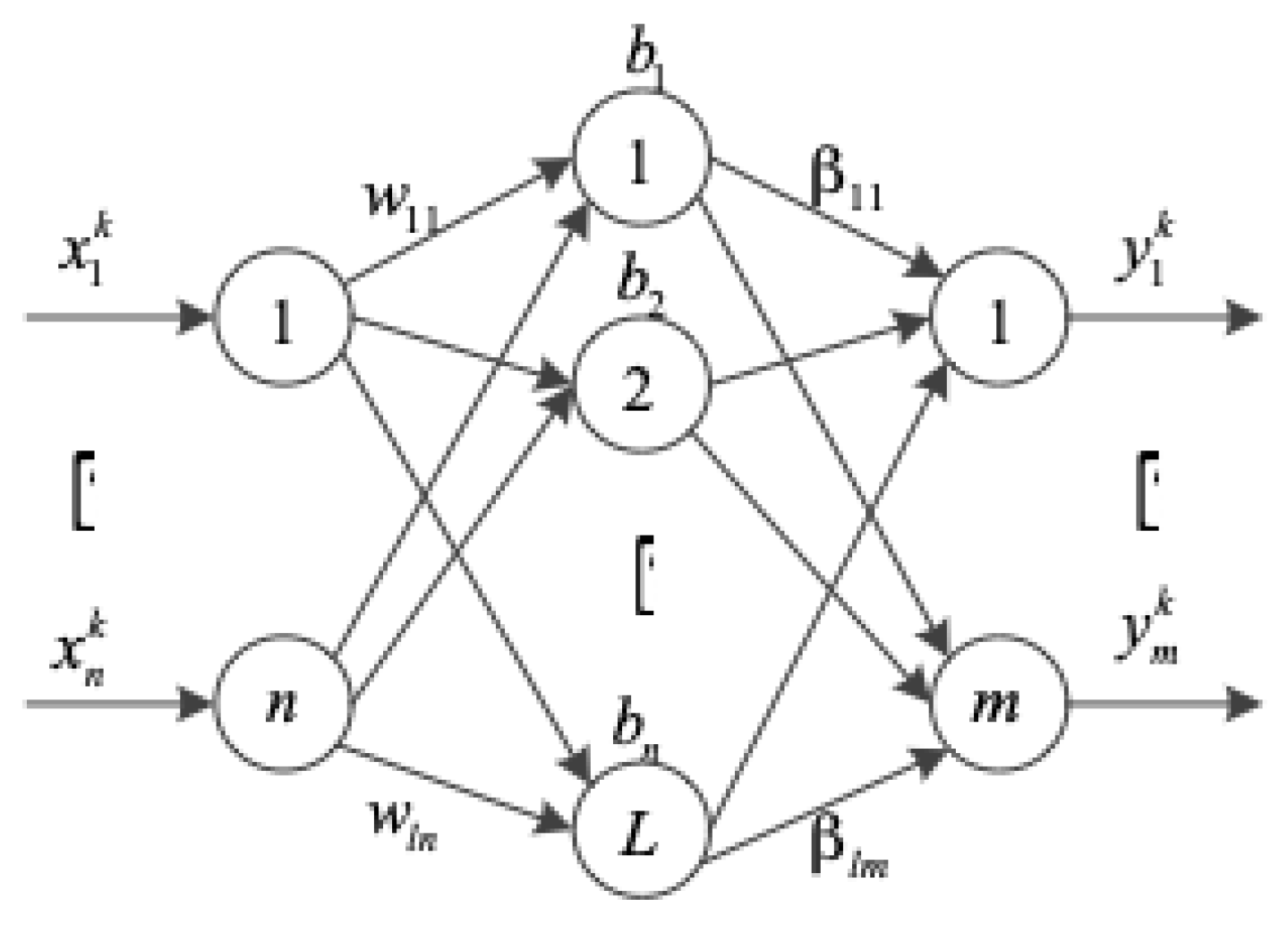
2.1. Extreme Learning Machine
2.2. Improved Cuckoo Search Algorithm-Based ELM (ICS-ELM)
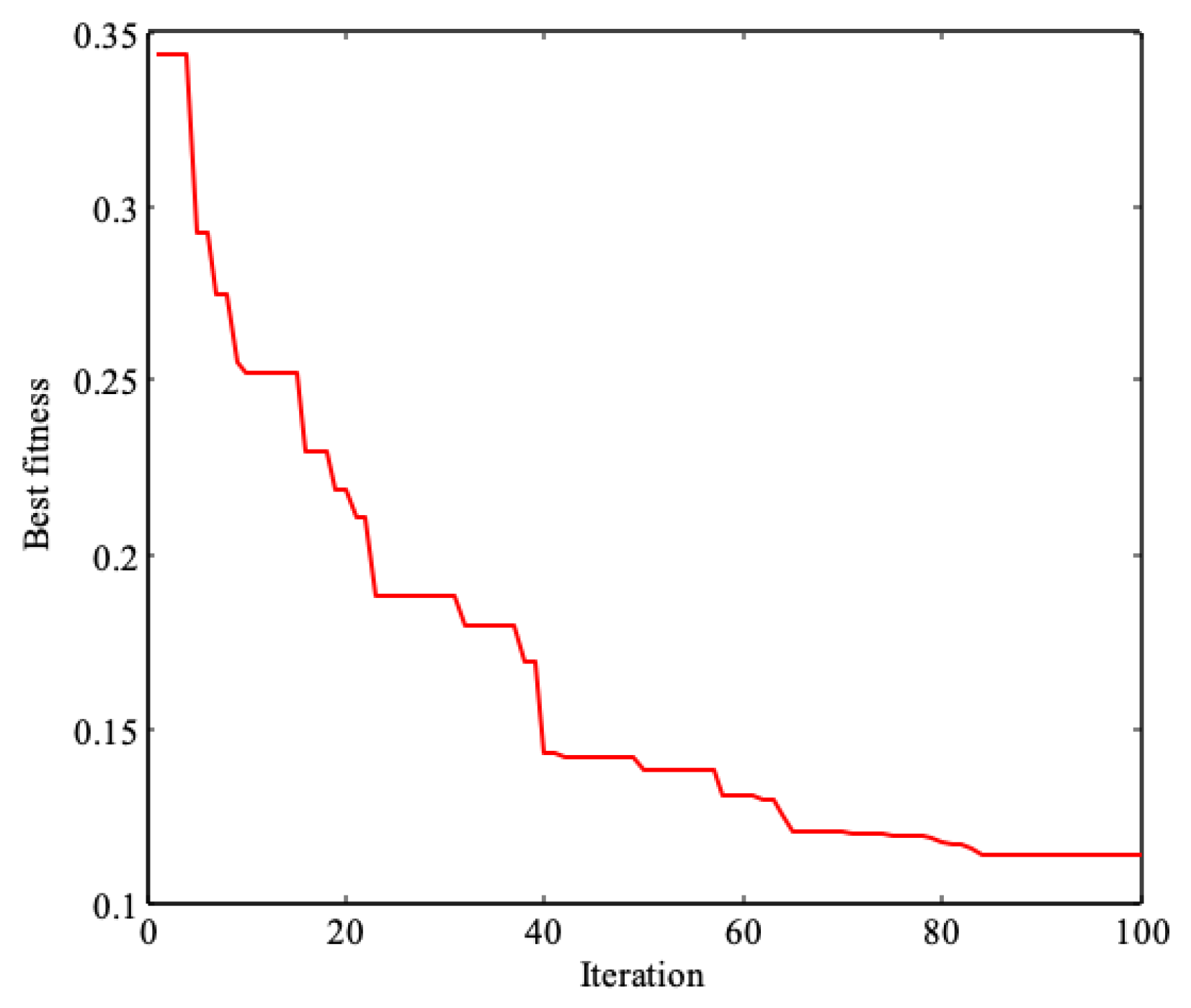
2.2.1. Improved Cuckoo Search (ICS) Algorithm
2.2.2. ICS-Based ELM
2.3. Experimental Data Processing
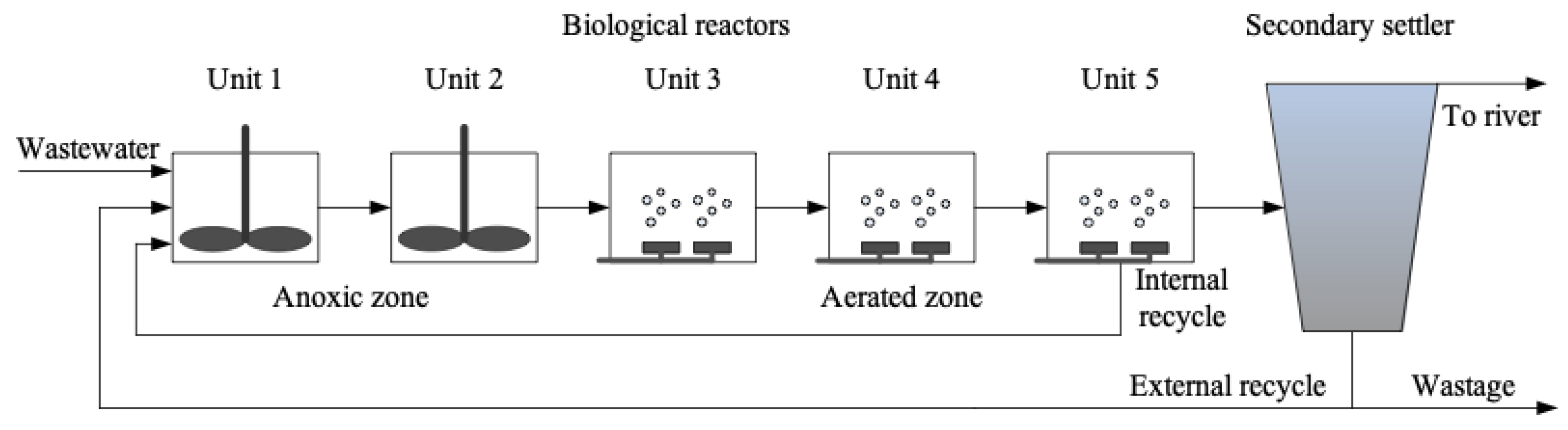
2.3.1. Acquisition of Experimental Data from Benchmark Simulation Model No. 1 (BSM1)
2.3.2. Fuzzy Rough Monotone Dependence Algorithm for Data Processing
3. Results and Discussion
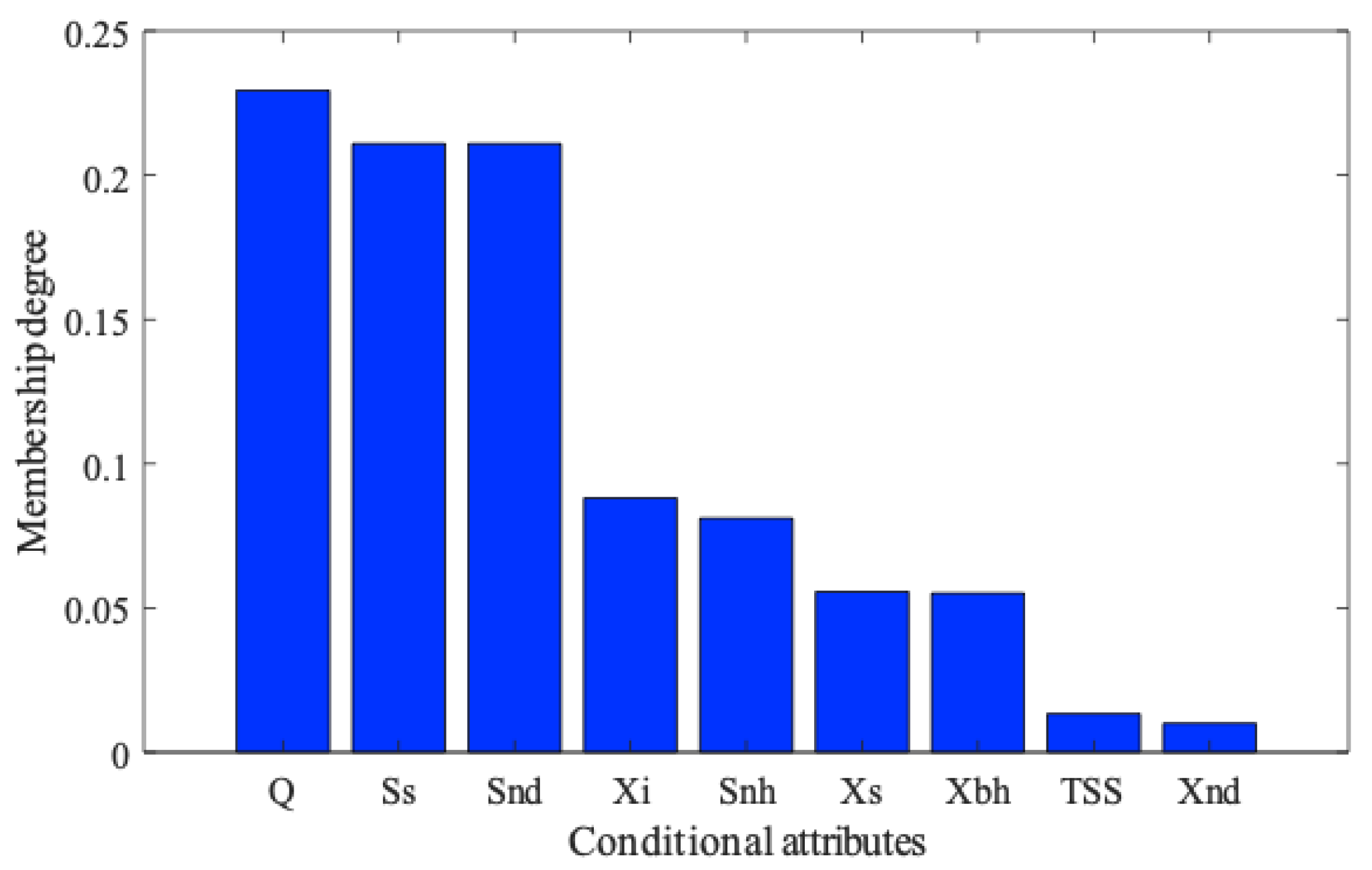
3.1. Data Attribute Reduction
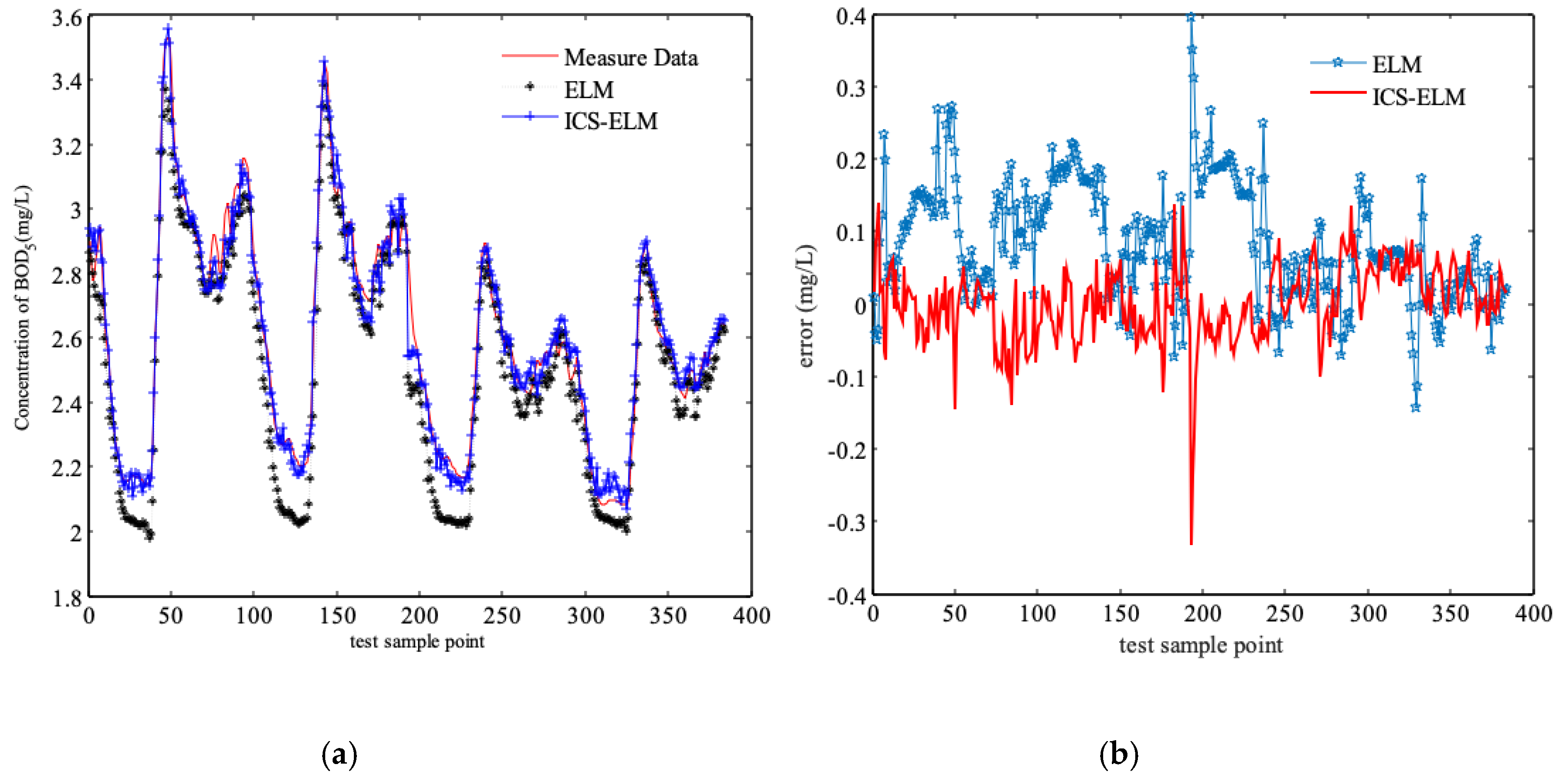
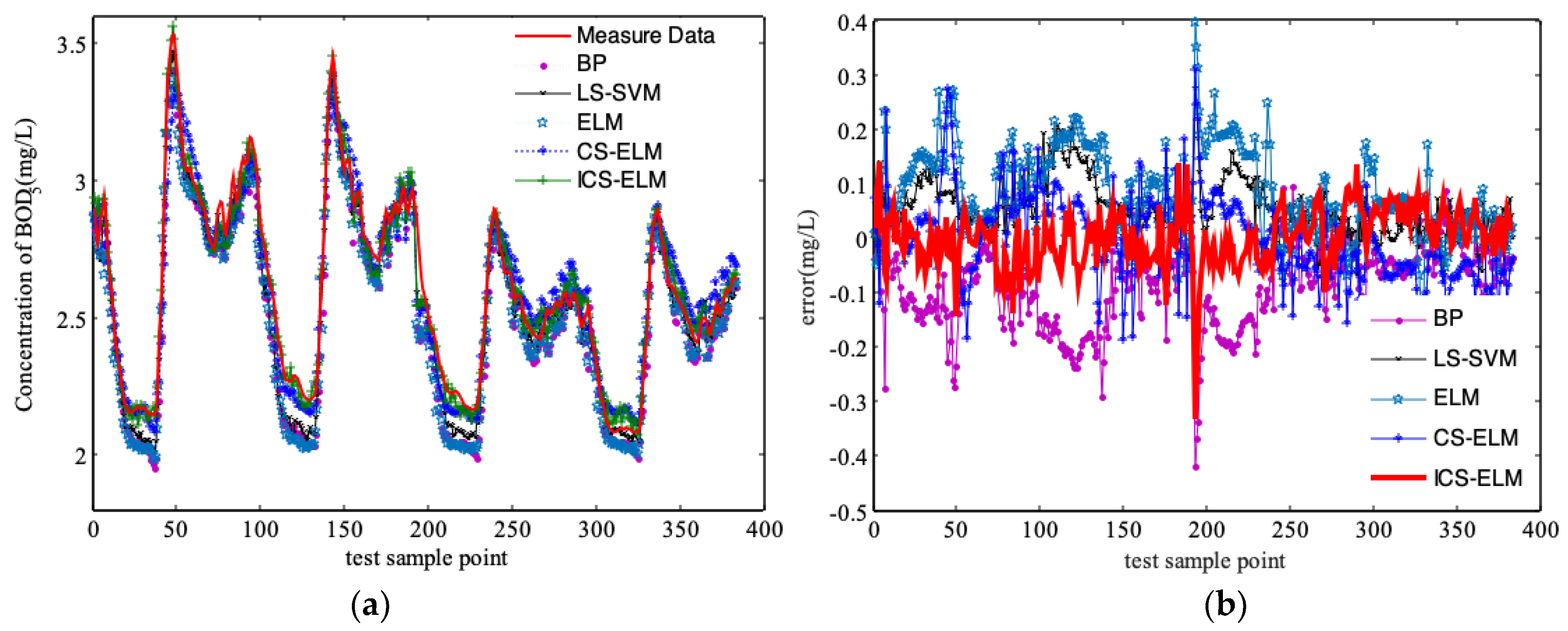
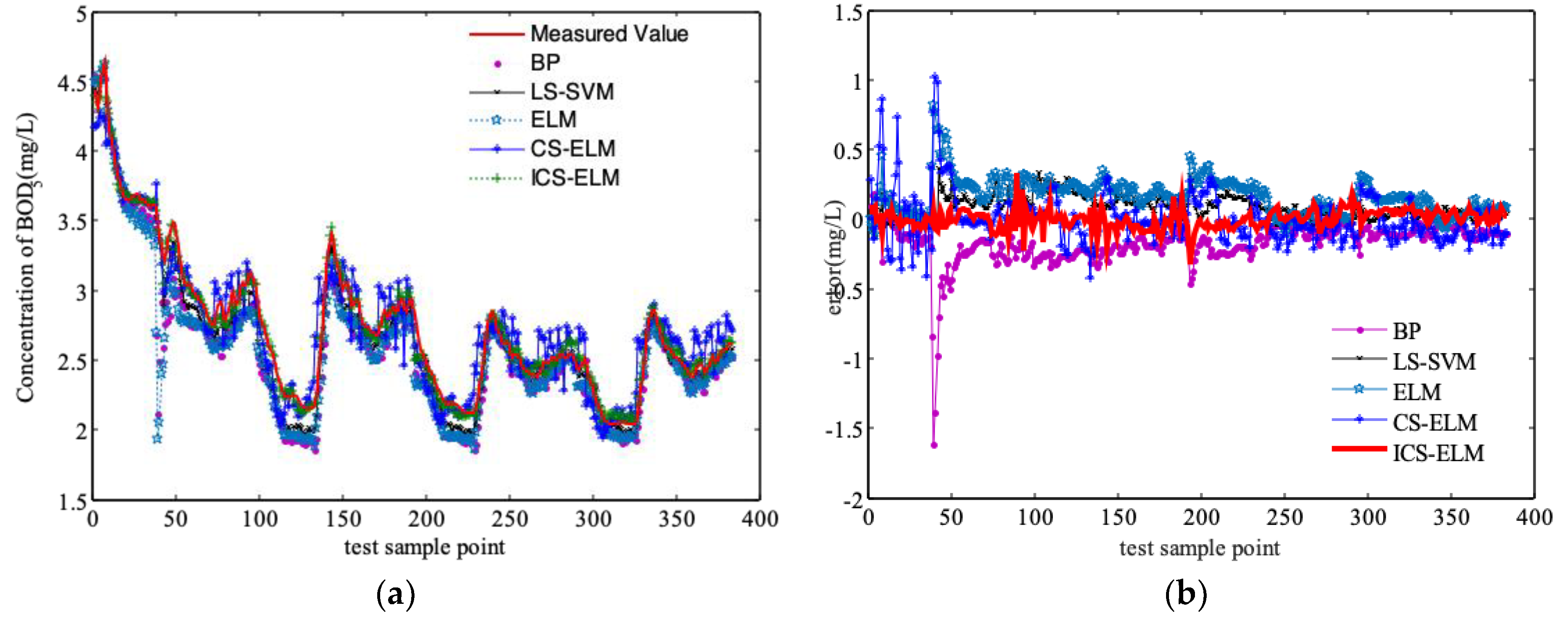
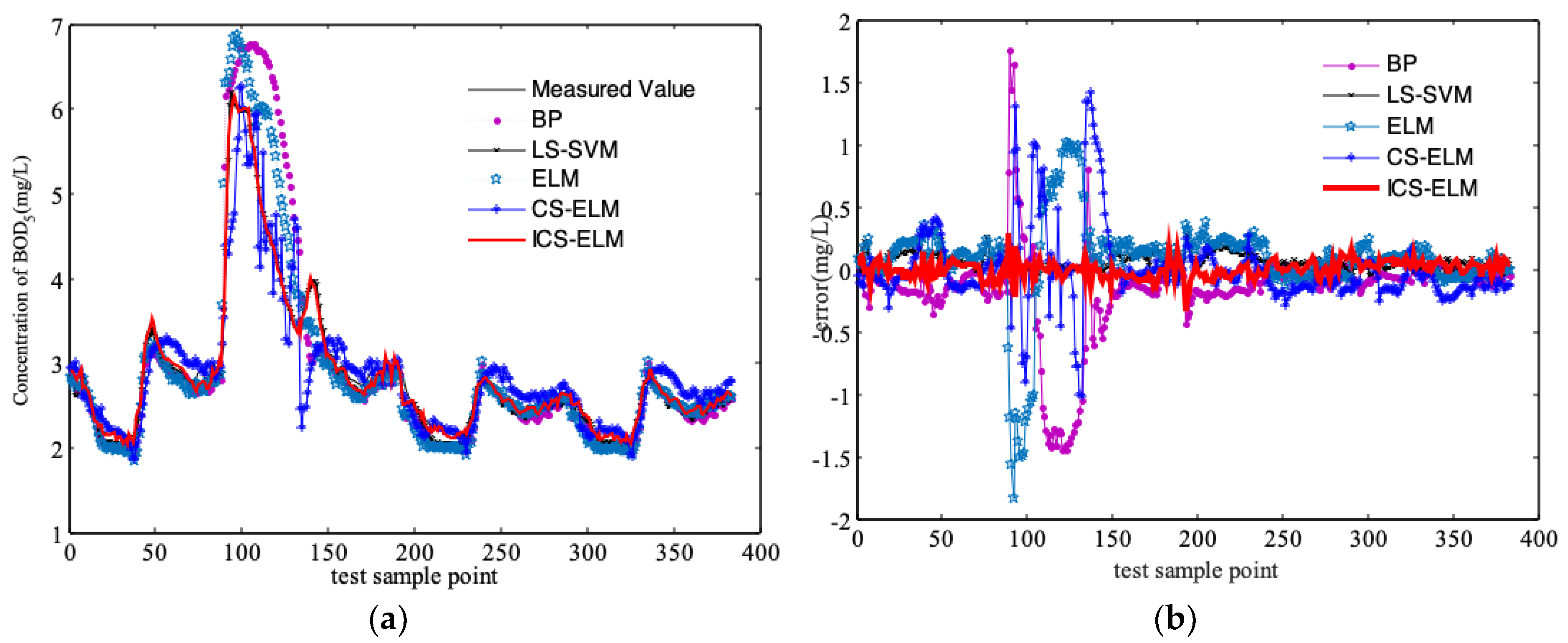
3.2. Comparison and Discussion of Simulation Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dellana, S.A.; West, D. Predictive modeling for wastewater applications: Linear and nonlinear approaches. Environ. Model. Softw. 2009, 24, 96–106. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y. Research advances in biosensor for rapid measurement of biochemical oxygen demand (BOD). Acta Sci. Circumstantiae 2007, 27, 1066–1082. [Google Scholar]
- Zhang, M.; Han, H.; Qiao, J. Research on dynamic feed-forward neural network structure based on growing and pruning methods. CAAI Trans. Intell. Syst. 2011, 6, 101–106. [Google Scholar]
- Qiao, J.; Ju, Y.; Han, H. BOD soft-sensing based on SONNRW. J. Beijing Univ. Technol. 2016, 42, 1451–1460. [Google Scholar]
- Liu, W. Online biochemical oxygen demand soft measurement based on echo state network. Comput. Meas. Control 2014, 22, 1351–1354. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Han, F.; Huang, D.S. Improved extreme learning machine for function approximation by encoding a priori information. Neurocomputing 2006, 69, 2369–2373. [Google Scholar] [CrossRef]
- Deng, C.; Huang, G.; Xu, J.; Tang, J. Extreme learning machines: New trends and applications. Sci. China Inf. Sci. 2015, 58, 1–16. [Google Scholar] [CrossRef]
- Wang, Y.; Di, K.; Zhang, S. Melt index prediction of polypropylene based on DBN-ELM. CIESC J. 2016, 67, 5163–5168. [Google Scholar]
- Li, R.; Wang, L. Soft Measurement modeling and chemical application based on ISOMAP-ELM neural network. Acta Metrol. Sin. 2016, 37, 548–552. [Google Scholar]
- Zhu, Q.Y.; Qin, A.K.; Suganthan, P.N.; Huang, G.B.; Patcog, J. Evolutionary extreme learning machine. Pattern Recognit. 2005, 38, 1759–1763. [Google Scholar] [CrossRef]
- Yan, D.; Chu, Y.; Zhang, H.; Liu, D. Information discriminative extreme learning machine. Soft Comput. 2018, 22, 677–689. [Google Scholar] [CrossRef]
- Kassani, P.H.; Teoh, A.; Kim, E. Sparse pseudoinverse incremental extreme learning machine. Neurocomputing 2018, 287, 128–142. [Google Scholar] [CrossRef]
- Du, X.; Wang, J.; Jegatheesan, V.; Shi, G. Parameter estimation of activated sludge process based on an improved cuckoo search algorithm. Bioresour. Technol. 2018, 249, 249–447. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Luo, F.; Xu, Y. Fuzzy rough monotone dependence algorithm based on decision table and its application. J. South China Univ. Technol. Nat. Sci. Ed. 2011, 39, 7–12. [Google Scholar]
- Alex, J.; Benedetti, L.; Copp, J. Benchmark Simulation Model No. 1 (BSM1); Technical Report; Lund University: Lund, Sweden, 2008. [Google Scholar]
- Jeppsson, U.; Pons, M.N. The COST benchmark simulation model—Current state and future perspective. Control Eng. Pract. 2004, 12, 299–304. [Google Scholar] [CrossRef]
- Huang, G.B. Learning capability and storage capacity of two hidden layer feedforward networks. IEEE Trans. Neural Netw. 2003, 14, 274–281. [Google Scholar] [CrossRef] [PubMed]
- Rao, C.R.; Mitra, S.K. Generalized Inverse of Matrices and Its Applications; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Serre, D. Matrices: Theory and Applications; Springer: New York, NY, USA, 2002. [Google Scholar]
- Yang, X.; Deb, S. Cuckoo search via Lévy flights. In Proceeding of the World Congress on Nature & Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009. [Google Scholar]
- Tao, T.; Zhang, J.; Xin, K.; Li, S. Optimal valve control in water distribution systems based on cuckoo search. J. Tongji Univ. Nat. Sci. 2016, 44, 106–110. [Google Scholar]
- Xu, Y.; Cao, T.; Luo, F. Wastewater effluent quality prediction model based on relevance vector machine. J. South China Univ. Technol. Nat. Sci. Ed. 2014, 42, 103–108. [Google Scholar]
| Parameters | Values | Units | Descriptions |
|---|---|---|---|
| KLa3, KLa4 | 240 | mg/day | Oxygen transfer coefficient of the 3rd and 4th bioreactors |
| KLa5 | 83 | mg/day | Oxygen transfer coefficient of the 5th bioreactor |
| Qint | 55338 | m3/day | Internal recirculation flow rate |
| Qr | 18446 | m3/day | Returned sludge flow rate |
| Qw | 385 | m3/day | Waste sludge flow rate |
| Component | Unit | Description |
|---|---|---|
| Si | mg COD/L | Soluble inert organic matter |
| Ss | mg COD/L | Readily biodegradable substrate |
| Xi | mg COD /L | Particulate inert organic matter |
| Xs | mg COD/L | Slowly biodegradable substrate |
| Xbh | mg COD /L | Active heterotrophic biomass |
| Xba | mg COD/L | Active autotrophic biomass |
| Xp | mg COD /L | Particulate product arising from biomass decay |
| So | mg -COD/L | Oxygen (negative COD) |
| Sno | mg N/L | Nitrate and nitrite nitrogen |
| Snh | mg N/L | NH4+ and NH3 nitrogen |
| Snd | mg N/L | Soluble biodegradable organic nitrogen |
| Xnd | mg N/L | Particulate biodegradable organic nitrogen |
| Salk | mole/m3 | Alkalinity |
| TSS | mg SS/L | Total amount of solids |
| Q | m3/day | Influent flow rate |
| Model | MSE | Hidden Nodes | Training Time (sec) |
|---|---|---|---|
| ELM | 1.3011 | 40 | 1.78 |
| CS-ELM | 0.0640 | 15 | 76.67 |
| RVM | 0.0513 | - | - |
| BP1 | 0.0909 | 25 | - |
| LS-SVM1 | 0.0865 | - | - |
| ICS-ELM | 0.0254 | 40 | 61.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, P.; Cao, J.; Jegatheesan, V.; Du, X. A Real-Time BOD Estimation Method in Wastewater Treatment Process Based on an Optimized Extreme Learning Machine. Appl. Sci. 2019, 9, 523. https://doi.org/10.3390/app9030523
Yu P, Cao J, Jegatheesan V, Du X. A Real-Time BOD Estimation Method in Wastewater Treatment Process Based on an Optimized Extreme Learning Machine. Applied Sciences. 2019; 9(3):523. https://doi.org/10.3390/app9030523
Chicago/Turabian StyleYu, Ping, Jie Cao, Veeriah Jegatheesan, and Xianjun Du. 2019. "A Real-Time BOD Estimation Method in Wastewater Treatment Process Based on an Optimized Extreme Learning Machine" Applied Sciences 9, no. 3: 523. https://doi.org/10.3390/app9030523
APA StyleYu, P., Cao, J., Jegatheesan, V., & Du, X. (2019). A Real-Time BOD Estimation Method in Wastewater Treatment Process Based on an Optimized Extreme Learning Machine. Applied Sciences, 9(3), 523. https://doi.org/10.3390/app9030523





