Quantum Bits with Macroscopic Topologically Protected States in Semiconductor Devices
Abstract
1. Introduction
2. Quantum Bits Based on Macroscopic Haldane Chains in Synthetic Semiconductor Systems
2.1. Haldane Phase in Synthetic Spin Chains
2.2. Macroscopic Singlet-Triplet Qubits
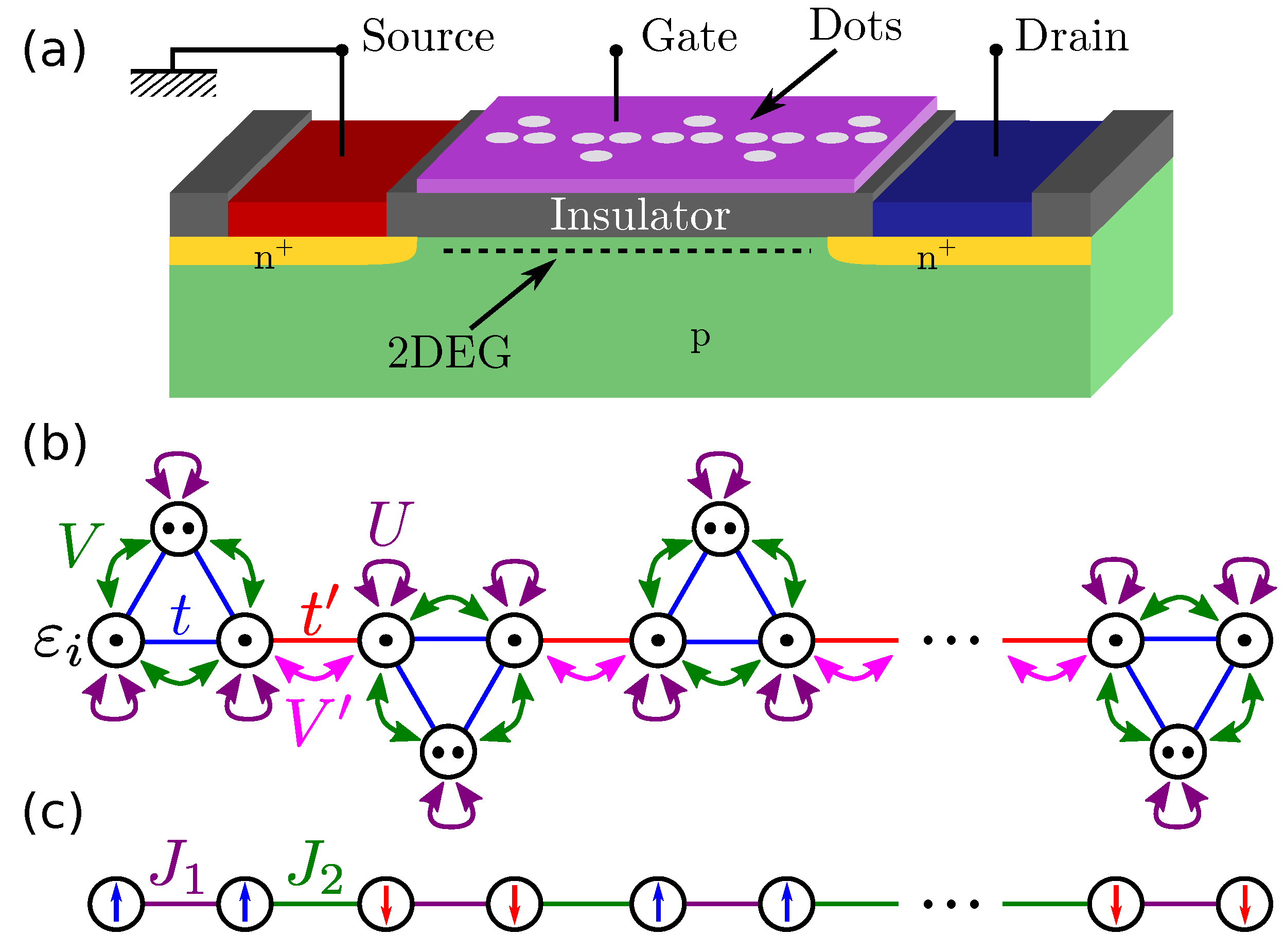
2.3. Haldane Phase in a Chain of Triple Quantum Dots in a Field Effect Transistor
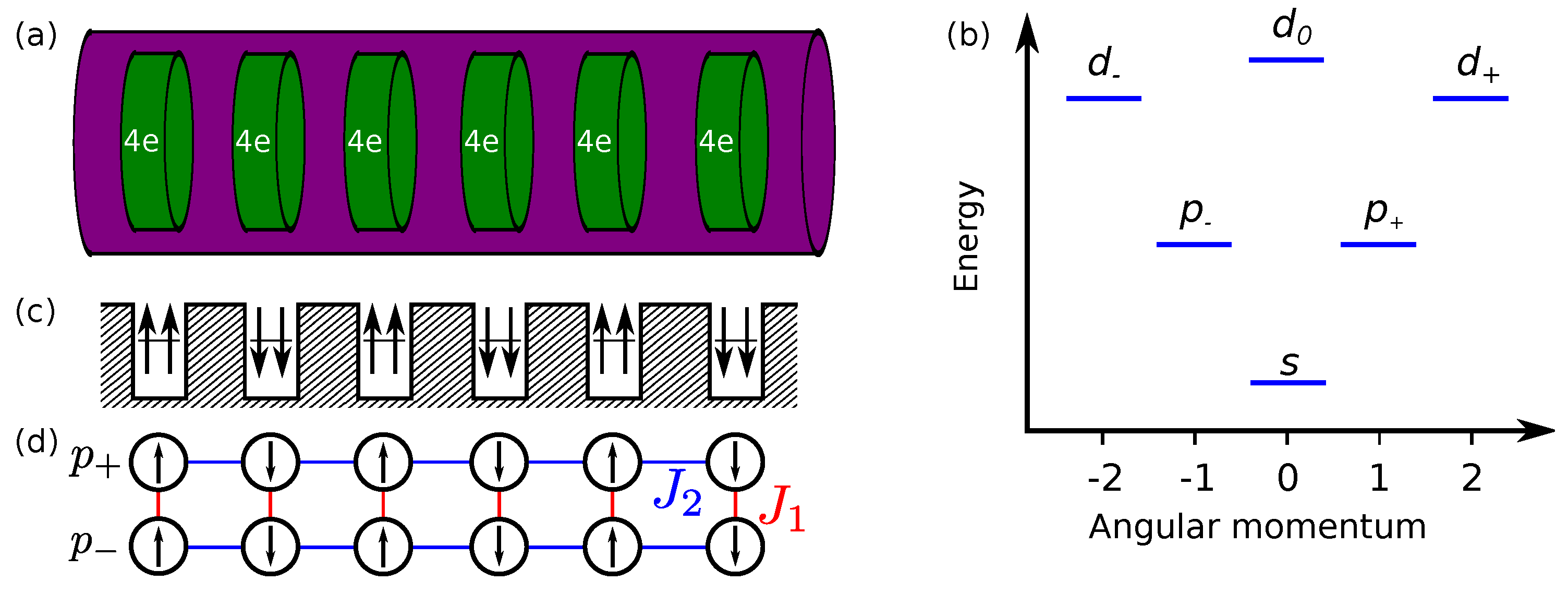
2.4. Haldane Phase in a Chain of Semiconductor Quantum Dots in a Nanowire
2.5. Implementation of the Qubit
3. Majorana Qubits
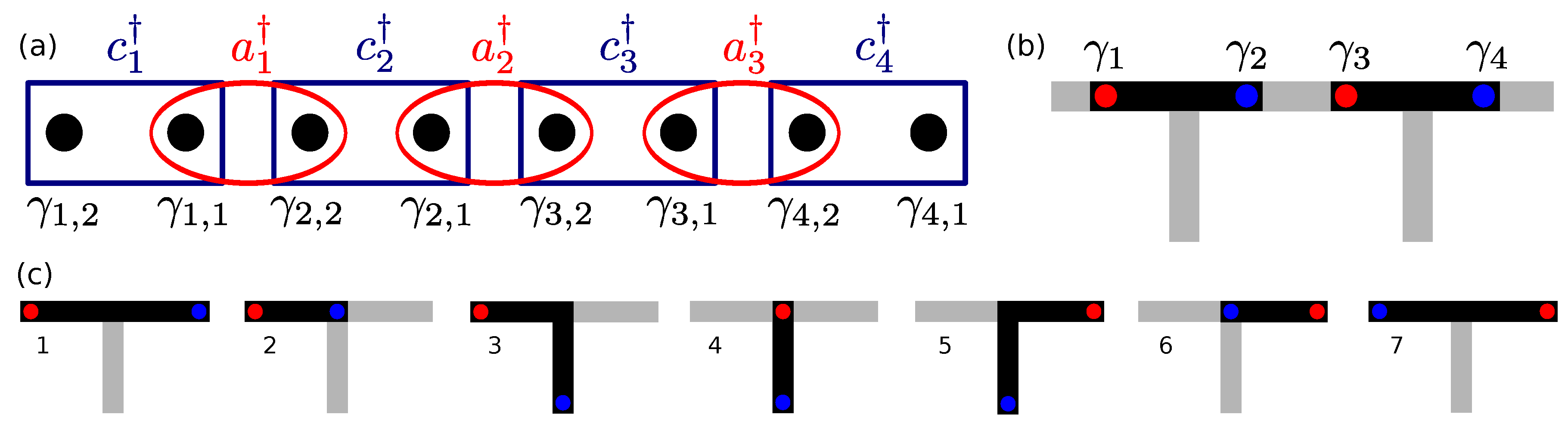
3.1. Kitaev Chain
3.2. Non-Abelian Statistics and Topological Quantum Computations
3.3. Physical Realization
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AKLT | Affleck, Kennedy, Lieb, Tasaki |
| QD | quantum dot |
| MZM | Majorana zero mode |
| SC | superconductor/superconducting |
References
- Brum, J.A.; Hawrylak, P. Coupled quantum dots as quantum exclusive-OR gate. Superlattices Microstruct. 1997, 22, 431–436. [Google Scholar] [CrossRef]
- Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120–126. [Google Scholar] [CrossRef]
- Ciorga, M.; Sachrajda, A.S.; Hawrylak, P.; Gould, C.; Zawadzki, P.; Jullian, S.; Feng, Y.; Wasilewski, Z. Addition spectrum of a lateral dot from Coulomb and spin-blockade spectroscopy. Phys. Rev. B 2000, 61, R16315–R16318. [Google Scholar] [CrossRef]
- Watson, T.F.; Philips, S.G.J.; Kawakami, E.; Ward, D.R.; Scarlino, P.; Veldhorst, M.; Savage, D.E.; Lagally, M.G.; Friesen, M.; Coppersmith, S.N.; et al. A programmable two-qubit quantum processor in silicon. Nature 2018, 555, 633–637. [Google Scholar] [CrossRef] [PubMed]
- Korkusinski, M.; Hawrylak, P. Coded qubits based on electron spin. In Semiconductor Quantum Bits; Benson, O., Henneberger, F., Eds.; Pan Stanford: Singapore, 2009. [Google Scholar]
- Hsieh, C.Y.; Shim, Y.P.; Korkusinski, M.; Hawrylak, P. Physics of lateral triple quantum-dot molecules with controlled electron numbers. Rep. Prog. Phys. 2012, 75, 114501. [Google Scholar] [CrossRef] [PubMed]
- Petta, J.R.; Johnson, A.C.; Taylor, J.M.; Laird, E.A.; Yacoby, A.; Lukin, M.D.; Marcus, C.M.; Hanson, M.P.; Gossard, A.C. Coherent Manipulation of Coupled Electron Spins in Semiconductor Quantum Dots. Science 2005, 309, 2180–2184. [Google Scholar] [CrossRef] [PubMed]
- Dial, O.E.; Shulman, M.D.; Harvey, S.P.; Bluhm, H.; Umansky, V.; Yacoby, A. Charge Noise Spectroscopy Using Coherent Exchange Oscillations in a Singlet-Triplet Qubit. Phys. Rev. Lett. 2013, 110, 146804. [Google Scholar] [CrossRef] [PubMed]
- Nizovtsev, A.P.; Kilin, S.Y.; Jelezko, F.; Gaebal, T.; Popa, I.; Gruber, A.; Wrachtrup, J. A quantum computer based on NV centers in diamond: Optically detected nutations of single electron and nuclear spins. Opt. Spectrosc. 2005, 99, 233–244. [Google Scholar] [CrossRef]
- Neumann, P.; Mizuochi, N.; Rempp, F.; Hemmer, P.; Watanabe, H.; Yamasaki, S.; Jacques, V.; Gaebel, T.; Jelezko, F.; Wrachtrup, J. Multipartite Entanglement Among Single Spins in Diamond. Science 2008, 320, 1326. [Google Scholar] [CrossRef]
- Saeedi, K.; Simmons, S.; Salvail, J.Z.; Dluhy, P.; Riemann, H.; Abrosimov, N.V.; Becker, P.; Pohl, H.J.; Morton, J.J.L.; Thewalt, M.L.W. Room-Temperature Quantum Bit Storage Exceeding 39 Minutes Using Ionized Donors in Silicon-28. Science 2013, 342, 830–833. [Google Scholar] [CrossRef]
- Pla, J.J.; Tan, K.Y.; Dehollain, J.P.; Lim, W.H.; Morton, J.J.L.; Zwanenburg, F.A.; Jamieson, D.N.; Dzurak, A.S.; Morello, A. High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 2013, 496, 334–338. [Google Scholar] [CrossRef] [PubMed]
- Barends, R.; Shabani, A.; Lamata, L.; Kelly, J.; Mezzacapo, A.; Heras, U.L.; Babbush, R.; Fowler, A.G.; Campbell, B.; Chen, Y.; et al. Digitized adiabatic quantum computing with a superconducting circuit. Nature 2016, 534, 222–226. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.W.; Amin, M.H.S.; Gildert, S.; Lanting, T.; Hamze, F.; Dickson, N.; Harris, R.; Berkley, A.J.; Johansson, J.; Bunyk, P.; et al. Quantum annealing with manufactured spins. Nature 2011, 473, 194–198. [Google Scholar] [CrossRef] [PubMed]
- Kitaev, A.Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Leinaas, J.M.; Myrheim, J. On the theory of identical particles. Il Nuovo Cimento B 1977, 37, 1–23. [Google Scholar] [CrossRef]
- Wilczek, F. Quantum mechanics of fractional-spin particles. Phys. Rev. Lett. 1982, 49, 957–959. [Google Scholar] [CrossRef]
- Fröhlich, J.; Gabbiani, F. Braid statistics in local quantum theory. Rev. Math. Phys. 1990, 2, 251–353. [Google Scholar] [CrossRef]
- Wen, X.G. Colloquium: Zoo of quantum-topological phases of matter. Rev. Mod. Phys. 2017, 89, 041004. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Nobel Lecture: Topological quantum matter. Rev. Mod. Phys. 2017, 89, 040502. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- Landau, L.D. The theory of phase transitions I. Zhurnal Eksperimental’noi i Teoreticheskoi Fiziki 1937, 7, 19–32. [Google Scholar] [CrossRef]
- Landau, L.D. The theory of phase transitions II. Zhurnal Eksperimental’noi i Teoreticheskoi Fiziki 1937, 7, 627. [Google Scholar]
- Moore, G.; Read, N. Nonabelions in the fractional quantum Hall effect. Nucl. Phys. B 1991, 360, 362–396. [Google Scholar] [CrossRef]
- Read, N.; Rezayi, E. Beyond paired quantum Hall states: Parafermions and incompressible states in the first excited Landau level. Phys. Rev. B 1999, 59, 8084–8092. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Physics-Uspekhi 2001, 44, 131. [Google Scholar] [CrossRef]
- Lutchyn, R.M.; Sau, J.D.; Das Sarma, S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef]
- Oreg, Y.; Refael, G.; von Oppen, F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 2010, 105, 177002. [Google Scholar] [CrossRef]
- Zhang, C.; Tewari, S.; Das Sarma, S. Bell’s Inequality and Universal Quantum Gates in a Cold-Atom Chiral Fermionic p-Wave Superfluid. Phys. Rev. Lett. 2007, 99, 220502. [Google Scholar] [CrossRef]
- Georgiev, L.S. Topologically protected gates for quantum computation with non-Abelian anyons in the Pfaffian quantum Hall state. Phys. Rev. B 2006, 74, 235112. [Google Scholar] [CrossRef]
- Bravyi, S. Universal quantum computation with the ν = 5/2 fractional quantum Hall state. Phys. Rev. A 2006, 73, 042313. [Google Scholar] [CrossRef]
- Camino, F.E.; Zhou, W.; Goldman, V.J. Realization of a Laughlin quasiparticle interferometer: Observation of fractional statistics. Phys. Rev. B 2005, 72, 075342. [Google Scholar] [CrossRef]
- Ferreira, G.J.; Loss, D. Magnetically Defined Qubits on 3D Topological Insulators. Phys. Rev. Lett. 2013, 111, 106802. [Google Scholar] [CrossRef] [PubMed]
- Michetti, P.; Recher, P. Bound states and persistent currents in topological insulator rings. Phys. Rev. B 2011, 83, 125420. [Google Scholar] [CrossRef]
- Xu, H.; Huang, L.; Lai, Y.C.; Grebogi, C. Superpersistent currents and whispering gallery modes in relativistic quantum chaotic systems. Sci. Rep. 2015, 5, 8963. [Google Scholar] [CrossRef] [PubMed]
- Miyake, A. Quantum computation on the edge of a symmetry-protected topological order. Phys. Rev. Lett. 2010, 105, 040501. [Google Scholar] [CrossRef]
- Else, D.V.; Schwarz, I.; Bartlett, S.D.; Doherty, A.C. Symmetry-protected phases for measurement-based quantum computation. Phys. Rev. Lett. 2012, 108, 240505. [Google Scholar] [CrossRef] [PubMed]
- Katsura, H.; Hirano, T.; Hatsugai, Y. Exact analysis of entanglement in gapped quantum spin chains. Phys. Rev. B 2007, 76, 012401. [Google Scholar] [CrossRef]
- Renard, J.P.; Verdaguer, M.; Regnault, L.P.; Erkelens, W.A.C.; Rossat-Mignod, J.; Stirling, W.G. Presumption for a quantum energy gap in the quasi-one-dimensional S = 1 Heisenberg antiferromagnet Ni(C2H8N2)2NO2(ClO4). Europhys. Lett. 1987, 3, 945. [Google Scholar] [CrossRef]
- Buyers, W.J.L.; Morra, R.M.; Armstrong, R.L.; Hogan, M.J.; Gerlach, P.; Hirakawa, K. Experimental evidence for the Haldane gap in a spin-1 nearly isotropic, antiferromagnetic chain. Phys. Rev. Lett. 1986, 56, 371–374. [Google Scholar] [CrossRef]
- Steiner, M.; Kakurai, K.; Kjems, J.K.; Petitgrand, D.; Pynn, R. Inelastic neutron scattering studies on 1D near-Heisenberg antiferromagnets: A test of the Haldane conjecture. J. Appl. Phys. 1987, 61, 3953–3955. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Nonlinear field theory of large-spin Heisenberg antiferromagnets: Semiclassically quantized solitons of the one-dimensional easy-axis Néel state. Phys. Rev. Lett. 1983, 50, 1153–1156. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Continuum dynamics of the 1-D Heisenberg antiferromagnet: identification with the O (3) nonlinear sigma model. Phys. Lett. A 1983, 93, 464–468. [Google Scholar] [CrossRef]
- Affleck, I.; Haldane, F.D.M. Critical theory of quantum spin chains. Phys. Rev. B 1987, 36, 5291. [Google Scholar] [CrossRef]
- Jaworowski, B.; Rogers, N.; Grabowski, M.; Hawrylak, P. Macroscopic Singlet-Triplet Qubit in Synthetic Spin-One Chain in Semiconductor Nanowires. Sci. Rep. 2017, 7, 5529. [Google Scholar] [CrossRef] [PubMed]
- Shim, Y.P.; Sharma, A.; Hsieh, C.Y.; Hawrylak, P. Artificial Haldane gap material on a semiconductor chip. Solid State Commun. 2010, 150, 2065–2068. [Google Scholar] [CrossRef]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. [Google Scholar] [CrossRef] [PubMed]
- Affleck, I.; Kennedy, T.; Lieb, E.H.; Tasaki, H. Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 1987, 59, 799–802. [Google Scholar] [CrossRef]
- Gu, Z.C.; Wen, X.G. Tensor-entanglement-filtering renormalization approach and symmetry-protected topological order. Phys. Rev. B 2009, 80, 155131. [Google Scholar] [CrossRef]
- Pollmann, F.; Berg, E.; Turner, A.M.; Oshikawa, M. Symmetry protection of topological phases in one-dimensional quantum spin systems. Phys. Rev. B 2012, 85, 075125. [Google Scholar] [CrossRef]
- Gaudreau, L.; Studenikin, S.A.; Sachrajda, A.S.; Zawadzki, P.; Kam, A.; Lapointe, J.; Korkusinski, M.; Hawrylak, P. Stability Diagram of a Few-Electron Triple Dot. Phys. Rev. Lett. 2006, 97, 036807. [Google Scholar] [CrossRef]
- Koppens, F.H.L.; Buizert, C.; Tielrooij, K.J.; Vink, I.T.; Nowack, K.C.; Meunier, T.; Kouwenhoven, L.P.; Vandersypen, L.M.K. Driven coherent oscillations of a single electron spin in a quantum dot. Nature 2006, 442, 766–771. [Google Scholar] [CrossRef] [PubMed]
- Gaudreau, L.; Kam, A.; Granger, G.; Studenikin, S.A.; Zawadzki, P.; Sachrajda, A.S. A tunable few electron triple quantum dot. Appl. Phys. Lett. 2009, 95, 193101. [Google Scholar] [CrossRef]
- Korkusinski, M.; Gimenez, I.P.; Hawrylak, P.; Gaudreau, L.; Studenikin, S.A.; Sachrajda, A.S. Topological Hunds rules and the electronic properties of a triple lateral quantum dot molecule. Phys. Rev. B 2007, 75, 115301. [Google Scholar] [CrossRef]
- Delgado, F.; Shim, Y.P.; Korkusinski, M.; Hawrylak, P. Theory of spin, electronic, and transport properties of the lateral triple quantum dot molecule in a magnetic field. Phys. Rev. B 2007, 76, 115332. [Google Scholar] [CrossRef]
- Shim, Y.P.; Hawrylak, P. Gate-controlled spin-spin interactions in lateral quantum dot molecules. Phys. Rev. B 2008, 78, 165317. [Google Scholar] [CrossRef]
- Hida, K. Crossover between the Haldane-gap phase and the dimer phase in the spin-1/2 alternating Heisenberg chain. Phys. Rev. B 1992, 45, 2207–2212. [Google Scholar] [CrossRef]
- Hung, H.H.; Gong, C.D. Numerical evidence of a spin-1/2 chain approaching a spin-1 chain. Phys. Rev. B 2005, 71, 054413. [Google Scholar] [CrossRef]
- Fernandes da Silva, E. GaAs: Effective Landé g-factors. In New Data and Updates for I-VII, III-V, III-VI and IV-VI Compounds; Roessler, U., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 214–215. [Google Scholar] [CrossRef]
- Reimer, M.E.; McKinnon, W.R.; Lapointe, J.; Dalacu, D.; Poole, P.J.; Aers, G.C.; Kim, D.; Korkusiński, M.; Hawrylak, P.; Williams, R.L. Towards scalable gated quantum dots for quantum information applications. Physica E 2008, 40, 1790–1793. [Google Scholar] [CrossRef]
- Sheng, W.; Hawrylak, P. Spin polarization in self-assembled quantum dots. Phys. Rev. B 2006, 73, 125331. [Google Scholar] [CrossRef]
- Dalacu, D.; Mnaymneh, K.; Wu, X.; Lapointe, J.; Aers, G.C.; Poole, P.J.; Williams, R.L. Selective-area vapor-liquid-solid growth of tunable InAsP quantum dots in nanowires. Appl. Phys. Lett. 2011, 98, 251101. [Google Scholar] [CrossRef]
- Wallentin, J.; Anttu, N.; Asoli, D.; Huffman, M.; Åberg, I.; Magnusson, M.H.; Siefer, G.; Fuss-Kailuweit, P.; Dimroth, F.; Witzigmann, B.; et al. InP Nanowire Array Solar Cells Achieving 13.8% Efficiency by Exceeding the Ray Optics Limit. Science 2013, 339, 1057–1060. [Google Scholar] [CrossRef] [PubMed]
- Haffouz, S.; Zeuner, K.D.; Dalacu, D.; Poole, P.J.; Lapointe, J.; Poitras, D.; Mnaymneh, K.; Wu, X.; Couillard, M.; Korkusinski, M.; et al. Bright single InAsP quantum dots at telecom wavelengths in position-controlled InP nanowires: The role of the photonic waveguide. Nano Lett. 2018, 18, 3047–3052. [Google Scholar] [CrossRef] [PubMed]
- Dalacu, D.; Mnaymneh, K.; Lapointe, J.; Wu, X.; Poole, P.J.; Bulgarini, G.; Zwiller, V.; Reimer, M.E. Ultraclean Emission from InAsP Quantum Dots in Defect-Free Wurtzite InP Nanowires. Nano Lett. 2012, 12, 5919–5923. [Google Scholar] [CrossRef] [PubMed]
- Kouwen, M.P.V.; Reimer, M.E.; Hidma, A.W.; van Weert, M.H.M.; Algra, R.E.; Bakkers, E.P.A.M.; Kouwenhoven, L.P.; Zwiller, V. Single Electron Charging in Optically Active Nanowire Quantum Dots. Nano Lett. 2010, 10, 1817–1822. [Google Scholar] [CrossRef]
- Van Weert, M.H.M.; den Heijer, M.; van Kouwen, M.P.; Algra, R.E.; Bakkers, E.P.A.M.; Kouwenhoven, L.P.; Zwiller, V. Surround-gated vertical nanowire quantum dots. Appl. Phys. Lett. 2010, 96, 233112. [Google Scholar] [CrossRef]
- Hida, K. Haldane gap in the spin-1/2 double chain Heisenberg antiferromagnet. J. Magn. Magn. Mater. 1992, 104–107, 783–784. [Google Scholar] [CrossRef]
- Van Bree, J.; Silov, A.Y.; Koenraad, P.M.; Flatté, M.E.; Pryor, C.E. g factors and diamagnetic coefficients of electrons, holes, and excitons in InAs/InP quantum dots. Phys. Rev. B 2012, 85, 165323. [Google Scholar] [CrossRef]
- Nonne, H.; Moliner, M.; Capponi, S.; Lecheminant, P.; Totsuka, K. Symmetry-protected topological phases of alkaline-earth cold fermionic atoms in one dimension. Europhys. Lett. 2013, 102, 37008. [Google Scholar] [CrossRef]
- Shulman, M.D.; Dial, O.E.; Harvey, S.P.; Bluhm, H.; Umansky, V.; Yacoby, A. Demonstration of Entanglement of Electrostatically Coupled Singlet-Triplet Qubits. Science 2012, 336, 202. [Google Scholar] [CrossRef]
- Hyman, R.A.; Yang, K.; Bhatt, R.N.; Girvin, S.M. Random Bonds and Topological Stability in Gapped Quantum Spin Chains. Phys. Rev. Lett. 1996, 76, 839–842. [Google Scholar] [CrossRef]
- Maune, B.M.; Borselli, M.G.; Huang, B.; Ladd, T.D.; Deelman, P.W.; Holabird, K.S.; Kiselev, A.A.; Alvarado-Rodriguez, I.; Ross, R.S.; Schmitz, A.E.; et al. Coherent singlet-triplet oscillations in a silicon-based double quantum dot. Nature 2012, 481, 344–347. [Google Scholar] [CrossRef]
- Hu, Y.; Churchill, H.O.H.; Reilly, D.J.; Xiang, J.; Lieber, C.M.; Marcus, C.M. A Ge/Si heterostructure nanowire-based double quantum dot with integrated charge sensor. Nat. Nanotechnol. 2007, 2, 622–625. [Google Scholar] [CrossRef] [PubMed]
- Rashidi, M.; Vine, W.; Dienel, T.; Livadaru, L.; Retallick, J.; Huff, T.; Walus, K.; Wolkow, R.A. Initiating and Monitoring the Evolution of Single Electrons Within Atom-Defined Structures. Phys. Rev. Lett. 2018, 121, 166801. [Google Scholar] [CrossRef]
- Sau, J.D.; Das Sarma, S. Realizing a robust practical Majorana chain in a quantum-dot-superconductor linear array. Nat. Commun. 2012, 3, 964. [Google Scholar] [CrossRef] [PubMed]
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Il Nuovo Cimento (1924–1942) 1937, 14, 171. [Google Scholar] [CrossRef]
- Ivanov, D.A. Non-Abelian Statistics of Half-Quantum Vortices in p-Wave Superconductors. Phys. Rev. Lett. 2001, 86, 268–271. [Google Scholar] [CrossRef] [PubMed]
- Alicea, J.; Oreg, Y.; Refael, G.; von Oppen, F.; Fisher, M.P.A. Non-Abelian statistics and topological quantum information processing in 1D wire networks. Nat. Phys. 2011, 7, 412–417. [Google Scholar] [CrossRef]
- Das Sarma, S.; Freedman, M.; Nayak, C. Majorana zero modes and topological quantum computation. NPJ Quantum Inf. 2015, 1, 15001. [Google Scholar] [CrossRef]
- Bravyi, S.; Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. A 2005, 71, 022316. [Google Scholar] [CrossRef]
- Bonderson, P.; Freedman, M.; Nayak, C. Measurement-Only Topological Quantum Computation. Phys. Rev. Lett. 2008, 101, 010501. [Google Scholar] [CrossRef]
- Hyart, T.; van Heck, B.; Fulga, I.C.; Burrello, M.; Akhmerov, A.R.; Beenakker, C.W.J. Flux-controlled quantum computation with Majorana fermions. Phys. Rev. B 2013, 88, 035121. [Google Scholar] [CrossRef]
- Choy, T.P.; Edge, J.M.; Akhmerov, A.R.; Beenakker, C.W.J. Majorana fermions emerging from magnetic nanoparticles on a superconductor without spin-orbit coupling. Phys. Rev. B 2011, 84, 195442. [Google Scholar] [CrossRef]
- Nadj-Perge, S.; Drozdov, I.K.; Li, J.; Chen, H.; Jeon, S.; Seo, J.; MacDonald, A.H.; Bernevig, B.A.; Yazdani, A. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 2014, 346, 602–607. [Google Scholar] [CrossRef] [PubMed]
- Mourik, V.; Zuo, K.; Frolov, S.M.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices. Science 2012, 336, 1003. [Google Scholar] [CrossRef] [PubMed]
- Rokhinson, L.P.; Liu, X.; Furdyna, J.K. The fractional a.c. Josephson effect in a semiconductor-superconductor nanowire as a signature of Majorana particles. Nat. Phys. 2012, 8, 795–799. [Google Scholar] [CrossRef]
- Laroche, D.; Bouman, D.; van Woerkom, D.J.; Proutski, A.; Murthy, C.; Pikulin, D.I.; Nayak, C.; van Gulik, R.J.J.; Nygård, J.; Krogstrup, P.; et al. Observation of the 4π-periodic Josephson effect in InAs nanowires. arXiv, 2017; arXiv:1712.08459. [Google Scholar]
- Lutchyn, R.M.; Bakkers, E.P.A.M.; Kouwenhoven, L.P.; Krogstrup, P.; Marcus, C.M.; Oreg, Y. Majorana zero modes in superconductor-semiconductor heterostructures. Nat. Rev. Mater. 2018, 3, 52–68. [Google Scholar] [CrossRef]
- Gangadharaiah, S.; Braunecker, B.; Simon, P.; Loss, D. Majorana Edge States in Interacting One-Dimensional Systems. Phys. Rev. Lett. 2011, 107, 036801. [Google Scholar] [CrossRef]
- Stoudenmire, E.M.; Alicea, J.; Starykh, O.A.; Fisher, M.P. Interaction effects in topological superconducting wires supporting Majorana fermions. Phys. Rev. B 2011, 84, 014503. [Google Scholar] [CrossRef]
- Lang, N.; Büchler, H.P. Topological states in a microscopic model of interacting fermions. Phys. Rev. B 2015, 92, 041118. [Google Scholar] [CrossRef]
- Iemini, F.; Mazza, L.; Rossini, D.; Fazio, R.; Diehl, S. Localized Majorana-Like Modes in a Number-Conserving Setting: An Exactly Solvable Model. Phys. Rev. Lett. 2015, 115, 156402. [Google Scholar] [CrossRef] [PubMed]
- Read, N.; Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect. Phys. Rev. B 2000, 61, 10267–10297. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef] [PubMed]
- Beenakker, C.W.J. Search for Majorana Fermions in Superconductors. Annu. Rev. Condens. Matter Phys. 2013, 4, 113–136. [Google Scholar] [CrossRef]
- Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 2012, 75, 076501. [Google Scholar] [CrossRef] [PubMed]
- Schuch, N.; Pérez-García, D.; Cirac, I. Classifying quantum phases using matrix product states and projected entangled pair states. Phys. Rev. B 2011, 84, 165139. [Google Scholar] [CrossRef]
- Fidkowski, L.; Kitaev, A. Topological phases of fermions in one dimension. Phys. Rev. B 2011, 83, 075103. [Google Scholar] [CrossRef]
- Verresen, R.; Moessner, R.; Pollmann, F. One-dimensional symmetry protected topological phases and their transitions. Phys. Rev. B 2017, 96, 165124. [Google Scholar] [CrossRef]
- Robinson, N.J.; Altland, A.; Egger, R.; Gergs, N.M.; Li, W.; Schuricht, D.; Tsvelik, A.M.; Weichselbaum, A.; Konik, R.M. Non-Topological Majorana Zero Modes in Inhomogeneous Spin Ladders. arXiv, 2018; arXiv:1806.01925. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaworowski, B.; Hawrylak, P. Quantum Bits with Macroscopic Topologically Protected States in Semiconductor Devices. Appl. Sci. 2019, 9, 474. https://doi.org/10.3390/app9030474
Jaworowski B, Hawrylak P. Quantum Bits with Macroscopic Topologically Protected States in Semiconductor Devices. Applied Sciences. 2019; 9(3):474. https://doi.org/10.3390/app9030474
Chicago/Turabian StyleJaworowski, Błażej, and Paweł Hawrylak. 2019. "Quantum Bits with Macroscopic Topologically Protected States in Semiconductor Devices" Applied Sciences 9, no. 3: 474. https://doi.org/10.3390/app9030474
APA StyleJaworowski, B., & Hawrylak, P. (2019). Quantum Bits with Macroscopic Topologically Protected States in Semiconductor Devices. Applied Sciences, 9(3), 474. https://doi.org/10.3390/app9030474




