Development of Low-Cost Fast Photoacoustic Computed Tomography: System Characterization and Phantom Study
Abstract
1. Introduction
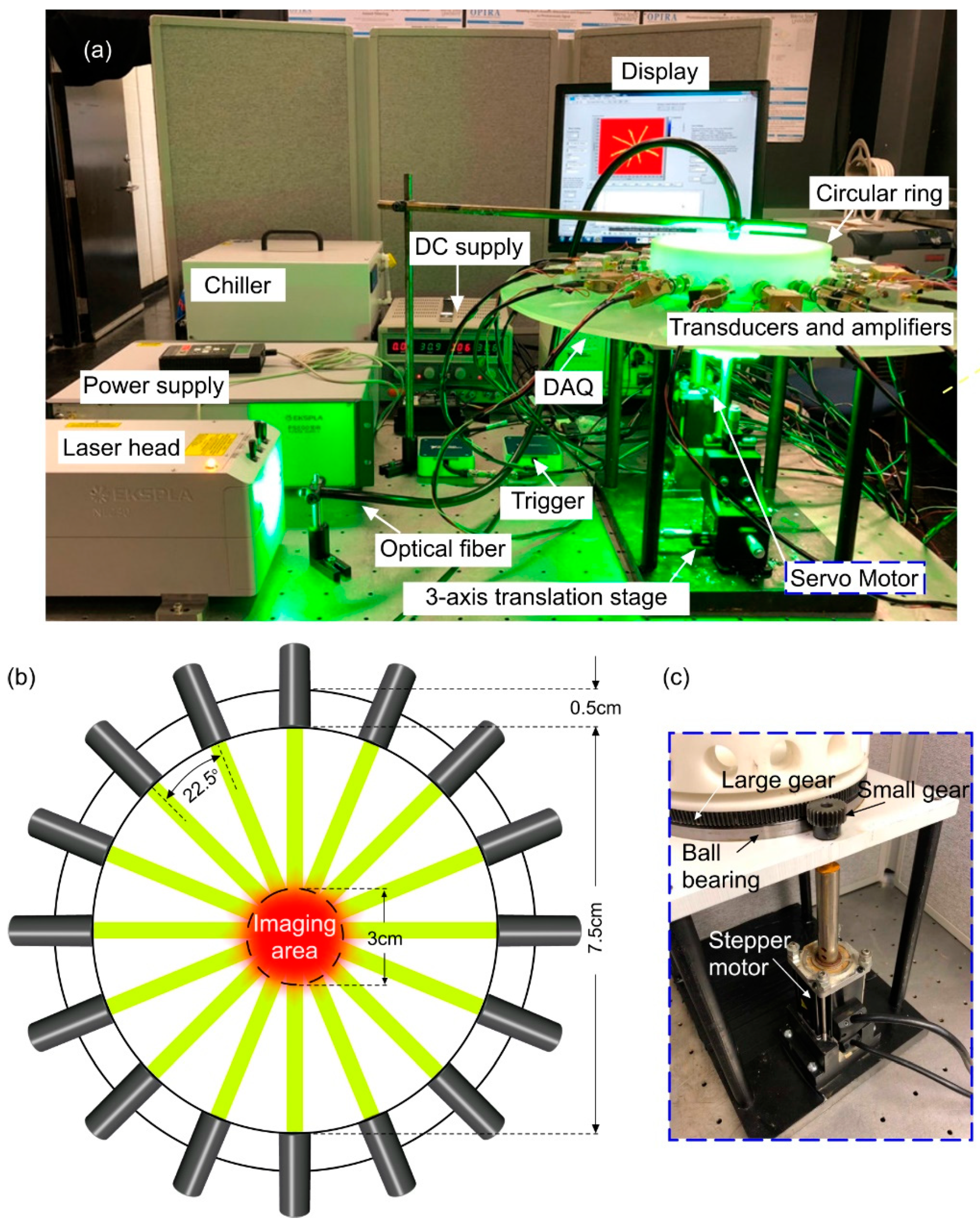
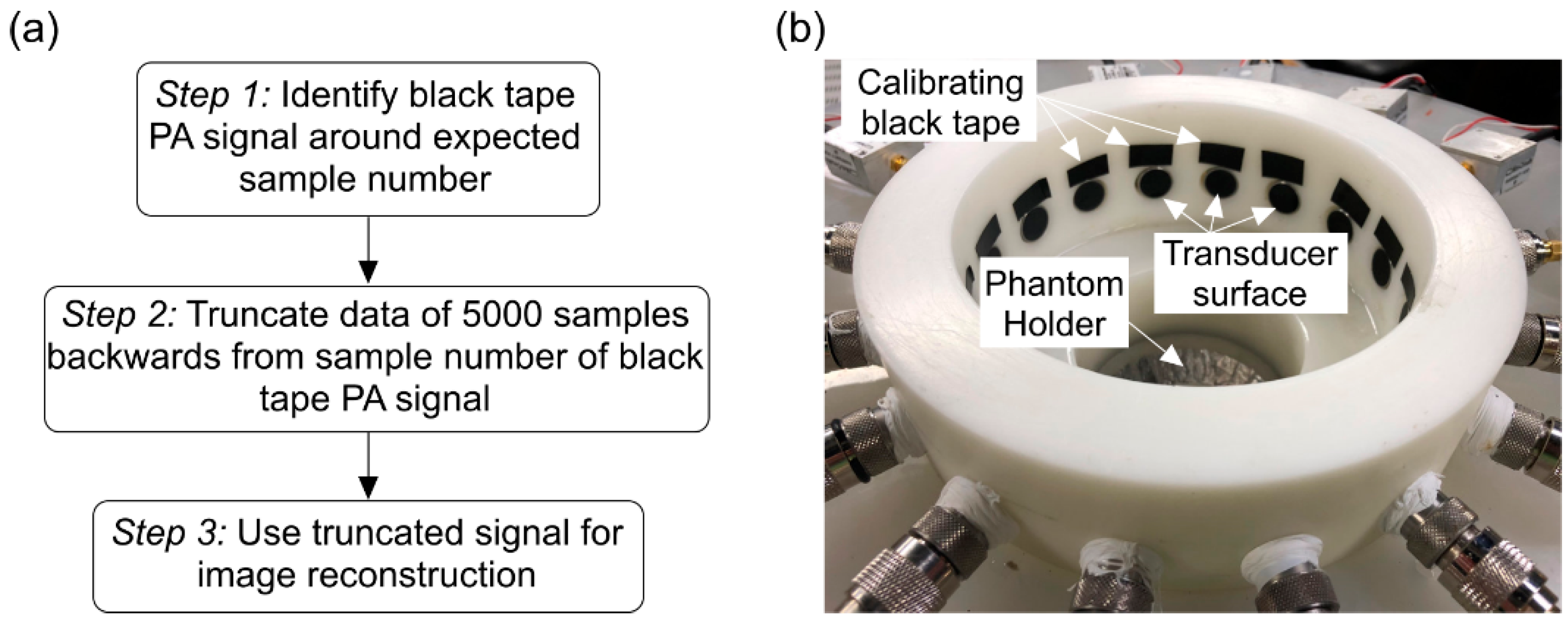
2. Materials and Methods
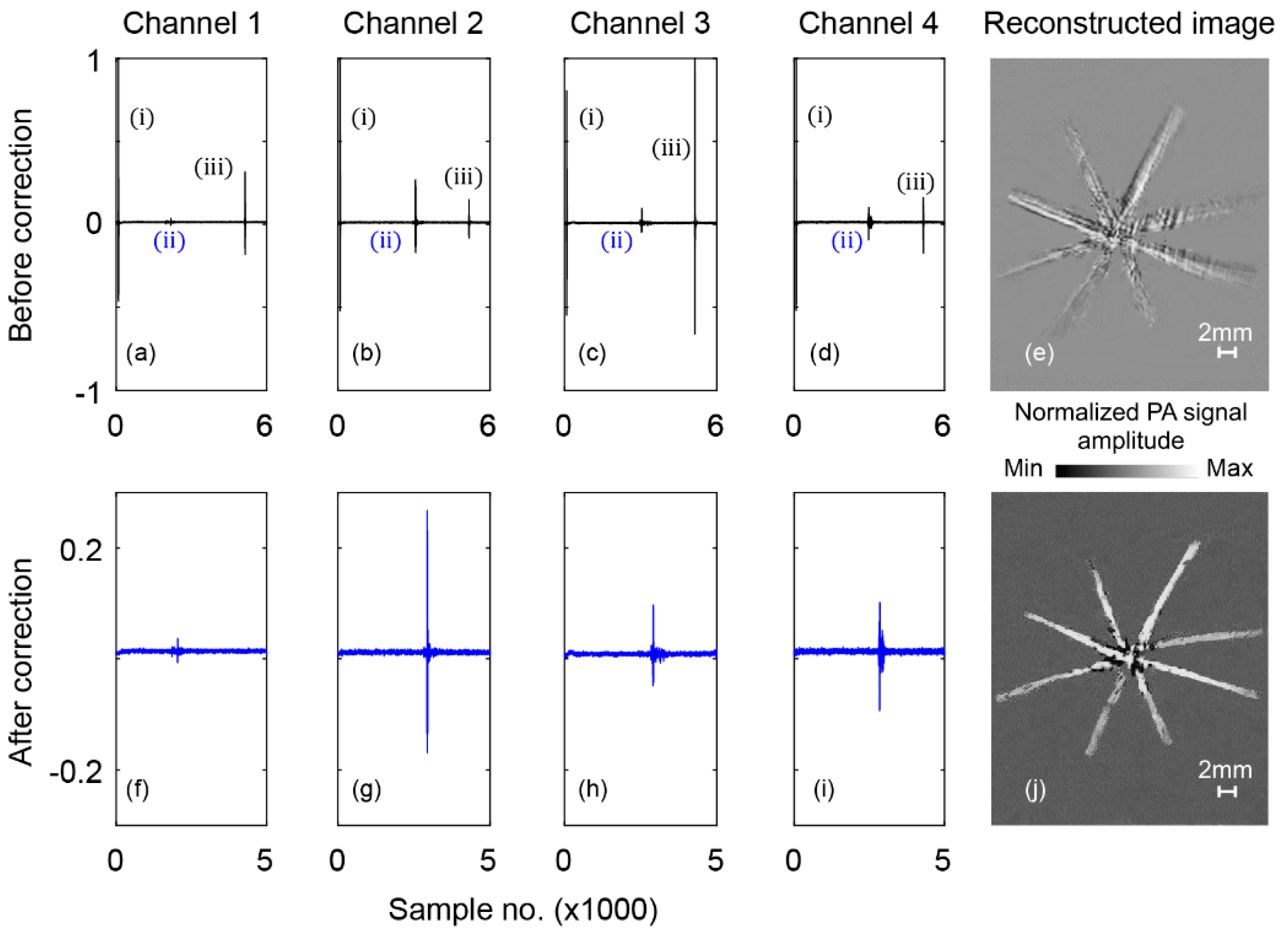
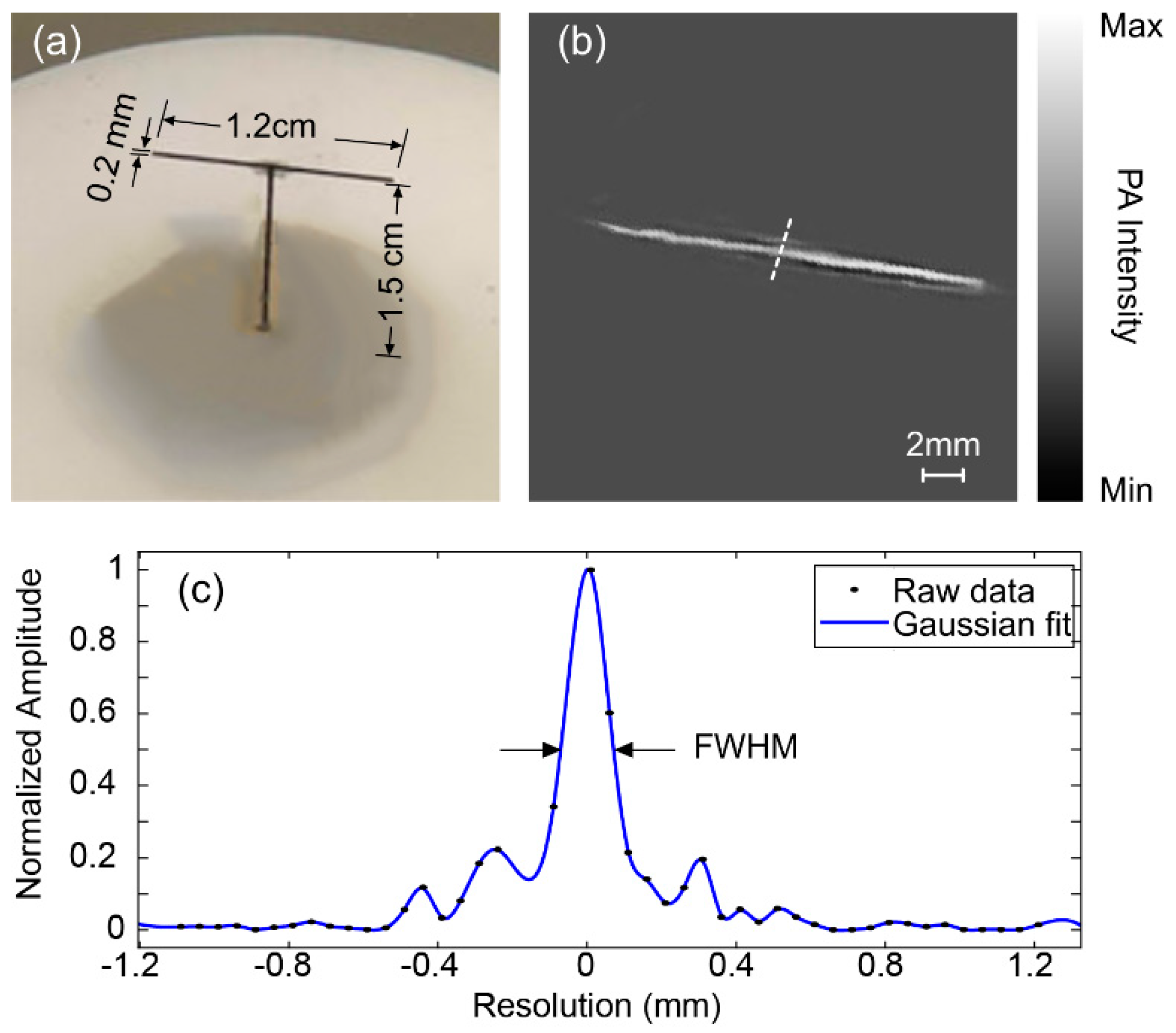
3. Results
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, L.V. Multiscale photoacoustic microscopy and computed tomography. Nat. Photonics 2009, 3, 503. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi-Nejad, A.-R.; Mahmoudzadeh, M.; Hassanpour, M.S.; Wallois, F.; Muzik, O.; Papadelis, C.; Hansen, A.; Soltanian-Zadeh, H.; Gelovani, J.; Nasiriavanaki, M. Neonatal brain resting-state functional connectivity imaging modalities. Photoacoustics 2018, 10, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Anwar, R.; Kratkiewicz, K.; Mohammad, R. Avanaki Photoacoustic Imaging: A Promising Alternative to Transcranial Ultrasound. Res. J. Opt. Photonics 2018, 2, 411–420. [Google Scholar]
- Wang, L.V. Tutorial on photoacoustic microscopy and computed tomography. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 171–179. [Google Scholar] [CrossRef]
- Zhou, Y.; Yao, J.; Wang, L.V. Tutorial on photoacoustic tomography. J. Biomed. Opt. 2016, 21, 061007. [Google Scholar] [CrossRef] [PubMed]
- Nasiriavanaki, M.; Xia, J.; Wan, H.; Bauer, A.Q.; Culver, J.P.; Wang, L.V. High-resolution photoacoustic tomography of resting-state functional connectivity in the mouse brain. Proc. Natl. Acad. Sci. USA 2014, 111, 21–26. [Google Scholar] [CrossRef] [PubMed]
- Mahmoodkalayeh, S.; Lu, X.; Ansari, M.A.; Li, H.; Nasiriavanaki, M. Optimization of light illumination for photoacoustic computed tomography of human infant brain. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing, San Francisco, CA, USA, 27 January–1 February 2018; p. 104946U. [Google Scholar]
- Manwar, R.; Hosseinzadeh, M.; Hariri, A.; Kratkiewicz, K.; Noei, S.; N Avanaki, M. Photoacoustic Signal Enhancement: Towards Utilization of Low Energy Laser Diodes in Real-Time Photoacoustic Imaging. Sensors 2018, 18, 3498. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Wang, L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006, 77, 041101. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, D.; Zhang, Y.; Chitgupi, U.; Geng, J.; Wang, Y.; Zhang, Y.; Cook, T.R.; Xia, J.; Lovell, J.F. A phosphorus phthalocyanine formulation with intense absorbance at 1000 nm for deep optical imaging. Theranostics 2016, 6, 688. [Google Scholar] [CrossRef] [PubMed]
- Adabi, S.; Hosseinzadeh, M.; Noei, S.; Conforto, S.; Daveluy, S.; Clayton, A.; Mehregan, D.; Nasiriavanaki, M. Universal in vivo textural model for human skin based on optical coherence tomograms. Sci. Rep. 2017, 7, 17912. [Google Scholar] [CrossRef] [PubMed]
- Choma, M.A.; Sarunic, M.V.; Yang, C.; Izatt, J.A. Sensitivity advantage of swept source and Fourier domain optical coherence tomography. Opt. Express 2003, 11, 2183–2189. [Google Scholar] [CrossRef] [PubMed]
- Cogliati, A.; Canavesi, C.; Hayes, A.; Tankam, P.; Duma, V.-F.; Santhanam, A.; Thompson, K.P.; Rolland, J.P. MEMS-based handheld scanning probe with pre-shaped input signals for distortion-free images in Gabor-domain optical coherence microscopy. Opt. Express 2016, 24, 13365–13374. [Google Scholar] [CrossRef] [PubMed]
- Monroy, G.L.; Won, J.; Spillman, D.R.; Dsouza, R.; Boppart, S.A. Clinical translation of handheld optical coherence tomography: practical considerations and recent advancements. J. Biomed. Opt. 2017, 22, 121715. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Nie, L.; Chen, X. Photoacoustic molecular imaging: from multiscale biomedical applications towards early-stage theranostics. Trends Biotechnol. 2016, 34, 420–433. [Google Scholar] [CrossRef] [PubMed]
- Hariri, A.; Tavakoli, E.; Adabi, S.; Gelovani, J.; Avanaki, M.R. Functional photoacoustic tomography for neonatal brain imaging: developments and challenges. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing, San Francisco, CA, USA, 28 January–2 February 2017; p. 100642Z. [Google Scholar]
- Mahmoodkalayeh, S.; Jooya, H.Z.; Hariri, A.; Zhou, Y.; Xu, Q.; Ansari, M.A.; Avanaki, M.R. Low temperature-mediated enhancement of photoacoustic imaging depth. Sci. Rep. 2018, 8, 4873. [Google Scholar] [CrossRef] [PubMed]
- Meimani, N.; Abani, N.; Gelovani, J.; Avanaki, M.R. A numerical analysis of a semi-dry coupling configuration in photoacoustic computed tomography for infant brain imaging. Photoacoustics 2017, 7, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V.; Yao, J. A practical guide to photoacoustic tomography in the life sciences. Nat. Methods 2016, 13, 627. [Google Scholar] [CrossRef] [PubMed]
- Laufer, J.; Delpy, D.; Elwell, C.; Beard, P. Quantitative spatially resolved measurement of tissue chromophore concentrations using photoacoustic spectroscopy: application to the measurement of blood oxygenation and haemoglobin concentration. Phys. Med. Biol. 2006, 52, 141. [Google Scholar] [CrossRef] [PubMed]
- Stein, E.W.; Maslov, K.I.; Wang, L.V. Noninvasive, in vivo imaging of blood-oxygenation dynamics within the mouse brain using photoacoustic microscopy. J. Biomed. Opt. 2009, 14, 020502. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xie, X.; Ku, G.; Wang, L.V.; Stoica, G. Noninvasive imaging of hemoglobin concentration and oxygenation in the rat brain using high-resolution photoacoustic tomography. J. Biomed. Opt. 2006, 11, 024015. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V.; Gao, L. Photoacoustic microscopy and computed tomography: from bench to bedside. Annu. Rev. Biomed. Eng. 2014, 16, 155–185. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V.; Hu, S. Photoacoustic tomography: in vivo imaging from organelles to organs. Science 2012, 335, 1458–1462. [Google Scholar] [CrossRef] [PubMed]
- Upputuri, P.K.; Pramanik, M. Performance characterization of low-cost, high-speed, portable pulsed laser diode photoacoustic tomography (PLD-PAT) system. Biomed. Opt. Express 2015, 6, 4118–4129. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Chatni, M.R.; Maslov, K.; Guo, Z.; Wang, K.; Anastasio, M.; Wang, L.V. Whole-body ring-shaped confocal photoacoustic computed tomography of small animals in vivo. J. Biomed. Opt. 2012, 17, 0505061–0505063. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Guo, Z.; Maslov, K.; Aguirre, A.; Zhu, Q.; Percival, C.; Wang, L.V. Three-dimensional photoacoustic tomography based on the focal-line concept. J. Biomed. Opt. 2011, 16, 090505. [Google Scholar] [CrossRef] [PubMed]
- Gamelin, J.K.; Aquirre, A.; Maurudis, A.; Huang, F.; Castillo, D.; Wang, L.V.; Zhu, Q. Curved array photoacoustic tomographic system for small animal imaging. J. Biomed. Opt. 2008, 13, 024007. [Google Scholar] [CrossRef] [PubMed]
- Buxton, R.B.; Wong, E.C.; Frank, L.R. Dynamics of blood flow and oxygenation changes during brain activation: the balloon model. Magn. Reson. Med. 1998, 39, 855–864. [Google Scholar] [CrossRef] [PubMed]
- Gamelin, J.; Maurudis, A.; Aguirre, A.; Huang, F.; Guo, P.; Wang, L.V.; Zhu, Q. A fast 512-element ring array photoacoustic imaging system for small animals. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing, San Jose, CA, USA, 24–29 January 2009; p. 71770B. [Google Scholar]
- Li, G.; Xia, J.; Wang, K.; Maslov, K.; Anastasio, M.A.; Wang, L.V. Tripling the detection view of high-frequency linear-array-based photoacoustic computed tomography by using two planar acoustic reflectors. Quant. Imaging Med. Surg. 2015, 5, 57. [Google Scholar] [PubMed]
- Kondo, K.; Namita, T.; Yamakawa, M.; Shiina, T. Three-dimensional photoacoustic reconstruction for sparse array using compressed sensing based on k-space algorithm. In Proceedings of the IEEE International Conference on the Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; pp. 1–3. [Google Scholar]
- Xiao, J.; He, J. Multispectral quantitative photoacoustic imaging of osteoarthritis in finger joints. Appl. Opt. 2010, 49, 5721–5727. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Pang, Y.; Ku, G.; Xie, X.; Stoica, G.; Wang, L.V. Noninvasive laser-induced photoacoustic tomography for structural and functional in vivo imaging of the brain. Nat. Biotechnol. 2003, 21, 803. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Li, D.; Yuan, Z. Photoacoustic tomography imaging of the adult zebrafish by using unfocused and focused high-frequency ultrasound transducers. Appl. Sci. 2016, 6, 392. [Google Scholar] [CrossRef]
- Xu, M.; Wang, L.V. Time-domain reconstruction for thermoacoustic tomography in a spherical geometry. IEEE Trans. Med. Imaging 2002, 21, 814–822. [Google Scholar] [PubMed]
- Xu, M.; Wang, L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E 2005, 71, 016706. [Google Scholar] [CrossRef] [PubMed]
- Omidi, P.; Zafar, M.; Mozaffarzadeh, M.; Hariri, A.; Haung, X.; Orooji, M.; Nasiriavanaki, M. A novel dictionary-based image reconstruction for photoacoustic computed tomography. Appl. Sci. 2018, 8, 1570. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Height, h | 31 cm |
| External radius, rext | 8 cm |
| Internal radius, rint | 7.5 cm |
| Motor weight, mr | 5 kg |
| Total weight, mt | 7.01 kg |
| Transducer no. | Distance to the Center (cm) |
|---|---|
| 1 | 7.61 |
| 2 | 7.65 |
| 3 | 7.67 |
| 4 | 7.69 |
| 5 | 7.58 |
| 6 | 7.62 |
| 7 | 7.64 |
| 8 | 7.62 |
| 9 | 7.65 |
| 10 | 7.67 |
| 11 | 7.63 |
| 12 | 7.62 |
| 13 | 7.64 |
| 14 | 7.63 |
| 15 | 7.68 |
| 16 | 7.68 |
| Components | Proposed/Full-Ring Array | Cost ($) |
|---|---|---|
| Transducer | 16 single elements/512 elements | ~5K/~65K |
| Amplifiers | Low noise 24dB/customized | ~5K/~25K |
| Servo Motor | Servo/NA | ~250/NA |
| DAQ | 16 channel/512 channel (or 64 channel with MUX) | ~5K/~50 K |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zafar, M.; Kratkiewicz, K.; Manwar, R.; Avanaki, M. Development of Low-Cost Fast Photoacoustic Computed Tomography: System Characterization and Phantom Study. Appl. Sci. 2019, 9, 374. https://doi.org/10.3390/app9030374
Zafar M, Kratkiewicz K, Manwar R, Avanaki M. Development of Low-Cost Fast Photoacoustic Computed Tomography: System Characterization and Phantom Study. Applied Sciences. 2019; 9(3):374. https://doi.org/10.3390/app9030374
Chicago/Turabian StyleZafar, Mohsin, Karl Kratkiewicz, Rayyan Manwar, and Mohammad Avanaki. 2019. "Development of Low-Cost Fast Photoacoustic Computed Tomography: System Characterization and Phantom Study" Applied Sciences 9, no. 3: 374. https://doi.org/10.3390/app9030374
APA StyleZafar, M., Kratkiewicz, K., Manwar, R., & Avanaki, M. (2019). Development of Low-Cost Fast Photoacoustic Computed Tomography: System Characterization and Phantom Study. Applied Sciences, 9(3), 374. https://doi.org/10.3390/app9030374





