Small Infrared Target Detection via a Mexican-Hat Distribution
Abstract
1. Introduction
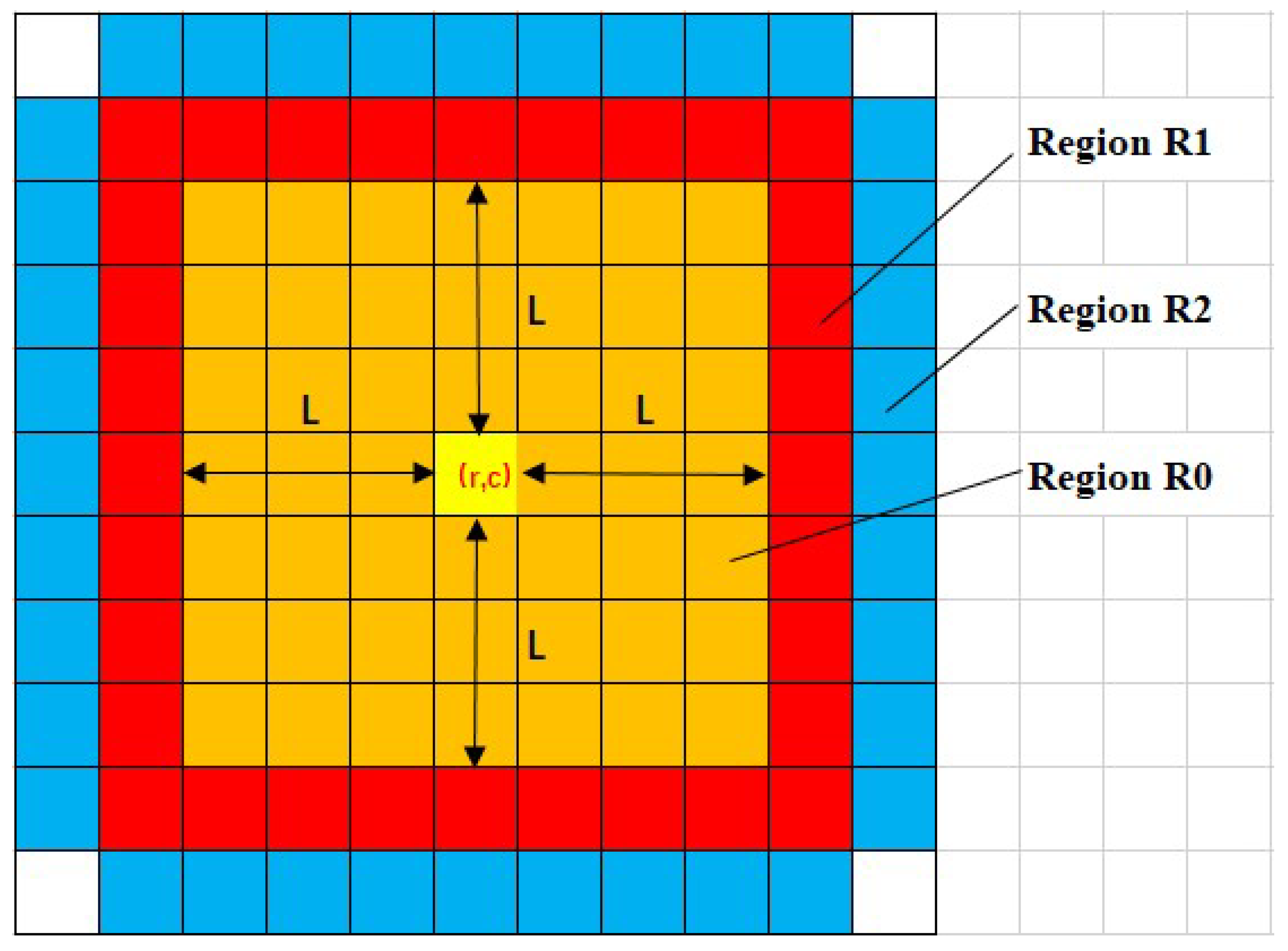
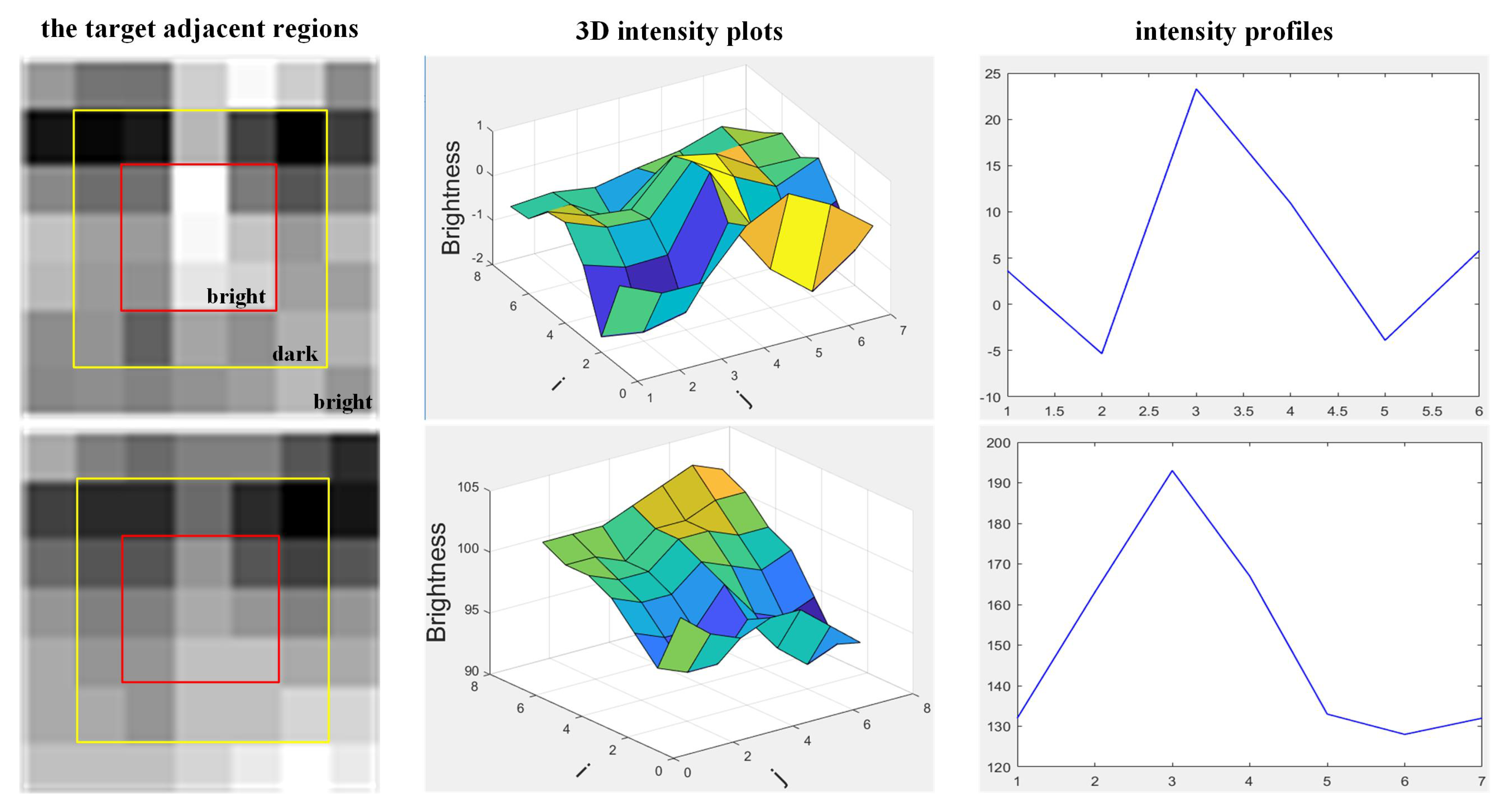
2. Mexican-Hat Distribution of the Adjacent Region around an IR Target
3. The Proposed Method
| Algorithm 1 Candidate target detection. |
|
| Algorithm 2 Our method for detecting small IR target. |
|
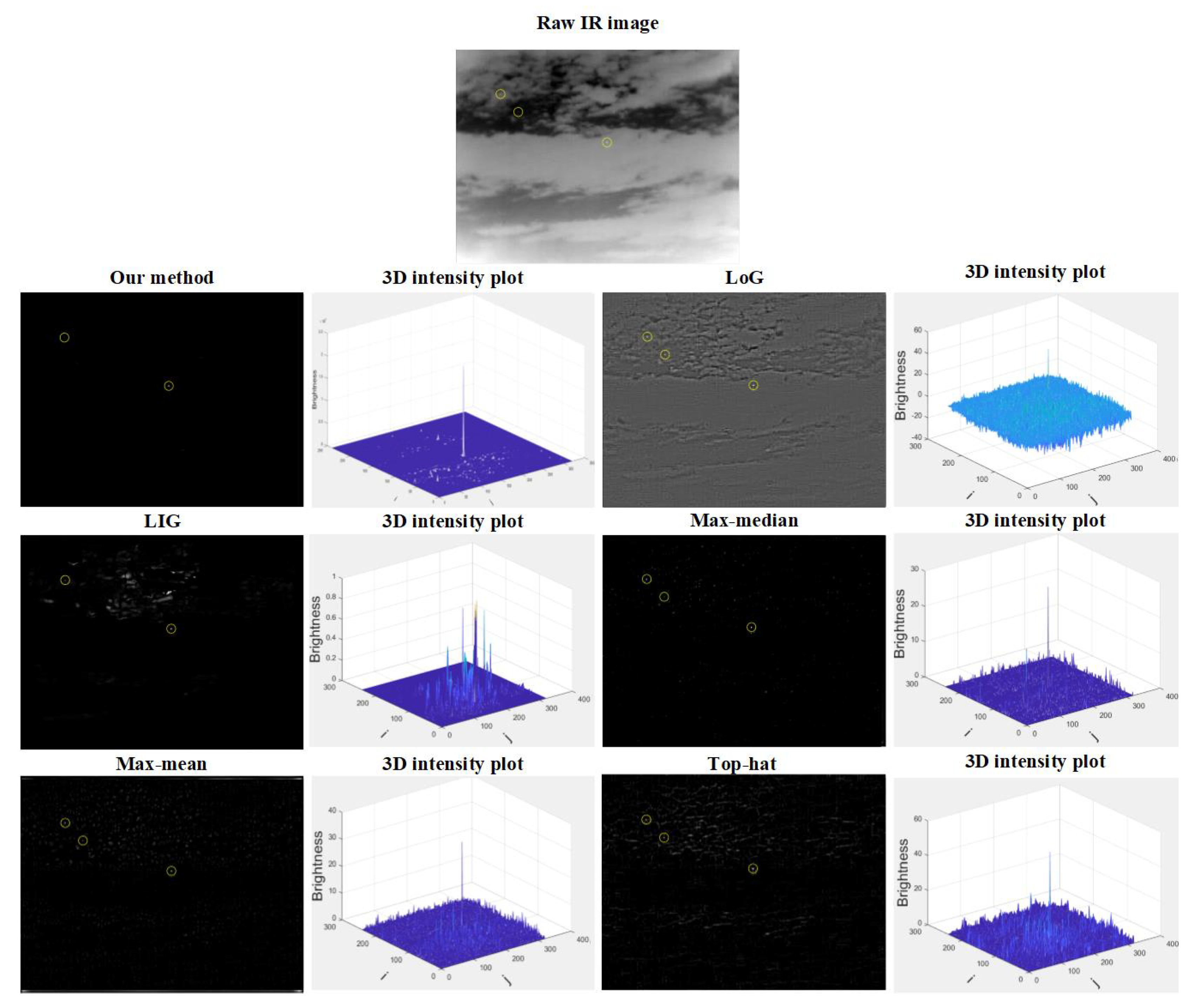
4. Experimental Results and Analysis
4.1. Influences of the Modified Top-Hat Transformation and the DoG
4.2. Step-By-Step Results
4.3. Comparison with Other Methods
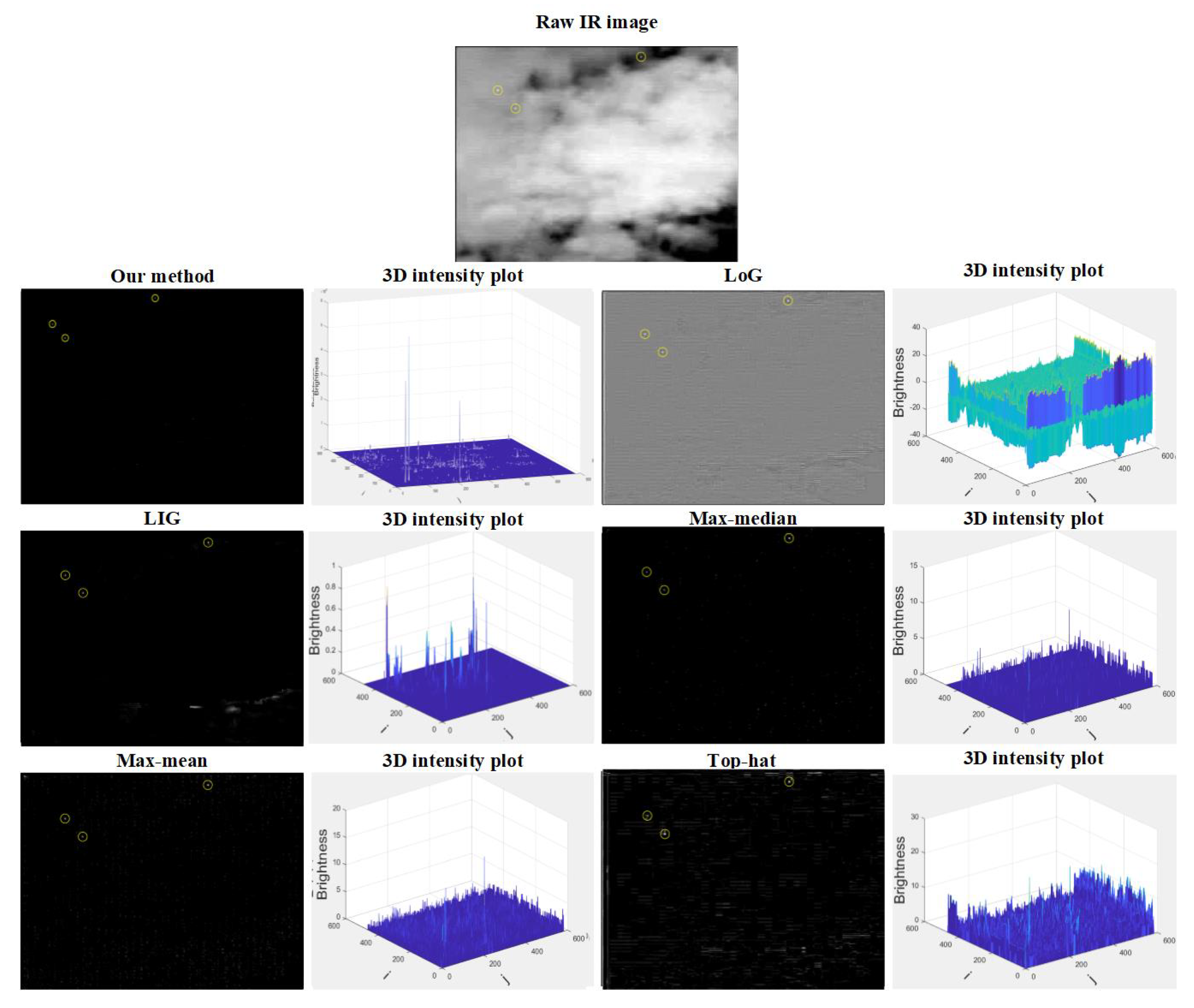
4.4. Multi-Target Detection Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Soni, T.; Zeidler, J.R.; Ku, W.H. Recursive estimation techniques for detection of small objects in infrared image data. In Proceedings of the ICASSP-92: 1992 IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992; Volume 3, pp. 581–584. [Google Scholar]
- Zhang, L.; Peng, Z. Infrared Small Target Detection Based on Partial Sum of the Tensor Nuclear Norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Bai, X. Morphological center operator for enhancing small target obtained by infrared. Opt.-Int. J. Light Electron Opt. 2014, 125, 3697–3701. [Google Scholar] [CrossRef]
- He, Q.; Mo, B.; Liu, F.; He, Y.; Liu, S. Small infrared target detection utilizing Local Region Similarity Difference map. Infrared Phys. Technol. 2015, 71, 131–139. [Google Scholar]
- Deng, L.; Zhu, H.; Zhou, Q.; Li, Y. Adaptive top-hat filter based on quantum genetic algorithm for infrared small target detection. Multimed. Tools Appl. 2017, 77, 10539–10551. [Google Scholar] [CrossRef]
- Itti, L.; Koch, C.; Niebur, E. A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 11, 1254–1259. [Google Scholar] [CrossRef]
- Li, W.; Pan, C.; Liu, L.X. Saliency-based automatic target detection inforward looking infrared images. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; Volume 153, pp. 327–333. [Google Scholar]
- Wang, X.; Lv, G.; Xu, L. Infrared dim target detection based on visual attention. Infrared Phys. Technol. 2014, 55, 513–521. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2014, 52, 574–581. [Google Scholar] [CrossRef]
- Yang, J.; Gu, Y.; Sun, Z.; Cui, Z. A Small Infrared Target Detection Method Using Adaptive Local Contrast Measurement. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; pp. 1–6. [Google Scholar]
- Wei, Y.; You, X.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Deng, H.; Sun, X.; Liu, M.; Ye, C.; Zhou, X. Small infrared target detection based on weighted local difference measure. IEEE Trans. Geosci. Remote Sens. 2016, 10, 4204–4214. [Google Scholar] [CrossRef]
- Han, J.; Ma, Y.; Huang, J.; Mei, X.; Ma, J. An infrared small target detecting algorithm based on human visual system. IEEE Geosci. Remote Sens. Lett. 2016, 13, 452–456. [Google Scholar] [CrossRef]
- Chen, Y.; Song, B.; Wang, D.; Guo, L. An effective infrared small target detection method based on the human visual attention. J. Abbr. 2018, 95, 128–135. [Google Scholar] [CrossRef]
- Nasiri, M.; Chehresa, S. Infrared small target enhancement based on variance difference. Infrared Phys. Technol. 2017, 10, 107–119. [Google Scholar] [CrossRef]
- Bai, X.; Bi, Y. Derivative entropy-based contrast measure for infrared small target detection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2452–2466. [Google Scholar] [CrossRef]
- Liu, J.; He, Z.; Chen, Z.; Shao, L. Tiny and dim infrared target detection based on weighted local contrast. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1780–1784. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, L.; Yuan, D.; Chen, H. Infrared small target detection based on local intensity and gradient properties. Infrared Phys. Technol. 2018, 89, 88–96. [Google Scholar] [CrossRef]
- Yi, X.; Wang, B.; Zhou, H.; Qin, H. Dim and small infrared target fast detection guided by visual saliency. Infrared Phys. Technol. 2019, 97, 6–14. [Google Scholar] [CrossRef]
- Li, L.; Li, Z.; Li, Y.; Chen, C.; Yu, J.; Zhang, C. Small Infrared Target Detection Based on Local Difference Adaptive Measure. IEEE Geosci. Remote Sens. Lett. 2019, 1–5. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, B.; Liu, P. Infrared small target detection based on salient region extraction and gradient vector processing. In Proceedings of the 2019 International Conference on Robotics, Intelligent Control and Artificial Intelligence, Shanghai, China, 20–22 September 2019; pp. 422–426. [Google Scholar]
- Bai, X.; Zhou, F. Infrared small target enhancement and detection based on modified top-hat transformations. Comput. Electr. Eng. 2010, 36, 1193–1201. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Nilufar, S.; Ray, N.; Zhang, H. Object detection with dog scale-space: A multiple kernel learning approach. J. Abbr. 2012, 21, 3744–3756. [Google Scholar] [CrossRef]
- Moradi, S.; Moallem, P.; Sabahi, M.F. A false-alarm aware methodology to develop robust and efficient multi-scale infrared small target detection algorithm. Infrared Phys. Technol. 2018, 89, 387–397. [Google Scholar] [CrossRef]
- Kim, S.; Yang, Y.; Lee, J.; Park, Y. Small target detection utilizing robust methods of the human visual system for IRST. J. Infrared Millimeter Terahertz Waves 2009, 30, 994–1011. [Google Scholar] [CrossRef]
- Deshpande, S.D.; Er, M.H.; Venkateswarlu, R.; Chan, P. Max-mean and max-median filters for detection of small targets. Signal Data Process. Small Targets 1999, 3809, 74–83. [Google Scholar]
- Hilliard, C.I. Selection of a clutter rejection algorithm for real-time target detection from an airborne platform. Signal Data Process. Small Targets 2000, 4048, 74–84. [Google Scholar]
- Gu, Y.; Wang, C.; Liu, B.; Zhang, Y. A kernel-based nonparametric regression method for clutter removal in infrared small-target detection applications. IEEE Geosci. Remote Sens. Lett. 2010, 10, 469–473. [Google Scholar] [CrossRef]







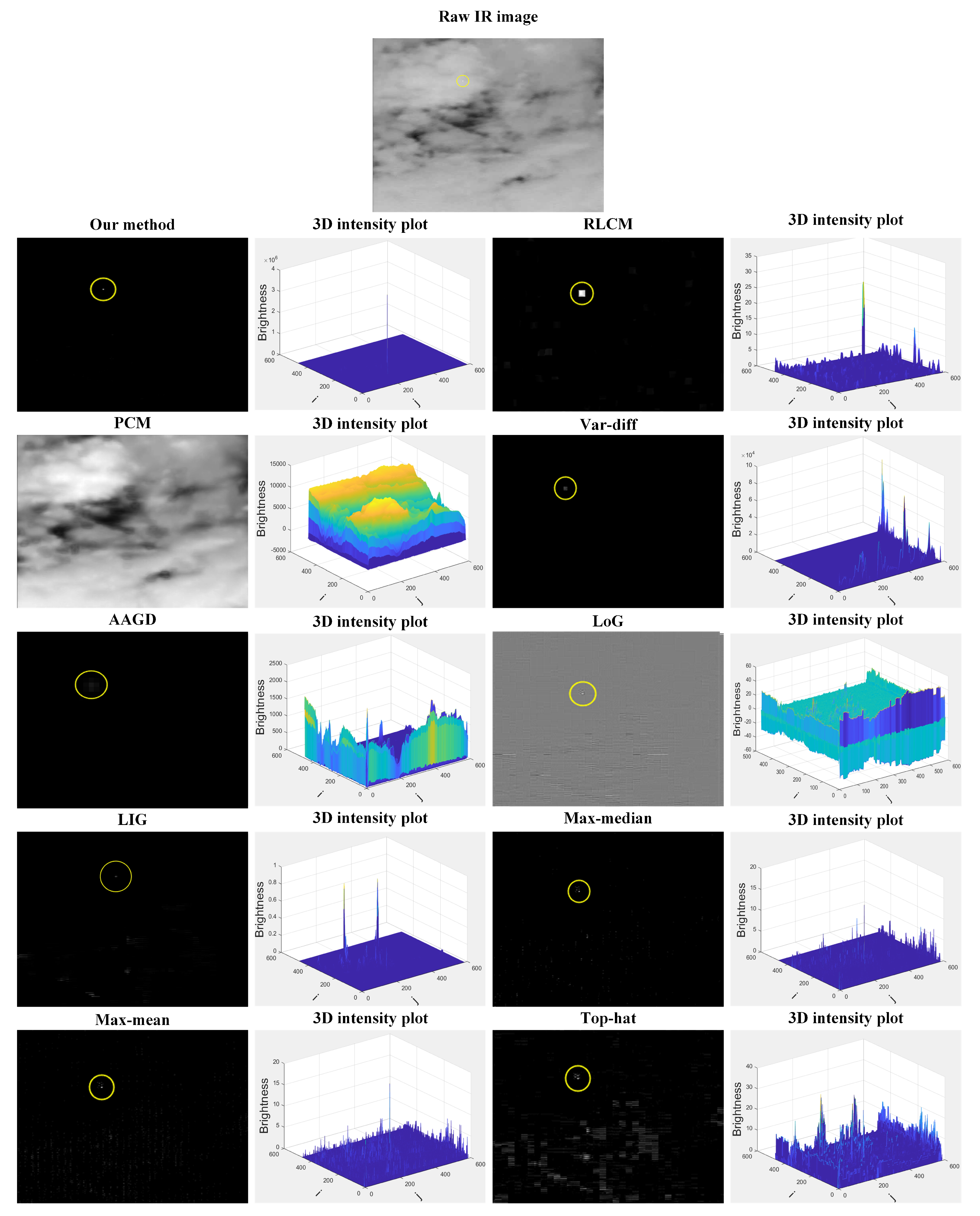

| Method | Our Method | RLCM | PCM | Var-Diff | AAGD | LoG | LIG | Max–Median | Max–Mean | Top-Hat |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.9900 | 0.0600 | 0 | 0.2600 | 0 | 0.3500 | 0.8100 | 1 | 0.9900 | 0.9000 | |
| 0.0100 | 0.0500 | 0 | 0.1300 | 0 | 0.2300 | 0.0900 | 0 | 0 | 0.0400 | |
| SCRG | 203.9131 | 0.3930 | 0.0025 | 0.4481 | 0.0055 | 0.0275 | 0.0275 | 0.3577 | 0.2193 | 0.1267 |
| BSF | 113.8130 | 0.0004 | 1.1872 | 0.2359 | 0.0703 | 0.0018 | 0.0018 | 0.00004 | 0.0001 | 0.0004 |
| Time (second) | 1.8572 | 40.3541 | 0.4709 | 0.1362 | 0.1537 | 0.1144 | 7.5586 | 6.8573 | 15.4546 | 0.1023 |
| Method | Our Method | RLCM | PCM | Var-Diff | AAGD | LoG | LIG | Max–Median | Max–Mean | Top-Hat |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.9688 | 0.3438 | 0 | 0.0313 | 0 | 0.9063 | 0.5313 | 0.8750 | 0.9063 | 0.9063 | |
| 0 | 0.5626 | 0 | 0.8750 | 0 | 0.0625 | 0.3125 | 0.1250 | 0.0625 | 0.0625 | |
| SCRG | 4920.8611 | 0.0029 | 0.0252 | 0.0632 | 0.0030 | 0.0172 | 0.1482 | 0.2515 | 0.0901 | 0.1482 |
| BSF | 612.0357 | 0.0005 | 7.8553 | 2.1969 | 0.1317 | 0.0019 | 0.0009 | 0.0002 | 0.0004 | 0.0009 |
| Time (second) | 0.8690 | 14.6853 | 0.1861 | 0.1057 | 0.1102 | 0.1040 | 2.1391 | 2.0189 | 4.6056 | 0.1294 |
| Method | Our Method | LoG | LIG | Max–Median | Max–Mean | Top-Hat |
|---|---|---|---|---|---|---|
| 0.9667 | 0.8000 | 0.8667 | 0.7111 | 0.7333 | 0.8444 | |
| 0.0333 | 0.2000 | 0.1333 | 0.2889 | 0.2667 | 0.1556 |
| Method | Our Method | LoG | LIG | Max–Median | Max–Mean | Top-Hat |
|---|---|---|---|---|---|---|
| 0.6556 | 0.8030 | 0.7396 | 0.5729 | 0.6979 | 0.7369 | |
| 0.3444 | 0.1969 | 0.2604 | 0.4271 | 0.3021 | 0.2604 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zheng, L.; Zhang, Y. Small Infrared Target Detection via a Mexican-Hat Distribution. Appl. Sci. 2019, 9, 5570. https://doi.org/10.3390/app9245570
Zhang Y, Zheng L, Zhang Y. Small Infrared Target Detection via a Mexican-Hat Distribution. Applied Sciences. 2019; 9(24):5570. https://doi.org/10.3390/app9245570
Chicago/Turabian StyleZhang, Yubo, Liying Zheng, and Yanbo Zhang. 2019. "Small Infrared Target Detection via a Mexican-Hat Distribution" Applied Sciences 9, no. 24: 5570. https://doi.org/10.3390/app9245570
APA StyleZhang, Y., Zheng, L., & Zhang, Y. (2019). Small Infrared Target Detection via a Mexican-Hat Distribution. Applied Sciences, 9(24), 5570. https://doi.org/10.3390/app9245570





