Predicting Students Success in Blended Learning—Evaluating Different Interactions Inside Learning Management Systems
Abstract
1. Introduction
- RQ1.
- Which are the most appropriate datasets to early predict at-risk students?
- RQ2.
- Is the sole use of the count of students interactions sufficient to early predict students’ failure in the course?
- RQ3.
- Does the use of oversampling techniques (SMOTE) help the models to achieve better performances?
- RQ4.
- Does the use of data from questionnaires applied at the beginning of the course help to improve model performance?
2. Related Work
2.1. Programming Courses
2.2. Computer Science/IT Courses
2.3. University
2.4. Fully Online
2.5. Blended Courses
2.6. Multiple Data Sources
2.7. Only Interaction Data/Log Files
2.8. Early Prediction
2.9. Approach Novelty
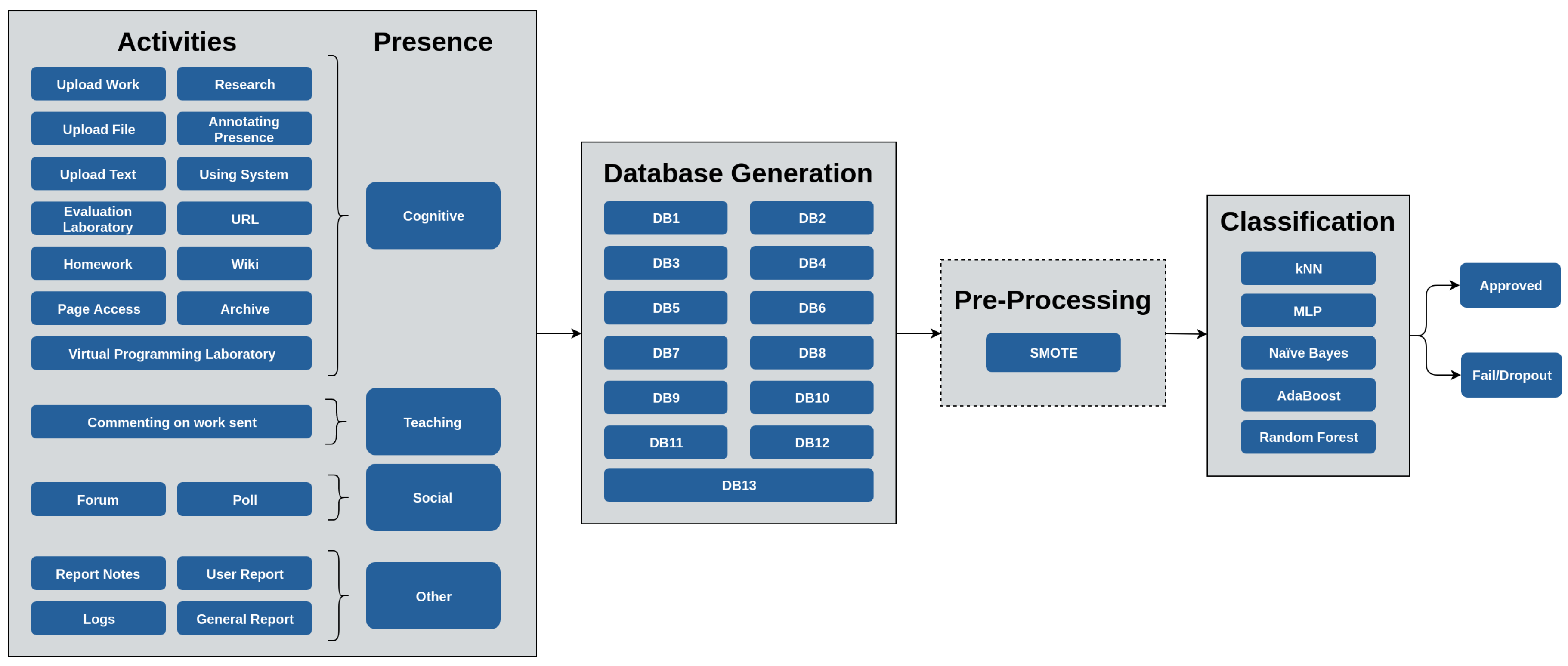
3. Methodology
3.1. Data Collection and Description
3.2. Dataset Generation
3.3. Data Pre-Processing
3.4. Generation and Evaluation of the Models
3.5. Comparison between Cases
4. Results
4.1. Research Questions
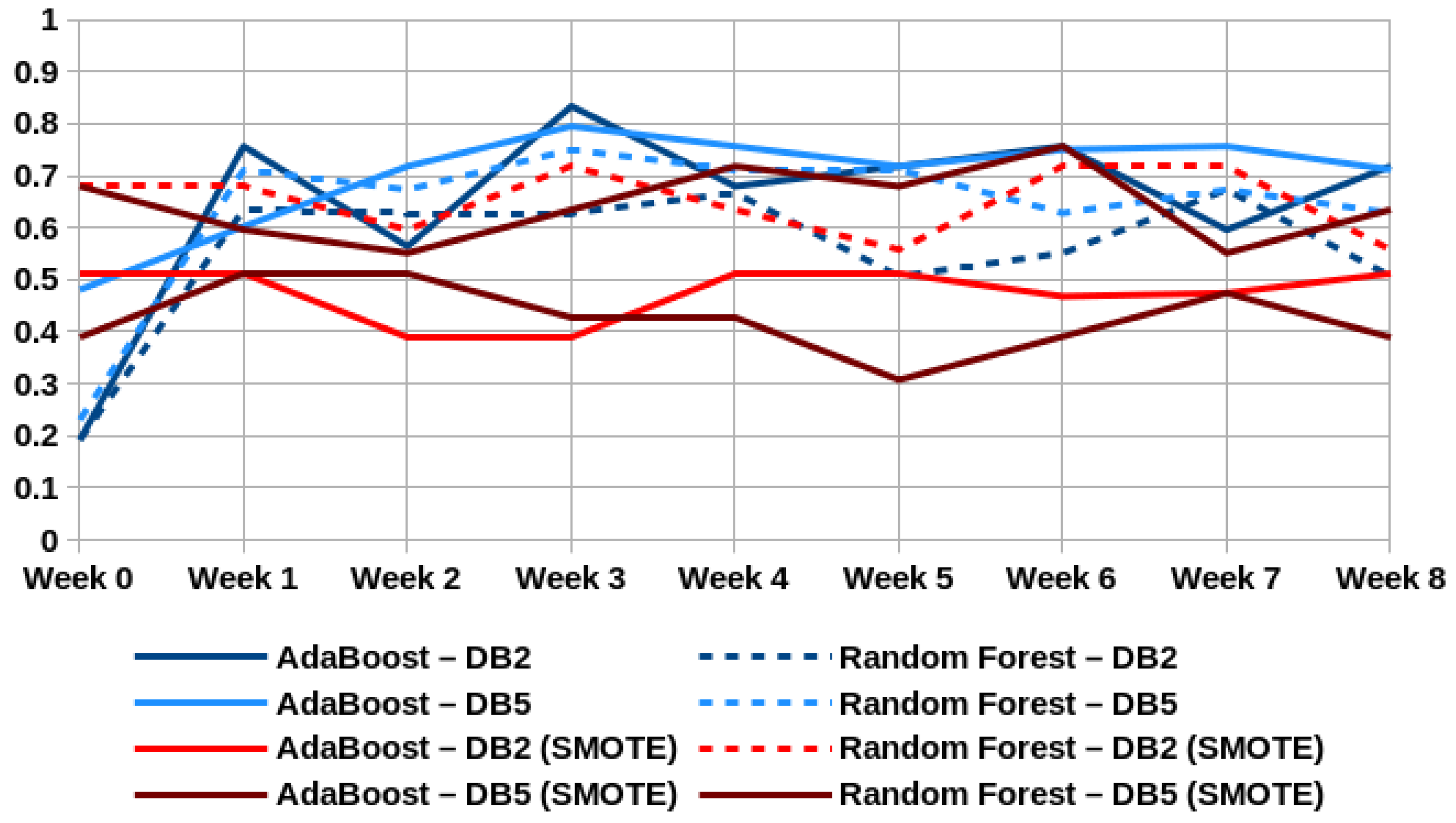
4.1.1. RQ1. Which Are the Most Appropriate Datasets to Early Predict at-Risk Students?
4.1.2. RQ2. The Sole Use of the Count of Student Interactions Is Sufficient to Early Predict Students’ Failure in the Course?
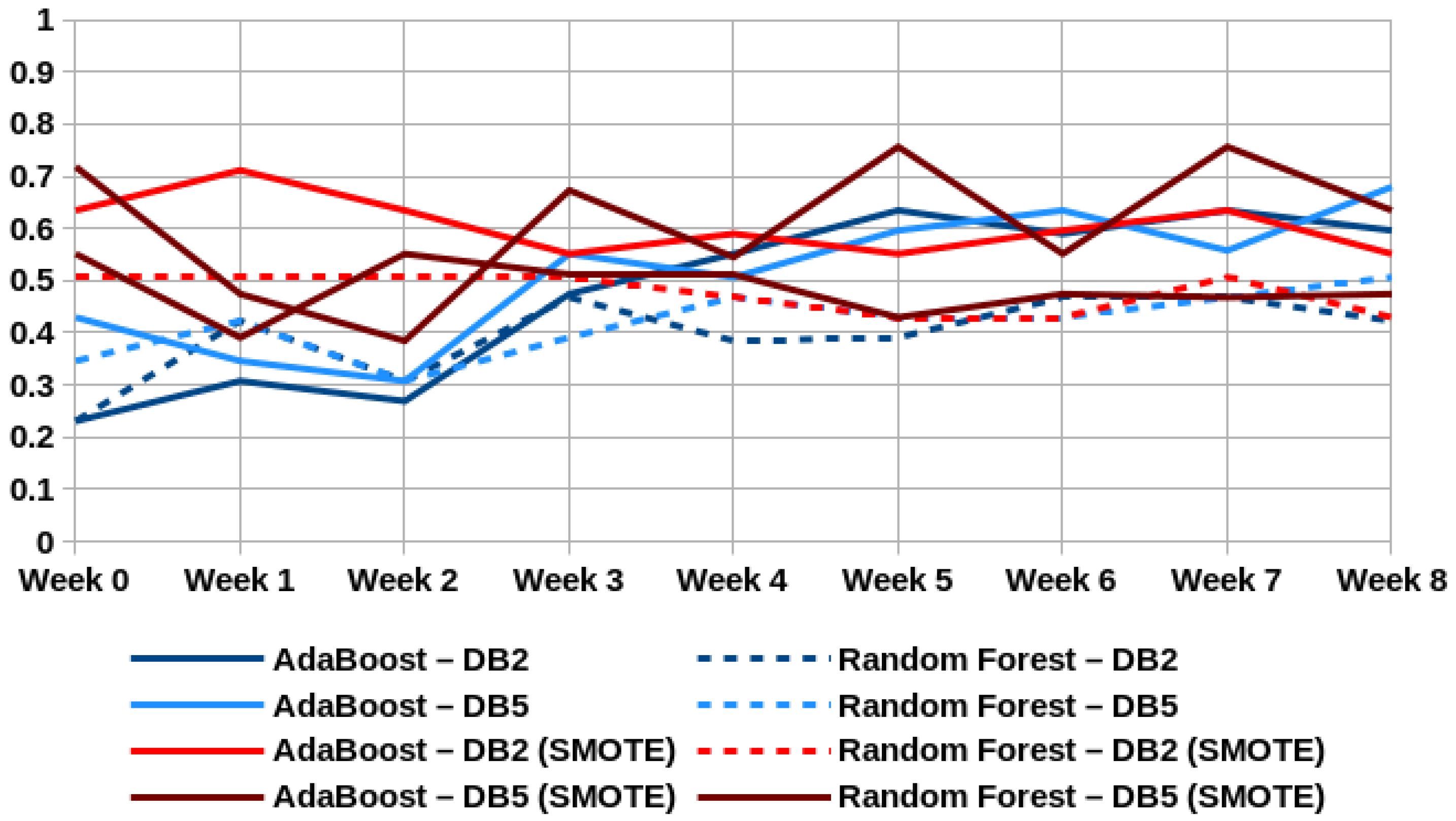
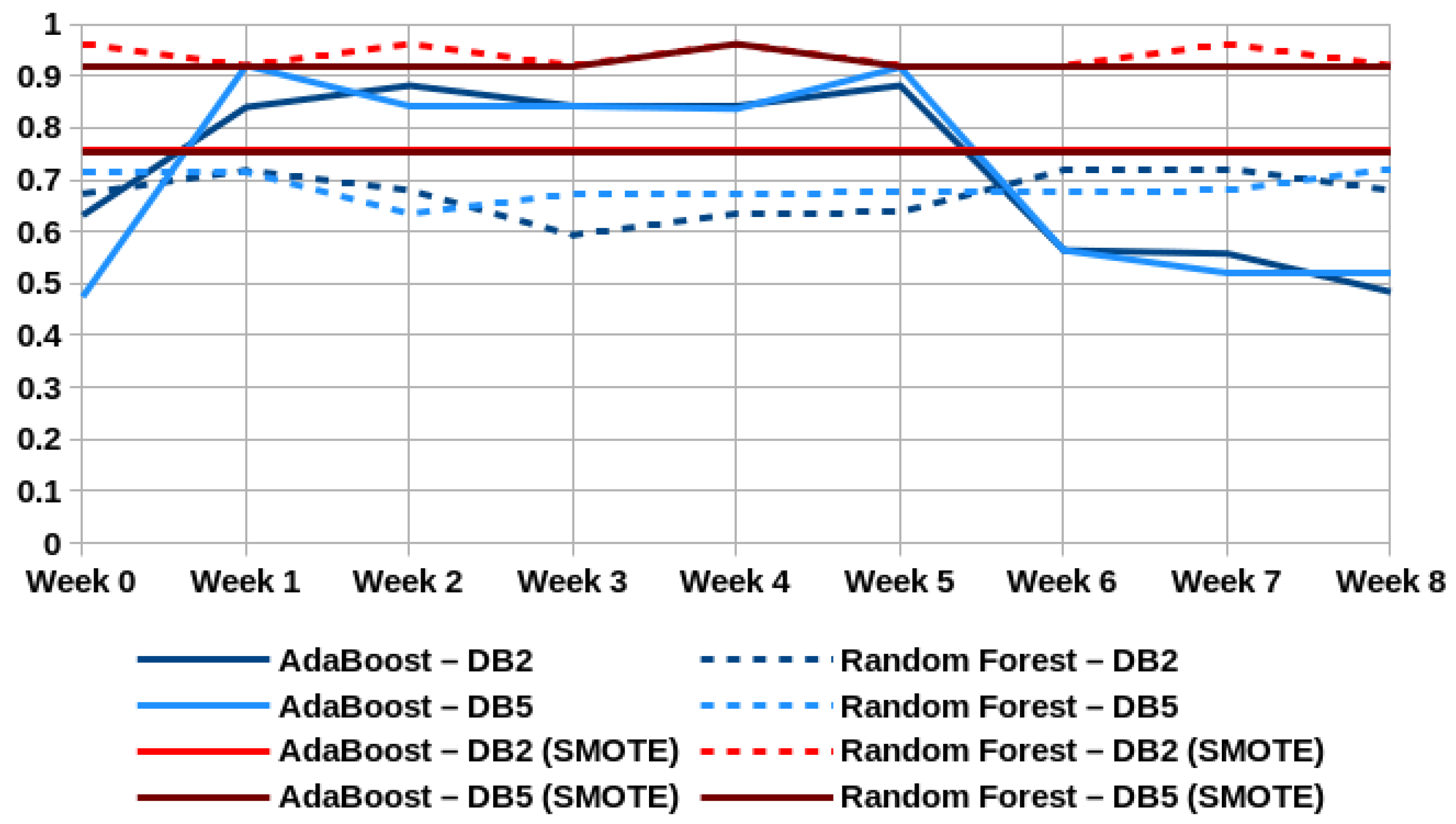
4.1.3. RQ3. Does the Use of Oversampling Techniques (SMOTE) Help the Models to Achieve Better Performances?
4.1.4. RQ4. Does the Use of Data from Questionnaires Applied at the Beginning of the Course Help to Improve Models Performance?
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| APA | Average prediction Accuracy |
| BART | Bayesian Additive Regressive Trees |
| DT | Decision Tree |
| e-SVR | e-insensitive Support Vector Regressors |
| EDM | Educational Data Mining |
| IT | Information Technology |
| kNN | k-Nearest Neighbor |
| LA | Learning Analytics |
| LMS | Learning Management Systems |
| MAE | Mean Absolute Error |
| MLP | Multilayer Perceptron |
| NN | Neural Networks |
| PAP | Percentage Accurate Predictions |
| PCR | Principal Components Regression |
| RF | Random Forest |
| RMSE | Root Mean Square Error |
| SVM | Support Vector Machine |
| VLE | Virtual Learning Environment |
| VPL | Virtual Programming Laboratory plugin |
Appendix A. Related Literature—Overview of Context and Main Characteristics
| Article | Number of Participants | Data-Mining/Machine Learning Techniques | Statistics Packages | Corpus | Measure |
| [24] | 423 | Naive Bayes, DT, NN, SVM | Pentaho Data Integration tool, WEKA, SMOTE | Distance education, On campus | F-measure, Precision, Recall |
| [26] | 950 | kNN, DT, RF, Logistic regression, Linear SVM, Gaussian SVM | Scikit-learn | Custom VLE | AUC, F-measure, precision, recall |
| [27] | 271 | Support Vector Classifiers, e-SVR | Not informed | Interaction with HTML elements | F-measure, R-squared |
| [28] | 145 | Multiple backwards stepwise regression, multiple squared correlation, binary logistic regressions | SPSS | LMS and Academic performance | Z-scores |
| [29] | 527 | Logistic regression, DT, and kNN | Not informed | Moodle, Piazza, Github Enterprise, WebAssign. | Kendall rank correlation coefficient, F-Measure |
| [30] | 1403 | Multiple linear regression | SPSS | home-grown EWS (early warning system) plug-in for Moodle | R-squared, ANOVA analysis |
| [31] | 21,314 | Linear regression, Robust linear regression, RF | Not informed | Student administrative information system, LMS | R2, MAE, RMSE, APA, PAP, Precision, Recall, F-score |
| [32] | 171 | Linear Regression, RF | Developed Analytics Tool and SPSS | VLE Interaction | R-squared |
| [34] | 646 | Logistic Regression, Hierarchical linear regression | SPSS | VLE Interaction and assignment score | ANOVA analysis |
| [35] | 3882 | C4.5 DT, Radial Basis Function, kNN, Naive Bayes, Reduced Error Pruning Tree, SVM (SMO), AdaBoost, LogitBoost, Rotation Forest, Linear Regression, M5’ Algorithm, M5’ Rules Algorithm, RBF Networks, kNN | Free Implementation | pre-university and performance data (17 attributes) | Accuracy, MAE |
| [36] | 608 courses. Not mention the number of students. | CART DT, kNN, Naive Bayes, SVM | Weka, Python and Scikit-learn | Universitat Oberta de Calanunya Data Mart | precision, recall, F-measure, classification error and RMS |
| [37] | 4989 | multi-level and standard regressions | STATA 14 | VLE Interaction and assignment score | Accuracy, F-measure, R-Squared |
| [38] | 717 | DT | Not informed | VLE Interaction | Accuracy, F-measure |
| [39] | 141 | DT, NN, SVM, Stacking Ensemble (combining the other three) | SPSS, Rapid Miner Studio | student record system, LMS, and survey | Precision, Recall, F-measures, classification error and RMS |
| [40] | 99 | RF, Naive Bayes, kNN, LDA | scikit-learn | VLE Interaction and assignment score | Accuracy, kappa coefficient, F-meassure, AUC |
| [41] | 78,722 | NN | Not informed | VLE Interaction | Accuracy, F-measure |
| [42] | 362 | Not informed | Not informed | VLE Interaction | Accuracy |
| [43] | 202 | Logistic Regression, RF, SVM | Not informed | VLE Interaction | Precision, recall, and F-measure |
| [44] | 515 | kNN, Naive Bayes, DT (Adaboost) | Weka | VLE Interaction | Accuracy |
| [25] | 578 | SVM, Naive Bayes, DT (Adaboost) | Not informed | VLE Interaction | False-Positive, False-Negative, AUC |
| [46] | 136 | BART, RF, PCR, Multivariate Adaptive Regression Splines, kNN, NN, and SVM, XGBoost | R | Students’ background information, continuous assessment, and VLE interaction | MAE |
| [47] | 59 | Principal Component Regression | Not informed | student learning profiles, out-of-class practice behaviors, homework and quiz scores, and after-school tutoring | MSE, R2, Q-Q, predictive MSE, predictive mean absolute, percentage correction |
| [48] | 9847 | Floating search, Sequential Forward Selection, C4.5, RF, RF Regression, Random Tree, Random Tree Regression, MLP, SOM, Naive Bayes, Decision Table, C4.5, kNN | Weka | 32 features | F-measure, accuracy, Precision, AUC, Recall |
References
- Bennedsen, J.; Caspersen, M.E. Failure rates in introductory programming: 12 years later. ACM Inroads 2019, 10, 30–36. [Google Scholar] [CrossRef]
- Watson, C.; Li, F.W. Failure rates in introductory programming revisited. In Proceedings of the 2014 Conference on Innovation & Technology in Computer Science Education, Uppsala, Sweden, 21–25 June 2014; pp. 39–44. [Google Scholar]
- Dasuki, S.; Quaye, A. Undergraduate Students’ Failure in Programming Courses in Institutions of Higher Education in Developing Countries: A Nigerian Perspective. Electron. J. Inf. Syst. Dev. Ctries. 2016, 76, 1–18. [Google Scholar] [CrossRef]
- Hawi, N. Causal attributions of success and failure made by undergraduate students in an introductory-level computer programming course. Comput. Educ. 2010, 54, 1127–1136. [Google Scholar] [CrossRef]
- Krpan, D.; Mladenović, S.; Rosić, M. Undergraduate Programming Courses, Students’ Perception and Success. Procedia- Behav. Sci. 2015, 174, 3868–3872. [Google Scholar] [CrossRef][Green Version]
- Jenkins, T. On the difficulty of learning to program. In Proceedings of the 3rd Annual Conference of the LTSN Centre for Information and Computer Sciences, The Higher Education Academy, Loughborough, UK, 27–29 August 2002; Volume 4, pp. 53–58. [Google Scholar]
- Dunican, E. Making the analogy: Alternative delivery techniques for first year programming courses. In Proceedings of the 14th Workshop of the Psychology of Programming Interest Group, London, UK, 18 June 2002. [Google Scholar]
- Byrne, P.; Lyons, G. The effect of student attributes on success in programming. Acm Sigcse Bull. 2001, 33, 49–52. [Google Scholar] [CrossRef]
- BRASSCOM. Relatório Setorial de TIC. Technical Report, Brasscom, 2019. Available online: https://brasscom.org.br/relatorio-setorial-de-tic-2019/ (accessed on 3 October 2019).
- Gareis, K.; Hüsing, T.; Birov, S.; Bludova, I.; Schulz, C.; Korte, W. E-Skills for Jobs in Europe: Measuring Progress and Moving Ahead; European Commission: Brussels, Belgium, 2014.
- Korte, W.; Hüsing, T.; Dashja, E. High-Tech Leadership Skills for Europe-Towards an Agenda for 2020 and Beyond; European Communities: Brussels, Belgium, 2017. [Google Scholar]
- European Political Strategy Centre (EPSC). Global Trends to 2030: The Future of Work and Workspaces. Technical Report, European Strategy and Policy Analysis System, 2018. Available online: https://espas.secure.europarl.europa.eu/orbis/sites/default/files/generated/document/en/Ideas%20Paper%20Future%20of%20work%20V02.pdf (accessed on 3 October 2019).
- Bughin, J.; Hazan, E.; Lund, S.; Dahlström, P.; Wiesinger, A.; Subramaniam, A. Skill Shift: Automation and the Future of the Workforce; McKinsey Global Institute. McKinsey & Company: Brussels, Belgium, 2018. [Google Scholar]
- Resnick, M. Mother’s Day, Warrior Cats, and Digital Fluency: Stories from the Scratch Online Community. In Proceedings of the Constructionism 2012 Conference: Theory, Practice and Impact, Athens, Greece, 21–25 August 2012; pp. 52–58. [Google Scholar]
- Macfadyen, L.P.; Dawson, S. Mining LMS data to develop an ’early warning system’ for educators: A proof of concept. Comput. Educ. 2010, 54, 588–599. [Google Scholar] [CrossRef]
- Lakkaraju, H.; Aguiar, E.; Shan, C.; Miller, D.; Bhanpuri, N.; Ghani, R.; Addison, K.L. A machine learning framework to identify students at risk of adverse academic outcomes. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; pp. 1909–1918. [Google Scholar]
- Romero, C.; Ventura, S. Data mining in education. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2013, 3, 12–27. [Google Scholar] [CrossRef]
- Mishra, T.; Kumar, D.; Gupta, S. Mining students’ data for prediction performance. In Proceedings of the 2014 Fourth International Conference on Advanced Computing & Communication Technologies (ACCT), Rohtak, India, 8–9 February 2014; pp. 255–262. [Google Scholar]
- Murray, M.; Pérez, J.; Geist, D.; Hedrick, A. Student interaction with content in online and hybrid courses: Leading horses to the proverbial water. In Proceedings of the Informing Science and Information Technology Education Conference, Porto, Portugal, 1–6 July 2013; Informing Science Institute: Porto, Portugal, 2013; pp. 99–115. [Google Scholar]
- Dickson, W.P. Toward a Deeper Understanding of Student Performance in Virtual High School Courses: Using qUantitative Analyses and Data Visualization to Inform Decision Making; Technical Report; NCREL/Learning Point Associates: Naperville, IL, USA, 2005; Available online: https://msu.edu/user/pdickson/talks/DicksonNCREL2005.pdf (accessed on 13 December 2019).
- Romero, C.; Ventura, S. Educational data mining: A review of the state of the art. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2010, 40, 601–618. [Google Scholar] [CrossRef]
- Garrison, D.R.; Anderson, T.; Archer, W. Critical inquiry in a text-based environment: Computer conferencing in higher education. Internet High. Educ. 1999, 2, 87–105. [Google Scholar] [CrossRef]
- Swan, K. Learning effectiveness online: What the research tells us. Elem. Qual. Online Educ. Pract. Dir. 2003, 4, 13–47. [Google Scholar]
- Costa, E.B.; Fonseca, B.; Santana, M.A.; de Araújo, F.F.; Rego, J. Evaluating the effectiveness of educational data mining techniques for early prediction of students’ academic failure in introductory programming courses. Comput. Hum. Behav. 2017, 73, 247–256. [Google Scholar] [CrossRef]
- Detoni, D.; Cechinel, C.; Matsumura, R.A.; Brauner, D.F. Learning to Identify At-Risk Students in Distance Education Using Interaction Counts. Rev. De Informática Teórica E Apl. 2016, 23, 124–140. [Google Scholar] [CrossRef][Green Version]
- Azcona, D.; Hsiao, I.H.; Smeaton, A.F. Detecting students-at-risk in computer programming classes with learning analytics from students’ digital footprints. In User Modeling and User-Adapted Interaction; Springer: Berlin, Germany, 2019; pp. 1–30. [Google Scholar]
- Leppänen, L.; Leinonen, J.; Ihantola, P.; Hellas, A. Predicting Academic Success Based on Learning Material Usage. In Proceedings of the 18th Annual Conference on Information Technology Education, Rochester, NY, USA, 4–7 October 2017; pp. 13–18. [Google Scholar]
- Tillmann, A.; Krömker, D.; Horn, F.; Gattinger, T. Analysing & Predicting Students Performance in an Introductory Computer Science Course; Hochschuldidaktik der Informatik HDI 2018; Universität Potsdam: Potsdam, Germany, 2018; pp. 29–46. [Google Scholar]
- Sheshadri, A.; Gitinabard, N.; Lynch, C.F.; Barnes, T.; Heckman, S. Predicting student performance based on online study habits: A study of blended courses. arXiv 2019, arXiv:1904.07331. [Google Scholar]
- Jokhan, A.; Sharma, B.; Singh, S. Early warning system as a predictor for student performance in higher education blended courses. Stud. Higher Educ. 2018, 44, 1900–1911. [Google Scholar] [CrossRef]
- Sandoval, A.; Gonzalez, C.; Alarcon, R.; Pichara, K.; Montenegro, M. Centralized student performance prediction in large courses based on low-cost variables in an institutional context. Internet High. Educ. 2018, 37, 76–89. [Google Scholar] [CrossRef]
- Mwalumbwe, I.; Mtebe, J.S. Using learning analytics to predict students’ performance in moodle learning management system: A case of mbeya university of science and technology. Electron. J. Inf. Syst. Dev. Ctries. 2017, 79, 1–13. [Google Scholar] [CrossRef]
- Hung, J.L.; Wang, M.C.; Wang, S.; Abdelrasoul, M.; Li, Y.; He, W. Identifying at-risk students for early interventions—A time-series clustering approach. IEEE Trans. Emerg. Top. Comput. 2017, 5, 45–55. [Google Scholar] [CrossRef]
- Soffer, T.; Cohen, A. Students’ engagement characteristics predict success and completion of online courses. J. Comput. Assisted Learn. 2019, 35, 378–389. [Google Scholar] [CrossRef]
- Kostopoulos, G.; Kotsiantis, S.; Pierrakeas, C.; Koutsonikos, G.; Gravvanis, G.A. Forecasting students’ success in an open university. Int. J. Learn. Technol. 2018, 13, 26–43. [Google Scholar] [CrossRef]
- Baneres, D.; Rodriguez-Gonzalez, M.E.; Serra, M. An Early Feedback Prediction System for Learners At-risk within a First-year Higher Education Course. IEEE Trans. Learn. Technol. 2019, 12, 249–263. [Google Scholar] [CrossRef]
- Conijn, R.; Snijders, C.; Kleingeld, A.; Matzat, U. Predicting student performance from LMS data: A comparison of 17 blended courses using Moodle. IEEE Trans. Learn. Technol. 2017, 10, 17–29. [Google Scholar] [CrossRef]
- Sukhbaatar, O.; Ogata, K.; Usagawa, T. Mining Educational Data to Predict Academic Dropouts: A Case Study in Blended Learning Course. In Proceedings of the IEEE TENCON 2018-2018 IEEE Region 10 Conference, Jeju, Korea, 28–31 October 2018; pp. 2205–2208. [Google Scholar]
- Adejo, O.W.; Connolly, T. Predicting student academic performance using multi-model heterogeneous ensemble approach. J. Appl. Res. High. Educ. 2018, 10, 61–75. [Google Scholar] [CrossRef]
- Umer, R.; Mathrani, A.; Susnjak, T.; Lim, S. Mining Activity Log Data to Predict Student’s Outcome in a Course. In Proceedings of the 2019 International Conference on Big Data and Education, London, UK, 30 March–1 April 2019; pp. 52–58. [Google Scholar]
- Olivé, D.M.; Huynh, D.; Reynolds, M.; Dougiamas, M.; Wiese, D. A Quest for a one-size-fits-all Neural Network: Early Prediction of Students At Risk in Online Courses. IEEE Trans. Learn. Technol. 2019, 12, 171–183. [Google Scholar] [CrossRef]
- Cohen, A. Analysis of student activity in web-supported courses as a tool for predicting dropout. Educ. Technol. Res. Dev. 2017, 65, 1285–1304. [Google Scholar] [CrossRef]
- Kondo, N.; Okubo, M.; Hatanaka, T. Early Detection of At-Risk Students Using Machine Learning Based on LMS Log Data. In Proceedings of the 2017 6th IIAI International Congress on Advanced Applied Informatics (IIAI-AAI), Hamamatsu, Japan, 9–13 July 2017; pp. 198–201. [Google Scholar]
- Usman, U.I.; Salisu, A.; Barroon, A.I.; Yusuf, A. A Comparative Study of Base Classifiers in Predicting Students’ Performance based on Interaction with LMS Platform. FUDMA J. Sci. 2019, 3, 231–239. [Google Scholar]
- Zhou, Q.; Quan, W.; Zhong, Y.; Xiao, W.; Mou, C.; Wang, Y. Predicting high-risk students using Internet access logs. Knowl. Inf. Syst. 2018, 55, 393–413. [Google Scholar] [CrossRef]
- Howard, E.; Meehan, M.; Parnell, A. Contrasting prediction methods for early warning systems at undergraduate level. Internet High. Educ. 2018, 37, 66–75. [Google Scholar] [CrossRef]
- Lu, O.H.; Huang, A.Y.; Huang, J.C.; Lin, A.J.; Ogata, H.; Yang, S.J. Applying Learning Analytics for the Early Prediction of Students’ Academic Performance in Blended Learning. J. Educ. Technol. Soc. 2018, 21, 220–232. [Google Scholar]
- Gray, C.C.; Perkins, D. Utilizing early engagement and machine learning to predict student outcomes. Comput. Educ. 2019, 131, 22–32. [Google Scholar] [CrossRef]
- Rodríguez-del Pino, J.C.; Rubio-Royo, E.; Hernández-Figueroa, Z.J. A Virtual Programming Lab for Moodle with automatic assessment and anti-plagiarism features. In Proceedings of the International Conference on e-Learning, e-Business, Enterprise Information Systems, and e-Government (EEE), Las Vegas, ND, USA, 16–19 July 2012; The Steering Committee of The World Congress in Computer Science, CSREA Press: Las Vegas, ND, USA, 2012; pp. 80–85. [Google Scholar]
- Detoni, D.; Cechinel, C.; Matsumura Araújo, R. Modelagem e Predição de Reprovação de Acadêmicos de Cursos de Educação a Distância a partir da Contagem de Interações. Revista Brasileira de Informática na Educação 2015, 23, 1–11. [Google Scholar]
- Moore, M.G. Three types of interaction. Am. J. Distance Educ. 1989, 3, 1–7. [Google Scholar]
- McKinney, W. Data structures for statistical computing in python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28–30 June 2010; Volume 445, pp. 51–56. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Lemaître, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Gašević, D.; Dawson, S.; Rogers, T.; Gasevic, D. Learning analytics should not promote one size fits all: The effects of instructional conditions in predicting academic success. Internet High. Educ. 2016, 28, 68–84. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Umer, R.; Susnjak, T.; Mathrani, A.; Suriadi, S. A learning analytics approach: Using online weekly student engagement data to make predictions on student performance. In Proceedings of the 2018 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 12–13 November 2018; pp. 1–5. [Google Scholar]
- Brooks, C.; Thompson, C.; Teasley, S. Who you are or what you do: Comparing the predictive power of demographics vs. activity patterns in massive open online courses (MOOCs). In Proceedings of the Second (2015) ACM Conference on Learning@ Scale, Vancouver, BC, Canada, 14–18 March 2015; pp. 245–248. [Google Scholar]

| Semester | Interaction Count | Average of Interaction | Students Approved | Students Reproved | Total of Students |
|---|---|---|---|---|---|
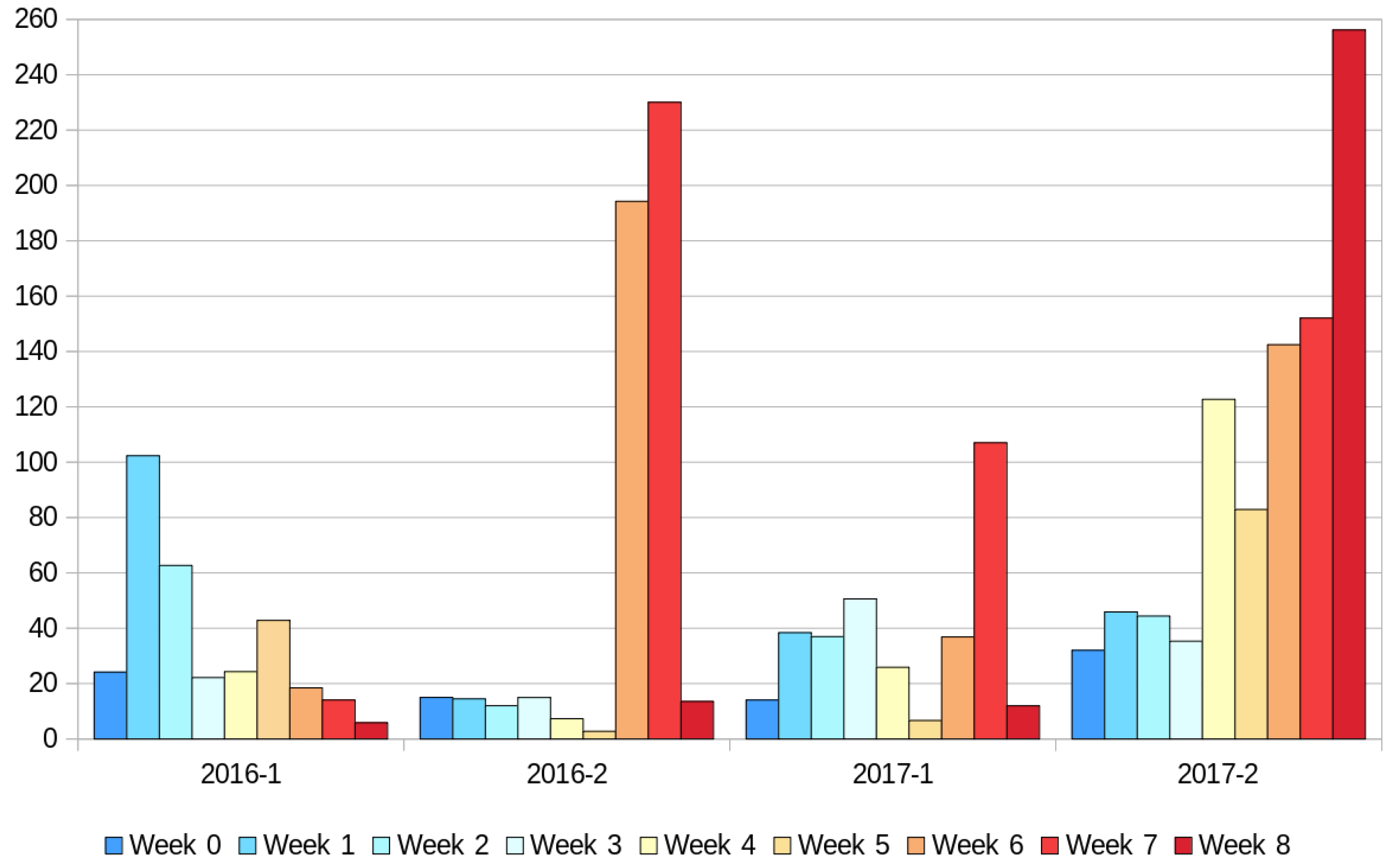
| 2016-1 | 10,395 | 547.10 | 6 | 13 | 19 |
| 2016-2 | 11,512 | 605.89 | 6 | 13 | 19 |
| 2017-1 | 23,457 | 902.19 | 9 | 17 | 26 |
| 2017-2 | 33,727 | 1349.08 | 12 | 13 | 25 |
| Attribute | Description |
|---|---|
| Count | Interaction count for each week |
| Average | Average of interactions on the week |
| Median | Median of interactions on the week |
| Zeroed weeks [50] | Number of weeks with zero interactions until the moment |
| Average of the difference [50] | Average of the difference between interactions on week i and week |
| Commitment factor [50] | Ratio between the student’s week interactions and the average class interaction for that week |
| Cognitive count [23] | Number of cognitive interaction on the week |
| Teaching count [23] | Number of teaching interaction on the week |
| Social count [23] | Number of social interaction on the week |
| Other count | Number of other types of interaction on the week |
| Attribute | Description |
|---|---|
| Cognitive count | Interactions involving content access and visualization: File upload/download, VPL exercise, URL access |
| Teaching count | Interactions with the professor: comments to the files sent |
| Social count | Interactions with other students: forum participation |
| Dataset | Variables |
|---|---|
| DB1 | Count |
| DB2 | Count, Average, Median |
| DB3 | Count, Cognitive Count, Teaching Count, Social Count, Other Count |
| DB4 | Count, Average, Median, Cognitive Count, Teaching Count, Social Count, Other Count |
| DB5 | Count, Average, Median, Zeroed Week, Commitment factor, Average of the difference |
| DB6 | Cognitive Count, Teaching Count, Social Count |
| DB7 | Cognitive Count, Teaching Count |
| DB8 | Cognitive Count, Social Count |
| DB9 | Teaching Count, Social Count |
| DB10 | Cognitive Count |
| DB11 | Teaching Count |
| DB12 | Social Count |
| DB13 | All variables |
| Semester | DB | Classifier | Median |
|---|---|---|---|
| 2016-1 | DB12 | AdaBoost | 0.62820 |
| DB2 | AdaBoost | 0.55128 | |
| DB5 | AdaBoost | 0.55128 | |
| DB9 | AdaBoost | 0.55128 | |
| DB12 | MLP | 0.55128 | |
| 2016-2 | DB2 | AdaBoost | 0.71795 |
| DB5 | AdaBoost | 0.71795 | |
| DB9 | kNN | 0.71795 | |
| DB12 | kNN | 0.71795 | |
| DB1 | Random Forest | 0.71154 | |
| 2017-1 | DB2 | AdaBoost | 0.66013 |
| DB5 | AdaBoost | 0.63072 | |
| DB6 | kNN | 0.60784 | |
| DB8 | kNN | 0.60784 | |
| DB10 | Random Forest | 0.60784 | |
| 2017-2 | DB2 | AdaBoost | 0.83974 |
| DB5 | AdaBoost | 0.83654 | |
| DB13 | AdaBoost | 0.75641 | |
| DB2 | Random Forest | 0.67949 | |
| DB4 | Random Forest | 0.67628 |
| Semester | Combination 1 | Combination 2 | p-Value |
|---|---|---|---|
| 2016-1 | DB12—AdaBoost | DB2—AdaBoost | 0.13032 |
| DB12—AdaBoost | DB5—AdaBoost | 0.19794 | |
| DB12—AdaBoost | DB9—AdaBoost | 0.48212 | |
| DB12—AdaBoost | DB12—MLP | 0.48224 | |
| 2016-2 | DB2—AdaBoost | DB5—AdaBoost | 0.32775 |
| DB2—AdaBoost | DB9—kNN | 0.50000 | |
| DB2—AdaBoost | DB12—kNN | 0.50000 | |
| DB2—AdaBoost | DB1—Random Forest | 0.42911 | |
| 2017-1 | DB2—AdaBoost | DB5—AdaBoost | 0.34448 |
| DB2—AdaBoost | DB6—kNN | 0.14441 | |
| DB2—AdaBoost | DB8—kNN | 0.14441 | |
| DB2—AdaBoost | DB10—Random Forest | 0.34525 | |
| 2017-2 | DB2—AdaBoost | DB5—AdaBoost | 0.41160 |
| DB2—AdaBoost | DB13—AdaBoost | 0.18712 | |
| DB2—AdaBoost | DB2—Random Forest | 0.32884 | |
| DB2—AdaBoost | DB4—Random Forest | 0.26740 |
| Semester | Combination | p-Value | Median (Normal) | Median (Oversample) |
|---|---|---|---|---|
| 2016-1 | DB2—AdaBoost | 0.03123 | 0.55128 | 0.59615 |
| DB5—AdaBoost | 0.07874 | 0.55128 | 0.63461 | |
| DB2—Random Forest | 0.00603 | 0.42308 | 0.50641 | |
| DB5—Random Forest | 0.01344 | 0.42949 | 0.47436 | |
| 2016-2 | DB2—AdaBoost | 0.00280 | 0.71795 | 0.51282 |
| DB5—AdaBoost | 0.00038 | 0.71795 | 0.42949 | |
| DB2—Random Forest | 0.02070 | 0.62820 | 0.67949 | |
| DB5—Random Forest | 0.36134 | 0.67308 | 0.63461 | |
| 2017-1 | DB2—AdaBoost | 0.06606 | 0.66013 | 0.54575 |
| DB5—AdaBoost | 0.01047 | 0.63072 | 0.51961 | |
| DB2—Random Forest | 0.16419 | 0.54902 | 0.57516 | |
| DB5—Random Forest | 0.00067 | 0.52287 | 0.63399 | |
| 2017-2 | DB2—AdaBoost | 0.35254 | 0.83974 | 0.75641 |
| DB5—AdaBoost | 0.35279 | 0.83654 | 0.75320 | |
| DB2—Random Forest | 0.00016 | 0.67949 | 0.91987 | |
| DB5—Random Forest | 0.00011 | 0.67628 | 0.91987 |
| Semester | Combination | p-Value | Median (Normal) | Median (Questionnaire) |
|---|---|---|---|---|
| 2016-1 | DB2—AdaBoost | 0.02081 | 0.55128 | 0.67308 |
| DB5—AdaBoost | 0.03846 | 0.55128 | 0.62820 | |
| DB2—Random Forest | 0.48202 | 0.42308 | 0.42308 | |
| DB5—Random Forest | 0.19819 | 0.42949 | 0.38461 | |
| 2016-2 | DB2—AdaBoost | 0.44679 | 0.71795 | 0.67949 |
| DB5—AdaBoost | 0.05542 | 0.71795 | 0.64103 | |
| DB2—Random Forest | 0.26698 | 0.62820 | 0.62820 | |
| DB5—Random Forest | 0.16124 | 0.67308 | 0.66667 | |
| 2017-1 | DB2—AdaBoost | 0.00302 | 0.66013 | 0.49020 |
| DB5—AdaBoost | 0.01466 | 0.63072 | 0.49346 | |
| DB2—Random Forest | 0.08310 | 0.54902 | 0.44118 | |
| DB5—Random Forest | 0.41219 | 0.52287 | 0.49673 | |
| 2017-2 | DB2—AdaBoost | 0.39453 | 0.83974 | 0.79808 |
| DB5—AdaBoost | 0.29755 | 0.83654 | 0.75641 | |
| DB2—Random Forest | 0.48230 | 0.67949 | 0.71154 | |
| DB5—Random Forest | 0.50000 | 0.67628 | 0.67628 |
| Semester | Combination | p-Value | Median (Oversample) | Median (Questionnaire Data with Oversample) |
|---|---|---|---|---|
| 2016-1 | DB2—AdaBoost | 0.06890 | 0.59615 | 0.58974 |
| DB5—AdaBoost | 0.21254 | 0.63461 | 0.58974 | |
| DB2—Random Forest | 0.00376 | 0.50641 | 0.50641 | |
| DB5—Random Forest | 0.13058 | 0.47436 | 0.46795 | |
| 2016-2 | DB2—AdaBoost | 0.00506 | 0.51282 | 0.34615 |
| DB5—AdaBoost | 0.1488 | 0.42949 | 0.39102 | |
| DB2—Random Forest | 0.0087 | 0.67949 | 0.71795 | |
| DB5—Random Forest | 0.03328 | 0.63461 | 0.71795 | |
| 2017-1 | DB2—AdaBoost | 0.28199 | 0.54575 | 0.57189 |
| DB5—AdaBoost | 0.2510 | 0.51961 | 0.49346 | |
| DB2—Random Forest | 0.0015 | 0.57516 | 0.66013 | |
| DB5—Random Forest | 0.0533 | 0.63399 | 0.60457 | |
| 2017-2 | DB2—AdaBoost | 0.0000 | 0.75641 | 0.79487 |
| DB5—AdaBoost | 0.0000 | 0.75320 | 0.79487 | |
| DB2—Random Forest | 0.2260 | 0.91987 | 0.95833 | |
| DB5—Random Forest | 0.02940 | 0.91987 | 0.96154 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buschetto Macarini, L.A.; Cechinel, C.; Batista Machado, M.F.; Faria Culmant Ramos, V.; Munoz, R. Predicting Students Success in Blended Learning—Evaluating Different Interactions Inside Learning Management Systems. Appl. Sci. 2019, 9, 5523. https://doi.org/10.3390/app9245523
Buschetto Macarini LA, Cechinel C, Batista Machado MF, Faria Culmant Ramos V, Munoz R. Predicting Students Success in Blended Learning—Evaluating Different Interactions Inside Learning Management Systems. Applied Sciences. 2019; 9(24):5523. https://doi.org/10.3390/app9245523
Chicago/Turabian StyleBuschetto Macarini, Luiz Antonio, Cristian Cechinel, Matheus Francisco Batista Machado, Vinicius Faria Culmant Ramos, and Roberto Munoz. 2019. "Predicting Students Success in Blended Learning—Evaluating Different Interactions Inside Learning Management Systems" Applied Sciences 9, no. 24: 5523. https://doi.org/10.3390/app9245523
APA StyleBuschetto Macarini, L. A., Cechinel, C., Batista Machado, M. F., Faria Culmant Ramos, V., & Munoz, R. (2019). Predicting Students Success in Blended Learning—Evaluating Different Interactions Inside Learning Management Systems. Applied Sciences, 9(24), 5523. https://doi.org/10.3390/app9245523





