1. Introduction
Mission- or safety-critical applications such as space, aerospace, nuclear, defense, electric power transmission and distribution, banking, financial, and industrial control and automation etc. usually employ some form of N-modular redundancy (NMR) for the hardware implementation to cope with unintended temporary faults and/or permanent failures of constituent circuits or systems [
1,
2]. In an NMR hardware, (N − 1) identical copies of a function module are used along with the original function module; the function module may be a circuit or a system. Out of the N function modules, at the maximum, the temporary faults or permanent failures of (N − 1)/2 function modules are tolerated. In other words, the correct operation of at least (N + 1)/2 function modules are necessary. Supposing each of the N function modules produce K primary outputs, the corresponding outputs of each of the N function modules are combined separately using K N-input majority voters to generate the actual NMR hardware outputs [
3]. A majority voter, as the name suggests, determines the output of an NMR implementation based on the Boolean majority. If N inputs are provided to a majority voter, the majority voter determines the primary output based on the identical values of (N + 1)/2 inputs. To implement NMR hardware, a total of N function modules and a requisite number of N-input majority voters, depending upon the number of outputs produced by the original function module, are required.
Triple modular redundancy (TMR or 3MR) is the minimum version of an NMR. In TMR, three function modules are used and the temporary fault or permanent failure of any one function module is tolerated. Thus, the correct operation of at least two function modules is necessary in TMR. A TMR implementation requires three-input majority voter(s). In fact, the three-input majority voter also finds use in majority and minority voted redundancy [
4] and self-healing redundancy [
5] schemes, which are relevant for mission- and safety-critical applications. In the literature, many designs for a three -input majority voter are discussed [
6,
7,
8,
9,
10]. However, [
6,
7,
8,
9] correspond to synchronous designs of the three-input majority voter, and [
10] corresponds to a bundled-data asynchronous design which is not delay insensitive. To our knowledge, delay insensitive designs of the three-input majority voter have not been discussed thus far. In this context, this article presents quasi delay insensitive (QDI) designs of the three-input majority voter based on some QDI logic synthesis methods and analyzes which majority voters are preferable in terms of speed, power, and area. A QDI three input majority voter is necessary for implementing a QDI TMR circuit/system.
QDI circuits form an attractive alternative to synchronous circuits because they are inherently modular and elastic due to being delay insensitive [
11], able to cope with variations in process, voltage, and temperature [
12], less susceptible to electromagnetic interference [
13], low power consuming [
14], more secure to attacks compared to synchronous circuits [
15], and self-checking [
16].
The rest of the article is organized into five sections.
Section 2 discusses the design preliminaries of QDI circuits.
Section 3 describes the architecture of a QDI TMR implementation.
Section 4 presents the QDI majority voter designs corresponding to some QDI logic synthesis methods utilizing delay insensitive dual rail data encoding and adhering to four-phase return-to-zero (RTZ) and four-phase return-to-one (RTO) handshake protocols. The simulation results obtained for the example QDI TMR implementations are given in
Section 5, and finally,
Section 6 concludes this article.
2. Basics of QDI Circuits
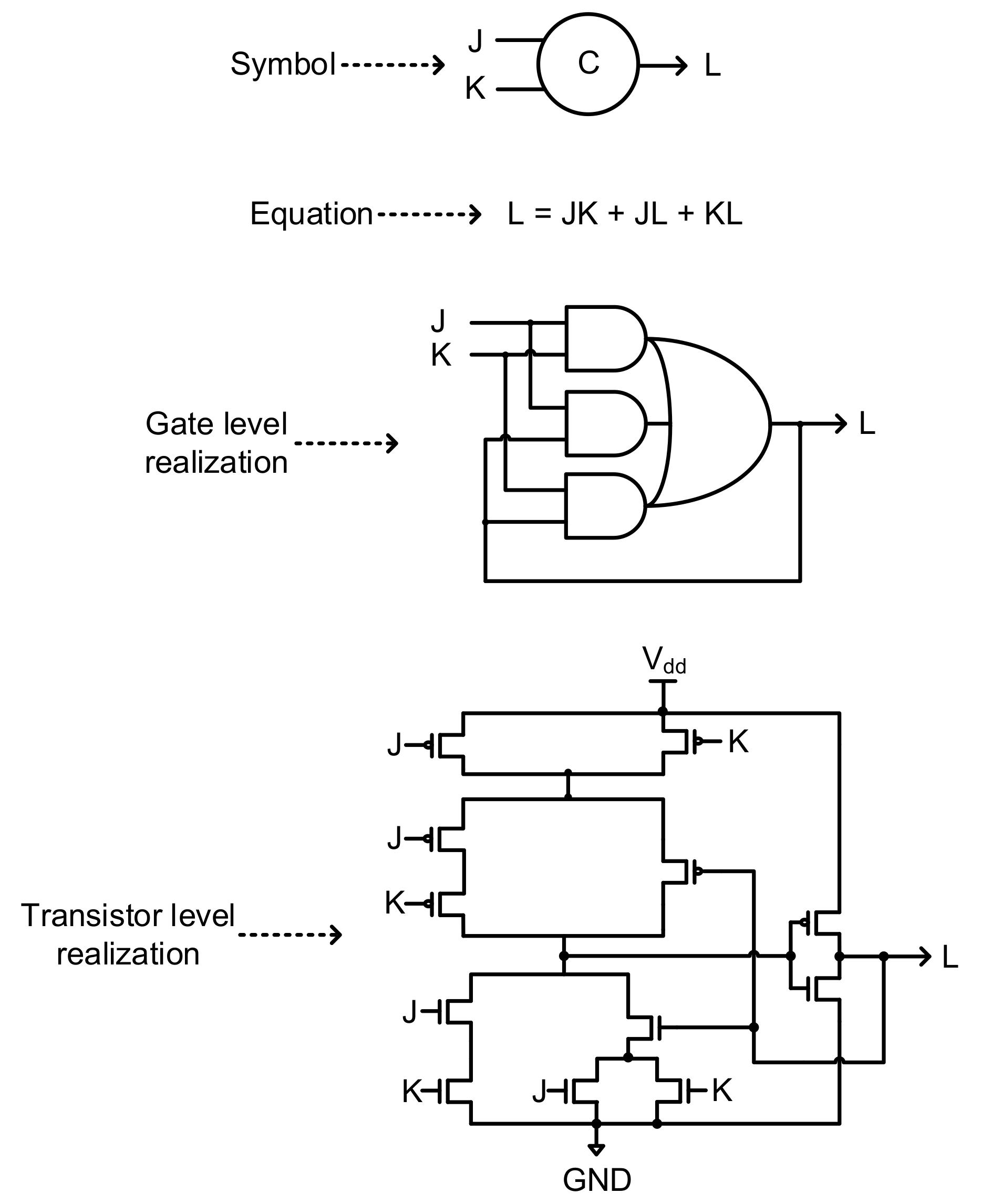
First, it should be noted that, practically, delay insensitive (DI) circuits could not be constructed. This is because the C-element [
17] and the inverter are the two DI gates available and the other simple gates such as AND, OR, XOR etc. and complex gates such as AO21, AO22, AO222 etc. are not DI. The symbol, logic equation, and gate-level and transistor-level realizations of a two-input C-element are shown in
Figure 1.
When a gate changes its output state, say from zero to one or from one to zero, it should be able to unambiguously convey the state of its inputs. Such a gate is said to be DI. The output of a DI gate duly indicates i.e., acknowledges its input(s). For example, if an inverter changes its output from say zero to one or from one to zero, it implies that its input has changed from one to zero or zero to one respectively. A C-element would output one if all its inputs are one, and would output zero if all its inputs are zero. If the inputs are not identical then the C-element will retain its existing steady state. Hence, if a C-element changes its output from zero to one or from one to zero, it implies that all its inputs have changed from zero to one or from one to zero respectively. However, using only the C-element and the inverter, it is not possible to construct practically useful digital circuits. Hence, a weak timing assumption has been introduced, called the isochronic fork [
18] to construct practically useful DI circuits, which are also called QDI circuits. An isochronic fork refers to two or more wires forking out from a node or junction. The isochronic fork timing assumption implies that a rising signal transition (i.e., 0 to 1) or a falling signal transition (i.e., 1 to 0) is assumed to happen concurrently on all the wires forking out from a node or junction. When the isochronic fork assumption is included in the design of a DI circuit, the resulting circuit is said to be QDI [
18]. Thus, although the isochronic fork assumption represents the weakest compromise to delay insensitivity, nevertheless, such an assumption enables the design of practical digital logic circuits in QDI style. Martin and Prakash [
19] have showed that the isochronic fork assumption is realizable in nano-meter scale design geometries, and hence QDI circuits are feasible in the nanoelectronics regime.
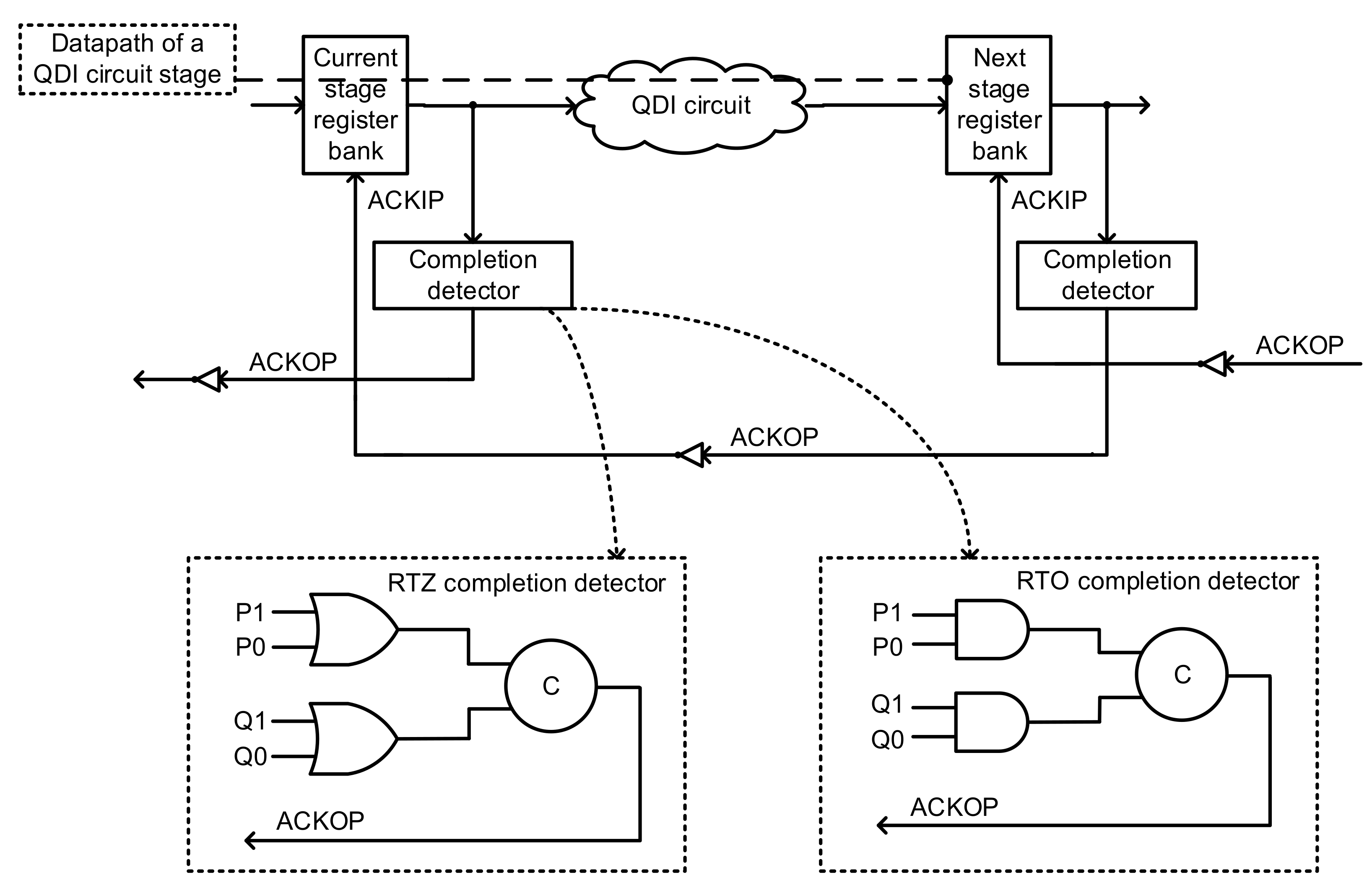
The block schematic of a QDI circuit stage employing delay insensitive dual rail data encoding and adhering to a four-phase handshaking is shown at the top of
Figure 2. A QDI circuit stage consists of a current stage register bank, a next stage register bank, a QDI circuit sandwiched between the current stage and next stage register banks, completion detectors, and acknowledgment input (ACKIP) and acknowledgment output (ACKOP) signals which are exchanged between the current stage and next stage register banks. ACKIP is the Boolean complement of ACKOP and vice-versa, i.e., if ACKIP = 0, ACKOP = 1, and if ACKIP = 1, ACKOP = 0.
A register bank in a QDI circuit stage comprises a series of registers, commensurate with the number of (dual rail) encoded inputs. For example, if M single rail inputs are encoded into 2M dual rail inputs, the number of registers in the current stage register bank will be 2M. Each register is a two-input C-element, which has ACKIP as one of its inputs and one of the rails of a dual rail encoded data as its other input. The circles with the marking ‘C’ denote the C-elements in the figures.
The completion detector is responsible for indicating, i.e., acknowledging the complete arrival of all the dual rail inputs to a QDI circuit. Assuming that there are 2M dual rail inputs, the completion detector for RTZ handshaking would comprise M 2-input OR gates to combine the dual rails of each encoded primary input. The completion detector for RTO handshaking would comprise M 2-input AND gates to combine the dual rails of each encoded primary input. All the two-input OR/AND gates present in the first logic level of the completion detector are combined using a two-input C-element or a tree of two-input C-elements and the output of the completion detector is ACKOP. Two example gate-level completion detectors corresponding to RTZ and RTO handshaking are shown at the bottom of
Figure 2 within the dotted boxes by assuming two dual rail inputs (P1,P0) and (Q1,Q0).
As mentioned earlier, the inputs and outputs of a QDI circuit are dual rail encoded. For example, a (single rail) input I is dual rail encoded as (I1,I0). Each single rail input is encoded into two rails as per the dual rail data encoding scheme [
20]. Depending on whether RTZ handshaking [
21] or RTO [
22] handshaking is followed for data communication between the current stage and next stage register banks, accordingly, the encodings of the dual rail inputs would differ.
Table 1 shows the dual rail encoding of an example single rail input (I) based on RTZ and RTO handshaking.
According to RTZ handshaking, I = 0 is represented by I0 = 1 and I1 = 0, and I = 1 is represented by I1 = 1 and I0 = 0. These two encodings are called ‘data’. I1 = I0 = 0 is referred to as the ‘spacer’. I1 = I0 = 1 is an indeterminate (i.e., illegal/invalid) state. According to RTO handshaking, I = 0 is represented by I0 = 0 and I1 = 1, and I = 1 is represented by I1 = 0 and I0 = 1. These two encodings are called ‘data’. I1 = I0 = 1 is referred to as the ‘spacer’. I1 = I0 = 0 is an invalid/indeterminate state. I1 = I0 = 1 and I1 = I0 = 0 are defined as indeterminate states with respect to RTZ and RTO handshaking respectively. This is because the data encoding scheme should be unordered [
23] and incomplete [
24] to be delay insensitive.
There are four phases involved in RTZ and RTO handshake schemes, which are described below with reference to
Figure 2. Handshaking is performed between the current stage (input) and next stage (output) register banks, involving the QDI circuit that is sandwiched between these register banks.
2.1. RTZ Handshake Signaling
According to RTZ handshaking, firstly, the dual rail data bus initially assumes the spacer and ACKIP = 1. After the current stage register bank sends data, rising signal transitions (i.e., zero to one) will occur on one of the rails of each dual rail encoded input of the dual rail data bus. Secondly, the next stage register bank, after receiving the processed data from the QDI circuit, would drive ACKOP to 1. Thirdly, the current stage register bank would wait for ACKIP to become zero, and after this happens, the dual rail data bus would once again assume the spacer. Finally (i.e., fourthly), after a finite and positive unbounded time duration elapses, the next stage register bank would receive the spacer from the QDI circuit and would drive ACKOP to 0. Consequently, ACKIP will become one. With this, one data transaction is deemed to have been completed and the next data transaction may commence. According to RTZ handshaking, the inputs are supplied following the sequence of data, spacer, data, spacer, and so forth.
2.2. RTO Handshake Signaling
According to RTO handshaking, firstly, ACKIP = 1. The current stage register bank now sends the spacer (i.e., all ones) and as a result, rising signal transitions will occur on all the rails of the dual rail data bus. Secondly, the next stage register bank, after receiving the spacer from the QDI circuit would drive ACKOP to 1. Thirdly, the current stage register bank would wait for ACKIP to become zero, and after this happens, the dual rail data bus would send the data by permitting falling signal transitions (i.e., one to zero) to occur on one of the rails of each dual rail encoded input of the dual rail data bus. Finally (i.e., fourthly), after a finite and positive unbounded time duration elapses, the next stage register bank would receive the processed data from the QDI circuit and subsequently drive ACKOP to 0. Consequently, ACKIP will become one. With this, one data transaction is deemed to have been completed and the next data transaction may commence. According to RTO handshaking, the inputs are supplied following the sequence of spacer, data, spacer, data, and so forth.
2.3. Timing Parameters of QDI Circuits
Forward latency, reverse latency, and cycle time are the important timing parameters of interest in a QDI circuit. Forward latency refers to the worst-case propagation delay encountered in the data path (shown in
Figure 2) for processing the data, and reverse latency refers to the worst-case propagation delay encountered in the data path for processing the spacer. From the above discussion, it may be noted that one complete data transaction in a QDI circuit would involve the forward latency as well as the reverse latency. The summation of forward and reverse latencies gives the cycle time. The speed of a QDI circuit is governed by the cycle time, which is equivalent to the clock period of a synchronous digital circuit.
2.4. Types and Characteristics of QDI Circuits
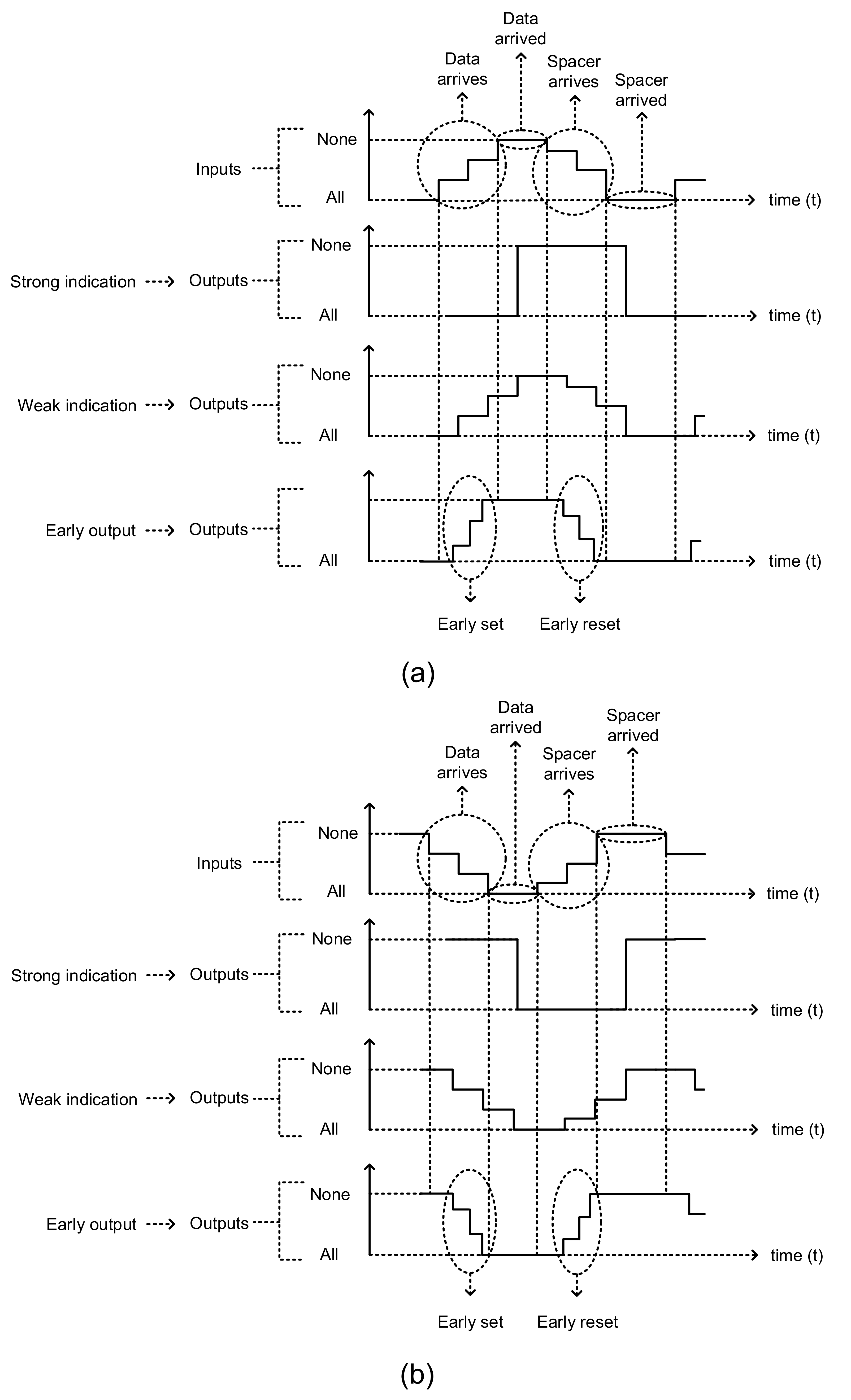
QDI circuits are classified as strong indication, weak indication, and early output circuits. Their input/output behavior are captured via a representative illustration in
Figure 3.
Strong indication (QDI) circuits [
25] will wait to receive all the primary inputs (data/spacer), and after receiving them would commence the processing to produce the required primary outputs (data/spacer). Weak indication (QDI) circuits [
25] can commence the processing after receiving a subset of the primary inputs (data/spacer) and are able to produce all but one of the required primary outputs (data/spacer). However, they are constrained by the rule that only after receiving the last primary input (data/spacer) can they process and produce the last primary output (data/spacer). Early output (QDI) circuits [
26] are very relaxed in terms of the timing compared to strong indication and weak indication circuits since they are allowed to process and produce all the primary outputs (data/spacer) after receiving a subset of the primary inputs (data/spacer). This characteristic of early output circuits implies that some of the late arriving primary inputs (data/spacer) to an early output circuit may not be acknowledged, which might give rise to wire orphans, and wire orphans are unacknowledged signal transitions occurring on the primary input wires. However, wire orphans are quite easily overcome in early output QDI circuits. This is because although an early output circuit may not acknowledge the late arriving primary inputs (data/spacer), the completion detector preceding the early output QDI circuit would properly acknowledge them. Thus, there does not arise any issue with respect to acknowledging the arrival of all the primary inputs (data/spacer) to an early output circuit. In addition, there are two sub-types of early output circuits called the early set type and the early reset type. If an early output circuit produces the primary output data early, it is said to be of early set type. Contrarily, if an early output circuit produces the spacer early, it is said to be of early reset type. The early set and reset behaviors of early output circuits with respect to RTZ and RTO handshaking are depicted within the dotted ovals in
Figure 3.
3. QDI TMR Implementation
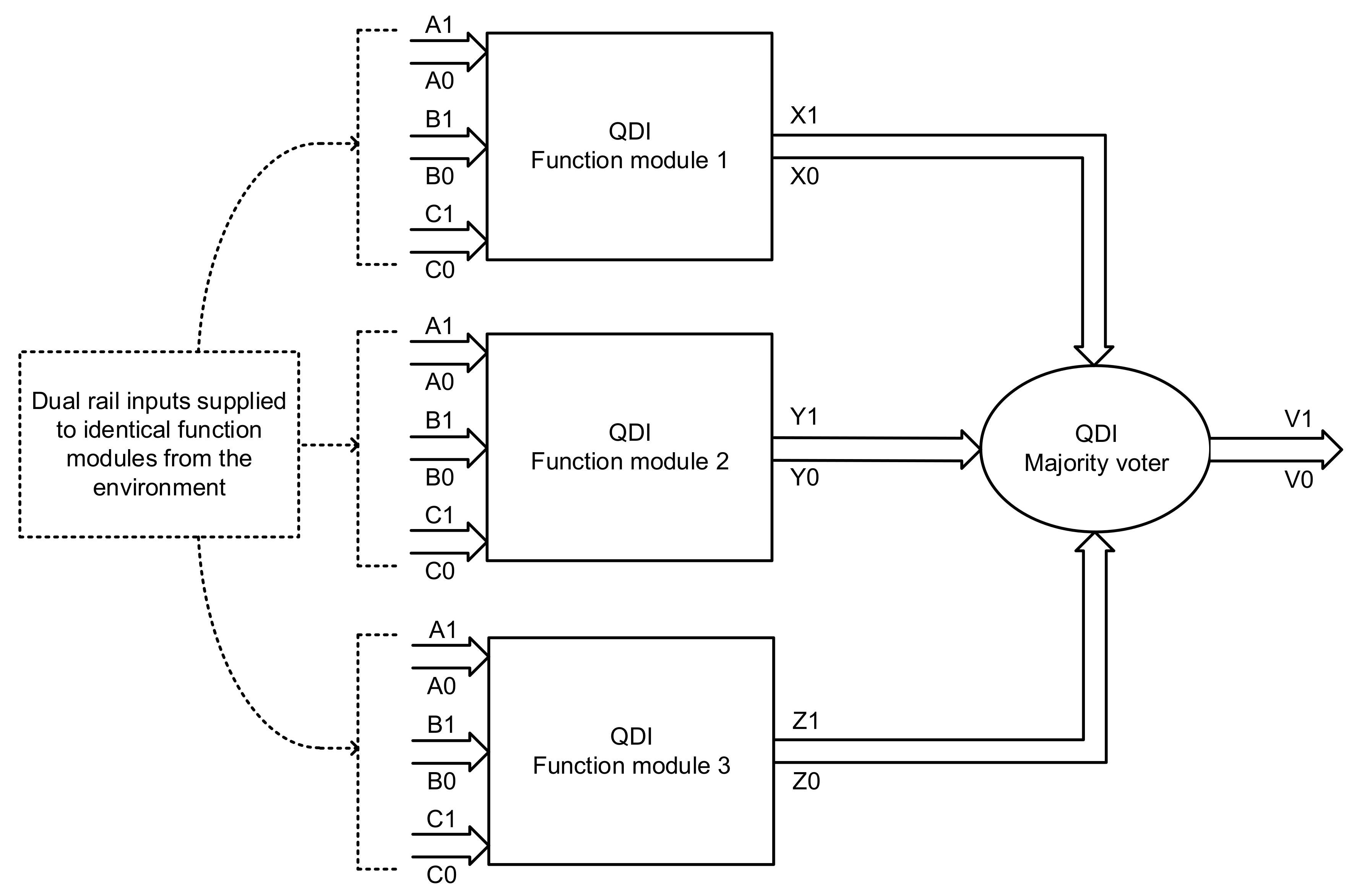
An example QDI TMR implementation is shown in
Figure 4 comprising three identical function modules 1, 2 and 3. Dual rail inputs (A1,A0), (B1,B0), and (C1,C0) are supplied to these function modules from the external world. The outputs of function modules 1, 2, and 3 are represented by (X1,X0), (Y1,Y0), and (Z1,Z0) respectively, which are given as inputs to the QDI majority voter. The dual rail output of the majority voter is denoted by (V1,V0).
Equations (1) and (2) are the classical expressions for V1 and V0. These equations consist of four terms out of which the first three terms viz. X1Y1, Y1Z1 and X1Z1 with respect to (1), and X0Y0, Y0Z0 and X0Z0, with respect to (2), signify the correct operation of any two function modules shown in
Figure 4. The fourth term viz. X1Y1Z1 with respect to (1) and X0Y0Z0 with respect to (2) signifies the correct operation of all the three function modules. However, X1Y1Z1 and X0Y0Z0 can be safely eliminated using Boolean axioms resulting in just three irredundant terms for (1) and (2).
A direct synthesis of (1) and (2) using C-elements and OR gates is depicted by
Figure 5a that corresponds to RTZ handshaking, and
Figure 5b is its counterpart, which corresponds to RTO handshaking.
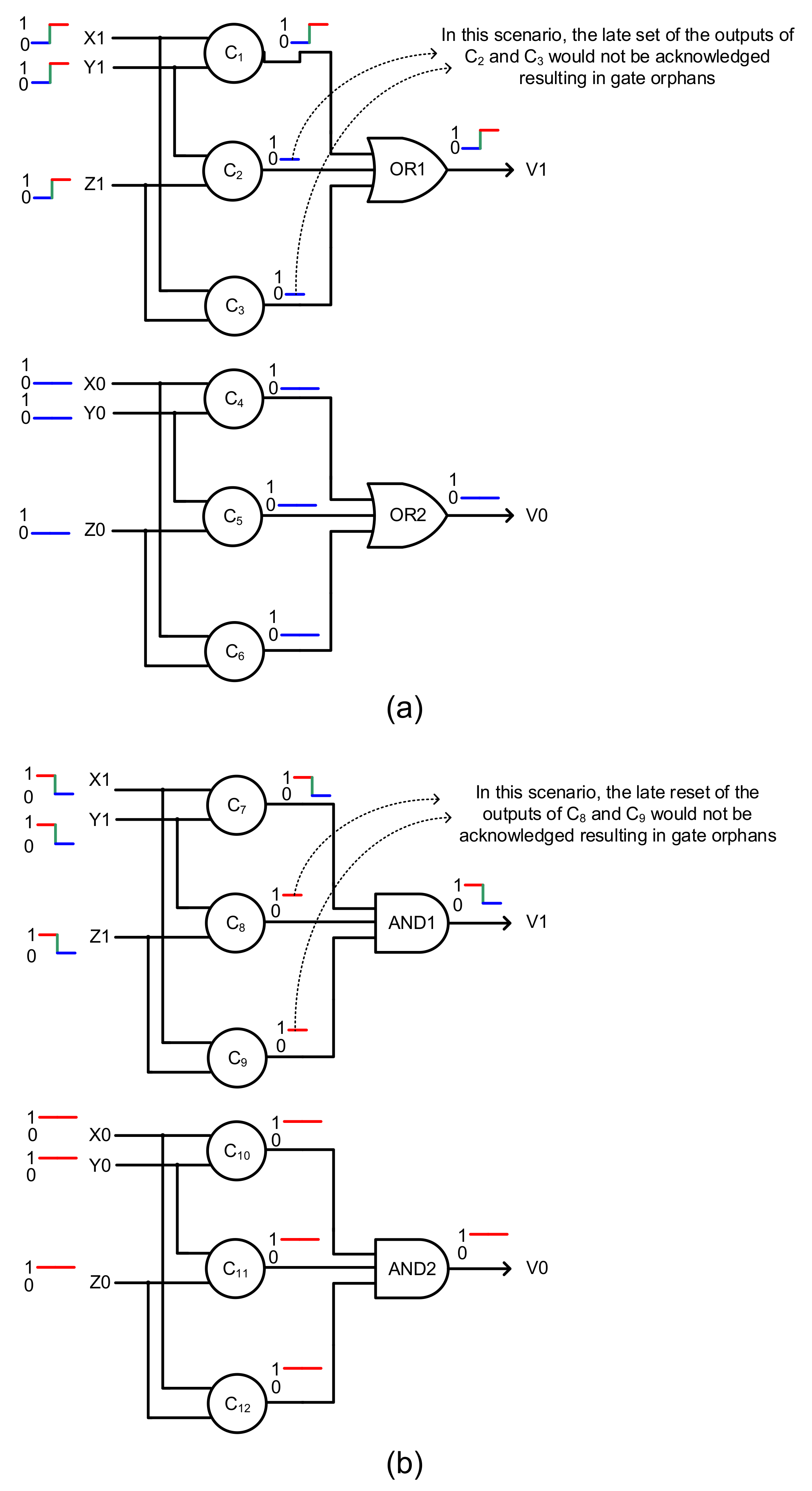
Figure 5 is provided mainly to illustrate why a naïve implementation of the majority equations described by (1) and (2) is inappropriate and how gate orphans could result. In
Figure 5, C
1 to C
12 represent the C-elements, OR1 and OR2 are the OR gates, and AND1 and AND2 are the AND gates.
To transform an asynchronous circuit that corresponds to RTZ or RTO handshaking into one that corresponds to RTO or RTZ handshaking respectively, all the gates i.e., simple and/or complex gates of the original circuit should be replaced by their respective duals according to the duality principle of Boolean algebra [
27]. However, this excludes any C-elements present in the original circuit, which should be left untouched while retaining their inputs. Nevertheless,
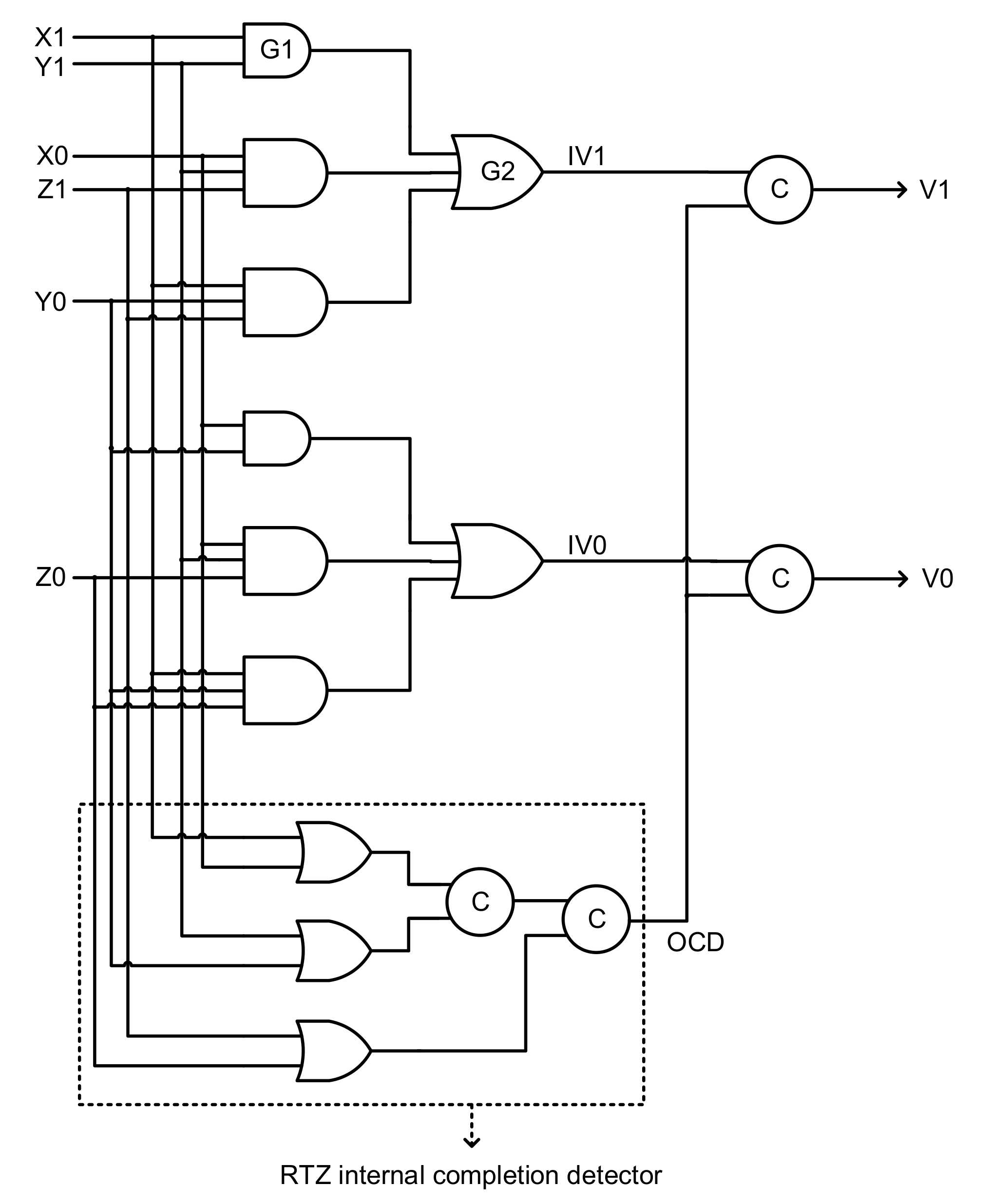
Figure 5a,b shows naïve implementations, since they are not QDI because they suffer from the problem of gate orphans, which are described below by considering some example input scenarios.
Wire orphans and gate orphans are the two circuit orphans which should be avoided in a QDI circuit as they could affect the robustness [
28,
29,
30], resulting in the circuit becoming non-QDI. For example, referring to
Figure 5a, let us assume that after a RTZ phase, all the dual rail inputs of the majority voter have assumed 0, i.e., X1 = X0 = 0, Y1 = Y0 = 0 and Z1 = Z0 = 0. In
Figure 5a,b, the steady state of 0 is highlighted by the blue line, the steady state of 1 is highlighted by the red line, and the signal transition from 0 to 1 or 1 to 0 is highlighted by the green line. Let us now assume that after the RTZ phase, the input data of X1 = Y1 = Z1 = 1 is applied to the majority voter in
Figure 5a. This implies X0, Y0 and Z0 continue to retain 0. Supposing that C-element C
1 alone has output 1 and assuming that C-elements C
2 and C
3 have not yet output 1, since one of the inputs to OR1 is 1, therefore OR1 will output 1 regardless of the receipt of 1 on its other two inputs, and thus V1 could assume 1. The late arrival of 1 on the other two inputs of OR1 after the production of 1 by C
2 and C
3 will not be acknowledged by V1, and V1 is said to have acknowledged the output of C
1 alone. Consequently, the late rising signal transitions on C
2 and C
3 would be called gate orphans, and gate orphans are signal transitions that occur on the output(s) of gate(s), which are not acknowledged. It may be noted that assuming the production of late outputs by C
2 and C
3 is not fictitious but practically likely, and in principle, a QDI circuit should remain insensitive to delays due to internal/external sources while processing the inputs. This implies that if an asynchronous circuit is sensitive to internal and/or external delays, it is not QDI.
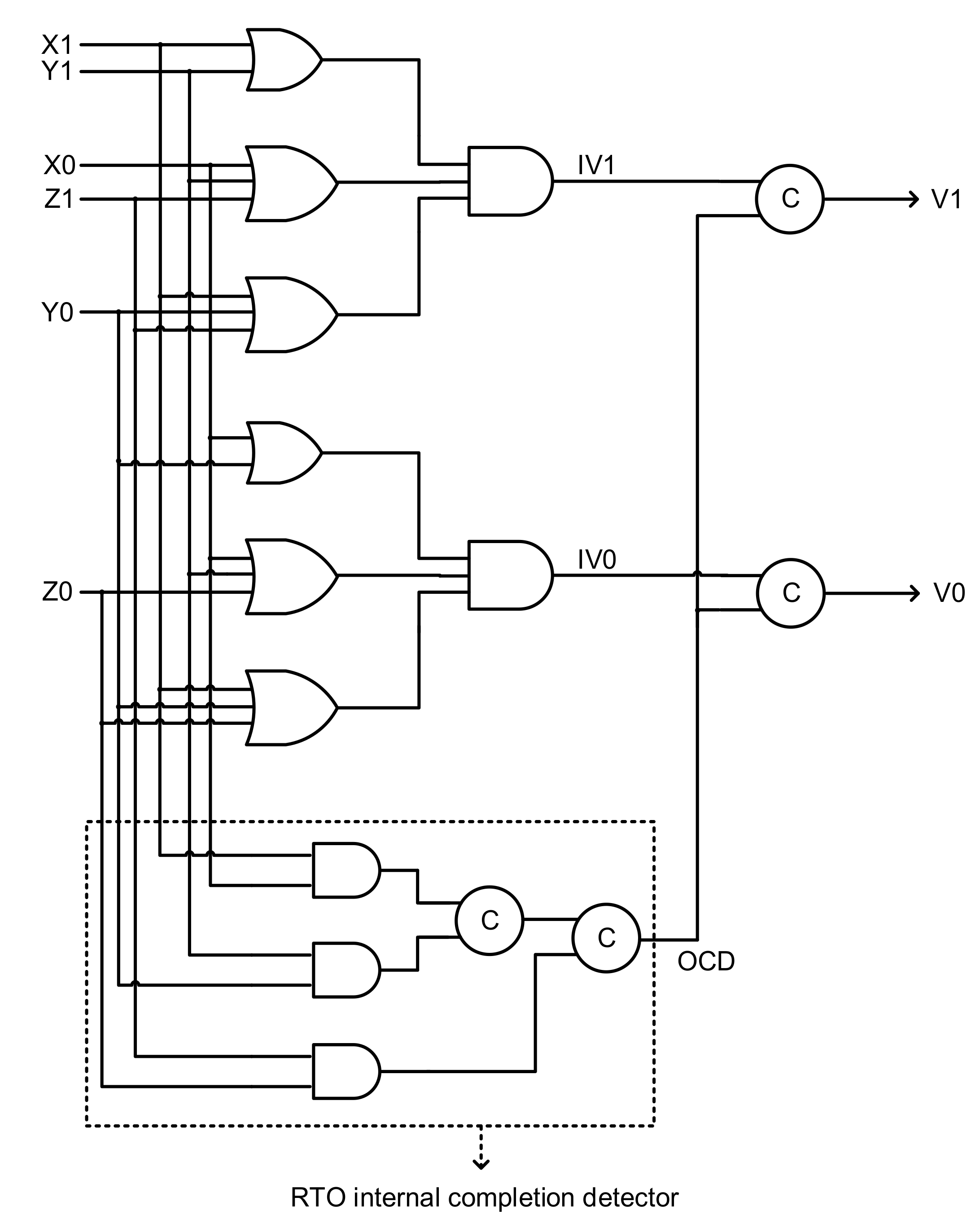
Now referring to
Figure 5b, let us consider the application of the spacer to the majority voter i.e., X1 = X0 = 1, Y1 = Y0 = 1 and Z1 = Z0 = 1. Subsequently, the C-elements C
7 to C
12 will output 1 and AND1 and AND2 will also output 1, and thus V1 = V0 = 1. After the RTO phase, let us assume that an input data of X1 = Y1 = Z1 = 0 is applied to the majority voter of
Figure 5b, which implies X0, Y0 and Z0 continue to retain 1. Subsequent to this, let us assume that C
7 outputs 0, and C
8 and C
9 also output 0, but lately i.e., after V1 assumes 0. This results in one of the inputs to AND1 becoming 0, and AND1 will output 0 resulting in V1 = 0. Given this, V1 is said to have acknowledged the output of C
7 alone and the late production of 0 by C
8 and C
9 would not be acknowledged by V1, thus giving rise to gate orphans.
With respect to
Figure 5a, the two input data of X1 = Y1 = Z1 = 1 and X0 = Y0 = Z0 = 1, which signify the correct operation of all the three function modules in
Figure 4, are likely to give rise to gate orphans. With respect to
Figure 5b, the two input data of X1 = Y1 = Z1 = 0 and X0 = Y0 = Z0 = 0, which also signify the correct operation of the three function modules in
Figure 4, are likely to give rise to gate orphans. If only two of the three function modules in
Figure 4 would maintain the correct operation, then gate orphans are unlikely to crop up in the majority voters shown in
Figure 5a,b. However, due to the likelihood of gate orphan occurrences in
Figure 5a,b, those majority voters are not QDI.
Contrary to a synchronous digital circuit, which is only required to produce the correct outputs based on the given inputs, the outputs of a QDI digital circuit are additionally responsible for indicating the completion of internal processing of data and spacer within the circuit [
21]. Moreover, in a QDI circuit, rising and falling signal transitions should occur monotonically throughout the entire circuit from the first logic level up to the last logic level [
31]. In the case of RTZ handshaking, rising signal transitions would occur monotonically throughout the circuit for the application of data and falling signal transitions would occur monotonically throughout the circuit for the application of spacer. On the contrary, in the case of RTO handshaking, rising signal transitions would occur monotonically throughout the circuit for the application of spacer and falling signal transitions would occur monotonically throughout the circuit for the application of data.
As mentioned earlier, wire orphans are overcome by imposing the isochronic fork assumption on the primary input nodes. On the other hand, gate orphans could be problematic [
26] and they are best avoided by incorporating the monotonic cover constraint (MCC) [
21] and/or by adhering to safe QDI logic decomposition principles [
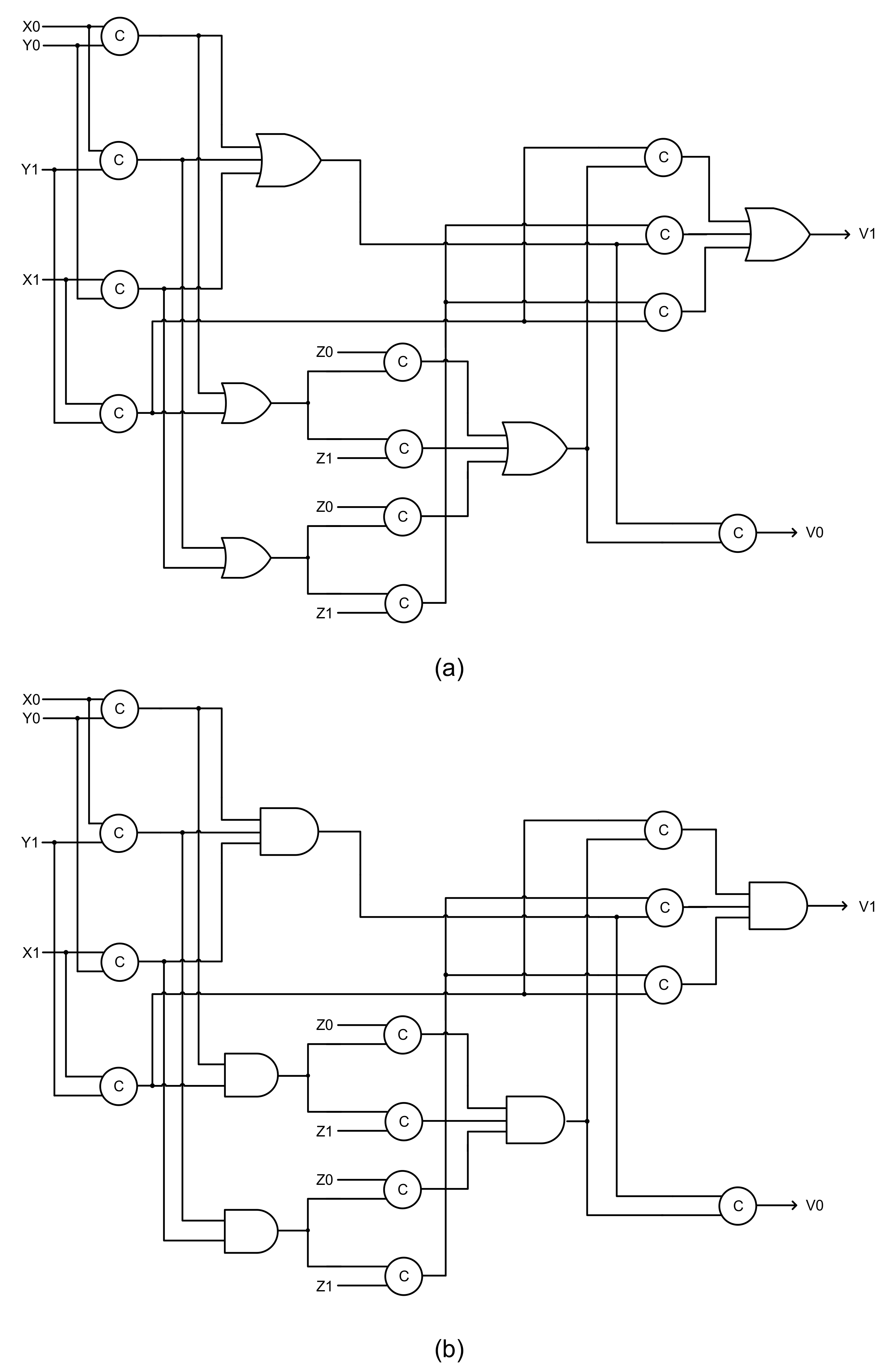
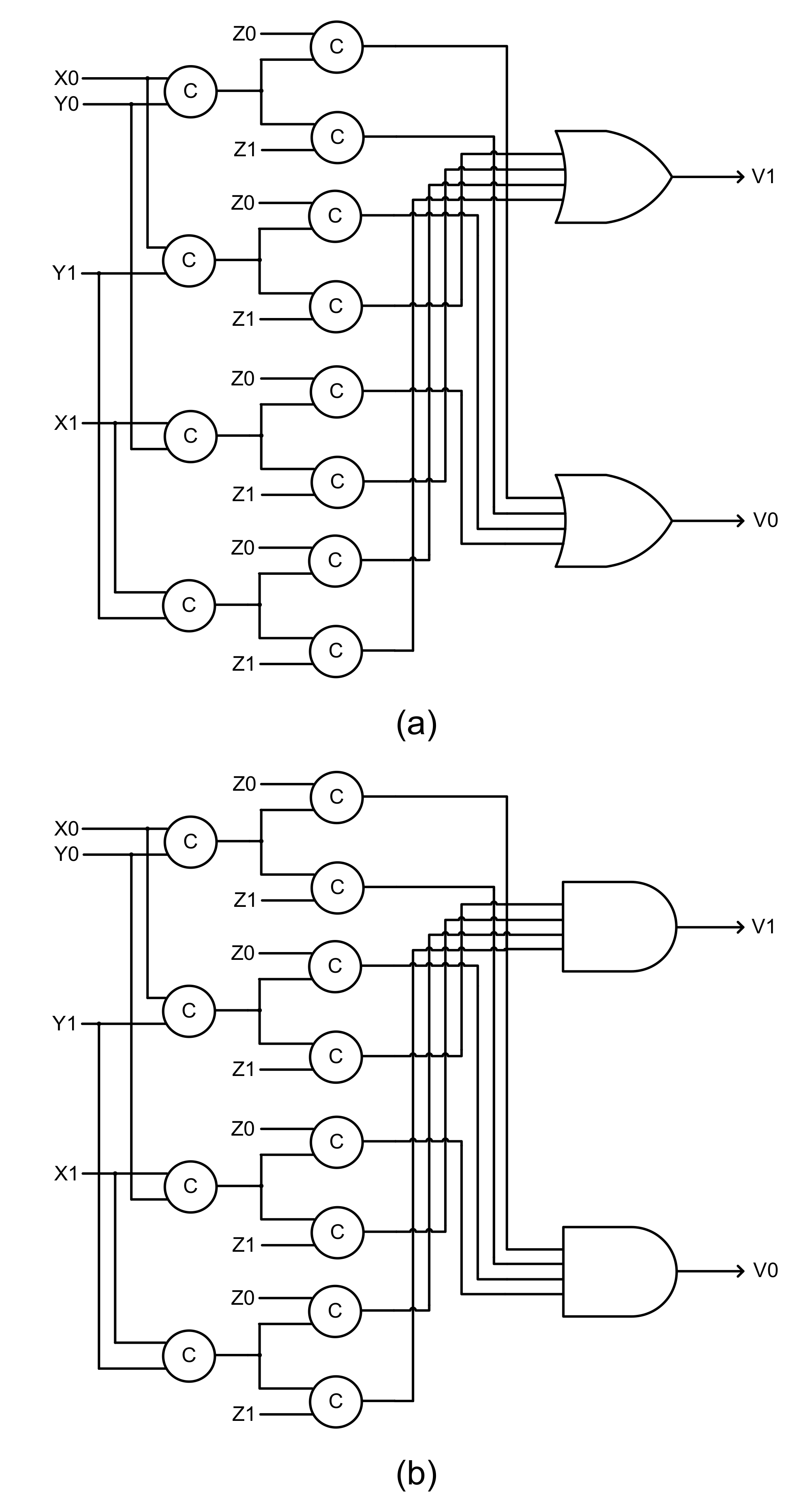
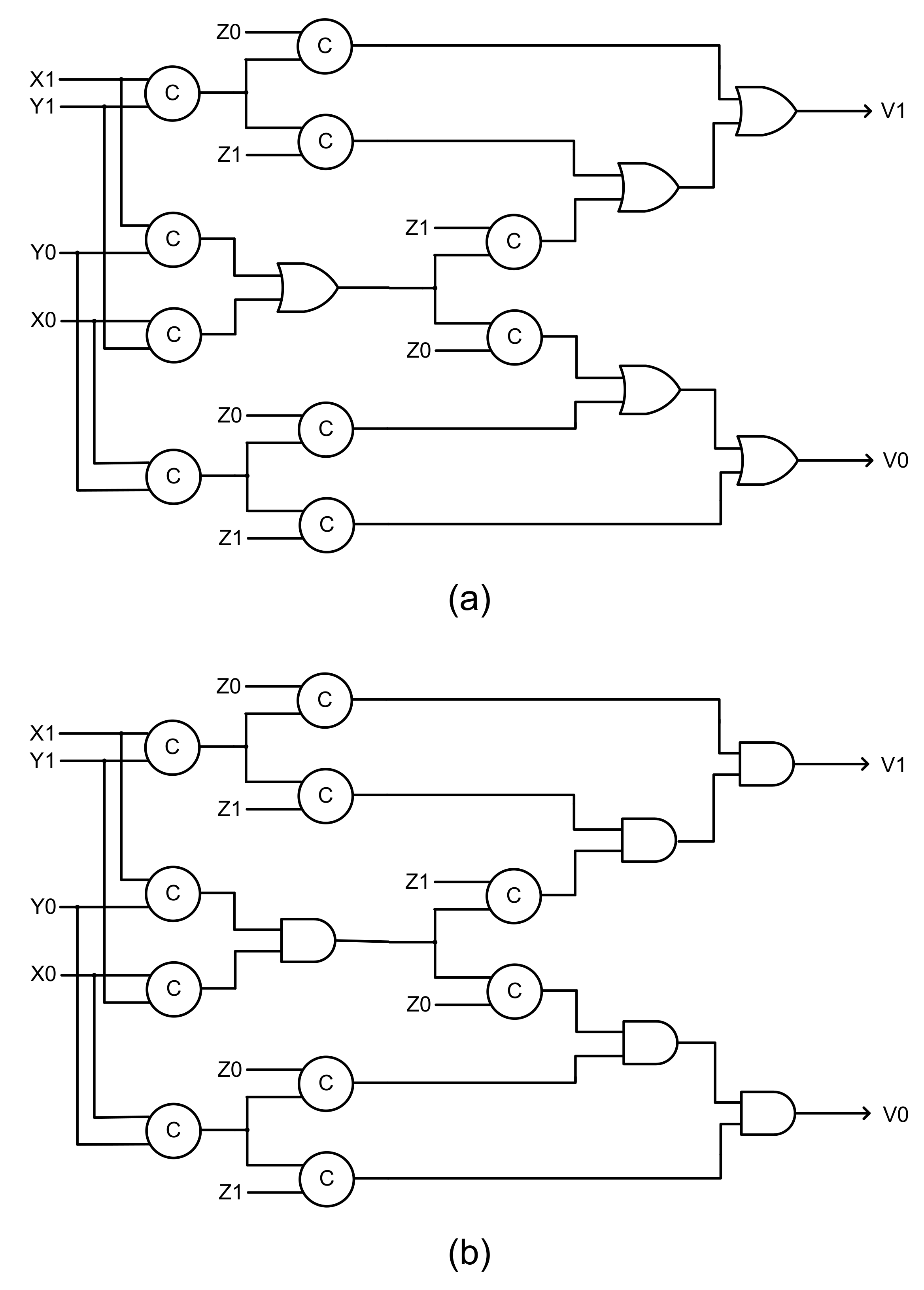
32]. The MCC mandates that, in say, a sum-of-products (SOP) expression, all the product terms should be mutually exclusive, i.e., the logical conjunction of any two product terms in a SOP expression should result in 0. Generally, this may not be achieved in a SOP expression. For example, the logical conjunction of any two product terms in Equations (1) and (2) would not result in zero. Alternatively, a SOP expression can be transformed into a disjoint SOP (DSOP) expression. This is because, by definition, a DSOP expression contains product terms, which are mutually exclusive to each other [
33].
5. Implementation Results
The example QDI TMR circuits were implemented as a typical QDI circuit stage (shown in
Figure 2) comprising a current stage register bank and the TMR circuit. The TMR circuits considered an early output QDI full adder [
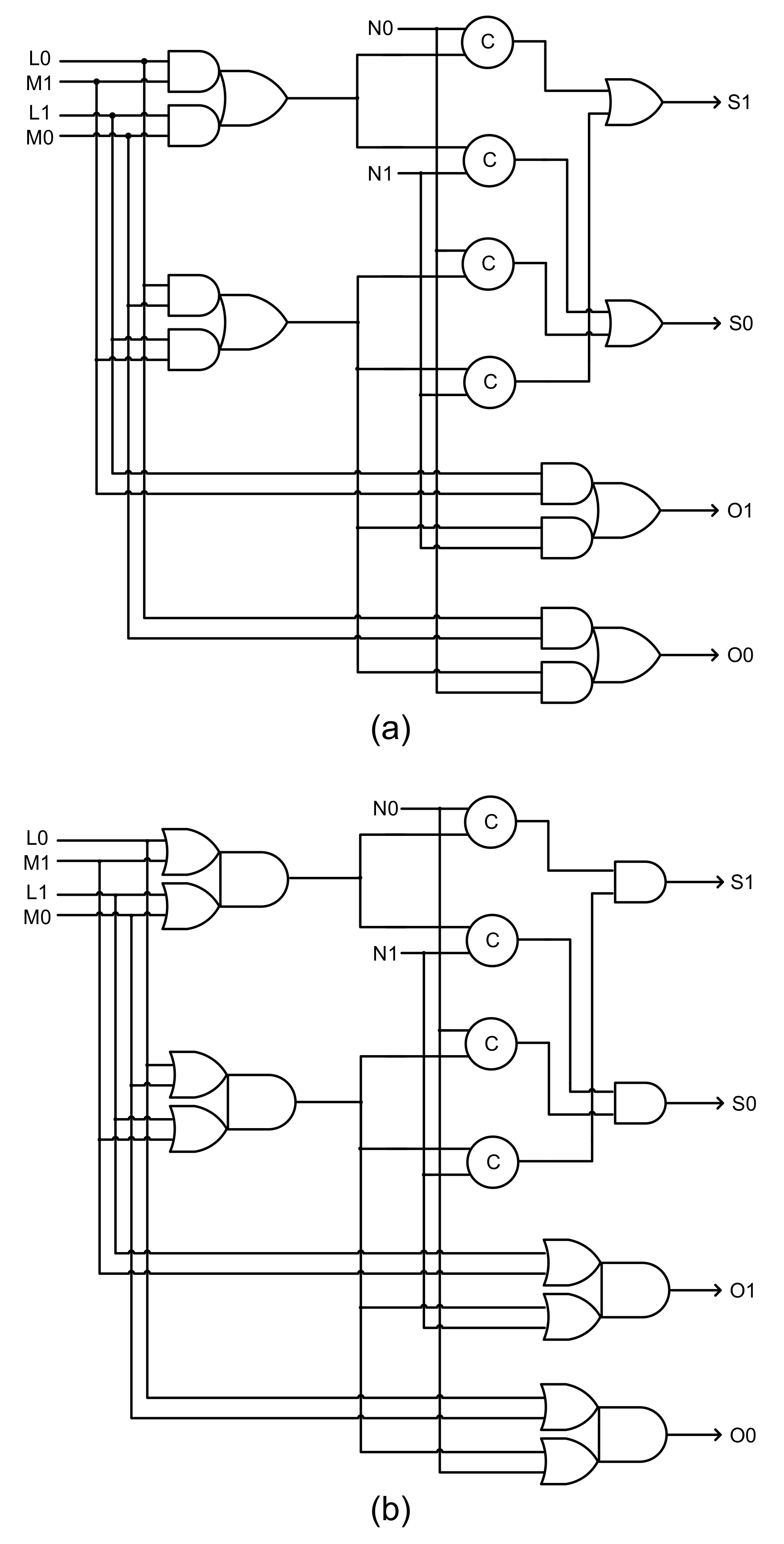
42] for the function modules and used the strong indication majority voters discussed in the previous section. A full adder adds two input bits (i.e., an augend bit and an addend bit) along with a carry input and produces two output bits, namely the sum bit and the carry output bit (overflow). Each TMR circuit implementation comprised three full adders and two majority voters with one majority voter assigned for the sum output and another majority voter assigned for the carry output. The gate level circuits of the early output QDI full adder [
42] are shown in
Figure 11a,b, which correspond to RTZ handshaking and RTO handshaking respectively. In
Figure 11, (L1,L0), (M1,M0), and (N1,N0) represent the dual rail augend, addend and carry inputs, and (S1,S0) and (O1,O0) represent the dual rail sum and carry (overflow) outputs of the full adder.
The physical implementations used a 32/28 nm bulk CMOS process [
38]. Excepting the 2-input C-element, which was alone custom-realized, all the other gates i.e., simple and complex gates used to construct the TMR circuits were directly utilized from the standard digital cell library [
38]. A typical case specification of the standard cell library was considered for the simulations using a (recommended) supply voltage of 1.05 V and an operating junction temperature of 25 °C. A virtual clock was used superficially to constraint the input and output ports of the TMR circuits; however, it did not form a part of the designs. The QDI TMR circuits were realized using dual rail data encoding and correspond to both RTZ and RTO handshaking.
A total of 256 input vectors, with half of them representing data and the remaining representing the spacer, were supplied to the function modules from the environment. A QDI full adder has six dual rail input signals, which gives rise to 26 i.e., 64 distinct input vectors. Considering an equal amount of return-to-zero or return-to-one spacers, given that the spacer is applied between successive applications of data, we end up with 128 input vectors covering both data and spacer which were applied twice. The input vectors considered for RTZ and RTO handshaking are logically equivalent to each other. The input vectors were supplied with a latency of 1.2 ns, which is greater than the worst-case latency of the QDI TMR circuit incorporating Singh_MV. Two test benches were used with one corresponding to RTZ handshaking and another corresponding to RTO handshaking. The behavioral simulations covered all possible scenarios for the function modules and it has been verified that majority voted outputs are produced.
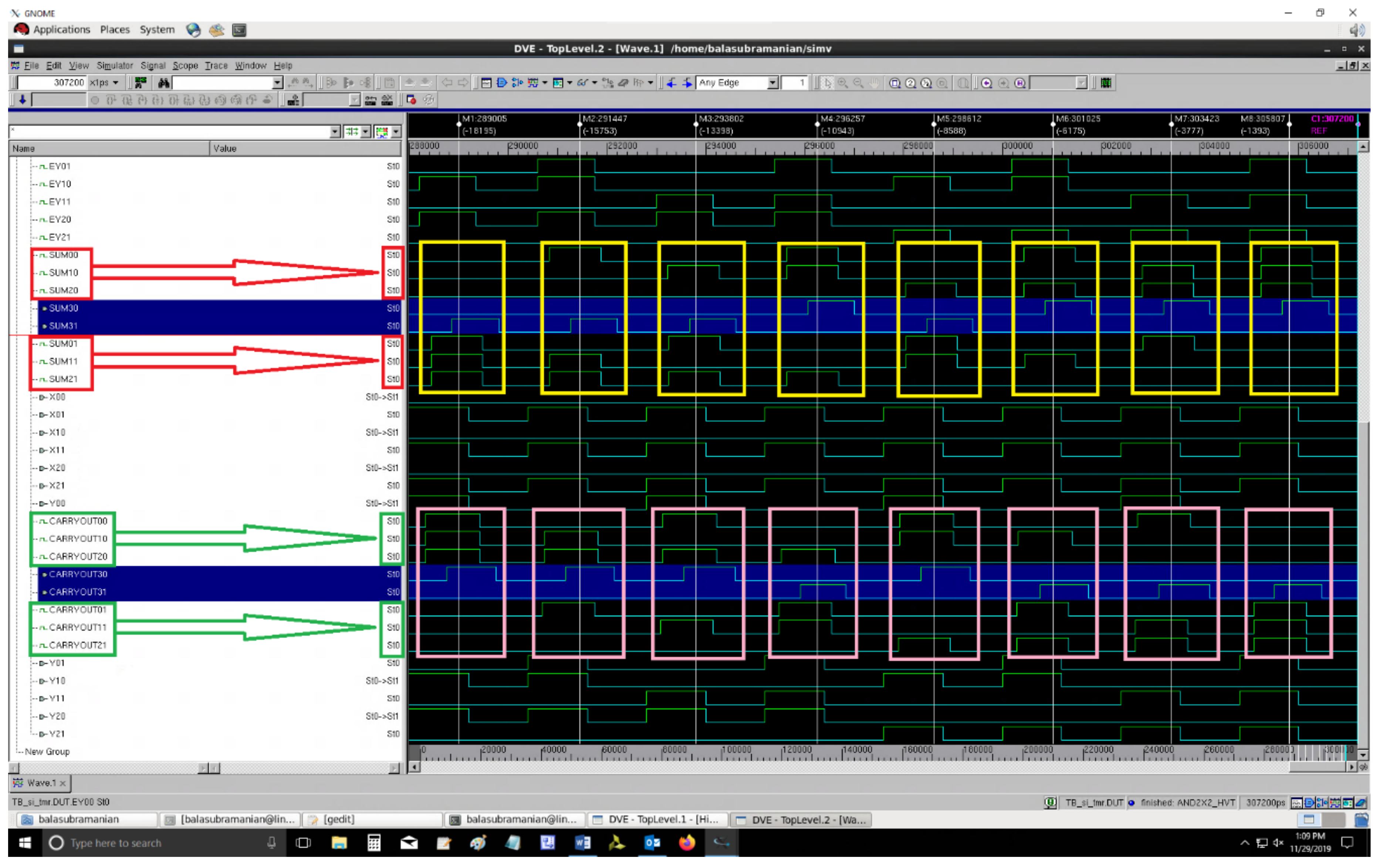
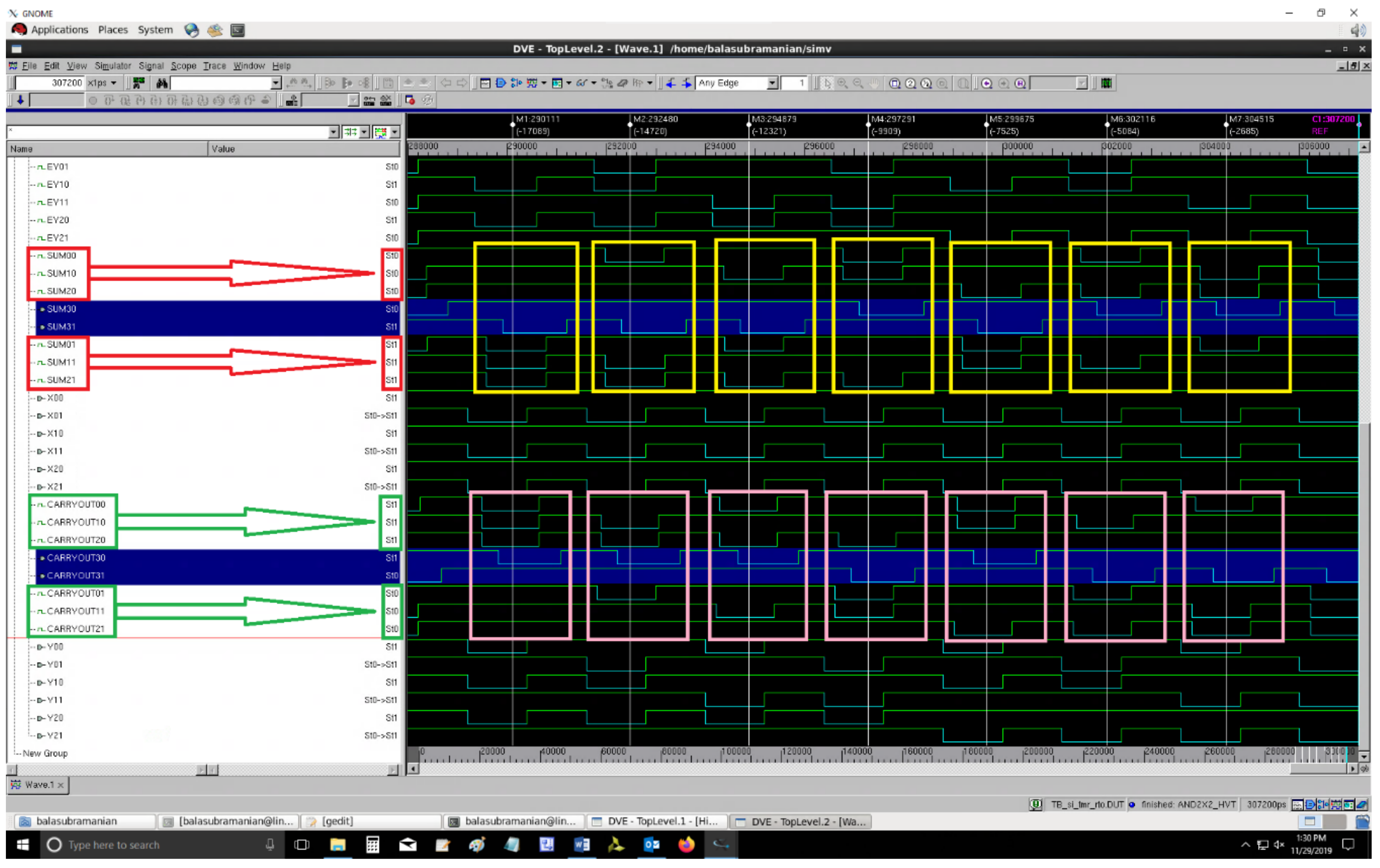
Figure 12 and
Figure 13 respectively portray the screenshots of example simulations of QDI TMR circuits comprising SI_MV corresponding to RTZ and RTO handshaking. In
Figure 12 and
Figure 13, on the left-side, (SUM01,SUM00), (SUM11,SUM10), and (SUM21,SUM20), given within the red boxes, represent the dual rail sum outputs, while (CARRYOUT01,CARRYOUT00), (CARRYOUT11,CARRYOUT10), and (CARRYOUT21,CARRYOUT20), given within the green boxes, represent the dual rail carry outputs of three identical QDI full adders (i.e., function modules). On the other hand, (SUM31,SUM30) and (CARRYOUT31,CARRYOUT30), highlighted in blue on the left-side, represent the majority voted sum and carry outputs of the QDI TMR circuit. Nevertheless, similar waveforms resulted for all the QDI TMR circuits comprising different majority voters. Some distinct combinations of inputs and majority voted sum and carry outputs are captured within the yellow and rose rectangles respectively in
Figure 12 and
Figure 13.
Synopsys tools were used to estimate the design metrics such as critical path delay, area, and average power dissipation. The critical path delay corresponds to the forward latency of a QDI circuit. Since strong indication majority voters are considered, the forward latency and reverse latency of the QDI TMR circuits are equal. This is because strong indication circuits tend to encounter the worst-case latency for the processing of data and spacer, as remarked in [
43]. Thus, the cycle time is the double of the forward latency. The design metrics are given in
Table 2.
The theoretical critical path delays associated with the function module (FM) are expressed by (45) and (46) with respect to RTZ and RTO handshaking. The theoretical cycle times of the QDI TMR circuits incorporating Singh_MV, DIMS_MV, Toms_MV and SI_MV are expressed by Equations (47) to (50) with respect to RTZ handshaking, and Equations (51) to (54) with respect to RTO handshaking. In the equations, the typical propagation delays of a two-input C-element, a four-input OR gate, a four-input AND gate, a two-input OR gate, a two-input AND gate, an AO22 complex gate, and an OA22 complex gate are denoted by TCE2, TOR4, TAND4, TOR2, TAND2, TAO22 and TOA22 respectively. Treg denotes the typical propagation delay of an input register, which is the same as TCE2. Equations (45) to (54) are rather approximate since the propagation delays of gates are alone accounted for and the interconnect delays have been neglected for simplicity.
From the above equations, it may be observed that the critical path traversed in the TMR circuit incorporating Singh_MV encounters an input register, a function module, three two-input C-elements, two three-input OR/AND gates and one two-input OR/AND gate. The critical path traversed in the TMR circuit incorporating DIMS_MV encounters an input register, a function module, two two-input C-elements and just one four-input OR/AND gate. The critical path traversed in the TMR circuit incorporating Toms_MV encounters an input register, a function module, two two-input C-elements and three two-input OR/AND gates. The critical path traversed in the TMR circuit incorporating SI_MV encounters an input register, a function module, one two-input OR/AND gate and three two-input C-elements. Hence, it is expected that the cycle time of the TMR circuit incorporating DIMS_MV would be less than the cycle times of its counterpart circuits incorporating Singh_MV, Toms_MV and SI_MV.
Table 2 substantiates this by showing that the cycle time of the TMR circuit incorporating DIMS_MV is the least amongst all with respect to RTZ and RTO handshaking.
In terms of area, the TMR circuit incorporating SI_MV consumes less silicon compared to the TMR circuits containing Singh_MV, DIMS_MV and Toms_MV, as seen from
Table 2. While the function modules, input registers and completion detectors would require the same area for all the TMR circuits pertaining to a specific handshaking, the areas of the majority voters would differ. This is the reason for the differences in area occupancies of different TMR circuits. With respect to RTZ handshaking, the areas of Singh_MV, DIMS_MV, Toms_MV and SI_MV are 50.57 µm
2, 46.76 µm
2, 43.20 µm
2 and 37.11 µm
2 respectively, and corresponding to RTO handshaking the areas of Singh_MV, DIMS_MV, Toms_MV and SI_MV are 50.57 µm
2, 44.73 µm
2, 43.20 µm
2 and 37.11 µm
2 respectively. Singh_MV requires the same area for both RTZ and RTO handshaking, which is the same case with SI_MV. A four-input AND gate requires less area than a four-input OR gate and hence DIMS_MV requires less area for RTO handshaking compared to RTZ handshaking. The areas of minimum-size two-input AND and OR gates are the same in [
38], and hence Toms_MV requires the same area for RTZ and RTO handshaking.
In terms of average power, the TMR circuits comprising DIMS_MV and Toms_MV dissipate almost the same power for RTZ handshaking. However, based on RTO handshaking, the TMR circuit comprising DIMS_MV dissipates less power compared to the TMR circuit comprising Toms_MV. The TMR circuit comprising Singh_MV dissipates more power compared to the TMR circuits comprising DIMS_MV and Toms_MV with respect to RTZ and RTO handshaking. This is due to the greater number of gates used to realize Singh_MV compared to DIMS_MV and Toms_MV. The TMR circuit comprising SI_MV dissipates more power than the counterpart TMR circuits for both RTZ and RTO handshaking. The main reason for this is attributed to the internal completion detector present in SI_MV, which is absent in Singh_MV, DIMS_MV and Toms_MV. In the cases of Singh_MV, DIMS_MV and Toms_MV, just one signal path would be activated from the primary inputs to the primary outputs for every application of data. Although the same phenomenon occurs in the logic of SI_MV as well, nevertheless, its internal completion detector will experience continuous switching activity for the application of spacer and data. Due to the frequent switching activity, the switching power and thus the dynamic power dissipation of SI_MV will be high, and this causes an increase in the average power dissipation of the TMR circuits comprising SI_MV compared to the TMR circuits containing Singh_MV, DIMS_MV and Toms_MV.
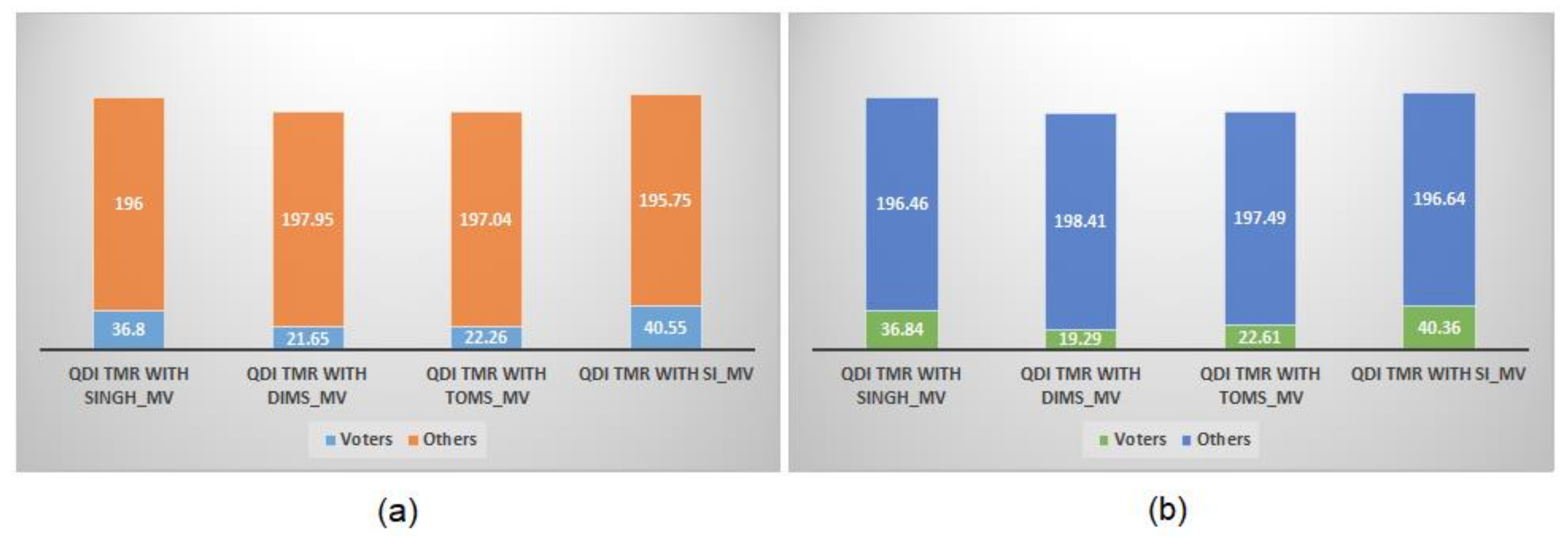
A split-up of the average power dissipation of different TMR circuits is shown in
Figure 14a for RTZ handshaking and
Figure 14b for RTO handshaking. The power dissipated by voters and others (i.e., function modules, registers and completion detector) are shown in
Figure 14. From
Figure 14, it is seen that SI_MV dissipates more power compared to Singh_MV, DIMS_MV and Toms_MV with respect to RTZ and RTO handshaking, and this is primarily due to the former’s internal completion detector.