Mechanical Response and Fracture Behavior of Brittle Rocks Containing Two Inverted U-Shaped Holes under Uniaxial Loading
Abstract
1. Introduction
2. Material and Methods
2.1. Sample Description
2.2. Experimental Facilities and Parameter Settings
3. Experimental Results and Analysis
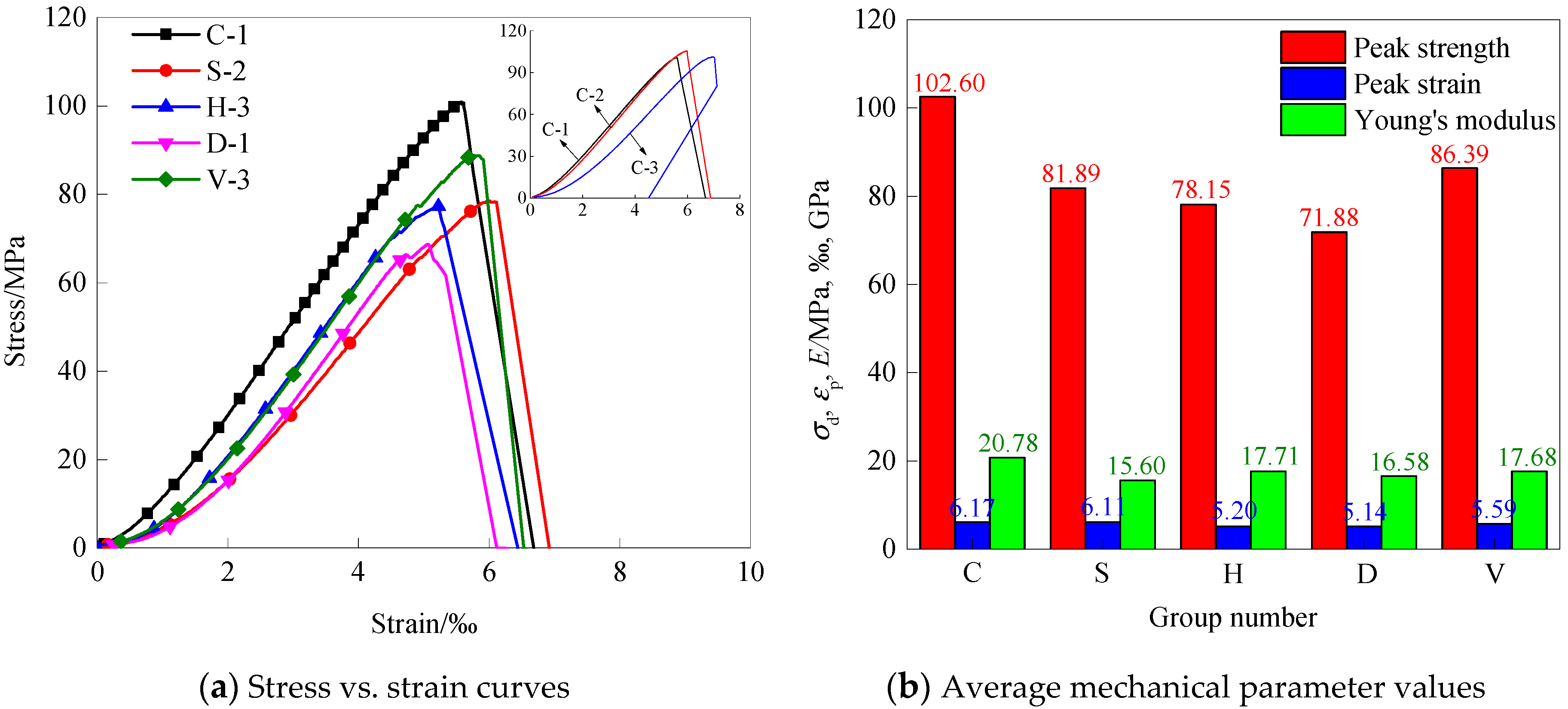
3.1. Strength and Deformation Properties
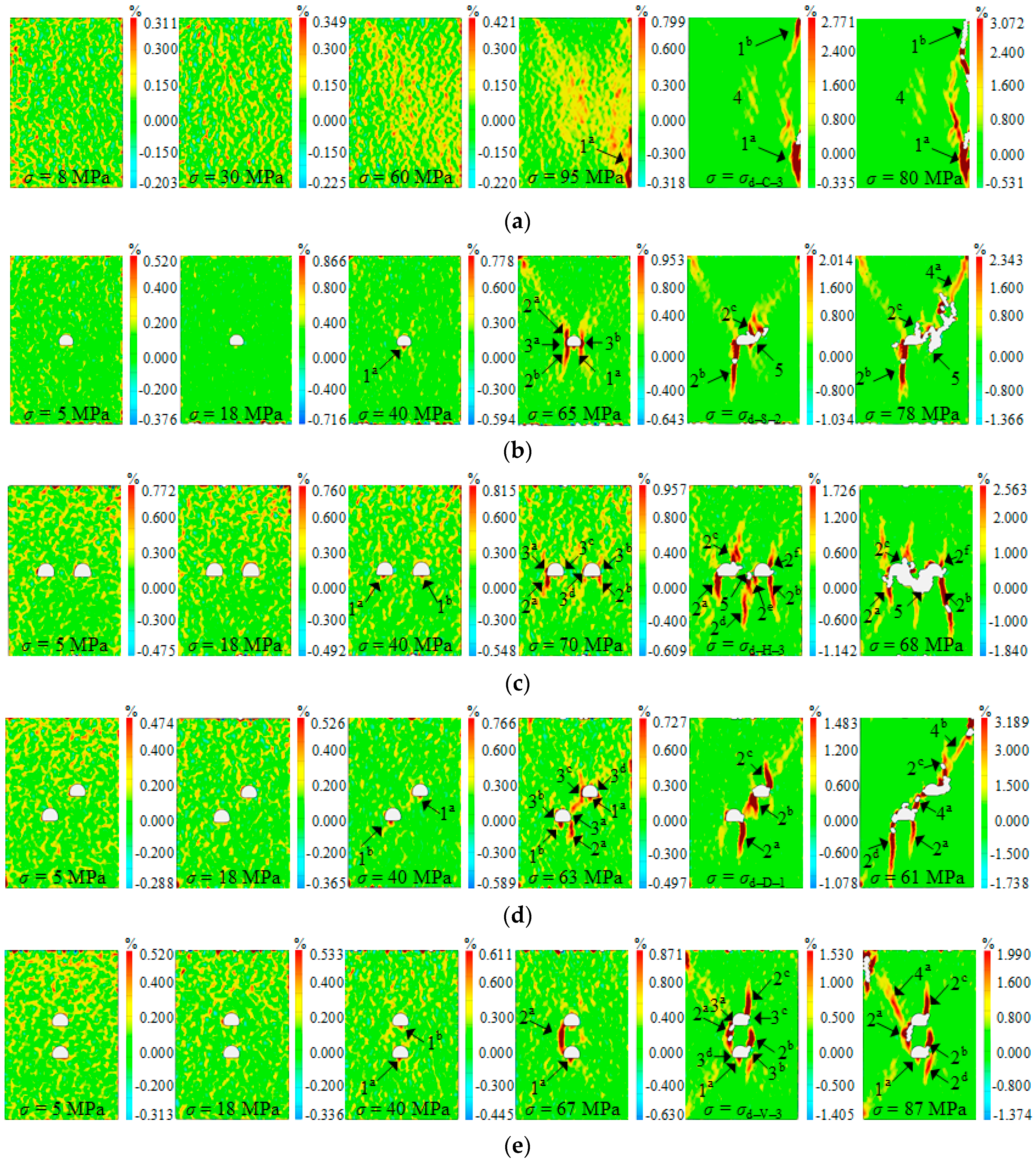
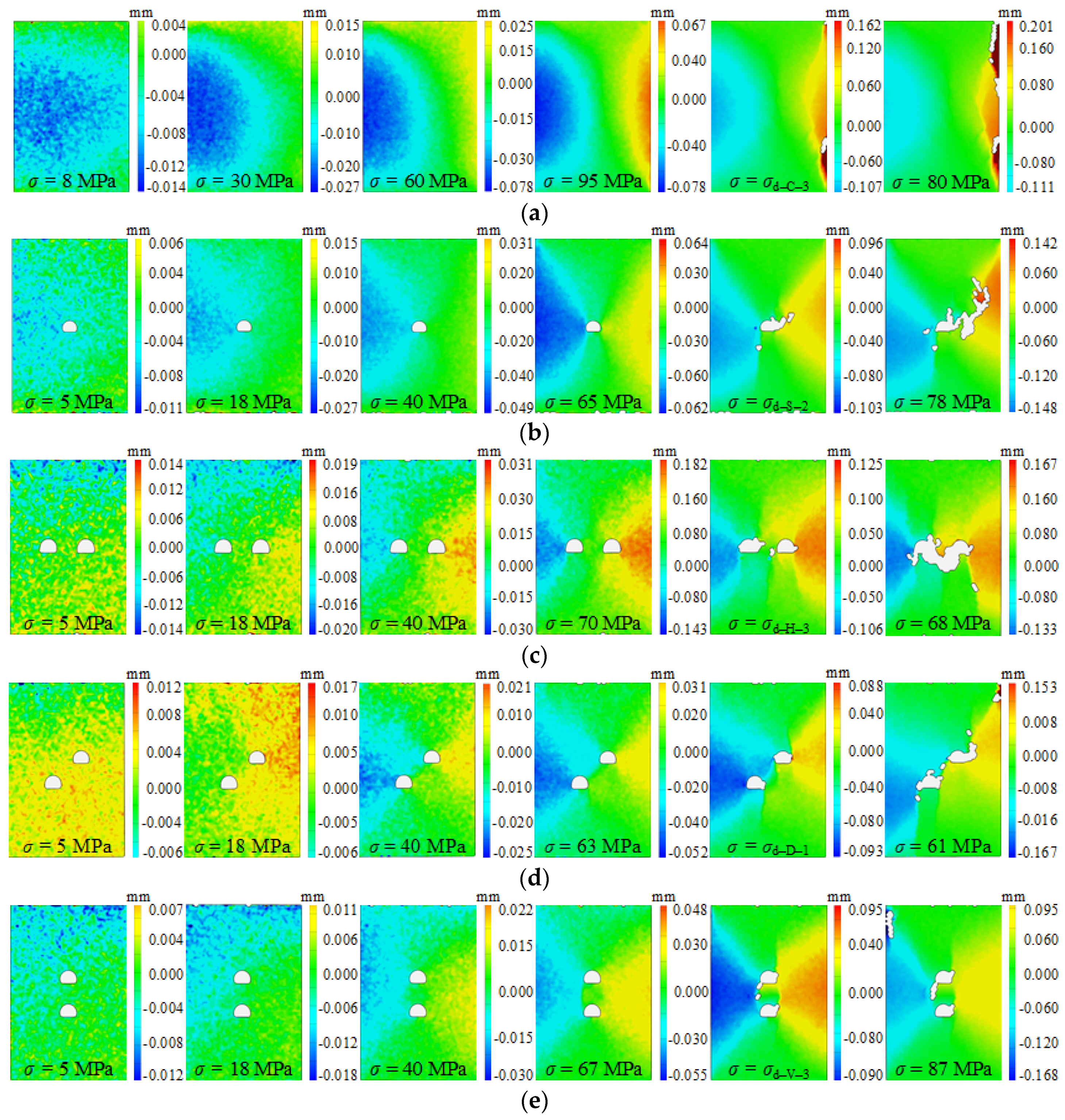
3.2. Fracture Development and Failure Patterns
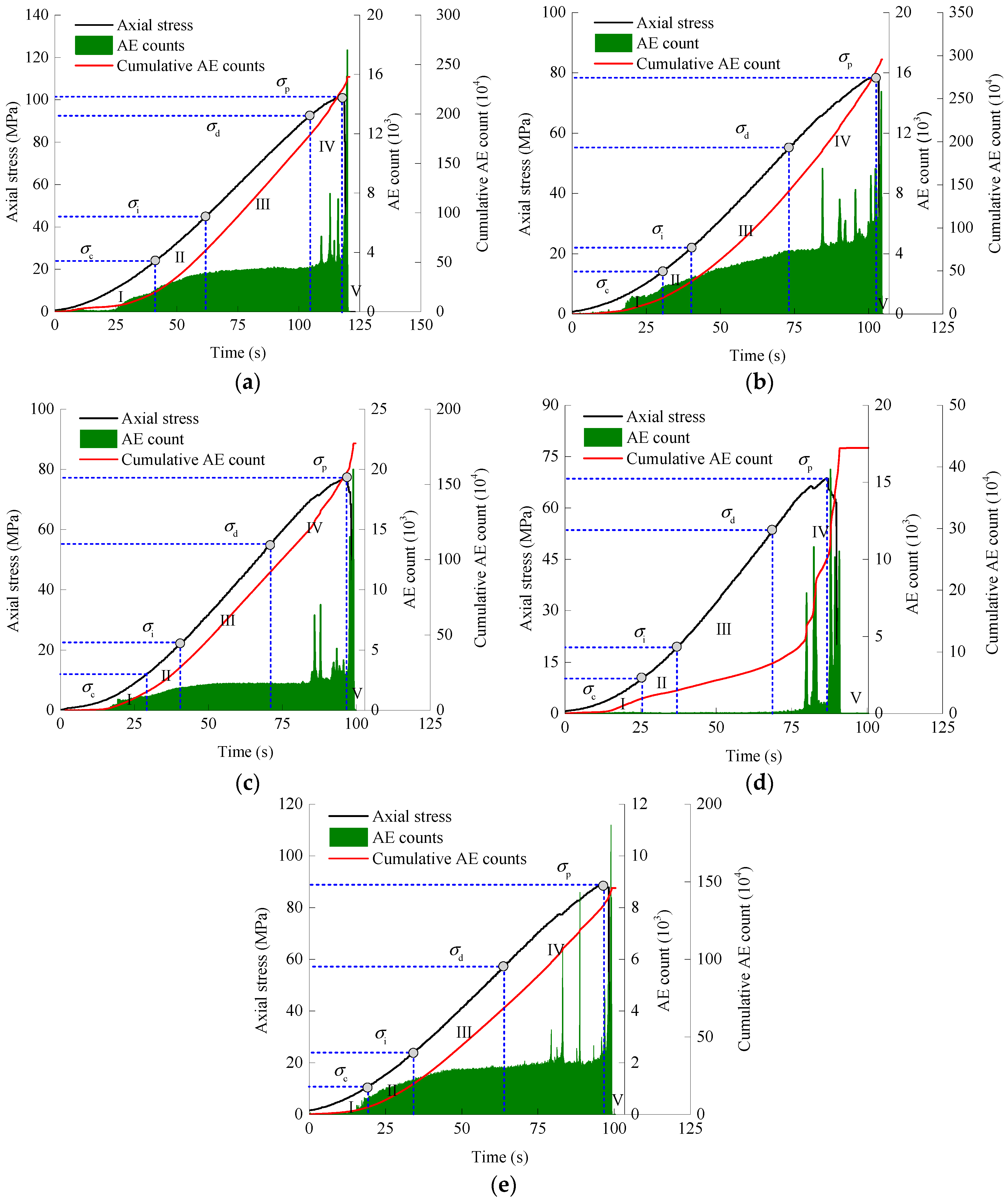
3.3. AE Activity and Threshold Stress
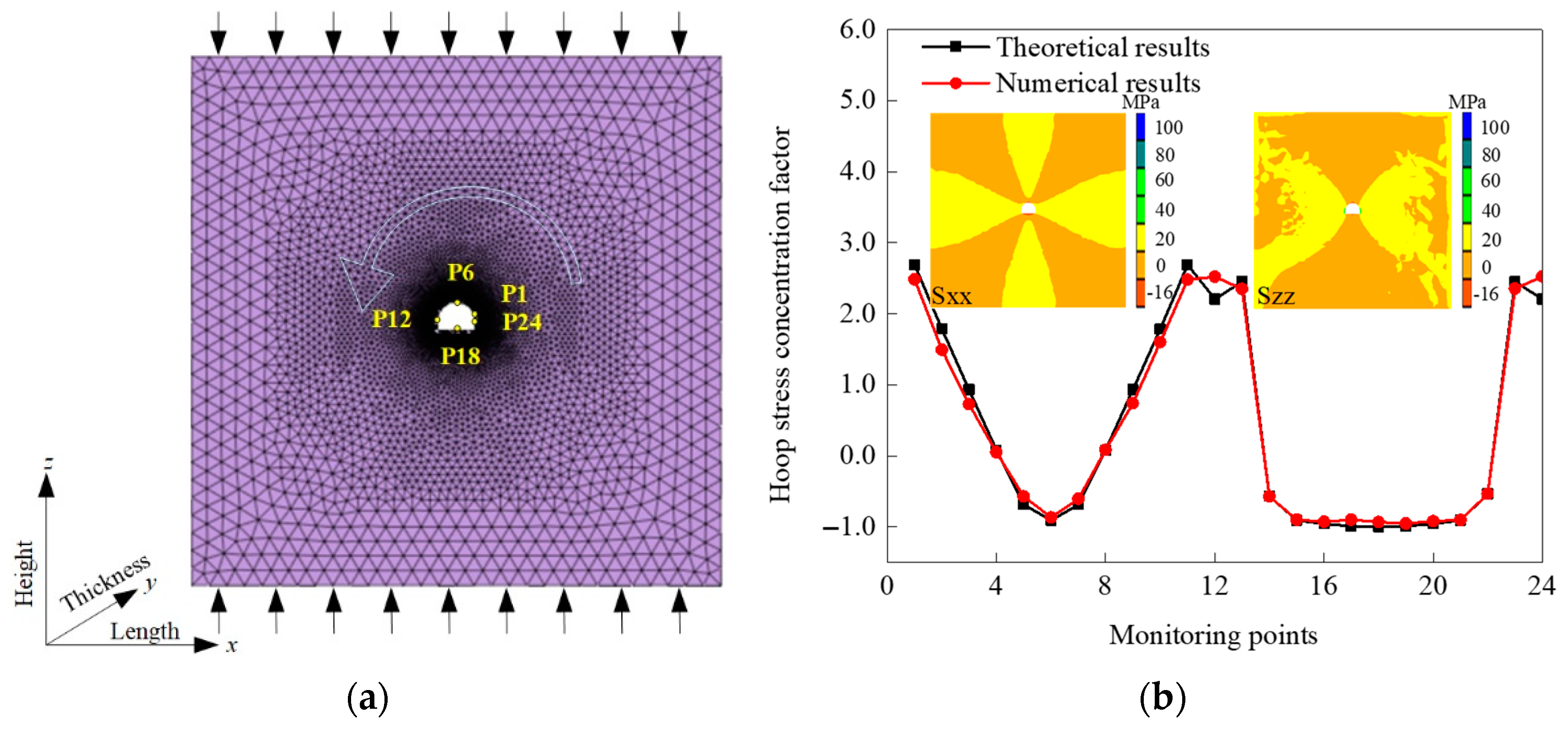
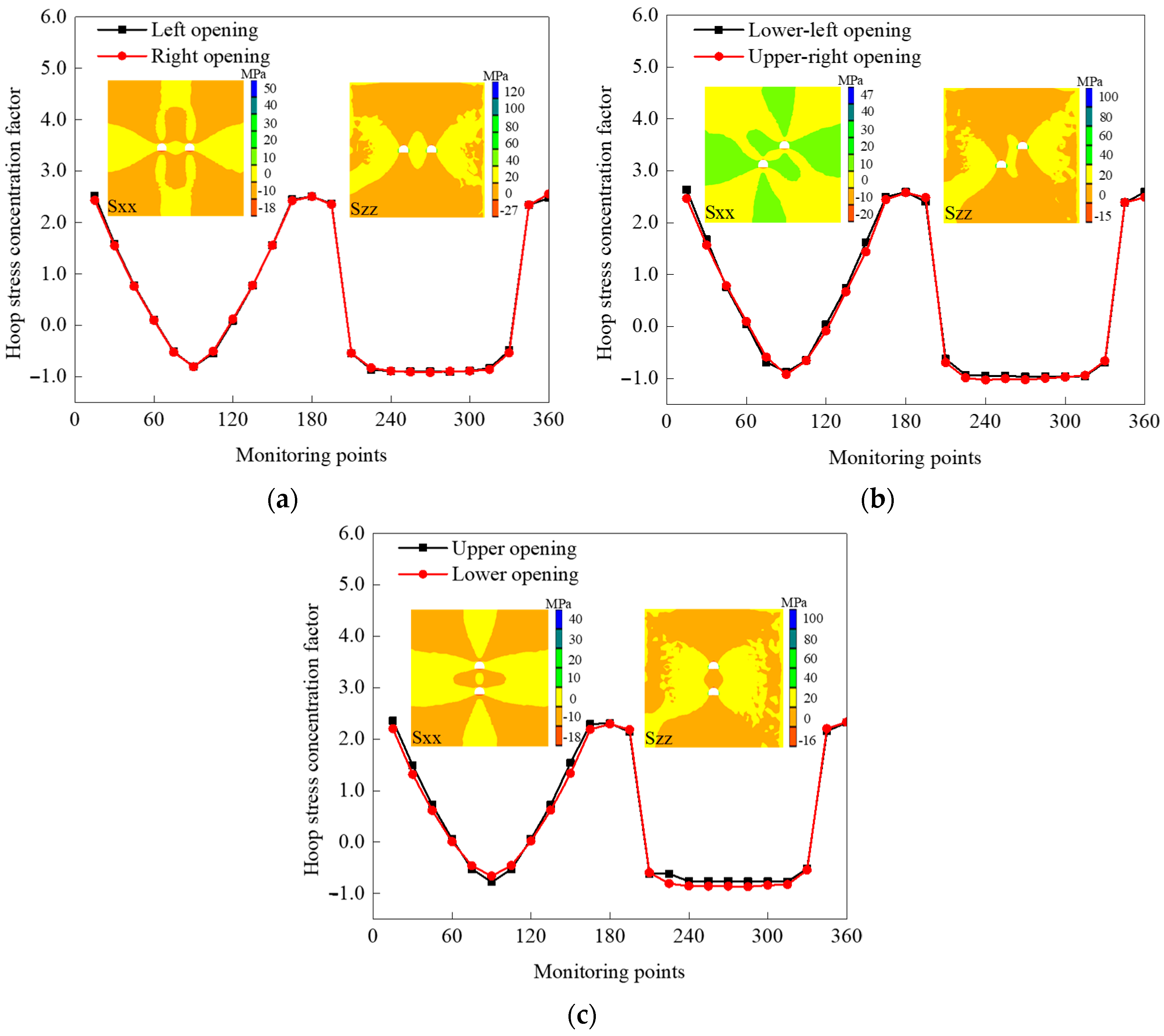
4. Stress Distribution around Opening
5. Discussion
6. Conclusions
- (1)
- Both the number and configuration of openings noticeably affected the strength and deformation properties of rock specimens. The uniaxial compressive strength of these groups could be ordered from large to small as: C > V > S > H > D, and the degree of attenuation ranged from 15.80% to 29.94%. For the Young’s modulus, Group C had the largest value, followed by Groups H, V, D and S, with a decrease extent of 14.76%–24.93%. Besides, the peak strains of the pre-holed specimens also showed a different degree of reduction from the intact specimen.
- (2)
- According to the distribution of strain localization and the variation of AE signals during loading, the crack development around the openings under increasing loads was clarified. Five sorts of cracks appeared around the openings, i.e., elementary tensile crack, posterior tensile crack, slabbing crack, shear crack and spalling crack. For specimens with two openings, three categories of hole coalescence, namely slabbing coalescence for Group H, shear coalescence for Group D and tensile coalescence for Group V, were formed. The failure mode of Groups S and D was shear failure, whilst that of the others was tensile-shear failure. With regard to the threshold stresses in the fracture process, the initiation stress of the intact specimen was 44.8 MPa, while that of the specimens with one single or two openings were 21.2 MPa, 22.9 MPa, 18.8 MPa and 24.6 MPa, respectively. Moreover, the damage stress of the intact specimen was 91% of the peak stress, while that of the specimens with openings was (0.65–0.78) times their peak stresses.
- (3)
- Under unidirectional compressive loads, tensile and compressive stresses concentrate on the roof-floor and both sides of the opening, respectively. The hoop SCFs on the boundaries of the two diagonal openings was the largest, while those of the two vertical openings were the smallest. On the whole, the stress distribution at the periphery of the opening could effectively interpret the formation, initiation location and sequence of the cracks. The order of the crack initiation stresses of the specimens with openings could also be verified on the basis of the magnitude of the SCF on the roofs or floors of the openings.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saadat, M.; Taheri, A. A numerical approach to investigate the effects of rock texture on the damage and crack propagation of a pre-cracked granite. Comput. Geotech. 2019, 111, 89–111. [Google Scholar] [CrossRef]
- Zhou, X.P.; Wang, Y.T.; Xu, X.M. Numerical simulation of initiation, propagation and coalescence of cracks using the non-ordinary state-based peridynamics. Int. J. Fract. 2016, 201, 213–234. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Zhang, L.Y.; Wang, W.J.; Pu, C.Z.; Wan, W.; Tang, J.Z. Cracking and stress-strain behavior of rock-like material containing two flaws under uniaxial compression. Rock Mech. Rock Eng. 2016, 49, 2665–2687. [Google Scholar] [CrossRef]
- Luo, Y.; Gong, F.Q.; Liu, D.Q.; Wang, S.Y.; Si, X.F. Experimental simulation analysis of the process and failure characteristics of spalling in D-shaped tunnels under true-triaxial loading conditions. Tunn. Undergr. Space Technol. 2019, 90, 42–61. [Google Scholar] [CrossRef]
- Liang, W.Z.; Zhao, G.Y.; Wang, X.; Zhao, J.; Ma, C.D. Assessing the rockburst risk for deep shafts via distance-based multi-criteria decision making approaches with hesitant fuzzy information. Eng. Geol. 2019, 260, 105211. [Google Scholar] [CrossRef]
- Liang, W.Z.; Zhao, G.Y.; Wu, H.; Chen, Y. Optimization of mining method in subsea deep gold mines: A case study. Trans. Nonferr. Met. Soc. 2019, 29, 2160–2169. [Google Scholar] [CrossRef]
- Su, G.S.; Zhai, S.B.; Jiang, J.Q.; Zhang, G.L.; Yan, L.B. Influence of radial stress gradient on strainbursts: An experimental study. Rock Mech. Rock. Eng. 2017, 50, 2659–2676. [Google Scholar] [CrossRef]
- Wu, H.; Kulatilake, P.H.S.W.; Zhao, G.Y.; Liang, W.Z.; Wang, E.J. Fracturing behaviour of sandstone specimens with a cavity formed by intersecting excavations under compression: Experimental study and numerical modelling. Strain 2019, 55, e12316. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Zhao, J.; Ju, M.H.; De Silva, R.V.S.; Rathnaweera, T.D.; Bandara, A.K.M.S. Opportunities and challenges in deep mining: A brief review. Engineering-PRC 2017, 3, 546–551. [Google Scholar] [CrossRef]
- Martini, C.D.; Read, R.S.; Martino, J.B. Observations of brittle failure around a circular test tunnel. Int. J. Rock Mech. Min. Sci. 1997, 34, 1065–1073. [Google Scholar] [CrossRef]
- Bobet, A.; Einstein, H.H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression. Int. J. Rock Mech. Min. Sci. 1998, 35, 863–888. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Chau, K.T. Crack coalescence in a rock-like material containing two cracks. Int. J. Rock Mech. Min. Sci. 1998, 35, 147–164. [Google Scholar] [CrossRef]
- Sagong, M.; Boet, A. Coalescence of multiple flaws in a rock-model material in uniaxial compression. Int. J. Rock Mech. Min. Sci. 2002, 39, 229–241. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Einstein, H.H. Systematic evaluation of cracking behavior in specimens containing single flaws under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2009, 46, 239–249. [Google Scholar] [CrossRef]
- Lee, H.; Jeon, S. An experimental and numerical study of fracture coalescence in pre-cracked specimens under uniaxial compression. Int. J. Solids Struct. 2011, 48, 979–999. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Sharrock, G.; Hebblewhite, B.K. Numerical investigation of the effect of joint geometrical parameters on the mechanical properties of a non-persistent jointed rock mass under uniaxial compression. Comput. Geotech. 2013, 49, 206–225. [Google Scholar] [CrossRef]
- Yang, X.X.; Kulatilake, P.H.S.W.; Chen, X.; Jing, H.W. Particle flow modeling of rock blocks with nonpersistent open joints under uniaxial compression. Int. J. Geomech. 2016, 16, 04016020. [Google Scholar] [CrossRef]
- Haeri, H.; Khaloo, A.; Marji, M.F. Experimental and numerical analysis of Brazilian discs with multiple parallel cracks. Arab. J. Geosci. 2015, 8, 5897–5908. [Google Scholar] [CrossRef]
- Feng, P.; Dai, F.; Liu, Y.; Xu, N.W.; Fan, P.X. Effects of coupled static and dynamic strain rates on mechanical behaviors of rock-like specimens containing pre-existing fissures under uniaxial compression. Can. Geotech. J. 2018, 55, 640–652. [Google Scholar] [CrossRef]
- Gao, Y.H.; Feng, X.T. Study on damage evolution of intact and jointed marble subjected to cyclic true triaxial loading. Eng. Fract. Mech. 2019, 215, 224–234. [Google Scholar] [CrossRef]
- Dang, W.G.; Konietzky, H.; Frühwirt, T.; Herbst, M. Cyclic Frictional Responses of Planar Joints Under Cyclic Normal Load Conditions: Laboratory Tests and Numerical Simulations. Rock Mech. Rock Eng. 2019. [Google Scholar] [CrossRef]
- Dang, W.G.; Konietzky, H.; Chang, L.F. Velocity-frequency-amplitude-dependent frictional resistance of planar joints under dynamic normal load (DNL) conditions. Tunn. Undergr. Space Technol. 2018, 79, 27–34. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Aliha, M.R.M.; Berto, F. Application of an average strain energy density criterion to obtain themixed mode fracture load of granite rock tested with the cracked asymmetric four-point bend specimens. Theor. Appl. Fract. Mech. 2018, 97, 419–425. [Google Scholar] [CrossRef]
- Wang, Y.S.; Hu, X.Z. Determination of tensile strength and fracture toughness of granite using notched three-point-bend samples. Rock Mech. Rock Eng. 2017, 50, 17–28. [Google Scholar] [CrossRef]
- Cao, R.H.; Cao, P.; Lin, H.; Fan, X.; Zhang, C.Y.; Liu, T.Y. Crack Initiation, propagation, and failure characteristics of jointed rock or rock-like specimens: A review. Adv. Civ. Eng. 2019, 2019, 6975751. [Google Scholar] [CrossRef]
- Carter, B.J.; Lajtai, E.Z.; Petukhov, A. Primary and remote fracture around underground cavities. Int. J. Numer. Anal. Methods Geomech. 1991, 15, 21–40. [Google Scholar] [CrossRef]
- Carter, B.J.; Lajtai, E.Z.; Yuan, Y.G. Tensile fracture from circular cavities loaded in com-pression. Int. J. Fract. 1992, 57, 221–236. [Google Scholar]
- Zhao, X.D.; Zhang, H.X.; Zhu, W.C. Fracture evolution around pre-existing cylindrical cavities in brittle rocks under uniaxial compression. Trans. Nonferr. Met. Soc. 2014, 24, 806–815. [Google Scholar] [CrossRef]
- Tang, C.A.; Wong, R.H.C.; Chau, K.T.; Lin, P. Modeling of compression-induced splitting failure in heterogeneous brittle porous solids. Eng. Fract. Mech. 2005, 72, 597–615. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Lin, P.; Tang, C.A. Experimental and numerical study on splitting failure of brittle solids containing single pore under uniaxial compression. Mech. Mater. 2006, 38, 142–159. [Google Scholar] [CrossRef]
- Dzik, E.J.; Lajtai, E.Z. Primary fracture propagation from circular cavities loaded in compression. Int. J. Fract. 1996, 9, 49–64. [Google Scholar] [CrossRef]
- Martin, C.D.; Kaiser, P.K.; Mccreath, D.R. Hoek–Brown parameters for predicting the depth of brittle failure around tunnels. Can. Geotech. J. 1999, 34, 136–151. [Google Scholar] [CrossRef]
- Fakhimi, A.; Carvalho, F.; Ishida, T.; Labuz, J.F. Simulation of failure around a circular opening in rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 507–515. [Google Scholar] [CrossRef]
- Wang, S.Y.; Sloan, S.W.; Sheng, D.C.; Tang, C.A. Numerical analysis of the failure process around a circular opening in rock. Comput. Geotech. 2012, 39, 8–16. [Google Scholar] [CrossRef]
- Wang, S.Y.; Sun, L.; Yang, C.; Yang, S.Q.; Tang, C.A. Numerical study on static and dynamic fracture evolution around rock cavities. J. Rock Mech. Geotech. Eng. 2013, 5, 262–276. [Google Scholar] [CrossRef]
- Yin, Q.; Jing, H.W.; Ma, G.W. Experimental study on mechanical properties of sandstone specimens containing a single hole after high-temperature exposure. Geotech. Lett. 2015, 5, 43–48. [Google Scholar] [CrossRef]
- Weng, L.; Li, X.B.; Taheri, A.; Wu, Q.H.; Xie, X.F. Fracture evolution around a cavity in brittle rock under uniaxial compression and coupled static–dynamic loads. Rock Mech. Rock Eng. 2018, 51, 531–545. [Google Scholar] [CrossRef]
- Li, X.B.; Feng, F.; Li, D.Y. Numerical simulation of rock failure under static and dynamic loading by splitting test of circular ring. Eng. Fract. Mech. 2018, 118, 184–201. [Google Scholar] [CrossRef]
- Haeri, H.; Khaloo, A.; Marji, M.F. Fracture analyses of different pre-holed concrete specimens under compression. Acta Mech. Sin. -PRC 2015, 31, 855–870. [Google Scholar] [CrossRef]
- Jespersen, C.; Maclaughlin, M.; Hudyma, N. Strength, deformation modulus and failure modes of cubic analog specimens representing macroporous rock. Int. J. Rock Mech. Min. Sci. 2010, 47, 1349–1356. [Google Scholar] [CrossRef]
- Lin, P.; Wong, R.H.C.; Tang, C.A. Experimental study of coalescence mechanisms and failure under uniaxial compression of granite containing multiple holes. Int. J. Rock Mech. Min. Sci. 2015, 77, 313–327. [Google Scholar] [CrossRef]
- Huang, Y.H.; Yang, S.Q.; Tian, W.L. Cracking process of a granite specimen that contains multiple pre-existing holes under uniaxial compression. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1341–1356. [Google Scholar] [CrossRef]
- Zhu, W.C.; Liu, J.; Tang, C.A.; Zhao, X.D.; Brady, B.H. Simulation of progressive fracturing processes around underground excavations under biaxial compression. Tunn. Undergr. Space Technol. 2005, 20, 231–247. [Google Scholar] [CrossRef]
- Li, X.B.; Weng, L. Numerical investigation on fracturing behaviors of deep-buried opening under dynamic disturbance. Tunn. Undergr. Space Technol. 2016, 54, 61–72. [Google Scholar] [CrossRef]
- Li, D.Y.; Zhu, Q.Q.; Zhou, Z.L.; Li, X.B.; Ranjith, P.G. Fracture analysis of marble specimens with a hole under uniaxial compression by digital image correlation. Eng. Fract. Mech. 2017, 183, 109–124. [Google Scholar] [CrossRef]
- Zeng, W.; Yang, S.Q.; Tian, W.L. Experimental and numerical investigation of brittle sandstone specimens containing different shapes of holes under uniaxial compression. Eng. Fract. Mech. 2018, 200, 430–450. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, G.Y.; Liang, W.Z. Investigation of cracking behaviour and mechanism of sandstone specimens with a hole under compression. Int. J. Mech. Sci. 2019, 163, 105084. [Google Scholar] [CrossRef]
- Liu, J.P.; Li, Y.H.; Xu, S.D.; Xu, S.; Jin, C.Y. Cracking mechanisms in granite rocks subjected to uniaxial compression by moment tensor analysis of acoustic emission. Theor. Appl. Fract. Mech. 2015, 75, 151–159. [Google Scholar]
- Zhou, L.; Zhu, Z.M.; Dong, Y.Q.; Fan, Y.; Zhou, Q.; Deng, S. The influence of impacting orientations on the failure modes of cracked tunnel. Int. J. Impact Eng. 2019, 125, 134–142. [Google Scholar] [CrossRef]
- Zhu, Q.Q.; Li, D.Y.; Han, Z.Y.; Li, X.B.; Zhou, Z.L. Mechanical properties and fracture evolution of sandstone specimens containing different inclusions under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2019, 115, 33–47. [Google Scholar] [CrossRef]
- Yang, S.Q.; Huang, Y.H.; Tian, W.L.; Zhu, J.B. An experimental investigation on strength, deformation and crack evolution behavior of sandstone containing two oval flaws under uniaxial compression. Eng. Geol. 2017, 217, 35–48. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Tan, L.H.; Cao, W.Z.; Zhou, Z.Y.; Cai, X. Fracture evolution and failure behaviour of marble specimens containing rectangular cavities under uniaxial loading. Eng. Fract. Mech. 2017, 184, 183–201. [Google Scholar] [CrossRef]
- Han, Z.Y.; Li, D.Y.; Zhu, Q.Q.; Liu, M.; Sun, Z. Dynamic fracture evolution and mechanical behavior of sandstone containing non-coplanar elliptical flaws under impact loading. Adv. Civ. Eng. 2018, 2018, 5649357. [Google Scholar]
- Wu, H.; Kulatilake, P.H.S.W.; Zhao, G.Y.; Liang, W.Z. Stress distribution and fracture evolution around a trapezoidal cavity in sandstone loaded in compression. Theor. Appl. Fract. Mech. 2019, 104, 102348. [Google Scholar] [CrossRef]
- Ulusay, R.; Hudson, J.A. The Complete ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 1974–2006; ISRM Turkish National Group: Ankara, Turkey, 2007. [Google Scholar]
- Liu, X.L.; Li, X.B.; Hong, L.; Yin, T.B.; Rao, M. Acoustic emission characteristics of rock under impact loading. J. Cent. South Univ. 2015, 22, 3571–3577. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Stimpson, B.; Read, R.S. Changes in acoustic event properties with progressive fracture damage. Int. J. Rock Mech. Min. Sci. 1997, 34, 71.e1–71.e12. [Google Scholar] [CrossRef]
- Shan, P.F.; Lai, X.P.; Liu, X.M. Correlational analytical characterization of energy dissipation-liberation and acoustic emission during coal and rock fracture inducing by underground coal excavation. Energies 2019, 12, 2382. [Google Scholar] [CrossRef]
- Wu, H.; Kulatilake, P.H.S.W.; Zhao, G.Y.; Liang, W.Z.; Wang, E.J. A comprehensive study of fracture evolution of brittle rock containing an inverted U-shaped cavity under uniaxial compression. Comput. Geotech. 2019, 116, 103219. [Google Scholar] [CrossRef]
- Dang, W.G.; Wu, W.; Koniezky, H.; Qian, J.Y. Effect of shear-induced aperture evolution on fluid flow in rock fractures. Comput. Geotech. 2019, 114, 103152. [Google Scholar] [CrossRef]

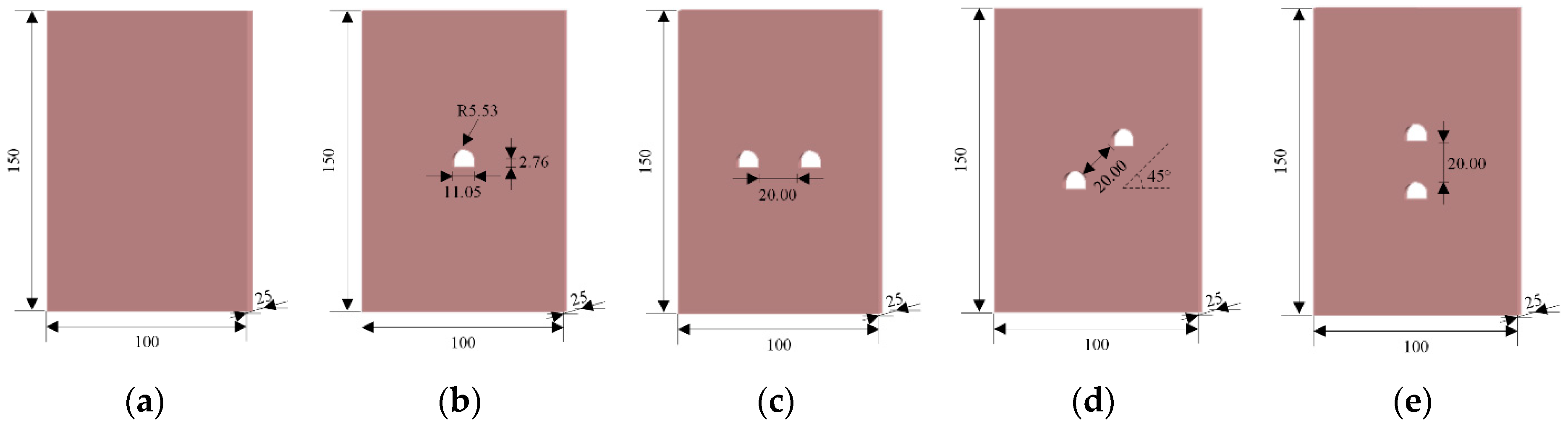
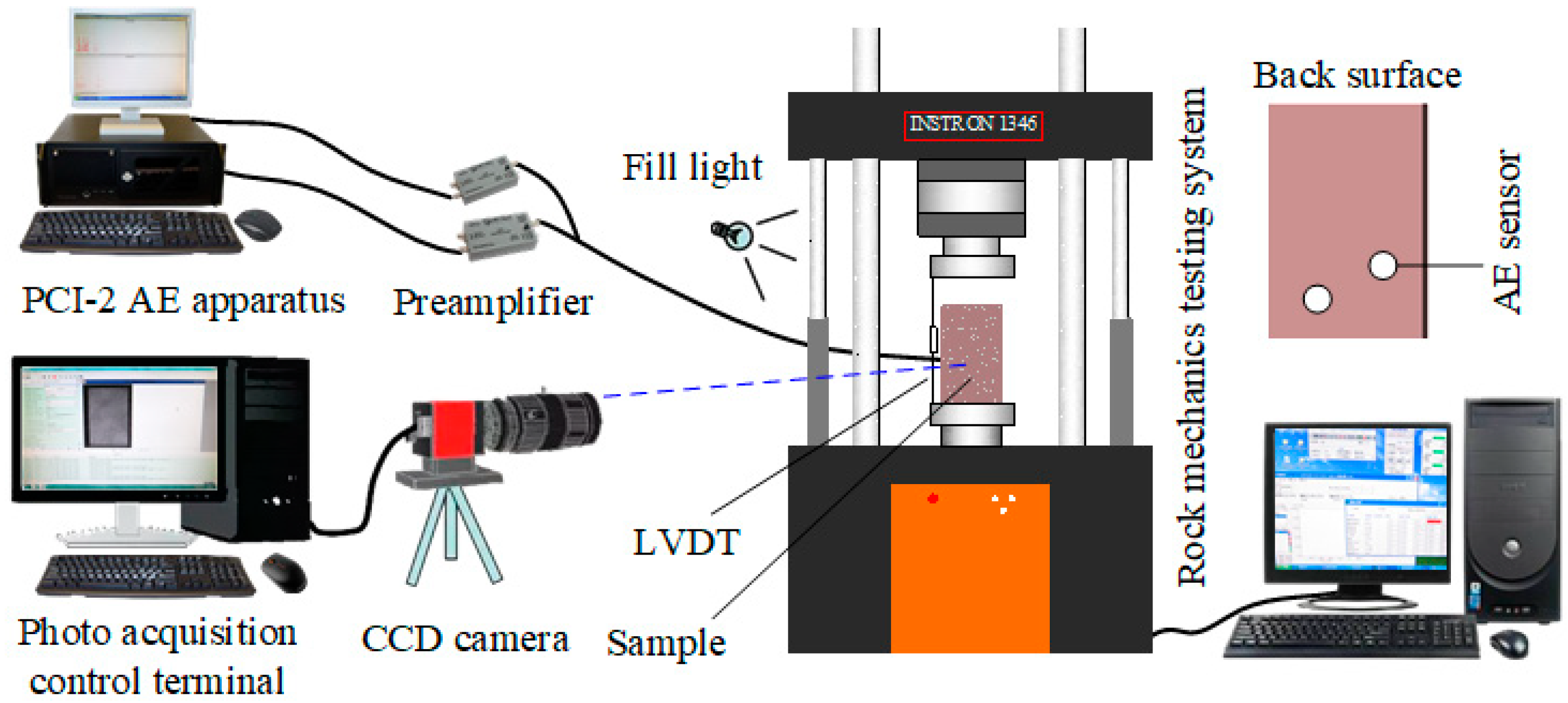

| v/(m/s) | ρ/(kg/m3) | σt/MPa | σp/MPa | E/GPa | μ | c/MPa | ϕ/° | KIC/(MPa·m½) |
|---|---|---|---|---|---|---|---|---|
| 3174.5 | 2472.2 | 5.3 | 99.3 | 24.4 | 0.26 | 19.0 | 40.4 | 0.6 |
| Detection Threshold/dB | Sampling Rate/Msps | Sampling Time/k | PtT/μs | PDT/μs | HDT/μs | HLT/μs |
|---|---|---|---|---|---|---|
| 45 | 10 | 5 | 256 | 50 | 20 | 300 |
| Sample No. | Length (mm) | Thickness (mm) | Width (mm) | Density (kg·m−3) | σp (MPa) | εp (‰) | E (GPa) |
|---|---|---|---|---|---|---|---|
| C-1 | 150.1 | 25.0 | 100.1 | 2391.4 | 100.9 | 5.57 | 21.63 |
| C-2 | 150.5 | 24.9 | 99.6 | 2427.5 | 105.6 | 5.96 | 21.63 |
| C-3 | 150.7 | 24.8 | 100.7 | 2385.5 | 101.3 | 6.97 | 19.07 |
| S-1 | 150.3 | 25.5 | 100.4 | 2462.2 | 89.22 | 6.08 | 16.90 |
| S-2 | 151.0 | 24.7 | 100.8 | 2415.4 | 78.50 | 6.01 | 14.95 |
| S-3 | 151.1 | 24.9 | 100.8 | 2404.6 | 77.95 | 6.23 | 14.95 |
| H-1 | 150.3 | 25.1 | 100.1 | 2407.1 | 82.44 | 5.17 | 18.36 |
| H-2 | 150.3 | 25.1 | 99.9 | 2390.3 | 74.73 | 5.22 | 17.46 |
| H-3 | 150.4 | 25.1 | 99.9 | 2362.7 | 77.28 | 5.22 | 17.32 |
| D-1 | 150.6 | 25.2 | 99.8 | 2370.2 | 68.74 | 5.06 | 15.63 |
| D-2 | 150.8 | 25.2 | 99.8 | 2380.2 | 70.44 | 4.93 | 16.76 |
| D-3 | 150.4 | 25.1 | 99.9 | 2362.7 | 77.28 | 5.22 | 17.32 |
| V-1 | 149.9 | 25.0 | 99.3 | 2360.7 | 87.01 | 5.88 | 18.06 |
| V-2 | 150.4 | 25.1 | 99.5 | 2358.2 | 83.35 | 5.43 | 17.37 |
| V-3 | 150.5 | 24.9 | 99.7 | 2401.5 | 88.82 | 5.77 | 17.60 |
| Sample No. | σc (MPa) | σi (MPa) | σd (MPa) | σp (MPa) |
|---|---|---|---|---|
| C-3 | 24.2 | 44.8 | 92.2 | 101.3 |
| S-2 | 14.0 | 21.2 | 55.2 | 78.5 |
| H-3 | 12.0 | 22.9 | 55.1 | 77.3 |
| D-1 | 10.2 | 18.8 | 53.6 | 68.7 |
| V-3 | 11.1 | 24.6 | 57.3 | 88.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Zhao, G.; Liang, W. Mechanical Response and Fracture Behavior of Brittle Rocks Containing Two Inverted U-Shaped Holes under Uniaxial Loading. Appl. Sci. 2019, 9, 5327. https://doi.org/10.3390/app9245327
Wu H, Zhao G, Liang W. Mechanical Response and Fracture Behavior of Brittle Rocks Containing Two Inverted U-Shaped Holes under Uniaxial Loading. Applied Sciences. 2019; 9(24):5327. https://doi.org/10.3390/app9245327
Chicago/Turabian StyleWu, Hao, Guoyan Zhao, and Weizhang Liang. 2019. "Mechanical Response and Fracture Behavior of Brittle Rocks Containing Two Inverted U-Shaped Holes under Uniaxial Loading" Applied Sciences 9, no. 24: 5327. https://doi.org/10.3390/app9245327
APA StyleWu, H., Zhao, G., & Liang, W. (2019). Mechanical Response and Fracture Behavior of Brittle Rocks Containing Two Inverted U-Shaped Holes under Uniaxial Loading. Applied Sciences, 9(24), 5327. https://doi.org/10.3390/app9245327






